差分进化算法是一种基于群体差异实现全局优化的进化算法,其简单高效,控制参数少,具有快速的全局寻优能力,在工程、管理以及科学领域获得了广泛的应用[1]。在实际应用中,当优化问题比较复杂时,差分进化算法和其他进化算法一样, 随着进化代数的增加,个体间的差异会逐渐降低,个体变异的多样性逐步减少,从而收敛到局部极值附近,陷入局部最优解.为了提高差分进化算法的寻优能力,加快收敛速度,克服一般进化算法常见的局部收敛现象,许多学者对其进行了改进,迄今对差分进化算法的研究和改进可以归纳为以下几方面:1)操作算子的改进;2)进化参数的自适应调整;3)多种群;4)混合算法[2-11].这些改进的算法虽然起到了一定的效果,但在求解一些复杂优化问题时仍显得不够理想.针对大规模欺骗函数和等级问题这类一般优化算法难以求解的高维复杂优化问题,本文将模拟退火算子嵌入到差分进化算法的循环中,提出了二者相结合的混合差分进化算法,以提高求解精度, 新算法既保留了差分进化算法具有较强的搜索能力,又克服了在复杂优化问题的求解上过早收敛而陷入局部解、进化后期收敛慢及求解精度不高的缺点。
1 差分进化算法与模拟退火算法 1.1 差分进化算法原理及操作本文是对欺骗函数和等级问题进行优化实验,根据所求解问题的特点,算法采用二进制编码方式。差分进化算法的基本原理与遗传算法类似,所不同的是,在遗传操作中采用种群个体间的差分向量进行变异,这充分利用了不可行解所携带的重要信息,减小了陷入局部最优解的机率。
1)种群初始化。
设Li=(l1i, l2i, …, lni)为一个n维向量,即种群中的一个个体,其中编码长度为n,种群大小为P,种群第1代个体按式(1)随机产生:
 |
(1) |
式中:rand[0, 1]随机产生0或者1,个体为随机产生的二进制串。初始化种群时产生种群大小为P,编码长度为n的个体。
2)变异操作。
算法的变异方式是在种群中随机选取2个不同的个体,将其向量差取绝对值后与待变异的个体进行向量叠加,变异方式如式(2)所示:
 |
(2) |
式中:Lig+1是g+1代种群中第i个要变异的个体,Lag、Lbg 、Lcg是g代种群中的3个互不相同的个体,由于是二进制编码,因此差分向量取绝对值。
3)交叉操作。
交叉操作是在种群中随机选择2个不同的个体,按式(3)产生新一代个体。
 |
(3) |
式中:rand为[0, 1]内均匀分布的随机数,Pc∈[0, 1]为交叉概率, i=1, 2, …, P, j=1, 2, …, n。
4)选择操作。
在差分进化算法中,选择操作采取优选策略,在变异操作和交叉操作完成后均进行选择操作,即只有当新产生的子代个体优于父代个体时才会保留,否则父代个体将继续保留在下一代中。
1.2 模拟退火算法原理及操作模拟退火算法来源于固体退火原理,通过降温来控制算法的搜索过程。模拟退火算法对当前解重复如下过程:产生新解→计算目标函数差→接受或舍弃,并在此过程中逐步衰减温度值,算法终止时,即得到近似最优解。
在模拟退火算法中,对个体Li按式(4)或者式(5)产生新个体。
1)方式1。
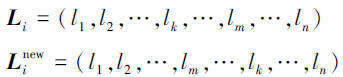 |
(4) |
式中:Li为当前种群中的个体,Linew为新产生的个体,n为个体的编码长度,1 < k < m < n。
2)方式2。
设原个体L=(l1, l2, …, ln),产生的新个体为a=(a1, a2, …, an),随机数p=rand(0, 1)(0和1之间的随机小数), 则产生新个体方式如下:
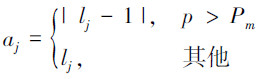 |
(5) |
式中:Pm∈[0, 1],新个体Linew=a, 1 < j < n。
为了对解空间进行充分的搜索,这2种方式都会被使用,在算法运行过程中随机选择其中的一种方式来产生新个体。新个体产生后计算适应度f(Linew)和新旧个体间的适应度增量△E=f (Linew)-f(Li),并计算p=exp(-△E/T),按概率p选用或者是舍弃新个体,重复上述过程一定次数后选择新搜索到的适应度高的个体进入下一代。
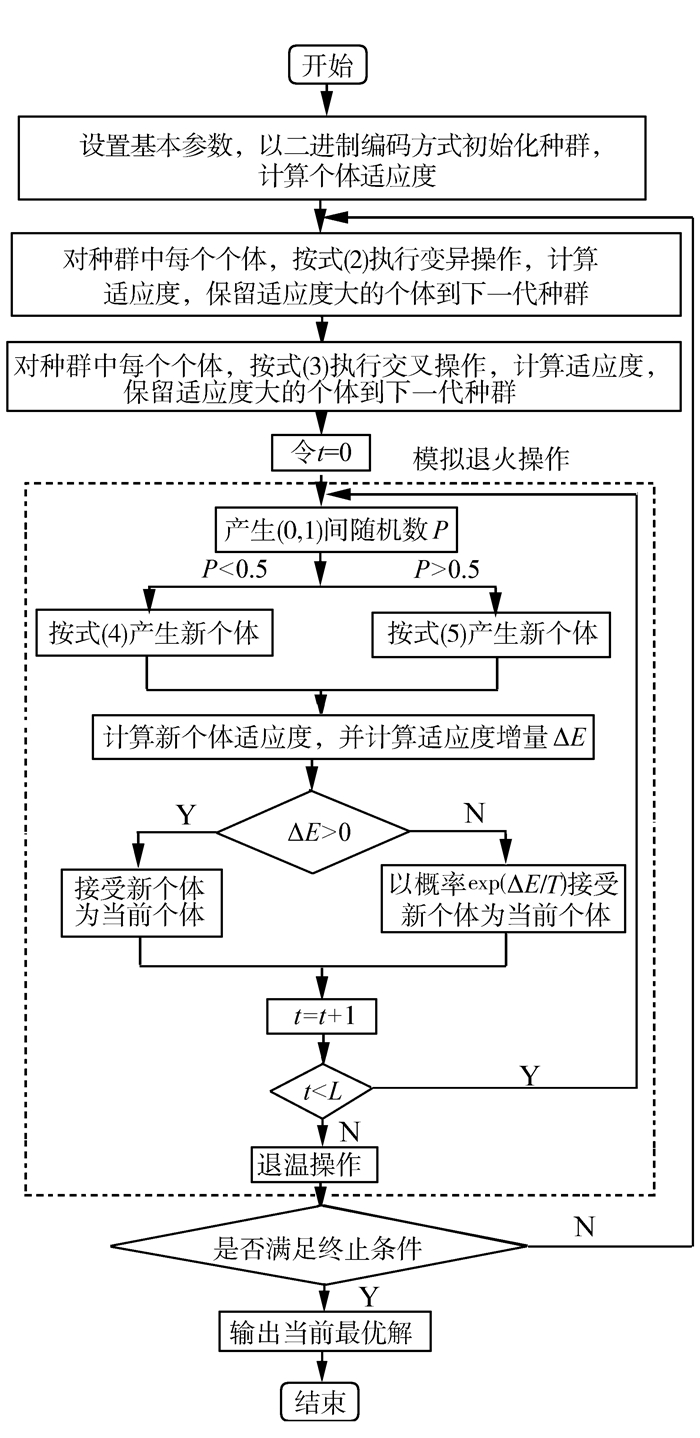
2 混合差分进化算法混合差分进化算法是差分进化算法和模拟退火算法的合理组合,首先由一组随机产生的初始解开始搜索,通过带有精英保留策略的遗传操作产生新个体,然后对每一个新个体进行独立的模拟退火操作,将操作完成后生成的个体作为混合算法的下一代个体,并进行退温操作,经过若干次迭代后,最终选择种群中最优解作为所求问题的解。混合差分进化算法流程如图 1所示。
|
| 图 1 混合差分进化算法 Fig. 1 Hybrid differential evolution algorithm |
进化算法在求解优化问题时一般具有通用性,在各个领域都能取得广泛的应用,但也有一些进化算法难以解决的优化问题,如实验中用到的欺骗函数和等级问题,欺骗问题中的低阶模式将搜索引向局部极值而非全局最优值,因此用欺骗函数来测试进化算法的性能是非常重要的[12]。
3.1 欺骗函数问题本文用4个常用的欺骗函数(Goldberg3、Deceptive3、Trap3、Bipolar6)[13]来测试混合差分进化算法的性能,其中每个输入变量的取值均为0或1,u为输入变量中1的个数。fdeceptive3、ftrap5函数的全局最优解为a=1,fbipolar6函数的全局最优解为a=1或a=0。以上4个函数具有不同的复杂度和特性, 由它们构成的大规模欺骗函数能比较全面地测试算法的性能。在实验中,按如下连接方式构成大规模欺骗函数:
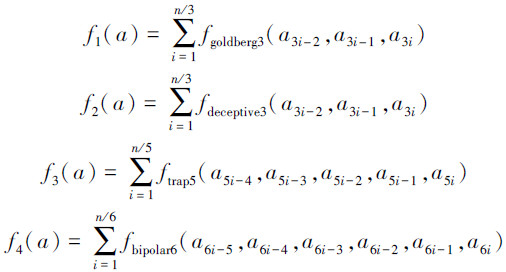 |
在算法中参数设置如下,种群大小为P=40,交叉概率Pc=0.4,变异概率Pm=0.2,取初始温度T0=1 000, 退火速率α=0.99, 每个温度段搜索次数L=10,迭代次数3 000或5 000次。分别取n=30, 60, 90的上述4个函数进行实验,并与优化能力较好的分区交叉差分进化算法(subarea crossover differential evolution, SCDE)[14]和组合优化多智能体进化算法(multi-agent evolutionary algorithm for combinatorial optimization, COMAEA)[13]进行性能对比,每个算法取50次运行结果的平均值,实验结果如表 1所示,DESA为本文改进差分进化算法(improved differential evolution algorithm)。
| 函数 | 维数n | 函数 最优解 | COMAEA | SCDE | DESA |
| Goldberg3 | 30 | 300 | 298.42 | 300.00 | 300.00 |
| 60 | 600 | 564.85 | 572.68 | 586.69 | |
| 90 | 900 | 796.84 | 842.75 | 889.36 | |
| Deceptive3 | 30 | 10 | 9.84 | 10.00 | 10.00 |
| 60 | 20 | 18.96 | 19.26 | 19.96 | |
| 90 | 30 | 28.96 | 28.78 | 29.46 | |
| Trap5 | 30 | 30 | 29.63 | 29.65 | 29.89 |
| 60 | 60 | 58.36 | 49.45 | 59.68 | |
| 90 | 90 | 78.95 | 82.68 | 88.61 | |
| Bipolar6 | 30 | 5 | 4.78 | 4.82 | 4.91 |
| 60 | 10 | 9.14 | 9.54 | 9.72 | |
| 90 | 15 | 13.68 | 14.56 | 14.89 |
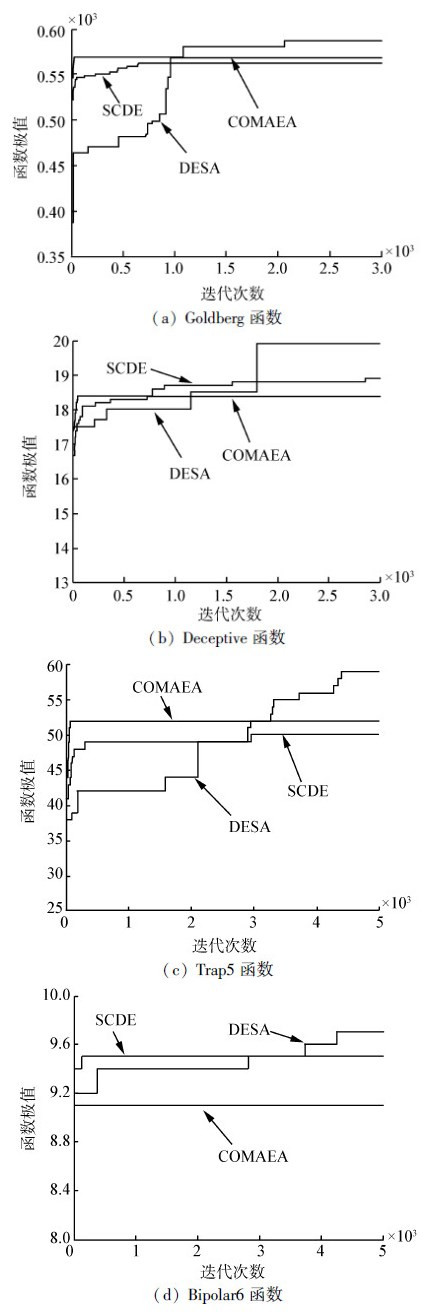
对n=60的上述4个函数某一次优化计算的收敛曲线如图 2所示。
|
| 图 2 60维函数收敛曲线对比图 Fig. 2 Comparison of 60-dimensional function convergence curve |
等级问题由等级结构、映射函数、函数值3部分组成,输入变量作为最底层,按照映射函数将下一层映射到上一层,便构成了树状结构,每一层的函数值之和即为最终的函数值。本文用HIFF (hierarchical if-and-only-if function)函数和HtrapI(hierarchical trap I)函数[13]这2个比较典型的等级函数来测试算法的性能。
1)HIFF函数。
按式(6)由下层向上层映射:
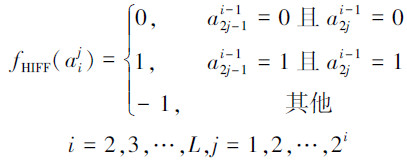 |
(6) |
式中:L为层数,每一层的函数值由式(7)计算:
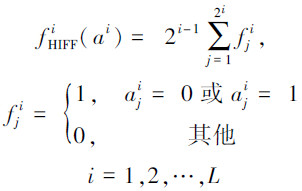 |
(7) |
总函数值由式(8)计算:
 |
(8) |
2)HtrapI函数。
HtrapI函数和HIFF函数映射过程类似,将下一层的3个变量映射为上一层的1个变量,问题规模满足n=3L,映射函数如式(9)所示:
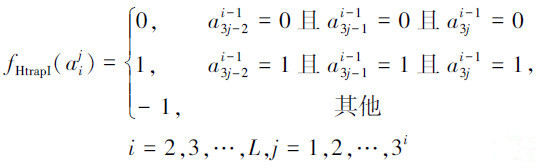 |
(9) |
各层的函数值由式(10)计算:
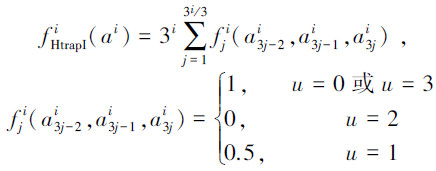 |
(10) |
式中:u表示a3j-2i、a3j-1i、a3ji中1的个数,最终的函数值由式(11)计算:
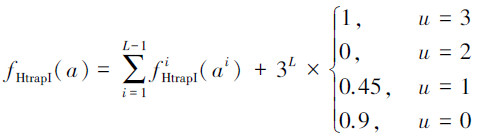 |
(11) |
在对这2个函数进行优化实验时,算法参数同上,每个算法取30次实验结果的平均值,实验结果如表 2所示。
| 函数 | 维数n | 函数 最优解 | COMAEA | SCDE | DESA |
| HIFF | 32 | 192 | 148.42 | 153.24 | 189.79 |
| 64 | 448 | 372.69 | 312.33 | 424.62 | |
| 128 | 1 024 | 836.54 | 821.35 | 989.36 | |
| HtrapI | 27 | 135 | 129.94 | 121.26 | 134.82 |
| 81 | 1 134 | 1 083.16 | 1 041.74 | 1 131.43 | |
| 243 | 9 963 | 9 228.76 | 9 128.13 | 9 927.31 |
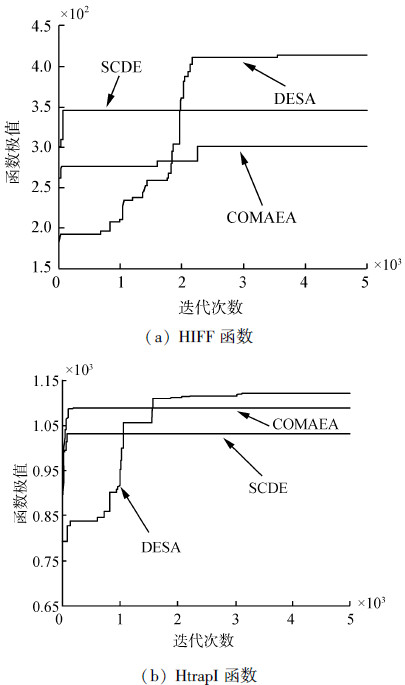
对于n=64的HIFF函数和n=81的HtrapI函数, 某一次优化计算的收敛曲线如图 3所示。
|
| 图 3 HIFF函数和HtrapI函数收敛曲线对比 Fig. 3 Comparison of HIFF function and HtrapI function convergence curve |
从以上的实验结果可以看出,对于复杂的、具有欺骗引导的优化问题,COMAEA算法和SCDE算法比较快地收敛到局部极值附近,出现早熟收敛现象,而改进的差分进化算法DESA随着迭代的进行,在算法运行的后期,能比较好地跳出局部最优解,收敛到全局最优解附近。
分析其原因在于:在算法运行的初期,利用模拟退火算子的突变搜索来减少陷入局部最优的个体,提高种群多样性,使差分进化算法能更好地利用群体差异进行全局搜索; 在算法运行末期,模拟退火算子以更大的机率接受好解,使种群朝着最优解的方向进化,从而保证收敛的稳定性。因此通过模拟退火算子和差分进化算法的有机结合,进一步增强了算法的求解能力。
4 结束语对于复杂的优化问题,一般进化算法在选择算子的作用下,优良个体的迅速增多使得种群失去多样性,从而陷入局部最优解。本文提出的混合差分进化算法在模拟退火操作的作用下,能较好地保持种群多样性,使差分变异更好地发挥作用,同时利用模拟操作的局部搜索功能,更有利地搜索到全局最优解。对欺骗函数问题和等级问题的仿真实验表明了混合差分进化算法的有效性和实用性。如何进一步改进该算法,使之适用于其他问题是本课题下一步工作的研究重点。
| [1] | 刘建平. 基于混沌和差分进化的混合粒子群优化算法[J]. 计算机仿真 , 2012, 29 (2) : 208-212 LIU Jianping. Hybrid particle swarm optimization algorithm based on chaos and differential evolution[J]. Computer Simulation , 2012, 29 (2) : 208-212 |
| [2] | 刘波, 王凌, 金以慧. 差分进化算法研究进展[J]. 控制与决策 , 2007, 22 (7) : 721-729 LIU Bo, WANG Ling, JIN Yihui. Advances in differential evolution[J]. Control and Decision , 2007, 22 (7) : 721-729 |
| [3] | 徐斌, 祁荣宾, 钱锋. 基于混合差分进化和alpha约束支配处理的多目标优化算法[J]. 控制理论与应用 , 2012, 29 (3) : 353-360 XU Bin, QI Rongbin, QIAN Feng. Constrained multi-objective optimization with hybrid differential evolution and alpha constrained domination technique[J]. Control Theory & Applications , 2012, 29 (3) : 353-360 |
| [4] | 刘若辰, 焦李成, 雷七峰, 等. 一种新的差分进化约束优化算法[J]. 西安电子科技大学学报:自然科学版 , 2011, 38 (1) : 47-53 LIU Ruochen, JIAO Licheng, LEI Qifeng, et al. New differential evolution constrained optimization algorithm[J]. Journal of Xidian University: Natural Science , 2011, 38 (1) : 47-53 |
| [5] | 张伟丰. 引入模拟退火算子的差分进化算法性能研究[J]. 数值计算与计算机应用 , 2011, 32 (4) : 301-304 ZHANG Weifeng. The performance research of differential evolution algorithm which introduced the simulated and annealing operator[J]. Journal on Numerical Methods and Computer Applications , 2011, 32 (4) : 301-304 |
| [6] | 郑建国, 王翔, 刘荣辉. 求解约束优化问题的ε-DE算法[J]. 软件学报 , 2012, 23 (9) : 2374-2387 ZHENG Jianguo, WANG Xiang, LIU Ronghui. ε-differential evolution algorithm for constrained optimization problems[J]. Journal of Software , 2012, 23 (9) : 2374-2387 DOI:10.3724/SP.J.1001.2012.04149 |
| [7] | ZOU Dexuan, GAO Liqun. An efficient improved differential evolution algorithm[C]//The 31st Chinese Control Conference. Hefei, China, 2012: 2385-2390. |
| [8] | LI Yinghai. Optimal scheduling of cascade hydropower system using grouping differential evolution algorithm[C]//2012 International Conference on Computer Science and Electronic Engineering. Hangzhou, China, 2012: 625-629. |
| [9] | 陶新明, 徐鹏, 刘福荣, 等. 组合分布估计和差分进化的多目标优化算法[J]. 智能系统学报 , 2013, 8 (1) : 39-45 TAO Xinmin, XU Peng, LIU Furong, et al. Multi-objective optimization algorithm composed of estimation of distribution and differential evolution[J]. CAAI Transactions on Intelligent Systems , 2013, 8 (1) : 39-45 |
| [10] | 杨振宇, 唐珂. 差分进化算法参数控制与适应策略综述[J]. 智能系统学报 , 2011, 6 (5) : 415-423 YANG Zhengyu, TANG Ke. An overview of parameter control and adaptation strategies in differential evolution algorithm[J]. CAAI Transactions on Intelligent Systems , 2011, 6 (5) : 415-423 |
| [11] | 阳春华, 钱晓山, 桂卫华. 一种混沌差分进化和粒子群优化混合算法[J]. 计算机应用研究 , 2011, 28 (2) : 439-441 YANG Chunhua, QIAN Xiaoshan, GUI Weihua. Hybrid algorithm of chaotic differential evolution and particle swarm optimization[J]. Application Research of Computers , 2011, 28 (2) : 439-441 |
| [12] | GOLDBERG D E, DEB K, KORB B. Messy genetic algorithms revisited: studies in mixed size and scale[J]. Complex Systems , 1990, 4 (4) : 415-444 |
| [13] | 钟伟才, 刘静, 刘芳, 等. 组合优化多智能体进化算法[J]. 计算机学报 , 2004, 27 (10) : 1341-1353 ZHONG Weicai, LIU Jing, LIU Fang, et al. Combinatorial optimization using multi-agent evolutionary algorithm[J]. Chinese Journal of Computers , 2004, 27 (10) : 1341-1353 |
| [14] | 刘荣辉, 郑建国. 分区交叉差分进化算法及其约束优化[J]. 计算机科学 , 2012, 39 (2) : 283-287 LIU Ronghui, ZHENG Jianguo. Subarea crossover differential evolution algorithm and its constrained optimization[J]. Computer Science , 2012, 39 (2) : 283-287 |



