岩层识别问题是地球物理勘探的重要课题之一,准确识别岩层对于地球物理勘探十分重要。较长时间以来,测井分析工作者主要根据测井曲线的形态变化特征及其与周围岩层之间的差异特征进行人工分层。这种十分原始的手工分层方法,会由于不同测井分析工作者在使用分层曲线和掌握分层标准的不同造成分层结果的差异[1]。相对于人工分层,自动分层可以避免人为分层的随意性,并在很大程度上提高工作效率[2]。
自从1982年Wolf等[3]首次根据测井数据自动判定地层岩性以来,目前已发展了很多分层方法,如有序聚类法[4]、极值方差聚类法[5]、支持向量机法[6-8]等。有序聚类法和极值方差聚类法是在没有先验类别条件下,通过测井数据内在的一些属性和联系,对岩层进行自动分层。这些方法在数学上比较严格,其分层结果是完美的数学结果,但并不能完全反映出测井数据与岩层类别之间的对应关系。
支持向量机(support vector machine, SVM)是Vapnik等[9]提出的一种基于结构风险最小化原理(structural risk minimization, SRM)和统计学习理论的VC维理论的机器学习方法,能够充分挖掘事物之间的对应关系。其根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度)和学习能力(即无错误识别任意样本的能力)之间寻求最佳折衷,以获得最好的分类能力[10]。目前,该算法被广泛应用于文本分类、图像分类、基因分析、字符识别、人脸识别等领域[11]。相对于许多传统的分类器,如参数估计和神经网络,它不仅有完善的理论支持,而且表现出良好的分类性能和推广能力,是一种专门针对有限样本分类的方法。SVM在很大程度上解决了非线性、高维数以及局部极值等问题[12]。近年来,更多的研究者开始致力于支持向量机对岩层识别的研究。宋延杰等[6]选取大庆油田中7口井的探井曲线资料作为样本数据,并依据先验经验,人为选取部分样本数据作为训练集,然后利用学习后的支持向量机预测岩层。赵军等[7]利用P油田18口井的解释结果,筛选出训练集和测试集,验证支持向量机在岩层识别中的有效性。文政等[8]利用同地区5口井的样本数据对支持向量机进行训练,并对剩余样本进行预测验证。然而,上述研究没有给出提取训练样本的具体方法,训练样本的选取依赖于先验经验或周边已知分层情况井的数据样本。为了克服支持向量机方法在岩层识别问题中的这种弊端,本文提出了一种基于有序聚类的支持向量机算法对岩层进行识别。
1 相关理论 1.1 支持向量机支持向量机的基本思想是寻找一个超平面,将属于2个不同类别的样本无误地分开,且分类间隙要最大。对于非线性问题,可以通过非线性映射φ:RN→H把数据从原空间(RN)映射到某个高维空间(H)里,在变换空间求最优分类面。
对于非线性样本集:
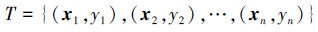 |
式中:xi∈RN为N维向量,yi∈{1, -1}。在高维空间中,则存在最优分类面:
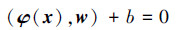 |
满足条件:
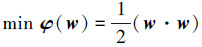 |
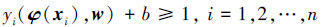 |
(1) |
式(1)是凸二次优化问题,引入拉格朗日函数:
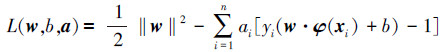 |
式中:ai≥0为拉格朗日乘子。为求L(w, b, a)的最小值,分别对w、b、a求偏导,得
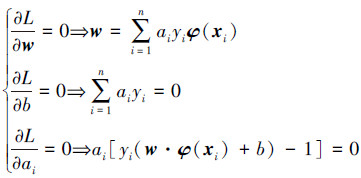 |
(2) |
根据式(1)和式(2)的约束条件,可转化成对偶问题为
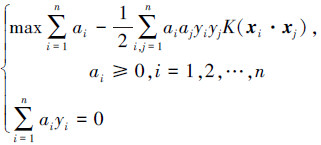 |
这是一个二次函数极值问题,故存在惟一解。若ai*为最优解,则有
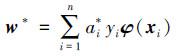 |
式中:ai*是不为零的样本,称为支持向量。b*是分类阈值,可由约束条件ai[yi(w·φ(xi)+b)-1]=0求解。
解得上述问题后可得到二分类最优分类函数为
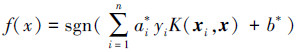 |
式中:K(xi, x)为核函数。
1.2 有序聚类算法有序聚类算法是多元统计分析中针对有序样本的一种统计分类方法。其基本思想是:首先将待分类的n个样本看作1类,然后根据离差平方和类内最小以及类间最大准则分为2类、3类……一直到所需的k类为止。
假设每个样本有m个特征指标,则n个样本形成的数据矩阵如下:
 |
式中:元素xij表示第i个样本第j个特征指标值。
首先利用这些特征指标值计算层内变差矩阵D=(dij)n×n,其中:
 |
然后记b(n, k)是有序样本分为k层的某一种方法,则其层内离差平方和为L[b(n, k)]。当L[b(n, k)]越小,即各层间的离差平方和越小,分层就越合理。要使L[b(n, k)]达到极小值的分法,就是寻求最佳分点(jk, jk-1, …, j2)。记P(n, k)为将有序样本分为k层的最佳分法,为得到最佳分层方法,利用递推公式:
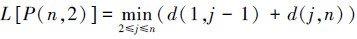 |
(3) |
 |
(4) |
由递推公式可以看出,要求得最佳分法P(n, k),需先找第k层最佳分点jk,使L[P(n, k)]达到最小。
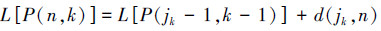 |
最后,利用类似的方法依次可得到最佳分点jk-1, jk-2, …, j2。
2 岩层自动分层基于上述理论,本文提出了一种基于有序聚类的支持向量机分类算法,首先对测井数据进行预处理:异常数据的处理、数据的滤波,其次选取测井曲线,并对其进行归一化处理,利用有序聚类算法初步分层,获取训练样本,最后利用训练后的支持向量机进行预测,实现岩层的自动分层。
2.1 处理异常数据在对岩层进行探测时,由于非岩层因素引起的干扰,会出现异常数据,即有的数据比相应测井曲线数据的平均值大很多或者小很多。异常数据不仅干扰有效数据,影响后面的数据处理,如归一化等,而且对后面岩层自动分层的精确度产生影响,故采用邻近数据平均值代替异常数据[13]。
2.2 平滑滤波经过异常数据处理后的测井曲线,从数字信号处理角度来看,由于自身携带了大量的噪声干扰信号,故测井曲线出现了毛刺,为了消除测井曲线的毛刺干扰,对测井曲线进行中值滤波。
假设测井数据序列:x1, x2, …, xN,选取窗口长度为2n+1的滤波器对该序列进行滤波,则步骤为如下:
1)选出以xi为中心的2n+1个数据xi-n, xi-n+1, …, xi, …, xi+n-1, xi+n,对这2n+1个数据排序;
2)选取排序后的中间项作为xi的滤波值;
3)自上而下迭代计算测井数据的滤波值。
2.3 选取测井曲线由于测井数据是按井深的递进变化对应着多种测井曲线的。1)由于测井曲线过多,导致分析问题的复杂度变大;2)实际上有的测井曲线之间相关性较大,故可对所有的测井曲线做相关性分析,找出高度相关的测井曲线,从这些高度相关的测井曲线中选择一种。相关性系数与相关程度对应关系如表 1。
| 相关系数 | 相关程度 |
| 0.00~±0.30 | 微相关 |
| ±0.30~±0.50 | 实相关 |
| ±0.50~±0.80 | 显著相关 |
| ±0.80~±1.00 | 高度相关 |
2.4 归一化处理
由于不同测井曲线的刻度和量纲各不相同,在采用多种曲线进行自动分层时,有必要将测井曲线归一化到[0, 1] 内,以消除因刻度和量纲所产生的影响。归一化公式为
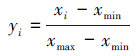 |
式中:xi为测井曲线上对应的测井深度i的测井值,yi为xi的归一化值,xmax和xmin分别为测井曲线中的最大值和最小值。
2.5 利用有序聚类初分层根据上述有序聚类算法,对岩层进行初步分层,首先利用测井数据值计算层内变差矩阵D,然后根据递推公式(3)、(4),可逐步求得岩层的最佳分点,即可获得岩层的初步分层结果{jk, jk-1, …, j2}。
2.6 利用支持向量机二次分层由于有序聚类算法所要求的分界点只满足层内离差平方和最小以及层间离差平方和最大,而没有完全反映出测井数据与岩层类别的对应关系,故利用支持向量机对岩层进行二次分层,其步骤如下:
1)获取训练样本:根据有序聚类初步分层结果,选取各层质心离差平方和最小的连续30个数据样本作为各层的训练样本。
2)训练支持向量机:选取“一对一”多类分类器作为支持向量机分类器,选取RBF核函数作为支持向量机的核函数[14-15],利用有序聚类算法获得的训练样本来训练支持向量机,最终获得多类分类器:
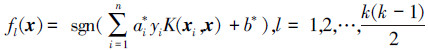 |
3)对岩层进行分层:利用训练后的支持向量机分类器去预测岩层类别。
3 实验结果与分析在CPU为2.53GHz、内存为2GB、操作系统为Windows7的PC机上,运用MATLAB7.1软件进行数字仿真。仿真实验所采用的测井数据来源于中国数学建模网,选取其中3口井进行预测。其中每口井各有66项指标。利用相关性分析方法对所有影响岩性的测井曲线进行筛选,最终选取10种测井曲线来指示岩性,选取结果见表 2。
| 序号 | 测井曲线名称 |
| 1 | 密度测井曲线(DEN) |
| 2 | 4M电阻率测井曲线(R4.0) |
| 3 | 自然电位测井曲线(SP) |
| 4 | 井斜测井曲线(DEVi) |
| 5 | 井斜方位测井曲线(AZIm) |
| 6 | 自然伽马测井曲线(GR) |
| 7 | 声波测井曲线(AC) |
| 8 | 微侧向电阻率测井曲线(RML) |
| 9 | 井径测井曲线(CAL) |
| 10 | 电阻率测井曲线(RT) |
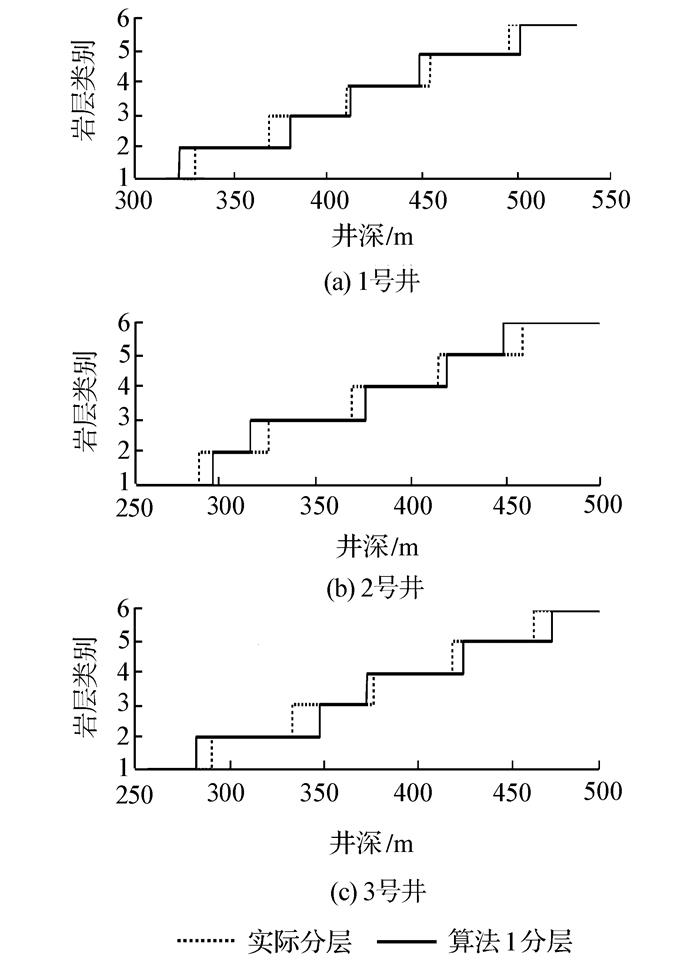
1~3号井各有6种岩层,从一定深度开始,对各口井进行岩层划分和命名,依次为岩1层, 岩2层, …, 岩6层。其中1号井的井深范围为294.0~530.2m,2号井的井深范围为257.0~297.5m,3号井的井深范围为249.4~496.0m,各口井中每米测试8个点,且已知各口井的实际分层情况。根据前述的岩层自动分层步骤,对1~3号井的实际测井数据利用新算法进行岩层的自动分层。同时,本文与文献[8]的算法做对比,以验证新算法的有效性。实验结果如图 1、图 2和表 3所示(本文提出的新算法简记为算法1,文献[8]的算法简记为算法2)。
|
| 图 1 算法1分层结果与实际分层结果对比 Fig. 1 Comparison of layered results of algorithm 1 and actual situation |

|
| 图 2 算法2分层结果与实际分层结果对比 Fig. 2 Comparison of layered results of algorithm 2 and actual situation |
| 预测 井号 | 岩1层 | 岩2层 | 岩3层 | 岩4层 | 岩5层 | 岩6层 | ||||||
| 算法1 | 算法2 | 算法1 | 算法2 | 算法1 | 算法2 | 算法1 | 算法2 | 算法1 | 算法2 | 算法1 | 算法2 | |
| 1号井 | 77.8 | 63.8 | 100.0 | 74.1 | 75.0 | 60.7 | 82.6 | 70.2 | 100.0 | 75.6 | 83.9 | 68.7 |
| 2号井 | 100.0 | 77.2 | 64.5 | 59.3 | 100.0 | 73.4 | 83.9 | 76.9 | 66.2 | 61.2 | 100.0 | 78.5 |
| 3号井 | 79.4 | 66.8 | 100.0 | 75.6 | 68.7 | 63.2 | 100.0 | 79.8 | 86.9 | 72.5 | 71.8 | 59.6 |
| 平 均 | 85.7 | 69.3 | 84.8 | 69.7 | 77.9 | 65.8 | 88.8 | 75.6 | 84.4 | 69.8 | 85.2 | 69.0 |
从图 1和图 2可以直观地看出,新算法分层结果更接近于实际分层情况,即新算法优于文献[8]的算法。同时,从表 3可以看出,利用新算法进行岩层识别,每种岩层的平均准确率能达到85%,而利用文献[8]的算法进行岩层识别,其平均准确率只能达到70%。主要原因在于文献[8]采用同地区其他井中已知岩层类别的测井数据作为训练集,虽然同地区相邻井在某些方面具有相同的属性和联系,但并不能完全反映出待预测井中每种岩层的特性。相对于文献[8]提出的算法,新算法主要优势在于利用有序聚类算法进行初步分层,然后根据初步分层结果来选取训练样本,所选取的训练样本能够很好地反映出各口井中岩层的特性,这样经测井数据训练后的支持向量机才具有更好的分类能力,分层准确率才会更高。
4 结束语岩层识别是地球物理勘探的基础性工作, 岩层识别的准确率将直接影响后续工作的有效开展,本文提出了一种基于有序聚类的支持向量机岩层识别算法。首先,该算法首先利用有序聚类进行初步分层;其次,根据初步分层结果提取出支持向量机所需的训练样本;最后,利用训练后的支持向量机进行第2次分层,得出相应的分类结果。该算法不同于常规的支持向量机算法,它不需要已知岩层类别的测井数据,也就是说能够间接通过有序聚类对未知岩层类别的测井数据进行初步识别,提高识别精度。仿真实验结果表明,该算法不仅很好地解决了已有算法必须依赖已知岩层类别的测井数据的弊端,而且具有较高的准确率,每种岩层的平均准确率为85%,明显高于以往研究的70%。然而,该算法仍具有局限性,如岩层分层数需要人为设定,以及如何选取核函数等,这都将是下一步的研究方向。
| [1] | 林海燕, 戴云, 肖慈珣. 一种基于沃希变换的测井自动分层方法[J]. 成都理工学院学报 , 1999, 26 (1) : 52-57 LIN Haiyan, DAI Yun, XIAO Cixun. A well-log automated identification of rock boundaries method based on Walsh transform[J]. Journal of Chengdu University of Technology , 1999, 26 (1) : 52-57 |
| [2] | 肖波, 韩学辉, 周开金. 测井曲线自动分层方法回归与展望[J]. 地球物理学进展 , 2010, 25 (5) : 1802-1810 XIAO Bo, HAN Xuehui, ZHOU Kaijin. A review and outlook of automatic zonation methods of well log[J]. Progress in Geophysics , 2010, 25 (5) : 1802-1810 |
| [3] | WOLF M, PELISSIER-COMBESCURE J. Faciolog automatic electrofacies determination[C]//SPWLA 23rd Annual Logging Symposium. Corpus Christi, USA, 1982: 6-9. |
| [4] | HAWKINS D M, MERRIAM D F. Optimal zonation of digitized sequential data[J]. Mathematical Geology , 1973, 5 (4) : 389-396 DOI:10.1007/BF02111989 |
| [5] | 张明玉. 极值方差聚类法在测井分层取值中的应用[J]. 新疆石油地质 , 2002, 23 (5) : 429-431 ZHANG Mingyu. Application of minimax variance cluster analysis method in well log layering[J]. Xinjiang Petroleum Geology , 2002, 23 (5) : 429-431 |
| [6] | 宋延杰, 张剑风, 闫伟林, 等. 基于支持向量机的复杂岩性测井识别方法[J]. 大庆石油学院学报 , 2007, 31 (5) : 18-20 SONG Yanjie, ZHANG Jianfeng, YAN Weilin, et al. A new identification method for complex lithology with support vector machine[J]. Journal of Daqing Petroleum Institute , 2007, 31 (5) : 18-20 |
| [7] | 赵军, 程鹏飞, 刘地渊, 等. 支持向量机在水淹层测井识别的应用[J]. 物探与化探 , 2008, 32 (6) : 652-655 ZHAO Jun, CHENG Pengfei, LIU Diyuan, et al. The application of the support vector machine to the recognition of flooding formation[J]. Geophysical and Geochemical Exploration , 2008, 32 (6) : 652-655 |
| [8] | 文政, 高松洋, 毕广武. 支持向量机在复杂岩性测井识别中的应用[J]. 大庆石油地质与开发 , 2009, 28 (1) : 134-137 WEN Zheng, GAO Songyang, BI Guangwu. Application of support vector machine (SVM) in complex lithology identification by well logging[J]. Petroleum Geology and Oilfield Development in Daqing , 2009, 28 (1) : 134-137 |
| [9] | VAPNIK V. The nature of statistical learning theory[M]. New York, USA: Springer-Verlag, 1995 . |
| [10] | 刘跃辉, 郑建东. 基于支持向量机原理的复杂地层岩性识别方法[J]. 国外测井技术 , 2011 (4) : 22-26 LIU Yuehui, ZHENG Jiandong. The lithology identification method based on support vector machine principle[J]. World Well Logging Technology , 2011 (4) : 22-26 |
| [11] | 李茂宽, 关键. 基于模糊C均值的支持向量机数据分类识别[J]. 系统仿真学报 , 2005, 17 (7) : 1785-1787 LI Maokuan, GUAN Jian. Data classification and recognition of support vector machines based on fuzzy C-means clustering[J]. Journal of System Simulation , 2005, 17 (7) : 1785-1787 |
| [12] | 柯永振, 张加万, 孙济洲, 等. 结合支持向量机与C均值聚类的图像分割[J]. 计算机应用 , 2006, 26 (9) : 2081-2083 KE Yongzhen, ZHANG Jiawan, SUN Jizhou, et al. Image segmentation combining support vector machines with C-means[J]. Journal of Computer Applications , 2006, 26 (9) : 2081-2083 |
| [13] | 万应明, 高峻, 董建平, 等. 多测井曲线合成应用方法初探[J]. 石油物探 , 2005, 44 (1) : 71-75 WAN Yingming, GAO Jun, DONG Jianping, et al. The primary discussion to the application of synthetic multiple-logging[J]. Geophysical Prospecting for Petroleum , 2005, 44 (1) : 71-75 |
| [14] | 赵磊, 李国和, 马现峰. 基于支持向量机的地层识别研究[J]. 计算机工程与应用 , 2006, 35 (1) : 230-232 ZHAO Lei, LI Guohe, MA Xianfeng. Research of stratum recognition based on support vector machine[J]. Computer Engineering and Applications , 2006, 35 (1) : 230-232 |
| [15] | 郑延斌, 李国和. 支持向量机在地层识别中的应用[J]. 河南师范大学学报:自然科学版 , 2009, 37 (2) : 37-39 ZHENG Yanbin, LI Guohe. Application of support vector machine to stratum recognition[J]. Journal of Henan Normal University: Natural Science , 2009, 37 (2) : 37-39 |



