基于内容的图像检索(content based image retrieval, CBIR)技术[1]是为了解决如何有效地从图像数据库中检索出相关图像的技术。通常CBIR中图像的表示是基于底层可视化特征,而这种表示方法不能直接表达用户的语义,因此出现了底层可视化特征和用户语义概念之间的“语义鸿沟”问题[2]以及“维度灾难”问题,严重限制了检索性能的提高。流形学习能够发现图像数据集内在的几何分布规律[3],不但能找出图像间内在的语义关系还能进行维数约减,已被广泛应用到图像检索问题中[4-6]。将用户反馈的语义融入到流形学习过程中能提高图像检索性能[7],流形排序(manifold ranking, MR)[8]就是一类融入用户反馈信息的基于拓扑图的图像检索排序算法。传统的基于流形排序的图像检索(manifold ranking based image retrieval, MRBIR)[9]对于查询图像位于数据库之外时,需要重新计算拓扑图,因此在线查询时效率低。在此基础上提出的广义流形排序图像检索算法(generalized manifold ranking based image retrieval, G-MRBIR)[10]及其变种EMR(efficient manifold ranking)[11]通过重复利用离线计算的近邻相似矩阵,大大减少了计算量,能有效地应用于在线图像检索。考虑到图像数据库中的图像很多时候是已经有分类标记的或者部分图像是有标记的,如人、动物、建筑、风景等,这些标记信息可以融入流形排序算法中,因此提出有监督和半监督的流形排序算法,可以提高图像检索的查准率;但是当用户查询结果的反馈是在无正反馈的情况下,用户语义却不能进一步改进流形排序算法的查询结果,针对这种情况,从全局出发引入不相关排序来校正检索图像对应的相关排序向量,从而获得进一步优化的排序结果。这就提出了一种新的有监督全局流形排序的图像检索算法(supervised global manifold ranking based image retrieval, SG-MRBIR),充分利用了图像库的局部与非局部的几何分布信息、标记信息以及用户的查询反馈信息,以进一步提高图像检索的查准率,并在著名的MSRA-MM图像库上进行对比实验来验证本文算法的性能。
1 基于流形排序的图像检索 1.1 流形排序图像检索算法基于流形排序算法应用于图像检索中的基本思想是:首先对图像库中的图像构建近邻连通图,然后通过此图将查询样例的值传播给其他每个节点,最后每个节点都会得到一个排序值,被排序数据便可以基于此值排序[7]。设图像数据库表示为X={x1, x2, …, xq, xq+1, …, xn},其中x1, x2, …, xq表示数据库中的q幅样例图像,xq+1, xq+2,…, xn表示n-q幅待检索的图像,在所有图像上实施如下步骤:
1)构建k最近邻(k-nearest neighbor, k-NN)图。
2)计算k-NN图中节点间边的权值,求得相似矩阵W,计算公式为
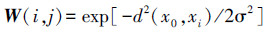 |
(1) |
式中:σ是热核常数。
3)正则化得到相似矩阵S,即S=D-1/2WD-1/2,其中D是对角矩阵,D(i, i)为矩阵W的第i行或列和。
4)根据用户相关性反馈y更新排序向量f,其中将检索到与查询图像相关图像的对应元素yi设置为1,否则为0。排序向量f的更新迭代式为
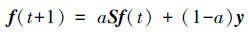 |
(2) |
式中:a为比例系数(常数)。获得一个与图像库X一一对应的排序向量f=[f1 f2…fn]T,根据f值大小的排序结果,判断查询样例图像跟待检索图像间的相似度,将与查询样例最相关的图像作为检索结果反馈给用户。
5)用户如果对查询结果不满意,则根据相关和不相关对图像进行标记,得到新的y,再返回步骤4),否则查询结束。
对于f的计算可以用式子f=(1-a)(I-aS )-1y近似代替[8],其中a为常数,I为单位阵,同时用如下f近似代替也不影响最后排序结果。
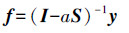 |
(3) |
流形排序图像检索算法(MRBIR)的不足是每次处理数据库外的图像时,需要重新计算n×n的相似矩阵S, 尤其是同样大小的矩阵I-aS的逆矩阵A=(I-aS)-1的计算,会使在线检索时间较长。但是广义流形排序算法(G-MRBIR)[10]能够避免这种问题。G-MRBIR相当于首先通过欧式距离找到图像数据集外的查询图像x0在图像数据集X ={x1, x2, …, xn}内相关的前m幅图像{xi, i=1, 2, …, m}, 相应的权值 e(i)=exp[-d2(x0,xi)/2σ2],剩余的e(i)取0,对e归一化处理后得到排序向量:
 |
(4) |
与流形排序不同的是,在面对图像数据集外新的待查询图像,利用相关反馈方法不用再重新计算S与A=(I-aS)-1了,具体步骤如下。
1)通过式(4)求得初始流形排序f0,即
 |
(5) |
2)对反馈的第i幅图像用yi*=1或-1进行标记,如果反馈的图像用户判断与查询图像是相关的就标记为1,否则标记为-1。这样就对反馈的前k幅(实际检索中一般取10~30幅是可以接受的)最相近图像进行了标记,其他未标记的设为0。首先,计算正相关向量y+和负相关向量y-分别为
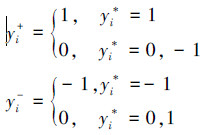 |
然后计算正相关排序向量f+=Ay+和负相关排序向量f-=Ay-,求得最终的流形排序f为
 |
(6) |
式中:η=exp(-ηr),ηr为y+中元素为1的个数。
3)如果用户对结果不满意,则返回步骤2),可以对反馈的图像中未标记的图像重新用同样的方法进行标记,得到新的y+与y-,在不需重新计算S与A的情况下更新f+与f-,这样就达到了更新排序f的目的,直到用户满意为止。
2 有监督全局流形排序的图像检索算法考虑到图像数据库中的图像可能是已经有类别标记的或者部分图像是有标记的,在广义流形排序图像检索算法(G-MRBIR)中融入检索图像库中图像的标记信息,能够改善查询结果的相关性,有利于提高检索性能。因此本文在求相似矩阵时引入了监督权值λ,目的是为了提高属于同一类2幅图像间的相似度及降低属于不同类2幅图像间的相似度。方法如下:假设图像xi与图像xj属于同一类,即有相同的标记时,存在集合β,满足集合中的元素对(i, j)所对应的图像xi、xj之间的相似度增加为原值的λ(λ≥1)倍,否则相似度设为0。于是有监督相似矩阵为W0(i, j)=W(i, j)·λ,其中W(i, j)为式(1)中所求相似矩阵,(i, j)∈β,其他为0。
将广义流形排序图像检索算法中的相似矩阵W(i, j)用有监督相似矩阵W0(i, j)代替后,就得到有监督流形排序图像检索算法(S-MRBIR)。对比实验表明,有监督流形排序图像检索算法使查准率得到一定提高,但存在一个问题就是当遇到没有用户的正反馈时,无法获得有价值的反馈信息,导致反馈后继续迭代无法改善查询结果,查准率可能依然得不到改进[10]。针对无正反馈的查询且反馈后的查询查准率依然为零的情况,从全局出发考虑到近邻图像与非近邻图像对检索都有不同程度的影响,引入不相关排序来校正相关排序向量,提出了有监督全局流形排序图像检索算法(SG-MRBIR)。SG-MRBIR算法充分利用了图像库的局部与非局部的几何分布信息、用户的查询反馈信息,以进一步提高检索性能。
2.1 相似矩阵近邻图像相似矩阵W表示的是近邻图像间的相似拓扑关系,非近邻图像相似矩阵W*描述的是非近邻图像间的拓扑关系。对于任意一幅图像r,根据欧氏距离可以判断出离r最近的k幅图像,这样得到近邻集合θr={x1r, x2r, …, xkr },则W与W*可由热核函数计算如下:
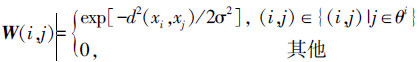 |
(7) |
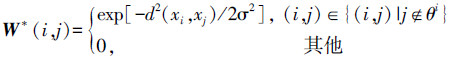 |
(8) |
式中:σ是热核常数,d2(xi, xj)是xi与xj的欧式距离。
引入监督信息,假设图像xi与图像xj属于同一类,即有相同的标记时,存放在集合β中,满足集合中的元素对(i, j)所对应的图像xi、xj间的相似度增加为原值的λ(λ≥1)倍,否则相似度为0。则有监督近邻图像相似矩阵为W0与有监督非近邻图像相似矩阵W0*应该满足:
 |
(9) |
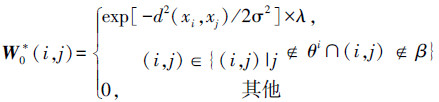 |
(10) |
检索过程中,图像数据集中除了少部分用户反馈标记的图像外,还有很大一部分未获得反馈标记,这些未获得反馈标记的非近邻图像势必会对排序有所影响,为此引入非近邻图像的不相关排序p来改善流形排序。不相关排序是指查询图像与非近邻图像相关度的一个排序。与非近邻图像相关度越小,不相关排序值就越小;反之,与非近邻图像相关度越大,不相关排序值也越大。
在MRBIR中,利用式子f(t+1)=aSf(t) + (1-a)y可迭代近似计算出排序向量f=(I-aS)-1y,其中y是标记后的相关向量,S是正则化近邻图像相似矩阵,a是平衡常数。若用不相关向量y*代替相关向量y,同时求得正则化非近邻图像相似矩阵S*,于是结合式子p(t+1)=aS*p(t)+(1-a)y*可迭代近似计算出不相关排序p=(I-aS*)-1y*,其中S*=(D*)-1/2W* (D*)-1/2,D*是对角矩阵,D*(i, i)为非近邻图像相似矩阵W*的第i行或列之和。不相关排序p反映的是与查询图像的无关度,相对来说对前一次迭代查准率为零的查询影响较大。
由于S*是正则化的非近邻图像相似矩阵,通过迭代计算出来的排序表示的是查询图像与y*中对应标记图像的关联值。而y*中标记的是与查询图像不相关的图像,那么排序对应的就是不相关排序,不相关排序值越大,与非近邻图像相关度就越大,反之说明与查询图像间的相关度越小。如果结合有监督近邻图像相似矩阵W0与有监督非近邻图像相似矩阵W0*,对应得到的S0与S0*就是带有监督信息的。
在G-MRBIR算法中,初始排序f0=a(I-aS)-1·e=aAe,其中e为相关权值向量,也就是说初始排序主要由近邻图像决定,对于图像数据集中大量的非近邻图像没有考虑。通过欧式距离查找最相关的前m幅图像求e的过程中,可以在其他非近邻图像中找到最不相关的n幅图像。于是可以得到不相关权值向量t,其中与n幅图像对应的不相关权值t(i)=exp[-d2(x0,xi)/2σ2],剩余t(i)取0。那么,可以得到初始不相关排序p0=a(I-aS*)-1t=aBt,其中B=(I-aS*)-1。如果非近邻图像相似矩阵采用的是有监督的非近邻图像相似矩阵W0*,那么得到的不相关排序p0就是带有监督信息的不相关排序了。
上述方法保证了查询图像与非近邻图像间不相关度越小的同时与近邻图像越相似,这样就可以求得有监督全局流形排序结果为
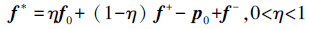 |
式中:f+=Ay+,f-=Ay-,f-为初始相关排序,p0为初始不相关排序。经过多次实验得到验证,在前一次查准率为零的情况下,与有监督流形排序图像检索算法的排序结果相比,利用f *进行下一步迭代,查准率更高。
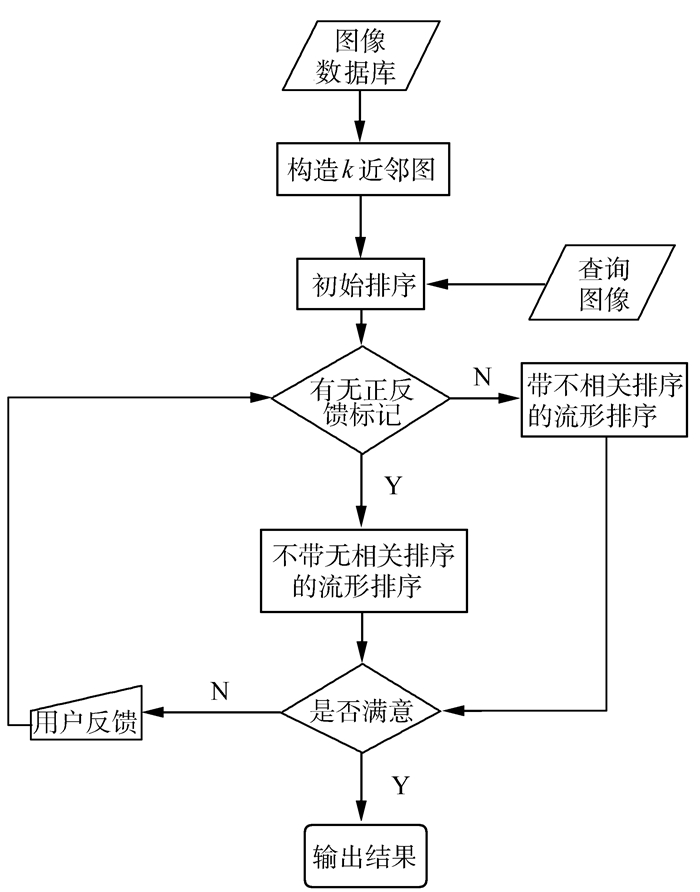
2.3 有监督全局流形排序的图像检索算法有监督全局流形排序图像检索算法SG-MRBIR的算法流程如图 1。
|
| 图 1 SG-MRBIR算法流程 Fig. 1 SG-MRBIR algorithm diagram |
具体步骤描述如下:
1)构建流形拓扑图。
通过构建k-NN图来尽可能逼近图像数据的流形子空间拓扑结构。计算k-NN图中节点间边的权值,求得有监督相似图像相似矩阵W0与有监督非近邻图像相似矩阵W0*,并进一步正则化得到近邻图像相似矩阵S0与非近邻图像相似矩阵S0*。
2)求对应的流形排序值。
根据欧式距离初步判断相关向量y与不相关向量y*,求得初始相关排序f0与初始不相关排序p0,对于图像集中的每个样本点xi一一对应每个排序值fi,利用fi的大小排序可以把与查询样例最相关的图像作为检索结果反馈给用户。
3)根据查询结果进行标记后反馈给系统。
用户如果对以上查询结果不满意,再依据相关和不相关对图像进行标记,根据相关反馈确定新的相关向量y与不相关向量y*。如果相关向量y全为0,即上次迭代查准率为0时,则采用新的排序f*=ηf0 + (1-η) f+ -p0 + f-,否则还是沿用排序f=ηf0+(1-η) f++ f-。再返回步骤2),将结果反馈给系统,直到用户满意。
3 实验结果与分析为了验证提出的有监督全局流形排序算法在图像检索中的性能,在微软亚洲研究院多媒体图像集(Microsoft Research Asia Internet Multimedia Dataset 1.0 & 2.0, MSRA-MM)上与广义流形排序作对比实验。MSRA-MM图像集为在线收集,包括68类,每类大约有1 000幅图像,一共是65 443幅图像,每幅图像附加了关联值(非常关联、关联、不关联3种相关性,对应3个关联值分别是2、1、0),其中每幅图像的有效特征包括:1)225D lack-wise color moment;2)64D SV颜色直方图;3)256D GB颜色直方图;4)144D颜色相关图;5)75D边缘分布直方图;6)128D纹理图;7)7D人脸特征,因此每个样本是899维。
为了实验方便,从这些数据集中只选用10类作为实验数据,分别是Panda、Ronaldinho、Birds、Baby、Trees、Cow、Flags、Football、Nokia、Hotels。然后从关联值为2和1的7 694幅图像中,选择每类的前300幅共3 000幅图用于实验。对3 000幅样本图像集进行10倍交叉验证,每次选取3 000幅中的每类30幅共300幅作为测试集,其他2 700幅作为训练集。
实验中热核常数σ取的是2,k取的是20,平衡常数a取的是0.8,监督权值λ取的是2。对每次反馈前20幅图像进行标记,依次迭代求出3 000幅图的平均查准率,对比结果如表 1、表 2所示。
| 反馈次数 | G-MRBIR | S-MRBIR |
| 无反馈 | 0.341 00 | 0.341 00 |
| 第1次 | 0.590 37 | 0.939 23 |
| 第2次 | 0.722 90 | 0.939 66 |
| 反馈次数 | S-MRBIR | SG-MRBIR |
| 无反馈 | 0.341 00 | 0.341 0 |
| 第1次 | 0.939 23 | 0.948 9 |
| 第2次 | 0.939 66 | 0.982 3 |
表 1比较了无监督与有监督情况下流形排序算法的查准率,可以看出引入监督信息后,S-MRBIR查准率比之前无监督的情况G-MRBIR有明显的提高,第1次反馈后相比提高了34.8%,第2次反馈后相比提高了21.7%。
实验中首次迭代是无反馈标记的,其中整个3 000次查询中有182次查询的查准率为零。经过一次反馈,传统方法查准率为零的次数仍然是182,但是引入不相关排序后得到查准率为零的次数减少到53,比之前少了129次,也正是这129次提高了图像查询的查准率。从表 2可以看出,SG-MRBIR与S-MRBIR相比,查准率有所提高,第1次反馈相比提高了1%,第2次反馈相比也提高了4.2%。
同时,对于2种算法在不同的反馈标记图像数目(10、20、30)情况下,在第2次反馈后的查准率统计结果如表 3所示。
| 反馈标记数目 | S-MRBIR | SG-MRBIR |
| 10 | 0.861 57 | 0.920 53 |
| 20 | 0.939 66 | 0.982 30 |
| 30 | 0.967 80 | 0.993 19 |
从表 3可以看出,无论反馈标记数目是多少,SG-MRBIR都比S-MRBIR算法查准率要高,进一步验证了基于有监督全局流形排序的图像检索算法的有效性。
图 2是S-MRBIR的检索情况,图 3是SG-MRBIR的检索情况,其中第1行是查询图像,其余的是检索结果,可以看出在无反馈时查准率为零的情况下经过一次反馈后的比较结果。图 2查询到的20幅图像中没有一幅与查询图像相关,即查准率依然为零;而图 3查询到的20幅图像中有8幅与查询相关。说明在本次查询中,经过一次反馈后采用SG-MRBIR检索效果更佳。

|
| 图 2 S-MRBIR第1次反馈后检索结果 Fig. 2 Retrieval results by S-MRBIR after first feedback |

|
| 图 3 SG-MRBIR第1次反馈后检索结果 Fig. 3 Retrieval results by SG-MRBIR after first feedback |
本文将图像集中图像已有的分类标记信息融入流形排序算法,提出了有监督流形排序图像检索算法,在MSRA-MM图像库上的实验表明,通过引入不相关排序,避免了不能通过用户的多次反馈改善初次反馈查准率为零的情况,进一步提高了图像检索性能。此外,现实生活中的图像可能同时具有多个标记信息,也就是同一幅图像同时属于不同的类,如果引入更加丰富的监督信息势必会更好地改善检索效果,这值得进一步探索。
| [1] | KATO T. Database architecture for content-based image retrieval[C]//Proceedings of the SPIE Vol. 1662—Image Storage and Retrieval Systems. San Jose, USA, 1992: 112-123. |
| [2] | RITENDRA D, DHIRAJ J, LI Jia. Image retrieval: ideas influence, and trends of the new age[J]. ACM Computer Surveys , 2008, 40 (2) : Article No. 5 |
| [3] | HE Xiaofei, NIYOGI P. Locality preserving projections[C]//Advances in Neural Information Processing Systems. Vancouver, Canada, 2003: 3-15. |
| [4] | HE Xiaofei. Incremental semi-supervised subspace learning for image retrieval[C]//Proceedings of the 12thAnnual ACM International Conference on Multimedia. New York, USA, 2004: 2-8. |
| [5] | LIN Yenyu, LIU Tyngluh, CHEN Hwanntzong. Semantic manifold learning for image retrieval[C]//Proceedings of the 13thAnnual ACM International Conference on Multimedia. Singapore, 2005: 249-258. |
| [6] | HE Xiaofei, CAI Deng, HAN Jiawei. Learning a maximum margin subspace for image retrieval[J]. IEEE Transactions on Knowledge and Data Engineering , 2008, 20 (2) : 189-201 DOI:10.1109/TKDE.2007.190692 |
| [7] | 刘利, 韦佳, 马千里. 基于流形学习的图像检索研究进展[J]. 北京交通大学学报 , 2010, 34 (5) : 164-171 LIU Li, WEI Jia, MA Qianli. State-of-the-art on image retrieval based on manifold learning[J]. Journal of Beijing Jiaotong University , 2010, 34 (5) : 164-171 |
| [8] | ZHOU Dengyong, JASON W, ARTHUR G. et al. Ranking on data manifolds[C]//Advances in Neural Information Processing Systems. Vancouver, Canada, 2003: 169-176. |
| [9] | HE Jingrui, LI Mingjing, ZHANG Hongjiang, et a1. Manifold-ranking based image retrieval[C]//Proceedings of the 12th Annual ACM International Conference on Multimedia. New York, USA, 2004: 9-16. |
| [10] | HE Jingrui, LI Mingjing, ZHANG Hongjiang. Generalized manifold ranking based image retrieval[J]. IEEE Transactions on Image Process , 2006, 15 (10) : 3170-3177 DOI:10.1109/TIP.2006.877491 |
| [11] | XU Bin, BU Jiajun, CHEN Chen, et al. Efficient manifold ranking for image retrieval[C]//The 34th Annual ACM SIGIR Conference. Beijing, China, 2011: 24-28. |



