粗糙逻辑是经典命题逻辑增加粗糙算子后的扩充，其推理形式也源于经典逻辑。但在语义研究方面，为了更准确地描述其涵义，粗糙逻辑采用了有别于经典命题逻辑的语义模型。在文献[1]中Pawlak将经典命题逻辑中的2个逻辑真值(“真”、“假”)扩展为粗糙逻辑中的5个逻辑真值(“真”、“假”、“粗糙真”、“粗糙假”、“粗糙不相容”)。之后，闫林等^[2-6]将粗糙公式扩展到了n维，给出公式的语义并讨论了语义推理。文献[7]中将模糊真值与粗糙逻辑真值结合，定义了5个模糊粗糙逻辑真值，并进行了语义和推理研究。本文在此基础上，将直觉模糊粗糙集引入到逻辑推理中，定义了5个直觉模糊粗糙逻辑真值，并讨论其语义推理。由于直觉模糊集增加了一个新的属性参数：非隶属度函数，因此直觉模糊粗糙逻辑的语义比粗糙逻辑和模糊粗糙逻辑的语义更加丰富，其推理也能够更加细腻地描述和刻画客观世界的模糊性本质。

1 预备知识

定义1^[8] 设U是一个非空有限论域，称U上形如A＝{〈x, μ_A(x), ν_A(x)〉|x∈U}的三元组为U上的一个直觉模糊集，其中，函数μ_A：U→[0, 1]和ν_A：U→[0, 1]分别表示U上元素x属于A的隶属度和非隶属度，并且满足0≤μ_A(x)+ν_A(x)≤1，∀x∈U．

为方便，记A(x)＝〈μ_A(x), ν_A(x)〉，U上所有直觉模糊集构成的集合为IFS(U)．

定义2^[9] 设U是一个非空有限论域，A, B∈IFS(U)，且具有下面的形式：

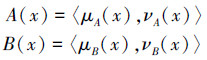规定序及运算如下：

1)A⊆B当且仅当μ_A(x)≤μ_B(x)且ν_A(x)≥ν_B(x)，∀x∈U；

2)A＝B当且仅当μ_A(x)＝μ_B(x)且ν_A(x)＝ν_B(x)，∀x∈U；

3)A∩B＝{〈x, min{μ_A(x), μ_B(x)}, max{ν_A(x), ν_B(x)}〉|x∈U}；

4)A∪B＝{〈x, max{μ_A(x), μ_B(x)}, min{ν_A(x), ν_B(x)}〉|x∈U}；

5)A^C＝{〈x, ν_A(x), μ_A(x)〉|x∈U}．

显然，〈IFS(U), ⊆〉是一个偏序集。

定义3^[9] 设(U, R)是Pawlak近似空间，U/R＝{X₁, X₂, …, X_n}是U上由R导出的所有等价类。直觉模糊集B在U中的上、下近似分别记为B、B，且被定义为U/R＝{X₁, X₂, …, X_n}上的直觉模糊集B, B：U/R→[0, 1]×[0, 1]，使得

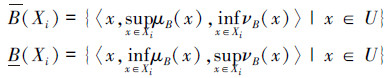式中：i＝1, 2, …, n．则称(B, B)为一个直觉模糊粗糙集。

2 直觉模糊粗糙逻辑的概念

在定义直觉模糊粗糙逻辑概念之前首先给出粗糙逻辑的定义。

定义4^[10] 设M＝(U, R)为Pawlak近似空间，ϕ为M下的原子公式, ‖为解释函数，‖:W→P(U)，|ϕ|→X∈P(U)，W为所有粗糙逻辑公式的集合，P(U)为U的幂集，则粗糙逻辑由经典的二值逻辑增加到5个逻辑真值：真、假、粗糙真、粗糙假和粗糙不相容。

1)若|ϕ|＝U，则称公式ϕ在M中真，记作|＝_Mϕ;

2)若|ϕ|≠U，则称公式ϕ在M中假，记作|≠_Mϕ;

3)若R|ϕ|＝U，则称公式ϕ在中M粗糙真，记作|＝_Rϕ;

4)若R|ϕ|＝∅，则称公式ϕ在M中粗糙假，记作|≠_Rϕ;

5)若R|ϕ|＝U且R|ϕ|＝∅，则称公式ϕ在M中粗糙不相容。

定义5 设M＝(U, R)为Pawlak近似空间，T为直觉模糊概念的真值，ϕ为U上的直觉模糊概念，‖为解释函数(直觉模糊映射)，‖:W→IF(U)，|ϕ|→A∈IF(U)，W为全体模糊概念的集合，IF(U)为全体直觉模糊集，|ϕ|的直觉模糊真值定义为T(|ϕ|)(x)＝A(x)＝〈μ_A(x), ν_A(x)〉，其直觉模糊粗糙真值定义为

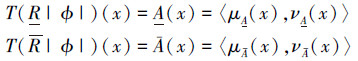则直觉模糊粗糙逻辑由粗糙逻辑中的5个逻辑值增加到无限多个值。做以下规定：

1)若μ_A(x)≥且ν_A(x) < ，则称ϕ在M中直觉模糊真，记作|＝_IFMϕ；

2)若μ_A(x) < 且ν_A(x)≥，则称ϕ在M中直觉模糊假，记作|≠_IFMϕ；

3)若μ_A(x)≥且ν_A(x) < ，则称ϕ在M中直觉模糊粗糙真，记作|＝_IFRϕ；

4)若μ_A(x) < 且ν_A(x)≥，则称ϕ在M中直觉模糊粗糙假，记作|≠_IFRϕ；

5)若μ_A(x)≥，ν_A(x) < 且μ _A(x) < ，ν_A(x)≥，则称ϕ在M中直觉模糊粗糙不相容。

3 直觉模糊粗糙集的逻辑运算

下面在直觉模糊粗糙逻辑语义的基础上，讨论直觉模糊粗糙逻辑的运算。

定义6 设ϕ、φ是近似空间K＝(U, R)上直觉模糊公式，其真值分别为T(|ϕ|)和T(|φ|)，则有

根据上述概念，给出直觉模糊粗糙逻辑的语义推理。

在经典命题逻辑中，语义推理是围绕公式的真值所展开的关于前提与结论的真值关系的讨论，粗糙语义推理是针对公式组成的前提和结论的粗糙逻辑值关系的讨论，而直觉模糊粗糙逻辑推理是针对直觉模糊公式的前提和结论的直觉模糊粗糙逻辑值关系进行的讨论^[11]。经典逻辑值只有真与假2个值，直觉模糊粗糙逻辑值有5个：直觉模糊真、直觉模糊假、直觉模糊粗糙真、直觉模糊粗糙假、直觉模糊粗糙不相容，其语义自然要丰富得多，主要性质在以下的定理中给出。

4 直觉模糊粗糙逻辑语义推理 4.1 含有“→”公式

这里主要讨论T(|ϕ→φ|)(x)和T(R|ϕ→φ|)(x)的一些性质，令

则有

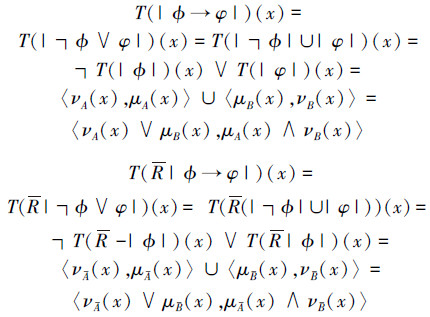设ϕ、φ是近似空间M＝(U, R)上的直觉模糊公式，则有下面的定理1~6成立。

定理1

1)若|＝_IFMφ, 则|＝_IFMϕ→φ，即若φ直觉模糊真，则ϕ→φ直觉模糊真；

2)若|≠_IFMϕ, 则|＝_IFMϕ→φ，即若ϕ直觉模糊假，则ϕ→φ直觉模糊真；

3)若|≠_IFMϕ→φ, 则|＝_IFMϕ且|≠_IFMφ，即若ϕ→φ直觉模糊假，则ϕ直觉模糊真，φ直觉模糊假。

证明

1)因为|＝_IFMφ，则μ_B(x)≥且ν_B(x) < ，所以对于T(|ϕ→φ|)(x)＝〈ν_A(x)∨μ_B(x), μ_A(x)∧ν_B(x)〉, 显然有ν_A(x)∨μ_B(x)≥且μ_A(x)∧ν_B(x) < ，因此可得结论。

2)因为|≠_IFMϕ，则μ_A(x) < 且ν_A(x)≥，所以对于T(|ϕ→φ|)(x)＝〈ν_A(x)∨μ_B(x), μ_A(x)∧ν_B(x)〉, 即有ν_A(x)∨μ_B(x)≥且μ_A(x)∧ν_B(x) < ，因此可得结论。

3)因为|≠_IFMϕ→φ，则ν_A(x)∨μ_B(x) < 且μ_A(x)∧ν_B(x)≥，所以ν_A(x) < ，μ_B(x) < 且μ_A(x)≥，ν_B(x)≥，故|＝_IFMϕ，|≠_IFMφ，因此可得结论。

定理2

1)若|＝_IFRφ, 则|＝_IFRϕ→φ，即若φ直觉模糊粗糙真，则ϕ→φ直觉模糊粗糙真；

2)若|≠_IFRφ, 则|＝_IFRϕ→φ，即若ϕ直觉模糊粗糙假，则ϕ→φ直觉模糊粗糙真；

3)若|≠_IFRϕ→φ, 则|＝_IFRϕ且|≠_IFRφ，即若ϕ→φ直觉模糊粗糙假，则ϕ直觉模糊粗糙真，φ直觉模糊粗糙假。

证明 类似定理1可证。

定理3

1)若|＝_IFMφ, 则|＝_IFRϕ→φ，即若φ直觉模糊真，则ϕ→φ直觉模糊粗糙真；

2)若|≠_IFMϕ, 则|＝_IFRϕ→φ，即若ϕ直觉模糊假，则ϕ→φ直觉模糊粗糙真。

证明

1)因为|＝_IFMφ, 则μ_B(x)≥且ν_B(x) < ，又由于|φ|⊆R|φ|，所以μ_B(x)≥且ν_B(x) < ，因此对于T(R|ϕ→φ|)(x)＝〈ν_A(x)∨μ_B(x), μ_A(x)∧ν_B(x)〉，总有ν_A(x)∨μ_B(x)≥且μ_A(x)∧ν_B(x) < ，因此可得结论。

2)同理可证。

在经典命题逻辑语义推理和模糊粗糙逻辑推理中，若(ϕ→φ)∧ϕ为真，则φ也为真，记作(ϕ→φ)∧ϕ|＝φ^[12].下面的定理表明：将其变为直觉模糊真和直觉模糊粗糙真后，上述结论仍成立。

定理4

1)若|＝_IFM(ϕ→φ)∧ϕ，则|＝_IFMφ；

2)若|＝_IFR(ϕ→φ)∧ϕ，则|＝_IFRφ.

证明

1) T(|(ϕ→φ)∧ϕ|)(x)＝T(|(┐ϕ∨φ)∧ϕ|)(x)＝T(|φ∧ϕ|)(x)＝T(|ϕ|)(x)∧T(|φ|)(x)＝〈μ_A(x)∧μ_B(x), ν_A(x)∨ν_B(x)〉。

因为|＝_IFM(ϕ→φ)∧ϕ，则有μ_A(x)∧μ_B(x)≥, ν_A(x)∨ν_B(x) < ，所以，μ_B(x)≥, ν_B(x) < ，因此可得结论。

2)T(R-|(ϕ→φ)∧ϕ|)(x)＝T(R|(┐ϕ∨φ)∧ϕ|)(x)＝T(R|φ∧ϕ|)(x)＝T(R(|ϕ|∩|φ|))(x)＝〈a, b〉

因为|＝_IFR(ϕ→φ)∧ϕ，则有a≥, b < ，由于R|ϕ∧φ|⊆R|ϕ|∩R|φ|，而T(R|ϕ|)(x)∧T(R|φ|)(x)＝〈μ_A(x)∧μ_B(x), ν_A(x)∨ν_B(x)〉，于是有μ_A(x)∧μ_B(x)≥a≥, ν_A(x)∨ν_B(x) < b < ，所以μ_B(x)≥, ν_B(x) < ，因此结论得证。

在定理4中，若把|＝_IFR(ϕ→φ)∧ϕ，则|＝_IFRφ改为：若|＝_IFRϕ→φ且|＝_IFRϕ，则|＝_IFRϕ, 其结论不成立。然而，若把上式中的条件加强，即把|＝_IFRϕ→φ改为|＝_IFMϕ→φ，|＝_IFRϕ改为|＝_IFMϕ，则结论成立，即有下面定理。

定理5 如果|＝_IFMϕ→φ且|＝_IFMϕ，则|＝_IFMφ，进而有|＝_IFRφ.

证明 因为|＝_IFMϕ→φ，所以对T(|ϕ→φ|)(x)＝〈ν_A(x)∨μ_B(x), μ_A(x)∧ν_B(x)〉, 有ν_A(x)∨μ_B(x)≥, μ_A(x)∧ν_B(x) < 。

又由|＝_IFMϕ，所以对T(|ϕ|)＝〈μ_A(x), ν_A(x)〉有μ_A(x)≥, ν_A(x) < 。于是μ_B(x)≥, ν_B(x) < , 即|＝_IFMφ成立。

又因为|φ|⊆R|φ|，故≤μ_B(x)≤μ_B(x), ν_B(x)≤ν_B(x) < ，因此可得结论。

上述条件过于严格，若把条件放宽，则结论仍然成立，即有下面的定理。

定理6

1)如果|＝_IFMϕ→φ且对于T(|ϕ|∪|φ|)(x)＝〈μ_A(x)∨μ_B(x), ν_A(x)∧ν_B(x)〉, 有μ_A(x)∨μ_B(x)≥, ν_A(x)∧ν_B(x) < ，则|＝_IFMφ且|＝_IFRφ.

2)如果|＝_IFMφ且对于T(|ϕ|∩|φ|)(x)＝μ_A(x)∧μ_B(x), ν_A(x)∨ν_B(x)〉, 有μ_A(x)∧μ_B(x) < , ν_A(x)∨ν_B(x)≥，则|≠_IFRϕ→φ且|≠_IFMϕ→φ.

证明

1)因为|＝_IFMϕ→φ，所以对T(|ϕ→φ|)(x)＝〈ν_A(x)∨μ_B(x), μ_A(x)∧ν_B(x)〉, 有ν_A(x)∨μ_B(x)≥, μ_A(x)∧ν_B(x) < ，又由μ_A(x)∨μ_B(x)≥, ν_A(x)∧ν_B(x) < ，则必有μ_B(x)≥，ν_B(x) < ，又因为|φ|⊆R|φ|，所以≤μ_B(x)≤μ_B(x), ν_B(x)≤ν_B(x) < ，因此可得结论。

2)因为|＝_IFMϕ，则有μ_A(x)≥, ν_A(x) < ，又因为μ_A(x)∧μ_B(x) < , ν_A(x)∨ν_B(x)≥，所以有μ_B(x) < , ν_B(x)≥。而T(|ϕ→φ|)(x)＝T(|┐ϕ∨φ|)(x)＝〈ν_A(x)∨μ_B(x), μ_A(x)∧ν_B(x)〉，因此有ν_A(x)∨μ_B(x) < , μ_A(x)∧ν_B(x)≥。又因为|ϕ→φ|⊇R|ϕ→φ|，所以对T(R|ϕ→φ|)(x)＝〈ν_A(x)∨μ_B(x), μ_A(x)∧ν_B(x)〉, 有ν_A(x)∨μ_B(x)≤ν_A(x)∨μ_B(x) < , μ_A(x)∧ν_B(x)≥μ_A(x)∧ν_B(x)≥，因此可证得结论。

4.2 含有“┐”公式

定理7 设ϕ是近似空间M＝(U, R)上的直觉模糊公式，则如果ϕ在M＝(U, R)上直觉模糊粗糙不相容，则┐ϕ在M上也直觉模糊粗糙不相容。

证明 令T(R|ϕ|)(x)＝〈μ_A(x), ν_A (x)〉，T(R|ϕ|)(x)＝〈μ_A(x), ν_A(x)〉。因为ϕ在M＝(U, R)上直觉模糊粗糙不相容，所以有μ_A(x)≥，ν_A(x) < 且μ_A(x) < ，ν_A(x)≥，又由R|┐ϕ|＝R(┐|ϕ|)＝┐R|ϕ|，R|┐ϕ|＝R(┐|ϕ|)＝┐R|ϕ|，所以T(R|┐ϕ|)(x)＝┐T(R|ϕ|)＝〈ν_A(x), μ _A(x)〉，T(R|┐ϕ|)(x)＝┐T(R|ϕ|)＝〈ν_A(x), μ_A(x)〉。

故┐ϕ在M上直觉模糊粗糙不相容。

4.3 含有“∧, ∨”公式

定理8 设ϕ是近似空间M＝(U, R)上直觉的模糊原子公式，若ϕ在M＝(U, R)上直觉模糊粗糙不相容，则对∀ϕ，有|＝_IFRϕ∨φ且|≠_IFRϕ∧φ, 即ϕ∨φ在M上直觉模糊粗糙真，ϕ∧φ在M上直觉模糊粗糙假。

证明

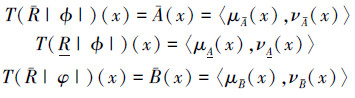由题意有|＝_IFRϕ和|≠_IFRϕ，即μ_A(x)≥，ν_A(x) < 且μ_A(x) < ，ν_A (x)≥。

所以对

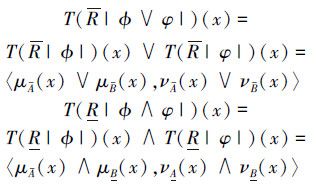可得

因此可得结论。

5 结束语

本文所讨论的直觉模糊粗糙逻辑的语义推理是在直觉模糊粗糙集的基础上进行的逻辑推理，这种逻辑推理拓展了经典逻辑中的语义推理。因此，在直觉模糊粗糙集基础上进行的直觉模糊粗糙语义推理为逻辑推理开辟了新径，与此同时逻辑推理也为直觉模糊粗糙集理论的研究提供新思路。因此，直觉模糊粗糙集理论与逻辑推理的融合为双方的深入研究互相指明了方向。