多机器人系统能克服单机器人在信息获取、处理和控制等方面的局限性,提高了任务执行效率和系统灵活性。任务分配是多机器人协作搬运的首要解决问题,分配的合理性将直接关系到系统的运行效率。目前多机器人任务分配主要通过基于行为、市场机制和线性规划等方法来设计,典型代表有合同网法、空闲链法和阈值法等[1]。Dahl等[2]在空闲链的基础上建立了奖赏函数,有效调节了平均奖赏值,较好地实现了任务分配,但存在着计算量大、效率低的不足。Bradford等[3]重新构建了拍卖的投标矩阵,并将任务分组与协同效应相结合,显现出计算量小、用时少的优点,但系统能耗大、效率低等问题有待解决。为了进一步提高多机器人系统的协作效率,近年来群体智能分配方法得到了重视。Ellips等[4]利用粒子群算法解决了机器人运动分配问题,但是在解空间中不易搜索到最优粒子。Zhang等[5]提出基于群集智能的自适应任务分配方法,通过自强化学习和蚁群算法完成觅食任务合作,但是计算量大、效率低。生物免疫的自组织、自适应性为解决工程问题,尤其是机器人系统提供了新思路。基于Farmer的免疫动力学模型,高云园等[6-7]实现了箱子搬运的任务分配,但执行效率还有待进一步提高。吴皓等[8]通过在模型中增加T细胞来控制抗体浓度,解决了未知环境的探测问题,但如何将局部探测转为全局探测还有待研究。为了解决全局环境中的任务分配,并进一步提高协作搬运效率,文中在Jerne独特型免疫网络基础上,通过定义干扰素调节因子等,实现分配网络的调节和优化,通过仿真来验证分配模型的有效性和优越性。
1 多机器人任务分配免疫网络模型 1.1 免疫网络模型生物免疫系统是一种高度进化的自适应信息处理系统。免疫学说理论之一的Jerne独特型免疫网络假设认为:抗原入侵会打破系统原先的平衡性,不同种类的抗体和淋巴细胞之间通过相互通讯进行相互激励或抑制,从而克服抗原,最终维持系统稳定[9]。图 1为独特型免疫网络假设示意图。

|
| 图 1 独特型免疫网络 Fig. 1 Idiotypic immune network |
根据该免疫网络假设,Farmer等[10-11]首次提出了计算抗体激励水平及浓度的动态方程,其表达式如下:
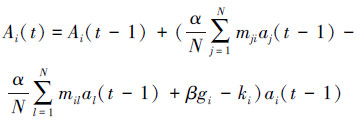 |
 |
式中:Ai(t)为t时刻抗体i的激励水平;N为抗体数;等号右边括号中第1项为抗体i、j之间的吸引力,mji为两者刺激系数;第2项为抗体i、k之间的排斥力,mik为两者抑制系数;第3项gi为抗原对抗体i的激励;第4项ki模拟抗体的自然消亡;α、β分别为抗体i对其他抗体和抗原的作用系数;ai(t)、aj(t)、ak(t)分别为t时刻抗体i、j、k的浓度,采用扁平S形函数来表示,目的是确保各抗体浓度值的稳定。
基于Farmer的免疫动力学模型,Ishiguro提出了行为仲裁系统,并在垃圾回收上得到了应用;Meshref等[12]解决了分布式自主机器人系统中的狗羊放牧问题。两者都较好地体现了人工免疫网络的柔韧性和鲁棒性。为了解决多机器人协作搬运问题,文中以搬箱问题为研究对象,在Jerne的独特型免疫网络假设基础上,借鉴Farmer的动力学模型提出了一种新的任务分配模型。在该人工免疫模型中,将机器人和箱子作为抗体和抗原,机器人搬运箱子的过程看作抗体消灭抗原过程,从而实现了多机器人的任务分配。
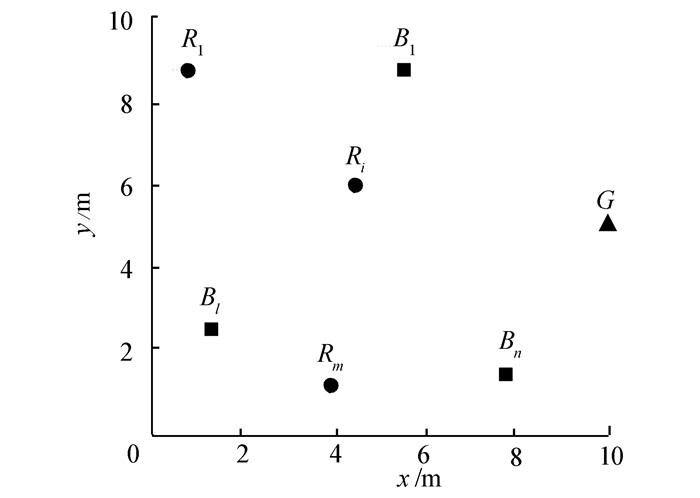
1.2 免疫分配模型的基本定义为了便于描述分配模型中的定义,给出如图 2所示的机器人分配环境,环境中分布着若干机器人Ri(i∈{1, 2,…,m})和若干箱子Bl(l∈{1, 2,…,n}),任务分配的目的是机器人通过合作方式,以最大性能和效率将箱子推到目标点G。
|
| 图 2 多机器人任务分配环境 Fig. 2 Task allocation environment of multi-robot |
箱子在初始时刻及搬运过程中的机器人分配,主要是根据两者之间的亲和度进行。设第i个机器人Ri与第l个箱子Bl之间激励为gi,则将gi定义为
 |
(1) |
 |
(2) |
式中:fi为机器人Ri的推力,dil是机器人Ri和箱子Bl之间距离,dlg是箱子Bl和目标点之间距离,λ1和λ2为调整系数,u为激励或抑制因子,r为调整系数。当机器人位于箱子左边时,fi越大,dil和dlg越小,gi越大。另外,按照实验模型,机器人在箱子左侧时gi得到正激励,反之为负激励。
1.2.2 抗体间亲合度根据独特型免疫网络假设,抗体间作用包括刺激和抑制。若机器人Ri无法独自搬运箱子Bl,则Ri产生抗体刺激其他机器人来协作搬运箱子;若机器人Ri可独自搬运箱子Bl,则Ri产生的抗体对其他机器人起到免疫抑制作用。为体现多机器人搬运中的刺激和抑制,定义如下亲合度系数m:
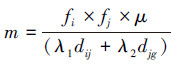 |
式中:fi、fj分别为Ri和Rj的推力大小,dij为机器人Ri和Rj之间的距离,djg为机器人Rj和目标点之间的距离,u、λ1、λ2的取值同上。
1.2.3 干扰素调节因子干扰素是人和动物细胞受到适宜刺激时产生的一种微量的且具有高度生物学活性的糖蛋白,由Issacs等于1957年利用鸡胚绒毛尿囊膜研究流感病毒干扰现象时发现。干扰素对体液免疫、细胞免疫均有免疫调节作用,对巨噬细胞和自然杀伤细胞也有一定的免疫增强作用[13]。临床医学表明:干扰素对免疫的调控作用有助于抑制乙肝、丙肝病毒的复制。为了进一步提高基于免疫网络的任务分配效果,将其引入并实现了免疫网络分配模型的调节。
干扰素调节因子di定义为
 |
(3) |
式中:di为机器人Ri需注射的干扰素剂量,N′为目前待搬运箱子的数目,δ=10-3为调整系数。由式(3)可以看出,当待搬运箱子数目减少时,干扰素注射量逐步增加,从而能自动调节机体的免疫水平。
1.3 任务分配的抗体选择模型根据多机器人协作搬运中的任务分配要求及Jerne的独特型网络模型假设,在Farmer的动力学模型基础上,利用文中所定义的抗体与抗原间亲合度、抗体间亲合度以及干扰素调节因子构建了多机器人新任务分配模型:
 |
(4) |
在多机器人任务分配过程中,若机器人需等待协作,则式(4)作为寻找协作机器人的依据。
1.4 多机器人协作搬运算法考虑到多机器人系统的分布式体系结构和通讯的灵活性要求,文中系统采用了黑板模式的通讯方式。系统中的每个机器人将其感知到的任务和自身信息写在“黑板”的共享区域内,同时从“黑板”上读取相关信息。黑板上的共享信息包括机器人信息、已搬运箱子信息和目标点信息。机器人之间通过相互通讯和激励值来完成任务分配和搬运。算法具体过程描述如下:
1)初始化抗原和抗体信息,根据式(1)和(2)计算机器人和箱子之间的激励;
2)根据激励值选择合适的机器人去搬运箱子,被选择机器人向相应箱子移动;
3)判断该机器人能否推动箱子,若能则转步骤5),同时抑制其他空闲机器人来协作;否则转步骤4)去寻找其他协作机器人;
4)根据式(4)计算等待搬运的箱子与空闲机器人的激励值,选择合适的机器人前来协作搬运,并转步骤3);
5)通过机器人或者多机器人协作将箱子搬运至目标点;
6)更新机器人和箱子的坐标等信息,重新计算未搬运箱子和机器人两两间的激励值,重复步骤2)~5),直至所有箱子被搬运至目标点。
在步骤4)中,当机器人都处于等待状态时,称为“任务死锁”。对此,文中采用Parker提出的“焦躁模型”[14],即当机器人等待队友协作过久,则选择不再等待,并通过减小其激励值来降低其再次被此任务选择的概率。
为了进一步清晰看出机器人的任务分配过程,上述免疫网络分配算法可以用图 3所示的流程图来描述。

|
| 图 3 多机器人任务分配流程 Fig. 3 Flow of multi-robot task allocation |
为了验证文中新免疫网络分配模型在多机器人协作搬运任务中的有效性,利用MATLAB7.1,在CPU 1.20 GHz、内存为2GB的计算机上进行了多环境任务分配测试,并将测试结果与文献[6, 8]中免疫算法进行了比较。环境共6种,参数设置如表 1所示。
| 环境 | NB | MB /kg | NR | FR /kg |
| 环境1 | 3 | 2、5、7 | 3 | 2、3、4 |
| 环境2 | 3 | 2、5、7 | 4 | 2、3、4、5 |
| 环境3 | 4 | 2、5、7、8 | 3 | 2、3、5 |
| 环境4 | 4 | 2、5、7、8 | 4 | 2、3、4、5 |
| 环境5 | 5 | 2、5、7、8、9 | 4 | 2、3、4、5 |
| 环境6 | 5 | 2、5、7、8、9 | 6 | 2、3、4、5、6、7 |
表中,NB为箱子数目,MB为箱子重量,NR为机器人数目,FR为机器人推力值。文中算法参数为α=0.5,β=0.1,k=0.002,Ai(0)=ai(0)=0.5,λ1=0.8,λ2=0.2。
2.2 分配结果及分析表 2为3种免疫算法在6种环境中的不同分配效果。由表 2不难看出,文中算法在6种环境中的分配是最优的。首先在机器人行驶总步数上,由于文中免疫网络加入了干扰素调节因子,使得其规划路径短于其他算法;其次在能量损耗上,新方法通过降低能力强的机器人重复参与搬运的可能性,减少了损耗值;最后协作机器人数量也得到了控制。因此基于干扰素调节机制的免疫网络模型,不仅能兼顾机器人行驶总路程和机器人推力损耗,还能提高多机器人系统的执行效率,实现了分配方案的优化。
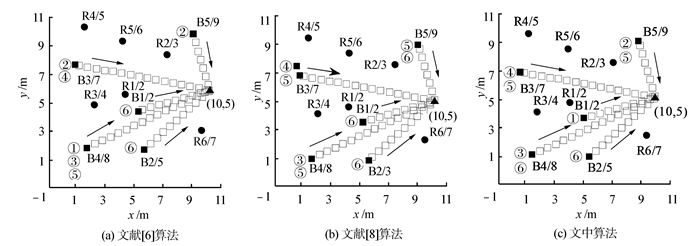
为了看出基于免疫网络模型的多机器人协作搬运情况,以相对较复杂的环境6为例来进行说明,结果如图 4所示。图中,“●”、“■”分别表示机器人和箱子的初始位置;“□”为箱子的搬运轨迹;“▲”为目标点;R1/2表示1号机器人,且推力值为2 kg;B1/2表示1号箱子,且重量为2 kg;1号箱子左侧的⑥表示1号箱子由6号机器人搬运。由图 4可以清晰地看出不同算法对应的机器人和箱子的分配情况。以图 4(c)为例,箱子1和2分别由1号和6号机器人单独搬完,箱子3由4号和5号机器人协作搬完,箱子4由3号和6号机器人协作搬完,箱子5由2号和5号机器人协作搬完。
|
| 图 4 3种算法在环境6中的多机器人协作搬运比较 Fig. 4 Comparisons of multi-robot cooperation handling of three algorithms in environment 6 |
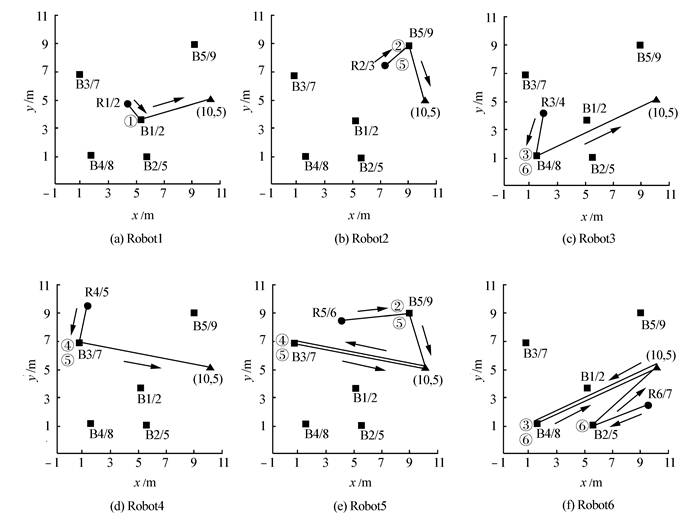
图 5给出了文中算法在环境6中的机器人搬运路径,由该路径可以进一步清晰看出机器人的协作过程。以图 5(e)为例,Robot5先被Box5选择,并与已经等候在Box5处的Robot2协作将箱子搬运至目标处;完成任务后,Robot5又被Box3选择,同时与守候在此处的Robot4协作将Box3搬运至目标处。
|
| 图 5 文中算法在环境6中的机器人搬运路径 Fig. 5 Robot handling path of proposed algorithm in environment 6 |
图 6给出了文中算法在环境6中的机器人浓度选择,1~6号机器人浓度通过不同纹理的柱高来表示,分配系统根据浓度来实现箱子的机器人分配。对应某个箱子,若某机器人的柱高为0,则表示该机器人已被选择执行其他任务;若某次选择时,所有机器人柱高均为0,则表示该箱子已被搬运至目标处,任务已完成。以图 6(c)来说明:对应箱子Box3,系统第1次选择Robot4去搬运,Robot4不能独自搬运Box3,需等待协作;系统第2次选择时,Robot3、Robot4、Robot6号机器人柱高为0,则表示在第1次分配时它们已经被成功分配任务,从而在空闲的Robot1、Robot2、Robot5三者中选择浓度最大的Robot5,于是Robot4和Robot5协作来搬运Box3;第3次选择时可以看出所有机器人柱高为0,表明搬运Box3的任务已经完成。图 6更为清晰地给出了文中算法在进行多机器人任务分配时,免疫系统模型中的浓度变化情况。浓度的变化体现出抗原抗体之间的激励和抑制结果,而分配结果表明了文中免疫网络模型的有效性和优越性。

|
| 图 6 文中算法在环境6中的机器人浓度选择 Fig. 6 Concentration selection of proposed algorithm in environment 6 |
为了解决多机器人系统协作问题,文中基于Jerne的独特型免疫网络假设和Farmer的动力学模型,根据干扰素作用机制,设计了一种新的基于干扰素调节的免疫网络分配模型。6种环境测试结果表明,利用干扰素调节可以显著减少机器人搬运路程;通过降低能力强的机器人重复参与次数,可以同时减少能量损耗和协作等待机器人数目。与已有的2种免疫网络分配算法相比,文中算法在多机器人的协作效率和完成质量方面都有明显提高,显示出该算法的有效性。与单机器人相比,多机器人系统的内在并行性和叠加性,使得其具有更高的任务执行效率和功能,而文中免疫分配模型将有助于进一步发挥多机器人系统的功效,因此该成果具有理论和实用价值。课题下一步将把重点放在如何根据机器人和任务信息,进一步提高机器人之间的协作以及免疫分配模型的实际应用上,在完善免疫网络分配算法的同时,发挥算法的实际应用价值。
| [1] | 董炀斌, 蒋静坪, 何衍. 基于适应度的多机器人任务分配策略[J]. 浙江大学学报:工学版 , 2007, 41 (2) : 272-277 DONG Yangbin, JIANG Jingping, HE Yan. Fitness-based task allocation strategy for multi robot system[J]. Journal of Zhejiang University:Engineering Science , 2007, 41 (2) : 272-277 |
| [2] | DAHL T S, MATARIC M, SUKHATME G S. Multi-robot task allocation through vacancy chain scheduling[J]. Robotics and Autonomous Systems , 2009, 57 (6) : 674-687 |
| [3] | BRADFORD H, MAURICE P. Sequential single-cluster auctions for robot task allocation[J]. Advances in Artificial Intelligence , 2011, 7106 : 412-421 |
| [4] | ELLIPS M, DAVOUD S. Multi-objective robot motion planning using a particle swarm optimization model[J]. Journal of Zhejiang University: Science , 2010, 11 (8) : 607-619 DOI:10.1631/jzus.C0910525 |
| [5] | ZHANG D, XIE G, YU J, et al. Adaptive task assignment for multiple mobile robots via swarm intelligence approach[J]. Robotics and Autonomous Systems , 2007, 55 (7) : 572-588 DOI:10.1016/j.robot.2007.01.008 |
| [6] | 高云园, 韦巍. 未知环境中基于免疫网络的多机器人自主协作[J]. 浙江大学学报:工学版 , 2006, 40 (5) : 733-737 GAO Yunyuan, WEI Wei. Multi-robot self-determination cooperation based on immune network in an unknown environment[J]. Journal of Zhejiang University : Engineering Science , 2006, 40 (5) : 733-737 |
| [7] | GAO Yunyuan, WEI Wei. Multi-robot autonomous cooperation integrated with immune based dynamic task allocation[C]//Proceedings of the Sixth International Conference on Intelligent Systems Design and Applications. Ji′nan, China, 2006: 586-591. |
| [8] | 吴皓, 田国会, 黄彬. 未知环境探测的多机器人协作策略研究[J]. 山东大学学报:工学版 , 2008, 38 (4) : 27-31 WU Hao, TIAN Guohui, HUANG Bin. Research on the collaboration strategy of multi robot for exploring unknown environment[J]. Journal of Shandong University: Engineering Science , 2008, 38 (4) : 27-31 |
| [9] | YUAN Mingxin, WANG Sunan, WU Canyang. Hybrid ant colony and immune network algorithm based on improved APF for optimal motion planning[J]. Robotica , 2010, 28 (6) : 833-846 DOI:10.1017/S0263574709990567 |
| [10] | FARMER J, PACKARD N, PERELSON A. The immune system, adaptation, and machine learning[J]. Physica D , 1986, 2 (3) : 187-204 |
| [11] | ISHIGURO A, WATANABE Y, KONDO T, et al. A robot with a decentralized consensus-making mechanism based on the immune system[C]//Proceedings of the International Symposium on Autonomous Decentralized Systems. Berlin, Germany, 1997: 231-237. |
| [12] | YUAN Mingxin, WANG Sunan, WU Canyang, et al. A novel immune network strategy for robot path planning in complicated environments[J]. Journal of Intelligent and Robotic Systems , 2010, 60 (1) : 111-131 DOI:10.1007/s10846-010-9408-9 |
| [13] | 刘颖, 侯利华, 陈薇. 干扰素的信号传导和抗病毒效应机制[J]. 生物技术通讯 , 2012, 23 (1) : 123-126 LIU Ying, HOU Lihua, CHEN Wei. Signal transduction and mechanisms of antiviral effect of interferon[J]. Letters in Biotechnology , 2012, 23 (1) : 123-126 |
| [14] | LI Guanghui, TAMURA Y, ASAMA H. Dynamical task allocation and reallocation based on body expansion behavior for multi-robot coordination[C]//Proceedings of 2011 International Conference on Mechatronics and Automation. Beijing, China, 2011: 537-542. |



