2. 诸暨市联系数学研究所,浙江 诸暨 311811;
3. 浙江大学 非传统安全与和平发展研究中心,浙江 杭州 310058
2. Zhuji Institute of Connection Mathematics, Zhuji 311811, China ;
3. Center for Non-traditional Security and Peaceful Development Studies, Zhejiang University, Hangzhou 310058, China
基于集对分析不确定性系统理论和方法[1-3],赵森烽与赵克勤在文献[4]中借助“白球加黑球”古典概型随机试验说明事物的随机性来自事物与事物的联系以及随机事件成对存在,并且给出了随机事件成对存在定理和联系概率的定义。文献[5]把联系概率应用于风险决策,得到了一种新的风险决策模型。文献[6]给出了几何概型的联系概率计算、随机事件的表现定理以及联系概率意义下的概率补数定理。由于这些概念与经典概率论中的相关概念在内涵上有重要区别,因此为了从形式上表明这种区别和应用上的方便,沿用经典概率论中的习惯记法,文献[6]把由赵森烽与赵克勤在文献[4]中提出的“联系概率”称为“赵森烽-克勤概率”,把随机事件成对存在定理称为“赵森烽-克勤存在定理”,把随机事件表现定理称为“赵森烽-克勤表现定理”,把联系概率意义下的概率补数定理称为“赵森烽-克勤补数定理”。
从概率论的历史看,以频率稳定值作为概率的理论值是概率的一个重要来源[7],与此相对应的随机试验称为频率型随机试验,“掷硬币”和“掷骰子”是2种典型的频率型随机试验[8]。人们会问:对于“掷硬币”和“掷骰子”这类随机试验,是否也能说明事物的随机性来自事物与事物的联系?是否也可以导出“赵森烽-克勤概率”?本文对此作出回答,并给出随机事件的“转化定理”和“大概率原理”,探讨它们与“小概率原理”的关系;借助“掷骰子”试验导出同异反联系概率(同异反赵森烽-克勤概率)和多元联系概率(多元赵森烽-克勤概率)的定义,据此说明基于频率的联系概率(赵森烽-克勤概率)与古典概型、几何概型的联系概率(赵森烽-克勤概率)具有同样的形式和性质,可统称为“赵森烽-克勤概率”。
1 2种不同的频率型随机试验 1.1 经典的掷硬币试验掷硬币试验是一种典型的频率型随机试验。历史上有不少学者做过掷硬币的随机试验[9](如表 1)。
| 实验者 | 投掷次数 | 正面朝上的次数 | 频率 |
| 德摩根 | 2 048 | 1 061 | 0.518 1 |
| 布丰 | 4 040 | 2 048 | 0.506 9 |
| 费勒 | 10 000 | 4 979 | 0.497 9 |
| 皮尔逊 | 24 000 | 12 012 | 0.500 5 |
| 罗曼诺夫斯基 | 80 640 | 40 173 | 0.498 2 |
学者们根据试验结果得出结论:随着投掷硬币次数增多,硬币正面朝上的频率稳定地在0.5左右摆动,这个0.5可以作为事件A (“硬币正面朝上”)的概率,本文把这种依据频率稳定性得到的概率称为频率型概率。
概率论历史上的掷硬币试验和根据试验得出的结论,以及与之相对应的频率型概率的形成,应该说无可非议。
1.2 掷硬币的赵森烽-克勤试验现在观察一种新的掷硬币随机试验:与传统掷硬币随机试验所不同的是,先掷一种两面都是“正面”的硬币,且不计硬币的厚度,并记A为“硬币正面朝上”;显然,这时的事件A是一个必然事件,无随机性可言;接下来,把这枚硬币变成同时有“正面”和“反面”的硬币,这时的事件A因具有随机性而成为一个随机事件。
由上面的试验看出:使事件A具有随机性而成为一个随机事件的客观原因是所掷的硬币同时存在“正面”和“反面”(先掷两面都是“反面”的硬币,再把这枚硬币变成有“正面”和“反面”的硬币也能得出同样的结论)。也就是说,硬币“正面”和硬币“反面”的客观存在,才使得掷一枚硬币的结果A(或事件A为“硬币反面朝上”)成为一个随机事件。进而言之,对于一个同时存在“正面”和“反面”的硬币来说,随机事件A与随机事件A成对存在,符合文献[4]中给出的“赵森烽-克勤存在定理”,并在此基础上再作随机表现。
1.3 经典的掷骰子试验掷骰子试验是另一种典型的频率型随机试验。通常在随机试验中用的骰子,是一个有上、下、左、右、前、后6个面的均质正立方体,每个面上依次刻有“1、2、3、4、5、6”6个数,任意抛掷一次,结果是随机地有一个面朝上,当抛掷次数足够多时,每个面朝上的频率将稳定地在1/6左右摆动,这个1/6就称为掷骰子出现某个点数的频率型概率,也简称概率。
1.4 掷骰子的赵森烽-克勤试验不难想见,可以用类似于1.2节中说的方法做一种新的掷骰子试验:先考虑一种6个面都是刻着相同数字(例如“2”)的骰子,这时,任意抛掷这个骰子,事件A为“2朝上”是一个必然事件,无随机性可言;接下来,把这个骰子的6个面依次刻上“1、2、3、4、5、6”,则事件A为“2朝上”就变为一个随机事件,说明事件A的随机性是不同事物(刻有“1、2、3、4、5、6”不同数字的面)相互关系的一个属性,随机事件A为“2朝上”与A为“除2以外的数朝上”成对存在,符合“赵森烽-克勤存在定理”,在此基础上再作随机表现。
需说明的是:为从形式上明确与经典的掷硬币随机试验与掷骰子随机试验相区别,这里称新给出的掷硬币与掷骰子随机试验为“赵森烽-克勤掷硬币与掷骰子随机试验”,并统一简称为“赵森烽-克勤随机试验”。连同文献[4]给出的新的“随机摸球试验”和文献[6]给出的新的“随机投针试验”,统称其为“赵森烽-克勤系列随机试验”。
2 基于频率的赵森烽-克勤概率 2.1 频率型概率1936年奥地利数学家冯·米西斯(R.Von Mises, 1883—1953)最早给出频率型概率定义[9]。现有文献给出的频率型概率定义如下。
定义1 在相同的一组条件S下,重复做n次试验,记nA为n次试验中事件A出现的频数,当试验的次数n很大时,如果事件A出现的频率nA/n总是在某一数值p附近摆动,而且在通常情况下随着试验次数n的增大,这种摆动的幅度越来越小,则称数值p为事件A的概率,记作P(A)=p。
基于频率的概率定义建立在试验和观察之上,克服了基本事件等可能要求的局限,具有重要的实际意义。当一个事件的概率不便求得时,可以取n较大时的频率作为这个事件概率的近似值。
2.2 基于频率的赵森烽-克勤概率 2.2.1 原理第1节中给出的赵森烽-克勤随机试验以及文献[4, 6]中给出的赵森烽-克勤系列随机试验表明:在随机试验E中,给定一个事件A,若存在伴随事件A,且A与A互不相容,则事件A与A各自为随机事件。因此,当需要定量描述A与A其中之一的随机性时,必须同时定量描述事件A与伴随事件A的随机性,并把描述结果组成一个相互联系的数学表达式,以刻划它们之间的关系。
以上原理为基于频率的赵森烽-克勤概率原理,以下简称原理。
2.2.2 定义根据上述原理和仿照定义1,给出基于频率的赵森烽-克勤概率定义如下。
定义2 在相同的一组条件S下,重复做n次试验,记nA为n次试验中事件A出现的频数,nA为n次试验中事件A(A的伴随事件)出现的频数;nA+ nA=n;当试验的次数n很大时,如果事件A出现的频率nA/n总是在某一数值p附近摆动,A出现的频率nA /n总是在某一数值q附近摆动,而且在通常情况下随着试验次数n的增大,这2种摆动的幅度越来越小,则称数值p为事件A的概率,记作P(A)=p;q为事件A的概率,记作P(A)=q,p+q=1,称
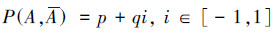 |
(1) |
为以A为主事件,A为A的伴随事件的赵森烽-克勤概率,或记为
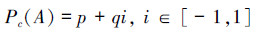 |
(2) |
根据文献[6]给出的赵森烽-克勤补数定理,还可以给出基于频率的赵森烽-克勤概率的另一个定义如下。
定义3 如果P(A)=p是事件A的一个频率型概率,事件A与事件A是互不相容的对立事件,则有事件A的基于频率的赵森烽-克勤概率Pc(A):
 |
(3) |
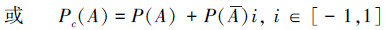 |
(4) |
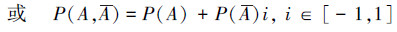 |
(5) |
定义2与定义3从不同角度阐述了基于频率的赵森烽-克勤概率,因而等价。定义2较为严格地叙述了基于频率的赵森烽-克勤概率的含义;定义3的实际意义是,当事件A的频率型概率P(A)已知时,可以直接根据P(A)写出事件A的赵森烽-克勤概率。
事实上,注意到定义2中P(A)=p,P(A)=q,式(5)即成为式(2)。
从定义2和定义3还可以看出,基于事件A频率的赵森烽-克勤概率与基于古典概型和几何概型的赵森烽-克勤概率具有相同的数学形式,且具有相同的性质(证明从略,可参见文献[4, 6])。
3 随机事件的转化定理 3.1 随机事件的转化定义4 设在随机试验E中,事件A与事件A客观存在,但表现为一对互不相容的对立事件,则称试验结果从A到第一次出现A(或从A到第一次出现A)为随机事件的转化。
3.2 转化定理“掷硬币”和“掷骰子”这类频率型随机试验的一个特点是试验次数n可以足够多,甚至无穷。对于这类次数可以足够多的随机试验,有以下定理。
定理1(随机事件转化定理的准备定理) 设事件A与事件A在随机试验E中客观存在,但表现为一对互不相容的对立事件,则在相同的一组条件S下重复做n次试验,当试验次数n足够大时,必然出现事件A和事件A。
证明 由于在随机试验E中,事件A与事件A是一对互不相容事件,根据随机事件的赵森烽-克勤存在定理可知事件A与事件A客观存在;又根据随机事件的赵森烽-克勤表现定理知,事件A和事件A在随机试验E中都有可能出现,当试验次数n足够大时,事件A和事件A必然出现。证毕。
定理2(随机事件转化定理) 在试验次数n足够大(n→∞)的一个频率型随机试验E中,如果在第K(K≥1, K∈n)次试验中第一次出现事件A,则必然在K+m(m≥1, K+m∈n)次试验中出现事件A。
证明根据定理1即得证。
为了方便地识别和记忆上述随机事件转化定理,称其为“赵森烽-克勤转化定理”,简称“转化定理”。“转化定理”在研究一些随机事件转化问题中有重要意义。
3.3 与小概率原理的关系“小概率原理”是经典概率统计中的一个重要原理,它是指如果一个事件发生的概率很小的话,那么它在一次试验中几乎不可能发生。但人们在陈述这个“小概率原理”时,会同时说明,概率很小的事件在多次重复试验中几乎会必然发生[7-9]。显而易见,这个说明其实就是前面给出的“赵森烽-克勤转化定理”所陈述的内容,从这个意义上说,这里给出的随机事件转化定理与“小概率原理”有异曲同工之意。
但重要的是:“赵森烽-克勤转化定理”是基于赵克勤集对分析联系数的一个定理,根据文献[4, 6]中给出的“赵森烽-克勤概率”定义和集对分析不确定性系统理论[1-3, 10],经典概率统计学中P(A)≤0.05或P(A)≤0.01这种“小概率”可以联系数化,例如P(A)≤0.01联系数化为Pc(A)=0.01+0.99i,从而表明,不仅仅是当试验次数足够多时小概率事件A会必然发生,例如Pc(A)=0.01+0.99i在直观上表明,小概率事件A(P(A)=0.01)几乎在100次随机试验中可能会发生1次。而且还从数学形式上直观表明当不确定因素(承载体为赵森烽-克勤概率Pc(A)=0.01+0.99i中的i)转化为有利于小概率事件A发生(赵森烽-克勤概率中的i=1时有Pc(A)=0.01+0.99i=1)时,此小概率事件A就将发生。指出和理解这一点具有重要的现实意义。因为“小概率原理”给人的印象性知识是:某小概率事件不大可能在一次试验中发生;但根据集对分析理论和“赵森烽-克勤概率”定义,如果在某次随机试验中,不确定性因素恰好全部转化为有利于小概率事件A发生,则小概率事件A就有可能在这一次试验中发生。前者侧重对A在随机试验过程宏观层面上的数量规律负责,而后者不仅对A在随机试验宏观层面上的数量规律负责,还要对A在每一次随机试验微观层面上的系统规律负责。为此需要对每次随机试验所涉及到的不确定因素(诸如观测者的因素、仪器仪表因素、观测对象自身因素、观测对象与其他事物的关联(时空关联、物理关联、化学关联等)因素、环境与温度因素、试验观察以及记录方法因素等,这些因素构成一个不确定性系统)展开系统分析,在数学形式上则表现为是对i展开系统分析。显而易见,小概率联系数化后得到的这种“赵森烽-克勤概率”既需要有“确定性的数学计算”,又需要有“不确定性的系统分析”。这种“确定性计算加上不确定性分析”的集对分析方法[11],是对“小概率事件”是否会在一次试验中出现作出的客观回答。这种回答在理论和实践两方面都有重要意义,因为在现实工作和生活中,不少“小概率事件”的发生会给人们带来灾难性的后果,例如航天飞机爆炸,大地震,山体滑坡,核泄漏,列车追尾相撞,高速行驶的汽车遭受不明物体的袭击,桥梁突然断裂等,为了防范这种灾难性“小概率事件”的发生,分析的侧重点显然不仅仅是发生的可能性是多少这个数字上,而是在各种不确定性因素的系统分析上,特别是其中的物理成因分析,从而采取有针对性的防范措施,杜绝人为的责任事故。对于不可抗拒的自然灾害这类“小概率事件”,则尽最大努力减少其损失。当然,对于“购彩票中大奖”这类小概率事件,既不需要防范,也没有必要进行系统分析。由此也看出,如果把所有的小概率事件作为一个集合,则从经济学的角度可以把这个集合中的元素分成2个有不同经济性质的子集合。
4 多元赵森烽-克勤概率 4.1 同异反赵森烽-克勤概率由前述知,在掷硬币的随机试验中,人们常常把硬币的厚度忽略不计,这样就只需考虑硬币“正面朝上”还是“正面不朝上”2件事。但实际掷的硬币都有厚度。试验还告诉人们,如果试验用的硬币越厚(如把多枚硬币粘在一起的“硬币组”),抛掷中也有可能出现硬币侧立的情况(见表 2).
| 硬币(角币) | 抛掷次数 | 正面朝上A | 反面朝上A1 | 侧立A2 |
| 1枚组 | 110 | 48 | 62 | 0 |
| 2枚组 | 110 | 52 | 58 | 0 |
| 3枚组 | 110 | 38 | 68 | 4 |
| 4枚组 | 110 | 48 | 47 | 15 |
| 5枚组 | 110 | 29 | 38 | 43 |
| 6枚组 | 110 | 31 | 31 | 48 |
| 7枚组 | 110 | 15 | 21 | 64 |
| 8枚组 | 110 | 13 | 22 | 75 |
这时的A(“硬币正面不朝上”)就成为一个复合事件,A由A 1(“硬币反面朝上”)和A2(“硬币侧立”)2个事件复合而成。相应的“赵森烽-克勤概率”P(A, A)=P(A)+P(A)i中的P(A)就要展开成P(A1)和P(A2)来表示,由此得到关于A、A1、A2的“赵森烽-克勤概率”为
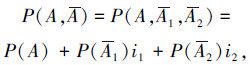 |
(6) |
按照集对分析同异反思想和赵森烽-克勤概率知识,当把事件A定义为主事件时,实际出现的“硬币正面朝上”事件A定义为“硬币正面朝上”事件A的“同事件”,实际出现的“硬币反面朝上”事件A1定义为A的“反事件”,实际出现的“硬币侧立”事件A2定义为介于事件A与A1之间的异事件,于是式(6)就称为基于事件A的同异反概率,为此给出“同异反赵森烽-克勤概率”定义如下。
定义5 在一个频率型随机试验E中,如果在一对互不相容的对立事件A与C(C=A)之间,还存在既异于A,也异于C,且与A和C都互不相容的中介事件B,则称中介事件B为与A和C皆异的异事件,简称异事件,并把A作为主事件时的联系概率
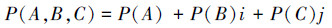 |
(7) |
称为“同异反赵森烽-克勤概率”。
式(7)中的j为“反事件”C概率P(C)的系数或标识,作为系数时通常取j=-1,不计值时,仅作为“反事件”C概率P(C)的标识。
按文献[1]中给出的“赵森烽-克勤概率”记法,以A为主事件,B、C为伴随事件时的“赵森烽-克勤概率”可写成:
 |
(8) |
根据集对分析理论,式(7)、(8)中的j=-1, i∈[-1, 1],但在随机事件转化现象和转化机理的研究中,i的取值范围需要扩展到[-∞,1],这一点将在后续研究中给予进一步的说明。
此外,根据集对分析同异反系统理论,定义5给定的同异反联系概率是一个同异反系统,该系统中的“同、异、反”可以在一定条件下相互转化[12],对此需要作深入研究。
4.2 多元赵森烽-克勤概率定义如果说前面考虑硬币厚度的随机试验导出多元赵森烽-克勤概率尚有牵强之意的话,那么由“掷骰子”试验来导出多元赵森烽-克勤概率就显得自然。因为从第1节中看到,“掷骰子”这类频率型随机试验结果要比“掷硬币”随机试验结果多,原因是骰子有6个面,因而在随机试验中有6个需要关注的基本事件,如果把“1朝上”设为“主事件A”,把“6朝上”设为“反事件C”,则其他的“2、3、4、5点朝上”就是介于A与C之间的“异事件”,依次记事件B1“2朝上”、事件B2“3朝上”、B3“4朝上”、事件B4“5朝上”,则仿照上一节的思路得到有关基于“主事件A”和“反事件C”的“同异反赵森烽-克勤概率”如下:
 |
(9) |
或者
 |
(10) |
式(9)、(10)既可以看作是一种“同异反赵森烽-克勤概率”(式(8))的展开式,也可以看作是一种用多元联系数表示的“赵森烽-克勤概率”。为此有如下的“多元赵森烽-克勤概率”定义。
定义6 在一个频率型随机试验E中,如果在一对互不相容的对立事件A与C(C=A)之间,还存在既异于A,也异于C的n(n≥1)个两两互不相容的中介事件Bk(k=1, 2, …, n),则称把A作为主事件(Bk、C为伴随事件)时的“赵森烽-克勤概率”
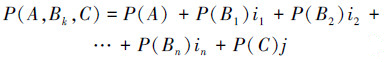 |
(11) |
称为“多元赵森烽-克勤概率”。
“多元赵森烽-克勤概率”中的B1, B2, …, Bn依次称为主事件A的第1伴随事件或第2关注事件、第2伴随事件或第3关注事件……第n-1伴随事件或第n关注事件,把C事件(主事件A的反事件)称为第n伴随事件或第n+1关注事件。相应的概率称为第1伴随事件或第2关注事件概率、第2伴随事件或第3关注事件概率……第n伴随事件或第n+1关注事件概率,它们同时是主事件“赵森烽-克勤概率”的组成部份,称为主事件赵森烽-克勤概率的“分概率”。而且一般地说,“多元赵森烽-克勤概率”中最后一个关注事件概率的系数j=-1,而其他“分概率”的系数i1, i2, …, in一般在[-1, 1]区间,视不同情况取值(i的取值范围是否需要扩展到[-∞,1]待另行研究)。
此外,“多元赵森烽-克勤概率”也可以从多元联系数的角度定义。
定义7 称用多元联系数表示的“赵森烽-克勤概率”为“多元赵森烽-克勤概率”。
4.3 多元赵森烽-克勤概率与全概率公式无论是4.1节给出的同异反事件定义,还是4.2节中对异事件(中介事件)的展开,都约定了所论述的事件是两两互不相容事件,按经典概率论,若A1, A2, …, An是一组两两互不相容事件,并且有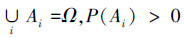
 |
(12) |
称式(12)为全概率公式,事件组A1, A2, …, An称为完备事件组。
显而易见,定义6给出的“多元赵森烽-克勤概率”其实是对完备事件组中每一事件发生概率的一种有序刻划(以主事件为第一关注事件,伴随事件依次为第二、三…关注事件),这种有序刻划与式(12)所示的全概率公式是从不同角度刻划完备事件组中每一事件发生概率相互关系的不同数学手段,两者之间的内在联系需要进一步研究。
另外,是否还可以直观地称“多元赵森烽-克勤概率”为“菜单概率”?因为需要时可以把主事件A以外的所有伴随事件都“压缩”到A中,这时的A就是一个“事件压缩包”,必要时又可以打开这个“事件压缩包”。这从一个侧面说明事件A的伴随事件A可能比事件A复杂得多,需要作进一步研究。此外,当多元联系概率的元数n→∞所对应的频率型随机试验实验,也需要进一步研究。
4.4 大概率原理“多元赵森烽-克勤概率”不仅具有“赵森烽-克勤概率”的一般性质,如系统性、可正可负性,还具有有序性、结构性,据此可以方便地看出一个随机试验多种不同结果以及不同结果发生的概率,比较不同结果发生概率的大小,容易从全局的角度对最可能出现结果进行判定。
仍以掷骰子试验为例,如果设事件A“1朝上”为“主事件”,则事件A“不是1的数字朝上”是A的伴随事件,这时以A为“主事件”的“赵森烽-克勤概率”为
 |
(13) |
由于A是一个复合事件,可以分解成若干个事件,设把它分解为事件B1“2朝上”和事件B2“3、4、5、6朝上”,B1∈A,B2∈A,则由式(13)得
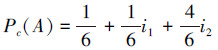 |
(14) |
由此可见,在以上设定条件下随机地掷骰子,最可能出现事件B2,因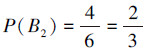
据此给出以下的定义8。
定义8 在一个存在t1, t2, …, tn共n≥2个不同试验结果(事件)的随机试验E中,如果在第K(K≥1)次试验中出现非最大概率事件,则在K+s(s≥1)次试验中必然出现最大概率事件, 称此陈述为基于赵克勤集对分析理论的“大概率原理”,简称“大概率原理”。
不难看出:“大概率原理”与“小概率原理”是一组“成对原理”。还需要进一步研究“大概率原理”与“小概率原理”的关系及其在随机事件转化中的应用。此外需进一步研究“多元赵森烽-克勤概率”在人工智能中的应用[13-16]。
5 结束语本文根据集对分析不确定性系统理论和关于经典概率需要联系数化的观点,借助不同于经典“掷硬币”和“掷骰子”频率型随机试验的“赵森烽-克勤随机试验”,介绍了经典的频率型概率联系数化原理和基于频率的“赵森烽-克勤概率”的计算方法,说明了基于频率的“赵森烽-克勤概率”与基于古典概型和几何概型的“赵森烽-克勤概率”具有同样的数学形式和数学性质,在此基础上给出了随机事件的“转化定理”、“多元赵森烽-克勤概率”以及“大概率原理”,粗略地讨论了这些新概念与经典概率统计中的“小概率原理”的关系,说明了“赵森烽-克勤概率”能客观地刻划随机试验结果,具有丰富的系统信息。本文的工作连同作者在前期文献中给出的“赵森烽-克勤存在定理”、“赵森烽-克勤表现定理”和“赵森烽-克勤补数定理”,为“赵森烽-克勤概率”的创建和实际应用提供了一定基础;但由于概率的概念由来已久且内容极为丰富,并已渗透到许多领域,要说明“赵森烽-克勤概率”在人工智能中的应用,还需要在后续工作中继续研究其与经典概率的关系。
| [1] | 赵克勤. 集对分析及其初步应用[M]. 杭州: 浙江科技出版社, 2000 : 44 -64. |
| [2] | 赵克勤. 集对分析的不确定性系统理论在AI中的应用[J]. 智能系统学报 , 2006, 1 (2) : 16-25 ZHAO Keqin. The application of uncertainty systems theory of set pair analysis (SPA) in the artificial intelligence[J]. CAAI Transactions on Intelligent Systems , 2006, 1 (2) : 16-25 |
| [3] | 赵克勤. 二元联系数A+Bi的理论基础与基本算法及在人工智能中的应用[J]. 智能系统学报 , 2008, 3 (6) : 476-486 ZHAO Keqin. The theoretical basis and basic algorithm of binary connection A+Bi and its application in AI[J]. CAAI Transactions on Intelligent Systems , 2008, 3 (6) : 476-486 |
| [4] | 赵森烽, 赵克勤. 概率联系数化的原理与联系概率在概率推理中的应用[J]. 智能系统学报 , 2012, 7 (3) : 200-205 ZHAO Senfeng, ZHAO Keqin. The principle of the probability of connection number and application in probabilistic reasoning[J]. CAAI Transactions on Intelligent Systems , 2012, 7 (3) : 200-205 |
| [5] | 赵森烽, 赵克勤. 联系概率的由来及其在风险决策中的应用[J]. 数学的实践与认识 , 2013, 43 (4) : 165-171 ZHAO Senfeng, ZHAO Keqin. The contact probability in risk decision-making medium application[J]. Mathematics in Practice and Theory , 2013, 43 (4) : 165-171 |
| [6] | 赵森烽, 赵克勤. 几何型概率的联系概率(复概率)和概率的补数定理[J]. 智能系统学报 , 2013, 8 (1) : 11-15 ZHAO Senfeng, ZHAO Keqin. Contact probability (complex probability) of geometry probability and probability of the complement number theorem[J]. CAAI Transactions on Intelligent Systems , 2013, 8 (1) : 11-15 |
| [7] | 茆诗松, 程依明, 濮晓龙. 概率论与数理统计教程[M]. 北京: 高等教育出版社, 2012 : 15 -17. |
| [8] | 王梓坤. 概率论基础及其应用[M]. 北京: 科学出版社, 1979 : 218 -219. |
| [9] | 赵秀恒, 米立民. 概率论与数理统计[M]. 北京: 高等教育出版社, 2008 : 1 -28. |
| [10] | 赵克勤. 基于集对分析的不确定性多属性决策模型与算法[J]. 智能系统学报 , 2010, 5 (1) : 41-50 ZHAO Keqin. Decision making algorithm based on set pair analysis for use when facing multiple uncertain attributes[J]. CAAI Transactions on Intelligent Systems , 2010, 5 (1) : 41-50 |
| [11] | 刘秀梅, 赵克勤. 基于联系数的不确定空情意图识别[J]. 智能系统学报 , 2012, 7 (5) : 450-456 LIU Xiumei, ZHAO Keqin. Inference method on intention with uncertain aerial information based on the connection number[J]. CAAI Transactions on Intelligent Systems , 2012, 7 (5) : 450-456 |
| [12] | 赵克勤. 集对分析的同异反系统理论及其在人工智能中的应用[J]. 智能系统学报 , 2007, 2 (5) : 476-486 ZHAO Keqin. The application of SPA based identical discrepancy contrary system theory in artificial intelligence research[J]. CAAI Transactions on Intelligent Systems , 2007, 2 (5) : 476-486 |
| [13] | 闫书亚, 殷明浩, 谷文祥, 等. 概率规划的研究与发展[J]. 智能系统学报 , 2008, 3 (1) : 9-22 YAN Shuya, YIN Minghao, GU Wenxiang, et al. Research and advances in probabilistic planning[J]. CAAI Transactions on Intelligent Systems , 2008, 3 (1) : 9-22 |
| [14] | 李德毅. 网络时代人工智能研究与发展[J]. 智能系统学报 , 2009, 4 (1) : 1-6 LI Deyi. AI research and development in the network age[J]. CAAI Transactions on Intelligent Systems , 2009, 4 (1) : 1-6 |
| [15] | 蔡自兴, 徐光佑. 人工智能及其应用[M]. 北京: 清华大学出版社, 2010 : 114 -116. |
| [16] | 谢安, 李冬红. 概率论与数理统计[M]. 北京: 清华大学出版社, 2012 : 7 -15. |



