2. 中国商用飞机有限责任公司 上海飞机设计研究院 综合航电设计研究部, 上海 201210
2. Integrated Avionics System Department, Shanghai Aircraft Design and Research Institute, Commercial Aircraft Corporation of China Ltd, Shanghai 201210, China
风切变广泛存在于机场环境, 已对民用飞机的起飞/着陆安全构成了巨大威胁, 是造成众多飞行事故的主要原因之一。由于大型民用飞机机体庞大、质量大, 因此极易受到风切变的影响而产生飞行轨迹的变化。而大型飞机状态响应较为缓慢, 在恶劣的风切变下极易发生操纵不当而引发恶性事故。
近年来, 航空技术发展突飞猛进, 特别是我国的大飞机已列为国家重大专项。国内外许多先进机场也增加了应对低空风切变的相应设备, 然而恶劣气象环境在起飞/着陆阶段对飞机的威胁却始终存在。据不完全统计, 过去20年间与风切变有关的飞行事故都发生在起飞和着陆阶段[1], 起飞/着陆阶段中复杂大气扰动造成的飞行事故日益引起航空界的密切关注, 已经成为一个亟待解决的关键难题[2]。
风切变对航空活动安全危害较大, 各国对风切变的相关研究投入了巨大的人力、物力和财力, 进行风切变下民用飞机的综合研究与试验。我国目前正在开展的大型飞机重大科技专项也把风切变列为关键技术难题之一。文献[1]研究了各种严重危害飞行安全的微下冲气流的有关问题。文献[2]利用机载低空风切变探测与回避技术规避风切变。文献[3]采用非线性动态逆法实现飞行控制系统的反馈解耦, 并将其最终用于风切变下的飞行控制。对于复杂风切变条件下大型民用飞机的起飞问题, 现在的仿真手段仍存在设计复杂、可视化不强等问题。
本文结合文献[4-5], 将虚拟实景应用于复杂风切变下大型民用飞机起飞仿真, 设计三维可视化仿真平台, 实现风切变下飞机的起飞轨迹模拟, 可对复杂风切变对大型民用飞机的影响进行有效地量化分析。通过某型民用飞机的仿真以验证该建模方法的有效性。
1 复杂风切变建模 1.1 微下击暴流建模通过在地面上方和下方分别布置强度相同的主涡环和镜像涡环, 根据涡环周围的流体模型, 可建立三维微下击暴流模型[6],如图 1所示。

|
| 图 1 涡环法建模 Fig. 1 Microburst model based on vortex method |
设置3个坐标系, 地面坐标系FO(OXYZ)、原像坐标系FP(OPXPYPZP)和镜像涡环坐标系FI(OIXIYIZI)。M为参考质点, 其坐标为(XM, YM, ZM)。
假设涡环面与地面平行, 由此涡环附近的气流方程可表示为
 |
式中: Γ为涡环强度, r1为M点距涡环最近点的距离, r2为M点距涡环最远点的距离,F1(K)和E1(K)为椭圆积分函数。在计算F1(K)-E1(K)时, 若0≤k2≤1, 可用式(1)来逼近。
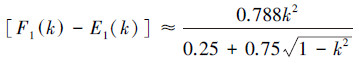 |
(1) |
式中:k=|(r2-r1)/(r1+r2)|。由流线方程可得到涡环径向和轴向诱导速度, 空间内受到涡环影响的任意点M, 其气流方程可表示为
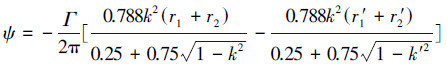 |
式中:r1′、r2′、k′分别为与主涡环对应的镜像涡环的参数。由此, 一对涡环对空间内任意点M的诱导速度可表示为
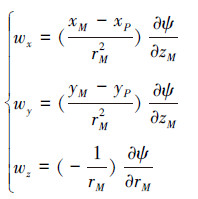 |
图 2给出了微下击暴流与大气紊流的仿真结果, 风场模型的基本参数为主涡环高度500 m、主涡环半径500 m、涡核半径r=500 m、中心轴处风场垂直速度10 m/s。
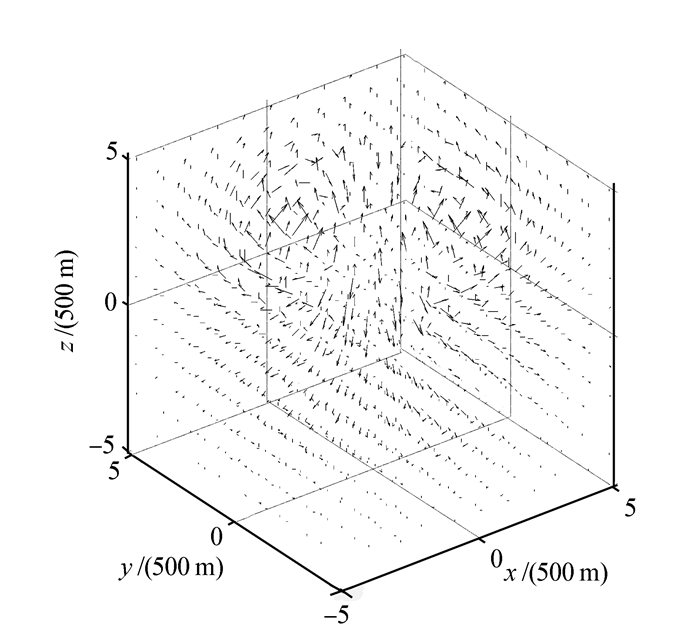
|
| 图 2 微下击暴流风场 Fig. 2 The simulation result of a typical microburst |
影响大型民用飞机运动的不仅有紊流速度本身u、v、w, 还有紊流速度的梯度, 特别是以下3个梯度: wx=∂wg/∂x, 即铅垂风速度沿飞行方向的变化; wy=∂wg/∂y, 即铅垂风速度沿翼展方向的变化; vx=∂vg/∂x, 即侧向风速度沿飞行方向的变化。根据Dryden双侧模型, 大气紊流速度和梯度的空间频谱表达式为[4]
 |
式中: Ω表示沿x轴的空间频率, 对于以速度V飞行的大型民用飞机, 它与时间频率ω的关系为Ω=ω/V; σu、σv和σw是3个方向的紊流强度,Lu、Lv和Lw是3个方向的紊流尺度, 对于各向同性紊流, 有σu=σv=σw,Lu=2Lv=2Lw; b为机翼展长。根据关系式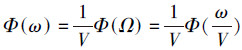
|
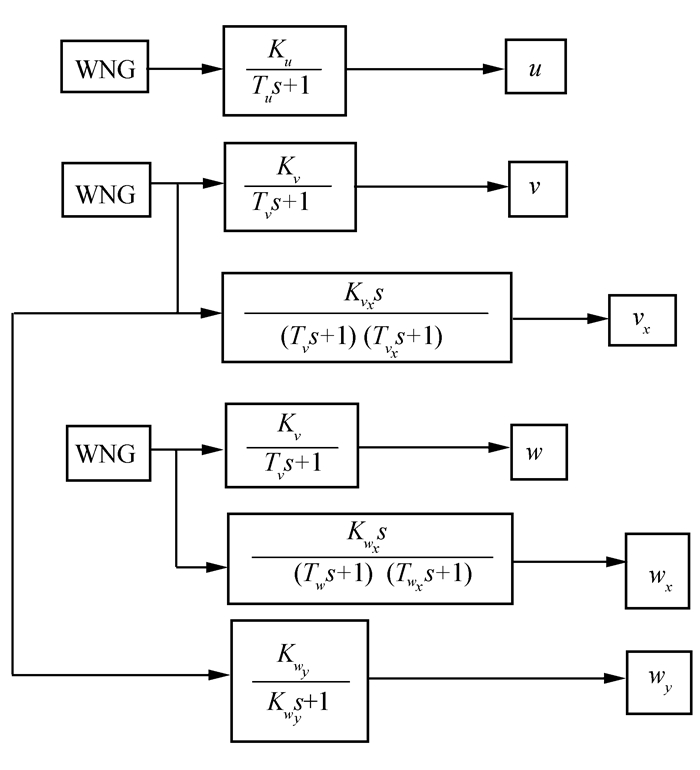
| 图 3 大气紊流生成器的结构 Fig. 3 The structure of the turbulence generator |
|
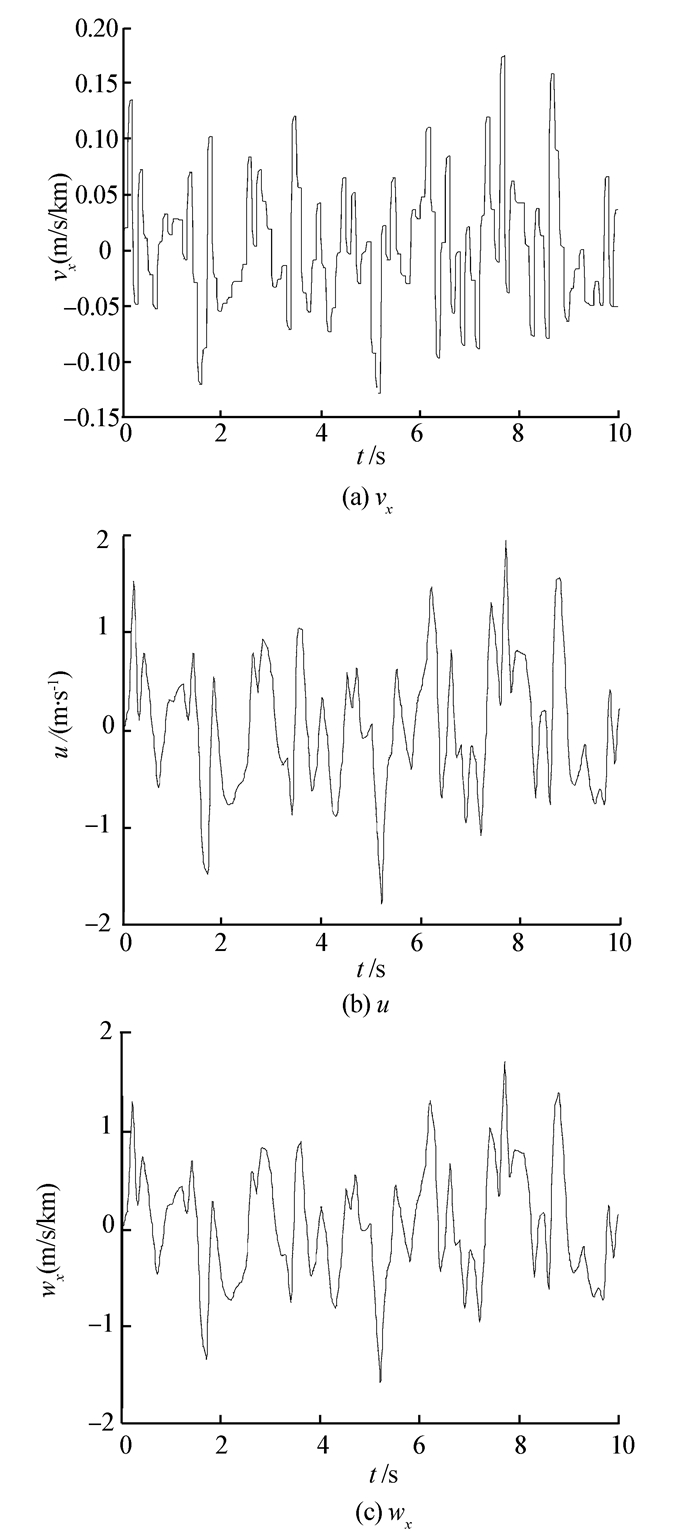
| 图 4 大气紊流生成器生成的紊流序列u、vx、wx片段 Fig. 4 The simulation results of a typical turbulence |
风切变对民用飞机运动的作用就是改变了作用于飞机上的相对气流, 从而改变了气动力。这种附加气动力的变化可通过民用飞机运动状态量的等价改变来表示[5]。
X方向的风速ug的作用相当于降低了前进速度, Y方向的风速vg的效果是引起侧滑角, Z方向的紊流速度wg的效果是引起迎角, 风切变速度梯度∂wg/∂x在气动效果方面相当于俯仰角速度q, 而∂wg/∂y相当于负的滚转角速度, ∂vg/∂y相当于偏航角速度。综合以上因素, 风切变对民用飞机飞行运动的影响可以表示为[7]
 |
式中:V0为未扰动的飞行速度。
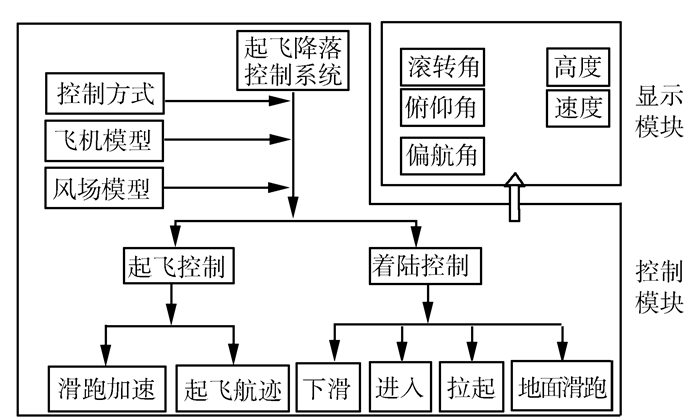
2 基于MATLAB虚拟现实的三维可视化仿真在建立复杂风切变风场模型, 完成复杂风场对民用飞机飞行运动影响研究的基础上, 使用MATLAB中的虚拟现实工具建立三维仿真平台。该虚拟现实工具箱是基于VRML技术的三维仿真工具, 具有较好的可视性与交互性, 通过相应的建模与链接方法, 可以建立不同的虚拟现实环境。需要建立虚拟仿真的动态系统可以用MATLAB语言和Simulink模块进行描述, 并通过虚拟现实工具箱来进行三维虚拟现实的拓展[5]。建立的三维仿真平台包括风场模型、民用飞机模型、飞行控制系统和虚拟现实显示等几个部分[7-8]。三维可视化仿真平台的结构如图 5所示。
|
| 图 5 仿真平台框架示意 Fig. 5 The architecture of simulation platform |
首先通过VRML建立真实世界场景的模型, 并进一步建立虚构的三维世界。建立模型可以使用程序语言或者使用建模工具, 使用建模工具进行大型民用飞机的过程如图 6所示, 主要包括机身轮廓和机翼等部件。在场景中加入跑道、塔台等附属建筑, 并进行相应的贴图, 完成后的场景如图 7所示。
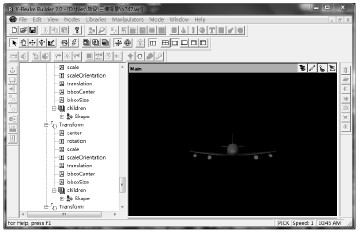
|
| 图 6 VRML工具建立的民用飞机模型 Fig. 6 The civil aircraft model in VRML |
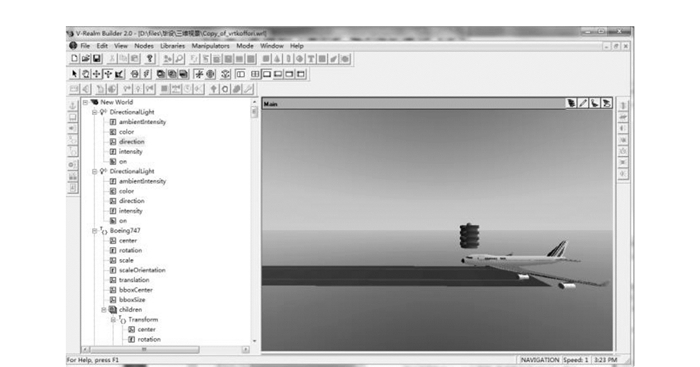
|
| 图 7 VRML建立的三维实景 Fig. 7 3D scene environment in VRML |
在完成虚拟视景的建模工作后, 对民用飞机动力学和飞行控制进行建模。
基于符号控制的新方法, 建立了大型民用飞机飞行控制系统模型。其控制思想是将大型飞机多模态运动分解成有限输入符号, 并构建相应的符号指令集, 指令集中的符号指令可通过有限传输信道发送给处理单元, 随后接收到所传符号指令的飞行器控制单元再将其解码成相应的控制行为指令[9]。符号控制由于其简洁灵活能够有助于快速准确地实现信息的传入传出。图 8为基于状态反馈的大型民用飞机纵向控制系统, 该系统通过反馈飞机的纵向状态, 利用符号控制理论进行控制输入的求解, 控制输入包括油门位置和升降舵位置。图 9为建立的飞行控制系统与三维实景连接的Simulink模块。
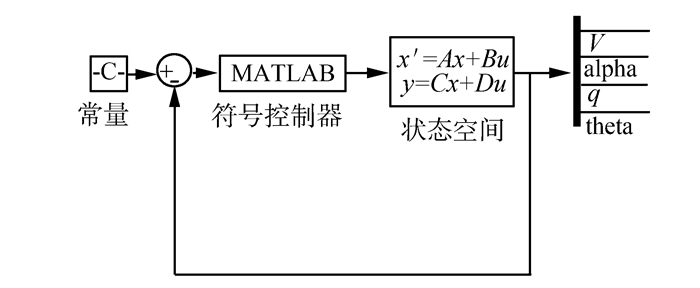
|
| 图 8 基于状态反馈的符号控制结构 Fig. 8 The symbolic control structure based on state feedback |
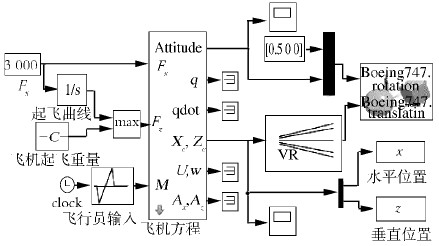
|
| 图 9 起飞航迹的Simulink模块 Fig. 9 The takeoff simulation module in Simulink |
在MATLAB框架内可以通过已有的标准模块将虚拟现实和一个Simulink模型连接起来进行模拟。
在Simulink的编辑窗口内, 双击VRSink模块。在出现的对话框中, 通过点击“browse”按钮选择已建立好的虚拟世界。当载入虚拟世界后, 在对话框右部“VRML tree”的窗口内, 将出现该虚拟世界所包含的结构(如图 10所示)。

|
| 图 10 VRML目录树 Fig. 10 The directory tree in VRML |
在目录树中可以看到已建立的民用飞机模型, 通过按标题左边的“+”标记, 可以展开飞机模型的结构目录树。点击平移(translation)和旋转(rotation), 则选择的区域被标记为虚拟世界的输入信号。不同的选项代表相应的飞机运动, 该运动以地轴坐标系为参考坐标系, 在复杂大气扰动的仿真中需要选择民用飞机的3轴滚转和3个方向的位移运动。
民用飞机的3轴滚转即第1个输入, 是一个具有4个元素的矢量, 其中前3个元素分布代表3个方向的旋转的坐标轴。民用飞机的航迹倾斜角通过关于X轴旋转表达, 围绕Y轴的旋转代表航迹滚转的角度, 而Z轴的旋转代表航迹方位角, 所有的角度都用弧度表示。
民用飞机3个方向的平移即第2个输入, 代表了虚拟视景中飞机的位置。该矢量由3个坐标x、y、z组成, Simulink中相应的输入矢量也必须有3个元素。在仿真实例中, 定义飞机的跑道与x轴平行, y轴代表与跑道垂直的方向, z轴代表飞机的海拔高度。
完成设置后点击“OK”, 在三维虚拟视景中民用飞机的运动状态就由Simulink产生的信号进行控制。
从Simulation菜单中点击Start, 大型民用飞机就开始从跑道的末端进行滑跑过程, 最终飞入空中, 滑跑的过程和空中飞行姿态如图 11和图 12所示。
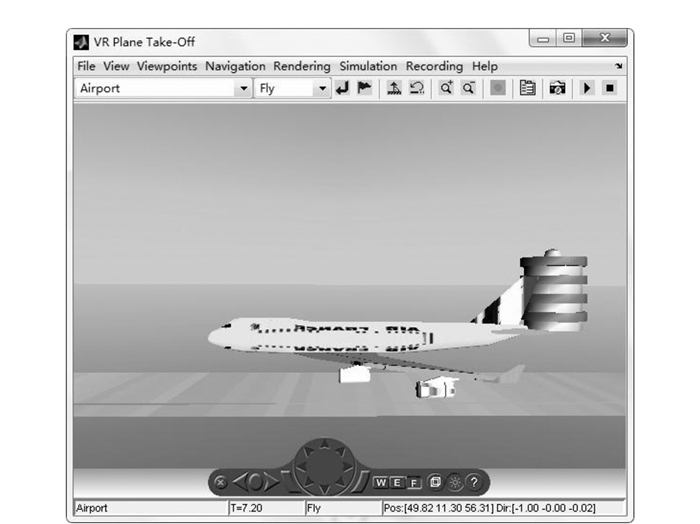
|
| 图 11 大型民用飞机起飞模拟 Fig. 11 Simulation of civil aircraft during takeoff |

|
| 图 12 大型民用飞机空中飞行模拟 Fig. 12 Simulation of civil aircraft during flying |
由于MATLAB的虚拟视景中无法对大型飞机的飞行状态进行实时显示, 在仿真过程中, 可以通过Simulink的基本显示工具对状态变量进行相应的查看, 如图 13所示。图 14给出了起飞后空中飞行阶段飞机迎角等变化量的曲线。
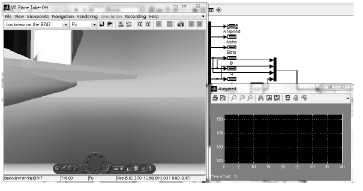
|
| 图 13 飞机空中飞行状态 Fig. 13 Flight states of the civil aircraft |
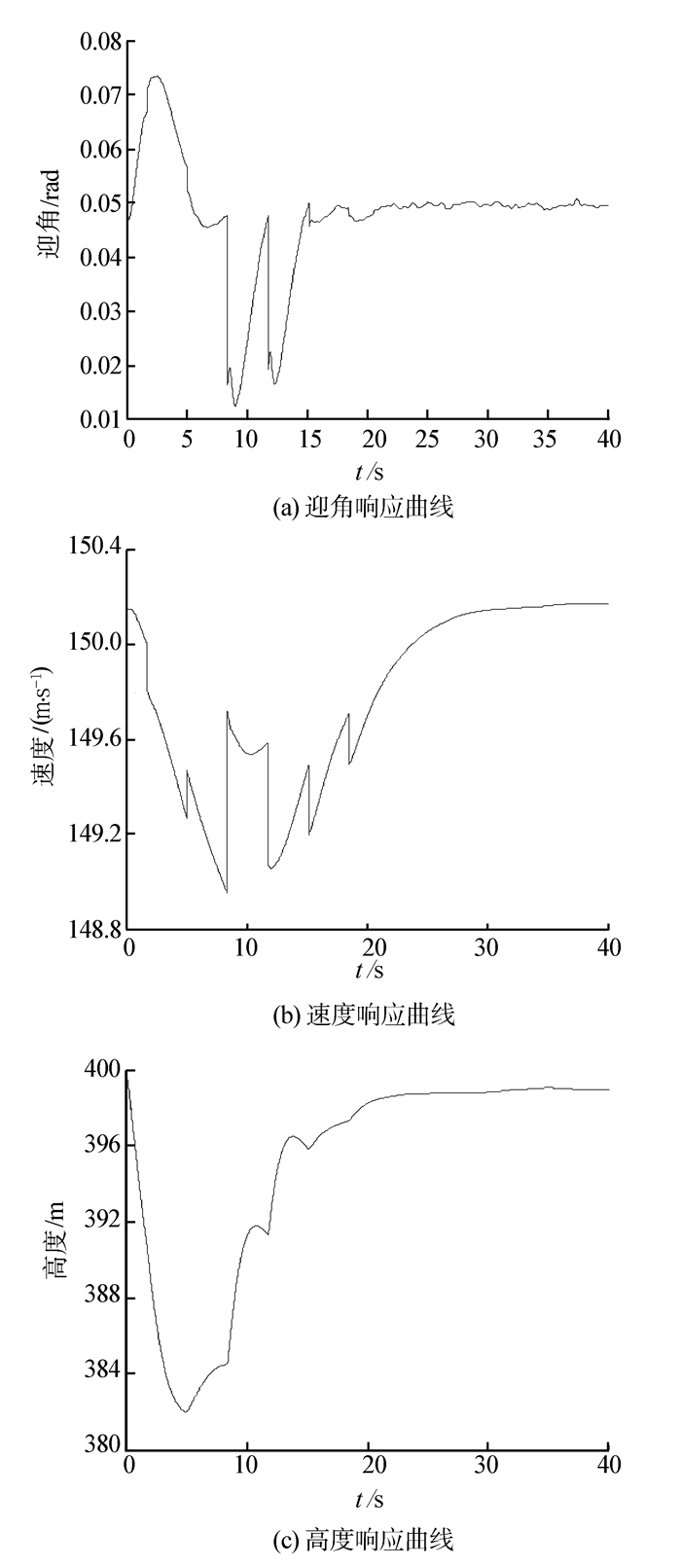
|
| 图 14 飞机空中飞行各状态响应曲线 Fig. 14 Response curves of the civil aircraft |
本文提出了一种复杂风切变下大型民用飞机起飞可视化仿真方案和控制方法, 并设计了一种基于MATLAB Simulink的三维可视化起飞模拟方法及实现流程, 且基于该方法构建了三维可视化仿真平台。
通过系列试验, 验证符号控制方法和平台能很好地满足飞机起飞模拟的要求。从仿真结果可以看出, 符号控制作为一种新方法, 能够有效降低飞行中风切变对大型飞机的干扰。搭建的仿真平台可用于验证风切变下大型民用飞机飞行控制系统性能, 为我国目前正在研发的ARJ21和C919大型民用飞机提供了关键技术支撑。
| [1] | 文传源, 屠巴宁, 高金源. 现代飞行控制[M]. 北京: 北京航空航天大学出版社, 2005 : 1 -303. |
| [2] | 高振兴, 顾宏斌. 用于飞行实时仿真的微下击暴流建模研究[J]. 系统仿真学报 , 2008, 20 (23) : 6524-6528 GAO Zhenxing, GU Hongbin. Research on modeling of microburst for real time flight simulation[J]. Journal of System Simulation , 2008, 20 (23) : 6524-6528 |
| [3] | MARIGO A. Optimal input sets for time minimality in quantized control systems[J]. Math Control Signal System , 2006, 18 (2) : 101-146 DOI:10.1007/s00498-005-0156-5 |
| [4] | 陈坪, 赵涛, 王建培. 无人机穿越变化风场起飞特性仿真研究[J]. 飞行力学 , 2002, 20 (2) : 22-26 CHEN Peng, ZHAO Tao, WANG Jianpei. Study of unmanned aircraft launch process simulation in the variable wind field[J]. Flight Dynamics , 2002, 20 (2) : 22-26 |
| [5] | SMAILI H, LABAN M, DOMINICUS J. New integrated modeling and simulation techniques for tesearch and training applications[C]//Proceedings of AIAA Modeling and Simulation Technologies Conference and Exhibit. San Francisco, USA, 2005: 148-157. |
| [6] | 刘刚, 洪冠新, 金长江. 复杂地形上空超低空风场的工程仿真方法[J]. 北京航空航天大学学报 , 2003, 29 (3) : 193-196 LIU Gang, HONG Guanxin, JIN Changjiang. Engineering simulation method for airfield over complex terrain at minimum altitude[J]. Journal of Beijing University of Aeronautics and Astronautics , 2003, 29 (3) : 193-196 |
| [7] | GUO Tongqing, LU Zhiliang, TANG Di, et al. A CFD/CSD model for aeroelastic calculations of large-scale wind turbines[J]. Science China: Technological Sciences , 2013, 56 (1) : 205-211 DOI:10.1007/s11431-012-5028-x |
| [8] | WANG Yamin, CUI Pingyuan, QIAO Dong. Opportunities search of transfer between interplanetary halo orbits in ephemeris model[J]. Science China: Technological Sciences , 2013, 56 (1) : 188-193 DOI:10.1007/s11431-012-5017-0 |
| [9] | TABUADA P. Symbolic control of linear systems based on symbolic subsystems[J]. IEEE Transactions on Automatic Control , 2006, 51 (6) : 1003-1013 DOI:10.1109/TAC.2006.876946 |



