计算机技术的发展使得三维模型得到了广泛应用,为了有效地利用由此产生的大量三维模型,需要高效的浏览与认知手段。根据成像原理以及Marr创立的视觉计算理论[1],三维模型需要映射到二维视图后,才能被人类浏览和认知。Blanz等[2]论证了人类对物体的认知依赖于视点位置,而使得人类能够最好地认知和理解三维模型的二维视图,被称为该三维模型的最优视图。在三维模型数据集的浏览过程中,应该选用最优视图作为缩略图来展示各个三维模型。人类能够合理地选择视点位置,得到三维模型的最优视图,但是对于大量的三维模型来说,完全由人工选择是不可行的。而且最优视图与人类的感知有关,难以确切地给出最优视图严格的数学定义,因而近年来不同的研究者提出了多种最优视图的定义以及相应方法。
一种是将二维视图的优劣定义为一个三维模型与视图相关的函数,使得该函数取得最大值的视图就是最优视图[3]。有很多方法基于这个定义,包括场景复杂性[4]、几何特征分布[5]、距离直方图的香农熵[6]等直接分析三维模型几何特征的方法,以及最小化对称性[7]、相似性[8],或者最大化视点熵[9]、形状差异[10]等对二维视图投影进行特征分析的方法[11]。但是三维模型种类多样,在这种定义下难以有适用于所有种类三维模型的视图评价函数。这些方法也不考虑在视觉上对模型加以区别,这样就难以保证同类模型具有人类感官上相似的最优视图,因此,这些方法不适用于对三维数据集的高效浏览。
另外一种定义基于如下假设:属于相同类别的三维模型具有相似的特征,这些特征使得属于不同类别的模型能够相互区分,同类模型的最优视图也具有相似性。一个三维模型的最优视图就是能区分该模型与其他类别模型的视图[12],这样可以联系到数据集中的上下文信息以及数据集中所属类别的语义信息,使得语义信息与几何信息建立关联,而这在前一种定义中是被忽视的。这样三维模型的最优视图选择问题就可以划归为评价视图分类能力问题。由此,最优视图随着数据集和分类的不同而变化,这更加适合于三维数据集的高效浏览。
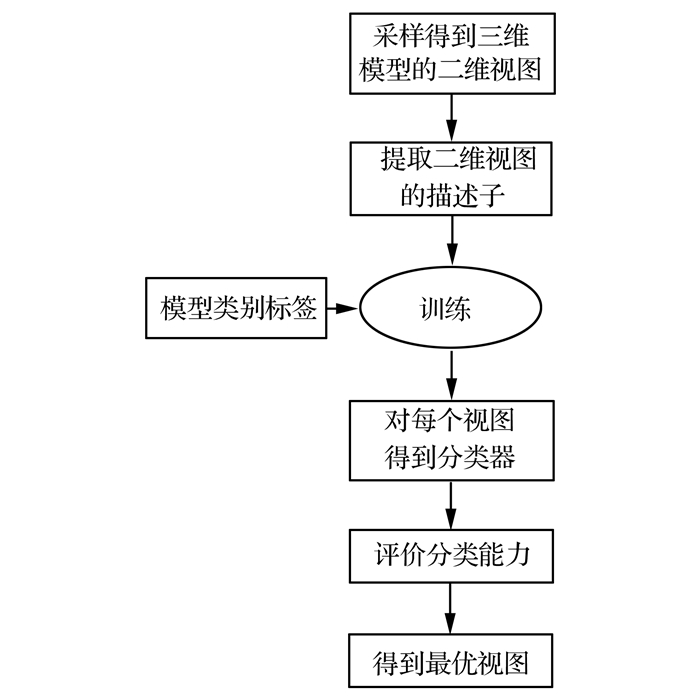
1 最优视图选择方法 1.1 方法概述图 1所示为本文方法的流程。
|
| 图 1 本文算法流程 Fig. 1 The flow chart of our method |
对于一个三维模型数据集来说,其具体流程如下。
1)首先对三维模型数据集进行预处理;
2)采样每个三维模型不同视点下的视图;
3)使用傅里叶描述子(Fourier descriptor, FD)以及Zernike矩描述子(Zernike moment descriptor, ZMD)来描述二维视图的特征,提取三维模型视图在二维形状空间中的几何特征;
4)在训练阶段,针对三维模型的每个视图特征使用随机森林算法训练分类器,并进行交叉验证,得到以该视图特征描述模型时的分类错误率;
5)最后选择使得分类错误率最小的视图作为最优视图。
1.2 三维模型预处理为了后续处理的方便,首先需要对输入的三维模型进行预处理。由于三维模型方向的不确定性,为了减小对二维视图的影响,需要对三维模型进行校正和归一化。尽管已有大量的相关研究,但是大部分方法仅适合人造物体[13],自动寻找任意三维模型合适的竖直方向仍然是很困难的。本文采用简单而快速的主成分分析(principal component analysis, PCA)方法计算得到模型的主轴方向,以此为模型所在坐标系的各个坐标轴方向,从而使得模型处于一致的姿态。最后将模型上的各个顶点到质心的距离进行归一化,得到经过姿态校正以及归一化的三维模型。
此外,如果某些三维模型没有类别标记,那么就需要判断其类别。这个问题在三维模型检索中得到了大量的研究,本文采用Vranic等[14]提出的由186维的深度视图特征、150维的轮廓特征、136维的射线特征组成的混合描述子作为三维模型的特征,使用已有数据集作为训练集进行有监督学习得到分类器。使用该分类器对输入的模型进行分类,可以得到输入模型的类别标记,将其作为数据集对应类别的模型进行后续步骤处理。
1.3 视图特征提取 1.3.1 视图采样本文的特征在二维视图上提取,需要取得三维模型的二维视图,首先是确定视点位置。由于视点可以在三维空间中连续变化,需要对视图采样选取离散化视点,减小样本空间。
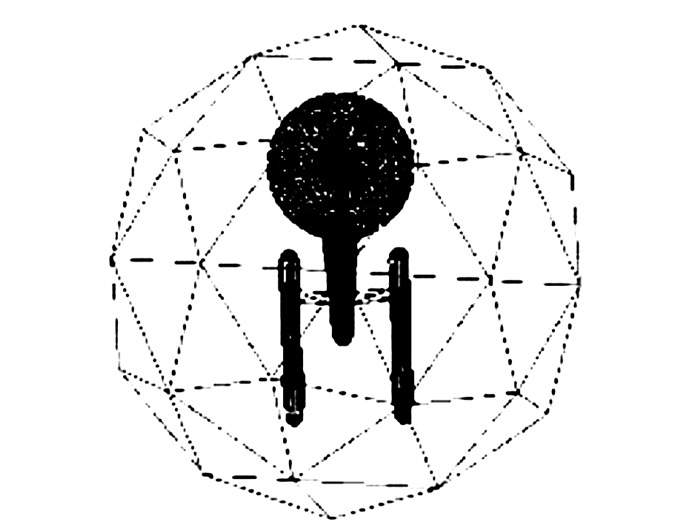
视点的选取方法有经纬度法、随机法、伪均匀法等。经纬度法在两极处采样稠密、中部稀疏,增大了两极视点的采样率,会漏掉中部的视点,而随机法运算量较大[6]。本文采用伪均匀法,以一个能够包住三维模型的多面体顶点作为视点位置,如图 2所示。这个多面体由正二十面体经过曲面细分得到,这样可以得到均匀分布的视点,而且根据不同的需要可以循环不同的次数来得到不同数量的视点位置。对于数据集中每个三维模型Mi,表面渲染为黑色,在每个视点上取得三维模型的投影,得到每个模型的n个二维视图,如图 3所示。
|
| 图 2 视点采样 Fig. 2 Viewpoints sampling |

|
| 图 3 部分二维视图 Fig. 3 Some 2D views |
获得最优视图样本之后,需要提取三维模型视图在二维形状空间中的特征。本文使用Zhang等[15]提出的结合傅里叶描述子和Zernike矩描述子的方法来描述每个视图。
Kauppien[16]比较了多类形状识别方法的能力,实验表明基于物体轮廓坐标序列的傅里叶描述子具有良好的形状识别性能,Zhang等[17]也说明了60个傅里叶描述子系数足以表示一个形状,由此可以使用傅里叶描述子来描述二维视图的特征。但是为了使得特征满足旋转、平移和缩放的几何不变性,需要对傅里叶描述子进行归一化操作。提取步骤如下。
1)二维视图经二值化处理后变成二值视图;
2)使用Canny算子提取二值视图的轮廓;
3)对轮廓序列进行傅里叶变换并进行归一化;
4)取前m个低频分量作为每个视图的特征。
但是傅里叶描述子是一种基于边界的描述方法,仅仅只利用了边界信息,丢失了形状的内部信息。而Zernike矩描述子可以利用形状的内部信息,作为傅里叶描述子的补充,更好地描述视图的特征。同样,为了使得特征满足旋转、平移和缩放的几何不变性,也需要进行归一化操作,其步骤如下。
1)二维视图经二值化处理后变成二值视图;
2)以视图的中心作为原点,把所有像素的坐标映射到以原点为圆心的单位圆中,使得Zernike矩具有平移和缩放的不变性;
3)用正交的Zernike多项式展开视图;
4)取得振幅作为Zernike矩描述子,得到旋转不变性。
由于在形状有缺口以及轮廓有凸起的情况下,傅里叶描述子的性能不佳,但Zernike矩的性能良好,而在形状分叉较多的情况下却相反[15]。因而把2个描述子结合起来,采用与文献[18]所述方法同样的参数,使用0~10阶的35个Zernike矩描述子和前10个傅里叶描述子来描述视图的特征,对数据集中每个三维模型Mi的每个视图Vik提取傅里叶描述子fikj和Zernike矩描述子zikj后,三维模型Mi将由n个视图的45维的特征向量表示,记为
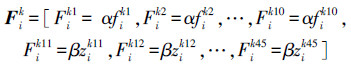 |
式中:α和β分别为傅里叶描述子和Zernike矩描述子的权重。在这里定义2个视图之间的相异性,即2个视图之间的距离为相应特征向量的欧式距离:
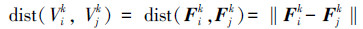 |
(1) |
式中:‖·‖是欧式范数。
1.4 分类能力评价为了衡量三维模型Mi中每个视图Vik的分类能力,这需要找到对于Vik而言其他三维模型的代表视图,使用这些代表视图构建特征矩阵和类别标记来训练分类器,进而衡量Vik的分类能力。
由于采样时存在视图对称或旋转等相似的情况,存在较大的数据冗余,为了减少计算开销,在选择代表视图之前,依照Yamauchi等[8]提出的方法,将相似度较高的视图聚集在一起,使得视图集合约减为数量较小、相似度较低的视图子集。由于存在着对称的影响,不相邻的视点相似度也可能很高,因此可以使用简单高效的k-means聚类算法代替文献[8]中的MeTis图划分方法,取得聚类中心作为候选视图,视图间的距离以式(1)度量。
下面定义三维模型Mj对于三维模型Mi的视图Vik的距离,将它看作是Mj的候选视图集合中所有视图Vjl与Vik间距离的最小值,即
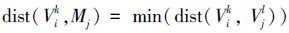 |
使得dist(Vik, Mj)取最小值的视图Vjl被选为Mj对于Vik的代表视图。
对于Mi的每个视图Vik,计算其他所有模型相对于Vik的代表视图后,对V ik训练得到一个二值分类器Φik,特征矩阵由其他所有模型相对于Vik的代表视图的特征组成。这个特征矩阵包括视图Vik的特征向量Fik以及每个代表视图Vjl的特征向量Fjl。如果模型Mi和Mj属于数据集中同一类别,那么特征Fjl的类别标记为1;否则,类别标记为-1。该分类器定义如下:
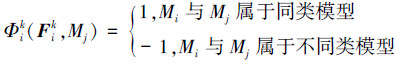 |
分类器采用随机森林算法进行训练。随机森林是Breiman[19]提出的一个分类器集成算法,它将许多决策树作为弱分类器集成一个强的分类器,以提升分类的正确率,随机森林的决策结果是所有决策树分类结果的平均。随机森林在图像检索方面的性能良好且快速[20],这有助于大量视图的高效学习。
然后,对分类器进行k折交叉验证,即将所有视图平均分成k份,每次以1份样本作为验证分类错误率的数据,其余k-1份作为训练分类器的数据,一共重复k次,对每次交叉验证的分类错误率进行累加,统计得到每次交叉验证的平均分类错误率,错误率最小的视图即为相应三维模型的最优视图。
1.5 数据集约减当数据集中有大量数据时,使用全部的数据进行学习需要大量的计算开销,为了减少计算量,可以对数据集进行约减。进行约减的主要思想是,属于同一类的三维模型具有相似的特征,那么同一类别的三维模型可以由几个代表性的三维模型来表示。对于输入的新模型,采用每个类别分类错误率较低的三维模型作为训练分类器的输入,这样可以按照用户的需要确定不同的分类器训练模型数量,而不需要使用全部的模型,减少对于新输入模型的计算和时间开销。
2 实验结果与分析为了验证方法的有效性,以普林斯顿形状基准(Princeton shape benchmark,PSB)[21]作为三维模型数据集,进行实验分析。普林斯顿形状基准是一个包含了1 814个从互联网上收集的模型分类基准数据库,该数据库包含4个层次的分类。最粗略的分类仅包括2个分类,分别是自然物体和人造物体,其余的3个分类,均是上一层次分类的细化。其中最精细(base)的分类下,包含161个类别,包括飞机、人类、车辆等。本文设置正二十面体的曲面细分迭代次数为2,这样产生了162个均匀分布的视点。参数α和β采用Zhang等[15]在实验得到的具有最佳检索性的参数α=0.7,β=0.3。k-means聚类数则设为10,交叉验证采用5折,这样可以得到性能和计算开销的折衷。
在第2个层次(coarse 1)的分类下,采用全部模型训练分类器,图 4展示了有翼飞行器模型前4个好的视图,左侧最好,往右依次降低。图 5展现了更多类别模型的实验结果,包括人类模型、液体容器和节肢动物,左右2列分别为不同模型前2个好的视图。从实验结果可以看出大部分最优视图符合人类观察物体的视觉习惯,而且同类模型的最优视图具有较高的一致性。

|
| 图 4 在coarse 1层次下,有翼飞行器的结果 Fig. 4 Results of winged vehicles of the coarse 1 |

|
| 图 5 在coarse 1层次下的结果 Fig. 5 Results of the coarse 1 |
为了衡量同类视图的稳定性,考虑到工程中一个物体往往由主视图、俯视图、左视图组成的三视图来表示,再加上一些转面视图如正侧视图等类别,本文将多个所有视图归并成主视图、俯视图、左视图、正侧视图和上侧视图,对模型的视图一致性进行了统计,对于第2个层次(coarse 1)分类的统计结果如表 1所示。
| 类别 | 视图比例 | 视图样例 | 视图比例 | 视图样例 |
| 飞行器 | 俯视图 44.7% | 
| 侧视图 16.0% | 
|
| 站立人体 | 正侧视图 50.3% | 
| 侧视图 22.1% | 
|
| 液体容器 | 正视图 67.8% | 
| 俯视图 27.1% | 
|
而在最精细的分类下对于有翼飞行器模型的实验结果如图 6所示,左侧最好,往右依次降低,对于该层次分类的统计结果如表 2所示,可以看到与前一个较为粗糙分类的情况不同,同类模型最优视图姿态的变化更小,一致性更高,由此可以看出,本文的方法对于数据集的分类情况具有依赖性,因此,三维模型的不同分类情况会对结果造成影响。

|
| 图 6 在最精细的分类下,有翼飞行器的结果 Fig. 6 Results of winged vehicles of the base classification |
| 类别 | 视图比例 | 视图样例 | 视图比例 | 视图样例 |
| 商用飞机 | 俯视图 61.9% | 
| 侧视图 23.8% | 
|
| 太空船 | 上侧视图 45.5% | 
| 俯视图 27.3% | 
|
其他的模型所选择的最优视图如图 7所示,其中同一行显示的是属于同一类别不同模型的最优视图。由于视图特征描述子是基于二维视图形状的,因此对于在不同视点下形状差别较大的模型效果较好。但是由于这种局限性,对于一些在每个视点下形状区别不大的模型,如人类头部模型,这些模型每个视图的特征较为相近,难以区分,一致性就较差。由于透视关系,在关于坐标原点对称的视点下得到的二维视图形状是完全一样的,例如一个模型的正面和背面,基于形状的视图描述子是无法区分的,这也导致了实验结果中会出现模型的背面视图,而这与人类的习惯是不相符的。

|
| 图 7 其他模型结果 Fig. 7 Results of some other models |
不同类别的三维模型的几何特征具有很大变化,因此难以得到通用的最优视图的精确数学定义。本文提出了一种三维模型最优视图的选择方法,将最优视图选择问题归结为视图对于三维模型类别的分类性能问题,该方法利用了三维模型数据集类别的语义信息,得到了比较符合人类习惯的最优视图。
新方法使用傅里叶描述子和Zernike矩描述子来描述三维模型的二维视图,但仅仅利用了不同视图的形状信息,无法区分三维模型关于坐标原点对称的2个视图,比如正面和背面。因此,怎样在对计算量影响不大的情况下能够描述不同视图下的三维空间信息将是后续工作的一个方面。此外,由于在不同的视角下得到的二维视图不一定是正立的,因此可以对最优视图进行校正以得到更好的结果,本文使用的是简单的校正视图到形状的主轴上的PCA方法,对于人类模型等细长的模型特别有效,但是对于任意类型的模型来说,这仍然是有待解决的问题。由于人类对于三维模型的类别认知可以有多种方式,往往是分层次或者模糊的,本文方法只是依据数据集中一个明确的固定分类,对于低类内变化的数据是鲁棒的,但对于高类内变化的数据性能会下降,因此本文得到的结果与人类的主观选择仍然会存在差异。对于最优视图的评价尚未形成统一的评价标准,如何度量这种差异以及引入人类主观选择的影响将是后续工作的另外一个方面。
| [1] | MARR D, POGGIO T, HILDRETH E C, et al. A computational theory of human stereo vision[M]. Boston: Birkhäuse, 1991 : 263 -295. |
| [2] | BLANZ V, TARR M J, BULTHOFF H H, et al. What object attributes determine canonical views?[J]. Perception , 1999, 28 (5) : 560-575 |
| [3] | POLONSKY O, PATAN G, BIASOTTI S, et al. What's in an image? Towards the computation of the "best" view of an object[J]. The Visual Computer , 2005, 21 (8\9\10) : 840-847 |
| [4] | FEIXAS M, DEL ACEBO E, BEKAERT P, et al. An information theory framework for the analysis of scene complexity[J]. Computer Graphics Forum , 1999, 18 (3) : 95-106 DOI:10.1111/cgf.1999.18.issue-3 |
| [5] | 杨利明, 王文成, 吴恩化. 基于视平面上特征计算的视点选择[J]. 计算机辅助设计与图形学学报 , 2008, 20 (9) : 1097-1103 YANG Liming, WANG Wencheng, WU Enhua. Viewpoint selection by feature measurement on the viewing plane[J]. Journal of Computer-Aided Design & Computer Graphics , 2008, 20 (9) : 1097-1103 |
| [6] | 曹伟国, 胡平, 李华, 等. 基于距离直方图的最优视点选择[J]. 计算机辅助设计与图形学学报 , 2010, 22 (9) : 1515-1521 CAO Weiguo, HU Ping, LI Hua, et al. Canonical viewpoint selection based on distance-histogram[J]. Journal of Computer-Aided Design & Computer Graphics , 2010, 22 (9) : 1515-1521 |
| [7] | JOSHUA P, PHILIP S, ALEKSEY G, et al. A planar-reflective symmetry transform for 3D shapes[J]. ACM Transactions on Graphics , 2006, 25 (3) : 549-559 DOI:10.1145/1141911 |
| [8] | YAMAUCHI H, SALEEM W, YOSHIZAWA S, et al. Towards stable and salient multi-view representation of 3D shapes[C]//Proceedings of the IEEE International Conference on Shape Modeling and Applications. Matsushima, Japan, 2006: 40. |
| [9] | VÁZQUEZ P P, FEIXAS M, SBERT M, et al. Automatic view selection using viewpoint entropy and its application to image-based modeling[J]. Computer Graphics Forum , 2003, 22 (4) : 689-700 DOI:10.1111/cgf.2003.22.issue-4 |
| [10] | SHILANE P, FUNKHOUSER T. Distinctive regions of 3D surfaces[J]. ACM Transactions on Graphics , 2007, 26 (2) : 7 DOI:10.1145/1243980 |
| [11] | VÁZQUEZ P P. Automatic view selection through depth-based view stability analysis[J]. The Visual Computer , 2009, 25 (5\6\7) : 441-449 |
| [12] | LAGA H. Data-driven approach for automatic orientation of 3D shapes[J]. The Visual Computer , 2011, 27 (11) : 977-989 DOI:10.1007/s00371-011-0628-1 |
| [13] | FU H, COHEN-OR D, DROR G, et al. Upright orientation of man-made objects[J]. ACM Transactions on Graphics , 2008, 27 (3) : 1-7 |
| [14] | VRANIC D V, SAUPE D. 3D model retrieval[C]//Proceedings of the Spring Conference on Computer Graphics and its Applications. Budmerice, Slovakia, 2000: 89-93. |
| [15] | ZHANG D, LU G. An integrated approach to shape based image retrieval[C]//Proceedings of 5th Asian Conference on Computer Vision. Melbourne, Australia, 2002: 652-657. |
| [16] | KAUPPIEN H, SEPANEN T. An experiment comparison of auto regressive and Fourier based descriptors in 2D shape classification[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 1995, 17 (2) : 201-207 DOI:10.1109/34.368168 |
| [17] | ZHANG D, LU G. Shape retrieval using Fourier descriptors[C]//Proceedings of 2nd IEEE Pacific Rim Conference on Multimedia. Beijing, China, 2001: 1-9. |
| [18] | CHEN D Y, TIAN X P, SHEN Y T, et al. On visual similarity based 3D model retrieval[J]. Computer Graphics Forum , 2003, 22 (3) : 223-232 DOI:10.1111/cgf.2003.22.issue-3 |
| [19] | BREIMAN L. Random forests[J]. Machine Learning , 2001, 45 : 5-32 DOI:10.1023/A:1010933404324 |
| [20] | BOSCH A, ZISSERMAN A, MUNOZ X. Image classification using random forests and ferns[C]//Proceedings of 11th IEEE International Conference on Computer Vision. Rio de Janeiro, Brazil, 2007: 1-8. |
| [21] | SHILANE P, MIN P, KAZHDAN M, et al. The Princeton shape benchmark[C]//Proceedings of the IEEE Shape Modeling International. Washington, DC, USA, 2004: 167-178. |



