2. 长春建筑学院 基础教学部,吉林 长春 130607;
3. 东北师范大学 计算机科学与信息技术学院,吉林 长春 130117
2. Department of Basic Subjects Teaching, Changchun Architecture & Civil Engineering College, Changchun 130607, China ;
3. School of Computer Science and Information Technology, Northeast Normal University, Changchun 130117, China
作为数理逻辑中形式化推理的一个分支,自动推理在人工智能发展初期就引起了研究者的广泛关注。定理证明是领域的研究热点,其发展深刻地影响着人工智能乃至计算机科学的其他研究方向,并在计算机工程中有着广泛的应用[1]。如在软件验证和硬件校验方面,Karlsruhe大学开发的KIV[2]已成功用于验证许多应用软件,包括图和树的表示等实验室软件和用于铁路转弯控制等工业软件,一些大公司如英特尔、摩托罗拉、AMD等都使用基于定理证明的硬件校验技术。在智能规划领域,把规划问题编译成SAT(satisfiablity)问题并利用高效的SAT求解器进行求解已成为一种主要方法。基于SAT的规划系统,在两年一度的国际规划器竞赛中屡获冠军,表现出优异的性能[3]。Grastien等[4]将基于模型的诊断问题转化成SAT问题,并且利用SAT求解算法进行诊断。与传统的方法相比,基于SAT的诊断方法能解决更复杂的诊断问题。
基于归结的方法[5-6]、基于表推演的方法、基于自然演绎的方法、基于公理系统的方法、基于相继式演算的方法和基于扩展规则的方法[7]是几类主要的定理证明方法。其中基于归结的定理证明方法一直是最重要也是最基本的方法,其基本思想是通过推出空子句判定给定子句集的不可满足性。相反于归结方法,基于扩展规则的方法的基本思想是将定理证明沿着归结的逆向进行,通过推出所有极大项组成的集合来判定子句集的可满足性。该方法不需要将所有极大项都扩展出来,而是巧妙地利用容斥原理直接计算扩展出的极大项的个数,降低了其空间复杂性,对于互补因子较高的SAT问题具有独特的求解优势,被国际著名的人工智能专家、DP过程的提出者Davis教授称为归结方法的补方法[8-9]。
基于扩展规则的定理证明方法于2003年由Lin等[7]提出,发表在国际重要杂志《Joumal of Automated Reasoning》上,该方法一经提出就受到了国内外学者的广泛关注,出现了大量研究成果。本文对扩展规则方法自提出以来10年的发展情况进行总结,旨在让对该方向感兴趣的学者有一个较为全面的了解。
1 相关概念在定理证明的几类求解方法中,扩展规则方法以其独特的特点和求解优势引起了研究者的广泛关注,这里介绍所涉及的相关概念。首先对文中符号进行约定:用Σ表示合取范式(conjunctive normal form, CNF),也看作子句集,有时也称为公式,用C表示单个的子句,可以理解为文字的集合;用小写英文字母表示布尔变量(简称变量),也称作原子,用|Σ|表示Σ中子句的个数,Var(Σ)表示出现在Σ中的变量,|C|表示子句中的变量个数,Mod(Σ)表示Σ所有模型组成的集合。
定义1(SAT问题) 给定一个命题公式Σ,SAT问题就是判断是否存在一个真值赋值使得公式的值为真。若存在,则称Σ是可满足的,否则为不可满足的。
定义2(碰集) 给定集合簇T,如果H⊆∪S∈TS,且对于每一个S∈T,都有H∩S≠∅,那么称H为T的一个碰集。如果H是满足上述性质的极小集合,则称H为极小碰集。
定义3(相近SAT问题)[10] 对于变量集M上的k (k>1)个子句集Σ1, Σ2, …, Σk,令Σ=Σ1∩Σ2∩…∩Σk,若对于∀1≤i≤k有|Σi-Σ|≤1,则称Σ1, Σ2, …, Σk相近,由它们构成的集合称为相近子句集簇,记为(Σ, Γ),
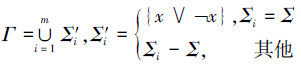 |
x为M中的任意变量。
定义4(#SAT问题) 给定一个命题公式Σ,#SAT问题就是计算Σ的可满足赋值(模型)个数。
定义5(加权模型计数问题)[11] 给定子句集Σ,Σ中的每个文字l的权记作w(l),每个模型ω的权为
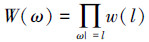 |
加权模型计数问题是计算满足Σ的所有模型的权之和。
#SAT问题可以看作是加权模型计数问题的特例,其中每个文字的权值为0.5。
隐蔽集(backdoor set)和骨架集(backbone set)是SAT问题的重要结构,与问题求解难度有着密切的关系[12]。
定义6(隐蔽集)[13] 给定一个命题公式Σ,B⊆Var(Σ)非空,如果B中变量的任意(存在一个)真值指派t使得简化公式Σ[t]在多项式时间内可解,那么B为Σ的强(弱)隐蔽集;如果简化公式Σ-B能在多项式时间内求解,那么B为Σ的删除隐蔽集。当基本类是封闭的,删除隐蔽集等价于强隐蔽集。
定义7(骨架集)[14] 给定一个命题公式Σ,B⊆Var(Σ)非空,如果在所有模型中,B中变量的赋值都相同,那么B为Σ的骨架集。
定义8(扩展规则)[7] 给定一个子句C和一个变量的集合M,D={C∨a, C∨¬a | a∈M并且a和¬a都不在C中出现},那么把从C到D中元素的推导过程叫做扩展规则,D中的元素叫做应用扩展规则的结果。
定义9(极大项)[7] 设C为变量集合M上的一个非重言式子句,且|M|=m,如果|C|=m,那么C为M上的极大项。
定义10(互补因子)[7] 给定子句集Σ,|Σ|=n,互补因子CF是含互补对的子句对个数与所有子句对个数的比值, 即CF=S/Cn2,其中S表示含互补对的子句对个数。
2 命题逻辑中的扩展规则求解方法扩展规则方法始于命题逻辑,本节分别讨论其在SAT问题、相近SAT问题和#SAT问题中的研究进展。
2.1 基于扩展规则的SAT求解方法 2.1.1 ER和IER算法2003年,Lin等[7]沿着归结原理的反向提出一条新的推理规则—扩展规则,使用扩展规则进行定理证明的算法ER(theorem proving based on extension rule),其基本思想是把给定的子句集Σ扩展成由极大项组成的子句集Σ′,然后根据极大项的个数|Σ′|来判定Σ的可满足性,如果|Σ′|=2m(m为Σ的变量数),则Σ是不可满足的;否则Σ可满足。事实上并不需要将Σ′扩展出来,只需计算出|Σ′|就可以判定Σ的可满足性。因此他们利用容斥原理直接计算出|Σ′|,降低了该方法的空间复杂性。一般情况下,ER算法的时间复杂性是指数级的,效率比较低,但是在任意2个子句都含有互补对的情况下,ER算法的效率较高,而使用基于归结的方法效率较低。可以用互补因子CF来比较基于扩展规则的方法和基于归结的方法。假设所有的SAT问题都在一个光谱上,其左端是互补因子为1的问题,其右端是互补因子为0的问题,在光谱左端用基于扩展规则的方法效率更高,而在光谱右端基于归结的方法效率更高。
ER算法实际上是在给定子句集的所有极大项组成的空间中进行搜索,看是否有不能被扩展出的极大项。为了减少搜索空间提高求解的效率,Lin等[7, 15]提出了一种高效的算法IER(improved extension rule)。该方法首先在极大项空间的一个子空间中搜索,如果在子空间中有不能被扩展的极大项,那么整个空间就有不能被扩展的极大项,这时子句集是可满足的;否则,不能判定子句集的可满足性,需要调用ER算法。IER算法是先运行一个高效但不完备的算法,希望它能解决大部分问题,对于无法解决的问题再调用完备的ER算法。
2.1.2 带化简规则的ER和IER算法通常,有些子句不会影响子句集不可满足性的判定,可以将之删除,如含纯文字的子句、被蕴含的子句等。Wu等[16-17]利用若干化简规则,包括重言式规则、单文字规则、纯文字规则和包含规则,对ER和IER算法进行了改进,提出了带化简规则的扩展规则算法RER(reduced extension rule)和RIER(reduced improved extension rule with heuristic)。其基本思想是对给定子句集进行化简并对其可满足性进行快速但不完备的判定,如果能判定子句集的可满足性,则返回判定结果;否则调用ER或IER算法对化简后的子句集进行判定。在大部分情况下,RER和RIER算法都提高效率,仅在化简规则不起作用的情况下,效率会降低。
2.1.3 基于启发式策略的IER算法IER算法通过随机选取子句C来限定极大项搜索空间,为了尽可能地在该子空间中判定出给定子句集的可满足性,以提高算法的效率,子句C的选取至关重要。Lin等在文献[7]中指出,对于具体的问题,通过问题的背景知识来调整子句C的输入可能会提高IER算法的效率,并将C的选取作为一个开放问题。
李莹等[18]根据具体给定子句集所包含的信息提出了2种用于选择限定搜索空间子句的启发式策略IMOM(improved maximum occurrences on clauses of maximum size)和IBOHM(improved BOHM)。IMOM是优先选择最长子句中出现频率高的文字的否定加入子句C,IBOHM是优先选择拥有极大向量(H1(Li), H2(Li), …, Hn(Li))的文字Li加入到子句C中,其中Hj(L)为子句集中长度为j的包含文字L的子句个数,并将其分别用于IER算法,提出了IMOMH_IER和IBOHMH_IER算法。IMOM和IBOHM策略利用子句集的相关信息选择子句C,可以得到更适合问题的极大项搜索子空间,对于可满足的问题可以直接返回SAT,不可满足的问题可以较早地调用ER算法,减少判定时间,提高了求解效率,其平均速度较DR(directional resolution)[6]和IER算法可以提高10~200倍。
2.1.4 与归结方法的结合基于扩展规则的方法和基于归结的方法是2种互补的方法,为了充分利用其各自的推理特点来提高SAT问题求解的效率,Wu等[19]将2种推理方法结合起来,即将有向归结DR和扩展规则方法ER结合,提出了综合的推理算法DR-ER。该方法利用子句集的互补因子CF来决定调用DR还是ER。如果CF≥0.5,调用ER进行推理;否则调用DR进行推理。DR-ER方法的求解效率优于单独使用DR或ER方法。
2.1.5 避开容斥原理的扩展规则方法利用容斥原理,ER算法可以巧妙地计算给定子句集可扩展出的极大项个数,解决了指数级的空间需求问题,但是其时间复杂性仍然是指数级的,严重影响了算法的求解效率,限制其在实际问题中的应用[20]。为了避开容斥原理复杂的求解过程,利用扩展规则的特性,研究人员提出了子句集合包含方法、极大项覆盖方法和碰集方法,下面分别给予介绍。
1)子句集合包含方法。
2009年,孙吉贵等[20]发现一个极大项能被子句集扩展出来,子句集中必须有子句包含于该极大项(子句看作文字集合)。基于该性质,孙吉贵等提出了一种新的基于扩展规则的定理证明方法NER,该方法将SAT问题转化为一系列文字集合的包含问题。NER算法按照一定次序判断极大项是否可被当前待判定的子句集Σ扩展,若存在某个极大项不能被扩展出来, 那么Σ是可满足的;否则,若所有极大项都可以被扩展出来,则Σ是不可满足的。其最优和最坏时间复杂度分别为O(m+n×k2)和O(2m×(m+n×k2)),m、n、k分别表示子句集中变量的个数、子句的个数和子句的平均长度。实验结果表明,无论是对于随机问题还是标准测试用例,NER算法的执行效率较IER和DR算法都有很大的提高,有些问题可以提高2个数量级。
NER算法将所有极大项按照一定顺序来一一判定其是否能由子句集扩展出来,直到某个极大项不能被扩展时或者所有极大项都可由子句集扩展出来时,才能判定出子句集的可满足性。事实上,当一个极大项可由某一子句扩展时,接下来的部分极大项可以不用判断其是否可由子句集扩展出来,从而减少了需要判断的极大项个数。张立明等[21]定义了半扩展规则,并且提出了基于半扩展规则的定理证明方法SRE(semi-extension rule)。SRE算法是在NER算法的基础上,按一定顺序判定极大项是否可被子句集扩展,当一个极大项可被子句集中的某一子句扩展时,那么基于此子句半扩展出的所有极大项都不需判断其是否可被子句集扩展,这样减少了需要判断的极大项个数,使计算复杂度由原来NER方法的O(2m×(m+n×k2))降为O(2d×(m+n×k2)+n2),其中d为子句集中子句的度的平均值。d越小,SRE算法的求解效率越高;当d趋近与m时,SRE算法的求解效率较NER算法提高较小。
进一步,他们提出了基于半扩展规则的并行定理证明方法PPSER(parallel theorem proving algorithm based on semi-extension rule)[22],该方法首先给出在极大项子空间中判定子句集可满足性的算法PSER,然后将子句集的极大项空间分解为若干个互不相交的子空间,对每个极大项子空间,并行地调用PSER方法进行判定,如果有一个极大项子空间中返回的结果为SAT,即该子空间中存在某个极大项不能被扩展出来,则子句集是可满足的;否则,如果所有极大项子空间返回的结果都为UNSAT,即所有极大项都能被扩展出来,那么子句集是不可满足的。由于并行处理,该算法在求解效率上较SRE算法有了较大的提高。
2)极大项覆盖方法。
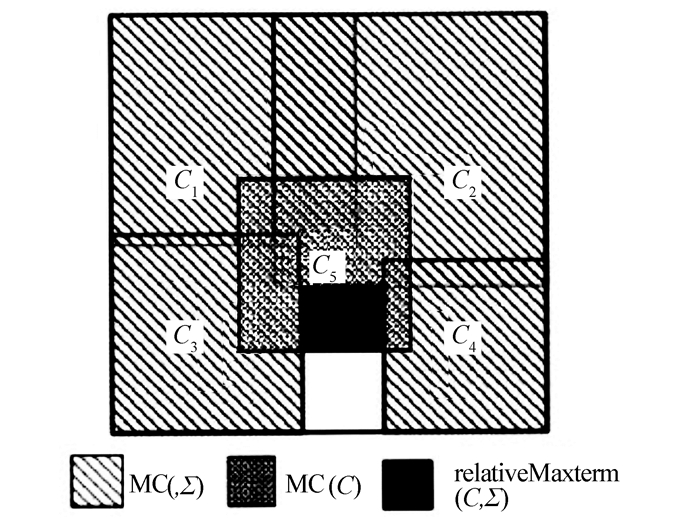
为了避开容斥原理求解的复杂性,Yin等[23]从相对极大项角度提出了一种基于极大项覆盖的有效SAT求解方法MC(maxterm covering for satisfiability)。子句C关于子句集Σ覆盖的相对极大项是C覆盖, 但不是Σ覆盖的极大项,表示为relativeMaxterm(C, Σ)=MC(C)\MC(Σ)。设子句集Σ={C1, C2, C3, C4},C关于Σ的相对极大项如图 1所示。
|
| 图 1 C关于Σ的相对极大项 Fig. 1 The relative maxterm of C with respect to Σ |
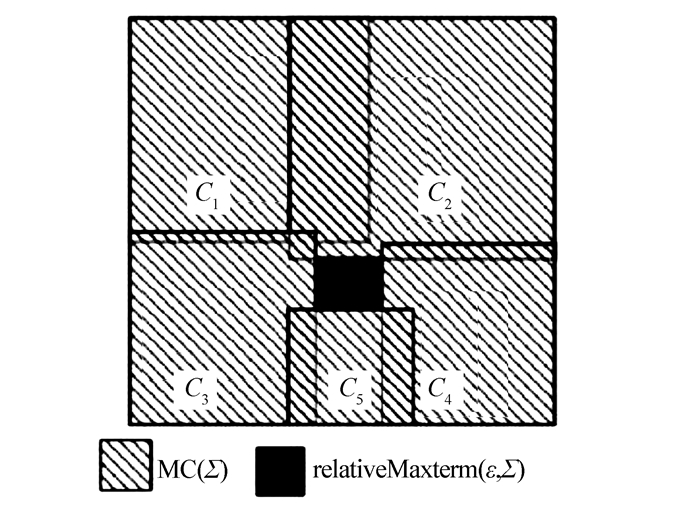
给定一个变量集合,设所有极大项集合为论域,那么空子句ε覆盖的极大项集合等于该论域。根据扩展规则方法可知,如果MC(Σ)=MC(ε),则子句集Σ是不可满足的;如果relativeMaxterm(ε, Σ)≠∅,则Σ是可满足的。图 2给出了一个可满足的问题实例。
|
| 图 2 一个可满足问题实例 Fig. 2 A satisfiable example |
MC方法利用空子句关于子句集的相对极大项的个数来判定子句集的可满足性。如果相对极大项个数为0,则子句集是不可满足的;否则,子句集是可满足的。与扩展规则方法根据扩展出的极大项个数来判断子句集的可满足性不同,该方法直接计算出不能由子句集扩展出来的相对极大项个数,然后根据相对极大项个数来判断子句集的可满足性,避开了容斥原理的复杂性。进一步,他们在基本MC算法的基础上提出了8种优化策略,极大地提高了算法的求解效率。
3)碰集方法。
Xu等[24-25]找出了不能被扩展出的极大项具有的特征,以此来回避容斥原理所带来的计算量。他们发现,若极大项与子句集Σ中的某个子句互补,则该极大项不能由这个子句扩展出来。进而可知,如果极大项与Σ中所有子句都互补,那么该极大项就不能由Σ扩展出来。假定存在与Σ中任意子句都互补的极大项CM,那么由CM可以构造极大项CM′,其中CM′由CM中每个文字的补文字构成。如果将子句看作文字集合,Σ看作文字集合簇,那么CM′与Σ中任意子句的交都不为空,即CM′是Σ的碰集。基于此,Xu等证明了子句集是可满足的, 当且仅当该子句集存在不包含互补文字的碰集,这样就将SAT问题转化成判定是否存在不含互补文字的碰集问题,并且提出了2种有效的方法CBHST(complementary binary hitting set tree)和RNHST(revised new hitting set tree)来进行求解。这2种算法与DR相比,在效率方面都有1~2个数量级的提高。RNHST算法与CBHST算法相比,RNHST更适合长子句的情况,而CBHST更适合短子句的情况。
2.1.6 基于扩展规则的知识编译方法1)基于KCER的知识编译方法。
Lin和Sun[26]指出扩展规则方法可以被应用于知识编译[27]中,他们定义了EPCCL(each pair contains complementary literal)理论(任意2个子句都含互补对子句集),证明了EPCCL理论是在“可满足可控制类”和“蕴含可控制类”中,并证明对于任意子句集一定能找到一个与之等价的EPCCL理论,因此EPCCL理论可以作为知识编译的目标语言,进而利用“桶删除”的思想提出将给定子句集编译成EPCCL理论的算法KCER(knowledge compilation using the extension rule)。该方法与现有其他知识编译方法的不同之处在于:在编译阶段和推理阶段该方法都是基于扩展规则的,而其他的知识编译方法都是基于归结原理的;当互补因子较大的时候,该方法得到的子句集规模相对较小,特别地,当待编译的子句集本身就是一个EPCCL理论,用该方法编译后的结果就是其本身,而用其他方法编译,结果可能是指数级大的。因此,该方法被Murray教授看作是与现有其他知识编译方法对偶的一种方法[28]。
2)基于启发式策略的知识编译方法。
在知识编译中,离线编译后生成的目标知识库的规模对在线查询的效率起着至关重要的作用。算法KCER在选择子句和变量进行扩展时,都采用顺序扩展的方式,几乎没有使用任何启发式策略。对于有些问题,这会导致编译后的子句集规模过大,从而影响之后的在线推理的效率。为此,笔者提出了2种启发式策略MCN(minimum complementary number)和MO(maximum occurrences)分别用于指导待扩展的子句和变量的选择[29],MCN策略是优先选择与其他子句互补的子句数较少的子句进行扩展,MO策略是在待扩展的子句中优先选择在其他未扩展子句中出现次数最多的变量进行扩展。前者使得需要扩展的子句数较少,后者使得子句被扩展出的子句数较少。使用随机生成的样例和处于相变区的Uniform Random-3-SAT标准用例进行测试,实验结果表明,MCN和MO策略都能大幅度地减小编译后的子句集规模,其中MCN的效果比MO更为明显。同时使用MCN和MO策略,可以使扩展后的子句集规模为算法KCER的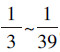
3)新的EPCCL编译框架。
赖永[30]证明了如下定理:给定子句集Σ=Σ1∧Σ2和EPCCL编译算法f,f(Σ1)∧f(¬Σ1∨Σ2)是与Σ等价的EPCCL理论。基于该定理,他提出了一种新的关于EPCCL理论的知识编译思想:对于给定的子句集,首先将其划分为2个子句集Σ1和Σ2,然后对它们分别进行编译,合取编译后的结果即可得到与原子句集等价的EPCCL理论。根据划分后|Σ1|、|Σ2|的不同,存在多种划分方式。如何编译¬Σ1∨Σ2又分为2种方式。根据子句集的划分方式、¬Σ1∨Σ2的编译方式和将DNF(disjunctive normal form)编译为EPCCL理论的方法的不同,给出多种不同的编译方法。
由于编译后的EPCCL理论的规模直接影响到在线查询效率,刘大有等[31]定义了一个规约规则,基于该规则提出了用于缩减EPCCL理论规模的算法,该算法具有多项式时间复杂度,然后结合基于DPLL的KCDP(knowledge compilation based on DPLL)算法,实现了C2E编译器。实验结果表明,不论是编译效率还是编译后子句集的规模都优于基于KCER的编译器。在目前的基于DPLL的SAT求解中,存在许多高效的技术,这些技术都能用于改进KCDP的编译效果,提升C2E编译器的性能。
2.2 基于扩展规则的相近SAT求解方法在实际应用中,通常需要判定仅相差一个子句的系列子句集的可满足性,即相近SAT问题。如在模型诊断系统和基于SAT的规划方法中,都需要判断相近SAT问题的可满足性。
赖永等[10]首先指出ER算法的实现存在以下不足:对于子句集Σ(|Σ|=n),在计算容斥原理的第i层时,需要搜索Cni 种情况,在实现过程中采用图搜索的策略进行搜索,保存第i层所有不含互补文字的子句组合,对空间要求较大;且对任意i个子句组合情况,在计算组合中出现的文字数时没有使用重用机制。基于以上不足,他们提出了一种更为高效的实现策略,在实现过程中采用了回溯法代替图搜索策略,降低了算法的空间需求,同时计算第i层的算法ER-i重用之前保存的结果, 避免了重复计算。
进而,他们发现将ER算法稍作修改就可以用于求解相近SAT问题。对于变量集M上的子句集Σ∪{Cn+1},其中Σ={C1, C2, …, Cn},按照是否包含Cn+1将所有由i个子句组成的子句集分为2类:由Σ中i个子句构成和由Σ中i-1个子句和Cn+1构成,那么容斥原理中的第i层为
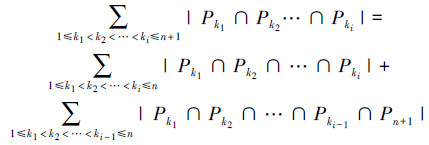 |
(1) |
式(1)中后一部分的计算如下:对于Σ的任一含i-1个子句的子集ΣΓ,若ΣΓ互补或者Cn+1与ΣΓ中任意子句互补,则ΣΓ∪{Cn+1}互补,值为0;否则,利用ER-i算法在第i-1层时能够额外地计算出后一部分的值。对于相近子句集簇(Σ, Γ),其中Σ={C1, C2, …, Cn},Γ={Cn+11, Cn+12, …, Cn+1m},可以一次性计算出Σ∪{Cn+11 }、Σ∪{Cn+1m }所包含的极大项,从而判定出它们的可满足性。因此提出求解相近SAT问题的nER算法。在多数情况下,算法nER求解相近SAT问题的时间仅相当于调用ER算法求解其中一个SAT问题的时间,nER算法的效率远远高于相近SAT问题中多个SAT问题单独求解的效率。
2.3 基于扩展规则的#SAT求解方法 2.3.1 利用容斥原理的#SAT方法笔者对扩展规则进行深入研究,发现赋值与极大项之间存在着一一对应的关系。一个赋值使得子句集为真, 当且仅当它的“非”形式的极大项不能被子句集扩展出来,即不能被扩展出的极大项对应于子句集的一个模型。由此可知,如果子句集扩展出的极大项个数为S,那么该子句集有2m-S个模型。基于此,将扩展规则推广到#SAT问题求解中,提出了一种基于扩展规则的模型计数方法CER(counting models using extension rule)。进而证明了EPCCL理论是在“模型计数可控制”类中,因此EPCCL理论可以作为模型计数知识编译的目标语言,基于KCER算法提出了基于知识编译的模型计数算法KCCER(knowledge compilation for counting models using extension rule)[32]。
笔者又进一步研究了如何使用扩展规则求解加权模型计数问题[33]。给定子句集Σ={C1, C2, …, Cn},M={a1, a2, …, am}为其变量集合,则Σ的所有可能的赋值的权之和为
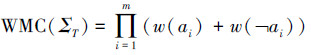 |
基于扩展规则的加权模型计数算法CWER(counting weighted models using extension rule)的思想是先计算出所有使得子句集Σ为假的模型的权和W(¬Σ),这样使得Σ为真的模型的权和为WMC(ΣT) -W(¬Σ)。其中计算W(¬Σ)需要利用容斥原理,当子句集Σ中任意2个子句都含互补文字时,不存在使得2个子句同时为假的赋值,这样只需要计算容斥原理公式的前n项。基于此,笔者提出基于知识编译的加权模型计数算法KCCWER(knowledge compilation for counting weighted models using extension rule)。
基于上述4种算法CER、CWER、KCCER、KCCWER, 笔者设计了JLU-WMCER系统,与传统的(加权)模型计数求解方法需要找出哪些赋值是给定子句集的模型(所有模型的权和)不同,该方法需要找出哪些赋值不是子句集的模型(所有使得Σ为假的赋值权和)。与ER方法类似,当互补因子较高时,基于扩展规则的(加权)模型计数方法一般要优于基于归结的方法;当互补因子较低时,基于扩展规则的方法要差于基于归结的方法,因此可以看作是目前其他(加权)模型计数问题求解方法的补方法。
2.3.2 避开容斥原理的#SAT方法1)与归结方法的结合。
由于容斥原理的复杂求解过程,降低了CER算法的效率,赖永等[9]利用|Mod(¬C)|=2m-|C|和求解子句集扩展出的极大项个数的容斥原理公式,得到了|Mod(Σ)|=|Mod(Σ′)|-|Mod(Σ′∧¬C)|,其中C∈Σ,Σ′=Σ\{C},Σ′∧¬C可以使用单文字规则进行化简。在此基础上提出了一种新的基于扩展规则的#SAT求解算法#ER,该算法继承了扩展规则方法的优点,能快速求解互补因子较高的问题。基于归结的算法#DPLL[34-35]主要借助单文字规则提高求解效率,在互补因子较高的情况下,单文字规则往往不能发挥作用,因此算法#DPLL效率较低。结合#ER和#DPLL算法的特点,赖永等提出了#CDE算法,该算法根据|Mod(Σ1∧Σ2)|=|Mod(Σ1)|-|Mod(Σ1∧¬Σ2)|,利用函数SelectClause(Σ)从Σ中选择适合算法#DPLL的子句集合Σ1,文中使用的是选出所有长度小于等于3的子句作为Σ1。当函数返回空集时,算法#CDE等价于#ER;当返回Σ本身时,算法#CDE等价于#DPLL。#CDE算法综合了#ER和#DPLL的优点,当互补因子较小时,#CDE表现出算法#DPLL的优点,当互补因子较大时,表现出#ER的优点。
2)碰集方法。
针对#SAT问题求解算法的效率会随着子句集的规模的增大而迅速降低的问题,许有军等[36]提出一种间接应用扩展规则求解#SAT问题的MCEHST(model counting with extension rule and hitting set tree)算法。在文献[24]中,他们发现不能被子句集扩展出的极大项可以构造出该子句集的一个碰集,即可以根据子句集是否存在不含互补文字的碰集来判定子句集是否为可满足的。任何不能由子句集扩展出的极大项都对应于该子句集的一个模型,而且该模型正好与子句集的碰集所扩展出的极大项相对应。MCEHST算法首先得到子句集的所有极小碰集,然后利用扩展规则计算出这些碰集扩展出的极大项个数,即模型数。当变量数一定,随着子句数的增加,子句集的极小碰集数显著减少。与已存在的其他#SAT算法比较,当子句数较大且子句较短时,该方法的执行效率较高;但是当子句数较小时,该算法的执行效率较低。实际应用时,可以根据情况来决定是否选择MCEHST算法。
3 扩展规则在其他逻辑中的应用目前,扩展规则方法已被推广到一阶逻辑、描述逻辑、模态逻辑、可能性逻辑和多值逻辑,下面分别讨论扩展规则方法在这些逻辑中的应用。
3.1 一阶逻辑利用Hooker提出的部分实例化推理方法PPI(primal partial instantiation)[37],Lin等[7]把扩展规则方法从命题逻辑提升到一阶逻辑。PPI算法的基本思想是把一阶逻辑的定理证明问题转化成一系列SAT问题,首先从较弱的SAT问题入手,然后通过进一步替换对问题逐渐加强,如果任何一步中返回不可满足,则原问题不可满足;如果在某一步返回可满足并且解释没有被阻塞,那么原问题是可满足的。由于PPI算法需要求出满足式映射,即模型,而ER算法只能判定可满足性,不能给出模型。因此他们又给出原子被潜在地阻塞的概念,以及2个原子被阻塞和被潜在地阻塞之间的关系,并对PPI算法进行修改,提出了基于扩展规则的一阶定理证明方法RPPI(revised primal partial instantiation)。
Wu等[38]指出Lin给出的原子被潜地阻塞的定义对新产生子句的条件限制过严,导致RPPI算法是不完备的,他们对潜在阻塞进行了重新定义,并且提出了一种新的一阶扩展规则算法RFOER(revised first-order extension rule),该算法与RPPI算法主要有以下3点不同:1)RPPI算法不完备,而RFOER算法完备;2)RPPI调用的是基本的ER算法,而RFOER调用的是更为高效的带化简规则和启发式策略的ER算法;3)RFOER中增加了M-可满足的情形,使得算法可以被更灵活地应用,更适合用于求解实际的问题。
3.2 描述逻辑描述逻辑是一种基于对象的知识表示形式化工具,是一阶谓词逻辑的可判定子集[39],研究有效的推理算法是描述逻辑的一个重要研究内容。Zou等[40]将扩展规则推广到描述逻辑ALC的推理中,定义了概念扩展规则CER(concept extension rule)和EPCCCL(each pair of clausal concept contains links)理论,即任意2个子句概念都包含链接(概念链接或关系链接)的规范概念合取式(conjunction normal concept,CNC),提出了基于概念扩展规则的推理方法,并且证明该方法能在多项式时间内完成任意EPCCCL理论的可满足性推理和蕴含推理,因此EPCCCL理论可以作为描述逻辑中知识编译的目标语言。进一步他们提出了基于概念扩展规则的描述逻辑知识编译方法,该方法首先利用CER-DLKC算法将CNC公式编译成EPCCCL理论,然后利用基于概念扩展规则的推理方法可以在多项式时间内回答任意查询。
3.3 模态逻辑模态逻辑为知识工程和并行程序的研究提供了一种形式化的途径[41]。目前常用的模态推理方法大致可分为以下2种:一种是直接推广经典的推理方法使之能应用于模态逻辑;另一种是利用转换方法将模态逻辑转换为经典逻辑,然后利用经典逻辑中的方法进行推理,其中关系转换方法、函数转换方法等是常用的转换方法。
Wu等[42]利用破坏性方法直接把扩展规则方法推广到模态逻辑中,提出了模态系统K中的破坏性扩展规则方法DMKER(destructive extension rule in modal logic K),该方法将利用化简规则进行简化和利用扩展规则判定不可满足性结合在一起,交替进行。DMKER算法能够快速地证明模态系统K中的所有公理和四类标准的benchmark问题。该方法继承了扩展规则方法的优点,当存在较多的互补公式时,模态逻辑推理的效率明显提高。此外,Wu等[43]分别将关系转换方法、函数转换方法与扩展规则方法相结合,提出了关系扩展规则方法MRER(modal relational extension rule)、连续模态逻辑中的函数扩展规则方法MFER(modal functional extension rule)和非连续模态逻辑的广义函数扩展规则方法GMFER(general modal functional extension rule)。
3.4 可能性逻辑可能性逻辑是适用于给定知识中含有不确定因素或者给定知识不完全一致的情况下进行知识表示和推理的逻辑。在可能性逻辑中,最主要和最基本的推理规则是基于Dubois和Prade提出的可能性归结原理[44]。笔者将扩展规则方法引入到可能性逻辑中[45],定义了可能性包含规则和可能性扩展规则,并且提出了基于可能性扩展规则的推理方法,即利用可能性扩展规则计算可能性知识库Σ的不一致程度。该方法的基本思想是:首先按照可能性子句的权值α对可能性知识库Σp中的子句从小到大进行排序,然后顺次考虑Σp的不同α截集Σα,利用公式ER算法判断Σα的可满足性:如果Σα不可满足,则Σp的不一致程度为α,否则继续考虑下一截集。与命题逻辑中的扩展规则方法ER类似,对于互补因子较高的问题可能性扩展规则方法效率较高,而对于互补因子较低的问题可能性归结方法的效率较高,因此,可能性扩展规则方法可以看作是任何可能性归结方法的补方法。
进一步,笔者扩展了经典逻辑的蕴含可控制类和可满足可控制类的概念,定义了可能性蕴含可控制类和不一致性程度计算可控制类。在可能性扩展规则的基础上,笔者提出了EPPCCCL(each pair of possibilistic clauses contains complementary literals)理论,即任意2个可能性子句的经典投影都含有互补对的可能性子句集,证明了该理论是在最优化形式蕴含可控制类和不一致性程度计算可控制类中的,可以作为可能性知识编译的目标语言,并且给出了一种可能性知识编译方法。该方法首先利用可能性知识编译算法SPL-KCER将任意给定的可能性知识库编译成EPPCCCL理论,然后利用上述的可能性扩展规则方法可以在多项式时间内完成推理。与可能性归结方法相比,该方法在有些情况下具有独特的优势,当待编译的可能性知识库本身就是一个EPPCCCL理论,新方法编译后的结果就是它本身,而可能性归结方法的结果一般为指数级别的。
3.5 多值逻辑经典逻辑对知识的表示能力是有限的,多值逻辑具有更强的表达能力。在许多领域中,不仅需要布尔变量,而且需要多值变量来表示实体的一些属性,直接向经典的命题公式中加入多值变量可能会增加原始问题的求解难度,笔者将扩展规则推广到多值逻辑中,提出了一种基于扩展规则的多值推理方法[46]。这里关注的是标记逻辑,因为任意一个多值逻辑知识库,都可以找到一个与之等价的标记逻辑知识库,反之亦然。文中定义了标记扩展规则以及最大项的概念,并且利用容斥原理来计算给定标记子句集所扩展出的最大项个数来判定标记子句集的可满足性。在此基础上定义了标记EPCCL (s-EPCCL)理论,即对于一个带有标记文字的子句集,其中每一对子句都含有互补文字,或者是互补的布尔文字,或者是互补的标记文字,并且证明s-EPCCL理论是在标记可满足可控制类和标记蕴含可控制类中,因此,s-EPCCL理论可以作为多值逻辑知识编译的目标语言。笔者提出了一种基于扩展规则的多值知识编译方法,该方法首先利用SKCER算法将标记知识库编译成一个与之等价的s-EPCCL理论,然后利用上述基于扩展规则的多值推理方法可以在多项式时间内回答查询。
4 待解决的问题扩展规则方法以其独特的优势使之成为自动推理的重要方法之一,目前还存在一些未解决的问题,值得研究人员进一步探讨。
1)如何利用扩展规则方法求解隐蔽集。
隐蔽集是SAT问题的一个重要结构,与求解难度有很大的关系,隐蔽集的选择使得剩下的问题能在多项式时间内求解。由于利用扩展规则方法和EPCCL理论是可以在多项式时间内判定可满足性的,如何求解隐蔽集使得剩下的问题都是EPCCL理论,是需要进一步研究的问题。
2)如何选择IER算法的子句C使之与骨架集相对应。
骨架集也是SAT问题中的一个重要结构,它是一个变量集合,在每一个模型中这些变量的赋值都相同。IER算法利用子句C来选择一个极大项空间中的子空间来进行搜索,由于不能扩展出的极大项与模型之间存在一一对应的关系,如果将骨架变量赋值的非作为子句C,那么对于可满足问题,C限定的子空间中肯定有不能扩展出的极大项。
3)探求扩展规则方法在其他逻辑中的应用。
目前,研究者主要集中于命题逻辑中扩展规则方法的研究,而在其他逻辑中的研究甚少,在可能性逻辑、多值逻辑等中,只是将最基本的ER算法进行推广。由于ER算法利用容斥原理进行推理,严重影响算法的求解效率。因此,在上述逻辑中扩展规则方法的效率还有很大的提升空间。另外,还可以考虑将扩展规则方法推广到模糊逻辑、概率逻辑等其他逻辑中。
5 结束语扩展规则方法是与归结方法对称的一种自动推理方法,它的提出为自动推理的研究提供了新的研究角度,注入了新的活力。本文较全面地介绍了扩展规则方法的发展,包括相关概念、各种基于扩展规则的求解方法以及待解决的问题,主要围绕命题逻辑中的各种扩展规则方法进行分析,并讨论了扩展规则方法在其他逻辑中的应用。尽管目前扩展规则方法的研究取得了一定的成果,但是在算法的提升、各种逻辑的应用方面仍有很大的研究空间。
| [1] | 殷明浩.自动推理和智能规划中若干问题研究[D].长春:吉林大学, 2008: 1-109. YIN Minghao. The research on several issues of automated reasoning and artificial intelligent planning[D]. Changchun: Jilin University, 2008: 1-109. http://cdmd.cnki.com.cn/article/cdmd-10183-2008126532.htm |
| [2] | WOLFGANG R. The KIV system: systematic construction of verified software[C]//Proceedings of the 11th International Conference on Automated Deduction. Saratoga Springs, USA, 1992: 753-757. |
| [3] | 吕帅, 刘磊, 石莲, 等. 基于自动推理技术的智能规划方法[J]. 软件学报 , 2009, 20 (5) : 1226-1240 LU Shuai, LIU Lei, SHI Lian, et al. Artificial intelligence planning methods based on automated reasoning techniques[J]. Journal of Software , 2009, 20 (5) : 1226-1240 |
| [4] | GRASTIEN A, ANBULAGAN A, RINTANEN J, et al. Diagnosis of discrete-event systems using satisfiability algorithms[C]//Proceedings of the Twenty-Second Conference on Artificial Intelligence. Vancouver, Canada, 2007: 305-310. |
| [5] | ROBINSON J A. A machine oriented logic based on the resolution principle[J]. Computer Machine , 1965, 12 (1) : 23-41 DOI:10.1145/321250.321253 |
| [6] | DECHTER R, RISH I. Directional resolution: the Davis-Putnam procedure, revisited[C]//Proceedings of the 4th International Conference on Principles of Knowledge Representation and Reasoning. Bonn, Germany, 1994: 134-145. |
| [7] | LIN Hai, SUN Jigui, ZHANG Yimin. Theorem proving based on the extension rule[J]. Journal of Automated Reasoning , 2003, 31 (1) : 11-21 DOI:10.1023/A:1027339205632 |
| [8] | DAVIS M, PUTNAM H. A computing procedure for quantification theory[J]. Journal of the ACM , 1960, 7 (3) : 201-215 DOI:10.1145/321033.321034 |
| [9] | DAVIS M, LOGEMANN G, LOVELAND D. A machine program for theorem-proving[J]. Communications of the ACM , 1962, 5 (7) : 394-397 DOI:10.1145/368273.368557 |
| [10] | 赖永, 欧阳丹彤, 蔡敦波, 等. 基于扩展规则的模型计数与智能规划方法[J]. 计算机研究与发展 , 2009, 46 (3) : 459-469 LAI Yong, OUYANG Dantong, CAI Dunbo, et al. Model counting and planning using extension rule[J]. Journal of Computer Research and Development , 2009, 46 (3) : 459-469 |
| [11] | SANG T, BEAME P, KAUTZ H. Solving Bayesian networks by weighted model counting[C]//Proceedings of the Twentieth National Conference on Artificial Intelligence. Pittsburgh, USA, 2005: 475-482. |
| [12] | 谷文祥, 李淑霞, 殷明浩. 隐蔽集的研究及发展[J]. 计算机科学 , 2010, 37 (3) : 11-16 GU Wenxiang, LI Shuxia, YIN Minghao. Research and development in backdoor set[J]. Computer Science , 2010, 37 (3) : 11-16 |
| [13] | NISHIMURA N, RAGDE P, SZEIDER S. Detecting backdoor sets with respect to Horn and binary clauses[C]//Proceedings of the 7th International Conference on Theory and Applications of Satisfiability Testing. Vancouver, Canada, 2004: 96-103. |
| [14] | MNASSON N, ZECCHINA R, KIRKPATRICK S. Determining computational complexity form characteristic 'phase transitions'[J]. Nature , 1999, 400 : 133-137 DOI:10.1038/22055 |
| [15] | 林海.基于扩展规则的定理证明和知识编译[D].长春:吉林大学, 2003: 1-40. LIN Hai. Theorem proving and knowledge compilation based on the extension rule[D]. Changchun: Jilin University, 2003: 1-40. http://d.wanfangdata.com.cn/Thesis/Y527971 |
| [16] | WU Xia, SUN Jigui, LU Shuai, et al. Improved propositional extension rule[C]//Proceedings of the First International Conference on Rough Sets and Knowledge Technology. Chongqing, China, 2006: 592-597. |
| [17] | 吴瑕.基于扩展规则的定理证明的研究[D].长春:吉林大学, 2006: 1-132. WU Xia. The research on the extension rule based theorem proving[D]. Changchun: Jilin University, 2006: 1-132. http://cdmd.cnki.com.cn/article/cdmd-10183-2006094302.htm |
| [18] | 李莹, 孙吉贵, 吴瑕, 等. 基于IMOM和IBOHM启发式策略的扩展规则算法[J]. 软件学报 , 2009, 20 (6) : 1521-1527 LI Ying, SUN Jigui, WU Xia, et al. Extension rule algorithms based on IMOM and IBOHM heuristics strategies[J]. Journal of Software , 2009, 20 (6) : 1521-1527 DOI:10.3724/SP.J.1001.2009.03420 |
| [19] | WU Xia, SUN Jigui, LU Shuai, et al. Propositional extension rule with reduction[J]. International Journal of Computer Science and Network Security , 2006, 6 (1A) : 190-197 |
| [20] | 孙吉贵, 李莹, 朱兴军, 等. 一种新的基于扩展规则的定理证明算法[J]. 计算机研究与发展 , 2009, 46 (1) : 9-14 SUN Jigui, LI Ying, ZHU Xingjun, et al. A novel theorem proving algorithm based on extension rule[J]. Journal of Computer Research and Development , 2009, 46 (1) : 9-14 |
| [21] | 张立明, 欧阳丹彤, 白洪涛. 基于半扩展规则的定理证明方法[J]. 计算机研究与发展 , 2010, 49 (7) : 1522-1529 ZHANG Liming, OUYANG Dangtong, BAI Hongtao. Theorem proving algorithm based on semi-extension rule[J]. Journal of Computer Research and Development , 2010, 49 (7) : 1522-1529 |
| [22] | ZHANG Liming, OUYANG Dantong, ZHAO Jian, et al. The parallel theorem proving algorithm based on semi-extension rule[J]. Applied Mathematics & Information Sciences , 2012, 6 (1) : 119-122 |
| [23] | YIN Liangze, HE Fei, HUNG W N N, et al. Maxterm covering for satisfiability[J]. IEEE Transactions on Computers , 2012, 61 (3) : 420-426 DOI:10.1109/TC.2010.270 |
| [24] | XU Youjun, OUYANG Dantong, YE Yuxin, et al. Solving SAT problem with a revised hitting set algorithm[C]//Proceedings of the 2nd International Conference on Future Computer and Communication. Wuhan, China, 2010: 653-656. |
| [25] | 许有军.基于扩展规则的若干SAT问题研究[D].长春:吉林大学, 2011: 1-91. XU Youjun. Research on several SAT issues based on extension rule[D]. Changchun: Jilin University, 2011: 1-91. http://cdmd.cnki.com.cn/Article/CDMD-10183-1011106010.htm |
| [26] | LIN Hai, SUN Jigui. Knowledge compilation using the extension rule[J]. Journal of Automated Reasoning , 2004, 32 (2) : 93-102 DOI:10.1023/B:JARS.0000029959.45572.44 |
| [27] | 谷文祥, 赵晓威, 殷明浩. 知识编译研究[J]. 计算机科学 , 2010, 37 (7) : 20-26 GU Wenxiang, ZHAO Xiaowei, YIN Minghao. Knowledge compilation survey[J]. Computer Science , 2010, 37 (7) : 20-26 |
| [28] | MURRAY N V, ROSENTHAL E. Duality in knowledge compilation techniques[C]//Proceedings of the 15th International Symposium on Foundations of Intelligent Systems. Saratoga Springs, USA, 2005: 182-190. |
| [29] | 谷文祥, 王金艳, 殷明浩. 基于MCN和MO启发式策略的扩展规则知识编译方法[J]. 计算机研究与发展 , 2011, 48 (11) : 2064-2073 GU Wenxiang, WANG Jinyan, YIN Minghao. Knowledge compilation using extension rule based on MCN and MO heuristic strategies[J]. Journal of Computer Research and Development , 2011, 48 (11) : 2064-2073 |
| [30] | 赖永.基于EPCCL理论的知识编译方法[D].长春:吉林大学, 2010: 1-46. LAI Yong. Research on the knowledge compilation method based on the EPCCL theory[D]. Changchun: Jilin University, 2010: 1-46. http://www.shangxueba.com/lunwen/v392830.html |
| [31] | 刘大有, 赖永, 林海. C2E:一个高性能的EPCCL编译器[J]. 计算机学报 , 2013, 36 (6) : 1254-1260 LIU Dayou, LAI Yong, LIN Hai. C2E: an EPCCL compiler with good performance[J]. Chinese Journal of Computers , 2013, 36 (6) : 1254-1260 |
| [32] | YIN Minghao, LIN Hai, SUN Jigui. Counting models using extension rules[C]//Proceedings of the Twenty-Second National Conference on Artificial Intelligence. Vancouver, Canada, 2007: 1916-1917. |
| [33] | 殷明浩, 林海, 孙吉贵. 一种基于扩展规则的#SAT求解系统[J]. 软件学报 , 2009, 20 (7) : 1714-1725 YIN Minghao, LIN Hai, SUN Jigui. Solving #SAT using extension rules[J]. Journal of Software , 2009, 20 (7) : 1714-1725 |
| [34] | BIRNBAUM E, LOZINSKII E. The good old Davis-Putnam procedure helps counting models[J]. Journal of Artificial Intelligence Research , 1999, 10 : 457-477 |
| [35] | BACCHUS F, DALMAO S, PITASSI T. Algorithms and complexity results for #SAT and Bayesian inference[C]//Proceedings of the 44th Symposium on Foundations of Computer Science. Cambridge, USA, 2003: 340-351. |
| [36] | 许有军, 欧阳丹彤, 叶育鑫, 等. 间接使用扩展规则求解#SAT问题[J]. 吉林大学学报:工学版 , 2011, 41 (4) : 1047-1053 XU Youjun, OUYANG Dantong, YE Yuxin, et al. Solving #SAT with extension rule indirectly[J]. Journal of Jilin University: Engineering and Technology Edition , 2011, 41 (4) : 1047-1053 |
| [37] | HOOKER J N, RAGO G, CHANDRU V, et al. Partial instantiation methods for inference in first-order logic[J]. Journal of Automated Reasoning , 2002, 28 (4) : 371-396 DOI:10.1023/A:1015854101244 |
| [38] | WU Xia, SUN Jigui, HOU Kun. Extension rule in first order logic[C]//Proceedings of the 5th International Conference on Cognitive Informatics. Beijing, China, 2006: 701-706. |
| [39] | BAADER F, CALVANESE D, MCGUINNESS D, et al. The description logic handbook: theory, implementation and applications[M]. New York: Cambridge University Press, 2003 . |
| [40] | ZOU Tingting, LIU Lei, LU Shuai. Knowledge compilation for description logic based on concept extension rule[J]. Journal of Computational Information System , 2012, 8 (6) : 2409-2416 |
| [41] | HALPERN J Y, MOSES Y. A guide to completeness and complexity for modal logics of knowledge and belief[J]. Artificial Intelligence , 1992, 54 (3) : 319-379 DOI:10.1016/0004-3702(92)90049-4 |
| [42] | WU Xia, SUN Jigui. Destructive extension rule in proposition modal logic K[M]//LIU G R, TAN V B C, HAN X. Computational Methods. Dordrecht, The Netherlands: Springer, 2006: 1087-1091. |
| [43] | WU Xia, SUN Jigui, LIN Hai, et al. Modal extension rule[J]. Progress in Natural Science , 2005, 15 (6) : 550-558 DOI:10.1080/10020070512331342540 |
| [44] | DUBOIS D, PRADE H. Possibilistic logic: a retrospective and prospective view[J]. Fuzzy Sets and Systems , 2004, 144 (1) : 3-23 DOI:10.1016/j.fss.2003.10.011 |
| [45] | 殷明浩, 孙吉贵, 林海, 等. 可能性扩展规则的推理和知识编译[J]. 软件学报 , 2010, 21 (11) : 2826-2837 YIN Minghao, SUN Jigui, LIN Hai, et al. Possibilistic extension rules for reasoning and knowledge compilation[J]. Journal of Software , 2010, 21 (11) : 2826-2837 |
| [46] | 谷文祥, 郭鸿鹤, 殷明浩, 等. 多值知识编译[J]. 东北师范大学学报:自然科学版 , 2011, 43 (4) : 44-48 GU Xenxiang, GUO Honghe, YIN Minghao, et al. Compiling multi-valued knowledge base[J]. Journal of Northeast Normal University: Natural Science Edition , 2011, 43 (4) : 44-48 |



