随着中国工业化进程的迅速加快和汽车保有量的急剧增长,能源危机迫在眉睫,同时,汽车发动机燃烧后排出的废气也严重污染了大气环境[1]。为应对这一系列问题,并把握我国交通能源动力系统的宝贵转型机遇,新能源汽车应运而生。但是,受制于电池技术发展的瓶颈,纯电动汽车无论在技术上还是市场上均难以普及。增程式电动汽车 (REEV) 因既具有纯电动汽车污染小、能耗低的优点,同时又能实现较长续驶里程, 已经成为传统内燃机汽车与纯电动汽车之间的理想过渡车型。能耗与污染气体排放是衡量新能源汽车的重要指标,CO是汽车主要的排放污染物之一,确定功率需求之后,以油耗和污染气体排放最小为目标,确定增程器工作点,是增程式电动汽车能量管理与运行优化的重要研究方向之一[2]。文献[3-5]分别通过不同的控制策略来实现电动汽车的节能优化;文献[6]以碳排放为优化对象进行了电动汽车充电站的规划;文献[7]也针对货车的污染物排放进行了研究;尽管上述方法都通过不同途径实现了汽车的运行优化,但是都没有在发动机实际限制条件下同时考虑油耗及污染物气体排放。为解决工业应用中经常遇到的各种优化问题,学者们提出了多种优化算法,文献[8]提出一种改进的教与学优化算法提高BP神经网络的输出精度;文献[9]基于鱼群算法完成了仿人机器人的步态优化。本文所选用的萤火虫算法 (FA) 是由剑桥学者Yang[10]在2008年提出的一种随机优化算法, 已经应用与多种工程实践之中,运用萤火虫优化算法,在考虑发动机的油耗的同时兼顾CO排放优化问题,实现了增程式电动汽车运行优化研究。
1 萤火虫优化算法 1.1 萤火虫优化算法以模拟自然界生物觅食或信息交换过程为特色的群智能优化算法是近年来备受关注的研究领域之一。萤火虫算法模拟自然界中萤火虫之间因觅食及择偶等活动中产生的依靠光照亮度而相互吸引的合作行为。每个萤火虫均是一个存在于种群中的独立个体,它们都具有一定的感知能力,不同的萤火虫发出的光强弱不一,搜索范围内发光弱的萤火虫被发光强的萤火虫所吸引,并在萤火虫之间的移动过程中实现位置迭代,寻找最优解的过程就是寻找最亮的萤火虫的过程,搜索过程就是不断的迭代过程,在不断的迭代中实现寻优[11]。
1.2 主要参数介绍FA算法中,萤火虫的寻优主要与几个重要参数相关,即萤火虫的荧光亮度和萤火虫的相互吸引度及种群规模。萤火虫的荧光亮度代表着萤火虫所处空间位置的“好坏”,荧光最亮的萤火虫位置就是所要寻找的最优点的位置,同时,荧光越亮的萤火虫对周围萤火虫的吸引度越高,且这两个重要参数均与距离成反比关系,即距离越大,两者吸引度越小。
1) 荧光亮度S(r):如式 (1) 所示,S0代表最亮的萤火虫荧光亮度,与寻优的目标函数值相关,目标函数值越优自身亮度越高;β表示光吸收系数,因为光在传播过程中荧光会随着距离增加而减弱,光吸收系数体现荧光减弱的速度,实际优化中,β ∈[0.01, 1, ], r表示萤火虫之间的距离。
 |
(1) |
2) 相互吸引度γ:如式 (2) 所示,γ0指最亮萤火虫的吸引度,即光源吸引度 (r=0)。
 |
(2) |
3) 种群规模M及最大迭代次数g:种群规模大小及迭代次数影响寻优的准确度及速度,一般选择20~60,特定问题可以取到100~200,而继续增大M对增强算法准确度并无明显效果,反而将显著增加计算量,反而不利于寻优。
确定几个重要参数之后,各萤火虫即可通过迭代不断寻优,其位置更新公式如式 (3):
 |
(3) |
式中:ζ是[0,1]上的随机常数,εi为[0,1]上服从正态分布的随机因子。
1.3 主要流程算法1 FA (t, β, γ0, g,M)
初始化: t=0,xi(t)=rand, β=0.4,γ0=1.0,g=60;
计算各萤火虫适应度值:Fi(t)=F(xi(t));
While (t<g)
for (i=1:M)
for (j=1:i)
计算萤火虫Xi荧光强度Si(r)
if (Si(r)<Sj(r))
萤火虫i向萤火虫j移动
end if
计算更新的荧光强度
end
end
萤火虫进行排序,找出当前最优解
end
FA算法中各萤火虫按照上述步骤迭代寻找到最优值。
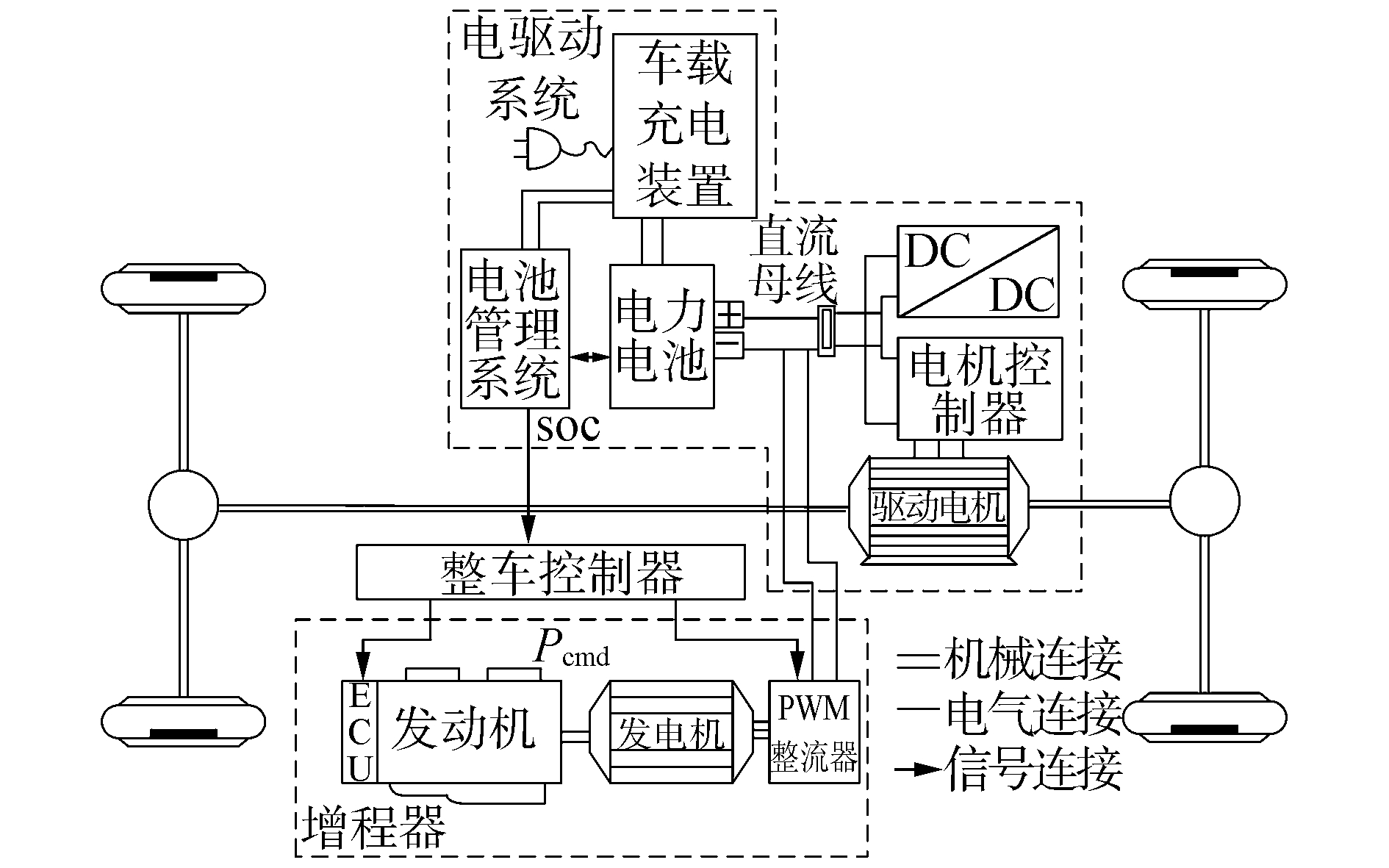
2 电动汽车运行优化问题文章所研究的增程式电动汽车动力系统结构如图 1所示,电驱动系统、增程器系统以及整车控制系统共同构成了车辆动力系统。电驱动系统与整车控制系统相互配合即可实现电动汽车的纯电行驶,但由于动力电池容量较小,纯电动行驶续驶里程较短。即当动力电池电量 (Soc) 消耗至最低临界限值Socmin时,需要启动增程器 (APU) 为整车提供能量从而延长汽车续驶里程。APU由发动机、发电机和PWM整流器组成。如式 (4):
|
| 图 1 增程式电动汽车动力系统结构示意图 Fig. 1 Schematic of the power-train of REEV |
 |
(4) |
车辆运行过程中,整车控制器根据动力电池提供的功率PBAT及整车实时功率需求P向APU发出功率需求PAPU。由于增程式电动汽车车辆驱动轮仅与驱动电机机械相连,而与APU相互隔离,因此发动机转速和转矩可以运行在满足功率要求的任意工作点上,而发动机的油耗和CO排放由其工作点决定,因此,控制发动机的工作点可以实现对其油耗及CO排放的优化。
为衡量增程式电动汽车燃油经济性能,常常用到有效燃油消耗率 (BSFC),它是指单位有效功的耗油量,通常用每千瓦小时有效功所消耗的燃油克数来表示,有效燃油消耗率越低,经济性越好。类似地,以每千瓦小时有效功所排放的气体克数来衡量增程式电动汽车排放性能。由于APU的有效燃油消耗率及有效CO排放率直接取决于起工作点 (N, T),根据发动机最佳BSFC和排放性能及实时功率需求来确定工作点可以有效减少能源消耗及CO排放。
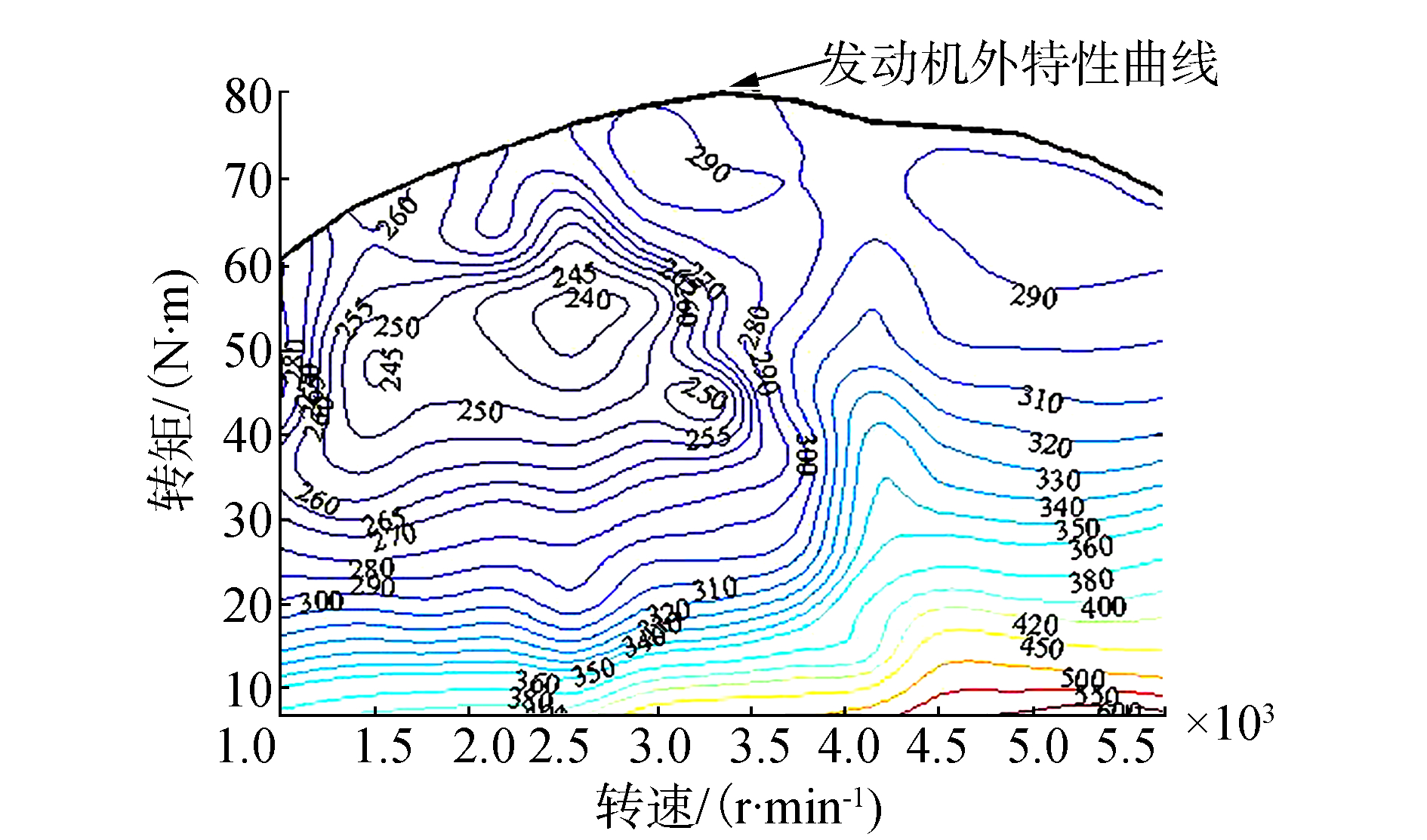
2.1 电动汽车增程器油耗及排放模型在MATLAB环境下,以某峰值功率为40 kW,排气量为1.0 L的自然吸气汽油发动机为研究对象,根据GB/T18297-2001规定的发动机试验方法[12],分别在27×8个转速、转矩点上测量发动机的油耗率及CO排放,然后采用双三次插值法,分别得到如图 2、图 3所示的发动机的转速-转矩-油耗率特性Map图及转速-转矩-CO排放特性Map图,其中的黑色粗实线表征的外特性曲线是指发动机工作在全负荷状态下时的速度转矩特性,它表示APU所能达到的最大动力性能,即APU实际可运行区域。
|
| 图 2 发动机转速-转矩-油耗率特性 Fig. 2 Speed-torque-fuel consumption rate characters of the engine |

|
| 图 3 发动机转速-转矩-CO排放率特性 Fig. 3 Speed-torque-CO consumption rate characters of the engine |
不同的工作点 (N,T) 对应不同的油耗率及CO排放,等高线分别为等油耗率线及等CO排放线。
由图 2、图 3可知,油耗与CO的优化方向并不完全重合,有时甚至会相互冲突。
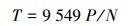 |
(5) |
式中:P、T、N分别为发动机功率、转矩、转速,整车控制器根据动力电池提供的功率及整车实时功率需求向APU发出功率需求PAPU,根据PAPU可以在转速-转矩-油耗率及转速-转矩-CO特性Map图上分别得到工作点可运行范围,在可运行范围上找到油耗率最低及CO排放最少的点即为分别的最优点。
如式 (6) 所示,APU油耗优化问题及CO排放优化问题可以等效为以油耗率及CO排放率为目标函数,以APU转速N和转矩T为优化变量的最小化优化问题,即
 |
(6) |
式中:W(N,T) 为APU对应的工作点,WFC及WCO分别为APU工作点对应的油耗率及CO排放率。
2.2 电动汽车增程器综合成本模型实际的增程器系统需要同时考虑燃油效率及CO排放多个目标,并且多个目标之间存在一定的冲突,难以寻找到一个能使多个目标均实现最优化的解。文章采用多目标加权求和的方法,构建增程器综合成本,赋予燃油效率及CO排放不同的权重值,将多目标优化问题转化为一个单目标优化问题,降低了计算量,同时能根据不同的实际需要分配不同权重值而实现对特定要求的工作点优化。由式 (7),先将目标函数转化为[0,1]内的无量量纲,
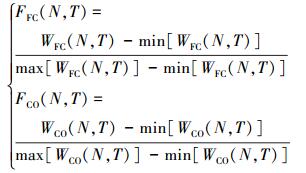 |
(7) |
归一化后,根据式 (8) 对增程器特性进行加权平均操作:
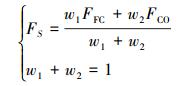 |
(8) |
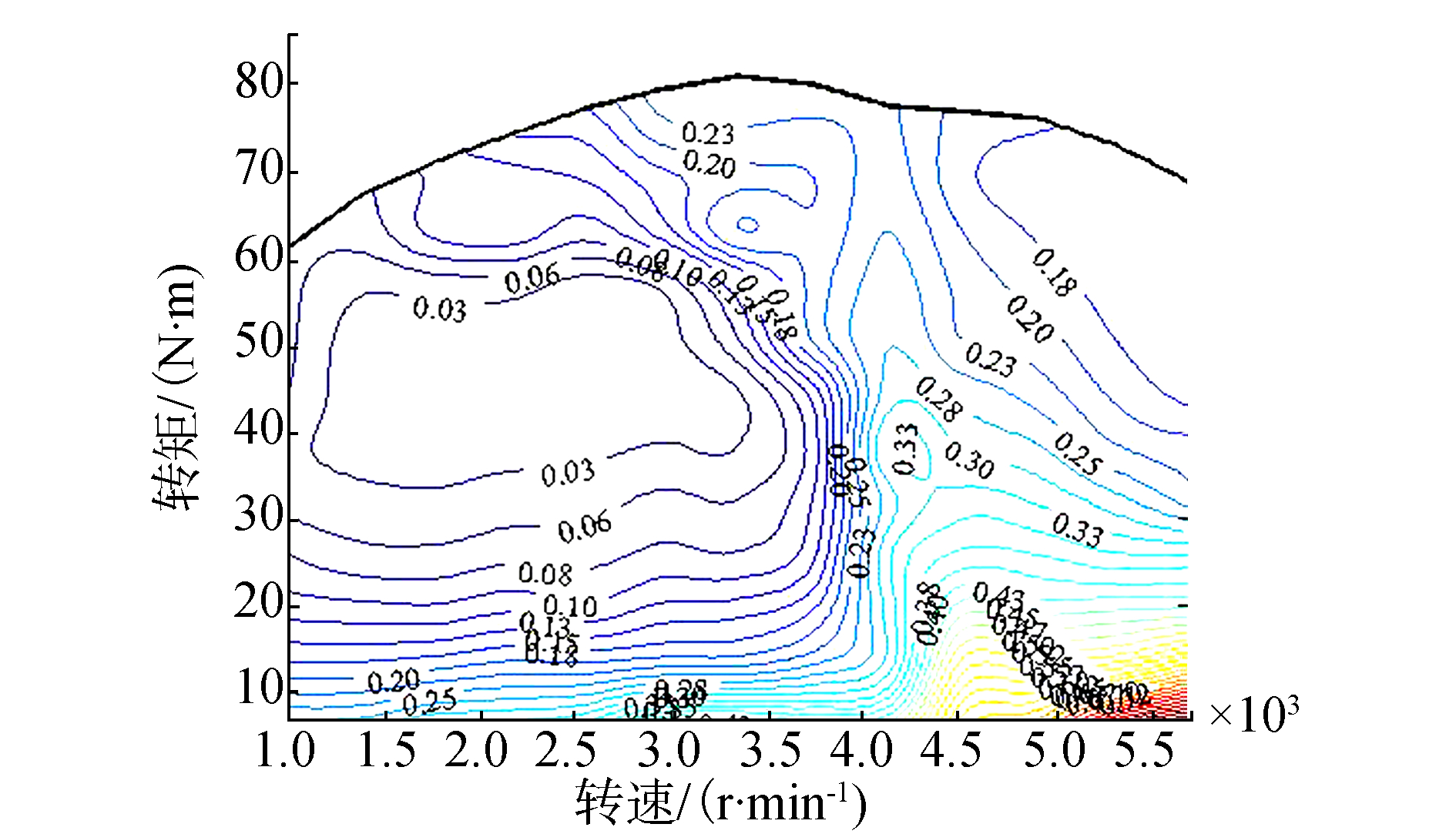
式中:w1及w2两项即为油耗率和CO排放的权重值,表示系统对两项分别的“重视程度”,通过调整w1及w2的值对油耗和CO排放进行优化。图 4为初始化设置w1=w2=0.5时,即同等程度重视油耗率及CO排放时的发动机转速-转矩-综合成本特性Map图。
|
| 图 4 发动机转速-转矩-综合成本特性 Fig. 4 Speed-torque-composite cost characters of the engine |
根据式 (8) 可以动态调整w1与w2的值来实现电动汽车综合成本运行优化,其运行优化的标准为:
1) 根据不同国家或者地区对汽车油耗率或者排放的不同规定,动态调整w1与w2的值,直至达标;
2) 根据车辆运行环境,动态调整w1与w2的值以避免环境的进一步恶化,例如当车辆行驶在空气质量较好的农村地带或者城市郊区时,可以通过增大w1来重点实现汽车油耗率的优化,而在空气污染严重的城市中心或者工业区时,增大w2以重点改善车辆排放性能。
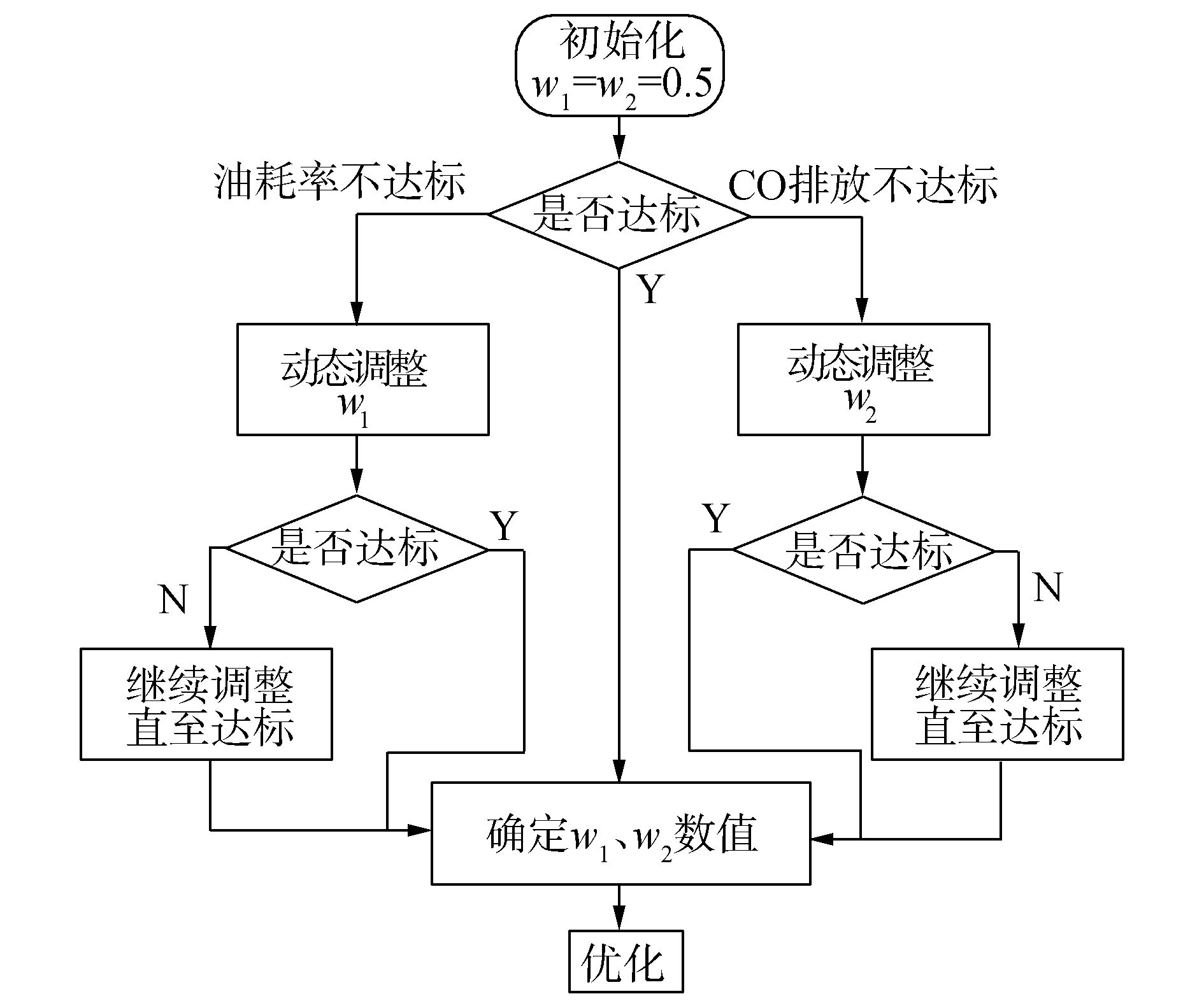
其中wi(i=1, 2) 按图 5所示流程及式 (9) 进行动态调整:
|
| 图 5 权重调整流程图 Fig. 5 Diagram of weight adjustment process |
 |
(9) |
至此,以发动机转速N和转矩T为优化变量,以APU油耗率和CO排放率构成的综合成本为优化目标,并通过发动机外特性作为约束条件的电动汽车增程器综合成本优化模型成功建立。
3 优化结果及对比分析根据以上分析,在已经建立的电动汽车增程器综合成本模型下,按照1.3节说明的算法执行流程,对发动机工作点进行FA优化。
3.1 全局优化全局优化模式下,首先初始化设置w1=w2=0.5时,萤火虫在满足外特性条件的全部范围内寻优,优化结果如图 6所示。此时,N= 2 540.8 r/m,T=49.3 N·m时,综合成本取得最小值FS=0.01。

|
| 图 6 全局优化时最优解分布情况 Fig. 6 Distribution of the firely optimal solution in solution space |
当整车控制器对APU发出特定的功率点需求PAPU时,发动机将工作在整车控制器指定的功率点上,此时的可运行工作点为功率为PAPU的等功率线上,如图 7所示黑色实线即为PAPU=25 kW时APU工作区间,优化变量需要满足式 (10)。

|
| 图 7 Pcmd=25 kW时APU工作区间 Fig. 7 Feasible operating area when Pcmd=25 kW |
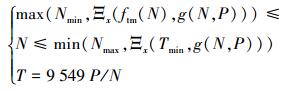 |
(10) |
式中:Ξx(ftm(N), g(N, P)) 表示APU外特性曲线ftm(N) 与等功率线g (N,Pmin) 的交点处转速,Ξx(Tmin, g(N, P)) 为APU最小功率与功率等高线g(n,P) 交点处的转速,图 8即为PAPU=25 kW,且w1=w2=0.5时综合成本优化结果。此时,N= 3 453.1 r·min-1,T=69.1 Nm时,综合成本取得最小值FS=0.19。

|
| 图 8 Pcmd=25 kW时最优解分布情况 Fig. 8 Distribution of the firely optimal solution when Pcmd=25 kW |
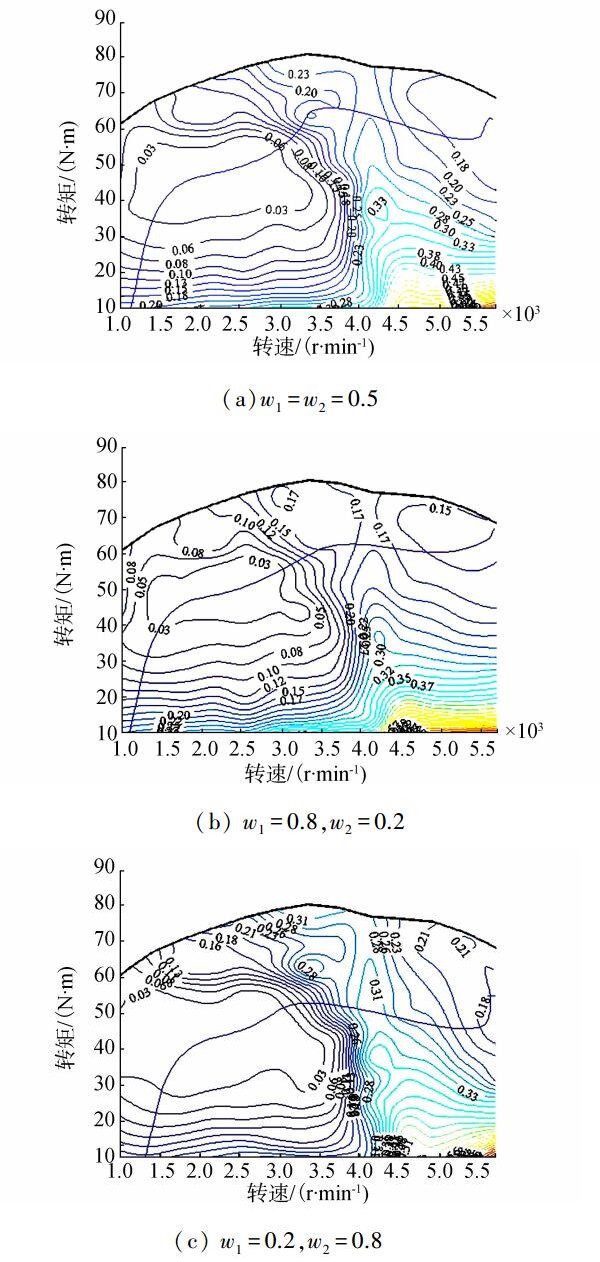
设定功率值从1 kW~40 kW,以每隔3 kW为间隔,在w1=w2=0.5时利用FA算法模型进行APU综合成本优化,即可得到APU最佳综合成本运行曲线,如图 9(a)所示, 当车辆需要更多考虑减小油耗率时,动态调整至w1=0.8,w2=0.2,而当车辆需要更多考虑减少CO排放时,动态调整w1=0.2,w2=0.8对工作点进行寻优,改善车辆的排放性能,而得到的APU最佳综合成本运行曲线的结果分别如图 9(b)、(c)所示。比较3张图,基于不同的权重考虑下,APU最佳综合成本运行曲线会发生明显变化,以寻求不同目的下的油耗率及CO排放率的共同优化。
|
| 图 9 基于PSO算法的最佳综合成本曲线 Fig. 9 The best composite cost curve based on PSO model |
为应对日益严峻的能源危机与环境污染问题,文章讨论的增程式电动汽车增程器发动机在其外特性基本限制条件下,综合考虑了燃油消耗及CO排放特性,并在MATLAB环境下建立了基于两者的综合成本模型,实现了基于萤火虫算法的全局优化及特定功率点的优化,最后在3种不同权重条件下完成了最佳综合成本运行曲线的绘制,通过3种曲线的对比表明,基于基于萤火虫算法的电动汽车综合成本研究能实现不同情况下的运行优化。
| [1] | 支树模. 汽车排放污染物控制与零排放净化技术[M]. 北京: 中国标准出版社, 2012: 1-5. |
| [2] | EHSANI M, GAO Yimim, EMADI A. Modern electric, hybrid electric, and fuel cell vehicles fundameentals, theory and design second edition[M]. 2nd ed. Boca Raton, FL: CRC Press, 2009. |
| [3] |
闵海涛, 叶冬金, 于远彬. 增程式电动汽车控制策略的优化[J].
汽车工程, 2014, 36(8): 899-903.
MIN Haitao, YE Dongjin, YU Yuanbin. Optimization of the control strategy for range extended electric vehicle[J]. Automotive engineering, 2014, 36(8): 899-903. |
| [4] | SUN Dongye, LIN Xinyou, QIN Datong, et al. Power-balancing instantaneous optimization energy management for a novel series-parallel hybrid electric bus[J]. Chinese journal of mechanical engineering, 2012, 25(6): 1161-1170. DOI:10.3901/CJME.2012.06.1161. |
| [5] | CERAOLO M, DI DONATO A, FRANCESCHI G. A general approach to energy optimization of hybrid electric vehicles[J]. IEEE transactions on vehicular technology, 2008, 57(3): 1433-1441. DOI:10.1109/TVT.2007.909268. |
| [6] |
陈光, 毛召磊, 李济沅, 等. 计及碳排放的电动汽车充电站多目标规划[J].
电力系统自动化, 2014, 38(17): 49-53. .
CHEN Guang, MAO Zhaolei, LI Jiyuan, et al. Multi-objective optimal planning of electric vehicle charging stations considering carbon emission[J]. Automation of electric power systems, 2014, 38(17): 49-53. DOI:10.7500/AEPS20140505005. |
| [7] |
王军方, 付明亮, 丁焰, 等. 低速货车的污染物排放特性[J].
农业工程学报, 2014, 30(14): 57-63. .
WANG Junfang, FU Mingliang, DING Yan, et al. Emissions characteristics of low speed vehicles[J]. Transactions of the Chinese society of agricultural engineering, 2014, 30(14): 57-63. DOI:10.3969/j.issn.1002-6819.2014.14.008. |
| [8] |
拓守恒. 一种优化神经网络的教与学优化算法[J].
智能系统学报, 2013, 8(4): 327-332.
TUO Shouheng. A modified teaching-learning-based optimization algorithm and application in neural networks[J]. CAAI transactions on intelligent systems, 2013, 8(4): 327-332. |
| [9] |
卢嘉敏, 杨宜民, 付根平. 基于鱼群算法的仿人机器人步态优化[J].
智能系统学报, 2013, 8(6): 526-531.
LU Jiamin, YANG Yimin, FU Genping. Research on the gait optimization of humanoid robots based on the fish swarm algorithm[J]. CAAI transactions on intelligent systems, 2013, 8(6): 526-531. |
| [10] |
曾冰, 李明富, 张翼, 等. 基于萤火虫算法的装配序列规划研究[J].
机械工程学报, 2013, 49(11): 177-184.
ZENG Bing, LI Mingfu, ZHANG Yi, et al. Research on assembly sequence planning based on firefly algorithm[J]. Journal of mechanical engineering, 2013, 49(11): 177-184. |
| [11] | 李瑞青. 改进的萤火虫算法及应用[D]. 长春: 吉林大学, 2015: 1-5. LI Ruiqing. Improved firefly algorithm and application[D]. Changchun: Jilin University, 2015: 1-5. |
| [12] | 汽车发动机标准化分技术委员会. GB/T 18297-2001, 汽车发动机性能试验方法[S]. 北京: 中国标准出版社, 2004. Automotive Engine Standardization Technical Committee. GB/T 18297-2001, Performance test code for road vehicle engines[S]. Beijing: China Standards Press, 2004. |



