2. 哈尔滨工程大学机电工程学院;
3. 海洋石油工程股份有限公司
2. College of Mechanical and Electrical Engineering, Harbin Engineering University;
3. Offshore Oil Engineering Co., Ltd
0 引言
吸力桩[1]是水下管汇、管汇终端、管道终端和水下脐带缆分配单元等水下生产结构物的基础形式,与其他基础结构(如长桩基础和防沉板基础)相比,具有较好的综合性能,其稳定性和安全性直接决定了水下生产设施的工作性能。因此,对吸力桩基础承载力进行研究具有重要意义[2]。
K.H.ANDERSEN等[3]采用有限元方法,对软黏土中吸力锚基础的承载力进行了研究,将空间三维问题简化为平面应变问题,建立了倾斜载荷作用下计算吸力锚基础承载力的数值方法。张金来等[4]通过有限元计算,分析了不同长径比下吸力桩载荷-位移曲线、水平向承载力和竖向承载力,并与试验结果进行对比分析,结果显示两者很接近。刘振纹等[5]通过数值方法,分析了竖向载荷作用下单筒式吸力桩的破坏模式,并将数值与相关理论公式计算结果进行了比较分析,显示采用汉森和魏西克公式可以较好地确定吸力桩竖向承载力。严驰等[6]通过小比尺模型试验研究了土性参数对桶型基础竖向承载力的影响,得到土体的内摩擦角、黏聚力和有效重度对桶型基础竖向承载力的影响规律,为桶型基础的设计和施工提供了理论依据。程光明等[7]对竖向载荷作用下吸力桩的受力模式进行了理论分析,并依据打入桩竖向承载力计算方法,提出了吸力桩竖向承载力的计算方法,进而分析了该方法的合理性与局限性。
综上所述,吸力桩的竖向承载力研究多集中于规律性的成果,所得到的理论公式计算方法局限性较强,导致实际应用中该方法计算结果误差较大。鉴于此,本文针对吸力桩的工作原理、特点及竖向承载力的计算方法进行探讨研究。
1 吸力桩工作原理及特点 1.1 工作原理吸力桩是一个顶端封闭、底部开口的钢圆筒结构,其外形如图 1所示。一般情况下,吸力桩顶部会使用较厚的钢板或者钢筋混凝土以便其贯入土体,并且设有可以关闭的排水/排气孔,以及与负压泵相连的抽水孔。吸力桩侧壁用钢板卷制而成,同时在桩体内焊接加强筋以提高其结构强度。有些学者建议将桩体开口端的外缘进行倒角,以减小土塞效应[8]。
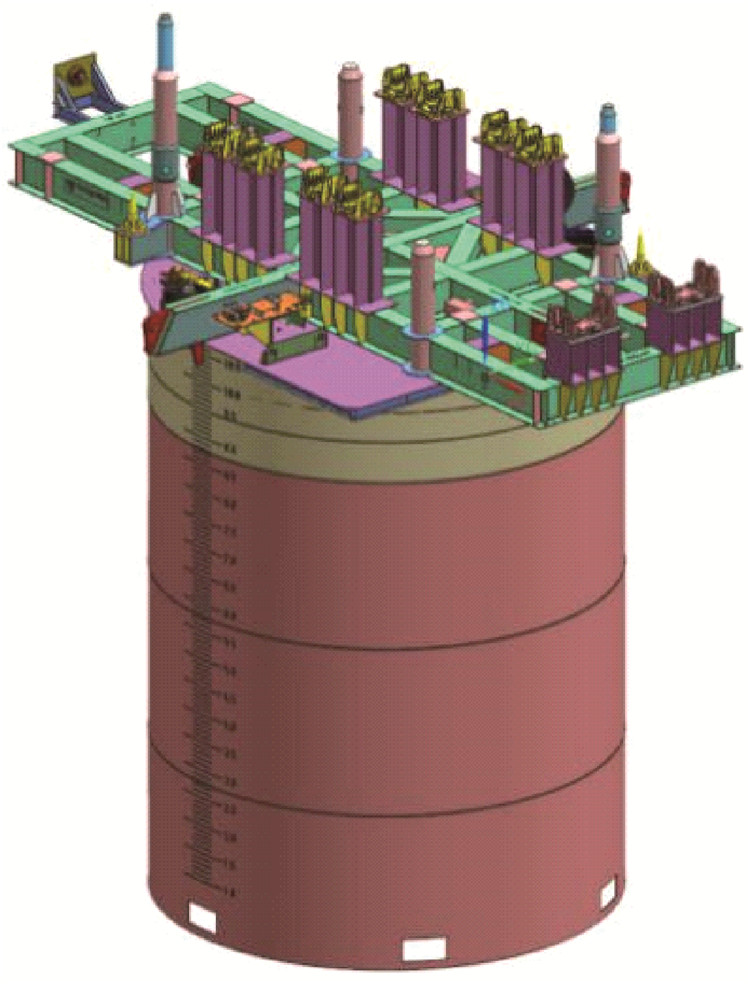
|
| 图 1 吸力桩 Fig.1 Suction pile |
在安装吸力桩时,首先通过自重贯入海底,此时桩体与土壤之间形成一个封闭空间,待贯入深度稳定后,借助负压泵以及桩顶盖上抽水口,通过吸力桩内外压差向外抽水及空气,使吸力桩以一定速度下沉,直至达到所要求的贯入深度。
当回收吸力桩时,操作负压泵,使吸力桩内部压力升高,当作用在吸力桩顶盖上的力超过其侧摩阻力、吸附力、静水压力和自重时,吸力桩开始向上运动,最终将其完全拔出,完成回收作业。
1.2 特点水下结构物的基础形式主要有长桩、吸力桩和防沉板3种。与长桩相比,吸力桩是一种非打入式基础,具有高度小和长径比大等特点,并且可以通过增大直径承受较大的外部载荷。从安装角度考虑,吸力桩埋置深度浅,通过自重和负压下沉,因此安装过程不需要动用打桩锤。当水深超过2 000 m时,打桩锤对船舶要求很高,安装施工造价昂贵,因此在超深水(1 500 m以上)长桩的应用受到了很大程度限制[9]。此外,吸力桩可以回收,进而重复利用,但长桩并不具备这一特点。
与防沉板相比,吸力桩适用于不同海床土层。对于表层较软的土层,为提供足够的承载力,通常防沉板基础尺寸较大[10],这样钢材耗费较多。
目前,在300 m以深的深水以及1 500 m以深的超深水水下生产系统中,绝大多数水下结构物的基础形式为吸力桩,其主要原因是吸力桩具有定位准确、便于回收利用、能够承受较大承载力及扭矩等优点,因此该基础形式在深水油气项目中应用越来越广泛[9, 11-12]。
2 吸力桩竖向承载力规范计算方法吸力桩作为水下结构物基础时,主要承受来自上部结构(如水下管汇和管汇终端等)的竖向载荷,其承载主要来自于桩体内外表面摩擦阻力和端部承载力[7]。因此,确定吸力桩竖向承载力就成为评价吸力桩稳定性和安全性首先要解决的问题。
考虑吸力桩外壁的摩擦阻力、桩头阻力及桩基冲刷深度,吸力桩竖向极限承载力计算式为[13]:
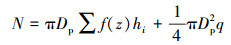
|
(1) |
式中:N为吸力桩极限竖向承载力,kN;Dp为吸力桩外径,m;hi为第i土层中吸力桩的高度,m;f(z)为第i土层吸力桩单位侧摩阻力,kPa;q为单位桩端承载力,kPa。
黏土中,沿吸力桩桩身任意一点的侧摩阻力f(z)可根据下式计算:
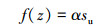
|
(2) |
式中:α为无量纲系数;su为土壤不排水抗剪强度,kPa。
系数α可参考API RP 2GEO 8.1.3节中桩的轴向承载力进行计算,即有:
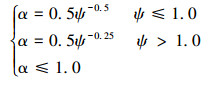
|
(3) |
其中
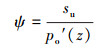
|
(4) |
式中:po′(z)为土体有效上覆压力,kPa。
单位桩端承载力可根据下式计算:
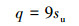
|
(5) |
非黏土中,沿吸力桩桩身任意一点的侧摩阻力f(z)可根据下式计算:
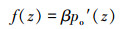
|
(6) |
式中:β为轴向无量纲系数。
单位桩端承载力可根据下式计算:
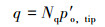
|
(7) |
式中:p′ o, tip为桩尖处有效覆盖土压力,kPa;Nq为无量纲系数。
3 吸力桩竖向承载力数值分析 3.1 竖向承载力数值模型和参数设置[14-17]本文采用满足Mohr-Coulomb强度准则的理想弹塑性本构模型描述土体的应力-应变关系,并根据空间上吸力桩-土的对称性,建立了二维轴对称有限元模型,以缩短计算时间,提高计算效率。
结合某海域实际海洋环境及吸力桩尺寸,建立了外径8 m、高度10 m、壁厚0.02 m的吸力桩有限元模型,如图 2所示。在有限元分析中,要用有限边界模拟无限边界,即在无限边界延伸的方向截取有限的边界[14-15],并假定截取边界上的位移完全约束。为避免模型边界对计算结果的影响,多数有限元分析模型尺寸取结构尺寸的3~5倍[16-17]。因此,建立了直径54 m、高度36 m的海床土层模型。

|
| 图 2 土体与吸力桩有限元模型 Fig.2 Finite element model of soil and suction pile |
有限元模型中,吸力桩物理和力学参数为:密度7 850 kg/m3,弹性模量210 GPa,泊松比0.3。黏性土体的参数为:有效容重7 kN/m3,弹性模量10 MPa,泊松比0.4,黏聚力10 kPa,内摩擦角0°。
为保证较高的计算精度且节省计算时间,采用二维轴对称数值分析吸力桩的竖向极限承载力,桩体和土体均采用八节点双线性轴对称四边形积分单元CAX8模拟。为了提高计算效率,桩体网格划分较粗。为明确桩-土之间的相互作用和屈服过程,吸力桩与土接触部分土体网格划分较细,将距吸力桩较远的土体网格划分较粗。
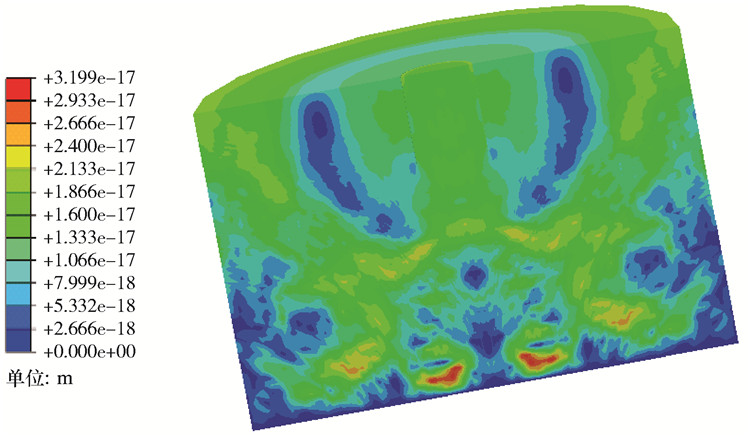
3.2 有限元计算结果及分析由于海床土体的初始地应力对计算结果的准确性有着直接影响,所以在进行吸力桩竖向承载力分析之前,先进行有限元模型的地应力平衡分析。在地应力平衡阶段,将吸力桩单元移除,仅对土体进行地应力平衡分析,在后续的分析步中激活吸力桩单元。图 3和图 4为地应力平衡完成后土体的应力分布与位移分布云图。从图 3和图 4可以看出,地应力平衡后,土体应力为103量级而无应变,能较好地模拟土体有应力、无位移的初始状态。

|
| 图 3 自重作用下土体的Mises应力云图 Fig.3 Mises stress distribution of soil under the action of suction pile |
|
| 图 4 自重作用下土体的位移云图 Fig.4 Displacement distribution of soil under the action of suction pile |
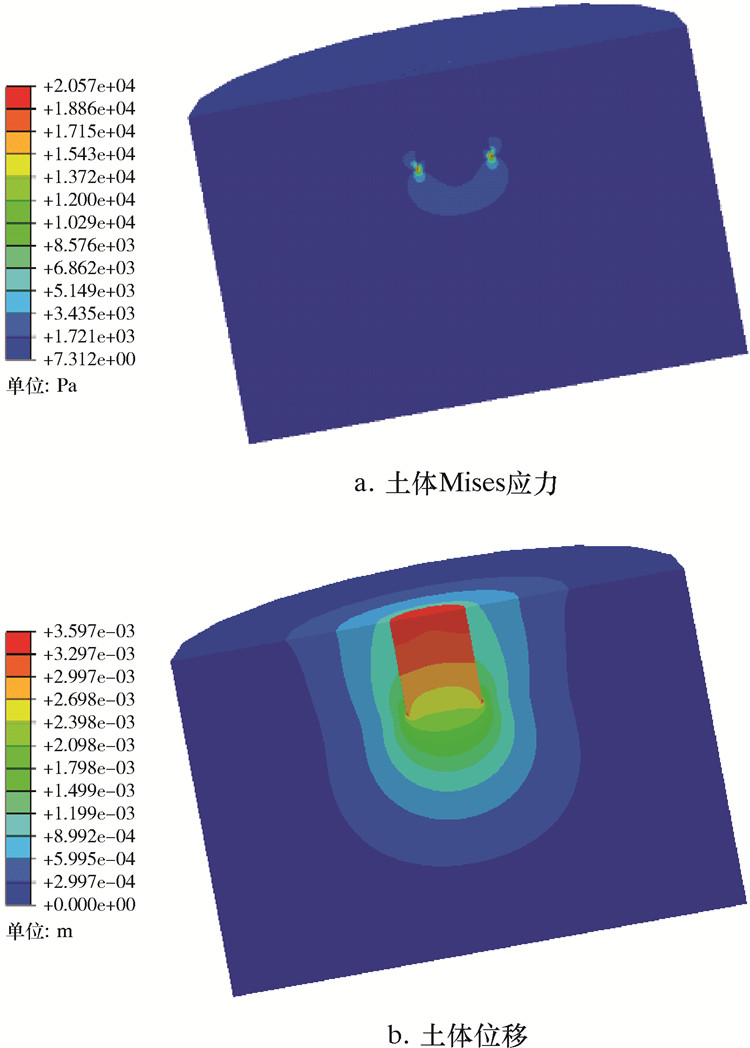
为了模拟自重作用下吸力桩的受力情况,在完成地应力平衡分析后,激活吸力桩单元和吸力桩与土体之间的接触,并施加吸力桩自重,保持土体边界条件不变。图 5为计算得到的吸力桩自重作用下土体的应力和位移分布图。由图 5可见,在吸力桩自重作用下,桩体和土体会发生一定的位移(沉降),为10-3~10-4 m量级。
|
| 图 5 吸力桩自重作用下土体Mises应力与竖直位移 Fig.5 Mises stress and vertical displacement of soil under the action of suction pile |
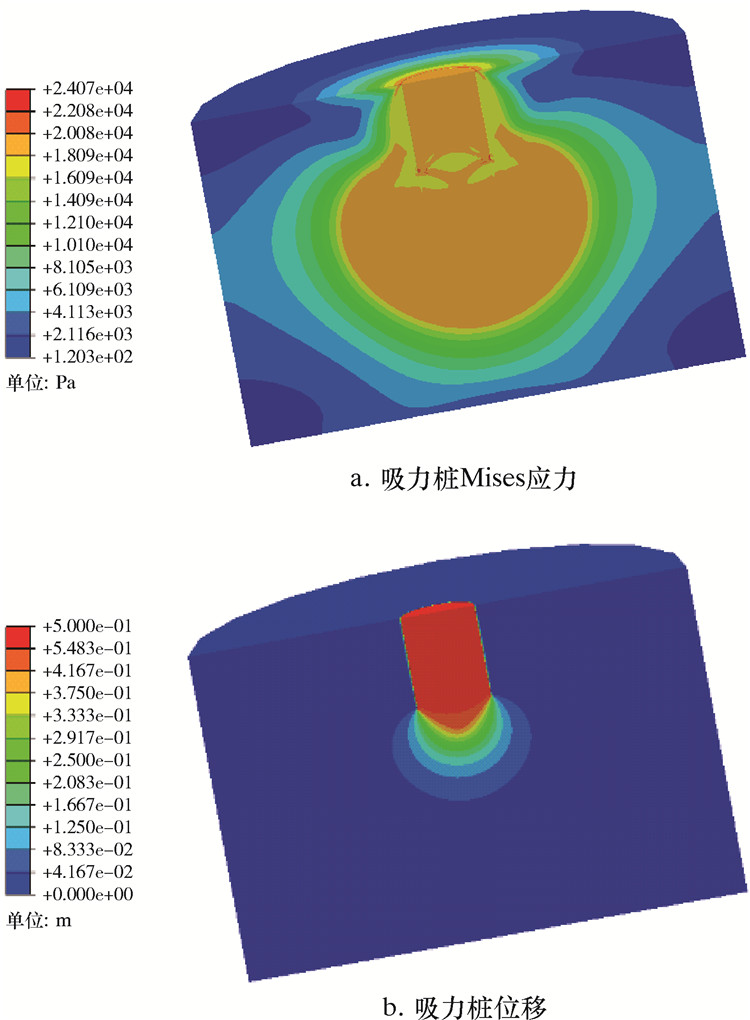
在以上分析后,进行竖向载荷作用下吸力桩极限承载力数值模拟。采用位移控制模式,分析吸力桩的竖向极限承载力。图 6为竖向载荷作用下吸力桩应力与位移分布云图。
|
| 图 6 吸力桩Mises应力与位移分布云图 Fig.6 Mises stress and displacement distribution of suction pile |
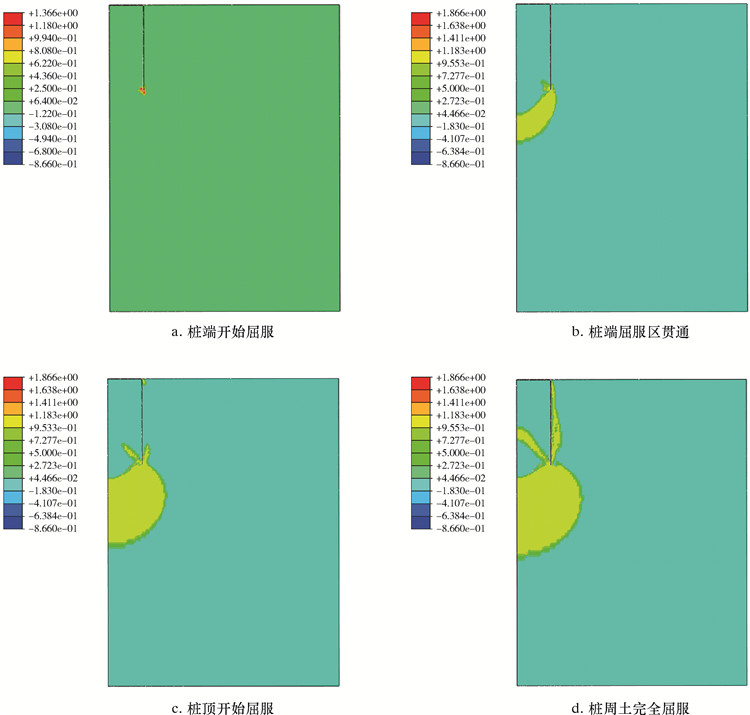
图 7为吸力桩周土体屈服过程图。图 7显示,加载初期,屈服主要出现在桩端土体。随着竖向位移的不断增加,桩端土体屈服区不断扩展,并最终完全贯通。随后,顶部土体开始出现屈服,并逐渐向下扩展,随着竖向位移的进一步增加,整个桩周土体屈服区完全贯通。这从侧面体现了吸力桩在竖向载荷作用下,桩端阻力先发挥,桩侧阻力后发挥。
|
| 图 7 吸力桩周土体屈服过程 Fig.7 Yield process of soil around suction pile |
提取吸力桩的载荷-位移曲线,结果如图 8所示。由图 8可以看出,吸力桩在竖向位移为0.13 m时达到拐点,此时对应的载荷约为7 000 kN。
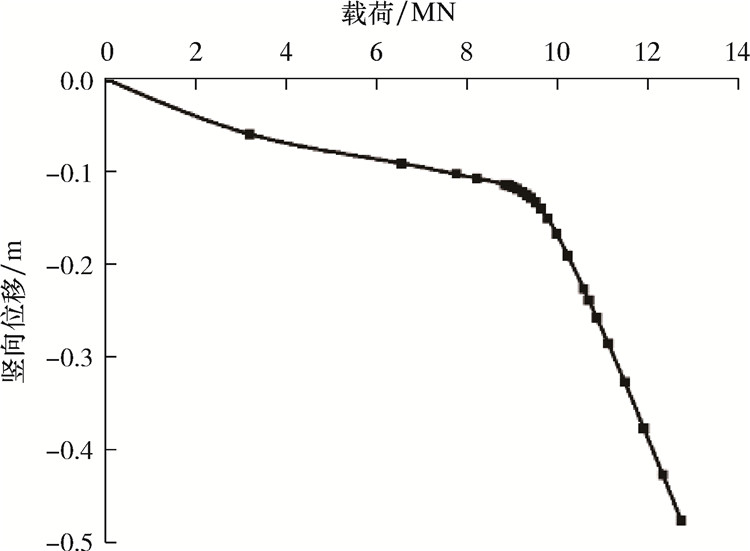
|
| 图 8 吸力桩竖向载荷-位移曲线 Fig.8 Vertical load-displacement curve of suction pile |
3.3 数值分析与规范计算结果对比
根据专著《海洋石油工程边际油气田开发技术》,吸力桩的竖向承载力计算式如式(1)所示。
根据API RP 2GEO,计算得吸力桩达到其竖向极限承载力时,侧摩阻力随深度的分布曲线,如图 9所示。
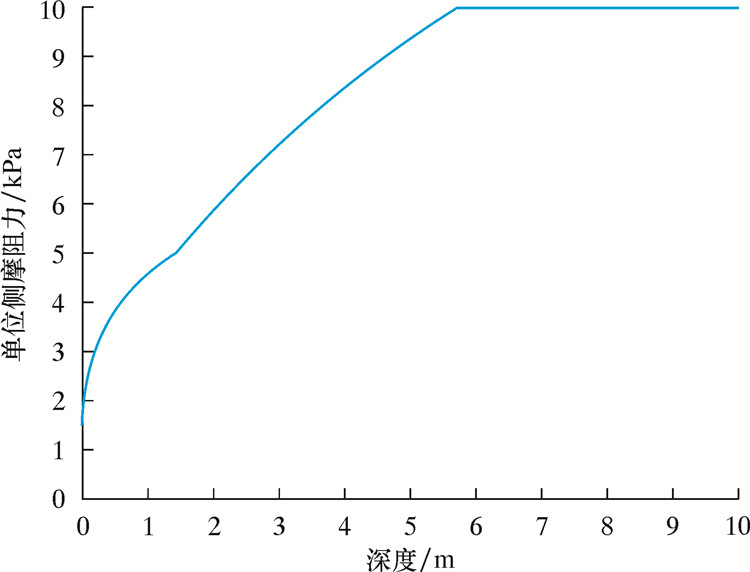
|
| 图 9 吸力桩侧摩阻力随深度的分布曲线 Fig.9 Distribution curve of lateral friction resistance of suction pile with depth |
从图 9可以看出,吸力桩在达到竖向极限承载力时,最初单位侧摩阻力随着深度的增加满足公式(8)。
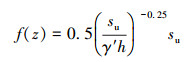
|
(8) |
式中:γ′为土体的有效容重。当深度达到1.429 m后,此时ψ≤1,单位侧摩阻力随着深度的增加满足下式:
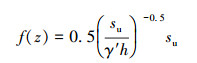
|
(9) |
当深度达到5.714 m后,单位侧摩阻力为10 kPa,不再发生变化。
公式计算得到的吸力桩竖向极限承载力为6 582.4 kN,有限元分析求得的竖向极限承载力与采用理论公式计算的结果偏差为6.34%,按规范计算与有限元仿真求得的结果很接近。
4 结论为了研究吸力桩的竖向承载力,采用理论公式计算和有限元仿真两种方法对极限承载力进行了求解,得到以下结论。
(1) 采用数值计算方法,得到了吸力桩的载荷-位移曲线,并得出吸力桩的竖向承载力约为7 000 kN。
(2) 根据理论公式计算得到了吸力桩竖向极限承载力为6 582.4 kN,并与数值分析结果进行对比,有限元分析求得的吸力桩竖向承载力与理论公式计算结果偏差为6.34%。
(3) 通过分析吸力桩桩周土体的屈服过程,发现在加载初期,屈服主要出现在桩端土体,随后桩端屈服区不断扩展,顶部土体开始出现屈服,并逐渐向下扩展,最终整个屈服区完全贯通。
| [1] |
李志刚, 贾鹏, 王洪海, 等. 水下生产系统发展现状和研究热点[J]. 哈尔滨工程大学学报, 2019, 40(5): 944-952. LI Z G, JIA P, WANG H H, et al. Development trend and active research areas of subsea production system[J]. Journal of Harbin Engineering University, 2019, 40(5): 944-952. |
| [2] |
朱焰.吸力式筒型基础承载力研究[D].天津: 天津大学, 2002. ZHU Y.The study of suction foundation bearing capacity[D]. Tianjin: Tianjin University, 2002. |
| [3] |
ANDERSEN K H, JOSTAD H P. Shear strength along outside wall of suction anchors in clay after installation[C]//Proceedings of 12th International Offshore and Polar Engineering Conference. Kitayushu, Japan: ISOPE, 2002: 785-794.
|
| [4] |
张金来, 鲁晓兵, 王淑云, 等. 桶形基础极限承载力特性研究[J]. 岩石力学与工程学报, 2005, 24(7): 1169-1172. ZHANG J L, LU X B, WANG S Y, et al. The characteristics of the bearing capacity of bucket foundation[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(7): 1169-1172. DOI:10.3321/j.issn:1000-6915.2005.07.014 |
| [5] |
刘振纹, 王建华, 袁中立, 等. 负压桶形基础地基竖向承载力研究[J]. 中国海洋平台, 2001, 16(2): 1-6. LIU Z W, WANG J H, YUAN Z L, et al. A study on the vertical bearing capacity of bucket foundation[J]. China Offshore Platform, 2001, 16(2): 1-6. DOI:10.3969/j.issn.1001-4500.2001.02.001 |
| [6] |
严驰, 李亚坡, 袁中立. 土性参数对桶形基础竖向地基承载力影响的敏感性分析[J]. 水运工程, 2009(1): 155-160. YAN C, LI Y P, YUAN Z L. Sensitivity analysis of the effect of soil parameters on the vertical bearing capacity of bucket foundation[J]. Port & Waterway Engineering, 2009(1): 155-160. DOI:10.3969/j.issn.1002-4972.2009.01.024 |
| [7] |
程光明, 段梦兰, 叶茂, 等. 深水生产系统中吸力桩的承载能力计算[J]. 石油矿场机械, 2013, 42(12): 46-50. CHENG G M, DUAN M L, YE M, et al. Bearing capacity of suction piles used in deep water subsea system[J]. Oil Field Equipment, 2013, 42(12): 46-50. DOI:10.3969/j.issn.1001-3482.2013.12.010 |
| [8] |
ZHOU H, RANDOLPH M F. Effect of caisson-tip geometry on flow pattern of soil plug, 2007[C]//The Society for Underwater Technology, September 11-13, 2007.
|
| [9] |
王丽勤, 庞然. 吸力式基础在深水油气田开发中的应用探讨[J]. 船海工程, 2011, 40(2): 98-103, 107. WANG L Q, PANG R. The application of suction pile in the deepwater oil and gas field development engineering[J]. Ship & Ocean Engineering, 2011, 40(2): 98-103, 107. DOI:10.3963/j.issn.1671-7953.2011.02.028 |
| [10] |
王志军, 崔雷. 水下管汇基础设计[J]. 广东化工, 2013, 40(10): 159-161. WANG Z J, CUI L. Base of subsea manifold[J]. Guangdong Chemical Industry, 2013, 40(10): 159-161. DOI:10.3969/j.issn.1007-1865.2013.10.085 |
| [11] |
王丽勤, 侯金林, 庞然, 等. 深水油气田开发工程中的基础应用探讨[J]. 海洋石油, 2011, 31(4): 87-92. WANG L Q, HOU J L, PANG R, et al. The application of foundations in deepwater oil and gas field development engineering[J]. Offshore Oil, 2011, 31(4): 87-92. DOI:10.3969/j.issn.1008-2336.2011.04.087 |
| [12] |
王朝阳, 付殿福, 孙友义. 水下生产系统基础型式对比分析[J]. 石化技术, 2017, 24(4): 11-13. WANG Z Y, FU D F, SUN Y Y. Comparative analysis of the foundation types for subsea production system[J]. Petrochemical Industry Technology, 2017, 24(4): 11-13. DOI:10.3969/j.issn.1006-0235.2017.04.008 |
| [13] |
周守为, 曾恒一, 安维杰, 等.海洋石油工程设计指南: 第十三册海洋石油工程边际油气田开发技术[M].北京: 中国石化出版社, 2010. ZHOU S W, ZENG H Y, AN W J, et al. Guidelines for offshore petroleum engineering design: volume 13 marginal oil and gas field development techniques for offshore petroleum engineering[M]. Beijing: China Petrochemical Press, 2010. |
| [14] |
李光銮, 李成军. 饱和粘土中导管架平台单桩水平承载力分析[J]. 石油机械, 2012, 40(10): 63-66. LI G L, LI C J. Analysis of the horizontal bearing capacity of the jacket platform single pile in saturated clay[J]. China Petroleum Machinery, 2012, 40(10): 63-66. |
| [15] |
朱百里, 沈珠江.计算土力学[M].上海: 上海科学技术出版社, 1990. ZHU B L, SHEN Z J. Computational soil mechanics[M].Shanghai: Shanghai Scientific & Technical Publishers, 1990. |
| [16] |
任永坚, 钟秉章, 丁浩江. 无限区域元及其在工程中的应用[J]. 水利学报, 1987(3): 67-71. REN Y J, ZHONG B Z, DING H J. Infinite domain element and its application in engineering[J]. Journal of Hydraulic Engineering, 1987(3): 67-71. DOI:10.3321/j.issn:0559-9350.1987.03.010 |
| [17] |
杜杰, 丁红岩, 刘建辉, 等. 筒型基础有限元分析的土体边界选取研究[J]. 海洋技术, 2005, 24(2): 109-113. DU J, DING H Y, LIU J H, et al. Research on boundary selection of soil of bucket foundation with finite element analysis[J]. Ocean Technology, 2005, 24(2): 109-113. DOI:10.3969/j.issn.1003-2029.2005.02.027 |



