0 引言
随着陆地石油资源的不断开发,石油资源不断减少,许多国家石油开发的重点已由陆地转向海洋。自升式平台作为海底油气资源开发的基础结构,数量已经占据海洋平台中的大部分,而桩腿作为平台的重要构件承担着支撑平台在海上安全作业的任务。桩腿分为壳体式结构和桁架式结构。壳体式桩腿适用于作业水深不超过60 m的环境中。深水自升式平台多采用桁架式结构,常用的3种结构分别为K型、倒K型和X型[1]。
自升式平台处于复杂的海洋环境中,承受着恶劣的环境载荷,世界上许多国家都发生过海洋平台倾覆事故,造成了巨大的经济损失。研究平台关键技术对海洋油气资源的勘探开发具有重大意义,许多学者对桩腿结构优化和仿真进行了研究。D.KARUNAKARAN等[2]讨论了自升式平台非线性随机响应的数学模型,研究了水动力载荷、阻尼和动力响应。M.S.WILLIAMS等[3]采用二维非线性有限元模型,对平台进行了动力分析和准静态研究,得到波高和波周期对平台结构动力响应的影响。顾永宁等[4]采用自升式平台内分析方法,将“渤海七号”作为一个统一的计算模型进行了计算。王兴国等[5]根据动力分析结果,利用优化算法软件对地震载荷作用下的海洋平台结构进行了优化设计。蒙占彬等[6]对某深水自升式平台动态载荷激励下的响应进行分析,所得结论为深水自升式平台的设计与动力控制提供了指导。为探究作业水深122 m(400 ft)自升式平台不同桩腿结构的性能,本文选取JU2000E自升式平台,分别选用K型、倒K型以及X型桩腿结构进行全尺度建模仿真,开展了自存工况下的静、动力学响应分析和平台稳定性分析,以期为自升式平台桩腿的选型和设计提供参考。
1 平台建模JU2000E自升式平台由F&G公司设计,并在世界各国广泛使用三桩式海洋平台。图 1为JU2000E自升式平台及桩腿结构图。该平台主要由平台主船体和桩腿组成,平台主船体为水密结构,拖航工况可提供相应浮力,作业工况可压载海水保证平台的稳定性,实现钻井和采油的功能。桩腿是由弦杆、横撑和斜撑焊接而成的桁架式结构,主弦杆上焊接齿条配合主船体齿轮升降系统和液压锁紧装置实现平台的升降[7]。桩腿通过桩靴插入海底以保证平台的稳定。JU2000E自升式平台几何参数如下:平台长75.90 m,平台宽70.38 m,平台型深9.45 m,桩腿总高166.98 m,弦管中心距13.10 m。表 1为桩腿杆件几何参数。

|
| 图 1 JU2000E自升式平台及桩腿结构图 Fig.1 JU2000E jack-up platform and pile structure |
| 参数名称 | 主弦杆 | 外横撑 | 斜撑 | 内横撑 |
| 直径 | 445 | 324 | 273 | 168 |
| 壁厚 | 83.50 | 28.58 | 21.41 | 10.97 |
随着计算机技术的发展,有限元技术在海洋工程中得到广泛应用,ANSYS作为一种大型CAE通用有限元分析软件,用于海洋工程中的诸多方面[8]。为准确分析3种桩腿结构性能,在ANSYS中建立了该平台桩腿的全尺度模型(见图 2)。

|
| 图 2 3种桩腿结构有限元模型 Fig.2 Finite element model of the three kinds of pile leg structure |
根据桩腿几何形式和受力特点,选择PIPE59单元对桩腿结构进行建模。PIPE59单元是ANSYS中专门用于模拟浸没在水中的杆件结构单元,应用该单元可以结合相应的波浪理论模拟实际波流与杆件结构的相互作用,进而计算水中构件所受的水流、波浪静载荷和动载荷。采用PIPE20单元模拟插入泥面以下的管体结构,该单元主要用于模拟泥线以下不受波流作用的管体构件。平台主体采用SOLID95单元模拟,该单元具有塑性、应力强化以及大变形等特性。
如图 2所示,根据JU2000E自升式平台的结构尺寸参数,采用不同的桁架结构建立平台模型。为对比不同结构型式桩腿的承载性能,3种平台桩腿构件中的所有弦杆、横撑和斜撑等均采用相同的材料和截面尺寸。
2 载荷及边界条件平台在工作过程中有多种不同的工作状态,如拖航、插桩和桩腿预压等,每种状态结构下的受力均不完全相同[9]。为保证自升式平台平稳安全作业,设计时将风暴自存工况下的环境载荷作为设计载荷。为了分析3种平台结构在恶劣海洋环境条件下的性能,笔者以平台自存工况下的环境条件为例进行加载,环境载荷为50 a一遇。平台在自存工况下的环境载荷为:平台及设备质量12 000 t,水深122 m,插桩深度3.05 m,波高13.41 m,波浪周期14.1 s,海面流速1.2 m/s,平均风速40 m/s,海冰厚度0.8 m,流动冰速1.03 m/s。
2.1 载荷计算及组合加载目前,确定作用于海洋结构物上的波浪载荷主要有两种方法:随机分析法和设计波法[10]。随机分析法以海况统计特征为基础,多用于海洋结构物的寿命分析中;设计波法计算简便,常被海洋工程设计所采用,通过给定一个大波浪并结合恰当的波浪理论来描述波浪的相应特征。本文选用设计波法结合Stokes五阶波浪理论计算平台所受的波流力载荷,计算公式为:

|
(1) |
式中:F为作用在桩腿上的波流力,N;ρ为流体密度,kg/m3;v1为设计流速,m/s;A1为构件在与流向垂直平面上的投影面积,m2;V为单位长度上的排水体积,m3;Cd为拖曳力系数;CM为惯性力系数;ux为水质点的水平速度,m/s;
风速只有在限定高程和持续时间下才有意义,风速和方向随空间和时间不断变化,对于典型的较大海洋结构,其水面以上平台主体部分载荷很大,并且有动力效应[11]。根据规定风压计算公式,海洋结构物所受风载的大小可以由受风构件的正投影面积乘以风压得到,即有:

|
(2) |
式中:FW为作用于结构物上的风载荷,N;K为风载体型系数;KZ风压高度变化系数;βZ为Z高度处的风振系数;α为风压系数,通常可以取0.613 (N·s2)/m4;v2为设计风速,m/s;A2为结构物正投影面积,m2。
对于冰载荷,巨大的冰原对平台产生的挤压力和流冰的冲击作用使平台遭到损坏和破坏[12]。在挤压过程中,大面积冰层破碎前的瞬间,作用在平台下部结构上的挤压力达到最大。影响冰载荷大小的因素很多,笔者采用基于桩柱切入大面积冰原理论的冰载荷计算公式,即有:

|
(3) |
式中:F1为冰载荷,kN;m为桩柱形系数,通常取0.9;K1为局部挤压系数;K2为桩柱与冰层接触系数,一般取0.3;Rj为冰块试样的极限抗压强度,Pa;b为桩柱宽度,m;h为冰层计算厚度,m。
平台处在复杂的海洋环境中,其载荷通常是随机、多方向及连续的[13]。为保证平台在恶劣的环境中安全工作,设计时通常将可能同时作用于平台上的载荷进行组合,把对平台最不利的几种载荷进行矢量相加,作用于同一方向。图 3为海洋平台桩腿所承受的载荷示意图。本文假设风、波浪、波流以及冰载荷以同一方向加载,即载荷指向单桩腿方向。

|
| 图 3 海洋平台桩腿所承受的载荷示意图 Fig.3 Schematic diagram of the loads on the legs of the offshore platform |
2.2 边界条件及基本假设
海洋平台桩腿在垂直方向承受主船体及设备自重,水平方向还受到风和波浪等载荷作用,这就要把握好桩-土之间的载荷传递情况[14]。在实际环境中,平台垂直方向的载荷施加给桩腿,桩腿通过表面与土壤的摩擦力传递给附近的土壤,这就要求在分析时要考虑桩-土的相互作用特性。本文采用6倍桩径来模拟桩-土的作用特性。
平台桩腿与主船体依靠齿轮齿条和锁紧装置连接,当桩腿站立时,主要是上导轨、下导轨及锁紧装置对桩腿施加载荷。考虑到升降机结构复杂,建立有限元模型比较困难,因此没有考虑复杂的边界约束条件,采用耦合的方式将平台主体与桩腿主弦杆的相应单元进行连接,并将主船体、设备自重和风载荷传递给桩腿。
3 平台有限元分析 3.1 平台静力学分析结构静力分析用来分析结构在给定静力载荷作用下的响应。海洋平台桩腿结构的位移和应力等参数是设计建造过程中非常重要的参数,为分析3种平台的力学性能,对平台模型施加极限工况下的环境载荷,载荷及边界条件如前所述。表 2为3种平台结构静力分析结果对比。图 4为3种平台结构最大应力图。图 5为3种平台结构最大位移图。

|
| 图 4 3种平台结构最大应力图 Fig.4 Maximum stress of the three types of platform structures |
|
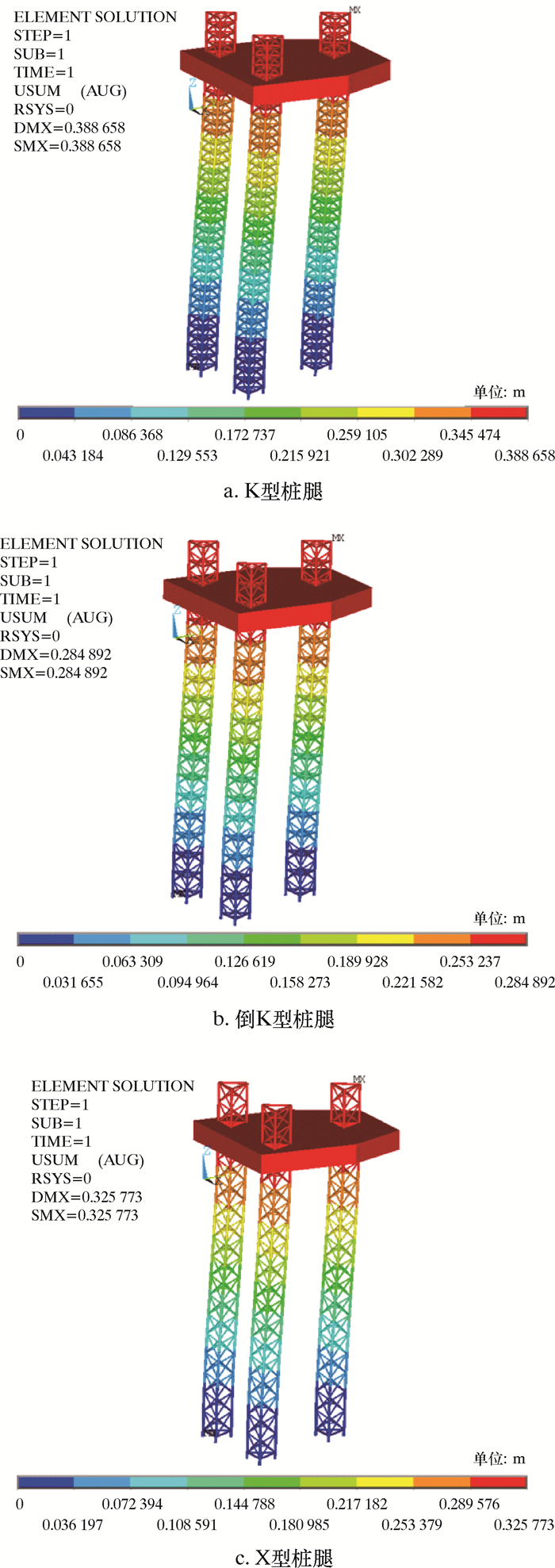
| 图 5 3种平台结构最大位移图 Fig.5 Maximum displacement of the three types of platform structures |
| 平台类型 | 最大应力/MPa | 最大位移/m | 单根桩腿质量/t |
| K型 | 397 | 0.389 | 915.3 |
| 倒K型 | 374 | 0.285 | 877.5 |
| X型 | 390 | 0.326 | 844.6 |
由图 4可知,在相同工况下,各平台内部桩腿间受力不均,位于载荷作用方向的单桩腿应力较大,极易引发因单桩失效而使平台倾覆的事故。进一步分析可知,倒K型桩腿的力学性能最好,最大应力值最小,为374 MPa,最大位移值为0.285 m;X型次之,最大应力为390 MPa,最大位移为0.326 m;K型桩腿的力学性能最差,最大应力与位移值最大,分别为397 MPa和0.389 m。模型中的最大应力点均属于危险点,极易发生破坏。由图 4还可以看出,倒K型平台的最大应力点位于弦杆与横撑的管节点处,而K型与X型结构桩腿的最大应力点均位于主弦杆最底部的桩靴连接处。通过提取3种桩腿模型的质量,倒K型桩腿的整体质量小于K型和X型桩腿质量,能达到节省材料和减少建造成本的目的。
3.2 平台动力分析波浪力是一种随时间变化的载荷,海洋平台在波浪等动态载荷激励下易发生振动响应,严重影响平台的使用安全和寿命。因此,对3种平台结构在动态载荷激励下进行动力分析。自升式平台动力响应的理论分析方法主要有时域分析法、频域分析法和动力放大系数法[15]。
笔者首先对3种平台结构进行模态分析,提取各个结构的1阶固有频率。然后采用时域分析方法,使用ANSYS软件的瞬态动力学技术计算3种平台结构在随机波浪载荷激励下的动力响应,得到平台在波浪载荷作用下随时间变化的位移与应力。瞬态动力学平衡方程为:

|
(4) |
式中:[M]为质量矩阵,[C]为阻尼矩阵,[K]为刚度矩阵,Fa为载荷向量,
根据静力学分析结果,选取3种平台的结构弱点为研究目标,即K型与X型桩腿平台弦杆最底部的最大应力点,倒K型桩腿的弦杆与横撑的管节点处,提取结构弱点在环境载荷作用下100 s内的应力值,并绘制时间-应力曲线,结果如图 6所示。选取3种平台顶端最大位移点为研究对象,提取3种平台在载荷激励后100 s内的位移值,并绘制时间-位移曲线,结果如图 7所示。表 3为3种平台结构动力学响应值比较。

|
| 图 6 3种平台结构时间-应力曲线 Fig.6 Time-stress curve of the three types of platform structures |

|
| 图 7 3种平台结构时间-位移曲线 Fig.7 Time-displacement curve of the three types of platform structures |
| 平台类型 | 1阶模态 频率/Hz |
动态应力幅值/MPa | 动态位移幅值/m |
| K型 | 0.126 11 | 8.5 | 0.45 |
| 倒K型 | 0.129 83 | 7.3 | 0.35 |
| X型 | 0.130 91 | 8.1 | 0.41 |
由图 6可知:3种平台结构在随机波浪载荷激励下,载荷作用初期应力急速增大,其中X型平台应力值最大,倒K型平台值最小;0~15 s范围内各点应力剧烈变化,20 s以后,3种平台的动态响应趋于稳定,各点应力值处于规律的变化之中。很明显,倒K型平台结构相比于K型和X型,应力曲线更接近于0刻度值,说明倒K型平台结构在动载荷激励下平均应力值小于K型与X型。由图 6还可以看出,在稳定状态下倒K型桩腿平台应力幅值最小,X型次之,K型最大,在一定程度上反映出在该动态载荷激励下,倒K型平台结构具有较长的疲劳寿命。
由图 7可以看出:动态载荷刚作用于平台结构时,3种平台结构位移迅速增大,其中K型平台结构位移值最大;20 s后,3种平台结构的位移响应平稳振荡,K型平台结构动态位移幅值为0.45 m,X型平台结构动态位移幅值为0.41 m,倒K型平台结构动态位移幅值最小,为0.35 m,说明倒K型桩腿结构在动态载荷激励下位移响应明显优于其余两种结构型式,在动态载荷作用下依然具有较好的刚度。由3种平台的1阶模态频率可以看出,倒K型平台的1阶固有频率为0.129 83 Hz,大于K型平台,可以远离波浪运动频率,避免共振的发生。
3.3 平台稳定性分析桁架式桩腿结构复杂,属于复杂的钢结构体系,不合理的设计极易造成平台发生整体失稳或局部失稳,甚至导致平台坍塌[16]。工程中常采用屈曲分析研究结构的稳定性,包括特征值屈曲分析和非线性屈曲分析。
特征值屈曲分析以结构模态为基础,根据模拟得到的最低阶屈曲模态可以预测结构的失稳状态。非线性屈曲分析在考虑材料非线性的基础上,通过分步施加恒定载荷增量直至解开始发散,得到结构的临界屈曲载荷。为对比分析3种平台结构的失稳状态及发生失稳时的屈曲临界载荷,笔者采用ANSYS有限元软件对平台进行特征值屈曲分析和非线性屈曲分析。图 8为非线性屈曲分析过程中3种平台结构的载荷-位移曲线。图 9为3种平台结构的1阶屈曲模态变形图。

|
| 图 8 3种平台结构载荷-位移曲线 Fig.8 Load-displacement curve of the three types of platform structures |

|
| 图 9 3种平台结构1阶屈曲模态变形图 Fig.9 Deformation of 1st order buckling mode of the three types of platform structures |
图 8准确反映了3种平台结构在施加恒定载荷增量的过程中载荷与结构位移的关系,可以追踪得到结构开始失稳时的最大临界载荷。图 9则分别反映了3种平台结构达到最大临界载荷时将发生的失稳破坏形式以及低阶屈曲载荷系数。低阶屈曲载荷系数在一定程度上反映出结构发生屈曲变形时的临界载荷,低阶屈曲载荷系数越小,则表明相应结构的临界屈曲载荷越小,K型、X型及倒K型平台在1阶模态频率时屈曲载荷系数分别为31.28、52.38和61.41,因此倒K型平台结构的1阶屈曲模态载荷最大,X型次之,K型最小。这一点可由图 8得到验证,倒K型平台结构最大临界载荷最大,为21 910 kN,此时倒K型平台结构将发生图 9b所示的破坏形式,桩腿整体产生屈曲变形。X型平台结构最大临界载荷为19 212 kN,此时平台桩腿底部1/2区域将发生屈曲变形,如图 9c所示。K型平台结构最大临界载荷最小,为17 256 kN,此时桩腿与桩靴连接处发生局部变形,但未扩展至整根桩腿,如图 9a所示。此外,在各平台的屈服极限内,当3种平台结构达到相同的位移值时,倒K型平台结构所需载荷大于其余两种。因此,倒K型平台结构具有较好的稳定性。
4 结论(1) 采用倒K型桩腿结构的海洋平台的力学性能优于其余两种,最大应力值与最大位移值最小;倒K型平台的单根桩腿质量最小,可以减少建造成本。针对3种平台结构最大应力点的出现位置,为避免平台在此处发生破坏失效,可以采取相应措施对最大应力点进行加固。
(2) 在动力响应分析中,3种平台结构具有一致的动态响应变化趋势,倒K型平台结构在弱点处的平均应力最小,X型次之,K型最大。倒K型桩腿结构在弱点处的应力幅值最小,说明倒K型桩腿具有好的疲劳特性。倒K型平台结构动态位移幅值最小,说明其具有较高的动态刚度,可有效减轻平台振动,有利于平台安全平稳作业。
(3) 倒K型平台结构的最大临界载荷最大,稳定性最好,X型次之,K型平台结构稳定性最差,且3种平台结构在失稳时的破坏形式不同,当载荷达到17 256 kN时K型平台结构发生桩腿局部破坏;当载荷达到19 212 kN时X型平台结构将在桩腿底部½处发生破坏;当载荷为21 910 kN时倒K型平台结构将发生整根桩腿破坏。
(4) 倒K型桩腿结构适合在水深122 m或更深的水深中作业,X型和K型桩腿结构适合稍浅水域作业。
| [1] |
张鹏飞, 于兴军, 栾苏, 等. 自升式钻井平台的技术现状和发展趋势[J]. 石油机械, 2015, 43(3): 55-59. ZHANG P F, YU X J, LUAN S, et al. Current technologies and future development of jack-up rig[J]. China Petroleum Machinery, 2015, 43(3): 55-59. |
| [2] |
KARUNAKARAN D, SPIDSQE N. Verification of methods for simulation of nonlinear dynamic response of jack-up platforms[J]. Marine Structures, 1997(10): 181-219. |
| [3] |
WILLIAMS M S, THOMPSON R S G, HOULSBY G T. A parametric study of the non-linear dynamic behaviour of an offshore jack-up unit[J]. Engineering Structures, 1999, 21(5): 383-394. DOI:10.1016/S0141-0296(97)00222-8 |
| [4] |
顾永宁, 束继兴. 自升式石油钻井平台整体结构静力分析[J]. 海洋通报, 1982(4): 86-94. GU Y N, SHU J X. Static analysis of integral structure of jack-up oil drilling platform[J]. Marine Science Bulletin, 1982(4): 86-94. |
| [5] |
王兴国, 贾默伊, 周晶. 地震作用下的导管架海洋平台结构动力优化设计研究[J]. 海洋工程, 2003, 21(2): 16-19. WANG X G, JIA M Y, ZHOU J. Dynamic optimization design for jacket platforms under earthquakes[J]. The Ocean Engineering, 2003, 21(2): 16-19. DOI:10.3969/j.issn.1005-9865.2003.02.003 |
| [6] |
蒙占彬, 张士华, 田海庆. 深水自升式平台动力响应分析研究[J]. 石油机械, 2018, 46(4): 35-41. MENG Z B, ZHANG S H, TIAN H Q. Analysis of dynamic response of deep water jack-up platform[J]. China Petroleum Machinery, 2018, 46(4): 35-41. |
| [7] |
陈建民, 娄敏, 王天霖. 海洋石油平台设计[M]. 北京: 石油工业出版社, 2012: 26-40. CHEN J M, LOU M, WANG T L. Offshore oil platform design[M]. Beijing: Petroleum Industry Press, 2012: 26-40. |
| [8] |
杨进, 刘书杰, 姜伟, 等. ANSYS在海洋石油工程中的应用[M]. 北京: 石油工业出版社, 2009: 11-17. YANG J, LIU S J, JIANG W, et al. Application of ANSYS in offshore petroleum engineering[M]. Beijing: Petroleum Industry Press, 2009: 11-17. |
| [9] |
张家齐, 刘远, 汪怡, 等. 自升式海洋平台桩腿拖航工况研究[J]. 船舶工程, 2013, 35. ZHANG J Q, LIU Y, WANG Y, et al. Research on leg structure analysis of self-elevating drilling units in transit condition[J]. Ship Engineering, 2013, 35(S2): 69-71. |
| [10] |
奚勇.自升式平台桩腿节距优化及强度分析[D].镇江: 江苏科技大学, 2016. XI Y. Pitch optimization and strength analysis of jack-up platform leg[D]. Zhenjiang: Jiangsu University of Science and Technology, 2016. |
| [11] |
杨炎华, 金书城, 金梦菊, 等. 自升式海洋平台桩腿结构优化设计[J]. 船海工程, 2011, 40(6): 150-152. YANG Y H, JIN S C, JIN M J, et al. Optimum structural design of jack-up platform leg[J]. Ship & Ocean Engineering, 2011, 40(6): 150-152. DOI:10.3963/j.issn.1671-7953.2011.06.039 |
| [12] |
TIAN X J, WANG Q Y, LIU G J, et al. Topology optimization design for offshore platform jacket structure[J]. Applied Ocean Research, 2019, 84: 38-50. DOI:10.1016/j.apor.2019.01.003 |
| [13] |
吕国兴.自升式海洋平台桩腿的结构强度分析及优化设计[D].舟山: 浙江海洋大学, 2016. LÜ G X. Structural strength analysis and optimum design of pile legs of jack-up offshore platform[D]. Zhoushan: Zhejiang Ocean University, 2016. |
| [14] |
朱亚洲.自升式平台桩土效应与桩腿结构构型研究[D].哈尔滨: 哈尔滨工程大学, 2015. ZHU Y Z. Research on effect of leg-soil and configurationof leg structure for self-elevating unit[D]. Harbin: Harbin Engineering University, 2015. |
| [15] |
徐长航, 陈国明, 谢静, 等. 自升式平台结构响应分析及可靠性评估研究综述[J]. 中国海洋平台, 2003, 18(4): 6-11. XU C H, CHEN G M, XIE J, et al. A general review of research works on the structure response analysis and reliability assessment for jack-up platform[J]. China Ocean Platform, 2003, 18(4): 6-11. DOI:10.3969/j.issn.1001-4500.2003.04.002 |
| [16] |
佟姝茜, 常思嘉, 邱成国, 等. 自升式平台桩腿相位差的敏感性分析[J]. 石油机械, 2018, 46(3): 42-47. TONG S Q, CHANG S J, QIU C G, et al. Sensitivity analysis of leg RPD of jack-up platform[J]. China Petroleum Machinery, 2018, 46(3): 42-47. |


