2. 中国石油青海油田公司钻采工艺研究院;
3. 中石油江汉机械研究所有限公司
2. Research Institute of Drilling and Production Technology, PetroChina Qinghai Oilfield Company;
3. Jianghan Machinery Research Institute Limited Company of CNPC
0 引言
理论与试验研究结果表明,水泥环质量影响套管的强度安全性[1]。在水平井固井过程中,由于套管偏心、井径变化、水泥浆流速不均匀及油气侵入等,水泥浆往往难以完全顶替环空中的钻井液,从而在套管和井眼环空形成不完整的固井水泥环[2],既影响封隔效果,也影响套管的强度安全性和井筒完整性[3]。因此,水泥环缺陷对套管强度影响问题引起了人们的广泛关注[4]。
文献[5]分析了水泥环失效后形成的局部载荷对套管变形的影响,提出了减小套管外径和增大套管壁厚的措施来防止套管变形。文献[6]分析了固井水泥环蠕变对套管围压的影响,结果表明水泥浆密度和水泥添加剂影响水泥环的蠕变性质。文献[7]利用数值分析法分析了缺失水泥环中束缚流体在温度与内压变化情况下对套管抗内压强度的影响。文献[8-9]建立了井筒组合体力学分析模型,分析了温压变化时完整水泥环与缺失水泥环对套管应力的影响。文献[10]应用有限元方法分析了套管磨损与水泥环缺陷位置对套管应力的影响,发现套管磨损位置与水泥环缺陷位置重叠会对套管应力产生非常大的影响。文献[11]分析了直井段水泥环第一界面环状缺失高度与厚度对套管应力的影响,发现环状缺失高度与厚度对套管应力影响不大。文献[12]应用有限元方法分析了水泥环性能、套管偏心及不同缺失角度对套管损坏的影响,发现套管承载力与缺失角度成正比。文献[13]研究了热采井中水泥环周向缺失不同角度时套管的应力与应变情况,得到温度载荷作用下套管应力和位移随周向缺失角度变化的规律。文献[14]考虑水泥环缺失角度与套管偏心的组合影响进行有限元分析,发现套管偏心与水泥环缺失同时存在将大幅增加套管应力。
实际上,水泥环的缺失形态复杂,应综合考虑缺失位置、缺失厚度与环向缺失角度对套管强度安全性的影响。鉴于此,本文利用有限元分析方法,建立了水平井套管-水泥环-地层力学模型,考虑非均匀地应力和套管内压的影响,模拟水平井中水泥环缺失段套管的应力分布情况,着重分析了水泥环第一胶结面和第二胶结面缺失不同厚度对套管强度安全性的影响,以及水泥环环向缺失角度对套管强度安全性的影响。所得结论可为水平井固井过程中套管的强度判断提供依据。
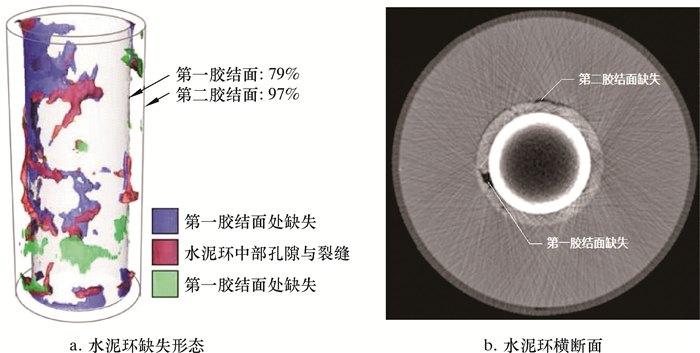
1 模型建立实际固井井下水泥环缺失形态十分复杂,很不规则,难以完全真实模拟。国外学者在研究温度循环变化对水泥环完整性的影响时,曾利用CT扫描技术,得到实验室固井水泥环的缺失形态[15],如图 1所示。图 1a显示了水泥环中不同位置存在的缺失情况,第一胶结面的缺失面积约为该界面总面积的21%,第二胶结面的缺失面积约为该界面总面积的3%,此外,在水泥环两个胶结面之间还存在空隙与裂缝。图 1b为水泥环横断面的扫描图。由图 1b可以看到,水泥环的内侧和外侧均存在缺失,缺失位置沿径向可能分布于第一胶结面(水泥环-套管胶结面)、第二胶结面(水泥环-地层胶结面)或两个胶结面中间,且缺失处形态沿径向厚度与环向角度均有变化。
|
| 图 1 利用CT扫描技术得到的固井水泥环缺失形态 Fig.1 Morphology of cement sheath absence obtained by CT scanning |
借鉴水泥环缺失扫描形态,以ϕ139.7 mm(5½ in)×7.72 mm P110套管与ϕ215.9 mm井眼组合为例,应用ANSYS Workbench有限元软件,建立水平井套管-水泥环-地层有限元分析模型。模型基本参数如表 1所示。假设地层和水泥环均为均质弹性体,根据圣维南原理,为消除远场应力的影响,地层模型边界到井眼的距离取为井眼尺寸的5倍以上,因此取地层模型边长3 000 mm。水泥环缺失部分通常是由水泥浆顶替钻井液不完全或油气侵入环空所致[16],将水泥环缺失处的填充物质设为密度1.0 g/cm3的液体。假设垂直地应力为32 MPa,最大水平地应力为48 MPa,套管服役过程中最大内压为76 MPa。
| 名称 | 密度/(kg·m-3) | 弹性模量/GPa | 体积模量/GPa | 泊松比 | 屈服强度/MPa | 极限强度/MPa |
| 套管 | 7 850 | 210 | 0.279 | 758 | 965 | |
| 水泥环 | 3 100 | 10 | 0.170 | 41 | ||
| 缺失处(流体) | 1 000 | 2.18 | 0.500 | |||
| 地层 | 2 600 | 22 | 0.230 | 49 |
2 水泥环径向缺失位置及缺失厚度对套管应力的影响
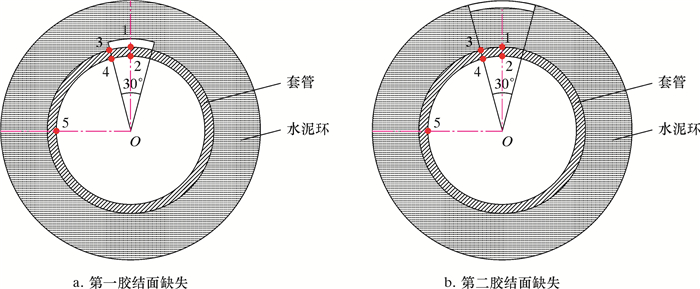
根据水泥环缺失位置的不同,分别使缺失部分位于水泥环顶部靠近第一胶结面与第二胶结面的两侧,缺失角度取圆心角30°且沿着垂直轴线两侧对称。水泥环径向缺失模型如图 2所示。定义水泥环径向厚度缺失比ε为:
|
| 图 2 水泥环径向缺失模型示意图 Fig.2 Schematic diagram of the radial cement sheath absence |
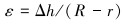
|
(1) |
式中:Δh为缺失部分径向厚度,mm;r、R分别为水泥环内、外半径,mm。
在进行有限元建模与分析时,依次取ε为0、1/6、1/3、1/2、2/3、5/6和1。如图 2所示,在套管上设置5个应力监测点,监测其Von Mises应力的分布与变化情况,考察水泥环径向缺失位置及缺失厚度对套管应力的影响。
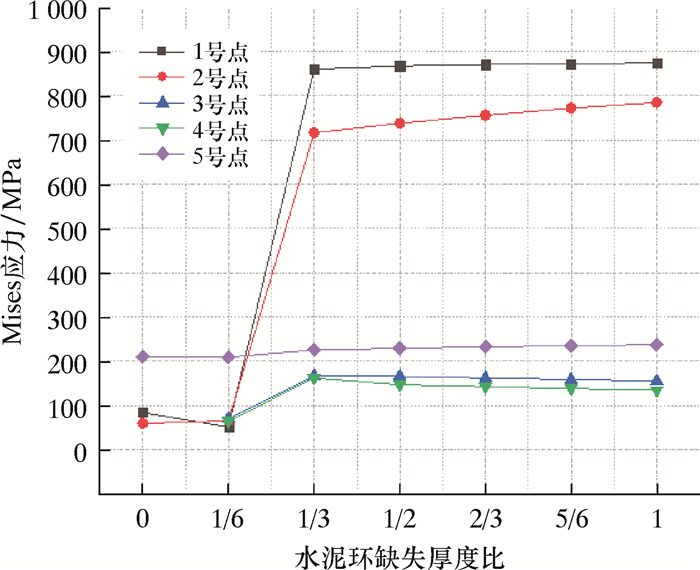
2.1 水泥环第一胶结面缺失通过有限元软件分析,得到水泥环第一胶结面缺失不同厚度时套管的应力变化情况,如图 3所示。由图 3可以看出:若水泥环完整无缺失,套管的最大应力出现在5号点处,即套管内壁两侧,最大应力为210.19 MPa;随着水泥环缺失厚度的增加,该点的应力也随之增大;若水泥环完全缺失,该点处应力达到最大值237.08 MPa,增幅为12.7%;在缺失厚度比达到1/6时,5号点仍是套管的应力极大值点;当缺失厚度达1/3时,位于套管顶部的1号、2号点应力急剧增大,套管顶部外侧的1号点成为套管应力的极大值点,该点处的最大应力由原来的51.21 MPa增大至860.49 MPa,增幅约16倍;随着缺失厚度的继续增加,该点的应力平缓增加至874.03 MPa。根据Mises屈服准则,在水泥环第一胶结面缺失厚度比达到1/3以后,缺失处的套管出现应力集中,将发生塑性变形。
|
| 图 3 水泥环第一胶结面缺失不同厚度时套管的应力变化 Fig.3 The casing stress under the first cementing surface absence at different cement sheath thicknesses |
为了进一步确定致使套管应力发生突变的缺失厚度值,利用二分法逐次改变缺失厚度进行进一步模拟。模拟结果表明,当缺失位置位于第一胶结面且缺失处径向厚度达到水泥环径向厚度的1/4时,套管的应力分布将发生突变。
以上分析结果表明:水泥环第一胶结面缺失对套管强度安全性影响较大,缺失厚度存在某一临界值(本例中该临界值为水泥环厚度的1/4);若缺失厚度小于该临界值,则套管的应力变化较小;若缺失厚度超过该临界值,套管1号、2号应力监测点位置将出现应力突变,导致套管的等效应力急剧增大。
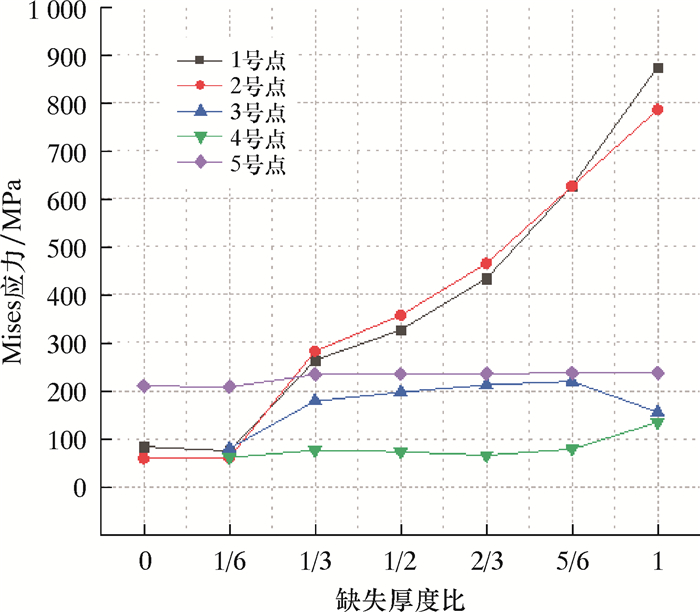
2.2 水泥环第二胶结面缺失通过有限元软件分析,得到水泥环第二胶结面缺失不同厚度时套管的应力变化情况,如图 4所示。由图 4可以看出:随着水泥环缺失厚度逐渐增大,1号、2号点的应力值也逐渐增大,增长趋势较为平稳;水泥环完全缺失时套管顶部的等效应力达到最大值873.78 MPa,而3号、4号和5号点的应力值未发生明显变化;当缺失位置位于水泥环外侧,即临近第二胶结面时,套管的应力极值随着缺失厚度的增大而逐渐增大;缺失厚度为1/6时,套管最大等效应力为208.60 MPa,而当水泥环完全缺失后,套管的最大等效应力达到最大,即873.78 MPa,超过套管材料的屈服强度。
|
| 图 4 水泥环第二胶结面缺失不同厚度时套管的应力变化 Fig.4 The casing stress under the second cementing surface absence at different cement sheath thicknesses |
以上分析结果表明:当水泥环缺失位置位于水泥环外侧,即临近第二胶结面时,套管1号和2号应力监测点位置处的应力随缺失厚度的增加而增大;当套管的应力极值超过材料的屈服强度时,套管将发生塑性变形。
3 水泥环环向缺失角度对套管应力的影响由于水泥环第一胶结面缺失对套管的强度安全性影响较大,故采用水泥环第一胶结面缺失1/3的套管-水泥环-地层有限元模型,分析缺失角度对套管应力的影响。水泥环环向缺失模型如图 5所示。缺失角度分别为15°、30°、……、150°、165°、180°,在套管模型上设置4个应力监测点(见图 5)。在分析过程中,考虑套管上的应力极大值点可能随着缺失角度的变化而改变,因此,将应力极大值点作为一个动监测点,编号为4号。

|
| 图 5 水泥环环向缺失模型示意图 Fig.5 Schematic diagram of the circumferential cement sheath absence model |
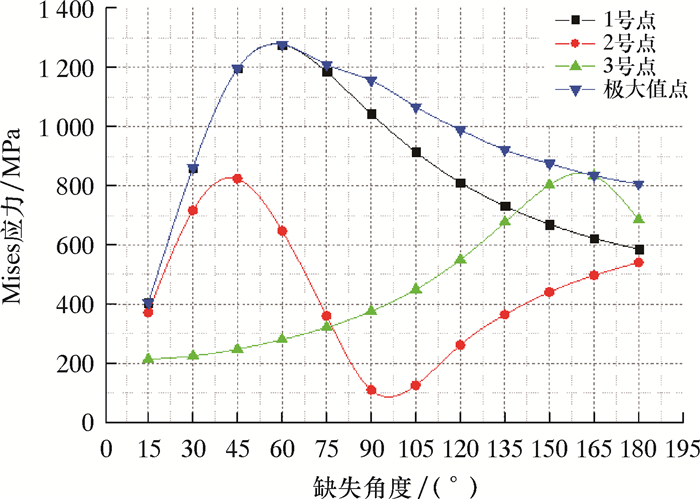
通过有限元软件分析,得到水泥环环向缺失角度对套管应力的影响,结果如图 6所示。
|
| 图 6 水泥环环向缺失不同角度时套管的应力变化 Fig.6 Casing stress under different circumferential cement sheath absence angles |
由图 6可以看出:随着缺失角度的逐渐增大,在0°~60°区间内,套管的应力极值逐渐增大,这一阶段的极值点位于套管顶部外侧1号点处;缺失角度达到60°时,套管的应力极值达到最大;当缺失角度大于60°时,套管的应力极值随着缺失角度的增大而逐渐减小,且位置随角度的变化而改变。
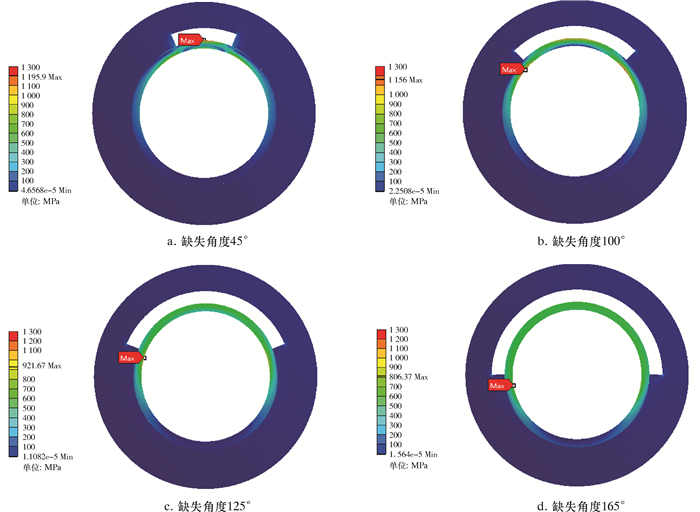
图 7为水泥环不同缺失角度下的套管应力极值点位置。由图 7可以看出:若缺失角度小于60°,应力极值点总是在1号和2号应力监测点附近;若缺失角度大于60°,应力极值点即4号监测点位置随角度的变化而变化,且总是位于套管内壁临近缺失角边线处;随着缺失角度的进一步增大,应力极值点的位置逐渐由1号监测点向3号监测点转移。
|
| 图 7 水泥环不同缺失角度下的套管应力极值点位置 Fig.7 Casing stress extreme point position at different cement sheath absence angles |
4 结论
(1) 水泥环第一胶结面缺失对套管的应力分布影响较大,缺失比存在一个临界值,若缺失厚度小于该临界值,套管的应力变化不大;若缺失厚度大于该临界值,套管的应力将发生突变,对算例套管,应力极值由208.76 MPa突变至860.49 MPa,增幅达3.12倍。
(2) 水泥环第二胶结面缺失时,随着水泥环缺失厚度的增加,算例套管的应力极值由210.19 MPa逐渐增大至873.78 MPa。平均缺失厚度比每增长1/6,算例套管的应力极值约增加133.20 MPa,直到套管屈服。
(3) 缺失角度小于60°时,环向缺失角度越大,算例套管的应力极值也越大;缺失角度为60°时,算例套管的应力极值达到最大值;缺失角度大于60°后,套管的应力极值随缺失角度的增加反而减小,且套管的应力极值点位置随着水泥环的环向缺失角度变化而变化,位于套管内壁靠近缺失角边缘处。
| [1] |
林凯, 杨龙, 史交齐, 等. 水泥环对套管强度影响的理论和试验研究[J]. 石油机械, 2004, 32(5): 13-16. LIN K, YANG L, SHI J Q, et al. The theory and test research about cement sheath influence to the casing strength[J]. China Petroleum Machinery, 2004, 32(5): 13-16. DOI:10.3969/j.issn.1001-4578.2004.05.005 |
| [2] |
BERGER A, FLECKENSTEIN W W, EUSTES A W, et al. Effect of eccentricity, voids, cement channels, and pore pressure decline on collapse resistance of casing[R]. SPE 90045-MS, 2004.
|
| [3] |
PATTILLO P D, KRISTIANSEN T G. Analysis of horizontal casing integrity in the Valhall Field[R]. SPE 78204-MS, 2002.
|
| [4] |
彭泉霖, 何世明, 章景城, 等. 水泥环缺陷对套管强度影响研究现状及展望[J]. 钻采工艺, 2015, 38(4): 35-37. PENG Q L, HE S M, ZHANG J C, et al. Research on the influence of defective cement ring on casing strength[J]. Drilling & Production Technology, 2015, 38(4): 35-37. DOI:10.3969/J.ISSN.1006-768X.2015.04.10 |
| [5] |
刘奎, 高德利, 王宴滨, 等. 局部载荷对页岩气井套管变形的影响[J]. 天然气工业, 2016, 36(11): 76-82. LIU K, GAO D L, WANG Y B, et al. Effects of local load on shale gas well casing deformation[J]. Natural Gas Industry, 2016, 36(11): 76-82. DOI:10.3787/j.issn.1000-0976.2016.11.010 |
| [6] |
窦益华, 唐俊才. 粘弹性围岩中套管围压分析及双层组合套管的使用[J]. 石油钻采工艺, 1988, 10(6): 29-42. DOU Y H, TANG J C. Analysis of casing confining pressure in viscoelastic surrounding rock and use of double-layer composite casing[J]. Oil Drilling & Production Technology, 1988, 10(6): 29-42. |
| [7] |
田中兰, 石林, 乔磊. 页岩气水平井井筒完整性问题及对策[J]. 天然气工业, 2015, 35(9): 70-76. TIAN Z L, SHI L, QIAO L. Research of countermeasure for wellbore integrity of shale gas horizontal well[J]. Natural Gas Industry, 2015, 35(9): 70-76. DOI:10.3787/j.issn.1000-0976.2015.09.010 |
| [8] |
范明涛, 柳贡慧, 李军, 等. 页岩气井温压耦合下固井质量对套管应力的影响[J]. 石油机械, 2016, 44(8): 1-5. FAN M T, LIU G H, LI J, et al. Effect of cementing quality on casing stress of shale gas well under heat-mechanical coupling[J]. China Petroleum Machinery, 2016, 44(8): 1-5. |
| [9] |
席岩, 李军, 柳贡慧, 等. 页岩气水平井多级压裂过程中套管变形研究综述[J]. 特种油气藏, 2019, 26(1): 1-6. XI Y, LI J, LIU G H, et al. Overview of casing deformation in multistage fracturing of shale gas horizontal wells[J]. Special Oil & Gas Reservoirs, 2019, 26(1): 1-6. |
| [10] |
庞秉谦, 杨松, 窦益华, 等. 套管磨损与水泥环缺陷位置对套管应力的影响[J]. 石油机械, 2009, 37(10): 1-3. PANG B Q, YANG S, DOU Y H, et al. The effect of casing abrasion and cement sheath's defect position on casing stress[J]. China Petroleum Machinery, 2009, 37(10): 1-3. |
| [11] |
练章华, 罗泽利, 步宏光, 等. 水泥环环状缺失套损机理及防控措施[J]. 石油钻采工艺, 2017, 39(4): 435-441. LIAN Z H, LUO Z L, BU H G, et al. Mechanical and control measures on casing damage due to annular absence of cement sheath[J]. Oil Drilling & Production Technology, 2017, 39(4): 435-441. |
| [12] |
于浩, 练章华, 林铁军. 油田固井质量对套管损坏影响的数值仿真[J]. 计算机仿真, 2014, 31(9): 161-164, 251. YU H, LIAN Z H, LIN T J. Numerical simulation of influence of cementing quality on casing failure for oil field[J]. Computer Simulation, 2014, 31(9): 161-164, 251. DOI:10.3969/j.issn.1006-9348.2014.09.035 |
| [13] |
陈勇, 练章华, 陈敏, 等. 水泥环周向缺失的热采井井筒热应力耦合分析[J]. 石油钻采工艺, 2008, 30(2): 108-110. CHEN Y, LIAN Z H, CHEN M, et al. Thermal-stress coupling analysis of the rmalrecovery wells with cement sheath circumferential discontinuity[J]. Oil Drilling & Production Technology, 2008, 30(2): 108-110. DOI:10.3969/j.issn.1000-7393.2008.02.027 |
| [14] |
蒋可, 李黔, 陈远林, 等. 页岩气水平井固井质量对套管损坏的影响[J]. 天然气工业, 2015, 35(12): 77-82. JIANG K, LI Q, CHEN Y L, et al. Influence of cementing quality on casing failures in horizontal shale gas wells[J]. Natural Gas Industry, 2015, 35(12): 77-82. DOI:10.3787/j.issn.1000-0976.2015.12.012 |
| [15] |
DE ANDRADE J, TORSAETER M, TODOROVIC J, et al. Influence of casing centralization on cement sheath integrity during thermal cycling[R]. SPE 168012, 2014.
|
| [16] |
李早元, 祁凌, 刘锐, 等. 空心微珠低密度水泥环完整性试验研究[J]. 石油钻探技术, 2017, 45(3): 42-47. LI Z Y, QI L, LIU R, et al. Experimental study on the integrity of low-density cement sheath with hollow microsphere[J]. Petroleum Drilling Techniques, 2017, 45(3): 42-47. |


