0 引言
大规模水力压裂是实现非常规油气藏商业开发的主要手段。然而大规模水力压裂会带来储层和地下水污染及水资源浪费等问题[1-3]。针对水力压裂存在的局限性,中国工程院沈忠厚院士率先提出利用超临界CO2进行储层压裂改造[4-6]。超临界CO2压裂不仅对储层和地下水无污染,而且能够使储层产生多而复杂的裂缝网络,大大提高油气采收率,同时还可以实现CO2埋存。然而超临界CO2压裂液与其他低黏压裂液相比,黏度更低,因此其在裂缝内支撑剂携带能力和规律不得而知。在超临界CO2携带支撑剂能力研究方面,L.HOU等[7]利用试验和模型推导的方法,建立了支撑剂在超临界CO2中的沉降末速计算模型,能够预测支撑剂在裂缝中沉降特性。郭斌[8]通过数值模拟证实了超临界CO2在连续管水平段和裂缝中携带支撑剂的可行性。侯磊等[9]在BBO方程的基础上,建立了支撑剂在超临界CO2中的跟随性计算模型,并通过试验验证了模型的准确性。
此前的研究主要关注超临界CO2在裂缝中携带支撑剂的可行性,而对超临界CO2在裂缝中携带支撑剂填充和铺设规律研究较少;此外,上述研究还忽略了超临界CO2压裂液黏度变化的影响,且所取砂比不符合超临界CO2压裂的特点。鉴于此,笔者采用计算流体力学(CFD)的方法,考虑支撑剂运移中流固和固固间耦合作用的影响,建立了求解裂缝中超临界CO2和支撑剂两相流动模型,并进行了关键参数敏感性分析,进而得到超临界CO2在裂缝中携带支撑剂的最优参数,可以为超临界CO2压裂参数优化及技术适应性研究提供借鉴和参考。
1 基本模型和模拟方案基于Eulerian-Eulerian的多相流模型主要包含VOF(Volume of Fluid)模型、Mixture(混合)模型和Eulerian(欧拉)模型。其中,VOF模型主要用来求解分层流和自由表面流,欧拉模型求解多相流,常将动量方程和连续性方程分开求解,计算量较大,而混合模型是一种简化的欧拉模型,适用于支撑剂运移和沉降问题,并且混合模型计算量较小,精度高。故笔者采用Mixture模型求解超临界CO2和支撑剂两相流动。为了考虑颗粒之间的相互作用,采用了颗粒动力学中固相的质量、动量及颗粒温度的输运方程[10-11]。
1.1 控制方程式(1)~式(3)分别给出了携砂液的连续性方程、动量守恒方程以及能量守恒方程。
连续性方程为:
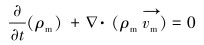
|
(1) |
式中:ρm为混合物密度,kg/m3;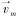
动量方程为:
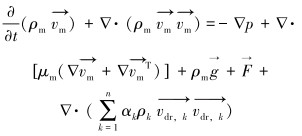
|
(2) |
式中:ρk为k相的密度,kg/m3;p为压力,Pa;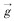


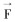
能量守恒方程为:
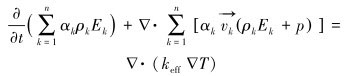
|
(3) |
式中:Ek为k相的能量,J;
根据颗粒流动模型能量理论可知,固相颗粒温度正比于颗粒随机脉动动能,其输运方程为:
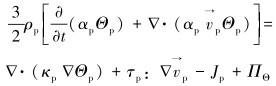
|
(4) |
式中:Θp为颗粒拟温度,m2/s2;κp为颗粒能量传导系数,kg/(m·s);τp为颗粒相的应变张量;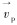
求解上述控制方程需要添加本构方程加以封闭,其中对于固相与液相之间的拖曳力计算,在裂缝内往往采用Gidaspow模型[12-14]。固液两相间的动量交换系数β计算式如下。
当α1≥0.8时,有:

|
(5) |
当α1<0.8时,有:

|
(6) |
其中:

|
(7) |
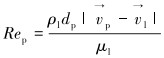
|
(8) |
式中:α1为液相的体积分数;vl为液相速度,m/s;ρl为液相的密度,kg/m3;dp为固相颗粒粒径,m;CD为固液两相间曳力系数;μl为液相的黏度,Pa·s;Rep为固液两相间滑脱速度定义的雷诺数。
在混合物体系中,颗粒黏度对混合物有效黏度的计算至关重要,因此在体积加权平均黏度的计算中需要考虑颗粒动能引起的剪切黏度。固体剪切黏度μs由碰撞黏度部分μs, col和动能黏度部分μs, kin组成。
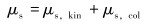
|
(9) |
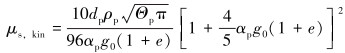
|
(10) |
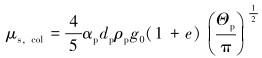
|
(11) |

|
(12) |
式中:e为弹性恢复系数;g0为径向分布函数,是当固体相稠密时用于修正颗粒之间碰撞概率的校正系数;s为颗粒之间的距离,m。
1.3 超临界CO2状态方程CO2的密度和黏度是影响其携带支撑剂性能的因素,考虑CO2黏度和密度受温度影响,利用Fluent中的Aungier-Redlich-Kwong真实气体模型及Vesovic模型分别计算CO2的密度和黏度[15-16]。
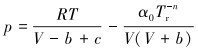
|
(13) |
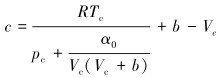
|
(14) |
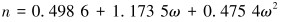
|
(15) |
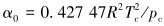
|
(16) |
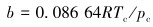
|
(17) |
式中:R为气体常数,J/(mol·K),k;Tr为对比温度,k;Tc为临界温度,K;pc为临界压力,Pa;Vc为临界体积,m3/kg;V为对比体积,m3/kg;ω为偏差因子。
1.4 几何模型和边界条件考虑超临界CO2压裂裂缝特点,确定采用与文献模型相似的尺寸,模拟裂缝的长、宽、高分别为3 000、10和400 mm,如图 1所示[17-21]。为了提高计算的准确性和收敛速度,网格划分采用结构化划分方式,且网格节点数72万个。入口的边界条件为质量流量入口,出口边界条件为压力出口。模型的其他部分边界条件为壁面,且假设壁面为无滑脱壁面,温度恒定。考虑到非常规油藏渗透率较低,故忽略超临界CO2的滤失效应。使用可实现k-ε(Realizable k-ε)模型描述支撑剂在裂缝内流动,同时为了提高计算的准确性,设置入口处的湍流强度和水力当量直径。此外,使用SIMPLE算法求解压力和速度耦合场,压力采用标准的离散格式,其他均采用一阶迎风的离散格式。

|
| 图 1 模拟裂缝二维网格模型 Fig.1 2D mesh model of simulated fracture |
1.5 模拟方案
为了探究支撑剂密度、粒径、携砂液的排量以及砂比等参数对超临界CO2在裂缝中携带支撑剂流动规律的影响,在参考滑溜水等低黏压裂液参数的基础上[22-23],制定了数值模拟方案(见表 1)。其中基准的模拟条件为支撑剂密度1 540 kg/m3,粒径为0.25 mm,砂比为0.3,携砂液排量为2 kg/s。
| 支撑剂密度/(kg·m-3) | 砂比 | 粒径/mm | 携砂液排量/(kg·s-1) |
| 1 540/1 750/ 2 040/2 350/ 2 540 |
0.08/0.10/ 0.15/0.20/ 0.30 |
0.250/0.300/ 0.425/0.500/ 0.850 |
1.0/1.5/ 2.0/3.0/ 4.0 |
数值模拟分4组进行,对每组模拟结果分析时,均取缝宽方向位于中心平面上的数据。
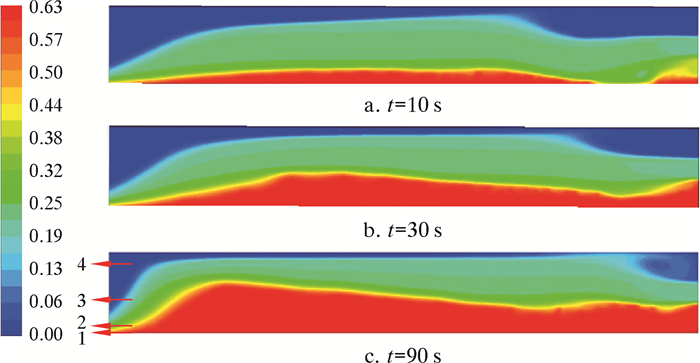
2 结果与讨论 2.1 超临界CO2携带支撑剂在裂缝中分布规律图 2为基准条件下不同时刻裂缝垂直剖面上支撑剂体积分数分布云图。由图 2a可知,当超临界CO2和支撑剂注入后,支撑剂由于重力作用在裂缝底部沉降形成砂丘;同时由于支撑剂密度较小,加上射流作用,其易被超临界CO2携带到深部裂缝,而在靠近入口位置形成凹陷。图 2b显示,随着注入时间持续,裂缝中的砂丘会影响携砂液射流速度,导致支撑剂因速度减小发生沉降,从而在距入口一定距离处形成堤峰。图 2c表明,由于堤峰的存在,致使裂缝中过流截面减小,流经裂缝中的支撑剂运移速度会加快,促使支撑剂向砂丘的背部方向堆积和运移,此时沙丘的高度不发生变化,长度不断向出口延伸。上述即是超临界CO2携带支撑剂在裂缝中沉降和运移的3个阶段,与文献[18]介绍的滑溜水携带支撑剂在裂缝中运移和铺设过程大致相同,说明超临界CO2同滑溜水具有相似的携带支撑剂的性能。
|
| 图 2 裂缝中支撑剂体积分数随时间变化的分布云图 Fig.2 Distribution of proppant volume fraction in the fracture over time |
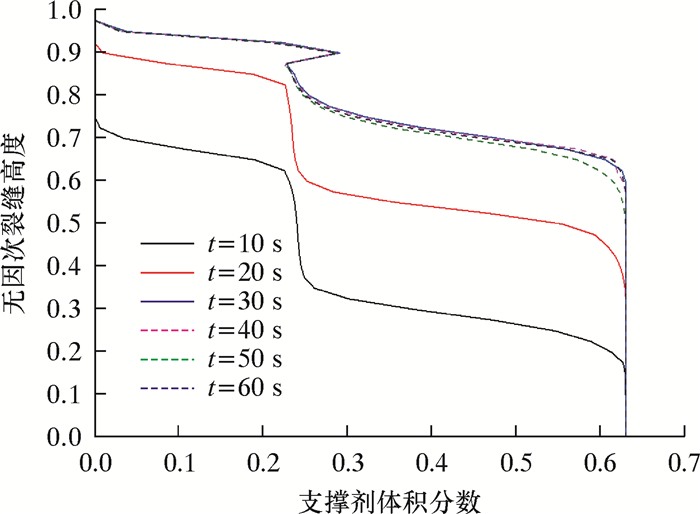
由图 2可知,支撑剂体积分数在裂缝垂直剖面上具有明显的差异,且由下到上依次可以分为4个区域:静止砂丘层(图中1)、接触层(图中2)、跃移层(图中3)和悬浮层(图中4)[17-18]。图 3为裂缝半长处支撑剂体积分数与无因次缝高关系。由图可知,在静止砂丘层支撑剂的体积分数维持在大于0.60的值保持不变,接触层体积分数在介于0.25~0.60之间缓慢变化,跃移层支撑剂体积分数在介于0.20~0.25范围内波动剧烈,而悬浮层的支撑剂体积分数则在介于0.0~0.2之间缓慢变化。此外,在10~30 s之间,随着时间的增加,静止砂丘层、接触层以及悬浮层在所占的面积比例不断增大,跃移层所占面积比例不断减小。而在40 s之后,裂缝中各层所占面积比例基本保持不变,即达到了平衡状态。
|
| 图 3 裂缝半长处支撑剂体积分数与无因次缝高关系 Fig.3 Relationship between proppant volume fraction and dimensionless fracture height at semi-length of fracture |
为了获得支撑剂在裂缝内铺设和填充规律,选取裂缝半长处的砂丘高度和支撑剂体积分数进行分析,并利用无因次平衡高度(平衡高度/裂缝高度)和无因次砂丘高度(当前砂丘堆积高度/裂缝高度)对影响超临界CO2携带支撑剂性能的参数进行优选。
2.2 支撑剂密度的影响图 4为无因次平衡高度和平衡时间随支撑剂密度变化的曲线。由图可知,随着支撑剂密度的增大,砂丘的无因次平衡高度逐渐增加,而平衡时间逐渐减小。其中支撑剂密度为1 540 kg/m3时,在裂缝中支撑剂形成的砂丘高度最小,约为裂缝高度的40%,平衡时间是50 s。支撑剂密度为2 540 kg/m3时,支撑剂形成的砂丘高度最大,约为裂缝高度的65%,平衡时间缩短为30 s。

|
| 图 4 无因次平衡高度和平衡时间随支撑剂密度变化的曲线 Fig.4 Dimensionless equilibrium height and equilibrium time under different proppant densities |
图 5为不同支撑剂密度下砂丘无因次高度随时间变化曲线。由图可知,不同密度的支撑剂所形成的砂丘高度均是先迅速增加,然后逐渐趋向稳定。这是因为当支撑剂和超临界CO2受到射流加速作用时,可以在射流的滞止点附近较快沉降。然而随着砂丘高度增加,携砂液的射流速度会受到影响,导致支撑剂沉降速度减慢。此外,由于携砂液的过流截面变窄而速度增大,支撑剂易被流化运移到砂丘背面。当支撑剂颗粒沉降数目和砂丘中支撑剂颗粒被流化数目相等时,则达到了平衡状态,砂丘高度不发生变化。

|
| 图 5 不同支撑剂密度下砂丘无因次高度随时间变化曲线 Fig.5 The dimensionless height of sand dunes versus time under different proppant densities |
图 5还表明,当支撑剂密度为2 540 kg/m3时,砂丘的高度随时间变化曲线在0~30 s之间的斜率最大,砂丘高度增加较快;而支撑剂密度为1 540 kg/m3时,曲线斜率变化相对较小,砂丘高度变化较慢。因此采用低密度支撑剂有利于其在裂缝中形成更加均匀的砂丘剖面,避免发生砂堵。
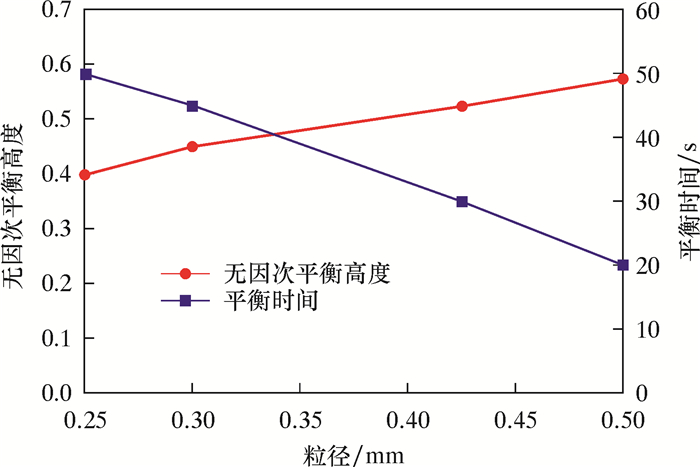
2.3 支撑剂粒径的影响图 6为无因次平衡高度和平衡时间随着支撑剂粒径变化曲线。由图可知,随着支撑剂粒径的增加,砂丘的无因次平衡高度不断增加,而平衡时间逐渐缩短。这是因为支撑剂的粒径越大,支撑剂颗粒越易受到裂缝壁面的影响,故支撑剂易于发生沉降。支撑剂的粒径为0.425 mm时,砂丘的无因次高度最大,约为裂缝高度的52.5%,平衡的时间约为30 s。而支撑剂粒径为0.250 mm时,砂丘的无因次高度最小,约为裂缝高度的40%;平衡的时间接近50 s。
|
| 图 6 无因次平衡高度和平衡时间随支撑剂粒径变化曲线 Fig.6 Dimensionless equilibrium height and equilibrium time under different proppant particle sizes |
图 7是在不同的支撑剂粒径条件下,砂丘的无因次高度随时间变化曲线。由图可知,不同的支撑剂粒径,无因次砂丘高度随时间变化的趋势均是先迅速增加,之后趋于稳定。其中支撑剂粒径越大,其前期沉降速度越大,无因次砂丘高度变化得越快;并且当支撑剂沉降达到平衡状态以后,支撑剂在裂缝中形成的砂丘高度也较高。因此,支撑剂粒径越大,越容易发生砂堵,不利于支撑剂在深部裂缝形成有效的支撑。故使用超临界CO2加砂压裂,建议选用高于20/40目数的支撑剂有利于支撑裂缝。

|
| 图 7 不同支撑剂粒径条件下无因次砂丘高度随时间变化曲线 Fig.7 The dimensionless height of sand dunes versus time under different proppant sizes |
2.4 砂比的影响
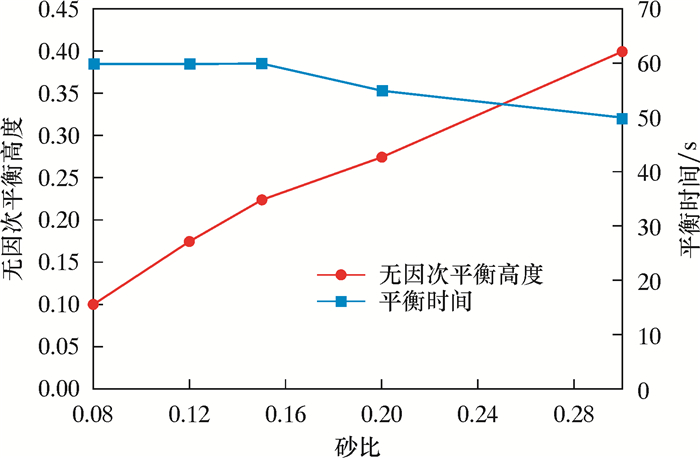
图 8为无因次平衡高度和平衡时间随着砂比变化曲线。由图可知,随着砂比的增加,无因次平衡高度逐渐增加,而平衡时间先在低砂比时保持不变之后逐渐缩短。这是因为随着砂比的增加,支撑剂颗粒之间及其与裂缝壁面的作用加剧,促使更易于发生沉降。其中支撑剂的砂比为8%,砂丘的无因次平衡高度最小,约为裂缝高度的10%,平衡时间约为60 s。支撑剂的砂比为3%,砂丘的无因次平衡高度最大,约为裂缝高度的40%,平衡时间接近50 s。
|
| 图 8 无因次平衡高度和平衡时间随砂比变化曲线 Fig.8 Dimensionless equilibrium height and equilibrium time under different sand ratios |
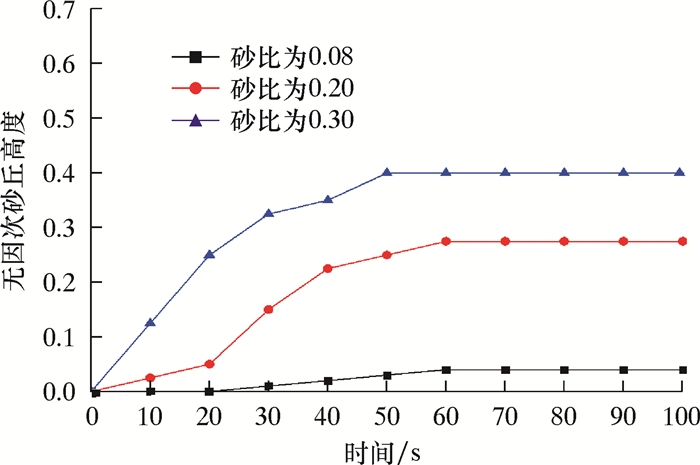
图 9是在不同的砂比条件下,砂丘的无因次高度随时间变化曲线。由图可知,不同的砂比条件下,无因次砂丘高度变化趋势先迅速增加,之后趋于稳定。同时随着砂比的增加,支撑剂颗粒之间的对流沉降作用加强,平衡时间逐渐缩短。此外,在达到平衡状态前,砂比越大,无因次砂丘高度随时间变化曲线斜率越大,支撑剂沉降越快;在达到平衡状态之后,砂比越大,无因次砂丘高度也越大。因此利用低黏的超临界CO2进行压裂时,适合采用低砂比(小于8%)的携砂液进行裂缝填充。
|
| 图 9 不同砂比条件下砂丘的无因次高度随时间变化曲线 Fig.9 The dimensionless height of sand dunes versus time under different sand ratios |
2.5 质量流量的影响
图 10为无因次平衡高度和平衡时间随着携砂液排量变化曲线。由图可知,随着携砂液排量的增加,无因次平衡高度降低,平衡时间缩短。这是因为入口质量流量越大,单位时间内注入的支撑剂质量越大,形成砂丘所需的时间就会缩短;同时注入的质量流量越大,注入支撑剂的速度较快,故悬浮区和跃移区的面积将变大,而静止砂丘的区域面积会变小。图中携砂液的质量流量为1 kg/s时,无因次平衡高度最大,约为裂缝高度的60%,平衡时间接近70 s;而携砂液的质量流量为4 kg/s时,无因次平衡高度最小,约为裂缝高度的5%,时间接近10 s。

|
| 图 10 无因次平衡高度和平衡时间随携砂液排量变化曲线 Fig.10 Dimensionless equilibrium height and equilibrium time under different displacement of the carrying liquid |
图 11是在不同的携砂液排量条件下,砂丘的无因次高度随时间变化的曲线。由图可知,随着时间的增加,无因次砂丘高度变化趋势是先增加之后趋于稳定。随着单位时间入口排量的增加,单位时间注入的支撑剂质量会增加,则平衡时间会逐渐减小。同时排量越小,达到平衡状态的时间越长,平衡高度越大,形成砂堵的风险越大。因此在实际的超临界CO2压裂作业中,应根据裂缝特点,选择合理的携砂液排量,避免发生砂堵。

|
| 图 11 不同携砂液排量条件下砂丘的无因次高度随时间变化曲线 Fig.11 The dimensionless height of sand dunes versus time under different carrying liquid displacements |
3 结论
(1) 超临界CO2携带支撑剂在裂缝中铺设时大致分为3个阶段:首先是支撑剂在射流的滞止点附近因重力发生沉降,在裂缝底部形成砂丘;其次砂丘随着支撑剂颗粒沉降不断抬高,在距离入口一定位置处形成凸起;最后,砂丘达到平衡高度后,支撑剂床不断向出口方向延伸。
(2) 使用超临界CO2携带支撑剂填充支撑裂缝时,支撑剂体积分数在裂缝垂直剖面上差异明显;静止沙丘层的支撑剂体积分数随注入时间增加基本保持不变,接触层和悬浮层体积分数变化较为平缓,而跃移层的体积分数变化剧烈。
(3) 当超临界CO2最初在裂缝中携带支撑剂流动时,静止砂丘层、接触层以及悬浮层所占的面积比例随着注入时间增加不断增大,而跃移层所占面积比例不断减小。而当达到一定时间后,裂缝中各层所占面积比例基本保持不变。
(4) 支撑剂的密度、粒径、携砂液的砂比以及排量会对超临界CO2携带支撑剂在裂缝中铺设规律和填充效果产生影响。在模拟条件下,建议选用密度小于1 540 kg/m3、粒径大于20/40目的支撑剂,并且携砂液的砂比要低于8%,排量要高于4 kg/s,从而有益于超临界CO2携带支撑剂在裂缝中形成均匀的砂丘形态,避免发生砂堵。
| [1] |
王海柱, 沈忠厚, 李根生. 超临界CO2开发页岩气技术[J].
石油钻探技术, 2011, 39(3): 30-35.
WANG H Z, SHEN Z H, LI G S. Feasibility analysis on shale gas exploitation with supercritical CO2[J]. Petroleum Drilling Techniques, 2011, 39(3): 30-35. DOI: 10.3969/j.issn.1001-0890.2011.03.005 |
| [2] |
李根生, 王海柱, 沈忠厚, 等. 超临界CO2射流在石油工程中应用研究与前景展望[J].
中国石油大学学报(自然科学版), 2013, 37(5): 76-80, 87.
LI G S, WANG H Z, SHEN Z H, et al. Application investigations and prospects of supercritical carbon dioxide jet in petroleum engineering[J]. Journal of China University of Petroleum (science edition), 2013, 37(5): 76-80, 87. DOI: 10.3969/j.issn.1673-5005.2013.05.011 |
| [3] |
张驰, 陈航. 超临界二氧化碳在非常规油气藏开发中的应用[J].
石油化工应用, 2014, 33(9): 57-59, 63.
ZHANG C, CHEN H. Application of supercritical carbon dioxide in unconventional oil-gas reservoirs[J]. Petrochemical Industry Application, 2014, 33(9): 57-59, 63. DOI: 10.3969/j.issn.1673-5285.2014.09.015 |
| [4] |
王香增, 吴金桥, 张军涛. 陆相页岩气层的CO2压裂技术应用探讨[J].
天然气工业, 2014, 34(1): 64-67.
WANG X Z, WU J Q, ZHANG J T. Application of CO2 fracturing technology for terrestrial shale gas reservoirs[J]. Natural Gas Industry, 2014, 34(1): 64-67. DOI: 10.3787/j.issn.1000-0976.2014.01.009 |
| [5] | CRAWFORD H R, NEILL G H, BUCY B J, et al. Carbon dioxide-a multipurpose additive for effective well stimulation[J]. Journal of Petroleum Technology, 1963, 15(3): 237-242. DOI: 10.2118/571-PA |
| [6] | MIDDLETON R S, CAREY J W, CVRRIER R P, et al. Shale gas and non-aqueous fracturing fluids:opportunities and challenges for supercritical CO2[J]. Applied Energy, 2015, 147(3): 500-509. |
| [7] | HOU L, SUN B, WANG Z, et al. Experimental study of particle settling in supercritical carbon dioxide[J]. The Journal of Supercritical Fluids, 2015, 100: 121-128. DOI: 10.1016/j.supflu.2015.02.020 |
| [8] |
郭斌.超临界CO2压裂携砂规律研究[D].北京: 中国石油大学(北京), 2015. GUO B. Numerical simulation of the proppant transport in supercritical carbon dioxide fracturing[D]. Beijing: China University of Petroleum(Beijing), 2015. |
| [9] |
侯磊, 孙宝江, 蒋廷学, 等. 支撑剂在超临界二氧化碳中的跟随性计算[J].
石油学报, 2016, 37(8): 1061-1068.
HOU L, SUN B J, JIANG T X, et al. Calculation on the following performance of proppant in supercritical carbon dioxide[J]. Act Petrolei Sinica, 2016, 37(8): 1061-1068. |
| [10] |
汪琦.气固流化床两相流动的CFD模型研究和实验验证[D].武汉: 华中科技大学, 2012. WANG Q. Comparative analysis of CFD models of gas-solid fluidized bed and experimental verification[D]. Wuhan: Huazhong University of Science & Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10487-1014025924.htm |
| [11] |
李东耀.基于Fluent软件的流化床的气固两相流模型研究[D].重庆: 重庆大学, 2009. LI D Y. Study on gas-solid flow model of fluidized bed based on fluent software[D]. Chongqing: Chongqing University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10611-2009149103.htm |
| [12] | JOHNSON P C, JACKSON R. Frictional-collisional constitutive relations for granular materials, with application to plane shearing[J]. Journal of Fluid Mechanics, 1987, 176: 67-93. DOI: 10.1017/S0022112087000570 |
| [13] | LUN C K K, SAVAGE S B, JEFFREY D J, et al. Kinetic theories for granular flow:Inelastic particles in Couette flow and slightly inelastic particles in a general flow field[J]. Journal of Fluid Mechanics, 1984, 140: 223-256. DOI: 10.1017/S0022112084000586 |
| [14] | LÜ H L, HE Y R, GIDASPOW D. Hydrodynamic modelling of binary mixture in a gas bubbling fluidized bed using the kinetic theory of granular flow[J]. Chemical Engineering Science, 2003, 58(7): 1197-1205. DOI: 10.1016/S0009-2509(02)00635-8 |
| [15] | LEMMON E W, JACOBSEN R T. Viscosity and thermal conductivity equations for nitrogen, oxygen, argon, and air[J]. International Journal of thermacphysics, 2004, 25(1): 21-69. DOI: 10.1023/B:IJOT.0000022327.04529.f3 |
| [16] | SPAN R. A reference equation of state for the thermodynamic properties of nitrogen for temperatures from 63.151 to 1000 K and pressures to 2200 MPa[J]. Journal of Physical and Chemical Reference Data, 2015, 29(6): 1361. |
| [17] | LIU Y, SHARMA M M. Effect of fracture width and fluid rheology on proppant settling and retardation: an experimental study[R]. SPE 96208, 2005. https://www.researchgate.net/publication/266663616_Effect_of_Fracture_Width_and_Fluid_Rheology_on_Proppant_Settling_and_Retardation_An_Experimental_Study |
| [18] | LIU Y. Settling and hydrodynamic retardation of proppants in hydraulic fractures[D]. Austin: The University of Texas at Austin, 2006. https://www.researchgate.net/publication/37256045_Settling_and_Hydrodynamic_Retardation_of_Proppants_in_Hydraulic_Fractures |
| [19] |
张涛, 郭建春, 刘伟. 清水压裂中支撑剂输送沉降行为的CFD模拟[J].
西南石油大学学报(自然科学版), 2014, 36(1): 74-82.
ZHANG T, GUO J C, LIU W. CFD simulation of proppant transportation and settling in water fracture treatments[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2014, 36(1): 74-82. |
| [20] |
温庆志, 高金剑, 刘华, 等. 滑溜水携砂性能动态实验[J].
石油钻采工艺, 2015, 37(2): 97-100.
WEN Q Z, GAO J J, LIU H, et al. Dynamic experiment on slick-water prop-carrying capacity[J]. Oil Drilling & Production Technology, 2015, 37(2): 97-100. |
| [21] |
温庆志, 胡蓝霄, 翟恒立, 等. 滑溜水压裂裂缝内砂堤形成规律[J].
特种油气藏, 2013, 29(3): 137-139, 158.
WEN Q Z, HU L X, ZHAI H L, et al. Study on the rule of forming sand bank in fractures of slick water fracturing[J]. Special Oil and Ras Reservoirs, 2013, 29(3): 137-139, 158. DOI: 10.3969/j.issn.1006-6535.2013.03.033 |
| [22] |
李靓.压裂缝内支撑剂沉降和运移规律实验研究[D].成都: 西南石油大学, 2014. LI L. Experimental study of proppant transport and settling in fracturing fracture[D]. Chengdu: Southwest Petroleum University, 2014. |
| [23] | ANSYS Inc. ANSYS FLUENT 12.0 user's guide[M].[S.l.]ANSYS Inc, 2009: 593-604. |




