0 引言
连续管作业设备广范应用于油气田修井、钻井、完井和测井等作业,在油气田勘探与开发中发挥着越来越重要的作用[1]。连续管在实际工作过程中条件极为恶劣,通常会存在一些机械损伤,例如在运输中表面碰伤、在清蜡作业中受到落入井下的刮蜡器的划伤、在注入过程中由于夹持过紧而在表面留下压痕等,这些损伤会加速连续管的疲劳破坏。如果将有缺陷的油管重新下入井内,有可能发生连续管穿孔或断裂事故,因此考虑初始缺陷对连续管作业造成的影响十分必要。根据现场观察,普通油管的初始缺陷以近似椭球体最为常见[2]。
连续管除了本身的制造缺陷外,由于其工作环境恶劣,还有碰伤和划痕等一些机械损伤以及腐蚀等化学损伤,以致在这些部位上截面尺寸发生突然变化。试验结果和理论分析表明:在零件尺寸突然改变处的横截面上 (几何不连续处),并在低循环载荷作用下,这些缺口会处产生较大的应变集中,从而导致较大的塑性应变,多次的循环载荷会导致局部应变累积增长,这往往成为疲劳裂纹萌生的危险部位[3]。因此,对于连续管的疲劳破坏来说,大都从应变较大的局部位置开始。对于缺陷的疲劳特性进行研究,有助于提高连续管设计水平和连续管使用寿命的预估能力,有助于减少疲劳事故所造成的人员和财产重大损失,具有非常重要的意义。
1 缺陷疲劳的研究状况疲劳破坏可以被描述为由3个过程组成:裂纹萌生、裂纹扩展和最终破裂。应变增长达到某一限度就会产生裂纹,在以后的加载过程中沿着某个方向开始扩展,进一步发展成宏观断裂。连续管的疲劳破坏属于多轴低周疲劳破坏,目前对于多轴低周疲劳破坏的损伤积累和寿命估算主要有2种方法[4]:等效应变法和临界面法。
定义合适的等效应变,对于多轴低周疲劳有[5]:
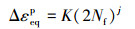
|
(1) |
式中:Δεeqp为等效塑性应变,K、j为材料常数。
Δεeqp可以定义为八面体剪应变、最大剪应变、最大正应变和Von Mises等效应变等。不同的等效应变之间差异不大,对于某些工程应用,它们是有效的,且简单实用。
临界面法认为失效是由裂纹引起的,裂纹的形成和扩展在一个临界平面上,其具最有利于裂纹产生和裂纹扩展的应力/应变条件,大量试验表明裂纹一般都产生于最大切应变平面上。运用这个方法有2步[6]:首先,计算疲劳临界面上的应力、应变历史;然后,将临界面位置的应力和应变历史转化成累积的疲劳损伤。
等效应变法简单实用,但不适合于非比例加载下的低周疲劳。临界面法是进行多轴低周疲劳分析比较合适的损伤判据,其类型有很多种。
在对含缺陷的连续管疲劳寿命预测方面,何春生等[7]用设计的专用连续管疲劳寿命装置做了含轴向划痕、环向划痕、方坑以及无损伤外径31.8 mm连续管的低周疲劳试验,发现含有轴向划痕的连续管在36次时发生断裂,比无损伤连续管循环次数减少15次左右,即使是有轴向划痕的试件其断裂方向仍是在环向,但发生在轴向损伤部位;具有环向划痕的连续管在试验过程中,循环次数只有7次左右就发生断裂,断裂处位于环向划痕根部;含有初始方坑的连续管循环次数在17次时发生断裂。3种损伤形式对连续管失效影响程度从大到小依次为:环向划痕、方坑、轴向划痕。
但是,对于连续管的疲劳寿命预测,国内外多数研究成果集中在无损伤连续管,而对表面出现各种缺陷后的连续管的疲劳寿命预测以及失效判别研究还很少,还没有成熟、统一使用的模型和方法。在连续管疲劳寿命试验研究方面,虽然国外的专用疲劳试验装置积累了大量疲劳试验数据,但还有各种损伤结构以及不同工况下的连续管疲劳试验需要开展研究。国内连续管试验装置较少,得到的疲劳试验数据还不够丰富,还不能完全满足工程应用的需要,仍需开展大量试验研究。
2 椭球缺陷连续管的疲劳寿命分析现场连续管椭球缺陷居多,因此下文开展不同尺寸椭球缺陷对连续管疲劳寿命的影响研究。在ANSYS软件中建立整个连续管卷绕模型 (见图 1),它由3部分组成:矫直模型、连续管模型和滚筒模型。其中连续管模型长度为1 000 mm,外径为50.8 mm,壁厚为4.78 mm,材料为CT90,滚筒模型的曲率半径为1 500 mm,矫直模型的曲率半径为7 000 mm。

|
| 图 1 连续管卷绕模型及加载 Fig.1 The winding model and loading of coiled tubing |
建立好整个卷绕模型后,在连续管中间部分建立椭球缺陷,中心点位置坐标为 (25.4,0,450)。由于建立了缺陷,使得缺陷附近划分网格会比较困难,而缺陷又是研究重点,必须使得缺陷部分网格质量尽量高,为此建立了更大的椭球面把缺陷单独分离出来,但被单独分出来的缺陷体部分还不是六面体,还要将其分成4小块,每一块都是六面体,然后划分成映射网格,如图 2所示。在整个模型的加载方面,滚筒和矫直模型为固定部分,限制其上所有节点所有方向的自由度,在连续管右端面施加合适的切向力和弯矩,加载方式为比例加载,泄载方式也是比例泄载,油管内零内压,由于建立的是1/2对称模型,所以要在y坐标为0的面上施加对称约束 (见图 1)。

|
| 图 2 连续管椭球缺陷网格划分 Fig.2 Meshing of the ellipsoid defect of the coiled tubing |
2.1 宽度和深度不变而长度不同的椭球缺陷 2.1.1 等效应变法
建立宽度 (y方向半轴长) 为0.25 mm,深度 (x方向半轴长) 为0.25 mm,长度 (z方向半轴长) 分别为0.3、0.4、0.5、0.6和0.7 mm的椭球坑缺陷。在连续管第1次弯曲完全贴在滚筒上后,找出应变最大的节点并标记,该节点在缺陷处才合理,然后找出在以后弯曲过程中该节点应变的3个分量的应变历程,这样根据式 (2) 和式 (3) 就可得出该节点3个方向的应变幅和平均应变[8]。
应变幅:
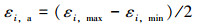
|
(2) |
平均应变:
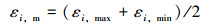
|
(3) |
i表示3个方向,即h为环向,x为轴向,r为径向 (分别为y方向、z方向、x方向)。εi, max表示在一次完整的卷绕矫直过程中某分量应变达到的最大值,εi, min则表示在一次完整的卷绕矫直过程中某分量应变达到的最小值。则该节点总的应变幅和平均应变为[8]:

|
(4) |
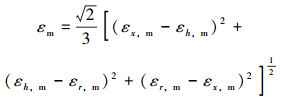
|
(5) |
最后得出的应变幅和平均应变可以合成一个Von Mises等效应变,根据等效应变法[8]:
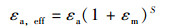
|
(6) |
式中:εa为应变幅,εm为平均应变,S是连续管的应变指数。
Manson-Coffin公式为[8]:
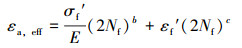
|
(7) |
式中:σf′为疲劳强度系数,b为疲劳强度指数,εf′为疲劳延性系数,c为疲劳延性指数,εa, eff为等效应变,E为弹性模量。
由公式 (7) 可以计算出2Nf,有关2Nf下文做说明。
在连续管疲劳寿命研究中,S.M.Tipton运用上述方法计算连续管疲劳寿命,他提出连续管的应变指数S通过连续管恒压疲劳试验获得,试验中连续管通过恒内压试验产生贯穿裂纹,出现连续管内压减小的现象时认为连续管失效,这样通过不同内压的试验获得S与内压之间有如下关系[9]:

|
(8) |
式中:Sy为连续管材料的屈服应力,Q和m为常数,环向应力σh用薄壁圆筒环向应力公式计算:
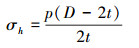
|
(9) |
式中:p为连续管的内压,D为连续管外径,t为连续管壁厚。
当内压p=0时,连续管环向应力σh=0,使得指数S=0,从而εa, eff=εa,即内压p为0时,等效应变可以由应变幅表示。然后根据Miner累积损伤准则有[10]:
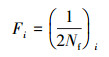
|
(10) |

|
(11) |
式中:Fi是第i次弯曲循环的损伤,当F=100%时认为发生失效,此时,i是总的累积次数,也就是总的弯曲循环次数,指的也就是疲劳寿命。
2.1.2 临界面法临界面法大多数采用最大剪切平面作为临界损伤平面,并利用该面上的最大剪切应变参数Δγmax和法向应变参数Δεn作为构造损伤参量的2个基本参数,循环剪应变有助于裂纹萌生,而法向正应变则有助于裂纹的扩展。在比例加载情况下最大剪应力平面方向固定, 仅在被开动的主滑移系与障碍物的交界处萌生微裂纹,但是非比例加载情况下会产生附加强化现象,若临界面法只以应变为损伤参量,则不能反映此现象。无论是比例加载还是非比例加载,尚德广等[11-12]给出了基于临界面法的缺口件疲劳寿命计算通式,由连续介质力学原理可以确定出3个主应变范围Δε1、Δε2和Δε3的值,则临界面上最大剪切应变范围为[11]:
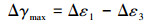
|
(12) |
临界面上最大法向应变范围为[11]:
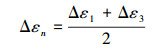
|
(13) |
如果利用Von Mises准则将临界面上2参数Δγmax和Δεn合成一个等效剪应变,与剪切形式的Manson-Coffin方程联系即可得出剪切形式的多轴疲劳寿命公式[12]:

|
(14) |
式中:G是剪切模量;τ′f、γ′f、b′和c′是纯扭循环加载下的疲劳材料常数。同理,如果将这2参数合成一个等效正应变幅,则可以得到拉伸形式的多轴疲劳寿命公式[12-13]:

|
(15) |
式中:E是弹性模量,σf′、εf′、b′和c′是单轴疲劳材料常数。
针对上述情况再次用临界面法计算。在ANSYS中提取出切应变最大的节点,标记该节点,提取出以后的弯曲循环过程中每一子步该节点的第一主应变ε1和第三主应变ε3,求出第一主应变的范围Δε1和第三主应变的范围Δε3,最后确定2个损伤参数,将它们合成的等效应变与Manson-Coffin方程联系起来,这样通过Miner累积损伤准则可以计算出疲劳寿命。笔者的计算取公式 (15)。
图 3是连续管模型缺陷附近应变分布云图。由图可以看出,缺陷中心处应变达到最大值,与预期结果相吻合。

|
| 图 3 应变分布云图 Fig.3 Strain distribution |
由于每次弯曲循环的应变幅和平均应变都不一样,从而合成的等效应变也不一样,所以每次的损伤Fi都不一样,笔者分别用上述2种方法计算出前10次弯曲循环的等效应变,发现相差非常微小,这说明前几次的损伤几乎一样,故求出前几次循环的等效应变平均值,代入Manson-Coffin公式求出2Nf的值就近似等于连续管的弯曲循环次数,从而达到估算疲劳寿命的目的。
将临界面法计算出的疲劳寿命数据与等效应变法计算出的疲劳寿命数据整合起来,结果如表 1和图 4所示。表中,L1为深度和宽度不变情况下椭球坑长度,εm等为通过等效应变法合成出的等效应变平均值,N等为通过等效应变法计算出的弯曲循环次数,εm临为通过临界面法合成出的等效应变平均值,N临为通过临界面法计算出的弯曲循环次数。有关连续管CT90的参数[14]:E=176 GPa,σf′=1 070 MPa,b=-0.117 5,εf′=0.346 56,c=-0.642 9。
| L1/mm | εm等 | N等 | εm临 | N临 |
| 0.3 | 0.020 18 | 112 | 0.019 39 | 120 |
| 0.4 | 0.015 96 | 172 | 0.015 71 | 177 |
| 0.5 | 0.014 27 | 213 | 0.013 68 | 231 |
| 0.6 | 0.012 66 | 268 | 0.012 45 | 277 |
| 0.7 | 0.012 24 | 287 | 0.011 93 | 302 |

|
| 图 4 弯曲循环次数随椭球坑长度变化曲线 Fig.4 The effect of the length of ellipsoid pit on the number of bending cycles |
由图 4可以看出,深度和宽度不变情况下,椭球坑长度越短,疲劳寿命越短。认为是由于深度和宽度不变,椭球坑长度越短,使得在xz截面上缺陷底部曲率半径越小,在xy截面上缺陷底部曲率半径不变,在yz截面上缺陷两侧曲率半径越小,但连续管在弯曲过程中,缺陷处是受到轴向的拉伸和压缩,缺陷轴向两侧的应变更加集中,缺陷底部的应变也更加集中,进而使得寿命缩短。
为了与无缺陷的连续管寿命相比较,在原有的连续管卷绕模型的基础上,只是除去了建立缺陷这一步骤,用等效应变法估算出无损连续管的弯曲循环次数在479次左右,由此可看出,即使是肉眼难以发现的缺陷对连续管疲劳寿命的影响还是很大。
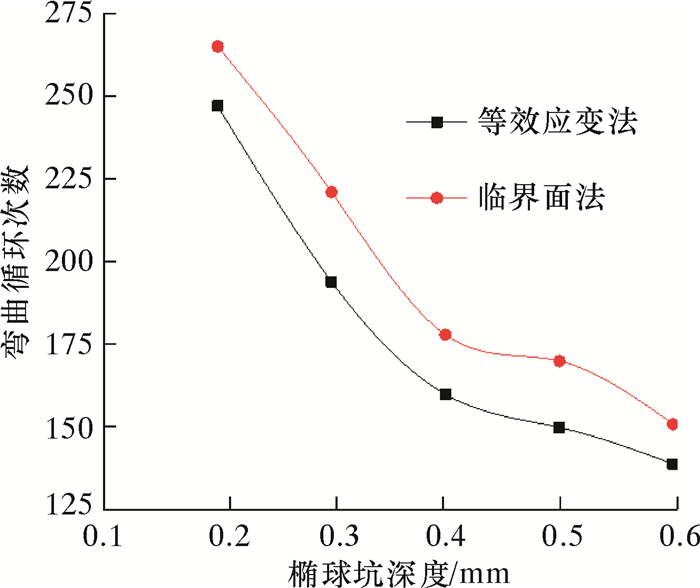
2.2 长度和宽度不变而深度不同的椭球缺陷继续分析长度和宽度不变而深度不同的椭球坑缺陷对连续管疲劳寿命的影响。建立宽度均为0.25 mm,长度均为0.5 mm,深度L2分别为0.2、0.3、0.4、0.5和0.6 mm的椭球缺陷,缺陷位置还是在同一位置。用等效应变法和临界面法计算出的有关数据如表 2和图 5所示。
| L2/mm | εm等 | N等 | εm临 | N临 |
| 0.2 | 0.013 20 | 247 | 0.012 75 | 265 |
| 0.3 | 0.015 01 | 194 | 0.014 00 | 221 |
| 0.4 | 0.016 59 | 160 | 0.015 66 | 178 |
| 0.5 | 0.017 20 | 150 | 0.016 07 | 170 |
| 0.6 | 0.017 90 | 139 | 0.017 14 | 151 |
|
| 图 5 弯曲循环次数随椭球坑深度变化曲线 Fig.5 The effect of the depth of ellipsoid pit on the number of bending cycles |
由图 5可看出,长度和宽度不变情况下,椭球坑深度越深,疲劳寿命越短。长度和宽度不变,椭球坑深度越深,使得在xz截面上缺陷底部曲率半径越小,在xy截面上缺陷底部曲率半径越小,在yz截面上缺陷两侧曲率半径不变,但连续管在弯曲过程中,缺陷处是受到轴向的拉伸和压缩,对缺陷两侧的应变集中影响不大,而缺陷底部应变更加集中,进而使得寿命缩短。
2.3 长度和深度不变而宽度不同的椭球缺陷继续分析长度和深度不变而宽度不同的椭球坑缺陷对连续管疲劳寿命的影响。深度均为0.25 mm,长度均为0.5 mm,宽度L3分别为0.2、0.3、0.4、0.5和0.6 mm的椭球缺陷,缺陷位置还是在同一位置。用等效应变法和临界面法计算出的有关数据如表 3和图 6所示。
| L3/mm | εm等 | N等 | εm临 | N临 |
| 0.2 | 0.013 50 | 237 | 0.013 03 | 254 |
| 0.3 | 0.014 79 | 199 | 0.014 31 | 212 |
| 0.4 | 0.016 07 | 170 | 0.015 70 | 178 |
| 0.5 | 0.017 35 | 147 | 0.016 90 | 155 |
| 0.6 | 0.018 23 | 134 | 0.017 77 | 141 |

|
| 图 6 弯曲循环次数随椭球坑宽度变化曲线 Fig.6 The effect of the width of ellipsoid pit on the number of bending cycles |
由图 6可看出,长度和深度不变情况下,椭球坑宽度越宽,疲劳寿命越短。长度和深度不变,椭球坑宽度越宽,在xz截面上缺陷底部曲率半径不变,在xy截面上缺陷底部曲率半径越大,在yz截面上缺陷两侧曲率半径越小,但是连续管在弯曲过程中,缺陷处是受到轴向的拉伸和压缩,对缺陷底部的应变集中影响不大,缺陷两侧应变更加集中,进而使得寿命缩短。
3 结论(1) 在其他方向尺寸不变的情况下,椭球缺陷长度越长,连续管疲劳寿命越长,椭球缺陷宽度越宽和深度越深,连续管疲劳寿命越短。如果3种方向尺寸变化范围一样,长度方向变化引起的弯曲循环次数范围大于深度方向和宽度方向引起的弯曲循环次数范围,深度方向变化引起的弯曲循环次数范围和宽度方向变化引起的弯曲循环次数范围差不多。这说明缺陷在笔者研究的图示位置时,缺陷尺寸在轴向的变化对疲劳寿命的影响大于环向和径向。
(2) 等效应变法和临界面法估算出的结果相差不大,但临界面法预估的疲劳寿命值略高于等效应变法预估的疲劳寿命值,从曲线的走向可以看出,2种方法算出的结果一致,具体哪种方法更接近实际值,还有待试验验证。
(3) 由于计算时间的限制,利用ANSYS仿真分析结合运用等效应变法和临界面法估算疲劳寿命时没有考虑累积损伤,得出的疲劳寿命值都高于准确值,因为在以后的弯曲循环过程中,会有累积的塑性应变增长,后几次弯曲循环的损伤高于前几次,但重点还是突出缺陷以及不同尺寸的缺陷对连续管疲劳寿命的影响。
| [1] | 李磊, 王鹏, 申昭熙, 等. 连续管在内压和循环弯曲作用下的试验研究[J]. 石油机械, 2011, 39(1): 5–7, 12. |
| [2] | 周思柱, 何迪, 吕志鹏. 用有限元方法研究含缺陷油管失效判据[J]. 石油矿场机械, 2006, 35(6): 19–22. |
| [3] | 刘鸿文. 材料力学[M]. 北京: 高等教育出版社, 2004. |
| [4] | 陈旭, 许爽燕. 多轴低周疲劳研究现状[J]. 压力容器, 1997(3): 58–61. |
| [5] | 丰崇友. 多轴非比例加载低周疲劳的研究综述[J]. 腐蚀科学与防护技术, 2010, 22(2): 124–127. |
| [6] | 刘克格. 多轴加载下缺口件应力应变分析与寿命预测的研究[D]. 北京: 北京工业大学, 2003. |
| [7] | 何春生, 刘巨保, 岳欠杯, 等. 基于椭圆度及壁厚参数的连续油管低周疲劳寿命预测[J]. 石油钻采工艺, 2013, 35(11): 15–18. |
| [8] | TIPTON S M.The achilles fatigue model[Z].CTES Tech Note, May, 1999. |
| [9] | TIPTON S M.Multiaxial plasticity and fatigue life prediction in coiled tubing:Fatigue lifetime predictive techniques:ASTM STP 1292[S].Philadelphia:American Society for Testing and Materials, 1996:283-304. |
| [10] | 姚卫星. Miner理论的统计特性分析[J]. 航空学报, 1995, 16(5): 601–604. |
| [11] | 尚德广, 王大康, 李明. 基于临界面法的缺口件多轴疲劳寿命预测[J]. 机械强度, 2003, 25(2): 212–214. |
| [12] | 尚德广, 姚卫星. 基于临界面法的多轴疲劳损伤参量的研究[J]. 航空学报, 1999, 20(4): 8–11. |
| [13] | 耿亚楠, 陈孝亮, 杨进, 等. 基于初始缺陷的钻柱疲劳寿命预测方法[J]. 石油钻采工艺, 2016, 38(6): 817–822. |
| [14] | TIPTON S M.Achilles 4.0 CT fatigue life prediction algorithm[Z].Tipton Engineering, May, 2003. |



