0 引言
连续波钻井液脉冲发生器因具有较高的传输速率而逐渐受到重视。连续波发生器的压力波信号质量主要由信号幅值和频谱特性决定,与其转子形状密切相关[1-6]。目前转子形状主要有三角形、矩形和扇形等[7-8]。若转子产生的压力波波形与简谐波相差较大,会导致其在传输过程中衰减较快。因此,需要合理设计转子形状以提高压力波信号的品质及传输距离。笔者以压力波信号与期望正弦波信号相关系数最大为评价指标,设计了三角形转子形状,对其压力波信号进行分析,并对优化所得的转子形状进行三维流体仿真,以验证其产生的波形。研究结果可为连续波钻井液脉冲发生器的结构优化提供参考。
1 转子设计准则 1.1 压力幅值设计准则在转子的形状设计中,应按式(1) 设计定子和转子的流通面积,以确保压力波幅值满足设计要求。

|
(1) |
式中:S为流通面积,m2;Δp为钻井液流过定转子产生的压降,Pa;Q为钻井液流量, m3/s;Cd为转阀阀口的流量系数;ρ为钻井液密度,kg/m3。
由于钻柱尺寸及结构的限制,最大流通面积不能过大, 同时最小流通面积过小会加大堵塞的概率,所以需要合理设计转子形状,在保证最大和最小流通面积的基础上使压力波信号幅值最大,以增加信号传输距离,减轻解码难度。
1.2 压力波与正弦波相关系数最大准则压力波信号在钻井液中传输时,信号中的谐波分量衰减较快,易导致信号损失。而正弦波是最简单的机械波,没有谐波分量,传输过程中衰减最小,因此以转子产生的波形接近正弦波为最优[9]。
标准正弦波方程为:
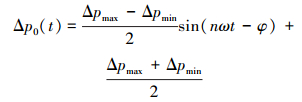
|
(2) |
式中:n为转阀阀瓣个数;ω为转阀转速,rad/s;φ为压力波信号的初始相位,rad。
压力波信号在单个周期内的相关系数为:
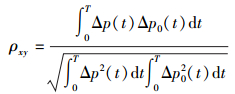
|
(3) |
在转子设计中,相关系数ρxy越大,则产生的压力波波形越接近正弦波。
2 转子形状参数化建模在笛卡尔坐标系中建立定子和转子的二维模型,根据其运动形式,用积分方法求出定子和转子的过流面积。由于三角形转子的形状主要由2条边线确定,所以先假设2条直线边的一般方程,推导出流通面积。然后通过程序优化求出2条直线边的最优方程。
钻井液脉冲发生器中定子和转子形状一致。定子和转子的初始状态如图 1所示。设定子2直线边一般方程为:

|
| 图 1 定子和转子的初始状态 Fig.1 Initial state of the stator and the rotor |
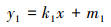
|
(4) |

|
(5) |
由于直线y1过点(R, 0),R为定转子半径,所以m1=y1-k1R。
转子2直线边一般方程y11(x)、y22(x)可视作由定子2直线边方程逆时针旋转γ-α所得,转子另一条边直线方程y3(x)由y2(x)顺时针旋转π/2-γ+α所得,令β=γ-α,由此可得:
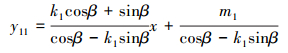
|
(6) |
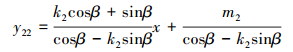
|
(7) |
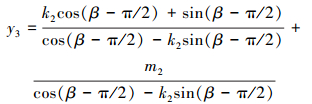
|
(8) |
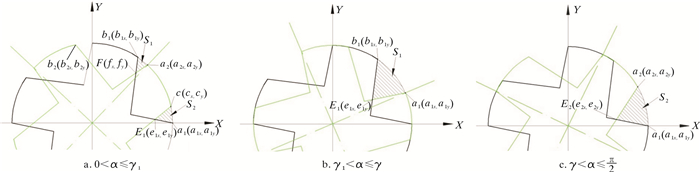
同理,可得a2、b2、c点(见图 2)横坐标为:
|
| 图 2 面积计算示意图 Fig.2 Schematic diagram of area calculation |
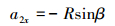
|
(9) |
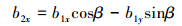
|
(10) |

|
(11) |
由于直线y2(x)与定转子半径R相交于b1(b1x, b1y)点,于是有:

|
(12) |
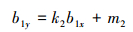
|
(13) |
进而可求出γ的计算式为:

|
(14) |
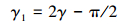
|
(15) |
(1) 当0<α≤γ1时,如图 2a所示,直线y11(x)与y2(x)相交于点E1(e1x, e1y),y3(x)与y1(x)相交于点F(fx, fy),将上述方程联立可求得E1和F点横坐标分别为:

|
(16) |
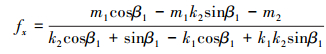
|
(17) |
式中:β1=β-π/2。
此时流通面积为:
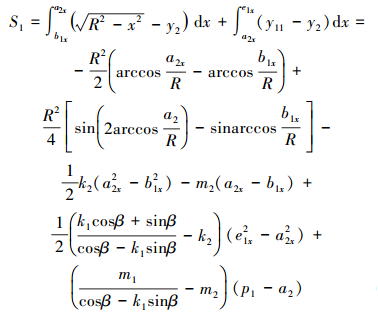
|
(18) |

|
(19) |
(2) 当γ1<α≤γ时,如图 2b所示,直线y11(x)与y2(x)相交于点E1(e1x, e1y),此时流通面积为:
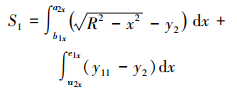
|
(20) |
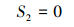
|
(21) |
(3) 当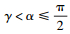
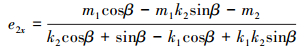
|
(22) |
此时流通面积为:

|
(23) |
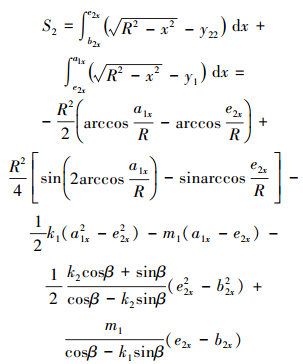
|
(24) |
根据式(18)、式(19)、式(20) 和式(24) 可以计算出不同情况下的面积S1和S2,各面积相加即为总过流面积。
3 转子形状优化 3.1 优化模型在定子和转子形状优化中,需要使其产生的压力信号幅值满足要求,同时使压力信号波形与正弦波形的相关系数最大。这属于多目标优化问题,由于目前在理论和算法上使多个分目标同时达到绝对最优解很困难,所以使用线性加权和法进行优化,分别设置各个分目标的权重,对其线性组合进行求解。同时考虑脉冲发生器受钻铤尺寸限制,对转子各尺寸进行约束。建立的三角形定子和转子形状优化数学模型为:
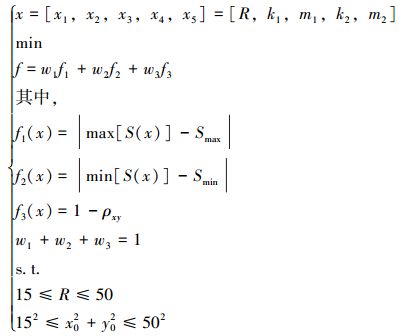
|
(25) |
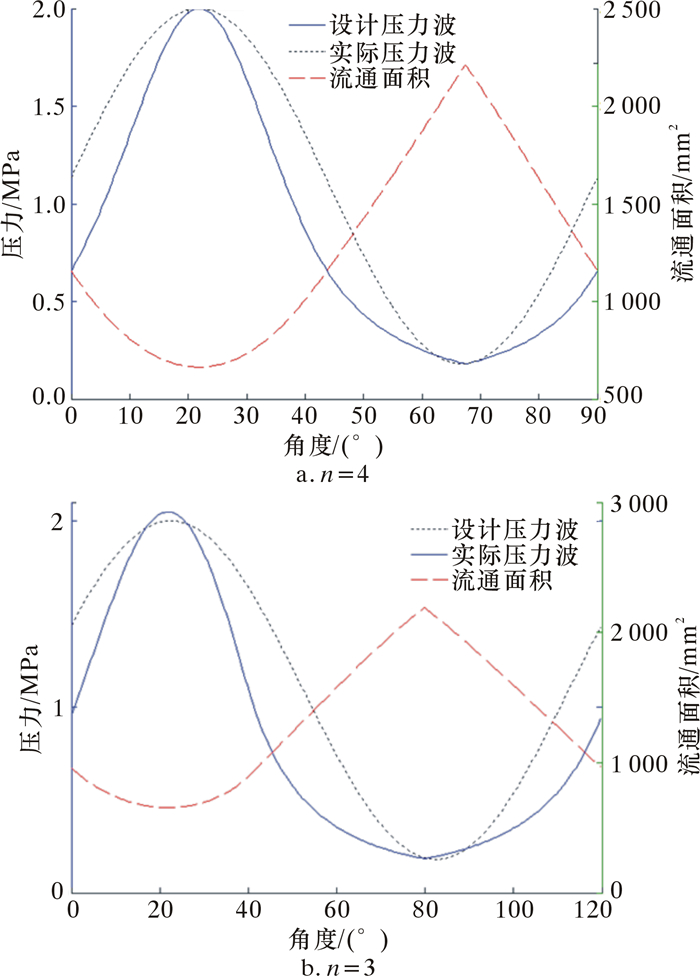
以实际工况对该三角形转子进行优化。所用参数为:钻井液流量25 L/s,钻井液密度1 280 kg/m3,压力波信号最大值2.00 MPa,最小值0.18 MPa,流量系数取0.7,优化结果如表 1所示。表中n表示阀瓣个数。优化后的三角形转子流通面积和压力信号随角度变化曲线如图 3所示。
| n | R | k1 | m1 | k2 | m2 | 相关系数 |
| 4 | 48.737 | -0.897 | 43.738 | -9.479 | 222.119 | 0.987 1 |
| 3 | 48.583 | -0.892 | 43.312 | 17.794 | -105.477 | 0.974 2 |
|
| 图 3 流通面积及压力信号变化曲线 Fig.3 The effect of angle on the circulation area and pressure signal |
由图 3可知,所得压力波信号较为理想,但流通面积在最大值处变化较陡。这是因为2直边直接相交,从而使定子和转子重合段内流通面积变化较为剧烈。为了改善这种情况,在2直边相交处应采用圆弧过渡。
4 流场仿真在实际工况中,流体在定子和转子间的流动十分复杂,笔者通过Fluent软件对上述优化结果进行流场仿真,从而确定优化后的定子和转子形状能否产生高品质的压力信号波。
4.1 模型与仿真设置将连续波钻井液脉冲发生器简化处理后建立三维模型。转子在工作过程中处于连续转动状态,需要采用滑移网格,因而将整个计算区域分为3个部分:定子区、转子区和出口区,同时加长进、出口流道,如图 4所示。不同区域间的交界面定义为interface进行数据传递。

|
| 图 4 脉冲发生器流道模型 Fig.4 Flow channel model of the mud pulse generator |
流体仿真中,认为钻井液为单相不可压缩液体,密度保持1 280 kg/m3不变,流量为25 L/s。入口设置为速度入口,流速为6.5 m/s,出口设置为压力出口。滑移网格旋转速度为300 r/min。钻井液脉冲发生器内钻井液为湍流,使用标准κ-ε模型、Simple算法及非定常求解器[10-12]。
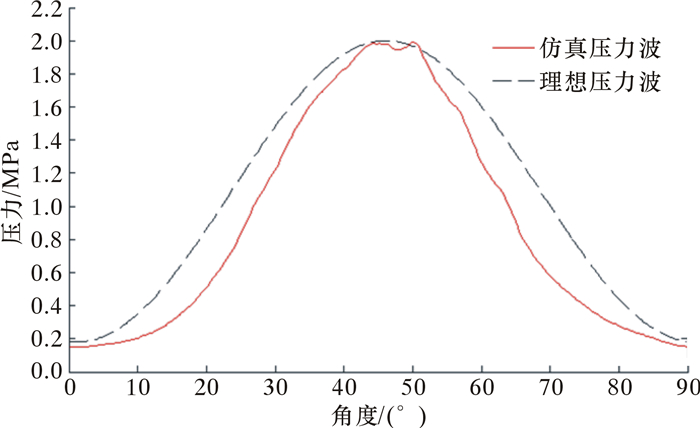
4.2 仿真结果图 5为流体仿真所得压力波形与理想压力波形的比较图。由图可知:仿真所得的压力波波峰值与波谷值均达到设计要求,且波形与正弦波形近似,相关系数为0.988 6。由此验证了上述优化所得的转子形状满足设计准则。
|
| 图 5 仿真波形与理想波形比较图 Fig.5 Comparison of simulation waveform and ideal waveform |
5 结论
(1) 根据最大和最小流通面积设计准则及相关系数最大准则,使设计所得的压力波信号幅值和频谱特性最优。
(2) 建立了三角形转子的流通面积计算模型,并依据设计准则建立了三角形转子形状优化模型,进行结构优化。
(3) 对所得转子形状进行流体仿真,仿真结果表明所得转子形状可以产生较为理想的正弦压力波形。
| [1] | 肖俊远, 王智明, 刘建领. 泥浆脉冲发生器研究现状[J]. 石油矿场机械, 2010, 39(10): 8–11. DOI: 10.3969/j.issn.1001-3482.2010.10.003 |
| [2] | 李荣喜, 房军. 井下旋转压力信号发生器的仿真[J]. 石油矿场机械, 2007, 36(2): 45–47. |
| [3] | 郑宏远, 白锐, 刘策. 石油钻井泥浆脉冲发生器数据传输速率分析[J]. 计算机仿真, 2016, 33(7): 194–199. |
| [4] | 张中伟, 孙峰. 基于卡尔曼滤波的钻井液脉冲信号处理方法[J]. 石油机械, 2015, 43(4): 39–42. |
| [5] | 耿亚楠, 李根生, 史怀忠, 等. 小井眼水力脉冲射流提速研究及应用[J]. 石油机械, 2015, 43(6): 1–5. |
| [6] | 房军, 王正旭, 贾朋, 等. 往复增流式井下压力信号发生器模型及特性分析[J]. 石油机械, 2016, 44(10): 11–16. |
| [7] | LAVRUT E, KANTE A, RELLINGER P, et al.Pressure pulse generator for downhole tool:6970398B2[P].2005. |
| [8] | HAHN D, PETERS V, ROUATBI C, et al.Oscillating shear valve for mud pulse telemetry and associated methods of use:6975244B2[P].2005. |
| [9] | 贾朋, 房军, 李林. 基于相关系数的连续波发生器转阀优化设计[J]. 石油矿场机械, 2012, 41(7): 37–42. |
| [10] | 郭仁生. 机械工程设计分析和MATLAB应用[M]. 4版. 北京: 机械工业出版社, 2014: 100-102. |
| [11] | 韩占忠, 王敬, 兰小平. FLUENT——流体工程仿真计算实例与应用[M]. 北京: 北京理工大学出版社, 2010. |
| [12] | 魏亮, 王赤忠, 程烨, 等. 泥浆脉冲发生器转子水力转矩多相流数值模拟[J]. 现代机械, 2015(6): 35–41. |



