0 引言
管道机器人作为特种机器人的一个重要研究领域,主要应用于管道、缆索和电缆等爬行检测作业中,其工业应用正在逐渐受到人们重视,产品种类越来越丰富[1, 2]。对加热炉炉管检测仅使用人力,或搭建脚手架或人工爬行检测,不但耗费大量的人力物力、效率低,且在许多场合下其环境不适宜人工作业[3]。爬管机器人在工业、农业、民用和军事等领域的突出性能,促使世界上各个国家均投入大量的人力、物力开展相应的研究[4, 5, 6]。
笔者利用SolidWorks软件建立机器人机构三维模型,对重要部件进行有限元分析,导入ADAMS软件开展了动力学仿真分析[7]。
1 炉管检测爬行机构建立目前很多化工企业和热电厂都有大型的加热炉,加热炉管道及大型锅炉排管都属于炉管爬行机器人的工作管路[8]。加热炉中的炉管直径一般较小,炉管竖直联排分布,横排管间距较小。研究针对上述工况开展工作的机器人系统应用前景广阔。
笔者研究的爬管机器人需在较小的管径和管柱间距条件下爬行。由于相邻2管的管间距很小,无法在管柱周向布置贴附及攀升机构。为了防止机器人从竖直管面上滑落,机器人必须与管面之间保持足够的夹紧力从而产生足够的摩擦力,并具有一定的抗倾覆能力。机器人本体结构采用剪刀型驱动轮式行走机构。该设计原理来源于人类爬树或爬杆时所用的脚扣,利用了机器人自身的重力来产生运动所需要的摩擦力,很好地解决了实现机器人附着所需要的复杂的施力机构。
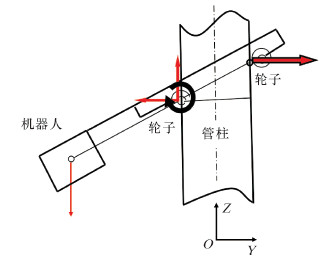
图1为爬管机器人的结构简图,该机构较好地利用了机器人自身的重力来产生运动所需要的摩擦力,很好地解决了实现机器人附着所需要的复杂的施力机构。该构型将重力这一对垂直爬行机器人最不利的因素转化为驱动能力,利用自身重力可实现自锁,结构简单,可满足要求。
|
| 图 1 爬管机器人结构简图 Fig.1 Structural schematic of the pipe climbing robot |
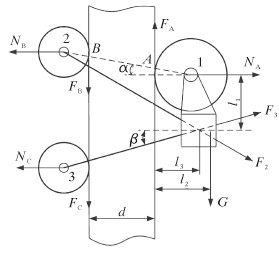
提出的机器人机构借鉴脚扣原理,爬管机器人能够较好地利用机器人自身重力产生运动所需要的摩擦力,较好地简化了实现机器人附着所需的复杂施力机构。力学模型如图2所示。
|
| 图 2 自重及拉紧受力分析模型 Fig.2 Self weight and tension stress analysis model |
图中:轮1、轮2和轮3分别为主驱动轮、主夹紧轮和从夹紧轮;NA、NB、NC分别为主驱动轮、主夹紧轮和从夹紧轮所受到的管壁正压力,N;FA、FB、FC分别为主驱动轮、主夹紧轮和从夹紧轮所受到的管壁摩擦力,N;F2、F3分别为主夹紧杆上、从夹紧杆上作用的拉力,N;d为爬行管柱直径,在本分析中是个常数,mm;G为机器人重力,N;l1为主驱动轮中心和主夹紧杆与从夹紧杆交点的竖直距离,mm;l2、l3分别为重心到管柱的水平距离、夹紧杆交点到管柱的水平距离,mm;α为主驱动轮与主夹紧轮中心连线和水平线的夹角;β为从驱动轮与重心连线和水平线的夹角。
建立机器人的力学平衡方程。考虑机器人系统在匀速运动状态,受到外力后处于平衡状态。
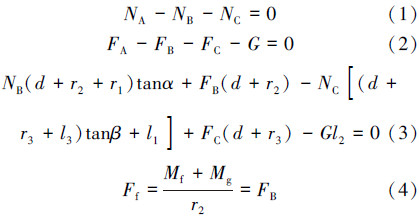
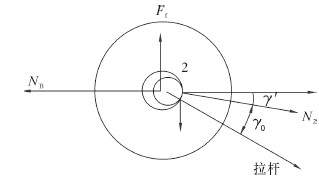
因为轮2的夹紧杆可以抽动,轮2受夹紧杆向斜下方的拉力作用,必然有向下滚动的趋势,轮2受力情况见图3。
|
| 图 3 机构处于静止状态时夹紧轮2受力图 Fig.3 The forces on the No.2 clamp wheel while the mechanism is at rest |
图中:N2为拉杆对主夹紧轮的作用力,N;γ′为N2与水平线的夹角;γ0为夹紧杆与水平线间夹角。
通过拉杆继续增大N2,由于垂直方向的摩擦力与滚轮2轴的滚动摩擦有关,增加比较小,所以N2的作用方向会趋向于水平。增加N2会增大NB,从而有效增加驱动轮1的压紧力。
分析可得到N2与NB之间的关系式为:
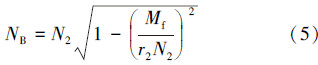
由于轮2采用滚动轴承,所以Mf很小,NB接近N2。下面对N2进行分析。
拉杆增大N2,使轮2和轮1能贴紧管壁,靠机器人的自重会在轮2夹紧杆中产生拉力。
FB与轮2轴的摩擦有关,数值很小,工程上可忽略,可求出NB:
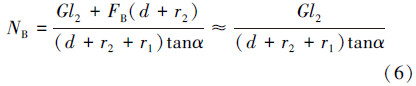
将式(5)带入式(6),可以得出当机器人匀速爬行时所需的N2:
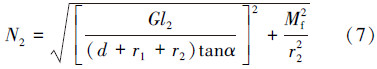
对夹紧杆进行受力分析,可以确定需要施加的夹紧杆力F2,从而增大N2,由图3可得出:

为使机器人匀速爬行时夹紧杆上所施加的弹簧拉力计算式为:
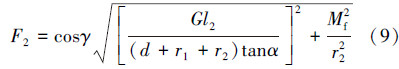
当F2达到该值时,则可使重力G充分发挥作用,如果这时还不能使机器人自锁或达到加速要求,则需要再增加F2的数值。
2.3 底座强度校核对机器人进行受力分析可知,机器人主要受力机构为底座调节栓机构。这部分是主要的受力机构,由于受夹紧力和自身重力的影响易产生疲劳变形,对工作影响较大[9]。拟模拟受力最大的工况进行计算、校核和修改。
底座选用强度较高的30Cr合金,材料屈服强度可达到685 MPa。机器人总重力为100 N,加载在支撑板的上表面;左、右两侧与调节栓通过螺栓装配,需仔细考虑力的传递情况。采用固定底座上表面的4个螺栓孔,管道给主、从夹紧轮的正压力通过夹紧杆作用在底座上,将力施加在空间点上。分析主、从夹紧轮所受到的正压力不同,对上侧点施加水平方向300 N、下侧施加水平方向80 N的力。通过SolidWorks Simulation中远程载荷选项,将该力传递给底座左、右两侧的螺栓孔上,如图4所示。

|
| 图 4 远程载荷施加图 Fig.4 The application of remote load |
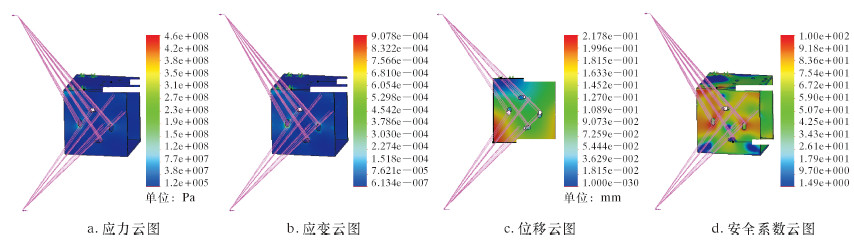
图5为底座有限元分析云图。
|
| 图 5 底座有限元分析云图 Fig.5 Finite element analysis on the foundation |
从图5a可见,最大应力460 MPa,小于30Cr的屈服强度。从图5b可见,最大应变为9.08×10-4。从图5c中可见,最大位移出现在螺栓孔附近,其值为0.22 mm。从图5d中可见,安全系数最小为1.5,这说明所设计夹紧杆满足强度要求。
3 ADAMS仿真分析在力学分析及有限元分析的基础上,运用ADAMS/View软件对机器人进行了动力学分析,以验证机器人设计的合理性[10]。
3.1 模型简化、添加约束及施加载荷模型从CAD软件导入到ADAMS后只具有几何形体以及构件间的相对位置关系,需要对构件或构件元素进行属性编辑。
PGR-Ⅱ机器人导入ADAMS后,需依次给各个关节添加运动副。其中待测管与大地之间添加固定副;机器人左右两侧的调节栓与夹紧杆之间添加滑移副;底座左右两侧从动轮与夹紧杆之间分别添加旋转副。
PGR-Ⅱ机器人需要考虑运动副上的摩擦、夹紧杆上的弹簧力以及轮子与爬行管之间的接触力等载荷的施加。在ADAMS中,接触力可分解成2部分:正压力和摩擦力。正压力使用冲击(impact)函数法进行计算,摩擦力使用库仑(Coulomb)法进行计算。
3.2 机器人复杂工况仿真分析 3.2.1 自锁在实际工作中,机器人要具有自锁能力,以便随时停止在管壁上进行测量,这就需要设置选取合适的拉杆弹簧力。
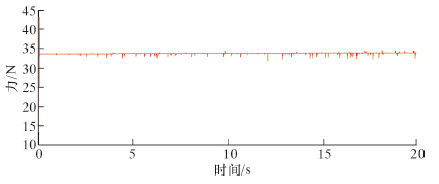
导入模型调节完毕后,针对该工况,试验施加不同的弹簧预紧力,试验选取仿真时间为20 s。为保证机器人自锁在管道表面,仿真结果表明,弹簧预紧力最小为35 N时,能够满足要求。图6和图7是弹簧在该预紧力下的弹簧力图像以及左驱动轮与管壁间接触力的幅值图像。
|
| 图 6 弹簧阻尼力图 Fig.6 The spring damp force |
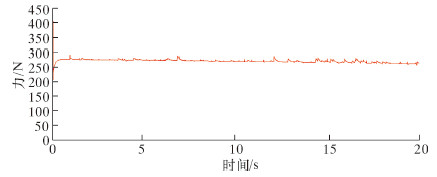
|
| 图 7 左驱动轮与管壁接触力幅值图 Fig.7 The magnitude of contact force of the left drive wheel and the pipe wall |
从以上分析可知,应用ADAMS仿真软件,在设置好构件间约束、接触、固定并选取合适摩擦因数后,仿真模拟出为保持机器人自锁状态应当将弹簧预紧力至少设置为35 N。
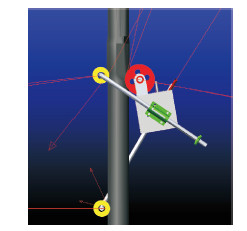
3.2.2 膨胀变粗炉管爬行仿真分析仿真试验中,为保证机器人本体不只具有自锁能力,还要具有一定的加速越障能力,因此将弹簧预紧力设置为50 N。机器人匀速驱动速度上行程达到0.2 m/s。试验仿真时间取9 s,爬行越障过程见图8。
|
| 图 8 炉管变粗膨胀爬升仿真图 Fig.8 Simulation of climbing on the expanded furnace pipe |
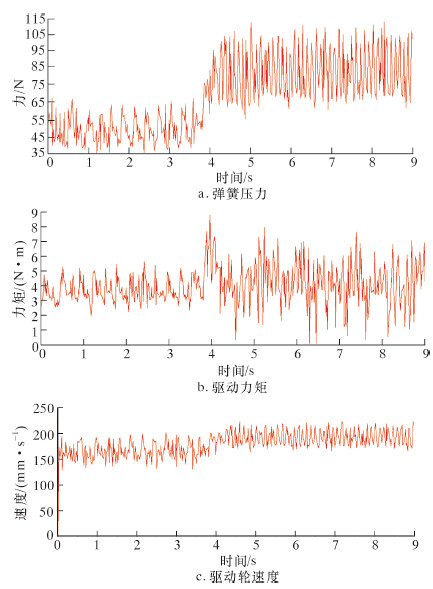
为仿真工厂真实情况下的最恶劣工况,试验选取的炉管管径为58 mm,加热变粗膨胀最大处管径为61 mm,变形区有60 mm过渡,62 mm最大膨胀区持续1 000 mm长进行分析。模拟分析经过膨胀区爬行时的弹簧力变化曲线以及驱动力矩曲线和主驱动轮爬行线速度曲线,结果见图9。
从图9a中可以看出,机器人在运行到4 s左右时,开始进入炉管膨胀区,爬行管径变大。由于主夹紧机构锁定,当机器人主驱动轮进入变粗膨胀区时,驱动轮与主夹紧轮中心连线与水平线的夹角减小以适应大管径爬行,此时由于机器人结构限制,从夹紧杆伸长弹簧被压缩。当机器人进入膨胀区时,弹簧力变大。
|
| 图 9 膨胀炉管爬升仿真曲线图 Fig.9 Simulation curve of climbing on the expanded furnace pipe |
从图9b可以看出,机器人在变形管道爬行时所需的平均驱动力矩为3.913 N·m,最大驱动力矩为8.660 N·m,普通电机的堵转矩远大于此峰值,因此机器人具有良好的驱动越障能力。从图9c可以看出,机器人爬行速度较为稳定,适应跨越加热炉管膨胀变形管道的爬行。
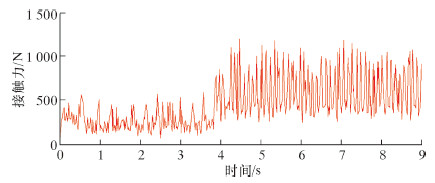
图10反映出在跨越膨胀变形管道时,驱动轮与管道之间接触力变化情况。从仿真图形可以看出,在4 s左右,机器人驱动轮爬行进入管道膨胀区后,接触力变大,最大峰值为1 192.9 N,平均值为449.4 N。接触力的大小满足膨胀区爬管机器人爬行要求。
|
| 图 10 膨胀炉管驱动轮接触力图 Fig.10 Contact force of the drive wheel and the expanded furnace pipe |
针对小间隙细长竖直联排炉管的爬行,研究了PGR-Ⅱ型管道爬行机器人,解决了传统爬管机器人无法适应管间距过小以及变管径条件下的爬管问题。建立了PGR-Ⅱ型炉管爬行机器人的力学模型,对机器人进行了整体受力分析,列出了机器人的平衡方程。用SolidWorks Simulation模块对爬管机器人主要受力构件进行了有限元分析和强度校核,得到了零件在最恶劣工况下的应力、应变和安全系数云图,优化了结构设计。
开展了ADAMS仿真分析,建立了爬管机器人虚拟样机模型,对机器人的自锁条件和管道加热膨胀变形后的越障能力进行了仿真分析。
研究了小间隙连排管爬行机器人的结构形式,通过理论分析和仿真分析建立的一套分析方法,不但能指导样机的设计和开发,而且对轮式爬管机器人的研究有良好的借鉴作用。
| [1] | 郑义,周淑芳,邓传云.关节式爬管机器人夹紧机构的优化研究[J].机电工程,2015,32(3):328-332. |
| [2] | 贾运行,张来斌,樊建春.多支撑轮式管道机器人运动仿真[J].石油机械,2009,37(8):39-41. |
| [3] | 常玉连,邵守君,高胜.石油工业中管道机器人技术的发展与应用前景[J].石油机械,2006,34(9):122-126. |
| [4] | 潘沛霖,韩秀琴,赵言正,等.日本磁吸附爬壁机器人的研究现状[J].机器人,1994,16 (6):379-382. |
| [5] | 潘焕焕,赵言正,高学山,等.水冷壁爬壁机器人的本体结构设计[J].机械设计与制造工程,2000,29(5):7-8,10. |
| [6] | 刘杰,刘永红,丛君丽,等.油井套管解堵机器人驱动机构的运动特性分析[J].石油机械,2008,36(3):34-37. |
| [7] | 陈霞,冷护基,王治国,等.一种新型爬缆机器人机构设计及实现[J].机械工程师,2008(12):20-21. |
| [8] | 张捍东,郑睿,岑豫皖.移动机器人路径规划技术的现状与展望[J].系统仿真学报,2005,17(2):439-443. |
| [9] | 安永植,姜国超,安永辰.管外移动机器人机构的研究[J].机器人,1994,16(5):275-280. |
| [10] | 何富君,李浩,常忠伟,等.储罐爬壁喷涂机构的运动学分析[J].机械设计与制造,2014(6):210-212,216. |



