2. 中国石化石油工程技术研究院;
3. 中国石油西部钻探工程公司
2. SINOPEC Research Institute of Petroleum Engineering;
3. CNPC Xibu Drilling Engineering Company Limited
0 引 言
为了克服深水钻井高压浅层气、浅层流以及窄密度窗口等问题,20世纪初期挪威AGR公司研发了双梯度钻井技术,即无隔水管钻井液回收钻井技术(Riserless Mud Recovery,简称RMR)[1, 2]。该技术先后在里海、Sakhalia半岛、Barents海域以及北海等地区进行了应用,经济效益明显[3]。与常规深水隔水管钻井不同,RMR无隔水管钻井技术主要特点有:①海水段不采用隔水管,钻柱直接裸露于海水中;②海底井眼环空顶部安装井口装置(海底吸入装置),隔离海水与环空井眼顶部钻井液,并为钻井液返回管线提供接口;③海底安置钻井泵,采用小尺寸回流管线将携带岩屑的钻井液举升至钻井平台;④通过海底泵系统保证井眼环空顶部压力与海底静水液压相等。钻井水力学主要是分析钻井液在钻柱、钻头和井眼环空等流道内复杂的流动过程,而国内关于无隔水管钻井技术水力学研究相对较少[4, 5, 6, 7],且循环压耗计算方法仍然基于适用性比较差的钻井液流变模式。基于此,笔者提出了适用于无隔水管钻井技术的水力学分析方法,并分析泵排量随水深和井深的变化规律,所得结论对无隔水管钻井系统平台泵排量的确定具有指导意义。
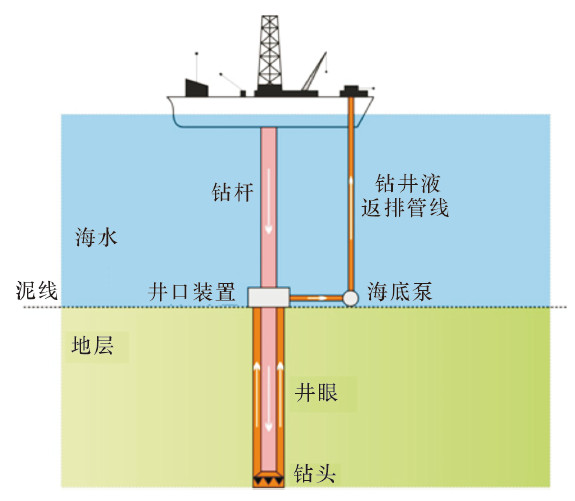
1 模型建立RMR无隔水管钻井系统循环过程如图 1所示。钻井液经钻杆通过钻头进入井眼环空,上返至井眼环空顶部,在海底泵吸入装置的作用下进入海底钻井泵,继而通过小尺寸返排管线返回到钻井平台。
|
| 图 1 RMR无隔水管钻井系统示意图 Fig. 1 Schematic of RMR riserless drilling system |
根据RMR无隔水管钻井系统循环过程平衡关系可得:
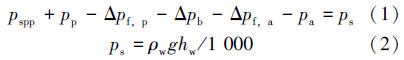
其中,pp=ρmg(hw+hbh)/1 000,pa=ρmghbh/1 000 ,联立式(1)和式(2)可得:
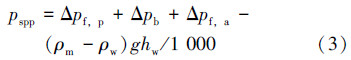
式中:pspp为立管压力,MPa;pp为钻柱内液柱压力,MPa;pa为井眼环空液柱压力,MPa;ps为井眼环空顶部压力,MPa;pf,p为钻柱内循环压耗,MPa;pf,a为井眼环空中循环压耗,MPa;pb为钻头压降,MPa;ρm为钻井液密度,g/cm3;g为重力加速度,m/s2;hw为水深,m;hbh为井深,m。
2 循环压耗分析 2.1 钻柱内循环压耗基于圆管流量方程的压耗计算方法能够准确地分析钻柱内循环压耗。为尽可能提高水力计算结果的精度,笔者选用兼具宾汉模式和幂律模式的罗伯特-斯蒂夫(Robertson-Stiff)模式[8],简称罗-斯模式。该模式能够较好地描述实际钻井液的流变性。符合罗-斯模式的流体在圆管内流动时满足如下关系式[7, 8, 9]:
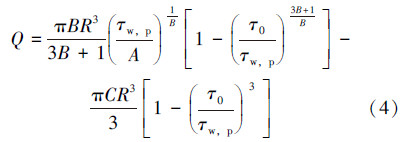
式中:Q为排量,L/s;τ0为流体屈服值,τ0=ACB,Pa;A为罗-斯模式稠度系数,Pa·sB;B为罗-斯模式流性指数;C为罗-斯模式剪切速率校正值,1/s;τw,p为钻柱内管壁处切应力,Pa。
给定泵排量,即可采用二分法和黄金分割等数值解方法得到管壁处切应力τw,p。根据樊洪海等[10]提出的广义流性指数法计算雷诺数,公式为:

式中:Reg,p为圆管广义雷诺数,ρ为流体密度,kg/m3;Deff,p为钻柱内有效管径,m;vp为钻柱内流体平均流速,m/s;μw,p为钻柱内管壁处有效黏度,Pa·s;n′p为钻柱内广义流性指数;D为钻杆内径,m。
F.J.Schuh[11]将流体流态划分为3个区域:层流、过渡流和紊流,并分别给出了相应的判别标准:
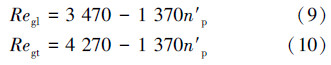
式中:Regl为层流雷诺数;Regt为紊流雷诺数。
若Reg,p≤Regl,则为层流;若Regl<Reg,p≤Regt,则为过渡流;若Reg,p>Regt,则为紊流。
层流条件下,范宁阻力系数fl与钻柱内雷诺数满足如下关系式:

紊流时范宁阻力系数ft采用文献[12]提出的非牛顿流体光滑管进行计算,即:
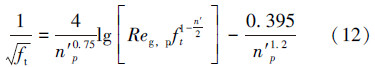
过渡流状态时,可采用线性差分原则求解范宁阻力系数ftr:
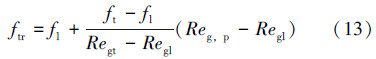
故钻柱内全流态循环压耗可由达西公式进行求解,即:
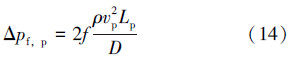
式中:Lp为钻柱的长度,m。
2.2 环空中循环压耗若将圆管流量方程扩展应用于环空中,可得罗-斯流体在环空流动时满足的关系式为[13]:
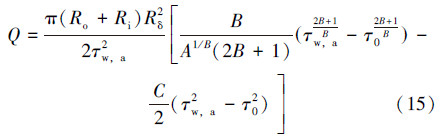
式中:τw,a为环空中管壁处切应力,Pa;Rδ为环空间隙,m;Ro为环空外半径,m;Ri为环空内半径,m。
同理,已知排量采用数值迭代方法可得管壁处剪切应力τw,a。
环空中采用周号博等[14]提出的环空广义流性指数法计算雷诺数,即:
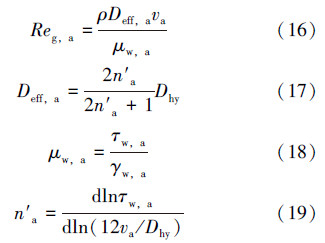
式中:Reg,a为环空广义雷诺数;Deff,a为环空有效管径,m;va为环空流体平均流速,m/s;μw,a为环空管壁处有效黏度,Pa·s;n′a为环空广义流性指数;Dhy为水力直径,m。
井眼环空中仍然可采用式(9)和式(10)进行流态判别。由环空广义流性指数计算模型的推导可知,范宁阻力系数的计算方法在环空中仍然适用。故井眼环空循环压耗计算式为:

式中:La为井眼环空的长度,m。
2.3 钻头压降及最小携岩返速工程上钻头压降一般采用下式进行计算[15]:
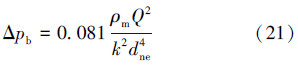
式中:k为喷嘴流量系数,取0.95;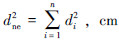 ,cm。
,cm。
工程上常用经验公式[16]

来确定环空携岩所需的最低返速。由于无隔水管钻井系统返排管线与井筒环空在流道上存在差异,设返排管线钻井液返速为vr,则有:
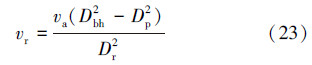
式中:Dr为返排管线内径,cm;Dbh为井眼直径,cm;Dp为钻柱的内径,cm;vr为返排管线内流速,m/s。
无隔水管钻井系统一般采用小尺寸的返排管线,即返排管线与环空井眼几何尺寸满足关系式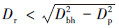 ,因此返排管线内流速要高于环空井眼中返速。在这种工况下,只需考虑井眼环空中最小携岩排量即可满足无隔水管钻井整个返回流道的携岩要求。
,因此返排管线内流速要高于环空井眼中返速。在这种工况下,只需考虑井眼环空中最小携岩排量即可满足无隔水管钻井整个返回流道的携岩要求。
采用RMR无隔水管钻井系统对某深水域储层进行勘探,分析RMR无隔水管钻井系统钻进过程中井筒水力参数。计算所需基本参数为:钻井液密度1.437 6 g/cm3,海水密度1.030 0 g/cm3,水深1 500 m,井深1 500 m,钻杆尺寸ø127.0 mm,钻头尺寸ø215.9 mm,钻头喷嘴直径18 mm,喷嘴数3个,返排管线内径152.4 mm,钻井液屈服值2.4 Pa·s,极限剪切黏度0.018 9 Pa·s,稠度控制系数0.795 6 Pa·sc,流性指数为0.492。
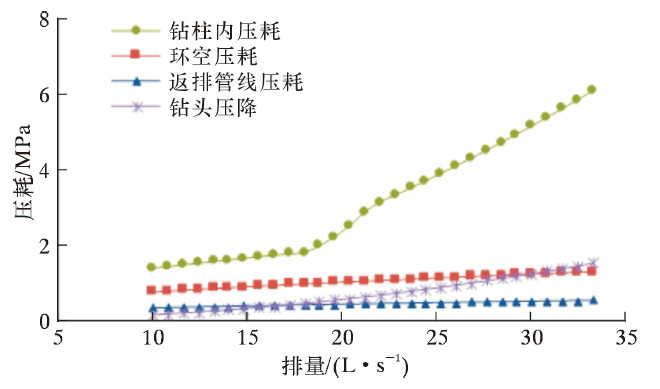
图 2为无隔水管钻井系统循环压耗随排量变化曲线。由图可知,无隔水管钻井系统各部分循环压耗均随着排量的增大而呈现不同趋势的增大。这主要是因为钻井液在各流道内呈现不同的流动状态。在钻柱内钻井液随着排量的增大,从层流(Q<17.9 L/s)逐渐转向过渡流(17.9 L/s≤Q<21.5 L/s)继而形成紊流(21.5 L/s≤Q),故钻柱内循环压耗层流阶段增大缓慢,转入过渡流时循环压耗出现小幅度快速增加,进入紊流后循环压耗快速增加。由于钻柱、返排管线及井眼环空几何尺寸存在如下关系:Dp<Dr<Dbh,随着排量增大,返排管线以及井眼环空中钻井液始终处于层流,经计算发现,Reg环空<Reg返排,f环空>f返排,故井眼环空及返排管线中循环压耗均随排量缓慢增大,且环空循环压耗始终大于返排管线循环压耗。
|
| 图 2 循环压耗随排量变化曲线 Fig. 2 The effect of displacement on the circulating pressure loss |
无隔水管钻井系统正常钻井过程中,立管压力pspp应保持为非负数。若无隔水管钻井系统以低排量钻进,井筒循环压耗(钻柱、钻头和环空循环压耗之和)不足以克服海水段钻井液与海水静液压力之差,根据式(3)可知,立管压力将出现负值,此时钻柱内液柱压力过大,在自身重力的作用下推着泥线下钻柱中钻井液经过钻头流向井眼环空中,产生U形管效应,钻柱中将出现真空段。当海水深度一定时,海水段钻井液、海水静液压之差也将是一常数,随着泵排量不断增大,由图 2可知,井筒循环压耗将不断增大,则势必存在一个排量,恰好使得井筒循环压耗与海水段钻井液、海水静液压之差相等,该排量称为临界排量。分析可知,若泵排量小于临界排量,则井筒中将产生U形管效应出现真空段,只有泵排量大于或等于临界排量时,才能保证无隔水管钻井系统正常钻进。
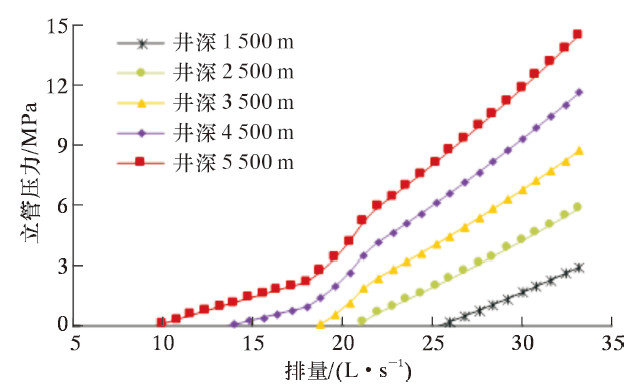
图 3揭示的是水深为1 500 m时,不同井深工况下立管压力随泵排量变化规律。其中,立管压力为0时对应的排量为临界排量。由图 3可知,随着井深逐渐增加,临界排量不断减小。这是因为随着井深增加,井筒循环压耗不断增大(钻柱、环空中沿程循环压耗也不断增大),而海水段钻井液、海水静液压之差却没有改变。不同井深条件下立管压力随排量增大趋势各不相同,主要与钻柱内钻井液的流态有关:层流状态下立管压力随排量增大缓慢,过渡流状态时立管压力小幅度迅速增加,进入紊流后立管压力随排量增大较快。由图 2可知,环空循环压耗与钻头压降对立管压力的影响程度比钻柱内循环压耗要小得多。
|
| 图 3 立管压力随排量变化曲线 Fig. 3 The effect of displacement on the standpipe pressure |
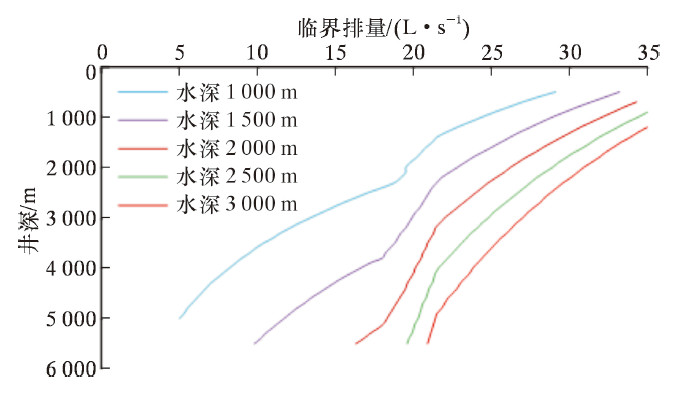
图 4为不同水深工况下,临界排量随着井深的变化规律。由图可知,不同水深条件下临界排量均随着井深的增加而减小;当井深相同时,水深较小的工况下临界排量也较小。其原因可归纳为,水深一定时,海水段钻井液、海水静液压之差也为定值,随着井深增大,井筒循环压耗不断增大,故临界排量减小;而当井深一定时,水深较小的工况下海水段钻井液、海水静液压之差较小,此时所需的循环压耗也较小,故临界排量也较小。
|
| 图 4 井深与临界排量关系曲线 Fig. 4 The relation of the well depth and the critical displacement |
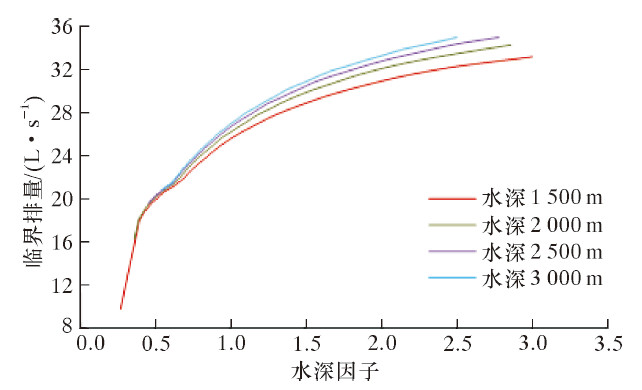
若将水深hw与井深hbh之比定义为水深因子η,则水深因子η与临排量的关系曲线如图 5所示。从单条曲线来看,图 5揭示的规律与图 4一致,即在水深一定的条件下,随着水深因子逐渐减小,对应于深井逐渐增大的过程,此时临界排量不断减小。结合多条曲线分析,在不同水深工况下,随着水深因子逐渐减小,不同水深工况下临界排量之间的差值不断减小,当水深因子位于0.38~0.65时,不同水深工况下临界排量几乎相等,且临界排量均在17.7~22.2 L/s的范围内。
|
| 图 5 水深因子与临界排量关系曲线 Fig. 5 The relation of the well depth and the water depth factor |
(1)基于无隔水管钻井的技术特点,采用罗-斯模式建立了适用于无隔水管钻井系统的全流态水力学分析方法。钻井液在圆管内和环空中全流态下循环压耗计算思路也得到了统一。
(2)无隔水管钻井系统正常钻进过程中,应保持泵排量大于或等于临界排量,否则立管压力将为负数,钻柱内将出现U形管效应而产生真空段。当水深一定时,钻柱内循环压耗对立管压力随排量变化的规律影响较大,而环空循环压耗和钻头压降对其影响相对较小。
(3)无隔水管钻井系统正常钻进过程中,立管压力为0时对应的泵排量称之为临界排量。不同水深条件下临界排量均随着井深的增加而减小;当井深相同时,水深较小的工况下临界排量较小。
(4)在不同水深工况下,随着水深因子的减小,各工况下临界排量之间差值不断减小,当水深因子处于0.38~0.65时,各工况下临界排量均在17.7~22.2 L/s范畴。
| [1] | Stave R,Farestveit R.Demonstration and qualification of a riserless dual gradient system[R].OTC17665,2005. |
| [2] | Johnny R,Rolv R.Riserless mud recovery (RMR) system evaluation for top hole drilling with shallow gas[R].SPE102579,2006. |
| [3] | 高本金,陈国明,殷志明,等.深水无隔水管钻井液回收钻井技术[J].石油钻采工艺,2009,31(2):44-47. |
| [4] | 刘杰,陈国明,周昌静,等.深水无隔水管钻井液回收钻井水力学计算[J].石油钻采工艺,2010,32(5):20-23. |
| [5] | 葛瑞一,陈国明,周昌静,等.无隔水管钻井泥浆举升系统管路特性计算与分析[J].石油矿场机械,2012,41(7):33-37. |
| [6] | 王国栋,陈国明,殷志明.深水无隔水管钻井MRL选型及参数优化[J].石油机械,2013,41(2):66-69. |
| [7] | 樊洪海,冯广庆,王果,等.一种新的流变模式及其应用性评价[J].中国石油大学学报:自然科学版,2010,34(5):89-93,99. |
| [8] | 黄逸仁.适用于钻井液的罗伯逊-斯蒂夫模式[J].西南石油学院学报,1982(2):16-28. |
| [9] | 樊洪海,彭齐,滕学清,等.不同流变模式钻井流体圆管层流压耗的通用精确算法[J].中国石油大学学报:自然科学版,2014,38(1):70-74. |
| [10] | Fan Honghai,Zhou Haobo,Peng qi,et al.A generalized hydraulic calculation model for non-newtonian fluid pipe flow and its application evaluation[J].SOCAR Proceedings,2014(2):22-29. |
| [11] | Schuh F J.Computer makes surge-pressure calculations useful[J].The Oil and Gas Journal,1964,62(31):96. |
| [12] | Doge D W,Metzner A B.Turblent flow of non-newtonian system[J].AICHE.Journal,1959,5(2):189-204. |
| [13] | 彭齐,樊洪海,周号博,等.不同流变模式钻井液环空层流压耗通用算法[J].石油勘探与开发,2013,40(6):752-756. |
| [14] | Zhou Haobo,Fan Honghai.A new utility calculation model for axial flow of non-newtonian fluid in concentric annuli[J].The Canadian Journal of Chemical Engineering,2014,91(5):945-952. |
| [15] | 樊洪海.实用钻井流体力学[M].北京:石油工业出版社,2014. |
| [16] | 陈庭根,管志川.钻井工程理论与技术[M].东营:石油大学出版社,2000. |



