随着互联网和智能设备愈来愈多地介入人们的日常生活以及大数据概念的提出,在社会科学研究领域,研究者们面对着一个新的非常巨大的数据源。不同于传统的问卷调查数据,这种新的数据来自各类智能设备的记录:手机信号塔所记录的在某个范围内的人群聚集状况,摄像头所捕捉到的人们在各个场所的出现,人们在互联网使用过程中所留下的轨迹或积累的信息等,例如微博的评论或转发、网络论坛上的发帖和回帖。也有一些数据早已进入研究者的视野,由于信息化手段的丰富多样,研究者们无需再大费周章专门进行数据录入或转换,例如人们的日常消费记录、学术文献的作者信息和引文信息、公司间的联动交易信息,等等。对于上述数据,研究者们往往关注其中的共现关系并探讨其潜在的社会机制。例如,在同一个论坛的帖子里进行讨论的用户可能对某一话题具有共同的兴趣,在科学文献作品中科学家之间合作关系的形成,图书购买记录背后所蕴含的共同的政治态度和价值观,等等。
一般来说,对上述数据的分析大多采用社会网络分析方法进行。从数据分析的角度来看,这类互动数据可以用一个发生矩阵 (incidence matrix) 来表示,例如一个n×m的二进制矩阵P:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\begin{array}{*{20}{c}} {{v_1}}&{{v_2}}&{{v_3}}&{{v_4}}&{{v_5}} \end{array}\\ {\rm{P}} = \begin{array}{*{20}{c}} {{e_1}}\\ {{e_2}}\\ {{e_3}}\\ {{e_4}}\\ {{e_5}}\\ {{e_6}} \end{array}\left[ {\begin{array}{*{20}{c}} 1&1&0&0&0\\ 3&0&1&0&0\\ 1&0&0&3&0\\ 0&4&0&1&0\\ 0&0&1&0&2\\ 0&0&0&0&3 \end{array}} \right] \end{array} $ |
其中矩阵的行表示某个场所或事件,例如微博的博文、学术文章或者购物清单等,矩阵的列则表示参与该事件的基本单位或成员,例如转发微博的用户、文章作者或者消费者所购买的商品的名称。若pij=1则表示第j个成员参与了第i次事件,反之则表示没有参与。矩阵P也可以采用权值的方式表示,即矩阵元素的取值表示参与的权值,例如回帖或转发的次数、所购买的商品数量、停留的时长等。在社会网络分析方法中,将上述社会网络结构称为双模网络,也称双重网络 (bipartite) 或“隶属网”。
在社会网络分析方法中,有很多对双模数据进行分析的方法,既有直接对双模网络的关联模式进行分析的方法,也有将双模网络变为单模网络的降模法。就行为观测数据而言,研究者通常只关心列模 (成员模) 的网络关联模式,行模 (事件模) 则作为协变量来考虑。将二进制双模数据进行一个简单的矩阵映射,就可得到一个单模矩阵,又称共生矩阵 (co-occurrence matrix)。这个单模矩阵既可以是表示列模的数据 (PT×P, m×m),也可以是表示行模的数据 (P×PT, n×n),数据的选择取决于研究者的需要。单模矩阵的数值则表示参与者两两之间共同出现的频次,因此该矩阵可视为有权网。从计算的角度来说,使用矩阵映射进行降模可以得到参与者的行为频次信息,非常简单高效。
但是,对于带权值的发生矩阵,降模映射则不太适用。其最大的缺点在于降模之后所得到的是一个密集矩阵。在原双模网络中,若节点的中心度为d的话,则降模之后变为[d×(d-1)]/2,从而放大了网络密度,并在某种程度上扭曲了网络结构 (Latapy et al., 2008)。因此,通常来说还需进一步处理,将其转换为二进制作为社会网络关系的量度。然而这种二值化量度的困扰在于如何确定阈值。若采用一个单一阈值对矩阵权值进行转换,则其潜在假设是参与者有相同的分布。例如,在网络社区中,网络成员之间的发帖数和回复数存在非常大的变差。假设成员x与z共有3次回复,成员y与z共有5次回复,但x的总回帖量是3次,而y的总回帖量是100次。我们该如何判定或比较x-z和y-z这两对关系呢?显而易见,基于单一阈值的二值化网络测度难以处理此类情形。在此基础上,可以考虑相对比例,例如3/3与5/100。巴拉特等人 (Barrat et al., 2004;Barthélemy et al., 2005;Newman,2004) 提出了改进型的加权方案,但其着重于探测网络的社区结构,而非节点间的关系测度。
除了降模映射法,典型的处理方式还包括直接计算列模的相关系数矩阵并作为社会网络测量。相关系数法的优点在于能够控制不同参与者的活跃程度,但缺点是无法识别虚假相关,同时相关系数矩阵作为一个稠密矩阵也不太适合对大规模网络进行测量。有学者 (Raeder and Chawla, 2011;Zweig and Kaufmann, 2011) 将双模数据视为“购物篮”问题,采用数据挖掘手段来发现列模之间的关联模式,然而其可信度和解释力不太能够得到保证。
在过去的十几年,在许多学科特别是在生物学 (Friedman et al., 2000)、基因学 (Ghazalpour et al., 2006)、神经科学 (Huang et al., 2010) 等领域,高斯图模型已经成为非常流行的对复杂系统进行抽象并获得关于大规模观测变量的关联模式的一种处理手段。相比于前述的降模映射法、相关系数法等处理方法,高斯图模型的计算结果不但避免了前述几种处理方法的缺点,能够较好地探测出真实的网络结构特征,而且具有可解释性强、扩展性高的特点,在面对不同问题时具有强大的解决能力。然而在社会科学领域,相关的研究尚不多见,仅有个别学者 (如陈华珊,2015) 用高斯图模型研究美国参议院投票网络、在线论坛发帖网络等。相较于图模型在自然科学领域应用的流行性,社会科学领域对它的认识和使用还非常粗浅。在此,本文尝试对高斯图模型进行介绍,以期引起社会科学界同仁的重视并推动相关的研究与应用。
二、 高斯图模型 (一) 高斯图模型的基本形式将观测数据的发生矩阵用一个n×p的矩阵X来表示:
| $ X = ({X_1}, \ldots ,{X_p})\sim N\left( {\mu ,\mathit{\Sigma} } \right) $ |
其中,n为观测数,p为变量数,观测之间相互独立,且X为多元正态分布随机变量。假设X的协方差矩阵∑为正定矩阵,那么分布的条件依赖结构可用高斯图模型g=(Γ, E) 来表示,其中Γ={1, …, p}表示节点集合;而E是一个Γ×Γ的边的集合。在高斯图模型中,节点表示变量,边表示一对变量的条件依赖关系。在控制所有其他变量的情况下,满足XΓ\{a, b}={Xk; k∈Γ\{a, b}}。两个节点的关系{a, b}出现在边集合E中,当且仅当Xa条件依赖于Xb。对于没有包含在集合E中的其他成对变量,意味着在控制所有其他变量的情况下条件独立。因此,高斯图模型也经常被称为条件依赖网络 (Lauritzen,1996),即如果一对变量为条件依赖,则其对应的两个节点之间可用一个连线 (边) 来连结,反之,节点之间不存在连线。
在此,对矩阵X中节点的两两关系的估计也被称为“邻域选择”(neighborhood selection),其实质是协方差选择问题。邻域选择的目的是对于给定的n个i.i.d观测X,分别估计每个变量 (节点) 的相邻变量。即对于集合Γ中的一个节点a(a∈Γ),它的邻域变量集合用Xnea表示,邻域选择的目标是让Xnea成为Γ\{a}的一个最小子集,使得给定Xnea,Xa条件独立于所有其他变量,进而邻域选择可以被转化为标准的回归问题并求解。
但在数学求解上,一般不直接计算协方差矩阵,而是估计其逆协方差矩阵。这是因为逆协方差矩阵具有独特的性质。假设存在一个从多元正态分布中独立抽取的n个样本,其协方差矩阵为∑,则表征样本变量之间条件依赖关系的高斯图模型可由逆协方差矩阵Θ=∑-1来表示。首先,逆协方差矩阵Θ与协方差矩阵∑具有对偶性,由于协方差矩阵为正定矩阵,那么逆协方差矩阵也为正定矩阵,因此它们互为对偶范数 (dual norm)。其次,逆协方差矩阵具有稀疏的特质 (Mardia et al., 1980;Lauritzen,1996),也就是说,当且仅当∑ij-1=0时,变量i与变量j条件独立;反之,变量i与变量j存在条件依赖关系。逆协方差矩阵在图模型中又称“精度矩阵”(precision matrix) 或“聚集矩阵”(concentration matrix)。逆协方差矩阵与协方差矩阵示例如下:
| $ \begin{array}{l} {\mathit{\Sigma} ^{ - 1}} = \left[ {\begin{array}{*{20}{c}} 2&{ - 1}&0&0&0\\ { - 1}&2&{ - 1}&0&0\\ 0&{ - 1}&2&{ - 1}&0\\ 0&0&{ - 1}&2&{ - 1}\\ 0&0&0&{ - 1}&2 \end{array}} \right]\\ \mathit{\Sigma} = \left[ {\begin{array}{*{20}{c}} {0.83}&{0.67}&{0.50}&{0.33}&{0.17}\\ {0.67}&{1.33}&{1.00}&{0.67}&{0.33}\\ {0.50}&{1.00}&{1.50}&{1.00}&{0.50}\\ {0.33}&{0.67}&{1.00}&{1.33}&{0.67}\\ {0.17}&{0.33}&{0.50}&{0.67}&{0.83} \end{array}} \right] \end{array} $ |
Θ矩阵与偏相关系数有如下关系:
| $ {\rho _{ij|(i,j)}} = \frac{{ - {\omega _{ij}}}}{{\sqrt {{\omega _{ii}}{\omega _{jj}}} }} $ |
就社会关系网络测量而言,当该偏相关系数矩阵的元素大于0,表示所对应的两个网络节点之间存在联带关系,且该数值可表示联带关系的强弱;反之则不存在联带关系。因此,对观测数据X进行计算的步骤为:先估计其样本逆协方差矩阵,再转换为偏相关系数矩阵就可得到该网络的关系测度。
一般采用最大似然法来估计精度矩阵∑-1。用S表示X的经验协方差矩阵,高斯对数最大似然的公式表达如下:
| $ log\;{\rm{det}}\mathit{\Theta} - trace\left( {S\mathit{\Theta} } \right) $ | (1) |
其中Θ表示逆协方差矩阵,即Θ=∑-1。使公式 (1) 最大化可得最大似然估计
1. 罚似然估计法
近几十年来,统计学家针对高维稀疏数据提出了很多解决方案,其中蒂施莱尼 (Tibshirani,1996) 所提出的罚似然回归法成为主流方法,并被其他研究者进一步扩展和引入到高斯图模型中 (Meinshausen and Bühlmann,2006;Yuan and Lin, 2007;Peng et al., 2009)。罚似然法是在线性回归公式中引入一个约束项 (regularizer) 或惩罚项 (penalty term)Θ,并由一个非负的优化参数 (tuning parameter)λ来控制。当λ足够大时,Θ的一些元素的值将等于0,也就是说λ值越大,所估计的逆协方差矩阵越稀疏。即使在p>n的情形下,公式仍能够求解,其表达式如下:
| $ maximiz{e_\mathit{\Theta} }\{ log\;{\rm{det}}\mathit{\Theta} - trace\left( {S\mathit{\Theta} } \right) - \lambda {\left\| \mathit{\Theta} \right\|_1}\} $ | (2) |
其中,‖Θ‖1为l1罚则,1表示对矩阵Θ的所有元素的绝对值求和。将公式 (2) 用社会统计学教材常用的残差最小化拟合公式来表示,就是将:
| $ {\rm{RSS}} = \sum\limits_{i = 1}^n {{{\left( {{y_i} - {\beta _0} - \sum\limits_{j = 1}^p {{\beta _j}{x_{ij}}} } \right)}^2}} $ |
1. 除了公式 (2) 提到的一范数 (l1),罚则范数的选择还包括零范数 (l0)、二范数 (l2)(岭回归)、核范数 (nuclear norm),以及混合一范数和二范数的弹性网回归 (Elastic Net)(Zou and Hastie, 2005),等等。更确切地说,本文所指的罚则模型是基于范数的罚则图模型 (lasso图模型),包括融合了l1范数和其他范数的扩展模型,本文后续所介绍的某些模型会采用弹性网或多种罚则范数来处理。
改写为:
| $ {\rm{RSS}} + \lambda \sum\limits_{j = 1}^p {|{\beta _j}|} $ | (3) |
在上式中,当λ=0时,即为常规的OLS回归残差项。由于λ为非负数,因此当整个回归模型保留的变量越多,残差惩罚越大,反之则残差惩罚越小,从而λ作为模型超参数能够控制模型中变量的稀疏程度。
梅豪森和布尔曼 (Meinshausen and Bühlmann,2006) 最早将罚似然回归应用到高斯图模型中,他们实际上是将网络的每一个节点作为因变量,其他所有节点作为自变量来构建一系列 (p个) 回归方程,从而得到一个近似解。其后,许多研究者提出了不同的求解法。有的学者 (Yuan and Lin, 2007) 借用万德伯格等人 (Vandenberghe et al., 1998) 提出的“内点搜索法”(interior-point) 进行求解;贝纳杰等人 (Banerjee et al., 2008) 则提出用“分块坐标递降法”(blockwise coordinate descent approach) 来求解;弗里德曼等人 (Friedman et al., 2008) 在此基础上进一步提出用坐标递降法 (coordinate descent procedure) 来求解,且证明了当p > n时,坐标递降法具有很高的计算效率。
所有采用罚则对高斯图模型进行稀疏求解的算法都可被称为图形罚极大似然法或罚似然高斯图模型 (以下简称glasso或图模型)。glasso模型近年来在基因研究、流行病学等领域被广泛应用,并且模型进一步从单一高斯图模型扩展为动态图模型 (Ahmed and Xing, 2009;Song et al., 2009)、多组图模型 (Guo et al., 2011;Danaher et al., 2014) 以及多层次图模型和潜变量图模型 (Ambroise et al., 2009;Chandrasekaran et al., 2012) 等。本文将在第二节详细介绍扩展模型。
2. 最优参数选择与模型评估
在公式 (2) 中,参数λ未知且无法通过样本数据对其进行推断,因此也称之为超参数 (hyper parameter),一般采用穷举法进行搜索;若有多个超参数则可使用网格搜索 (Grid Search) 等方法。为了更好地评估模型以及避免模型的过度拟合,在机器学习理论中,一般采用交叉验证 (cross validation) 的方式来进行,即将样本数据集分为训练集和测试集,前者用来建立模型,后者则用来评估模型对未知样本进行预测时的精确度。也有学者 (如Chen and Chen, 2008;Foygel and Drton, 2010) 采用贝叶斯信息准则 (BIC) 来评估模型,并针对其稀疏约束的特点提出扩展贝叶斯信息准则 (eBIC)。
(三) 应用与示例在社会科学领域,最为著名的数据集是美国南方黑人妇女数据集,2被很多研究者所使用 (Freeman,2003;Neal,2013)。该数据是由人类学家戴维斯和加纳等人 (Davis et al., 1941) 通过访谈、观察记录、访客名单以及报纸记载所收集的社区妇女参与社区活动的信息 (下文简称DGG)。该数据包括18名参与者,14次社会事件。研究者们用他们的人类学观察直觉以及经验洞察力对这些妇女的社会网络进行了归纳,把她们分成两个子群体,并且在每组中区分出核心成员、主要成员和边缘成员三个层次。在他们汇报的结果中,编号1至编号8的妇女被分到第一组,其中编号1、2、3、4作为核心成员,编号5、6、7为主要成员,编号8为边缘成员。编号10到18被归为第二组,其中编号13、14、15是核心成员,编号11、12为主要成员,编号10、16、17、18为边缘成员。编号9被标识为同时属于两个组,且都作为边缘成员。
2. 该数据由戴维斯和加纳 (Davis,Gardner and Gardner) 收集,故简称DGG。社会网络分析软件UCINet及R软件包latentnet均附带了该数据,单独的数据下载及更详细的介绍见该网站:https://networkdata.ics.uci.edu/netdata/html/davis.html。
根据罚似然图模型计算结果,可以用两种方式来构建社会关系网络矩阵。方式一为根据所估计的样本逆协方差矩阵,将非0元素转换为1,可得到常规的社会关系网络表示矩阵,用这种测量方式所得到的网络为无向网络。方式二为根据样本逆协方差矩阵进一步计算偏相关系数矩阵,作为社会关系网络的测量,其中偏相关系数可作为关系的权重,3由此,可得到无向有权网络 (undirected valued network)。在实际应用中,上述方式所得到的关系矩阵很可能不是对称矩阵,还需进行对称化处理。对于样本逆协方差矩阵可采用“或法则”(OR rule,即矩阵中每一对对角元素若任一个值不等于0则视为存在条件依赖) 或“且法则”(AND rule,每一对对角元素均不等于0才视为存在条件依赖);对于偏相关系数矩阵则用对每一对对角元素求平均值、最大值或最小值等方式来处理。
3. 偏相关系数矩阵中有可能出现负相关,即小于0的数值。对于负相关与网络关系的关联需根据具体的研究问题予以处理。在共现数据中,负相关往往出现在两个参与者没有发生共现行为的情形中。本文对负相关数值进行了技术处理,将其设为0,表示不存在网络关系。
| 表 1 美国南方妇女社会活动日常参与记录 (DGG) |
使用glasso法对这18位妇女的社会关系网络判定的结果见图 1,随着罚则系数rho数值的增大,所估计的网络密度愈加稀疏。根据eBIC法则,选择rho=0.1的模型为最优模型,可以区分出三个群体:编号1至7为第一组,编号8、编号10至16为第二组,编号17和编号18为第三组。编号9被判定为同时属于两个组,也就是说她承担了网桥的作用,连接两个群体。弗里曼 (Freeman,2003) 汇总了21种计算方法对DGG数据进行元分析,glasso法的判定结果与这21种分析方法的绝大多数判定结果是一致的。稍有不同的是,glasso法单独将编号17和编号18两人判定为第三个组别,从原始数据上可以看到,她们两人仅共同出席了两次活动。在弗里曼所进行的分析中,BGR74和OSB00这两个方法也都将她们判定为单独的组别。戴维斯和加纳在人类学分析中虽然将她们与编号10至16合为一组,但是将她们判定为边缘成员。由此可见,glasso法对小群体估计也具有敏感性。
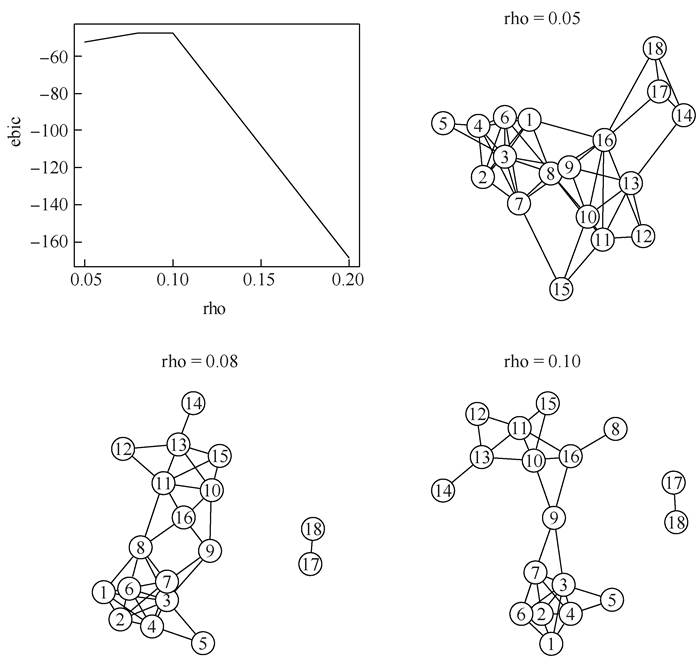
|
图 1 用glasso法计算的网络关联 (DGG)4 |
4. 这里采用偏相关系数矩阵作为社会关系网络测量的工具。为了更好地呈现网络关系的稀疏性,在构建网络时,通过设定阈值对偏相关系数进行二值化也是常见的做法。需要强调的是,不同于直接对频次的二值化,对偏相关系数的二值化与样本活跃度无关。本示例共拟合了5个模型,限于篇幅仅展示其中3个。本文示例数据、代码以及详细结果可从《社会》杂志官网下载。
三、 罚似然图模型的扩展基于罚似然回归方法的社会网络关系测度不仅适用于小群体的网络数据,更适用于大规模的社会网络数据。罚似然回归本质上是回归估计和模型变量选择,统计学家们通过模拟分析已经证明其具有非常好的稳健性,对于几千甚至上万的自变量选择具有一致性 (Tibshirani,1996)。另外,使用罚似然图模型进行社会关系网络测度,可以根据无向无权的二分双模网络数据估计得到无向有权的关系网络矩阵,不仅可以对关系的有无进行判定,还可以进行强度的比较,大大丰富了分析内容。除此之外,罚似然图模型还具有很强的扩展性,本节将对此进行详细介绍。
经典的高斯图模型假设变量为多元正态分布,但在社会科学研究中,往往会遇到多种类型的数据,甚至是混合类型的数据,包括二分数据、定类数据、定序数据、计数数据、有偏分布的连续数据,等等。例如,前述的美国南方妇女数据即为二分变量;网民在论坛的发帖回帖数量为计数型变量;在某个场所停留的时间可视为计数型变量或有偏的连续变量。关于健康领域的社会学大数据研究则可能要考虑性别 (二分)、年龄 (连续)、行为模式 (计数)、事件发生的场所 (类别)、用药的剂量 (连续) 等各类数据之间的关联模式。基于此,统计学家们发展了多种特殊模型予以解决。5略有遗憾的是,目前为止,尚未有一个软件包将所有数据类型综合到一个框架下进行处理。
5. 针对二项分布数据的估计问题可进一步参考:Banerjee et al., 2008;Ravikumar et al., 2008;van Borkulo et al., 2014。针对泊松分布数据可参考:Allen and Liu, 2012,2013。针对多分类分布可参考:Dai et al., 2013。针对混合数据类型的估计问题可参考:Chen et al., 2015;Haslbeck and Waldorp, 2015。
(一) 带协变量的罚似然图模型在罚似然模型中,除了对所有变量加罚,还可以仅对部分变量加罚。将公式 (3) 的罚则项
| $ \lambda \sum\limits_{p = 1}^p {|{b_p}|} $ |
改写为:
| $ \lambda \sum\limits_{p = 1}^m {|{b_p}|} $ |
其中m < p表示仅对部分自变量加罚。因此,很容易引入其他协变量进入模型。以DGG数据为例,由于所记录的事件来自多种聚会类型,尽管人类学家们没有记录事件的具体类型从而缺失了相关信息,但是可以假设不同的活动类型与参与规模相关,进而影响不同人的参与程度。因此,在本示例中,将参与活动的人数作为协变量引入图模型,得到的结果如图 2所示。与图 1相比,在控制了参与规模这个因素之后,图 2仍然保留了基本相同的网络结构,编号17和编号18通过编号16与其他成员相关联。但与图 1不同的是,编号1、编号8和编号16处在网络桥的位置,而编号9不再作为网络桥,而是成了第一网络子群的成员。在弗里曼 (Freeman, 2003) 的元分析中,编号8的分组其实存有争议,21个方法中有4个将其判定为第二分组,另有7个方法无法处理编号8只能将其剔除。从原始数据来看,编号9所参与的4次活动均是这个群体参与人数最多的活动。因此,关于编号9的网络地位,忽略技术问题 (由于观测数太少而导致估计不稳定),可能的推论有两个:编号为9的妇女是从众的边缘成员或者重大事件才出席的核心人物。选择何种推论取决于对活动信息的了解而不能仅依赖于网络指标。遗憾的是,原始数据缺乏相关信息。
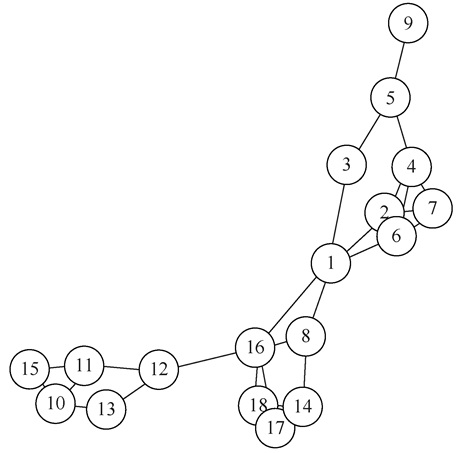
|
图 2 控制聚会规模以后的网络关联 (DGG) |
若协变量为类别变量,则观测样本可能来自不同的子总体,那么有两种策略:一是用不加罚的方式将协变量引入模型,此时估计得到的是一个总体网络,消除了不同类别之间的异质性;二是对子总体分别建模,从而得到多个网络,该方式的缺点在于无法进一步分析网络之间的共性。
除了来自不同子总体的样本之外,在时点观测数据中往往需要假设存在一定的异质性:在一个随时点变化的观测中,存在一个公共的网络结构,在不同时间段网络结构发生缓慢变化或者突变。例如,对于学术引文网络来说,在20世纪六七十年代,由于布劳—邓肯地位获得模型的成功,社会流动领域的研究的引文可能会更多涉及路径模型和结构方程模型方面的文献;而在20世纪八九十年代之后,引文中可能更多地出现对数线性模型方面的文献。在统计技术变迁的过程中,核心的关注主题并没有发生变化,不同时段的引文仍然具有一定的共性。
对于这种异质性数据,有不同的分析策略:一是在考虑异质性的条件下,估计一个平滑的共同网络结构 (Zhou et al., 2010;Kolar and Xing, 2011);二是假设不同子总体之间存在一个公共网络结构,但每个子总体由于其自身的结构特殊性而具有独特的网络结构,需同时估计多个子网络结构。就后一种分析策略来说,针对观测的独立同分布 (i.i.d) 假设,可以将glasso模型进一步扩展为联合glasso模型,在一个统一的分析框架下考察在同一个群体中不同性质的网络关系如何叠加和扩展。针对该问题,需要使用两个惩罚因子,一个惩罚因子用来控制所有子样本中的公共因子θj, j′的稀疏度,另一个惩罚因子用来控制子样本内部的稀疏度。有学者 (Zhu et al., 2014) 提出的解决方案是为每一个子总体估计一个稀疏图结构,同时也估计跨子图的网络凝聚点。也有学者 (Guo et al., 2011) 使用分层罚模型估计来保留公共的图结构,同时允许组间差异,当plog (p)/n趋向于0时 (其中p为变量个数,n为样本规模),该方法可实现弗罗贝尼乌斯范数 (Frobenius norm) 收敛;但这也意味着当p > n时,并不能获得稳定的估计。达纳赫等人 (Danaher et al., 2014) 使用融合罚则 (FGL, fused graphical Lasso) 和分组罚则 (GGL, grouped graphical Lasso) 使罚似然对数最大化,但并未给出其估计量统计收敛的理论验证。蔡天文等人 (Cai et al., 2015) 提出了一个改进型模型 (MPE) 联合估计K个稀疏精度矩阵,并对其统计收敛属性进行了理论验证。
上述几种方法的分析思路是将网络边作为分析的核心,即假设网络中某些边是公共的或是特殊的。莫汉等人 (Mohan et al., 2014) 则提出了一个以网络节点为核心的视角,即某些节点的连结在子图中具有共性,而另一些节点的连结在不同子图中具有特殊性。
本节的示例为学术文献关键词关联网络,数据来自《社会学研究》和《社会》这两本学术杂志2006年至2015年发表的所有文章的关键词。在社会学专业的学术文章中,关键词是反映一篇文章现实关注点、理论切入口和方法流派的重要指标。通过构建关键词关联网络,不仅可以发现社会学专业研究中的核心关注要素,还可以比较这两本杂志在文章题材选择方面的偏好差异。据统计,该数据包括1 348篇文章、492个关键词。由于本示例主要是为了展示模型特点,在此仅提供初步的模拟拟合结果。使用GGL法拟合的结果表明《社会学研究》的关键词关联有79对,《社会》有83对;两种杂志共同的关键词关联41对。关键词关联网络如图 3、图 4、图 5所示。

|
图 3 两本杂志 (2006—2015) 学术论文关键词关联网络 |

|
图 4 《社会学研究》(2006—2015) 学术论文关键词关联网络 |
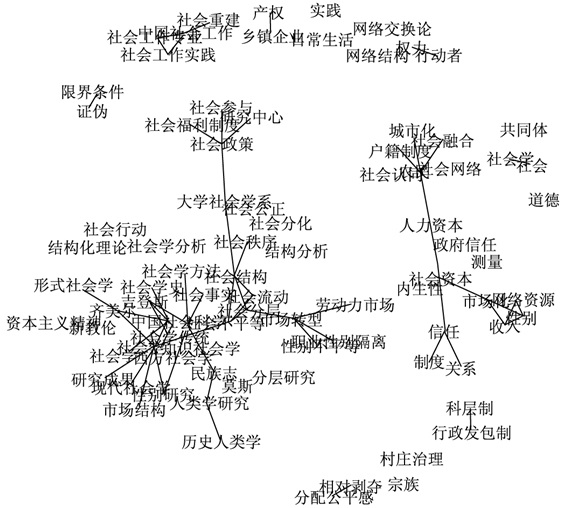
|
图 5 《社会》(2006—2015) 学术论文关键词关联网络 |
使用高斯图模型的目的是根据观测到的多元正态分布数据推断其潜在的网络结构。若观测数据来自不同的子总体且可区分,可采用前节所述的多组罚似然图模型;若子总体不可观测,则需假设观测数据来自不同的分布密度,用公式表示即为:
| $ {\pi _1}{N_1}\left( {{\mu _1},{\sum _1}} \right),{\pi _2}{N_2}\left( {{\mu _2},{\sum _2}} \right), \ldots {\pi _k}{N_k}({\mu _k},{\sum _k}), $ |
其中N(μ, ∑) 为多元正态分布,均值为μ,方差协方差矩阵为∑,πk为混合比例。该问题类似于有限混合聚类模型,但在图模型中,需根据样本数据和给定的稀疏度约束来估计潜在的网络结构。罗茨和维特 (Lotsi and Wit, 2013) 在有限混合聚类模型的基础上提出了glassomix模型。与有限混合聚类模型一样,glassomix也是一个探索性分析的模型,需指定分类的数目,并在事后根据对数似然值或eBIC值评估不同模型拟合的效果。
仍以DGG数据为例,假设DGG数据来自不同类别的事件 (子总体),则采用glassomix模型拟合的结果如图 6所示 (程序中分别拟合了二分类和三分类模型,其中二分类模型的拟合指标优于三分类模型)。可以看到,在图 6(1)中,仍然保留了与图 1相一致的结构,有两个较大的连接子群和编号16、17、18这个游离的子群。在图 6(2)中,大致也呈现为两个子群,但是网络密度大于图 1的glasso基本模型。对照观测值的聚类结果 (见表 2),图 6(2)的事件中包括e8和e9这两次参与人数最多的活动,以及e11、e13和e14这三次由特定小规模群体参与的活动,因此可以认为图 6(1)表示的是日常事件网络,而图 6(2)表示的则是特殊活动网络。
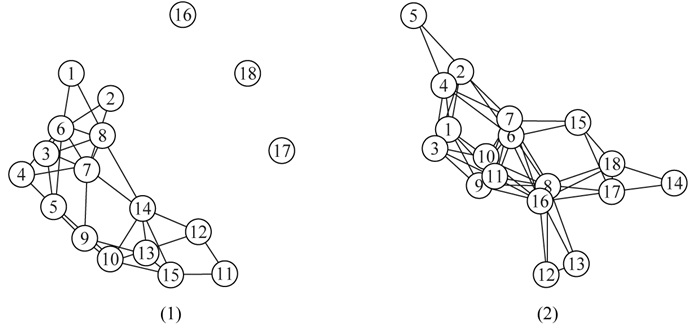
|
图 6 DGG数据的两个子网络 |
| 表 2 glassomix模型对事件进行聚类的结果 |
1. 分组罚似然图模型
在罚似然图模型中,当自变量中含有定类变量时,由于采用虚拟编码的形式,每个定类变量构成一个变量组。在这种情况下,直接对模型的每个变量施加惩罚项就不太合适,会造成一个定类变量的部分虚拟编码变量被剔除出模型,而实际上需要保留全部虚拟编码变量组以表示该定类变量。因此,惩罚项应加在变量组这一层次,而非单个虚拟变量上,这样才能保证同一组的虚拟变量同进同出。有学者 (Yuan and Lin, 2006) 提出了分组的罚似然回归模型,并用于图模型拟合 (Yuan and Lin, 2007),弗里德曼等人 (Friedman et al., 2010) 在此基础上进一步提出了能够改善组稀疏度的罚似然模型。
分组罚似然模型并不局限于在技术层面上处理定类数据或变量之间的交互效应,在其他领域也有很多应用。例如,在文本语义模型中,同义词或相近含义的词通常不会同时出现在一个句子中,从而形成一定程度的“互斥”,通过将相近语义的词设置为同一组变量并将罚似然加在组的层次,往往可以得到更好的拟合效果。
2. 潜变量罚似然图模型
分组罚似然模型的要求是变量的依赖关系可观测,但如果假设变量之间存在条件依赖且变量的分组未被观测,则上述组内依赖关系变为潜变量问题。在复杂网络理论中,网络连接并非随机生成,由于小世界现象 (Watts and Strogatz, 1998) 和幂律的存在,网络中存在着大量的网络聚合点或结构洞 (Burt,1995)。有学者 (Zhu et al., 2014) 在估计多组图模型的稀疏结构时考虑了网络的聚合点效应。安布鲁瓦兹等人 (Ambroise et al., 2009) 使用潜结构的方式来估计精度矩阵。该模型假设网络中的节点从属于某个未被观测到的潜分组 (latent group)。网络边即为条件依赖于这些潜分组的独立同分布 (i.i.d) 随机变量,其分布依赖于其所连接的节点所属的潜分组。
在本文的分析中,用潜结构模型去拟合DGG数据并没有得到较好的结果。但为了查看DGG数据中的变量依赖关系,笔者仍然选取了其中一个模型的结果来查看。如图 7所示,网络节点依赖于两个潜变量,其中编号8、12、13、16、17和18依赖于一个潜变量,并形成一个网络子群;其他成员依赖于另一个潜变量,但在控制了潜变量之后,这些成员之间没有形成网络关系。
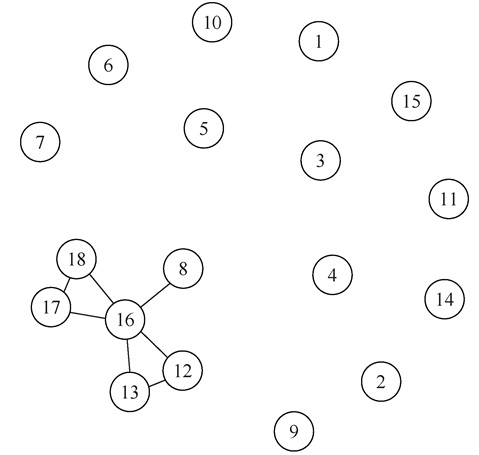
|
图 7 DGG数据的潜结构模型 |
针对变量未被观测或者观测变量缺失的问题,一些学者 (Chandrasekaran et al., 2012;Ma et al., 2012;Yuan,2012) 进一步提出了一个更加广义的潜变量罚似然图模型,其做法是将逆协方差矩阵拆成两个部分,一部分稀疏的矩阵代表观测变量之间的条件独立性,另一部分是低秩的矩阵,代表潜变量之间的条件独立性。
四、 小结与讨论本文简述了基于罚似然估计的高斯图模型及其扩展模型在社会科学领域的应用。通过展示基本的罚似然估计原理以及一些特定的扩展模型,可以看出相对于传统的双模数据处理方法,罚似然图模型具有非常强的扩展性,在社会科学领域的应用潜力也非常大。通过对DGG数据的示例以及不同的假设设置,本文用罚似然图模型进一步发掘了数据潜力,得到了与以往分析不同的结果。本文使用了两个示例数据集,DGG是非常小的数据,而论文关键词示例规模相对适中 (492个节点),罚似然图模型在大规模数据分析中的应用可参考陈华珊 (2015)对业主论坛讨论的测量。
除了罚似然图模型,适合对高维稀疏双模数据进行网络关系判别的方法还有很多,例如线性判别模型、潜狄氏聚类模型 (Latent Dirichlet Allocation)(Blei et al., 2003;Blei,2011) 等,甚至可以采用神经网络领域的词向量模型 (Mikolov et al., 2013;Pennington et al., 2014))。通过这些模型将双模数据中的事件和成员映射到一个低维的向量空间,再构建相互之间的关联矩阵,就可以得到一个新的表示网络关系的结构。但是,上述模型对数据的生成机制有其特定的假设,因此对最终网络关系的理解也会发生变化,研究者应谨慎对待。
在社会网络分析方法中,本文认为有必要区分两种不同的社会网络测量类型。一是表征状态的社会网络,例如代表感知和情感关系的友谊、信任、结盟等,这类数据通常以一种较为稳定的状态出现,比较适合由受访者进行自我评估,用问卷调查的方式进行社会网络关系测量。二是表征行为的社会网络数据,例如借贷行为网络、沟通行为网络、学术论文的引证网络,等等。在以问卷调查为主要手段的数据收集过程中,可收集到的后一类数据的规模通常较小,因此往往采取与前者同样的方式处理。但随着大数据概念的深入和各类数据源的丰富,表征行为的社会网络会越来越多地出现在社会学学者的视野中,且数据规模远超以往。对于这类数据,除了描述事件的概貌之外,研究者们有理由假设行为背后存在一个较为稳定的网络关系状态,因而需要对潜在的网络关系模式进行推断。本文展示了用罚似然图模型对该类数据进行潜在网络关系推断的优点。
表征事件的社会网络数据通常具有时序特征,例如本文所采用的两个示例数据均包含时序信息。就时序数据而言,用罚似然图模型去拟合实际上是对观测进行了静态的测量,从而损失了大量时序信息,无法拟合社会网络的变迁。折衷的办法是设定一个时间间隔,将事件分成不同的时间片段再予以测量,但该方法的缺点是时间周期完全由人工选择,因此推论将完全依赖于所选择的时间周期,无法保证结果的一致性。目前来看,采用罚似然图模型对时序网络的分析主要集中于对离散时段数据的探测 (Zhou et al., 2010;Kolar and Xing, 2011),对连续时段数据探测的相关研究非常少,威特和阿布鲁 (Wit and Abbruzzo, 2015) 对一个变动比较缓慢的网络结构进行了分析。除此之外,时序数据往往伴随着样本的变动 (加入/离开),这些问题对罚似然图模型来说都是比较艰巨的挑战。
最后,随着R语言的发展和成熟,有相当多罚似然图模型均提供了相应的R软件包,据笔者的不完全收集,已有200个左右的R包。本文在此仅列举部分,并对其特点进行简单归纳,以方便读者学习 (见表 3)。不同于常规的统计学模型,由于超参数的存在,尤其是潜变量罚似然模型中存在两个超参数,对最优的拟合模型的寻找和判定往往比较困难,需要研究者的努力和耐心。
| 表 3 罚似然图模型相关R包 |
必须要提醒的是,尽管罚似然图模型解决的是高维问题,但不同的模型和优化求解算法均有特定的数据前提,有的模型并不适合特定的情形,有的模型只适合中小型网络规模,还有的受限于网络稀疏度。实际应用中针对各种数据场景选择合适的模型和优化求解算法仍需十分小心。
罚似然估计法与图模型相结合的研究方法发展时间不过十来年,但进展非常迅速,特别是在基因学、机器学习等领域,相关论文层出不穷,不仅包括对罚似然模型的进一步扩展和延伸,还包括从工程应用角度进行计算上的优化及并行化应用等。罚似然图模型的扩展还有很多,本文提到的文献仅仅是冰山一角。同时,受作者学识水平所限,此综述可能会遗漏一些重要的文献,谨以此文唤起社会科学研究者的关注,与有志者共勉。
| [] | 陈华珊. 2015. 虚拟社区是否增进社区在线参与?一个基于日常观测数据的社会网络分析案例. 社会, 35(5): 101. |
| [] | Ahmed Amr, Xing Eric P.. 2009. Recovering Time-Varying Networks of Dependencies in Social and Biological Studies. Proceedings of the National Academy of Sciences, 106(29): 11878-11883. DOI:10.1073/pnas.0901910106 |
| [] | Allen, Genevera I. and Zhandong Liu. 2012. "A Log-Linear Graphical Model for Inferring Genetic Networks from High-Throughput Sequencing Data." Arxiv:1204.3941[Stat]. |
| [] | Allen Genevera, Zhandong Liu. 2013. A Local Poisson Graphical Model for Inferring Networks from Sequencing Data. IEEE Transactions On Nanobioscience, 12(3): 189-198. DOI:10.1109/TNB.2013.2263838 |
| [] | Ambroise Christophe, Julien Chiquet, Catherine Matias. 2009. Inferring Sparse Gaussian Graphical Models with Latent Structure. Electronic Journal of Statistics, 3: 205-238. DOI:10.1214/08-EJS314 |
| [] | Banerjee Onureena, Laurent El Ghaoui, Alexandre d'Aspremont. 2008. Model Selection through Sparse Maximum Likelihood Estimation for Multivariate Gaussian or Binary Data. Journal of Machine Learning Research, 9: 485-516. |
| [] | Barrat Alain, Marc Barthélemy, Romualdo Pastor-Satorras, Alessandro Vespignani. 2004. The Architecture of Complex Weighted Networks. Proceedings of the National Academy of Sciences of the United States of America, 101(11): 3747-3752. DOI:10.1073/pnas.0400087101 |
| [] | Barthélemy Marc, Alain Barrat, Romualdo Pastor-Satorras, Alessandro Vespignani. 2005. Characterization and Modeling of Weighted Networks. Physica A:Statistical Mechanics and its Applications, 346(1-2): 34-43. DOI:10.1016/j.physa.2004.08.047 |
| [] | Blei, David M. 2011. "Introduction to Probabilistic Topic Models." Communications of the ACM:1-16. |
| [] | Blei David M., Ng Andrew Y., Jordan Michael I.. 2003. Latent Dirichlet Allocation. The Journal of Machine Learning Research, 3: 993-1022. |
| [] | Burt, Ronald S. 1995. Structural Holes:The Social Structure of Competition. Cambridge:Harvard University Press. |
| [] | Cai Tony, Hongzhe Li, Weidong Liu, Jichun Xie. 2015. Joint Estimation of Multiple High-Dimensional Precision Matrices. The Annals of Statistics, 38: 2118-2144. |
| [] | Chandrasekaran Venkat, Parrilo Pablo A., Willsky Alan S.. 2012. Latent Variable Graphical Model Selection via Convex Optimization. The Annals of Statistics, 40(4): 1935-1967. DOI:10.1214/11-AOS949 |
| [] | Chen Jiahua, Zehua Chen. 2008. Extended Bayesian Information Criteria for Model Selection with Large Model Spaces. Biometrika, 95(3): 759-771. DOI:10.1093/biomet/asn034 |
| [] | Chen Shizhe, Witten Daniela M., Ali Shojaie. 2015. Selection and Estimation for Mixed Graphical Models. Biometrika, 102(1): 47-64. DOI:10.1093/biomet/asu051 |
| [] | Chiquet, Julien, Gilles Grasseau, Camille Charbonnier, and Christophe Ambroise. 2016. SIMoNe:Statistical Inference for Modular Networks. |
| [] | Dai Bin, Shilin Ding, Grace Wahba. 2013. Multivariate Bernoulli Distribution. Bernoulli, 19(4): 1465-1483. DOI:10.3150/12-BEJSP10 |
| [] | Danaher Patrick, Pei Wang, Witten Daniela M.. 2014. The Joint Graphical Lasso for Inverse Covariance Estimation Across Multiple Classes. Journal of the Royal Statistical Society:Series B (Statistical Methodology), 76(2): 373-397. DOI:10.1111/rssb.2014.76.issue-2 |
| [] | Davis, Allison, Burleigh B. Gardner, Mary R. Gardner, and J. W. Silver. 1941. Deep South. Chicago:University of Chicago Press. |
| [] | Foygel Rina, Mathias Drton. 2010. Extended Bayesian Information Criteria for Gaussian Graphical Models. Advances in Neural Information Processing Systems, 2010: 604-612. |
| [] | Freeman, Linton C. 2003."Finding Social Groups:A Meta-Analysis of the Southern Women Data." In Dynamic Social Network Modeling and Analysis:Workshop Summary and Papers (2003), edited by Ronald Breiger, Kathleen Carley and Philippa Pattison. Washington:The National Academies Press:39-97. |
| [] | Friedman, Jerome and Robert Tibshirani. 2014. "Glasso:Graphical Lasso-Estimation of Gaussian Graphical Models." R Package Version 1. |
| [] | Friedman Jerome, Trevor Hastie, Robert Tibshirani. 2008. Sparse Inverse Covariance Estimation with the Graphical Lasso. Biostatistics, 9(3): 432-441. DOI:10.1093/biostatistics/kxm045 |
| [] | Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. 2010. Applications of the Lasso and Grouped Lasso to the Estimation of Sparse Graphical Models. Technical report, Stanford University:1-22. |
| [] | Friedman Nir, Michal Linial, Iftach Nachman, Dana Pe'er. 2000. Using Bayesian Networks to Analyze Expression Data. Journal of Computational Biology, 7(3-4): 601-620. DOI:10.1089/106652700750050961 |
| [] | Ghazalpour Anatole, Sudheer Doss, Bin Zhang, Susanna Wang, Christopher Plaisier, Ruth Castellanos, Alec Brozell, Schadt Eric E., Drake Thomas A., Lusis Aldons J., et al. 2006. Integrating Genetic and Network Analysis to Characterize Genes Related to Mouse Weight. PLoS Genetics, 2(8): PLoS Genetics. DOI:10.1371/journal.pgen.0020130 |
| [] | Guo Jian, Elizaveta Levina, George Michailidis, Ji Zhu. 2011. Joint Estimation of Multiple Graphical Models. Biometrika, 98(1): 1-15. DOI:10.1093/biomet/asq060 |
| [] | Haslbeck, Jonas M. B. and Lourens J. Waldorp. 2015. "Structure Estimation for Mixed Graphical Models in High-Dimensional Data." Arxiv:1510.05677[stat.AP]. |
| [] | Huang Shuai, Jing Li, Liang Sun, Jieping Ye, Adam Fleisher, Teresa Wu, Kewei Chen, Eric Reiman. 2010. Learning Brain Connectivity of Alzheimer's Disease by Sparse Inverse Covariance Estimation. Neuroimage, 50(3): 935-949. DOI:10.1016/j.neuroimage.2009.12.120 |
| [] | Kolar Mladen, Xing Eric P.. 2011. On Time Varying Undirected Graphs. Journal of Machine Learning Research, 10001(15): 407-415. |
| [] | Latapy Matthieu, Clémence Magnien, Nathalie Del Vecchio. 2008. Basic Notions for the Analysis of Large Two-Mode Networks. Social Networks, 30(1): 31-48. DOI:10.1016/j.socnet.2007.04.006 |
| [] | Lauritzen Steffen L.. 1996. Graphical Models. Oxford: Clarendon Press. |
| [] | Lotsi, Anani and Ernst Wit. 2013. "High Dimensional Sparse Gaussian Graphical Mixture Model." Arxiv:1308.3381. |
| [] | Ma, Shiqian, Lingzhou Xue, and Hui Zou. 2012. "Alternating Direction Methods for Latent Variable Gaussian Graphical Model Selection." Arxiv:1206.1275[Math, Stat]. |
| [] | Mardia Kanti V., Kent John T., Bibby John M.. 1980. Multivariate Analysis. London & New York: Academic Press. |
| [] | Meinshausen Nicolai, Peter Bühlmann. 2006. High-Dimensional Graphs and Variable Selection with the Lasso. The Annals of Statistics, 34(3): 1436-1462. DOI:10.1214/009053606000000281 |
| [] | Mikolov, Tomas, Kai Chen, Greg Corrado, and Jeffrey Dean. 2013. "Efficient Estimation of Word Representations in Vector Space." Arxiv:1301.3781. |
| [] | Mohan Karthik, Palma London, Maryam Fazel, Daniela Witten, Su-In Lee. 2014. Node-Based Learning of Multiple Gaussian Graphical Models. Journal of Machine Learning Research, 10001(15): 445-488. |
| [] | Neal Zachary. 2013. Identifying Statistically Significant Edges in One-Mode Projections. Social Network Analysis and Mining, 3(4): 915-924. DOI:10.1007/s13278-013-0107-y |
| [] | Newman, Mark E. J. 2004. "Analysis of Weighted Networks." Physical Review. DOI:https://doi.org/10.1103/PhysRevE.70.056131. |
| [] | Peng Jie, Pei Wang, Nengfeng Zhou, Ji Zhu. 2009. Partial Correlation Estimation by Joint Sparse Regression Models. Journal of the American Statistical Association, 104(486): 735-746. DOI:10.1198/jasa.2009.0126 |
| [] | Pennington Jeffrey, Richard Socher, Manning Christopher D.. 2014. Glove:Global Vectors for Word Representation. EMNLP, 10001(4): 1532-1543. |
| [] | Raeder Troy, Chawla Nitesh V.. 2011. Market Basket Analysis with Networks. Social Network Analysis and Mining, 1(2): 97-113. DOI:10.1007/s13278-010-0003-7 |
| [] | Ravikumar, Pradeep, Garvesh Raskutti, Martin J. Wainwright, and Bin Yu. 2008. "Model Selection in Gaussian Graphical Models:High-Dimensional Consistency of L1-Regularized MLE." Advances in Neural Information Processing Systems:1329-1336. |
| [] | Song Le, Mladen Kolar, Xing Eric P.. 2009. Time-Varying Dynamic Bayesian Networks. Advances in Neural Information Processing Systems, 22: 1732-1740. |
| [] | Tibshirani, Robert. 1996. "Regression Shrinkage and Selection via the Lasso." Journal of the Royal Statistical Society:Series B (Methodological):267-288. |
| [] | van Borkulo, Claudia D. and Sacha Epskamp. 2014. "IsingFit:Fitting Ising Models Using the eLasso Method." R package version 0.2.0. |
| [] | van Borkulo, Claudia D., Denny Borsboom, Sacha Epskamp, Tessa F. Blanken, Lynn Boschloo, Robert A. Schoevers, and Lourens J. Waldorp. 2014. "A New Method for Constructing Networks from Binary Data." Scientific Reports 4. |
| [] | Vandenberghe Lieven, Stephen Boyd, Wu Shao-Po. 1998. Determinant Maximization with Linear Matrix Inequality Constraints. Journal On Matrix Analysis and Applications, 10001(19): 499-533. |
| [] | Watts Duncan J., Strogatz Steven H.. 1998. Collective Dynamics of 'Small-World' Networks. Nature, 393(6684): 440-442. DOI:10.1038/30918 |
| [] | Wit Ernst C., Antonino Abbruzzo. 2015. Inferring Slowly-Changing Dynamic Gene-Regulatory Networks. Bmc Bioinformatics, 16(Suppl. 6): S5. |
| [] | Yuan Ming. 2012. Discussion:Latent Variable Graphical Model Selection via Convex Optimization. The Annals of Statistics, 40(4): 1968-1972. DOI:10.1214/12-AOS979 |
| [] | Yuan Ming, Yi Lin. 2006. Model Selection and Estimation in Regression with Grouped Variables. Journal of the Royal Statistical Society:Series B (Statistical Methodology), 68(1): 49-67. DOI:10.1111/rssb.2006.68.issue-1 |
| [] | Yuan Ming, Yi Lin. 2007. Model Selection and Estimation in the Gaussian Graphical Model. Biometrika, 94(1): 19-35. DOI:10.1093/biomet/asm018 |
| [] | Zhao, Tuo, Xingguo Li, Han Liu, Kathryn Roeder, John Lafferty, and Larry Wasserman. 2015. "Huge:High-Dimensional Undirected Graph Estimation." R package version 1.6. |
| [] | Zhou Shuheng, John Lafferty, Larry Wasserman. 2010. Time Varying Undirected Graphs. Machine Learning, 80(2-3): 295-319. DOI:10.1007/s10994-010-5180-0 |
| [] | Zhu Yunzhang, Xiaotong Shen, Wei Pan. 2014. Structural Pursuit over Multiple Undirected Graphs. Journal of the American Statistical Association, 109(508): 1683-1696. DOI:10.1080/01621459.2014.921182 |
| [] | Zou Hui, Trevor Hastie. 2005. Regularization and Variable Selection via the Elastic Net. Journal of the Royal Statistical Society:Series B, 67: 301-320. DOI:10.1111/rssb.2005.67.issue-2 |
| [] | Zweig Katharina Anna, Michael Kaufmann. 2011. A Systematic Approach to the One-Mode Projection of Bipartite Graphs. Social Network Analysis and Mining, 1(3): 187-218. DOI:10.1007/s13278-011-0021-0 |
 2017, Vol. 37
2017, Vol. 37