文章信息
- 杨茹元, 万佳, 孙友富, 张晓凤, 翟伟
- YANG Ruyuan, WAN Jia, SUN Youfu, ZHANG Xiaofeng, ZHAI Wei
- 钢-木组合梁抗弯性能的数值模拟及参数分析
- Numerical simulation and parametric study of the flexural behaviour of steel-timber composite beams
- 森林与环境学报,2021, 41(1): 96-103.
- Journal of Forest and Environment,2021, 41(1): 96-103.
- http://dx.doi.org/10.13324/j.cnki.jfcf.2021.01.013
-
文章历史
- 收稿日期: 2020-08-21
- 修回日期: 2020-10-29
2. 太原理工大学土木工程学院, 山西 太原 030024;
3. 南京林业大学林业资源高效加工利用协同创新中心, 江苏 南京 210037
2. College of Civil Engineering, Taiyuan University of Technology, Taiyuan, Shanxi 030024, China;
3. Co-Innovation Center of Efficient Processing and Utilization of Forest Resources, Nanjing, Jiangsu 210037, China
为提高木质构件的承载性能,扩大木结构的应用范围,木材可以与其他材料进行组合[1-3],形成新的组合结构,如木-混组合(timber-concrete composite, TCC)结构[4-5]、木-木组合(timber-timber composite, TTC)结构[6],这些组合结构作为建筑构件具有巨大优势。尽管对于TCC和TTC构件的结构性能已有大量的理论和试验研究,但对于钢-木组合(steel-timber composite, STC)结构的关注和应用还相对较少。STC梁通过剪力连接件对胶合木翼板与“H”形钢梁进行组合,不仅能发挥木材抗压能力强的优势,还能避免钢构件由于局部屈曲和畸变导致的承载能力降低的缺点[7],充分发挥两种材料的力学性能。在组合结构的研究中,有限元模拟是一种常用的研究方法,HASSANIEH et al[8]对STC梁进行了四点弯曲试验,并建立STC梁的非线性有限元模型,研究STC梁中螺钉和螺栓作为剪力连接件的不同模式对STC梁承载性能的影响;XU et al[9]通过循环试验和非线性有限元模拟,研究了钢梁-胶合木柱组合构件的受力性能;NOURI et al[10]对带有双腹板的STC梁柱节点进行了试验研究,并采用三维(three-dimensional, 3D)连续非线性有限元模拟研究了这种节点的结构性能。STC结构具有优异的结构性能,但由于与其相关的研究理论还不成熟,未出现专门的设计标准,在我国还未得到广泛的应用,因此,有必要对STC梁在短期荷载作用下的力学性能进行系统的研究,为STC梁的实际应用提供更多理论依据。
鉴于此,可使用有限元软件ABAQUS 2017建立STC梁的3D有限元模型,模拟四点弯曲试验的加载条件,采用合理的材料本构关系、屈服准则以及接触单元模型,与现有试验结果进行对比,验证该有限元模型的准确性和可靠性。同时,对STC梁抗弯性能的影响因素进行参数分析,研究剪力连接件类型、间距对STC梁承载性能和组合效率的影响。
1 钢-木组合梁抗弯性能试验 1.1 试验材料试验以兴安落叶松[Larix gmelinii (Rupr.) Kuzen.]规格材为原材料,经过干燥处理后,质量含水率为9%~12%,制备两层层板胶合木,每层层板厚度相同,胶黏剂选用间苯二酚-甲醛树脂胶;钢材选用的热轧“H”形钢,型号为HW100×100,等级Q235级,翼缘厚度8 mm,腹板厚度6 mm,在“H”形钢上翼缘与胶合木相应位置进行激光导孔,确保“H”形钢与胶合木对孔准确,开孔直径7 mm,长度方向上的开孔间距100 mm,宽度方向上的开孔间距50 mm;剪力连接件选用直径6 mm,等级为6.8级的高强螺栓,螺栓为双排布置,间隔100 mm(沿跨度方向),采用10 mm×10 mm的垫圈防止木材由于应力集中被局部压溃,并使用扳手拧紧螺栓,以提供400 N的预拉力。分别参照ASTM D143—2014[11]和ASTM A370—16[12],对木材及同批次钢板进行材性试验,得到材料参数见表 1。
| 试验材料 Material |
受力方式 Forced form |
极限强度 Ultimate strength/MPa |
屈服强度 Yield strength/MPa |
泊松比 Poisson′s ratio |
弹性模量 Elastic modulus/GPa |
| 木材Timber | 顺纹受压Compress parallel to grain | 50.62 | 0.32 | 13.716 | |
| 顺纹受拉Tensile parallel to grain | 117.10 | 0.32 | 14.014 | ||
| 顺纹剪切Shear parallel to grain | 9.25 | ||||
| 钢材Steel | 拉伸Tensile | 375.14 | 312.62 | 0.29 | 197.056 |
共设计6组18根试件,试件总长度均为2.70 m,跨度2.52 m,试件具体参数见表 2。所有试件中,钢梁的尺寸及剪力连接件的数量保持不变,为确保试验结果的精度和重复性,每组制备并测试了3个相同的试件。
| 组别 Group |
胶合木厚度 Glulam thickness /cm |
胶合木宽度 Glulam width /cm |
截面宽度 Section width /cm |
截面高度 Section height /cm |
| A | 3 | 15 | 15 | 13 |
| B | 4 | 15 | 15 | 14 |
| C | 5 | 15 | 15 | 15 |
| D | 6 | 15 | 15 | 16 |
| E | 4 | 10 | 10 | 14 |
| F | 4 | 20 | 20 | 14 |
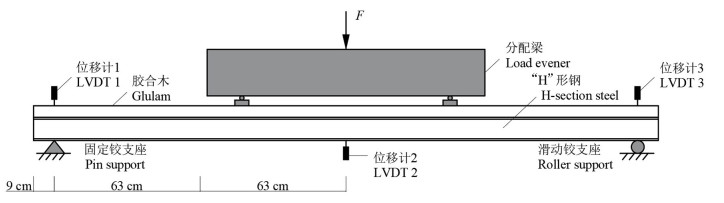
试验依据ASTM D198—15[13]进行,利用分配梁在距离试验梁中线42 cm的两个截面处施加对称荷载,两端支座处设置顶针式位移传感器,梁跨中处底部设置激光位移传感器,分别测量梁两端支座沉降及跨中挠度变化。采用微机控制电液伺服万能试验机作动器设计,最大推力300 kN,所有数据由TDS-530静态数据采集仪同步采集。以5 mm·min-1的恒定速率施加荷载,直至荷载下降至峰值荷载的90%,或试件出现明显损伤,即停止试验。图 1为用于验证有限元模型的STC梁抗弯性能试验加载装置设计图。
|
图 1 钢-木组合梁抗弯性能试验加载装置设计图 Fig. 1 Design of a loading device for the flexural performance test of steel-timber composite beams |
螺栓连接件对STC梁钢-木交界面的连接是一种柔性连接,产生组合梁的部分组合行为,其组合程度可以通过组合效率(ηef)进行量化,计算方法如下:
| $ {\eta _{{\rm{ef}}}}/\% = \frac{{{\omega _{\rm{p}}} - {\omega _0}}}{{{\omega _\infty } - {\omega _0}}} \times 100 $ | (1) |
式中:ωp表示部分剪力连接组合梁的跨中挠度(mm); ω0表示无剪力连接组合梁的跨中挠度(mm);ω∞表示完全剪力连接组合梁的跨中挠度(mm)。
2 钢-木组合梁抗弯性能数值模拟 2.1 有限元模型的建立与网格划分在有限元软件ABAQUS 2017中,建立与四点弯曲试验A~F组相对应的计算模型FE-A~FE-F。STC梁在试验中有两个对称面,若不计大变形后钢梁平面外的变形[14],则模型能够按对称模型对待。为降低计算成本,有限元模型为试验对象的1/4。“H”形钢梁使用四节点S4R壳单元进行模拟,壳沿厚度方向有5个积分点,胶合木翼板则采用八节点C3D8R缩减积分立方体单元进行模拟。
图 2为有限元模型网格划分图,钢梁和木梁的单元尺寸为10 mm;为模拟实际情况,在加载点与支座处添加钢板,加载钢板和支座钢板网格尺寸大于钢梁和木梁,为25 mm。

|
图 2 有限元模型的网格划分 Fig. 2 Mesh grid of finite element model |
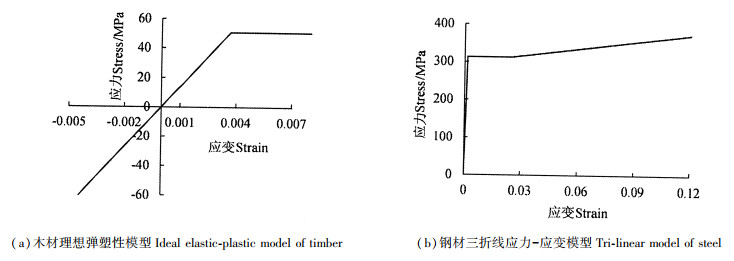
木材在顺纹受压时,具有较好的塑性变形能力,而顺纹抗拉为脆性破坏。由于受弯木构件在受压边缘纤维屈服后,构件仍能够承受荷载,故其破坏应以受拉区域边缘纤维应力达到其屈服极限为准(木梁下翼缘达到屈服强度即破坏)。试验所用的层板胶合木,胶层厚度在0.1 mm左右,大多数情况下认为,胶层对胶合木整体力学性能影响较小,可以忽略。对于胶合木翼板的受力情况,忽略了木材横向强度性能差异,其在顺纹受压作用下,表现出应变软化的特性,故在有限元模拟中,可采用理想弹塑性模型[图 3(a)]表征木材的顺纹承压屈服[15]。
|
图 3 材料的本构模型 Fig. 3 Constitutive model of materials |
钢材被视为各向同性的理想弹塑性材料,考虑到钢材屈服后的应力强化效应,有限元数值模拟中,将钢材的本构模型选为各向同性的三折线应力-应变模型[图 3(b)][16-17]。钢材采用Von Mises屈服准则,该准则规定:在一定的变形条件下,当受力物体内一点的等效应力达到某一常数时,材料则进入屈服阶段。
2.3 有限元模型接触单元的模拟有限元模型使用连接器“Connector”对钢、木螺栓连接的切向和法向力学行为进行模拟,连接器的位置与试验中螺栓的位置对应。钢-木构件交界面的垂直相互作用以硬接触模拟,切向作用简化为库仑摩擦模型,参照《机械设计手册》[18]中的常用设计参数,钢、木之间的摩擦系数设置为0.4。钢-木构件交界面的切向行为完全由STC节点推出试验[19]的荷载-滑移曲线确定,采用与四点弯曲试验相同胶合木厚度、连接件类型及间距的推出试件,模拟STC梁受弯时连接器切向(即梁长度方向)的非线性行为,考虑到螺栓预拉力会对分析结果产生影响,推出试验中螺栓与四点弯曲试验采用相同的方式,施加400 N的后张拉力;钢-木构件交界面法向弹簧主要承受法向压力,且法向变形远小于纵向和横向变形,故法向弹簧刚度可取较大值[20]或作为刚性连接[8]对待,以螺栓的轴向刚度作为法向刚度的数值。
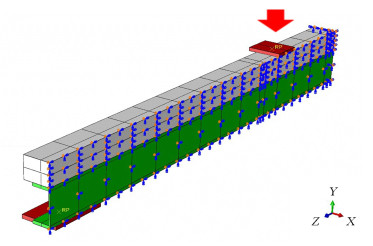
2.4 有限元模型边界条件与加载方式的确定有限元模型为对于X轴平面和Z轴平面分别对称的1/4模型,模型X轴平面的对称面上施加Y-Z轴平面的对称边界条件,Z轴平面的对称面上施加X-Y轴的对称边界条件。四点弯曲试验中,“H”形钢的下翼缘直接放置于支撑钢板上,加载板则直接放置于木梁顶面,为了准确模拟实际边界状况,加载板与支撑钢板与组合梁的接触都使用硬接触模拟法向行为,罚函数模拟切向行为。支撑板与钢梁底部的摩擦系数为0.2,加载板与木梁顶部的摩擦系数为0.4。对于支撑钢板,约束X、Y轴方向的平动释放Z轴方向的平动,约束Y、Z轴方向的转动释放X轴方向的转动;对于加载钢板,约束X轴方向的平动和Y、Z轴方向的转动,释放X轴方向的转动;位移施加于加载板上,沿Y轴方向以1 mm为步长,逐步施加至200 mm(图 4)。四点弯曲试验为静力试验,故分析时不计惯性力的影响,将求解器选为“Standard”中的“Static General”。
|
图 4 有限元模型的边界条件 Fig. 4 Boundary condition of finite element model |
四点弯曲试验中,加载初期,STC梁处于弹性工作阶段,荷载-跨中挠度关系呈线性变化;随着荷载增大,试验梁的变形开始加快,交界面开始出现滑移,剪力连接件发生变形,木梁每隔一段时间会发出木纤维断裂的脆响;随着荷载进一步增大,与前一阶段相比,荷载增加的速度开始变慢,STC梁变形明显变快,此时STC梁已经进入塑性阶段,此阶段交界面的滑移和剪力连接件的变形更加明显,木梁中木纤维断裂发出的脆响更加密集,最终STC梁发生延性破坏。试验主要出现两种典型破坏模式:破坏模式Ⅰ中试验梁由于挠度过大,两加载点附近胶合木梁底部木纤维被拉断,木材出现脆性劈裂导致试件最终破坏;破坏模式Ⅱ中试验梁出现较大的平面外变形,构件发生侧向失稳,同时加载点附近钢梁的上翼缘出现局部屈曲。随着STC梁胶合木翼缘厚度和宽度的增加,破坏模式逐渐由Ⅱ向Ⅰ转变,说明胶合木翼板可以有效限制试验梁的侧向变形以及“H”形钢局部屈曲变形,提升构件稳定性。试验过程中,所有试件剪力连接件均未发生断裂,未出现胶合木与钢梁构件上下掀起现象,两种材料协同工作能力较好。
以模型FE-D为例,在有限元结果中选取5个数据点,分别对应了STC梁在加载过程中不同的屈服状态(图 5)。A点处,挠度为20 mm荷载为64.58 kN,两加载板间钢梁的底部材料开始屈服;B点处,挠度为36 mm荷载为79.36 kN,钢梁底部的屈服发展至腹板,钢梁上翼缘首次出现了材料屈服,木梁处于弹性状态;C点处,挠度为55 mm荷载为86.32 kN,钢梁下翼缘材料的屈服向梁跨度方向发展,腹板处材料的屈服沿梁高方向发展,加载板间木梁的顶部首次出现了屈服区域;D点处,挠度为70 mm荷载为89.22 kN,钢梁上下翼缘和腹板处的屈服区域逐渐稳定,木梁顶部的屈服区域向木梁两侧和深度方向发展;E点处,挠度为82 mm荷载为90.70 kN,钢梁上下翼缘和腹板的屈服区域发展缓慢,木梁底部首次出现材料的屈服;F点处,挠度为126 mm荷载为93.20 kN(到达极限荷载),加载板间钢梁和木梁的大部分区域都进入屈服状态。从以上分析可以看出,有限元模型的受力形态与试验过程吻合较好。

|
图 5 有限元模型加载过程中屈服状态的变化 Fig. 5 Development of the yield state of the finite element model during loading |
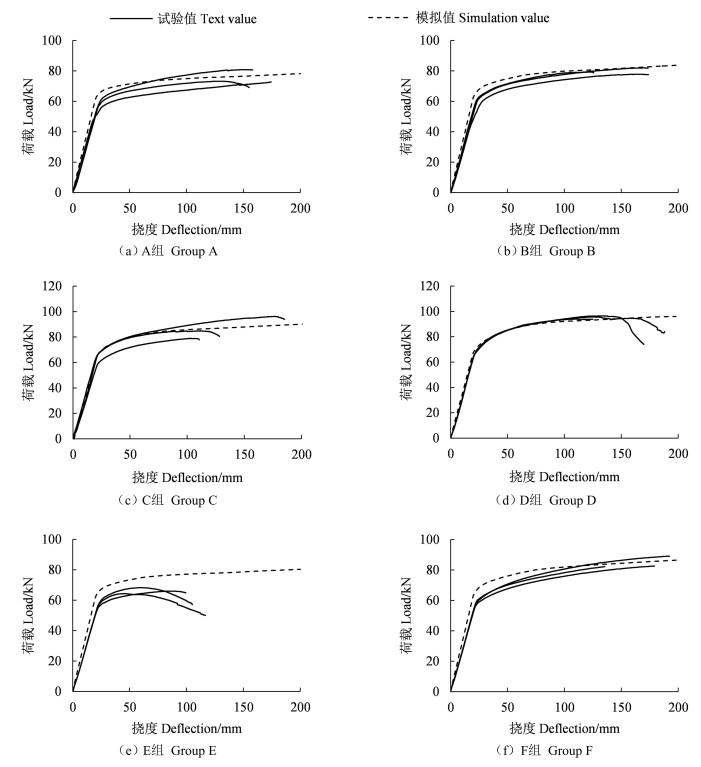
图 6为STC梁有限元模拟和四点弯曲试验荷载-挠度曲线的对比。除模型FE-E由于试验中出现了较大的平面外变形,有限元和试验曲线存在偏差[图 6(e)],其余模型与对应试验组的荷载-挠度曲线吻合较好。随着胶合木翼板厚度和宽度的增加,有限元模型和试验组之间的差异逐渐减小,至模型FE-D[图 6(d)]时,胶合木翼板厚度最大,模型与试验结果差异最小,几乎完全吻合,进一步说明了增加胶合木翼板的厚度与宽度能有效提高STC梁的侧向刚度。
|
图 6 荷载-挠度曲线试验值与有限元模拟值的对比 Fig. 6 Comparison of test and finite element values |
表 3为有限元模型FE-A~FE-F与试验荷载-挠度曲线关键点的对比,屈服荷载模拟值与试验值的最大平均误差为14.85%,屈服挠度最大平均误差为12.94%,极限荷载最大平均误差为16.79%。产生误差主要有3个原因:第一,有限元模型是理想的对称模型,无法模拟STC梁平面外的变形;第二,模型未考虑STC梁中钢梁和木材的缺陷以及加载初期加载装置和支座产生的滑移,因此,有限元的荷载-挠度曲线在加载初期普遍要高于试验曲线,且未出现曲线的初期滑移现象。加载后期,木梁和钢梁在局部进入了塑性强化阶段,有限元模型使用的木材本构模型无法准确模拟木材进入强化阶段后,材料存在的刚度损失以及各向异性下的复杂应力状态;第三,螺栓连接件在局部进入塑性强化阶段之后,其连接的非线性曲线也与推出试验得到的荷载-滑移曲线有差异,故有限元模型的计算结果在大位移情形下的延性和强度均高于试验组,但关键点误差均未超过17%(在合理范围内),证明所建立的有限元模型、选用的材料参数及接触单元模型,可以较好地模拟STC梁的抗弯性能。
| 组别 Group |
屈服荷载Yeild load/kN | 误差 Error /% |
屈服挠度Yeild deflection/mm | 误差 Error /% |
极限荷载Ultimate load/kN | 误差Error /% | |||
| 试验值Test value | 模拟值Simulation value | 试验值Test value | 模拟值Simulation value | 试验值Test value | 模拟值Simulation value | ||||
| A | 56.46 | 64.84 | 14.84 | 21.54 | 21.03 | -2.38 | 72.85 | 75.16 | 3.17 |
| B | 58.55 | 66.72 | 13.95 | 22.38 | 21.24 | -5.09 | 77.81 | 80.09 | 2.93 |
| C | 65.30 | 69.84 | 6.95 | 21.54 | 21.29 | -1.15 | 86.61 | 86.14 | -0.54 |
| D | 66.61 | 73.99 | 11.08 | 20.30 | 22.93 | 12.94 | 93.92 | 92.76 | -1.24 |
| E | 59.68 | 65.98 | 10.56 | 23.49 | 21.24 | -9.59 | 66.23 | 77.35 | 16.79 |
| F | 58.71 | 67.43 | 14.85 | 22.37 | 21.24 | -5.04 | 79.80 | 82.28 | 3.11 |
| 注:极限荷载取5倍屈服挠度所对应的荷载值,对于试验曲线,若5倍屈服挠度超过峰值荷载所对应的挠度值,则取峰值荷载为极限荷载;误差/%=[(模拟值-试验值)/试验值]×100。Note: the ultimate load denotes the load value corresponding to five times the yield deflection. For the test curves, if the five-time yield deflection exceeds the deflection value corresponding to the peak load, the peak load is used as the ultimate load. Error/%=[(Simulation value-Test value)/Test value]×100. | |||||||||
STC梁涉及两种不同材料的组合工作,受力形式较为复杂,诸多因素会对其抗弯性能造成不同程度的影响,仅仅依靠耗时长、投入高的试验研究是不够的,为了提高研究效率,需要借助其他分析手段。上述分析已经验证了STC梁有限元模型的可靠性,在此基础上,以有限元模型FE-C作为基本模型,改变STC梁中接触单元的特性,研究STC梁抗弯性能随这些参数的变化规律。
钢-木组合梁参数研究共设计4组计算模型,模型中胶合木翼板的厚度、宽度均与模型FE-C相同,宽度均为15 cm,厚度均为5 cm,其他参数见表 4。模型FE-C-150、FE-C-200和FE-SDS的连接属性均由节点推出试验确定[19],模型FE-C-150和FE-C-200的螺栓间距(沿跨度方向)分别为15和20 cm;模型FE-SDS是以钻尾自攻螺钉(self-drilling screw, SDS)作为剪力连接件的有限元模型;模型FE-C-Rigid为刚性连接有限元模型,其连接属性通过设置连接器切向和法向的属性为“Rigid”实现。
| 组别 Group |
连接件类型 Connector type |
连接件直径 Connector diameter /mm |
连接件间距 Connector spacing /mm |
| FE-C-150 | 螺栓Bolt | 6.0 | 150 |
| FE-C-200 | 螺栓Bolt | 6.0 | 200 |
| FE-SDS | 钻尾自攻螺钉SDS | 5.5 | 100 |
| FE-C-Rigid | 刚性连接Rigid connection | 100 |
STC梁中剪力连接件的分布密度和连接的力学特性会影响STC梁整体的力学行为,不同连接特性STC梁的有限元分析结果见表 5。随着连接件刚度提高,STC梁的承载性能及初始抗弯刚度随之增加,在连接件布置方式不变的情况下,STC梁的组合效率也相应提高,对STC梁进行设计时,为提高其承载性能,可考虑选择刚度较大的剪力连接件;连接件的间距与STC梁的承载性能成反比,间距越小STC梁承载性能越高,当间距为150 mm时,构件组合效率最好,连接件的布置更加经济。
| 组别 Group |
屈服荷载 Yield load /kN |
差异 Difference /% |
屈服挠度 Yield deflection /mm |
差异 Difference /% |
极限荷载 Ultimate load /kN |
差异 Difference /% |
初始割线刚度 Initial secant stiffness /(kN·mm-1) |
差异 Difference /% |
组合效率 Combination efficiency/% |
| FE-C | 69.84 | 21.29 | 86.14 | 3.25 | 33.65 | ||||
| FE-SDS | 70.60 | 1.09 | 21.19 | -0.47 | 87.25 | 1.29 | 3.37 | 3.69 | 40.97 |
| FE-C-150 | 69.61 | -0.33 | 20.88 | -1.93 | 85.12 | -1.18 | 3.29 | 1.23 | 35.48 |
| FE-C-200 | 67.69 | -3.08 | 21.34 | 0.23 | 82.81 | -3.87 | 3.14 | -3.38 | 26.33 |
| FE-C-Rigid | 78.81 | 12.84 | 18.98 | -10.85 | 91.99 | 6.79 | 4.18 | 28.62 | 90.36 |
| 注:差异/%=[(模拟值-模型FE-C模拟值)/模型FE-C模拟值]×100。Note: Difference/%=[(Simulation value-FE-C value)/FE-C value]×100. | |||||||||
采用有限元软件ABAQUS2017建立计算模型,模拟STC梁四点弯曲试验,结果表明,模拟值和试验值吻合较好,各关键点误差均在合理范围内。同时,有限元模型的受力形态、荷载-挠度曲线与试验相比,均有较好的吻合度,说明建立的有限元模型、选定的材料参数和接触单元模型能较好地模拟STC梁的抗弯性能,为进一步研究STC梁的抗弯性能提供了有限元分析方法。在验证了有限元模型准确性的基础上,对影响STC梁抗弯性能的因素进行参数研究,结果表明,剪力连接件的分布密度、连接的力学特性,能够影响STC梁整体的力学行为,今后在对STC梁进行设计时,为提高其承载性能,可考虑选择刚度较大的剪力连接件,目前钢-木构件的连接形式还较为有限,在后续研究中可以对其进行探索与尝试。此外,连接件的间距越小,STC梁的承载性越高,但在实际应用中还应当把材料利用率也作为考虑因素,使连接件的布置更加经济。
| [1] |
吴建飞, 王纬, 袁红梅, 等. 竹木复合建筑混凝土模板的工艺研究[J]. 森林与环境学报, 2020, 40(3): 329-335. |
| [2] |
郝丹, 王佳阳, 付帅, 等. 高湿环境下杨木单板层积材销槽的承压性能[J]. 森林与环境学报, 2020, 40(5): 554-560. |
| [3] |
杨文斌, 文月琴, 徐建锋. 可逆热致变色木塑复合材料的制备及性能表征[J]. 森林与环境学报, 2015, 35(3): 199-204. |
| [4] |
DAŇKOVÁ J, MEC P, ŠAFRATA J. Experimental investigation and performance of timber-concrete composite floor structure with non-metallic connection system[J]. Engineering Structures, 2019, 193: 207-218. DOI:10.1016/j.engstruct.2019.05.004 |
| [5] |
YEOH D, FRAGIACOMO M, DE FRANCESCHI M, et al. State of the art on timber-concrete composite structures:literature review[J]. Journal of Structural Engineering, 2011, 137(10): 1085-1095. DOI:10.1061/(ASCE)ST.1943-541X.0000353 |
| [6] |
NAUD N, SORELLI L, SALENIKOVICH A, et al. Fostering GLULAM-UHPFRC composite structures for multi-storey buildings[J]. Engineering Structures, 2019, 188: 406-417. DOI:10.1016/j.engstruct.2019.02.049 |
| [7] |
陈爱国, 李登辉, 方超, 等. H形钢-木组合梁受弯性能试验研究[J]. 建筑结构学报, 2016, 37(S1): 261-267. |
| [8] |
HASSANIEH A, VALIPOUR H R, BRADFORD M A. Experimental and numerical study of steel-timber composite(STC) beams[J]. Journal of Constructional Steel Research, 2016, 122: 367-378. DOI:10.1016/j.jcsr.2016.04.005 |
| [9] |
XU B H, BOUCHAÏR A, RACHER P. Mechanical behavior and modeling of dowelled steel-to-timber moment-resisting connections[J]. Journal of Structural Engineering, 2015, 141(6): 04014165. DOI:10.1061/(ASCE)ST.1943-541X.0001119 |
| [10] |
NOURI F, VALIPOUR H R, BRADFORD M A. Structural behaviour of steel-timber composite(STC) beam-to-column connections with double angle web cleats subjected to hogging bending moment[J]. Engineering Structures, 2019, 192: 1-17. DOI:10.1016/j.engstruct.2019.04.092 |
| [11] |
ASTM International.Standard test methods for small clear specimens of timber: ASTM D143-2014[S].West Conshohocken, PA, USA: ASTM International, 2014.
|
| [12] |
ASTM International.Standard test methods and definitions for mechanical testing of steel products: ASTM A370-16[S].West Conshohocken, PA, USA: ASTM International, 2016.
|
| [13] |
ASTM International.Standard test methods of static tests of lumber in structural sizes: ASTM D198-15[S].West Conshohocken, PA, USA: ASTM International, 2015.
|
| [14] |
CHYBIÑSKI M, POLUS L. Theoretical, experimental and numerical study of aluminium-timber composite beams with screwed connections[J]. Construction and Building Materials, 2019, 226: 317-330. DOI:10.1016/j.conbuildmat.2019.07.101 |
| [15] |
CHEN Y X.Flexural analysis and design of timber strengthened with high strength composites[D].New Brunswick: Rutgers the State University of New Jersey, 2003.
|
| [16] |
何朝红.胶合木-钢夹板螺栓连接力学性能试验研究[D].长沙: 中南林业科技大学, 2017.
|
| [17] |
董宇光.型钢与混凝土粘结-滑移关系及型钢混凝土剪力墙抗震性能研究[D].上海: 同济大学, 2006.
|
| [18] |
闻邦椿. 机械设计手册[M]. 5版. 北京: 机械工业出版社, 2010: 25.
|
| [19] |
YANG R Y, LI H T, LORENZO R, et al. Mechanical behaviour of steel timber composite shear connections[J]. Construction and Building Materials, 2020, 258: 119605. DOI:10.1016/j.conbuildmat.2020.119605 |
| [20] |
李登辉.钢-木组合梁抗弯性能研究[D].北京: 北京交通大学, 2016.
|

 2021, Vol. 41
2021, Vol. 41


