文章信息
- 冯辉荣, 周成军, 周新年, LIMCheewah, 陈立群
- FENG Huirong, ZHOU Chengjun, ZHOU Xinnian, LIM Cheewah, CHEN Liqun
- 重刚比对悬索静态位形影响的建模与分析
- Modeling and analysis of the static configuration of cableway suspension by the ratio of cable weight to stiffness
- 森林与环境学报,2017, 37(3): 302-308.
- Journal of Forest and Environment,2017, 37(3): 302-308.
- http://dx.doi.org/10.13324/j.cnki.jfcf.2017.03.009
-
文章历史
- 收稿日期: 2017-02-11
- 修回日期: 2017-05-17
2. 福建农林大学交通与土木工程学院, 福建 福州 350002;
3. 香港城市大学土木与建筑工程系, 香港 999077;
4. 上海大学力学系, 上海 200444
2. College of Transportation and Civil Engineering, Fujian Agriculture and Forestry University, Fuzhou, Fujian 350002, China;
3. Department of Architecture and Civil Engineering, City University of Hongkong, Hongkong 999077, China;
4. Department of Mechanics, Shanghai University, Shanghai 200444, China
工程索道从静态分析与设计逐步向动力学研究深入,不论是在静态分析还是动态研究过程中,悬索静态位形均是悬索设计计算的重要基础[1-4]。17世纪,伽俐略第一个研究了不可伸长索或链的“悬链曲线”,1794年FUSS提出了在悬索桥设计中的“抛物线”,直到1862年“抛物线”理论才形成体系[1]。目前,工程索道的主要设计理论是悬链线、摄动法、悬索曲线及抛物线四大理论,其中抛物线理论因为计算简便,在林业架空索道中得到了长期的实际应用[2]。在考察悬索的静态位形时,悬链线理论把悬索自重的影响考虑为一个无穷级数,是最精确的,而摄动法则是在悬链线理论基础上取级数的有限项截断,悬索曲线则是取级数前两项的改造计算,而抛物线理论只是取第一项进行改造后的近似计算,大大简化了计算过程。在抛物线理论中,悬索的自重折合到水平位移上是一个常数,简化了悬索自重对静态位形的影响,不考虑悬索刚度对静态位形的影响。在很长的时期内,悬索无荷自由振动及各类动力学的研究中,学者常以不考虑刚度的静态平衡位形为平衡的参考位形[2-5]。此外,在绘制悬索侧型简图及传统设计中,影响悬索静态位形的主要描述参数是悬索自重、中央挠度系数、跨距与张力等,基本上不考虑悬索的刚度[5-8]。这些不考虑刚度的模型虽然能在工程中满足基本静态设计要求,但是在动力学研究中也逐步显示出不足,尤其对于大挠度、小刚度的悬索动力学的研究会产生较大误差,需要更加精确的静态参考位形。值得借鉴的是,SHIH et al[6]在研究悬索自由振动时,为考虑静态平衡位形,引入了张力与自重的比值和悬索自重与抗拉压刚度的比值,并进行了考虑弹性伸长的无荷悬索的静态位形分析,其研究结果表明,当悬索的重刚比小到一定范围时,其静态位形可以看成不可伸长索的性能来处理。但是该文献尚未研究有分布荷载及自重同时作用下悬索的静态位形,只是为其后期的振动研究找出无荷平衡位形是否考虑弹性伸长的范围进行了界定,尚未考虑有集中力作用或分布荷载作用下,静态平衡位形的不确定性。例如,悬索在移动荷载作用下的静态位形是随荷载位置的不同发生变化的,这就要求在动力学建模中不能轻易消除自重项[3]。FENG et al[3]尝试同时考虑刚度与自重作用的欧拉梁的模型来综合考虑悬索的弯曲刚度及表面接触模型等性质对跑车与悬索的耦合振动建模,为后期综合考虑刚度的退化动力学模型提供了基础。鉴此,为了更好地考虑悬索自重与刚度的综合影响,并有效引入移动荷载,在文献[6]的基础上考虑了分布载荷与自重的共同作用下,悬索自然未变形状态、自重拉伸状态、分布荷载与自重共同作用下的悬索自身刚度及几何、物理与材料参数特性的关系,并为研究不等高支座悬索及不同材料特性的悬索的动力学性能提供静态参考位形基础,亦可为林业索道在冬季出现的悬索全线履冰现象、悬索在分布风荷载作用下、海底缆索在流体冲击力作用下的动力学建模、增加中间支架的多跨动力学、振动与噪声及钢索的无损检测等探索可行的平衡位形参考[9-14]。为了研究的对称性与简便性,建立了支座水平等高索道的相关静力学模型,但不乏钢索静态位形受自重与刚度影响的一般性,并在传统假设基础上对悬索研究条件作了更切实际的修正。
1 悬索基本静态位形分析 1.1 静力学模型基本假设(1) 假设悬索支座两端固定,悬索在垂直平面内的任一部分的运动相比于悬索长度非常小。(2) 由于受力是沿悬索长度的张力,假设其应力应变遵循虎克定律。(3) 对悬索静态性能的分析时将所有的摩擦力、空气阻力和支座的窜动位移忽略不计。(4) 在悬索建模和静态位形分析时,考虑悬索自重和悬索刚度的影响。(5) 悬索平均直径相对于其长度非常小,在索长参与计算中可忽略不计。
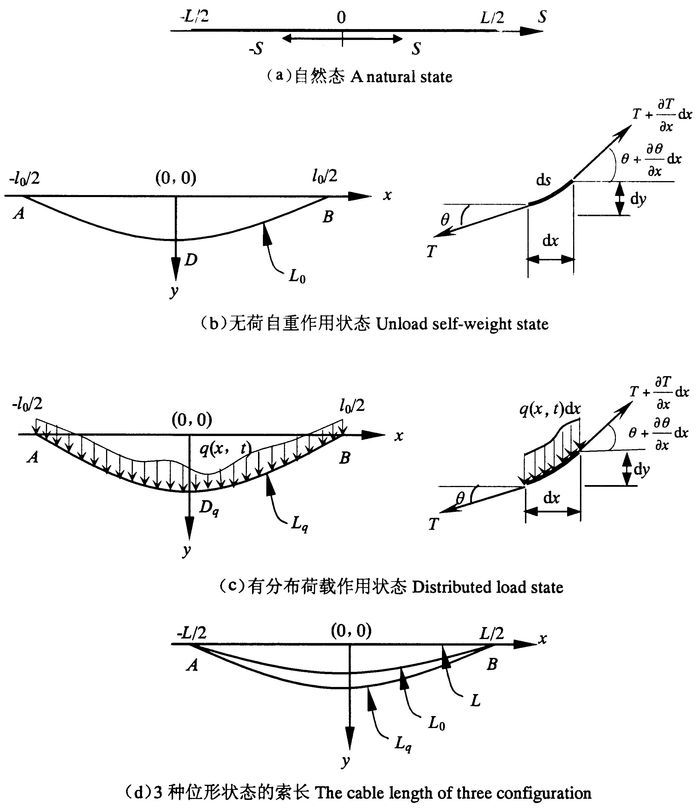
1.2 悬索基本静态位形分类图 1建立了坐标系OS和Oxy,两坐标系具有同一水平轴和零点。现将悬索分为未变形长(L)、自重拉伸长(L0)和载荷拉伸长(Lq)3种状态,如图 1(a)、(b)和(c)所示,并绘在图 1(d)中,由于自重和载荷作用,其索长将发生变化。
|
图 1 弹性悬索的3种位形状态 Fig. 1 Three configuration of elastic cable |
在图 1(a)坐标系OS中,-L/2≤S≤L/2代表悬索自然态的跨距范围。在图 1(b)坐标系Oxy中,代表在索的均匀自重作用下的施工态;图 1(c)表示索在自重作用或施工态的基础上,在索上各点位置加上任意分布荷载q(x, t),用x(s, t),y(s, t)和S表示坐标关系。
1.3 分布力与重刚比影响下的静态位形建模考虑悬索的弹性应变e,可以由弹性变形公式(1) 给出[6]
| $e={{\left[ {{\left( \frac{\partial x}{\partial S} \right)}^{2}}+{{\left( \frac{\partial y}{\partial S} \right)}^{2}} \right]}^{1/2}}-1$ | (1) |
根据虎克定律,“真实”的轴向力T,可由公式(2) 确定
| $T=EeA=Ee\frac{{{A}_{0}}}{1+e}$ | (2) |
式中:A0为变形前索的截面积(mm2);E为弹性模量(MPa);其中A是索在载荷作用下变形后的截面积(mm2)。
图 1(c)表明,悬索受到的任意分布的荷载力q(x, t)。
在变形状态下的悬索长度可以由公式(3) 给出
| ${{L}_{0}}=2\int _{0}^{\frac{{{l}_{0}}}{2}}\sqrt{{{\left( \frac{\partial x}{\partial S} \right)}^{2}}+{{\left( \frac{\partial y}{\partial S} \right)}^{2}}}\text{d}s$ | (3) |
此外,跨中挠度f0,单位长度的索力和几何关系可从图 2(a)中截取微元段,并以图 2(b)和图 2(c)表示。

|
图 2 在自重作用下弹性伸长索的位形 Fig. 2 The configuration of elastic extensible cable with self-weight |
x0(S),y0(S)和T0(S)表示静态参量,可以通过公式(1) 和公式(2) 得出,从公式(2) 中可以得到
| ${{T}_{0}}=\frac{{{T}_{0}}\left( 0 \right)}{\text{cos}\theta }=\frac{{{H}_{0}}\left( 1+e \right)}{x_{0}^{\prime }}={{\left\{ H_{0}^{2}+{{[\rho g+q\left( x,t \right)]}^{2}}{{s}^{2}} \right\}}^{1/2}}$ | (4) |
| $x_{0}^{\prime }=\left( 1+e \right)\text{cos}\theta =\frac{{{H}_{0}}}{{{T}_{0}}}{{(1-\frac{{{T}_{0}}}{E{{A}_{0}}})}^{-1}}$ | (5) |
| $y_{0}^{\prime }=\left( 1+e \right)\text{sin}\theta =\frac{\rho gs+q\left( x,t \right)s}{{{T}_{0}}}{{(1-\frac{{{T}_{0}}}{E{{A}_{0}}})}^{-1}}$ | (6) |
引入无量纲参数,
因此,方程组可以改写为公式(7)~(9)。
| ${{T}_{0}}=\rho gL{{\left\{ {{\alpha }^{2}}+{{[1+\bar{q}\left( x,t \right)]}^{2}}{{\xi }^{2}} \right\}}^{1/2}}$ | (7) |
| $x_{0}^{\prime }=\alpha {{\left\{ {{\alpha }^{2}}+{{[1+\bar{q}\left( x,t \right)]}^{2}}{{\xi }^{2}} \right\}}^{-1/2}}\langle 1-\beta {{\left\{ {{\alpha }^{2}}+{{[1+\bar{q}\left( x,t \right)]}^{2}}{{\xi }^{2}} \right\}}^{1/2}}{{\rangle }^{-1}}$ | (8) |
| $y_{0}^{\prime }=-[1+\bar{q}\left( x,\text{ }t \right)]\xi {{\left\{ {{\alpha }^{2}}+{{[1+\bar{q}\left( x,\text{ }t \right)]}^{2}}{{\xi }^{2}} \right\}}^{-1/2}}\langle 1-\beta {{\left\{ {{\alpha }^{2}}+{{[1+\bar{q}\left( x,t \right)]}^{2}}{{\xi }^{2}} \right\}}^{1/2}}{{\rangle }^{-1}}$ | (9) |
从ξ=-0.5~0.5并利用边界条件y=(y)ξ=±0.5=0积分方程式,可以得到图 3。图 3表示了不同的重刚比下,悬索挠度y随着ξ=s/L的变化关系。重刚比β越大,悬索挠度y也相应增大。当重刚比β=10-2~10-8时,也就是重刚比很小,相对刚度而言,悬索的自重很小时,可伸长的弹性悬索的静态位形基本是重合的,也就是接近于不可伸长的悬索状态[6]。当β≤ 10-2时,此时在106倍率的量级内的无量纲悬索最大挠度y=0.06是基本相同的。并且从两支座向跨中逐渐增大,说明此时悬索重量对悬索的静态位形基本没有影响。但是,当重刚比β≥10-1时,如β=0.10, 0.25, 0.30时,重刚比增加2.5,3.0和1.2倍时,无量纲悬索最大挠度y=0.067, 0.130, 0.158,相应的增幅为1.94,2.36与1.22倍,增幅明显。说明此时悬索的静态位形受悬索的重刚比影响明显。

|
图 3 悬索挠度y随ξ的变化关系 Fig. 3 The relationship of deflection yand ξ |
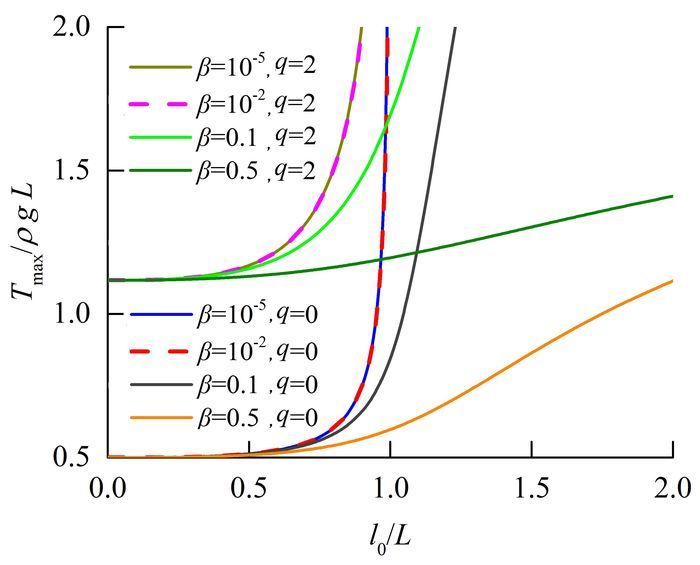
通过公式(7)~(9),可以得到图 4~图 6,分别表示水平等高支座悬索的最大拉力、水平拉力与中央挠度随跨距l0/L的变化关系。
|
图 4 不同重刚比下悬索单元最大拉力与水平支座间距的关系 Fig. 4 Relationship between Tmax/ρgL and l0/L of cable with different ratio of weight to stiffness |

|
图 5 不同重刚比下悬索水平拉力与水平支座间距的关系 Fig. 5 Relationship between H0 /ρgL and l0/L of cable with different ratio of weight to stiffness |
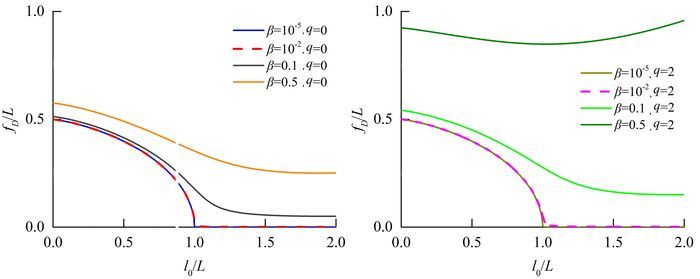
|
图 6 不同重刚比下悬索中央挠度与水平支座间距的关系 Fig. 6 Relationship between fD/L and l0/L of cable with different ratio of weight to stiffness |
图 4描述了悬索最大张力随跨距l0/L的变化关系,随着跨距从0向L增加时,最大张力随着增大,可以看出重刚比越大时,最大张力增加得越慢;反之,重刚比越小,也就是刚度越大时,最大张力随跨距增大越快,刚度越大也就是EA0越大,钢索的抗拉刚度越大,虽然β=10-2与β=10-5的重刚比相差103倍,但其最大拉力曲线在图 4中是完全重合的,说明钢索的刚度性能越接近于不可伸长悬索的特性。考虑钢索自重与均布荷载同时作用(3条不同颜色的实线与1条虚线表示)、考虑自重但不考均布荷载作用(3条不同颜色的实线与1条虚线表示)时,最大张力会相差一个与均布荷载有关的初值,尤其是均布荷载增加了最大张力的初值,将对悬索产生预应力。另外,重刚比β≤10-2时的2条最大拉力曲线是重合的,图 4中用不同色的虚、实线表示。
图 5描述了水平张力随跨距l0/L的变化关系,随着跨距增加,水平张力也随着增大,重刚比越小,也即刚度越大时,水平张力增大越快,当重刚比β≤10-2的较大范围内,也就是自重小刚度大的钢索的水平张力曲线在重刚比小到一定范围时,张力曲线也基本重合,另外,重刚比β≤ 10-2时的2条水平拉力曲线是重合的,图 5中用不同色的虚、实线表示。
图 6表示在变形前索长相同的前提下,不考虑均布载荷[图 6 (a)]与考虑均布载荷[图 6 (b)]的2种情况下,随着跨距增大,悬索的中央挠度相应减小。对于重刚比β≤10-2时,当跨距接近原长时,中央挠度明显减小,接近于零。对于自重大,刚度小的悬索,其中央挠度越大,悬索的中央挠度与重刚比呈递增关系,考虑自重与均布荷载的悬索中央挠度比不考虑均布荷载时大;当跨距达到一定值时,也就是超过变形前的索长一定值时,中央挠度曲线开始趋向一个较大取值范围内的水平线,这也说明悬索不断伸长,不断施以张拉力的情况下,也难以改变中央挠度的大小,所以在设计中应控制张力的大小,不应通过盲目张紧来改变中央挠度的大小。另外,图 6(a)中重刚比β≤10-2时的2条曲线是基本重合的,同样可以看出图 6(b)中β≤10-2时的2条中央挠度曲线也是重合的。说明重刚比小到一定程度时,悬索的中央挠度曲线接近于不可伸长悬索的曲线特性,也就是刚度大到一定程度时,中央挠度曲线受均布荷载作用的影响可以忽略。因此,在工程中,若在一定的重刚比的情况下,张力的大小主要取决于安全系数,林业索道的安全系数应控制在2.5以上,过大不经济,过小则不安全;对于合理的跨度设计要结合中央挠度系数综合考虑,目前工程上主要推荐无荷中挠系数为0.03~0.05之间,防止过于张紧悬索。
3 小重刚比悬索静态参数测定与结果分析为了验证重刚比小到一定程度时,悬索的静态位形可以看成不可伸长索的静态位形来处理。现对3种不同直径的钢丝绳进行实验测定,并与理论值进行对照(表 1)。
| 型号与直径 Type and diameter |
l0/m | l0/L | β(×10-6) | fD/m | 理论对照 Theoretical checks fD/m |
相对误差 Relative error /% |
H0/N | 理论对照 Theoretical checks H0/N |
相对误差 Relative error /% |
Tm/N | 理论对照 Theoretical hecks Tm/N |
相对误差 Relative error /% |
| 6×7-2 | 0.000 | 0.00 | 1.91 | 1.902 | 2.000 | 4.90 | 0.000 | 0.000 | 0.00 | 0.301 | 0.290 | 3.79 |
| 0.800 | 0.20 | 1.91 | 1.846 | 1.891 | 2.38 | 0.064 | 0.061 | 4.92 | 0.304 | 0.290 | 4.83 | |
| 1.610 | 0.40 | 1.91 | 1.683 | 1.711 | 1.64 | 0.132 | 0.127 | 3.94 | 0.306 | 0.294 | 4.08 | |
| 2.410 | 0.60 | 1.91 | 1.431 | 1.445 | 0.97 | 0.201 | 0.197 | 2.03 | 0.312 | 0.305 | 2.30 | |
| 3.200 | 0.80 | 1.91 | 1.057 | 1.062 | 0.47 | 0.301 | 0.292 | 3.08 | 0.361 | 0.350 | 3.14 | |
| 3.644 | 0.91 | 1.91 | 0.771 | 0.782 | 1.41 | 0.436 | 0.420 | 3.81 | 0.473 | 0.456 | 3.73 | |
| 4.000 | 1.00 | 1.91 | 0.032 | 0.031 | 3.23 | 9.551 | 9.334 | 2.32 | 9.552 | 9.336 | 2.31 | |
| 4.010 | 1.002 5 | 1.91 | 0.024 | 0.023 | 4.35 | 241.059 | 231.073 | 4.32 | 241.077 | 231.091 | 4.32 | |
| 6×7-3 | 0.000 | 0.00 | 4.18 | 1.902 | 2.000 | 4.90 | 0.000 | 0.000 | 0.00 | 0.642 | 0.636 | 0.94 |
| 0.800 | 0.20 | 4.18 | 1.846 | 1.891 | 2.38 | 0.138 | 0.135 | 2.22 | 0.651 | 0.637 | 2.20 | |
| 1.610 | 0.40 | 4.18 | 1.683 | 1.711 | 1.64 | 0.283 | 0.278 | 1.80 | 0.657 | 0.644 | 2.02 | |
| 2.410 | 0.60 | 4.18 | 1.431 | 1.445 | 0.97 | 0.441 | 0.431 | 2.32 | 0.685 | 0.670 | 2.24 | |
| 3.200 | 0.80 | 4.18 | 1.057 | 1.062 | 0.47 | 0.650 | 0.641 | 1.40 | 0.779 | 0.768 | 1.43 | |
| 3.600 | 0.91 | 4.18 | 0.771 | 0.782 | 1.41 | 0.930 | 0.920 | 1.09 | 1.012 | 1.001 | 1.10 | |
| 4.000 | 1.00 | 4.18 | 0.032 | 0.031 | 3.23 | 21.162 | 20.472 | 3.37 | 21.165 | 20.474 | 3.38 | |
| 4.010 | 1.002 5 | 4.18 | 0.023 | 0.022 | 4.55 | 519.757 | 506.772 | 2.56 | 519.792 | 506.806 | 2.56 | |
| 6×7-5 | 0.000 | 0.00 | 3.47 | 1.901 | 2.000 | 4.95 | 0.000 | 0.000 | 0.00 | 1.212 | 1.188 | 2.02 |
| 0.800 | 0.20 | 3.47 | 1.850 | 1.891 | 2.17 | 0.256 | 0.251 | 1.99 | 1.212 | 1.190 | 1.85 | |
| 1.610 | 0.40 | 3.47 | 1.635 | 1.711 | 4.44 | 0.553 | 0.531 | 4.14 | 1.251 | 1.202 | 4.08 | |
| 2.410 | 0.60 | 3.47 | 1.428 | 1.445 | 1.18 | 0.812 | 0.807 | 0.62 | 1.259 | 1.251 | 0.64 | |
| 3.200 | 0.80 | 3.47 | 1.028 | 1.062 | 3.20 | 1.220 | 1.207 | 1.08 | 1.450 | 1.434 | 1.12 | |
| 3.600 | 0.90 | 3.47 | 0.698 | 0.717 | 2.65 | 1.790 | 1.743 | 2.70 | 1.920 | 1.870 | 2.67 | |
| 4.000 | 1.00 | 3.47 | 0.033 | 0.032 | 3.13 | 40.120 | 38.239 | 4.92 | 40.126 | 38.244 | 4.92 | |
| 4.005 | 1.001 3 | 3.47 | 0.024 | 0.023 | 4.26 | 989.162 | 946.605 | 4.50 | 989.236 | 946.676 | 4.50 | |
| 1)此表为提高小挠度时的计算精度,不以小数点后的位数一致,而以小数点后的有效数字一致。Note: to improve the deflection caculation accuracy in the table, number after radix pointis calculate dusing significance digit. | ||||||||||||
表 1所测钢丝绳的公称直径分别为2、3、5 mm,为合成纤维芯6×7钢丝绳,实验自然标记长度L为4 m,自重分别为0.580、1.272、2.376 N,弹性模量E均为8.5×104 MPa,因考虑纤维芯的影响,钢丝绳的总断面积参照GB/T 20118—2006[15], 分别取2.35、3.58与8.06 mm2。实验采用定自然索长的挂重法,通过两端挂重进行加载,实验中调节两端挂重量来保证其有效测定长度在两水平支座之间,注意在测定l0/L接近1.0或超过1.0时的悬索中央挠度时,应使用游标卡尺进行高精度测定,并注意悬索要保持完全静止状态。根据图 4~图 6测得不同跨间距所对应的悬索的中央挠度、水平拉力与最大拉力参数列于表 1,并与理论值进行对照。由表 1可知,当l0/L的值在0.8以内时索的水平张力与最大张力均比较小,当l0/L的值接近1.0或超过1.0时,也就是索长接近自然长度时,索的水平张力和最大张力均急剧增大,索的中央挠度则急剧变小,与图 4~图 6的结果相吻合。如,6×7-2的钢丝绳中央挠度从1.057 m急剧变小为0.031 8 m,索的水平张力与最大张力分别从0.436和0.473 N急剧增大到9.551和9.552 N,分别增大了21.9和20.2倍。当l0/L接近1.0以后的悬索中央挠度变化不明显,但随着索的张紧,水平张力和最大张力拉力均急剧增大。表 1中的实验数据与理论数据的相对误差均在4.95%以内。说明了实验值与图 4~图 6的结果相吻合,也说明了理论模型的正确性与可行性,并达到了工程应用相对误差不超过5%的精度。
4 讨论与结论重刚比β≤10-2时,悬索的静态位形的结果与不可伸长索的静态位形一致,悬索的静态位形相关曲线基本重合。若将自重忽略不计,悬索的刚度对静态位形起主导作用,与不考虑悬索自重的研究结果相吻合[6]。重刚比β≥10-1时,悬索的自重与分布载荷对静态位形起主导作用,悬索的中央挠度与自重及分布载荷呈递增关系,此时张紧悬索对中央挠度的影响不明显。因此,设计中控制悬索中央挠度不能盲目通过张紧悬索来实现,应该防止悬索张得过紧,张力过大,影响安全性能。另外,建模研究中引入分布荷载可以模拟工程实际中的荷载作用,并为后期通过狄拉克函数引入移动集中荷载进行相关动力学建模提供基础。重刚比是影响悬索静态位形的重要参数,不宜把悬索自重与刚度孤立考虑。实验结果与理论对照具有较好的一致性,说明了力学模型的正确性与可行性。今后还应加强用重刚比参数来综合优化选择钢索、尼龙索、麻索与复合材料索等新材质悬索的静态位形的比较实验测定,同时考虑工程实际应用案例、仿真及其振动与噪声测定[10-12],钢索工作张力及无损检测等实验研究[13-14],为悬索设计探索相关特性。
| [1] | 周新年. 架空索道理论与实践[M]. 北京: 中国林业出版社, 1996: 10-36. |
| [2] | 周新年. 工程索道与悬索桥[M]. 北京: 人民交通出版社, 2013: 18-33. |
| [3] | FENG H R, CHEN L Q, YUAN T C, et al. Modeling and analysis of coupled vibration of a carriage and skyline[J]. Journal of Vibration Engineering & Technologies, 2015, 3(6): 779–792. |
| [4] | 冯辉荣, 周成军, 周新年. 埃特金加速迭代法及其在单跨悬索状态方程中的应用[J]. 福建农林大学学报(自然科学版), 2013, 42(3): 333–336. |
| [5] | 冯辉荣, 周成军, 周新年, 等. 单跨架空索道货物脱钩跳跃弦振动响应分析[J]. 力学与实践, 2014, 36(2): 190–194, 189. DOI:10.6052/1000-0879-13-349 |
| [6] | SHIH B, TADJBAKHSH I G. Small-amplitude vibrations of extensible cables[J]. Journal of Engineering Mechanics, 1984, 110(4): 569–576. DOI:10.1061/(ASCE)0733-9399(1984)110:4(569) |
| [7] | 王小桃, 周新年, 冯辉荣, 等. 基于VB 6.0的悬链线理论单跨索道侧型图设计[J]. 福建农林大学学报(自然科学版), 2012, 41(2): 149–152. |
| [8] | 周新年, 赖阿红, 周成军, 等. 山地森林生态采运研究进展[J]. 森林与环境学报, 2015, 35(2): 185–192. |
| [9] | 周成军, 巫志龙, 周新年, 等. 多跨索道的可移动中间支架设计[J]. 森林与环境学报, 2016, 36(1): 104–110. |
| [10] | 卢秀琳, 周成军, 周新年, 等. 集材绞盘机噪声及其对环境的影响[J]. 森林与环境学报, 2015, 35(3): 225–229. |
| [11] | 冯辉荣, 周新年, 李闽晖, 等. 轻型索道集材与开路集材三大效益对比分析[J]. 林业科学, 2012, 48(8): 129–134. DOI:10.11707/j.1001-7488.20120821 |
| [12] | FENG H R, LIM C W, CHEN L Q, et al. Sustainable deforestation evaluation model and system dynamics analysis[J]. The Scientific World Journal, 2014, 2014: 106209. |
| [13] | SPINELLI R, MARCHI E, VISSER R, et al. Skyline tension, shock loading, payload and performance for a European cable yarder using two different carriage types[J]. European Journal of Forest Research, 2017, 136(1): 161–170. DOI:10.1007/s10342-016-1016-1 |
| [14] | PETERKA P, KRESAK J, SIMONAK J, et al. Tractive work of the aerial cableway towing haul rope[J]. Measurement, 2017, 100: 322–328. DOI:10.1016/j.measurement.2017.01.006 |
| [15] | 中国钢铁工业协会. 一般用途钢丝绳: GB/T 20118—2006[S]. 北京: 中国标准出版社, 2016: 1-18. |

 2017, Vol. 37
2017, Vol. 37


