2. 浙江海洋大学 水产学院, 浙江 舟山 316022
光诱捕捞是利用鱼类的趋光特性,将鱼类诱集至渔船周围进行捕捞的作业方式,具有操作简单、效率高等特点,广泛应用于我国近海及远洋捕捞[1]。常见的光诱渔业有灯光围网、光诱鱿钓、灯光罩网、光诱敷网等[2-5]。集鱼灯是光诱渔业的重要装备[6],起到诱鱼与集鱼的作用,且集鱼灯的自身特性和渔船灯光配置直接影响渔船周围照度分布,进而影响鱼类诱集效果与捕捞产量。目前,对于鱼类趋光特性、海洋光学性质、渔船集鱼灯配置等已有较多的研究,但对于集鱼灯照度分布理论模型的研究较少。日本学者[7-8]分别使用点光源和线光源模型对光诱渔船海面照度分布进行计算;郑国富[9]使用经验计算方法对光诱鱿鱼浮拖网周围光场分布进行计算;钱卫国等[10]提出叠加法,并对集鱼灯海面照度分布及鱿钓渔船的集鱼灯合理配置进行研究,以往的模型均将衰减系数设置为常数,并未考虑环境因子对不同波段光吸收与散射的影响。而且,渔船在不同海域作业时的海况及海水光学性质不同,其作业海域的大气与整个海水水体的衰减系数也存在显著差异。官文江等[11]建立了集鱼灯的水下照度分布模型,虽考虑了海水水体的散射与吸收,计算船底阴影部分的照度分布及不同水层照度分布,但未考虑灯光在大气中衰减的影响。
蒙特卡洛方法利用随机数和概率统计研究光子与介质相互作用关系,是解决辐射传输问题的经典方法之一[12-14],广泛应用于光学辐射传输计算[15]。海洋大气的光学特性主要由海洋性气溶胶决定[16]。海洋性气溶胶粒子的密度和粒子谱受到风速和相对湿度的影响,通过经验公式计算粒子半径谱、复折射指数与气溶胶粒子数密度,采用米氏散射理论计算大气吸收、散射系数和不对称因子,可得到蒙特卡洛方法所需的基本参数。本文尝试将集鱼灯灯光看作是很多光子,根据光子与大气介质中气溶胶粒子随机碰撞的统计结果,采用蒙特卡洛方法建立海面照度模型,旨在为集鱼灯照度计算模型的优化提供一种新的方法。
1 材料与方法 1.1 渔船集鱼灯布置参数“浙岱渔13461”渔船船长为46.0 m,船宽为6.6 m,甲板离水面高1.0 m;渔船左右两侧集鱼灯对称布置,同侧集鱼灯根据与船首、船尾的距离分为两列,同侧两列灯首尾相距为2.5 m,灯离水面高6.2 m,左右两侧集鱼灯间距6.5 m;靠近船首部位一列灯灯带长为14.4 m,共25盏灯;靠近船尾部位一列灯灯带长为21.0 m,共35盏灯;左侧60盏均为2 kW白光直筒型集鱼灯,假设各个灯发光性能一致,单个集鱼灯光通量为220 000 lx,其灯各个垂直方向的发光强度计算公式[17]为
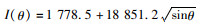 (1)
(1)
(1) 式中:θ为集鱼灯发光天底角,rad;I(θ)为角度为θ时的发光强度,cd。
1.2 相关数据采集数据于2019年4月26日采集,风速数据来源于NOAA网站(https://oceanwatch.pifsc.noaa.gov)遥感数据,海域范围为27°N~28°N、123°E~124°E,空间分辨率为0.5°×0.5°,时间分辨率为周;光谱分布由上海海洋大学国家远洋渔业工程技术研究中心集鱼灯实验室使用HASS-2000积分球测得(图 1),测量范围为380~780 nm,步长5 nm;湿度计为DT-321S型(深圳市华盛昌科技实业股份有限公司),量程为0~100%,精度0.1%;海面照度使用水下照度计测量,测量位置为离渔船右舷2 m处的海面(-0 m水层)照度,照度测量间隔2 m,每个位点测量3次,取其平均值,实验所用的照度计为ZDS-10W-2D型(上海嘉定学联仪表厂),量程为0~2×104 lx,精度为0.1 lx。

|
图 1 2 kW金属卤化物集鱼灯光谱分布图 Fig. 1 Spectrum distribution of 2 kW metal halide fishing lamp |
已有大量的实验和理论研究[18-22]证明,对数正态分布能够较好地描述气溶胶的粒子尺度分布。本文采用对数正态分布对海洋性大气粒子的尺度分布进行描述,计算公式为
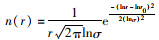 (2)
(2)
式中:r为气溶胶粒子半径,μm;n(r)为半径为r处单位间隔内的气溶胶相对粒子数;r0、σ为平均模态半径及其均方差,分别取0.3 μm、0.51[18]。
1.3.2 复折射指数海洋性气溶胶复折射指数由干气溶胶海盐粒子和凝结在干气溶胶粒子上的液态水所组成的气溶胶共同决定。随着相对湿度的变化,气溶胶的复折射指数也随之变化,HÄNEL[23]通过大量实验和理论计算总结出了相对湿度和复折射指数的关系,公式为
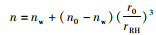 (3)
(3)
式中:r0和rRH分别是干、湿气溶胶粒子半径,μm;n0和nw分别是干、湿气溶胶粒子复折射指数,干海盐与液态水复折射率由HITRAN 2008数据集提供。干、湿气溶胶粒子半径比值的经验公式[24]为
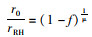 (4)
(4)
式中:μ为常数,对于海洋性大气气溶胶粒子取3.9[24];f为相对湿度。
1.3.3 气溶胶粒子密度研究[23]表明,近地层面的大气分子对消光系数的贡献可以忽略,因此大气消光系数即等于气溶胶消光系数。海洋性气溶胶一般与风浪破碎有关[24-25]。在海上,气溶胶密度主要依赖风速引起的风浪破碎与气体之间交换,海上气溶胶质量密度经验公式[21]为
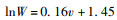 (5)
(5)
式中:W为气溶胶质量密度,μg/m3;v为风速,m/s。
气溶胶粒子密度参考杨玉峰等[26]通过质量密度换算方法,单位体积气溶胶粒子数计算公式为
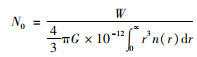 (6)
(6)
式中:N0为单位体积气溶胶粒子数,1/m3;G为海盐密度,g/m3。
1.3.4 气溶胶粒子群米氏散射大气中吸收和散射是单位体积内不同尺寸多个粒子集体贡献的结果,假设气溶胶粒子为球形气溶胶粒子,对具有一定尺寸分布的球形气溶胶粒子的消光、散射和吸收系数计算公式[17]为
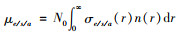 (7)
(7)
式中:μe、μs、μa分别为气溶胶粒子群的消光、散射和吸收系数,1/m;σe(r)、σs(r)、σa(r)分别为粒子半径为r时单粒子的消光、散射、吸收效率因子,具体计算方法见文献[27]。
粒子不对称因子表示光子前后散射的程度,粒子的等效不对称因子计算方法[28]为
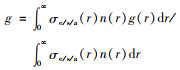 (8)
(8)
式中:g为等效不对称因子;g(r)表示粒子半径在r时的不对称因子,可通过米氏散射理论得出[27]。
1.4 照度模型建立 1.4.1 基本思路蒙特卡洛方法是根据概率分布函数模拟辐射在随机介质中的传输过程,将光看作是由许多光子组成的辐射,描述光子在大气介质中发生散射或吸收的随机过程。根据集鱼灯光子初始发射角度概率分布函数、渔船集鱼灯坐标系及光子比例计算公式,按照一定方向、坐标位置和比例发出光子,光子在大气介质中依据自由程的累积概率函数传播一段距离后,判断光子路径是否与甲板描述方程或海面所在平面相交,若都未相交,进一步判断光子与气溶胶粒子碰撞发生散射或吸收,若光子被吸收,不再对该光子进行追踪,若光子被散射,光子依据散射相函数与散射方位角分布改变传播方向后继续传输,直至光子到达海面或被甲板和气溶胶粒子吸收,在经过海面时根据海面毛细波概率分布函数及反射系数判断光子是否被反射,被反射的光子不再继续追踪,最终光子穿过海面,统计到达海面的光子数,计算出海面照度。在计算过程中模型有如下假设条件:(1)远离陆地,假设大气中仅含有海洋性气溶胶粒子;(2)海洋天气稳定;(3)光子经过海面时仅发生一次折射或反射。
1.4.2 建立渔船集鱼灯坐标系如图 2所示,分别以船尾、船中线在海面上的投影为Y轴、X轴,X轴与Y轴交于O点,Z轴过O点且垂直于X轴与Y轴建立的渔船集鱼灯坐标系。其中:L为渔船船长;L1为船首与船首部最靠前的一个集鱼灯之间连线在X轴上的投影距离;L2为靠近船首一列集鱼灯灯带长;L3为靠近船首和船尾两列集鱼灯的间距;L4为靠近船尾一列集鱼灯灯带长;L5为船尾与船尾部最靠后的一个集鱼灯之间连线在X轴上的投影距离;h为集鱼灯距离甲板的高度;d为左、右船舷两侧集鱼灯之间的距离;船体宽为a;靠近船首和靠近船尾两列集鱼灯数量为n1、n2;左舷两列集鱼灯的坐标为L1i(x1i,d/2)和L2i(x2i,d/2),i为每列集鱼灯的序数;每盏集鱼灯的坐标为

|
图 2 集鱼灯坐标示意图 Fig. 2 Sketch map of the fishing lamps |
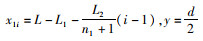 (9)
(9)
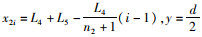 (10)
(10)
船身左、右舷描述方程为
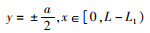 (11)
(11)
船首左、右舷描述方程为
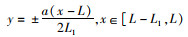 (12)
(12)
上述方程中,光子通过距甲板高度Z所对应的水平面时,若光子传递过程中Zi+1 < Z、Zi>Z(Zi表示第i次散射时在Z轴上的值)时,且Zi至Zi+1的光线传播路径与上述描述方程围成的面相交,即判断为光子被甲板吸收。
1.4.3 光子各波段发射比例不同波段发射的光子数不相同。根据干、湿气溶胶现有已知复折射率和本文集鱼灯波长分布范围,选择波长为400、488、515、550、633、694 nm,各波段光子数比例计算公式为
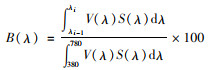 (13)
(13)
式中:λi-1、λi分别为波长间隔下、上限;B(λ)为波长在λi-1到λi占总光子数的百分比,%;V(λ)为标准光度函数;S(λ)相对光谱分布。总的光子数根据实际结果的稳定性和计算时间等确定。
1.4.4 光子发射初始角度光子从集鱼灯按一定角度发射时,天底角范围为0~π,方位角范围为0~2π。天底角与方位角概率分布函数分别为
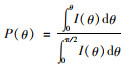 (14)
(14)
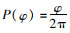 (15)
(15)
式中:θ、φ分别为集鱼灯天底角、方位角,rad。天底角与方位角确定方法:产生两个均匀分布的随机数ξ1、ξ2∈[0, 1],使P(θ)和P(φ)分别等于ξ1、ξ2,求出θ和φ。以下ξ均为此类随机数。
1.4.5 光子在大气中的传输光子与气溶胶粒子碰撞前有一段步长,其步长由平均自由程的累积概率函数决定,步长计算公式为
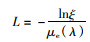 (16)
(16)
式中:L为光子行进步长,m。
光子与气溶胶中的粒子发生碰撞后,若ξ>μs(λ)/μe(λ),光子被吸收,否则发生散射。碰撞后的散射方位角服从0~2π均匀分布,空间散射角可通过H-G相函数较好的模拟[29-32],对该函数抽样得到空间散射角为
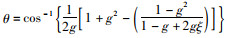 (17)
(17)
式中:θ为空间散射角,rad;g为不对称因子。
1.4.6 光子经过海面的传输光子穿过大气介质到达海面时,由风作用在海面而形成的毛细波影响光子在海面的入射角,相应的反射系数也会发生变化。海面入射角、折射角的确定方法参见文献[11],反射系数计算公式[33]为
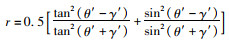 (18)
(18)
式中: γ′、θ′分别为入射角、折射角,rad;r为反射系数。取随机数ξ,当ξ < r时光子被反射。
1.5 照度计算方法如图 3所示,以船中线中点在海面投影为中心,将300×300 m海面划分成1×1 m方格。光子穿过海面后,根据光子到达海面的位置,统计落入每个方格的光子数,每个方格内平均照度计算公式为

|
图 3 海面照度计算示意图 Fig. 3 Sketch map of sea surface illumination calculation |
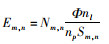 (19)
(19)
式中:Em, n为海面第m行、第n列方格内平均照度,lx;Nm, n为光子到达海面第m行、第n列方格内的光子数;Φ为集鱼灯光通量,lm;nl和np分别为集鱼灯个数和集鱼灯发射光子总数;S为方格的面积,m2。
2 结果 2.1 理论值与实测值比较根据环境数据和位置,利用上述模型计算出理论值,比较理论值与实测值之间关系(图 4)。由图 4a可知,理论值与实测值线性拟合斜率为1.04,斜率系数接近于1,实测值与理论值的比值均匀分布在拟合趋势线两侧。由图 4b可知:叠加法理论值与实测值线性拟合斜率为1.97;蒙特卡洛模型与叠加法模型理论值与实测值均显著相关(P < 0.05)。

|
图 4 实测值与理论值相关性分析(虚线为实测值=理论值,实线为实测值与理论值回归线) Fig. 4 Correlation analysis between measured value and theoretical value (The dotted line shows that the measured value is equal to the theoretical value, the solid line is the regression line between measured value and theoretical value) |
为研究不同风速与不同相对湿度的海面照度分布变化,根据上述建立的模型及渔船配置参数,分别计算风速为0 m/s,相对湿度为50%、60%、70%、80%时与相对湿度为78%,风速为0、2、4、6、8、10 m/s时的海面照度分布、照度值随与船中线中点距离变化(图 5和图 6)。

|
图 5 不同相对湿度下海面照度分布图(风速为0m/s时,a、b、c、d对应的相对湿度分别为50%,60%,70%,80%) Fig. 5 Distribution of sea surface light-field under different relative humidity(The wind speed is 0 m/s, the relative humidity corresponding to a, b, c, and d is 50%, 60%, 70%, and 80%, respectively) |

|
图 6 不同风速下海面照度分布图(相对湿度为78%,a、b、c、d、e、f对应的风速分别为0、2、4、6、8、10 m/s) Fig. 6 Distribution of sea surface light-field at different wind speeds(The relative humidity is 78%, and the wind speeds corresponding to a, b, c, d, e, and f is 0, 2, 4, 6, 8, and 10 m/s, respectively) |
分析海面照度分布,由图 5a可知,距离船中线25.0 m内照度等值线较密集,30.0 m以外照度均在120.0 lx以下,30.0 lx等照度曲线与船中线最远距离约为47.4 m。靠近船中线附近的海面照度有两个照度峰值,相对湿度为50%时,照度峰值分别为3 772.8 lx和3 507.6 lx;相对湿度为60%时,照度峰值分别为3 778.9 lx和3 511.8 lx;相对湿度为70%时,照度峰值分别为3 779.5 lx和3 505.5 lx;相对湿度为80%,照度峰值分别为3 806.9 lx和3 502.6 lx,不同相对湿度间照度变化不明显。照度随与船中线中点距离的增加,均呈先增大后减小的变化趋势,最终趋向于零。
由图 6可知,不同风速与不同相对湿度的照度值变化趋势相同。分析不同风速海面照度分布可以看出:30 lx和2 500 lx等照度曲线范围有明显变化,风速为0、2、4、6、8、10 m/s时,30.0 lx照度距离船中线最远距离分别为46.3、48.5、50.2、51.6、52.1、52.3 m,随风速增大而增大;2 500.0 lx照度距离船中线最远距离分别为10.1、9.2、8.3、7.3、7.2、6.9 m,随风速增大而减小。不同风速与不同相对湿度的海面照度分布一致,在靠近船舷附近均有两个照度峰值,但不同风速的照度峰值变化更显著;风速为0 m/s时,照度峰值分别为3 841.1 lx和3 524.5 lx;风速为2 m/s时,照度峰值分别为3 783.2 lx和3 527.5 lx;风速为4 m/s时,照度峰值分别为3 781.3 lx和3 556.2 lx;风速为6 m/s时,照度峰值分别为3 731.3 lx和3 536.2 lx;风速为8 m/s时,照度峰值分别为3 602.1 lx和3 445.9 lx;风速为10 m/s时,照度峰值分别为3 578.2 lx和3 437.2 lx,照度峰值随着风速的增大而减小。
2.3 海面照度的衰减变化根据2.2节设置的参数计算结果,绘制距离船舯线中点20.0 m内的海面照度变化与衰减率变化图(图 7和图 8)。

|
图 7 风速对海面照度的影响 Fig. 7 Influence of wind speed on sea surface illumination |

|
图 8 相对湿度对海面照度的影响 Fig. 8 Influence of relative humidity on sea surface illumination |
由图 7a可知:距船中线0~4.0 m为船与海面的接触区域,海面照度为零;照度随与船中线距离的增加,呈先增大后逐渐减小的趋势;风速为0、2、4、6、8、10 m/s时,照度峰值分别为3 826.4、3 781.6、3 774.3、3 731.3、3 602.1、3 598.1 lx,随着风速的增加而减小。由图 7b可知:不同风速的照度衰减率变化明显,衰减率随与船舯线距离的增加,先增大后减小,最终趋向于零;距离船中线4.0~4.8 m时,风速越小衰减率越大,4.8~8.3 m时,风速越大衰减率越大,之后随与船舯线距离的增加,风速越小衰减率越大;风速为0、2、4、6、8、10 m/s时,最大衰减率分别为485.5、489.1、569.1、782.2、953.7、1 044.0 lx/m,随风速增加而增大。
由图 8a可知,距离船舯线20.0 m内的海面照度分布,不同相对湿度对照度与衰减率变化影响较小,照度峰值均分布在距离船舯线6.0~8.0 m处;相对湿度为50%、60%、70%、80%时,照度峰值为3 767.4、3 778.9、3 779.5、3 806.9 lx,变化不明显。由图 8b可知,海面照度衰减率随与船舯线的距离增加至8.0~10.0 m之间达到最大,随后逐渐减小,最终趋向于零;不同风速与不同相对湿度的衰减变化趋势一致。
3 讨论 3.1 理论值与实测值比较分析目前,针对集鱼灯照度计算的主要方法有点光源法、线光源法、经验法、叠加法[7-10]。点光源法、线光源法、经验法没有考虑灯光的各向异性(即随不同发光角度的发光强度不相同),对金属卤化物集鱼灯等各向异性光源计算存在较大误差,故不适用光诱渔船的照度计算。叠加法虽考虑了集鱼灯的各向异性,在此基础上对每个集鱼灯的照度进行叠加,但未考虑集鱼灯在大气中的散射与吸收。本文模型从光子微观角度出发,基于蒙特卡洛随机方法模拟光子在实际环境中的传输路径,不仅考虑了集鱼灯的发光特性,还考虑了大气、海面波浪对照度的影响,模型实际计算结果更加符合真实环境情况,对模型验证程度更高。
根据本文照度模型与叠加法照度模型计算结果,由图 4b可知,叠加法理论值与实测值线性拟合斜率为1.97,本文蒙特卡洛模型相比于叠加法照度模型拟合斜率更接近于1,实际测量值与理论值有更显著的对应关系。叠加法计算结果与理论值相比偏大(除两点之外),主要原因是叠加法忽略了大气中衰减的影响,即光子在大气中无损失,高估了海面照度。本模型假设忽略大气对照度衰减的影响(模型参数吸收与散射系数均为零),并假设海面平静无波浪时(模型风速参数为零),本文模型与叠加法模型计算结果相一致。
3.2 环境因素对海面照度分布的影响由图 5和图 6可知,不同相对湿度与不同风速海面照度分布图中均有两个照度峰值,可能是渔船同侧集鱼灯排列不连续导致,渔船同侧集鱼灯有两列,靠近船首和船尾部位两列集鱼灯的灯间距约为0.6 m,且两列集鱼灯首尾之间间隔2.5 m,两列集鱼灯首尾之间存在的间距较大,因此在海面形成两个照度峰值;海面照度随与船中线距离的增加,先增加后减小,海面照度先增加这可能与金属卤化物集鱼灯发光特性有关,天底角越大,发射的有效光子数越多,因此在距离海面船中线一定位置接收到光子的数量最多;照度达到最大值后逐渐减小,原因有两方面,一方面是光子在大气中传输更容易被散射或吸收,另一方面是距离船中线越远,光线越发散,海面单位面积接收到光子数量越少。
大气相对湿度是描述大气水蒸气含量的参数,是指水在大气中的蒸汽压与同温度同压强下水的饱和蒸汽压的比值[34]。不同相对湿度间海面照度分布有差异,在一定范围内,相对湿度越大海面照度越小,随着相对湿度的增加,湿气溶胶粒子直径随之增大,湿气溶胶粒子复折射指数也发生变化,从而光子在大气中的衰减参数也发生变化,但不同相对湿度间照度衰减差异较小其主要原因是相对湿度的变化未引起气溶胶粒子数密度的变化。巨养锋等[35]利用米氏散射对脉冲激光在大气中传输时辐照度进行计算分析发现,大气相对湿度对激光散射截获半径影响较小,与本文相一致。有研究[23]表明,天气状况良好时,海洋性气溶胶成分相对稳定,且本文数据在海上测量时,天气状况良好,因此模型中忽略雾和降雨对照度衰减的影响,模型需要对雾天和降雨天气情况进一步研究。
不同风速间照度有明显差异,主要原因有两方面,一方面可能是风速使大气中气溶胶粒子数密度增加引起的海面照度变化,另一方面可能是风速可以改变海面粗糙程度引起的海面反射系数的变化[33]。官文江等[11]通过模型研究发现,海面照度随风速增加而增加,与本文结论不一致,是因为本文考虑了大气对光的衰减,风速增加虽然使海面粗糙程度发生变化,会增加光子穿过海面的概率,但风速还会导致气溶胶密度增加,气溶胶密度越大,其衰减系数越大。在距离船中线6 m左右范围内,海面照度随风速的增加而增加,在距离船中线6~20 m时,海面照度随风速增加呈减小趋势,其原因很可能与金属卤化物集鱼灯配光曲线和气溶胶粒子数密度变化有关,金属卤化物集鱼灯随天底角的增加,发光强度逐渐增加,天底角为90°时发光强度达到最高,船舷附近海面与集鱼灯的距离较小,受到大气吸收与散射的影响相比于离船舷较远位置的影响小,同时距离船舷较远位置集鱼灯配光曲线发光角度对应的发光强度较大,故距离船舷较近光子散射到较远位置相比于较远位置散射到较近位置的贡献低,随风速增加,较远位置与较近位置之间的相互贡献差距更加明显。随风速增加,海面照度峰值与船中线距离减小,能进一步说明较远位置与船舷附近之间的相互贡献差。由此表明,以往的照度计算模型忽略风速对海面照度影响的计算存在较大误差。
光诱渔船利用合理可靠的照度模型能准确的掌握光诱捕捞作业时鱼类最适宜的照度区域,且能节约燃油成本,实现更高效、绿色捕捞作业。本文考虑了大气对照度衰减的影响,提出一种基于蒙特卡洛方法海面照度计算模型,并分析环境因素对海面照度的影响,为今后海面照度分布研究提供理论基础。
| [1] |
花传祥, 李非, 朱清澄, 等. 基于点光源和球面光源的集鱼灯照度模型比较研究[J]. 中国光学, 2019, 12(2): 274-288. HUA C X, LI F, ZHU Q C, et al. Comparative study on the illumination model of fishing lamps based on point light sources and spherical light sources[J]. Chinese Optics, 2019, 12(2): 274-288. |
| [2] |
AN Y I, HE P G, ARIMOTO T, et al. Catch performance and fuel consumption of LED fishing lamps in the Korea hairtail angling fishery[J]. Fisheries Science, 2017, 83(3): 343-352. DOI:10.1007/s12562-017-1072-6 |
| [3] |
NGUYEN K Q, WINGERP D, MORRIS C, et al. Artificial lights improve the catchability of snow crab (Chionoecetes opilio) traps[J]. Aquaculture & Fisheries, 2017, 2(3): 124-133. |
| [4] |
MATSUSHITAY, YAMASHITAY. Effect of a stepwise lighting method termed "stage reduced lighting" using LED and metal halide fishing lamps in the Japanese common squid jigging fishery[J]. Fisheries Science, 2012, 78(5): 977-983. DOI:10.1007/s12562-012-0535-z |
| [5] |
钱卫国, 官文江, 陈新军. 1 kW国产金属卤化物灯光学特性及其应用[J]. 上海海洋大学学报, 2012, 21(3): 439-444. QIAN W G, GUAN W J, CHEN X J. The optical characteristics of domestic metal halide lamp(1 kW) and its applications[J]. Journal of Shanghai Ocean University, 2012, 21(3): 439-444. |
| [6] |
钱卫国, 陈新军, 钱雪龙, 等. 国产LED水下集鱼灯光学特性与节能分析[J]. 渔业现代化, 2010, 37(6): 56-61. QIAN W G, CHEN X J, QIAN X L, et al. Analysis of optical characteristics of domestic underwater fish aggregation LED lamp and its energy saving[J]. Fishery Modernization, 2010, 37(6): 56-61. DOI:10.3969/j.issn.1007-9580.2010.06.013 |
| [7] |
崔淅珍, 中村善彦, 有元貴文. 集魚灯による小型イカ釣り漁船周辺の海面照度分布[J]. 日本水産学会誌, 1997, 63(2): 160-165. CHOI S, NAKAMURA Y, AIRMOTO T. Horizontal illuminance of line source model for fishing lamps around the coastal squid jigging boats[J]. Nippon Suisan Gakkaishi, 1997, 63(2): 160-165. |
| [8] |
崔淅珍, 荒川久幸, 有元貴文, 等. 線光源モデルを用いた小型イカ釣り漁船集魚灯の水中照度分布解析[J]. 日本水産学会誌, 2003, 69(1): 44-51. CHOI S, ARAKAWA H, ARIMOTO T, et al. Underwater illuminance of line light source model for fishing lamps of coastal squid jigging boats[J]. Nippon Suisan Gakkaishi, 2003, 69(1): 44-51. |
| [9] |
郑国富. 诱鱼灯光场计算及其对光诱鱿鱼浮拖网作业的影响[J]. 台湾海峡, 1999, 18(2): 215-220. ZHENG G F. Light-field calculation of light-attraction lamp and discussion on its suitabilities to fishing gear and methods in light-pelagic trawl for squid[J]. Journal of Oceanography in Taiwan Strait, 1999, 18(2): 215-220. DOI:10.3969/j.issn.1000-8160.1999.02.018 |
| [10] |
钱卫国, 王飞. 集鱼灯海面照度计算方法的比较研究[J]. 浙江海洋学院学报(自然科学版), 2004, 23(4): 285-290. QIAN W G, WANG F. Comparative study on the calculated methods of illuminate of sea surface about aggregating fish lamps[J]. Journal of Zhejiang Ocean University(Nature Science), 2004, 23(4): 285-290. DOI:10.3969/j.issn.1008-830X.2004.04.002 |
| [11] |
官文江, 钱卫国, 陈新军. 应用Monte Carlo方法计算水上集鱼灯向下辐照度在一类海水中的分布[J]. 水产学报, 2010, 34(10): 1595-1604. GUAN W J, QIAN W G, CHEN X J. Computing underwater downward irradiance of fish aggregation lamps in class Ⅰ ocean water based on Monte Carlo method[J]. Journal of Fisheries of China, 2010, 34(10): 1595-1604. |
| [12] |
LIU S Y, CHANT L. A stochastically weighted operator splitting Monte Carlo (SWOSMC) method for the numerical simulation of complex aerosol dynamic processes[J]. International Journal of Numerical Methods for Heat and Fluid Flow, 2017, 27(1): 263-278. DOI:10.1108/HFF-08-2015-0335 |
| [13] |
FANG Q Q, BOAS D A. Monte Carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units[J]. Optics Express, 2009, 17(22): 20178-20190. DOI:10.1364/OE.17.020178 |
| [14] |
LIU Q, RAMANUJAM N. Scaling method for fast Monte Carlo simulation of diffuse reflectance spectra from multilayered turbid media[J]. Journal of the Optical Society of America A, 2007, 24(4): 1011-1025. DOI:10.1364/JOSAA.24.001011 |
| [15] |
王婷, 徐军, 赵选科, 等. 基于Monte Carlo方法的雾红外传输仿真及分析[J]. 光子学报, 2018, 47(12): 122-131. WANG T, XU J, ZHAO X K, et al. Simulation and analysis of infrared radiation transmission in fog based on Monte Carlo method[J]. Acta Photonica Sinica, 2018, 47(12): 122-131. |
| [16] |
郝增周, 龚芳, 潘德炉, 等. 沙尘气溶胶粒子群的散射和偏振特性[J]. 光学学报, 2012, 32(1): 14-22. HAO Z Z, GONG F, PAN D L, et al. Scattering and polarization characteristics of dust aerosol particles[J]. Acta Optica Sinica, 2012, 32(1): 14-22. |
| [17] |
钱卫国. 鱿钓渔业中集鱼灯的优化配置研究[D]. 上海: 上海水产大学, 2005. QIAN W G. Study on the optimal allocation of fish aggregation lamps in squid jigging fisheries[D]. Shanghai: Shanghai Fisheries University, 2005. |
| [18] |
UGOLNIKOV O S, MASLOV I A. Stratospheric aerosol particle size distribution based on multi-color polarization measurements of the Twilight sky[J]. Journal of Aerosol Science, 2018, 117: 139-148. DOI:10.1016/j.jaerosci.2018.01.002 |
| [19] |
MALININA E, ROZANOV A, ROZANOV V, et al. Aerosol particle size distribution in the stratosphere retrieved from SCIAMACHY limb measurements[J]. Atmospheric Measurement Techniques, 2018, 11(4): 2085-2100. DOI:10.5194/amt-11-2085-2018 |
| [20] |
ONISCHUK A A, VALIULIN S V, BAKLANOV A M, et al. Determination of the aerosol particle size distribution by means of the diffusion battery: Analytical inversion[J]. Aerosol Science and Technology, 2018, 52(8): 841-853. DOI:10.1080/02786826.2018.1473839 |
| [21] |
SHETTLE E P, FENN R W. Models for the aerosols of the lower atmosphere and the effects of humidity variations on their optical properties[M]. Air Force Geophysics Laboratory, Air Force Systems Command, United States Air Force, 1979: 26-30.
|
| [22] |
YAN Q, DI H G, ZHAO J, et al. Improved algorithm of aerosol particle size distribution based on remote sensing data[J]. Applied Optics, 2019, 58(29): 8075-8082. DOI:10.1364/AO.58.008075 |
| [23] |
HÄNEL G. The properties of atmospheric aerosol particles as functions of the relative humidity at thermodynamic equilibrium with the surrounding moist air[J]. Advances in Geophysics, 1976, 19: 73-188. |
| [24] |
王菲菲, 李学彬, 郑显明, 等. 相对湿度和风速对海洋大气气溶胶粒子谱的影响[J]. 红外与激光工程, 2019, 48(s1): S117003. WANG F F, LI X B, ZHENG X M, et al. Effect of relative humidity and wind speed on marine atmospheric aerosol particle size distribution[J]. Infrared and Laser Engineering, 2019, 48(s1): S117003. |
| [25] |
鲁先洋, 李学彬, 秦武斌, 等. 海洋大气气溶胶粒子谱分布及其消光特征分析[J]. 红外与激光工程, 2017, 46(12): 1211002. LU X Y, LI X B, QIN W B, et al. Particle size distribution and extinction characteristic analysis of marine atmospheric aerosol[J]. Infrared and Laser Engineering, 2017, 46(12): 1211002. |
| [26] |
杨玉峰, 蒋明争, 李挺. 海雾和陆雾的光散射特性研究[J]. 电子测量与仪器学报, 2018, 32(9): 163-168. YANG Y F, JIANG M Z, LI T. Study on the light scattering characteristic of sea fog and land fog[J]. Journal of Electronic Measurement and Instrument, 2018, 32(9): 163-168. |
| [27] |
项建胜, 何俊华. Mie光散射理论的数值计算方法[J]. 应用光学, 2007, 28(3): 363-366. XIANG J S, HE J H. Numerical calculation of Mie theory[J]. Journal of Applied Optics, 2007, 28(3): 363-366. |
| [28] |
TAMINIAU T H, MOERLAND R J, SEGERINK F B, et al. λ/4 resonance of an optical monopole antenna probed by single molecule fluorescence[J]. Nano Letters, 2007, 7(1): 28-33. |
| [29] |
罗双, 尹球. 辐射传输计算中散射相函数截断近似方法对比分析[J]. 光学学报, 2017, 37(2): 0229002. LUO S, YIN Q. Comparison and analysis of scattering phase-function truncation approximations in radiative transfer calculation[J]. Acta Optica Sinica, 2017, 37(2): 0229002. |
| [30] |
WANG Z, CUI S C, YANG J, et al. A novel hybrid scattering order-dependent variance reduction method for Monte Carlo simulations of radiative transfer in cloudy atmosphere[J]. Journal of Quantitative Spectroscopy & Radiative Transfer, 2016, 189: 283-302. |
| [31] |
白璐, 汤双庆, 吴振森, 等. 紫外到可见波段外混合气溶胶的传输特性[J]. 光学学报, 2010, 30(8): 2175-2179. BAI L, TANG S Q, WU Z S, et al. Transmission characteristic of external mixture of aerosol from ultraviolet to visible-light band[J]. Acta Optica Sinica, 2010, 30(8): 2175-2179. |
| [32] |
黄朝军, 吴振森, 刘亚锋, 等. 大气气溶胶粒子散射相函数的数值计算[J]. 红外与激光工程, 2012, 41(3): 580-585. HUANG C J, WU Z S, LIU Y F, et al. Numerical calculation of phase function of atmospheric aerosol particles[J]. Infrared and Laser Engineering, 2012, 41(3): 580-585. |
| [33] |
LI H K, PINEL N, BOURLIER C. Polarized infrared reflectivity of 2D sea surfaces with two surface reflections[J]. Remote Sensing of Environment, 2014, 147: 145-155. |
| [34] |
张淑平, 韩立建, 周伟奇, 等. 冬季PM2.5的气象影响因素解析[J]. 生态学报, 2016, 36(24): 7897-7907. ZHANG S P, HAN L J, ZHOU W Q, et al. Relationships between fine particulate matter(PM2.5) and meteorological factors in winter at typical Chinese cities[J]. Acta Ecologica Sinica, 2016, 36(24): 7897-7907. |
| [35] |
巨养锋, 梁冬明, 薛建国, 等. 气象条件对激光散射截获半径的影响[J]. 应用激光, 2011, 31(4): 338-341. JU Y F, LIANG D M, XUE J G, et al. The influence of meteorology parameter on laser scatter intercept radius[J]. Applied Laser, 2011, 31(4): 338-341. |
2. Fisheries College, Zhejiang Ocean University, Zhoushan 316022, Zhejiang, China
 2021,
Vol. 30
2021,
Vol. 30


