2. 国防科技大学 第63研究所, 江苏 南京 210007
2. The 63 rd Institute, National University of Defense Technology, Nanjing 210007, China
随着大数据应用的发展, 数据规模呈现爆发式增长, 数据中心的数据量从PB(1PB=240B), EB(1EB=250B)级已经迈入了ZB(1ZB=260B), YB(1YB=270B)级.当前的互联网数据, 半结构化和非结构化数据已经占数据总量的85%以上, 如文本、网页、图像、基因等, 其中, 高维性是这些数据的重要特征[1].收集存储仅是大数据应用的第1步, 如何利用存储的数据描述应用特征, 预测未来的发展, 为业务决策和科学研究提供有力的支撑, 是大数据应用的出发点和落脚点.降维是高维数据重要的预处理步骤, 常用的方法有特征抽取和特征选择.由于特征选择保留了数据的原始特征, 因此具有良好的可解释性, 成为主要的数据降维方法[2, 3].
特征选择, 即从原始特征集合中选择使得评价准则最大化的最小特征子集, 通过运用特征选择可以减少原始数据获取的时间, 缩减数据的存储空间, 提高分类模型的可解释性, 更快地获得分类模型, 提高分类性能, 并且有助于对数据和知识进行可视化[4].长期以来, 针对特征选择方法的研究主要集中在提高算法的分类性能、减少时间复杂度等方面.然而在众多实际应用中, 如基因筛选、生物识别、癌症检测等, 不但要求选择的特征具有良好的分类性能, 也对特征选择的稳定性提出了需求[5, 6].在某些领域, 特征选择稳定性的重要程度甚至要高于分类性能[7], 但是目前, 对特征选择稳定性的研究相对较少[8-12].
特征选择稳定性是指特征选择方法对训练样本的微小扰动具有一定的鲁棒性, 一个稳定的特征选择方法应当在训练样本具有微小扰动的情况下生成相同或相似的特征子集[13].提高特征选择的稳定性可以发现相关特征, 增强领域专家对结果的可信度, 进一步降低获取数据的复杂性和时间消耗.近年来, 随着高维数据研究领域的发展, 特征选择稳定性逐渐成为特征选择研究领域的热点.在脑科学领域, 通过功能性核磁共振成像技术来测量脑部活动是一种流行的方法, 然而由于样本的获取代价高昂, 同时对特定的测试状态而言, 仅存在较少的脑部区域被激活使用, 导致样本同时具有高维性和稀疏性, 若仅采用分类准确性评价特征选择, 会造成在未知数据集上训练模型时产生不稳定的泛化错误, 因此, 对特征选择稳定性同时进行考虑具有现实的必要性[14, 15].随着社交网络的发展, 社交网站每天都会产生大量的数据, 如用户状态信息、评论和公告等.这些社交网络数据最重要的特点是其内容长度较短且特征空间维度较高, 导致产生高维稀疏样本.针对此类应用数据的特点, 众多研究人员提出了行之有效的特征选择方法, 然而这些方法普遍缺乏对稳定性的考虑.如何确保特征子集具有优异分类性能的同时具备良好的稳定性, 是该领域面临的挑战[16].特征选择稳定性的应用场景还包括癌症基因识别和DNA微阵列数据的基因表达等[17, 18].
特征选择方法有两种分类方式.
● 按照选择特征时是否具有独立性, 特征选择方法可分为单变量法和多变量法:单变量法采用特定的评价准则独立评估每个特征; 多变量法在评估某个特征时同时考虑该特征与其他特征之间的关联关系;
● 按照结果返回类型的不同, 可将特征选择方法分为权重法、排序法和子集法这3种类型[13]:权重法是指特征选择方法返回的是赋予特征的权重值, 排序法返回的是特征的排序列表, 子集法返回的是选择的特征子集.
本文对特征选择稳定性的研究做详细的总结, 为从事特征选择稳定性方面的研究人员了解相关领域的进展提供参考.本文将特征选择稳定性提升方法分为扰动法和特征法两种, 分别总结两种方法的研究进展和特点; 阐述演化算法在特征选择稳定性中的应用; 归纳特征选择稳定性中的评估, 包括特征选择稳定性度量指标、特征选择算法稳定性以及影响因素评估等; 在人工和标准测试集上, 对典型的子集法稳定性度量指标的性能做比较分析, 在此基础上, 分析4种集成单变量与多变量的集成方法在稳定性、分类性能和分类器上的相关性; 最后展望特征选择稳定性未来的研究方向.
1 特征选择稳定性提升方法本节对特征选择稳定性提升方法做详细的归纳, 总结方法的特点和适用范围, 并介绍演化算法在特征选择稳定性方面的应用.
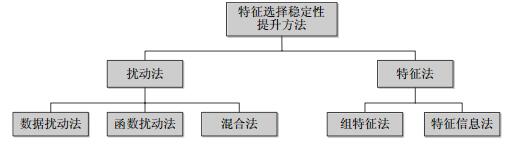
为了提高特征选择方法的稳定性, 近年来出现了众多有效的方法和研究成果, 按照特征选择稳定性提升技术是否与特征本身相关, 将其分为扰动法和特征法:扰动法包括数据扰动法、函数扰动法和混合法, 特征法包括组特征法和特征信息法.如图 1所示.
|
Fig. 1 Classification of feature selection improvement methods 图 1 特征选择稳定性提升方法分类 |
1.1 扰动法
扰动法是从输入的训练样本集和特征选择方法入手, 采用扰动数据集、增加新的数据或集成多种特征选择方法等方式提高特征选择结果的稳定性, 它一般与集成学习技术相结合.扰动法仅在数据集或者特征选择方法层面采用一种或多种手段提高特征选择的稳定性, 是一种宏观的提升方法.具体而言, 数据扰动法采用抽样、采样和样本分割等方式对原始数据集进行重新组合作为训练样本, 或者采用样本注入增加新的训练样本, 在此基础上, 使用特征选择方法选择特征子集并进行集成, 提高选择相似特征子集的概率, 进而提升特征选择的稳定性[19]; 函数扰动法是在同一数据集上采用不同的特征选择方法进行特征选择, 并对结果进行集成, 得到稳定特征子集; 混合法融合了数据扰动法和函数扰动法, 在对训练样本进行扰动的基础上, 利用不同的特征选择方法在新的训练样本上选择特征, 并融合特征选择结果, 选出稳定的特征子集.
在数据扰动法研究方面, 采用Bootstrap抽样方法提高特征选择稳定性的技术较为常见.文献[20]提出一种随机集成ReliefF方法, 首先使用Bootstrap方法对原始数据进行抽样得到多个抽样子集, 再随机移除每个抽样子集中的特征, 然后采用ReliefF特征选择方法对去除特征后的抽样子集进行特征排序, 将生成的多个特征排序列表进行集成形成最终的特征排序.文献[21]设计了一种集成框架, 在框架内对训练样本进行Bootstrap抽样, 在抽样数据上进行特征选择, 并用中值法、均值法和指数法这3种策略集成特征选择结果.此外, 文献[22, 23]同样利用Bootstrap对训练样本进行抽样, 提高特征选择稳定性.在使用采样技术方面, 文献[24]对原始数据进行不同规模的采样, 并在采样规模相同的前提下, 运行多次采样生成训练样本, 集成训练样本上的特征选择结果, 提高特征子集的稳定性.文献[25]则对训练数据进行随机欠采样, 并在样本上随机移除特征, 然后使用特征选择方法选择相关特征, 并将被选次数大于设定阈值的特征作为最终特征, 有效提升了算法的稳定性.此外, 样本分割技术也可以用来提高特征选择的稳定性.文献[26]提出了一种提高特征选择稳定性的Booster方法, 该方法使用交叉检验生成训练样本, 将训练样本分割为不相交的子集, 采用特征选择方法在划分的每个子集数据上选择特征, 将生成的特征子集合并成为最终的特征子集.
抽样、采样和样本分割等数据扰动法仅仅是对原始数据样本的重新组合, 并不增加新的样本.另一种数据扰动法是通过样本注入, 即增加训练样本个数提高特征选择稳定性, 如获取更多真实样本或构建新样本等[27].然而获取新的真实样本通常在时间和开销上较为可观, 另一方面, 在某些应用中, 如癌症检测和故障诊断, 获取新的样本是比较困难的.构建新样本有两种方式:一种是使用测试数据作为新的训练样本, 另一种方法是基于原始训练样本分布概率生成新的人工训练样本[28].但是它们也存在难以解决的问题:采用测试数据作为训练样本会导致对特征选择方法的评估存在偏差; 而生成新的人工训练样本会造成过拟合, 并且在疾病诊断等领域, 生成人工训练样本并不可行, 因为它们的诊断结果依赖于真实数据[29].因此在实际研究中, 通过样本注入提高特征选择稳定性的方法使用较少.
在函数扰动法研究方面, 文献[30]集成信息增益(information gain)、增益率(gain gatio)、基于相关性的特征方法(correlation based feature approach)、基于一致性搜索(consistency based search)和卡方检验(chi squared)等5种常用的特征排序法对同一训练样本进行特征选择, 减少不相关特征对分类的影响, 提高特征选择的稳定性.文献[31]采用集成的方法融合了基于相关性的快速过滤法(fast correlation based filter)、基于相关性的特征选择(correlation based feature selection)、ReliefF、增益率和卡方检验等5种特征选择方法的结果, 提升特征子集的稳定性.此外, 文献[32]使用了基于相关性的特征方法、信息增益、ReliefF、基于一致性搜索和INTERACT等5种特征选择方法进行集成.文献[33]则集成了增益率、卡方检验、单规则(one rule)、信息增益和基于相关性的特征选择等方法.经过研究可以看出:采用函数扰动法提高特征选择稳定性, 通常是采用集成单变量与多变量的方法来实现, 提高特征选择方法的多样性, 从而增强特征选择稳定性, 如单变量方法中的信息增益、增益率、单规则与卡方检验, 多变量方法中的ReliefF、基于相关性的快速过滤法、基于一致性搜索、基于相关性的特征方法、INTERACT和基于相关性的特征选择等.同时说明:若仅集成单变量或多变量方法, 其稳定性提升效果并不显著[34].
混合法是同时采用数据扰动法与函数扰动法的一种方法, 通常先使用数据扰动法生成多组训练数据, 再利用多种特征选择方法选择特征并集成结果.文献[35]通过欠采样生成新的训练样本组, 采用信息增益、增益率、对称不确定(symmetrical uncertainty)、费舍尔率(Fisher ratio)以及ReliefF这5种方法选择特征, 并提出一致性函数聚合特征排序列表.文献[36]使用Bootstrap抽样生成多个训练样本, 然后采用10种不同的方法在训练样本上进行特征选择, 并将特征排序结果进行集成.
在应用扰动法时, 各种方法的适用范围以及各自的优缺点是主要考虑的因素.数据扰动法的使用较为简单, 适用于训练样本较多、获取数据较为容易的场景, 但是数据扰动法并不适用于一些小样本应用, 如癌症检测、故障诊断等, 因为在小样本数据上, 采用数据扰动法易造成过拟合.函数扰动法对小样本应用而言较为适用, 其缺点在于难以根据数据集的特点选择合适的特征选择方法进行集成[37].由于混合法是一种结合数据扰动法与函数扰动法的方法, 因此其缺点也显而易见, 如不适用于小样本应用且特征选择方法的选用较为困难等; 然而其优点在于经过精心的设计, 该方法的提升效果最为显著, 且具有良好的泛化性能.
1.2 特征法特征法是在特征层面对其进行进一步处理, 在此基础上与特征选择方法相融合, 提高特征选择的稳定性, 它是一种在特征层面的微观方法.组特征法是通过某种方式将高度相关的特征聚集成组, 从特征组中选择相关特征构成稳定的特征子集; 特征信息法是利用特征本身的信息对当前的特征选择方法进行改进, 即, 采用某种度量准则给予重要特征更高的权重, 然后根据权重值选择稳定的相关特征.
组特征方法在近年来得到了快速的发展, 它基于一个经验观测结论:在高维数据中, 相关特征是高度关联的, 因此可以生成多组相关的特征集合.特征选择算法从各组中选择特征, 组合成最终的特征子集.由于这些特征组对输入样本的扰动具有一定的鲁棒性, 因此, 基于组特征的特征选择方法对输入样本的微小扰动同样具有稳定性[38, 39].常用的获取特征组的方法包括核密度估计、正则化和相关性.
核密度估计是一种非参数密度估计方法, 通过使用核密度估计, 可以得出特征与密度波峰的距离, 然后将距离小于阈值的特征合并作为特征组.文献[40]考虑了特征选择的泛化性能及其稳定性, 通过核密度估计得出一组紧密特征组, 并将组内的特征作为特征选择的相关实体, 然后提出采用紧密相关属性组选择器算法, 在紧密特征组上选择特征.
为了解决文献[40]中核密度方法在高维空间上容易忽略稀疏区域相关特征的问题, 文献[38]利用Bootstrap方法对训练样本抽样, 在抽样样本中, 采用核密度估计得出紧密特征组, 最后通过层次聚类得出特征组.
正则化是回归模型常用的方法, 采用正则化技术可以进行特征选择.例如, 最小绝对收缩选择算子(least absolute shrinkage and selection operator, 简称LASSO)就是一种常用的基于正则化技术的特征选择方法, 它通过构造具有正则化项的回归模型, 使得平方误差和最小化, 从而产生较少的非零分量, 这些非零分量对应选择的特征.文献[28]为了解决LASSO特征选择方法在电子医疗记录数据上的不稳定性, 提出一种称为预测聚组弹性网络的方法将相关特征划分为组, 然后选择具有丰富判别信息的组而非单个特征, 将模型转换为具有限制条件的优化问题, 同时提出一种收敛的迭代方法进行求解.此外, 文献[41]采用桥正则化技术求解非零分量, 选择稳定特征.文献[42]在朴素弹性网络的基础上提出弹性网络正则化技术, 解决了LASSO在高维相关特征中易产生相似回归系数的问题, 有效提升了LASSO的稳定性.
相关性的方法是通过相关性函数得出特征的相关性值, 基于相关性值, 采用某种策略得出特征组.文献[43]提出了聚类组LASSO稳定性特征选择方法:首先, 基于典型相关分析方法采用层次聚类将特征聚集成组, 并计算特征组的相关性表示矩阵; 再对原始训练样本进行抽样, 每次抽样原始训练样本的一半; 在抽样数据上使用LASSO从特征组中选择特征, 将被选次数大于设定阈值的特征作为最终特征子集的元素.
其他获得特征组的方法还包括如自组织映射、K均值、逻辑回归和图理论等[44-47].
特征信息法常用的度量准则包括相关性度量、基于信息理论的度量、基于距离的度量和基于损失函数的度量等.
在使用相关性度量方面, 文献[48]提出了最小独立支配集技术:先采用皮尔逊相关系数(Pearson correlation coefficient)度量特征间的相关性, 并设定阈值, 将大于设定阈值的特征之间用边相连; 在此基础上, 寻找到一组最小独立支配集, 即, 使得集合中的特征相互之间没有边相连, 集合之外的特征至少存在一条边与集合中的特征相连.最小独立支配集中的特征就是最能够代表全部特征的稳定特征子集.
基于信息熵度量的研究中, 文献[49]将训练样本随机分割为不重复的子样本, 再将特征分割成不重复的子集, 使用条件互信息最大化(conditional mutual information maximization)和LASSO对每个子样本和特征子集做特征选择, 最后, 将被选次数大于阈值的特征作为特征子集的组成元素.文献[50]提出在随机森林特征选择中采用过滤式特征选择方法计算特征的信息增益, 再从中选择最好的特征进行节点分裂, 提高选择相关特征的概率.
基于距离度量方面, 文献[51]通过假设样本间隔计算出样本的权重, 再将已被分配权重的样本作为输入, 由基于距离度量的权重特征选择法Simba评估样本中特征的权重, 从而选择出稳定的特征子集.文献[52]提出了最大相关最大距离特征排序方法, 该方法用皮尔逊相关系数度量特征子集与分类目标之间的相关性, 使用欧式距离、余弦相似度和谷元距离(Tanimoto distance)衡量特征之间的距离, 然后计算特征的平均距离, 最后选择使得相关性指标与平均距离之和最大的特征.
利用损失函数度量特征信息方面, 文献[53]分别采用L1与L2正则化泛化损失函数计算样本中特征的权重, 根据特征的权重值选择特征子集, 并通过实验得出L2正则化泛化损失函数在提升特征选择稳定性方面性能较好.此外, 也有相关工作结合多种度量准则提高特征选择稳定性.文献[54]提出一种结合相关性偏差约减策略的算法, 其利用特征的距离间隔与高斯损失函数对支持向量机递归特征消除(support vector machine recursive feature elimination)算法中每次被移除的特征组内特征做相关性计算, 若该特征与至少Tg个组内特征的相关性大于设定阈值Tc, 且该特征与已选特征子集内特征的相关性不大于Tc, 则将该特征保留作为选择的特征.
组特征法研究成果较多, 取得了较好的效果, 特别是基于核密度估计和正则化技术的方法, 在组特征法中被广泛采用.但组特征法的局限性在于缺乏较为系统的理论依据, 目前, 组特征法的发展仍然基于经验观察的结论, 且组特征法并不适用于数据集特征规模较小的情况, 同时也难以适应特征组边界并不清晰的数据集.
特征信息法则能够适用于数据的特征规模较小的情况, 但其缺点在于需要根据问题及数据集的特点选用合适的度量准则.基于相关性和基于距离的度量难以适应特征维度较高的情况, 当特征维度较高时, 其特征的相关性和距离值差异较小, 导致难以选择合适的特征子集.而基于信息理论的度量存在同样的问题[29].基于损失函数的度量需要根据数据集的特点构造有效的损失函数.正是由于特征信息法的特点, 导致其泛化性较弱.
1.3 特征选择稳定性中的演化算法特征选择是典型的NP难问题, 即, 无法在多项式时间内获得最优解.一类重要的解决方法是利用演化算法获取次优解.基于演化算法选择特征子集是常用的特征选择方法, 其在提升特征选择稳定性的研究中也得到了重视和应用.
目前, 提高演化算法特征选择稳定性主要有两种方式:一种是与扰动法或特征法相结合, 一种是采用集成策略.文献[55]提出一种结合组特征法与遗传算法(genetic algorithm)的特征选择方法, 通过基于信息理论的对称不确定度量准则将相关特征聚集成组, 使用遗传算法从特征组中选择相关特征构成特征子集, 有效提升了特征子集的稳定性.文献[17]将演化算法与函数扰动法相结合, 采用T检验、费舍尔判别准则和ROC曲线下面积(area under ROC curve)等3种特征选择方法对训练数据进行特征选择, 并集成特征排序结果, 然后使用遗传算法选择稳定的特征子集.针对遗传算法在高维数据中选择特征耗时的问题, 文献[56]将函数扰动法与演化算法相融合, 提出采用最小冗余最大相关(minimum redundancy maximum relevance)、联合互信息(joint mutual information)、条件互信息最大化(conditional mutual information maximization)和交互覆盖(interaction capping)等4种过滤式特征选择方法对特征进行筛选, 将选择次数大于阈值的特征集作为输入, 由遗传算法进一步选择相关特征.
在采用集成策略方面, 文献[57]将多个相同的基于粒子群优化(particle swarm optimization)的特征选择算法并行运行, 对每个算法搜索到的最优特征组合, 利用提出的类别可分性指标对特征组合进行加权集成, 权值高的特征被选频次高同时对分类贡献度大, 然后采用递归特征消除策略选择权值高的特征构成特征子集, 进一步提升粒子群优化算法的特征选择稳定性和分类性能.
基于演化算法的特征选择是一类重要的特征选择方法, 目前, 对于特征选择稳定性及提升方法的研究主要聚焦于过滤式特征选择方法, 而针对基于演化算法的特征选择稳定性提升方法研究还不成体系, 研究成果相对较少, 这也是未来特征选择稳定性研究的主要方向和亟待解决的问题[58].
2 特征选择稳定性中的评估除了提升方法, 特征选择稳定性评估也是特征选择稳定性研究的一项重要内容, 具体包括3个方面:一是特征选择稳定性度量指标的研究与评估, 二是对特征选择算法的稳定性评估, 三是对影响特征选择稳定性因素的研究.特征选择稳定性度量指标是特征选择稳定性研究的基础工作, 具备良好性能的度量指标对正确评估特征选择稳定性的相关研究内容至关重要; 对特征选择算法本身进行稳定性评估, 能够使我们了解“稳定”方法的内在机制, 从而进一步发展性能优异的特征选择方法; 特征选择稳定性影响因素的研究是进一步提高特征选择方法稳定性能的理论基础, 只有充分了解造成特征选择方法不稳定的原因才能“对症下药”, 提出合理的解决方案.
2.1 特征选择稳定性度量指标及性质在特征选择稳定性的研究中, 关键问题之一就是采用何种指标度量特征选择算法的稳定性.通常, 我们是通过比较特征选择结果的相似程度来度量特征选择稳定性.本节将特征选择方法分为权重法、排序法和子集法等3种, 归纳每种方法对应的度量指标及各自的特点, 在此基础上讨论特征选择稳定性度量指标的性质.常见的度量指标见表 1.
| Table 1 Measures of stability of feature selection 表 1 特征选择稳定性度量指标 |
2.1.1 权重法稳定性度量指标
为了度量给定特征选择方法生成的两个权重向量w和w’之间的相似度, 可以使用皮尔逊相关系数进行计算, 如公式(1)[21]:
| $ {D_W}\left( {\mathit{\boldsymbol{w}}, \mathit{\boldsymbol{w'}}} \right) = \frac{{\sum\nolimits_i {\left( {{w_i}-{\mu _w}} \right)\left( {{{w'}_i}-{\mu _{w'}}} \right)} }}{{\sqrt {\sum\nolimits_i {{{\left( {{w_i}-{\mu _w}} \right)}^2}} \sum\nolimits_i {{{\left( {{{w'}_i} - {\mu _{w'}}} \right)}^2}} } }} $ | (1) |
其中, wi和
目前, 度量权重法稳定性的指标仅有皮尔逊相关系数一种方法.由于我们可以根据特征的权重值将其进行排序或选出合适的特征子集, 因此可以将特征的权重值转换为特征排序或特征子集的方式, 进而采用排序法或子集法度量指标评估特征选择方法的稳定性.
2.1.2 排序法稳定性度量指标对排序法稳定性的度量可以分为3种情况, 即全排序列表、部分排序列表(top-k排序列表)和部分子集列表(top-k列表).全排序列表是指对全部特征的排序结果进行度量, 其度量指标包括斯皮尔曼排序相关系数法(Spearman rank correlation coefficient)和兰氏距离(Canberra distance)等[13, 59]; 部分排序列表是指对特征排序列表中前k个特征构成的排序列表进行度量, 其代表性的度量指标是权重兰氏距离(weight Canberra distance)[60]; 部分子集列表是指对特征排序列表中前k个特征构成的特征子集进行度量, 典型的度量指标是叠加评分(overlap score)[60].最近, 文献[61]提出一种基于詹森-香农距离的度量指标, 它的适用范围最为广泛, 可以应用在排序法的任意情况中.下面对典型的排序法度量指标作简要的介绍.
在全排序列表中, 为了度量两个特征全排序向量r和r’的相似性, 可以采用斯皮尔曼排序相关系数法进行计算, 如公式(2):
| $ {D_S}\left( {\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{r'}}} \right) = 1-6\sum\limits_{i = 1}^c {\frac{{{{\left( {{r_i}-{{r'}_i}} \right)}^2}}}{{c\left( {{c^2}-1} \right)}}} $ | (2) |
其中, ri和
另一种度量全排序列表的指标是兰氏距离, 其计算如公式(3):
| $ {D_{CD}}\left( {\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{r'}}} \right) = \sum\limits_{i = 1}^c {\frac{{\left| {{r_i}-{{r'}_i}} \right|}}{{{r_i} + {{r'}_i}}}} $ | (3) |
DCD的取值在[0, +∞)之间, 兰氏距离值越小, 两个排序特征选择结果越相似.
而权重兰氏距离可以度量部分排序列表的相似性, 其计算如公式(4):
| $ {D_{WCD}}\left( {\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{r'}}} \right) = \sum\limits_{i = 1}^c {\frac{{\left| {\min \left\{ {{r_i}, k + 1} \right\}-\min \left\{ {{{r'}_i}, k + 1} \right\}} \right|}}{{\min \left\{ {{r_i}, k + 1} \right\} + \min \left\{ {{{r'}_i}, k + 1} \right\}}}} $ | (4) |
其中, k(1≤k≤c)是参数, 表示从特征排序的结果中选择前k个特征作为分类器输入特征, min(ri, k+1)表示取ri和k+1两个值中的较小者.
度量部分子集列表相似性的典型指标是叠加评分, 其计算如公式(5):
| $ {D_{OS}}\left( {\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{r'}}, \alpha } \right) = \sum\limits_{k = 1}^c {w_\alpha ^{\left( k \right)}} \cdot \sum\limits_{i = 1}^c {I\left( {{r_i} \leqslant k \wedge {{r'}_i} \leqslant k} \right)} $ | (5) |
其中, k表示从特征排序的结果中选择前k个特征作为特征子集; I表示指示函数(如果表达式A是正确的, 则I(A)=1, 否则I(A)=0);
基于詹森-香农距离的度量指标, 可以用在全排序列表、部分子集列表和部分排序列表的计算中.设由M个特征子集组成的系统R, 它们的新詹森-香农距离指标计算如公式(6):
| $ {D_{JS}}\left( \mathit{\boldsymbol{R}} \right) = 1-\frac{{{T_{JS}}\left( \mathit{\boldsymbol{R}} \right)}}{{T_{JS}^*\left( \mathit{\boldsymbol{R}} \right)}} $ | (6) |
其中,
●
●
设排序向量为r=(r1, r2, r3, …, rc), qi可通过公式(7)计算:
| $ {q_i} = \frac{1}{{2c}}\left( {1 + \frac{1}{{{r_i}}} + \frac{1}{{{r_i} + 1}} + \cdots + \frac{1}{c}} \right) $ | (7) |
其中, qi满足概率的性质, 即
针对子集法的特征选择结果, 研究人员也提出了许多有效的稳定性度量指标.需要注意的是:分类器或领域专家更为关注特征选择返回的特征子集, 并非是全部特征的排序或权重.对排序法和权重法而言, 其返回结果一般是根据要求按照排序列表或权重的降序给出满足规模的特征子集, 因此, 子集法稳定性度量指标同样适用于度量排序法和权重法的特征选择结果.
子集法稳定性度量指标可以分为4类:基于相似度(距离)的指标、基于频次的指标、基于信息理论的指标和基于相关性的指标.基于相似度(距离)的指标包括杰卡德距离、谷元距离、昆彻瓦相似度度量(Kuncheva similarity measure)指标、扩展昆彻瓦相似度度量(extensions of Kuncheva similarity measure)指标、邓恩稳定性指标(Dunne stability index)、海明距离(Hamming distance)和戴斯系数(Dice coefficient)等[13, 62, 63].基于频次的指标是基于特征在多个子集列表中出现的频次进行稳定性度量, 包括权重一致性(weighted consistency)指标和叠加基因比例(percentage of overlapping gene)等[64-66].基于信息理论的典型指标是对称不确定[67].基于相关性的指标是抽样皮尔逊相关系数(sample Pearson’s correlation coefficient)[68].
下面介绍4类方法中常用的子集法特征选择稳定性指标, 我们将在第3节通过实验对这些指标的性能做进一步的比较分析.
对两个特征子集s和s’, 可以直接采用谷元距离度量它们的相似性, 如公式(8):
| $ {D_T}\left( {\mathit{\boldsymbol{s}}, \mathit{\boldsymbol{s'}}} \right) = 1-\frac{{\left| \mathit{\boldsymbol{s}} \right| + \left| {\mathit{\boldsymbol{s'}}} \right|-2\left| {\mathit{\boldsymbol{s}} \cap \mathit{\boldsymbol{s'}}} \right|}}{{\left| \mathit{\boldsymbol{s}} \right| + \left| {\mathit{\boldsymbol{s'}}} \right|-\left| {\mathit{\boldsymbol{s}} \cap \mathit{\boldsymbol{s'}}} \right|}} $ | (8) |
|·|表示特征子集的基; ST的值在[0, 1]之间, 值为0表示两个子集之间没有相交的子集, 1表示两个子集完全相同.
对两个基相同的特征子集s和s’, 它们的昆彻瓦相似度度量指标计算如公式(9):
| $ {D_K}\left( {\mathit{\boldsymbol{s}}, \mathit{\boldsymbol{s'}}} \right) = \frac{{\left| {\mathit{\boldsymbol{s}} \cap \mathit{\boldsymbol{s'}}} \right| \cdot c-{d^2}}}{{d\left( {c-d} \right)}} $ | (9) |
其中, d(1≤d≤c)表示两个特征子集的基.昆彻瓦相似度度量指标的取值是在[-1, 1]之间, 昆彻瓦相似度度量指标取值越大, 两个特征子集相似度越高.
扩展昆彻瓦相似度度量指标, 该指标是昆彻瓦相似度度量指标的扩展, 可以用来度量不同特征个数的特征子集相似性.当两个特征子集规模一致时, 它的值就等于昆彻瓦相似度度量指标的值.设两个基不相等的特征子集s和s’, 它们的扩展昆彻瓦相似度度量指标值的计算如公式(10):
| $ {D_E}(\mathit{\boldsymbol{s}}, \mathit{\boldsymbol{s'}}) = \frac{{|\mathit{\boldsymbol{s}} \cap \mathit{\boldsymbol{s'}}|- \frac{{|\mathit{\boldsymbol{s}}| \cdot |\mathit{\boldsymbol{s'}}|}}{c}}}{{\max \left[{-\max (0, |\mathit{\boldsymbol{s}}| + |\mathit{\boldsymbol{s'}}|-c) + \frac{{|\mathit{\boldsymbol{s}}| \cdot |\mathit{\boldsymbol{s'}}|}}{c};\min (|\mathit{\boldsymbol{s}}|, |\mathit{\boldsymbol{s'}}|)-\frac{{|\mathit{\boldsymbol{s}}| \cdot |\mathit{\boldsymbol{s'}}|}}{c}} \right]}} $ | (10) |
与昆彻瓦相似度度量指标类似, 扩展昆彻瓦相似度度量指标的取值是在[-1, 1]之间, 扩展昆彻瓦相似度度量指标取值越大, 两个特征子集相似度越高.
邓恩稳定性指标计算方式如公式(11):
| $ {D_D}(\mathit{\boldsymbol{s}}, \mathit{\boldsymbol{s'}}) = \frac{{|\mathit{\boldsymbol{s}}-\mathit{\boldsymbol{s'}}| + |\mathit{\boldsymbol{s'}}-\mathit{\boldsymbol{s}}|}}{c} $ | (11) |
其中, s-s’表示特征子集s中与特征子集s’不相交的特征集.邓恩稳定性指标的取值在[0, 2]之间, 当两个特征子集完全不一致时为2, 完全一致时为0.
设S为M个特征子集组成的系统,
| $ {D_{CW}}(\mathit{\boldsymbol{S}}) = \sum\limits_{i \in c} {\frac{{{N_i}}}{N}} \cdot \frac{{{N_i}-1}}{{M-1}} $ | (12) |
权重一致性指标的取值范围在[0, 1]之间, 当且仅当N=c时为0, 当且仅当N=M·c时为1.
抽样皮尔逊相关系数由公式(13)计算:
| $ {D_S}(\mathit{\boldsymbol{s}}, \mathit{\boldsymbol{s'}}) = \frac{{\frac{1}{c}\sum\nolimits_{i = 1}^c {({x_i}-\bar x)({{x'}_i}-\bar x')} }}{{\sqrt {\frac{1}{c}\sum\nolimits_{i = 1}^c {{{({x_i}-\bar x)}^2}} } \sqrt {\frac{1}{c}\sum\nolimits_{i = 1}^c {{{({{x'}_i} - \bar x')}^2}} } }} $ | (13) |
其中:xi表示第i个属性是否出现在特征子集s中, 出现为1, 否则为0;
目前, 对特征选择稳定性度量指标性质的研究相对较少, 仅有少量相关文献对其做了初步的研究和探索.
文献[62]提出特征选择稳定性指标应具有6个特性, 即有界性、单调递增性、随机校正性、完全定义性、对称性和冗余反馈等.文献[68]在文献[62]的基础上进行了进一步探讨, 提出特征选择稳定性指标应具有4个特性, 即完全定义性、有界性、单调递增性和随机校正性.本文在文献[68]的基础上, 对特征选择稳定性度量指标性质做进一步的探讨.
首先给出完全定义性、有界性、单调递增性和随机校正性的定义.
● 完全定义性:特征选择稳定性指标能够度量不同规模的特征子集;
● 有界性:特征选择稳定性指标的评估值要具有上下界;
● 单调递增性:特征选择稳定性指标值应当随着选择的特征子集相似度的增加而增加;
● 随机校正性:特征选择稳定性指标要能够反映出特征选择算法选择的特征是否具有随机性, 并返回确定的常量值.
对上述4个性质做进一步分析.
● 完全定义性对度量指标而言并非是必要的性质, 它仅仅表明度量指标的适用范围是否足够广泛.在实际研究中, 对特征选择算法稳定性的度量多数是建立在选择相等特征个数的基础上.事实上, 只要研究的对象是在度量指标的适用范围内即可;
● 有界性是度量指标必须满足的性质, 否则我们无法准确地判定特征子集的相似度.例如, 若不存在上下界, 那么我们就无法准确判别完全一致的两个特征子集和完全不一致的两个特征子集的差异程度, 而仅仅只能说明前者相似性大于后者;
● 单调递增性也是一个度量指标应当具备的基本性质, 否则无法对指标的结果做出正确的评判;
● 随机校正性对特征选择稳定性度量指标而言是一个重要的基本性质, 它是间接反映特征选择方法有效性的途径.例如:当有100个特征时, 采用随机方法选择2个特征个数为10的特征子集, 2个子集包含的特征完全一致的概率仅为1%;若将特征个数提高到90, 则2个特征子集包含的特征完全一致的概率将达到81%.因此, 为了避免度量结果无法真实反映出特征选择结果是否具有随机性, 度量指标必须要具备随机校正性.
2.2 特征选择算法的稳定性评估在对特征选择算法本身的稳定性进行评估方面, 相关文献做了一些初步的验证与分析.
文献[69]表明:提出的基于树形表示的TREE-LASSO特征选择算法与LASSO、信息增益、ReliefF和T检验特征选择方法进行对比, 拥有较好的稳定性.文献[70]通过实验得出结论:单变量特征选择方法能够获得较好的稳定性, 但是具有较弱的分类性能; 而多变量方法——最小冗余最大相关特征选择算法在分类性能和稳定性方面达到较好的平衡.文献[71]提出一种固定重叠分割的数据抽样方法, 该方法采用参数控制抽样数据之间重复样本的规模, 然后使用谷元距离指标度量特征选择稳定性, 结果表明, ReliefF具有较好的稳定性.文献[72]通过在软件质量度量数据中对典型的过滤式和封装式特征选择算法进行对比实验得出结论:ReliefF具有较好的稳定性; 同时, 提高数据扰动生成样本的重复率可以提高算法的稳定性.文献[73]在癌症数据集上得出结论, 贝叶斯错误估计法(Bayesian error estimator)在分类性能和稳定性上具有较好的综合性能.文献[74]经过比较分析认为:在训练数据扰动和数据分布不平衡存在的情况下, 基于相关性的特征选择算法具有较好的稳定性能.此外, 文献[75]比较了单变量方法和多变量方法的稳定性能, 并得出结论:单变量方法选择特征子集的相似度较高, 即, 不同的单变量方法在稳定性方面具有相似性, 如卡方检验、信息增益、对称不确定、增益率和单规则等; 多变量方法的稳定性能差异度较大, 如ReliefF、支持向量机递归特征消除和支持向量机特征选择等; 且基于支持向量机的特征选择方法对参数设置较为敏感, 不同参数条件下选择的特征子集相似度具有较大的差异.
虽然较多研究成果对特征选择算法本身的稳定性做了比较分析, 但是这些工作仍然存在需要进一步分析解释的问题:一是这些研究并没有在统一的标准数据集上进行实验与分析, 因此其结论难以具有普适性, 甚至有可能得出相对立的结论; 二是并没有对特征选择算法内在的稳定性做深层的分析, 即, 造成这些方法稳定的原因是什么, 这是特征选择算法稳定性评估的目的和落脚点.
2.3 特征选择稳定性影响因素评估对影响特征选择稳定性的因素进行评估与研究方面, 研究人员主要从理论和实验两个方面进行分析.
● 理论分析方面
文献[76]通过概率理论和随机生成样本数据的方法, 对造成特征选择不稳定的原因及提升方法做了初步研究.首先构造满足高斯分布的数据集, 并采用参数控制数据集分布的复杂程度.在此基础上, 经过概率分析得出结论:对分布较为简单的数据集, 选择相关特征的概率会随着输入样本规模的增长而增加; 对于分布较为复杂的数据集, 输入样本规模的增长不会显著提高选择相关特征的概率; 同时, 即使在分布较为简单的情况下, 输入样本规模较小时, 选择相关特征的概率存在较低的上限.在人工和真实数据集上的实验结果进一步验证了上述理论分析结论, 并给出了提高特征选择稳定性的两种方法:一种是增加输入样本的规模, 另一种是采用可靠的方法进行数据降维.
● 实验分析方面
文献[70]指出:特征选择算法的稳定性与数据集的复杂性具有较强相关性, 而与分类性能之间并不存在显著的相关性, 提高特征选择稳定性并不能提高算法的分类性能.文献[77]在核磁共振成像分类数据上对过滤法和封装法等两种类型的特征选择方法的稳定性进行了比较分析, 研究表明:特征选择稳定性与选择特征的数量具有强相关性, 与分类性能具有弱相关性, 而与平均分类性能无关.文献[78]认为:在非独立高维数据中, 基于统计理论的特征选择方法是不适用的, 数据的微小变化会导致结果产生较大幅度的变化; 同时, 数据分布的不均匀也是造成特征选择不稳定的原因.
通过上述相关研究工作可以看出, 数据的分布复杂性、样本规模、特征之间的相关性等都是影响特征选择稳定性的因素; 同时也可以看出, 特征选择稳定性与分类性能之间并无确定的相关性.然而, 这些都是在假设仅存在一种影响因素的前提下得出的结论, 当存在多种影响因素的情况下对特征选择稳定性有何影响, 以及在什么样的数据集中特征选择稳定性与分类性能之间存在确定相关性, 这些都需要我们进一步研究.
3 实验分析由于在分类过程中, 分类器要求的输入并非是特征的权重或排序, 而是特征子集.因此当特征选择方法返回权重值或排序列表时, 都必须转换为特征子集并构造训练样本作为输入, 例如按照权重值由大到小排列后选择前m个特征组成特征子集, 或者是按照排序列表选择前m个特征组成特征子集.因此, 子集法度量指标的适用范围最为广泛; 同时, 目前也鲜有从指标的性质出发评估指标性能的相关工作.本节对子集法中5种稳定性度量指标做比较分析, 在此基础上, 选择合适的指标对融合单变量与多变量的集成方法做进一步的分析研究.
实验数据使用二分类数据集, 包括典型的高维数据领域, 即文本数据和基因数据.数据集来源于网站: http://featureselection.asu.edu/datasets.php, 数据集的有关基本信息见表 2.
| Table 2 Characteristics of experiment datasets 表 2 实验数据集属性 |
3.1 特征选择稳定性指标分析
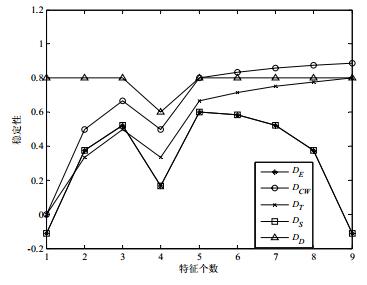
本节对5种子集法特征选择稳定性指标进行分析, 即邓恩指标DD、谷元距离指标DT、抽样皮尔逊相关系数DS、权重一致性指标DCW、扩展昆彻瓦指标DE.按照文献[79]中的方法, 假设一个特征选择方法生成2个特征个数为10的特征子集S1和S2(M=2, c=10), 其中, S1={x9, x7, x2, x1, x3, x10, x8, x4, x5, x6}, S2={x3, x7, x9, x10, x2, x4, x8, x6, x1, x5}, 在这两个数据集上比较5种指标随着特征个数变化的性能表现.
图 2描述了这5种指标随特征个数d变化时的度量趋势, 从图中可以看出:所有的稳定性指标在d=4时都正确出现了下降的趋势; 但是当d>5的时候, 不同指标表现出不同的取值趋势, DT, DD和DCW的值随着特征子集个数的增加而增长.这是由于特征个数的增加导致特征子集中包含相同特征的概率也同样增加, 即, 它们不具备随机校正性; 而另外两种指标DE和DS则能够正确反映出该情况.
|
Fig. 2 Comparisons of stability indicators in feature subset S1 and S2 图 2 特征子集S1和S2上稳定性指标比较 |
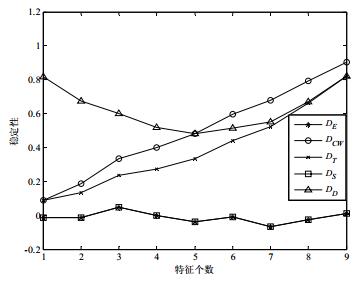
为了进一步验证这5种稳定性指标在随机生成特征子集情况下的性能表现, 按照文献[63]的方法, 随机生成10组特征个数为10的特征子集(M=10, c=10)作为实验数据集, 并用稳定性指标度量在特征子集个数变化的情况下随机特征选择方法的稳定性, 结果如图 3所示.
|
Fig. 3 Comparisons of stability indicators in ten random feature subsets 图 3 10组随机生成特征子集稳定性指标比较 |
从图 3中可以看出:只有DE和DS指标的度量值趋于0, 而其他3种指标的取值都在一定程度上随着特征子集个数的增加而增长.说明DT, DD和DCW指标不具备随机校正性的属性.
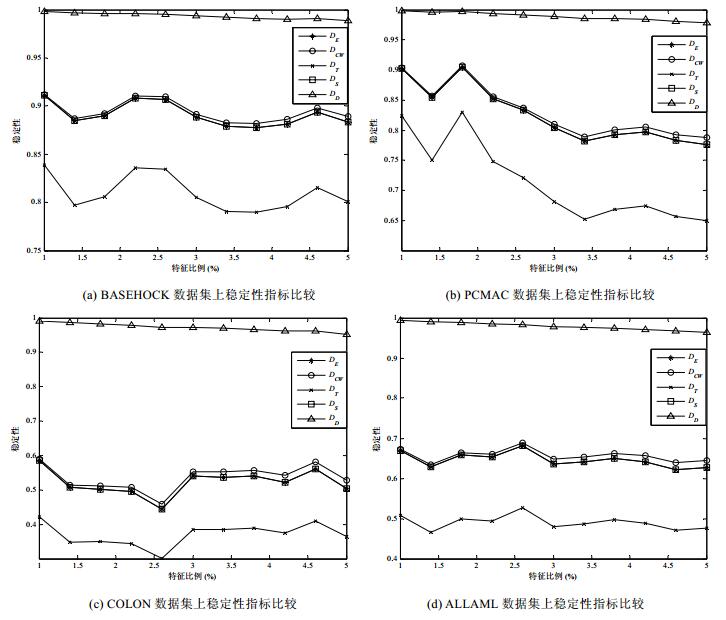
为了验证5种特征稳定性指标在真实数据集上的度量性能, 使用单变量排序法卡方检验(χ2)对4个数据集进行特征选择.在此基础上, 选择特征比例从1%~5%的特征组成特征子集, 并使用稳定性指标进行度量, 实验采用5重交叉检验, 测试结果如图 4所示.
|
Fig. 4 Comparisons of stability indicators in four real datasets 图 4 4组真实数据集上的稳定性指标比较 |
从图 4中可以看出:DE, DS和DCW指标提供了相似的精确结果, 3种指标对特征比例的变化具有一定的鲁棒性; 相反, DD受高维数据的影响, 无法度量测试条件下特征选择的稳定性, 即, 该指标在高维数据的测试条件下不可用.DT指标与DE, DS和DCW指标的结果相比, 其度量值偏低, 但其变化趋势与DE, DS和DCW指标的变化趋势相近, 可在一定程度上反映特征选择方法的稳定性.
通过实验比较可以看出:DE, DS和DCW指标在多数测试条件下能够较准确反映出特征选择的稳定性; DD受高维数据的影响, 无法准确度量特征选择的稳定性, 在真实实验测试数据条件下, 该指标甚至不可用.进一步分析, 在随机生成特征子集上的测试表明, DT, DD和DCW指标无法度量出随机特征选择的稳定性, 即不具备随机校正性, 因此, DE和DS指标在度量特征选择稳定性方面具有较好的综合性能.
3.2 特征选择稳定性集成方法分析在特征选择稳定性的研究中, 研究人员广泛采用了集成方法提高算法的稳定性, 但是这些工作仅表明了集成方法的有效性, 并未对集成方法特别是结合单变量与多变量算法的集成方法在稳定性、分类性能与分类器之间的相关性上做进一步的分析评估.
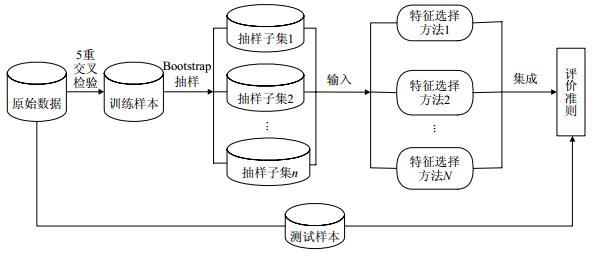
本节从这3个方面入手, 对结合单变量与多变量特征选择的集成方法在稳定性提升效果、分类性能与分类器间的关系做深入的实验分析.使用5重交叉检验方法将原始数据分为训练样本和测试数样本, 训练样本经过Bootstrap抽样生成n个抽样数据, 每个特征选择方法在n个抽样数据上进行特征选择, 对N×n个特征选择结果进行集成形成最终的特征子集, 采用测试样本得出分类正确率.文献[21]验证了不同的集成策略之间并无显著的差异, 因此这里使用中值法集成特征选择结果, 即, 给特征赋予其在多个排序列表中处于中间位置的序号.实验的框架如图 5所示(这里n=5).选用的单变量特征选择方法为χ2和信息增益(IG), 多变量特征选择方法为ReliefF和支持向量机递归特征消除(SVM-RFE), 选用支持向量机(SVM)、K近邻(KNN)和朴素贝叶斯(NB)等3种分类器.第3.1节通过实验表明, DE和DS指标在度量特征选择稳定性方面具有较好的性能表现, 因此本节使用分类正确率和DE指标对结果进行度量.
|
Fig. 5 Framework of experiments 图 5 实验框架图 |
为了分析单变量和多变量特征选择方法在集成条件下的性能表现, 设计4种集成方式对上述4种特征选择方法进行组合, 见表 3.
| Table 3 Ensemble feature selection methods 表 3 集成特征选择方法 |
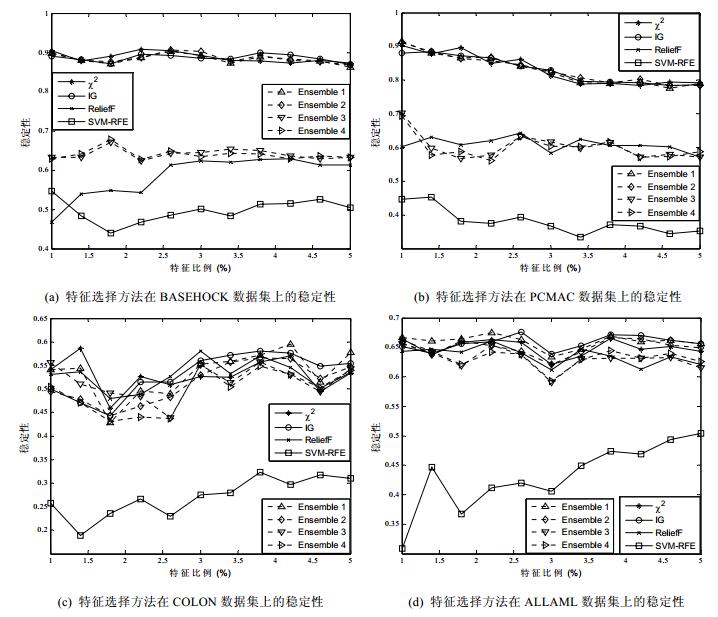
在4个数据集上, 4种集成特征选择方法和4种基本特征选择方法的稳定性度量结果如图 6所示, 其中, 横坐标表示选择的特征占全部特征的比例.
|
Fig. 6 Stability comparisons among ensemble feature selection methods 图 6 集成特征选择方法稳定性比较 |
首先观察在文本数据集上集成方法的稳定性提升效果.从图 6中的(a)可以看出, 在BASEHOCK数据集上, 对于稳定性较好的χ2和IG而言, 增加稳定性较弱的ReliefF或SVMFS方法的Ensemble 1和Ensemble 2在稳定性方面并没有显著的提升, Ensemble 1和Ensemble 2的稳定性要弱于χ2, 较IG有微弱的提升.相对ReliefF方法, Ensemble 1在稳定性方面有显著的提升, Ensemble 2对于SVMFS方法也具有显著的提升.Ensemble 3和Ensemble 4两种集成方法在稳定性方面都要好于ReliefF和SVMFS方法.但Ensemble 3和Ensemble 4的稳定性要弱于χ2和IG.从图 6中的(b)同样可以看出, 在PCMAC数据集上, Ensemble 1和Ensemble 2的稳定性与χ2和IG相比并没有显著提升, 但都要好于ReliefF或SVMFS方法.Ensemble 3和Ensemble 4的稳定性要好于ReliefF和SVMFS, 而弱于χ2或IG.
观察4种集成特征选择方法在基因数据集上的提升效果, 即图 6中的(c)和(d).首先, 对比稳定性表现较弱的SVMFS方法, 在COLON和ALLAML数据集上, Ensemble 2、Ensemble 3和Ensemble 4在稳定性上都具有显著的提升效果.在这两个数据集上, 4种集成方法与χ2, IG和ReliefF方法的稳定性随着特征比例的增加而不断变化, 并无明显的优劣区分.
综上所述, 对于稳定性较强的特征选择方法(如χ2和IG), 采用集成方法对其稳定性的提升效果并不显著.而对于稳定性较弱的特征选择方法(如ReliefF和SVMFS), 采用集成方法能够在一定程度上提高特征选择稳定性.因此, 采用集成方法能够在一定程度上综合保证特征选择结果的稳定性, 即, 能够在不同的数据集上确保特征选择稳定性的提升.进一步观察可以看出, 单变量方法χ2和IG的稳定性要好于多变量方法ReliefF和SVMFS.这也是显然的, 单变量方法采用特定内在的度量方式独立评估每个特征, 而多变量方法在评估特征的同时也会考虑该特征与其他特征的关联.因此, 由于高维数据特征间复杂关系的存在, 导致多变量特征选择方法的稳定性也在一定程度上受到了影响.
表 4~表 7给出了在4个数据集上, 4种基本特征选择方法和4种集成特征选择方法在3种不同分类器上的分类正确率, 特征比例仍然设置为1%~5%.
| Table 4 Classification accuracy of feature selection methods in BASEHOCK 表 4 特征选择方法在BASEHOCK数据集上的分类正确率 |
| Table 5 Classification accuracy of feature selection methods in PCMAC 表 5 特征选择方法在PCMAC数据集上的分类正确率 |
| Table 6 Classification accuracy of feature selection methods in COLON 表 6 特征选择方法在COLON数据集上的分类正确率 |
| Table 7 Classification accuracy of feature selection methods in ALLAML 表 7 特征选择方法在ALLAML数据集上的分类正确率 |
通过表 4~表 7可以看出:除了COLON数据集, 使用SVM分类器时, 4种基本特征选择方法和4种集成特征选择方法在多数情况下能够取得较好的分类正确率.因此从分类器的角度, SVM分类性能要好于KNN和NB分类器.其次, 从集成方法的角度看, 与基本的单变量和多变量特征选择方法相比, 4种集成特征选择方法在多数情况下都能够获得较好的分类性能, 特别是在BASEHOCK数据集上, 4种集成方法提供了全面较好的结果.而针对具体的集成方法而言, 4种集成方式并无明显的差异.这说明在单变量和多变量方法同时存在的情况下, 集成选择能够有效提高分类性能, 而集成的算法对分类性能并无明显的影响.最后, 从分类性能的角度, 单变量方法与多变量方法相比, 在分类性能上并无明显的差异.这说明多变量方法能够获得在分类性能上较好的特征子集, 但是由于多变量方法稳定性较弱, 因此其生成特征子集与单变量方法相比变化程度较强, 即可信度较低.
综上, 与基本特征选择方法相比, 使用结合单变量与多变量方法的集成方法能够确保选择的特征子集在不同数据集上具有良好稳定性, 同时也具有优越的分类性能; 其次, 集成方法在分类性能上的提升效果与分类器并无显著关联性, 采用SVM分类器能够获得较好的分类性能.
4 结束语本文总结了特征选择稳定性提升方法的研究进展, 概要阐述了演化算法在特征选择稳定性中的应用, 归纳特征选择稳定性中的评估, 通过实验分析典型的子集法稳定性度量指标的性能, 并验证了结合单变量与多变量算法的集成方法能够同时提高算法的稳定性和分类性能.
尽管特征选择稳定性在近两年得到了学术界的重视和发展, 但其仍属于起步阶段, 还有一些亟待解决的问题:在高维数据中, 除了特征维度较高之外, 还有一些常常被忽略的因素, 如样本的不平衡、数据分布的漂移和噪声数据等, 而目前的提升特征选择稳定性的方法并未考虑这些情况的存在, 因此结合高维数据蕴含的特点, 提高特征选择方法的稳定性是一项值得深入研究的课题; 特征选择稳定性度量指标是特征选择稳定性研究的基础, 虽然研究人员提出或借鉴了一些度量指标, 但由于在稳定性度量指标应当具备的性质方面并未有统一的标准, 造成不同指标度量的结果可能存在差异性, 导致我们不能客观全面地评价特征选择稳定性的研究成果, 因此对特征选择稳定性度量指标的研究仍然任重道远; 目前, 多数特征选择稳定性提升方法的研究成果仍然是建立在集成或扰动的机械方法之上, 虽然特征法在特征层面对提高稳定性做了进一步的探索, 但其泛化能力也是值得商榷的, 是否可以针对特征选择稳定性发展出专用的特征选择算法, 也是值得探讨的问题; 当前, 对特征选择稳定性的研究主要聚焦于独立于分类器的过滤式特征选择方法, 而作为重要分支的基于进化算法的特征选择方法, 在稳定性方面的研究还存在较多的空白.基于进化算法的特征选择方法的稳定性是否与采用的进化算法相关, 其与分类器和评价准则之间是否具有关联性, 如何提高基于进化算法特征选择的稳定性, 也是需要进一步探索的研究方向; 对影响特征选择稳定性因素的深入研究和探索, 这是从根本上解决特征选择稳定性问题的出发点和落脚点.对不同的数据集或不同的应用而言, 造成特征选择不稳定的因素不尽相同, 如特征规模、样本数量、数据分布等, 然而目前鲜有研究成果对其进行深入探讨.对导致特征选择不稳定的因素以及这些因素之间相互的影响做判断及分析, 并以此作为依据提出对应的解决方案, 是特征选择稳定性研究的重要内容.
| [1] |
Emani CK, Cullot N, Nicolle C. Understandable big data:A survey. Computer Science Review, 2015, 17: 70–81.
[doi:10.1016/j.cosrev.2015.05.002] |
| [2] |
Fakhraei S, Soltanian-Zadeh H, Fotouhi F. Bias and stability of single variable classifiers for feature ranking and selection. Expert Systems with Applications, 2014, 41(15): 6945–6958.
[doi:10.1016/j.eswa.2014.05.007] |
| [3] |
Li JD, Liu H. Challenges of feature selection for big data analytics. IEEE Intelligent Systems, 2016, 32(2): 9–15.
[doi:10.1109/MIS.2017.38] |
| [4] |
Bolon-Canedo V, Sanchez-Marono N, Alonso-Betanzos A. Feature selection for high dimensional data. Progress in Artificial Intelligence, 2016, 5(2): 65–75.
[doi:10.1007/s13748-015-0080-y] |
| [5] |
Goh WW, Wong L. Evaluating feature selection stability in next generation proteomics. Journal of Bioinformatics and Computational Biology, 2016, 14(5): 1650029.
[doi:10.1142/S0219720016500293] |
| [6] |
Du W, Cao ZB, Song TC, Li Y, Liang YC. A feature selection method based on multiple kernel learning with expression profiles of different types. BioData Mining, 2017, 10: 4.
[doi:10.1186/s13040-017-0124-x] |
| [7] |
Chlis NK, Bei ES, Zervakis M. Introducing a stable bootstrap validation framework for reliable genomic signature extraction. IEEE/ACM Trans. on Computational Biology and Bioinformatics, 2016, PP(99): 1-1. [doi: 10.1109/TCBB.2016.2633267] |
| [8] |
Yu K, Wu XD, Ding W, Pei J. Scalable and accurate online feature selection for big data. ACM Trans. on Knowledge Discovery from Data, 2016, 11(2): Article 16. [doi: 10.1145/2976744] |
| [9] |
Iglesias F, Zseby T. Analysis of network traffic features for anomaly detection. Machine Learning, 2015, 101(1): 59–84.
[doi:10.1007/s10994-014-5473-9] |
| [10] |
Wang YL, Li ZQ, Wang YF, Wang XN, Zheng JJ, Duan XJ, Chen HF. A novel approach for stable selection of informative redundant features from high dimensional fMRI data. Computer Science, 2016, 146: 191–208.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=Arxiv000001318081 |
| [11] |
Park CH, Kim SB. Sequential random K nearest neighbor feature selection for high dimensional data. Expert Systems with Applications, 2015, 42(5): 2336–2342.
[doi:10.1016/j.eswa.2014.10.044] |
| [12] |
Aldehim GN. Heuristic ensembles of filters for accurate and reliable feature selection[Ph. D. Thesis]. Norwich: University of East Anglia, 2015. |
| [13] |
Kalousis A, Prados J, Hilario M. Stability of feature selection algorithms:A study on high dimensional spaces. Knowledge and Information Systems, 2007, 12(1): 95–116.
[doi:10.1007/s10115-006-0040-8] |
| [14] |
Fan M, Chou CA. Exploring stability based voxel selection methods in MVPA using cognitive neuroimaging data:A comprehensive study. Brain Informatics, 2016, 3(3): 193–203.
[doi:10.1007/s40708-016-0048-0] |
| [15] |
Tohka J, Moradi E, Huttunen H. Comparison of feature selection techniques in machine learning for anatomical brain MRI in dementia. Neuroinformatics, 2016, 14(3): 1–18.
[doi:10.1007/s12021-015-9292-3] |
| [16] |
Tommasel A, Godoy D. Short text feature construction and selection in social media data:A survey. Artificial Intelligence Review, 2016: 1–38.
[doi:10.1007/s10462-016-9528-0] |
| [17] |
Alkuhlani A, Nassef M, Farag I. Multistage feature selection approach for high dimensional caner data. Soft Computing, 2016: 1–12.
[doi:10.1007%2Fs00500-016-2439-9] |
| [18] |
Gangeh MJ, Zarkoob H, Ghodsi A. Fast and scalable feature selection for gene expression data using Hilbert-Schmidt independence criterion. IEEE/ACM Trans. on Computational Biology and Bioinformatics, 2017, 14(1): 167-181. [doi: 10.1109/TCBB.2016.2631164] |
| [19] |
Schirra LR, Lausser L, A.Kestler H. Selection stability as a means of biomarker discovery in classification. Studies in Classification, Data Analysis, and Knowledge Organization, 2016: 79–89.
[doi:10.1007/978-3-319-25226-1_7] |
| [20] |
Zhou QF, Ding JC, Ning YP, Luo LK, Li T. Stable feature selection with ensembles of multi ReliefF. In: Proc. of the 201410th Int'l Conf. on Natural. 2014. 742-747. [doi: 10.1109/ICNC.2014.6975929] |
| [21] |
Pes B, Dessi N, Angioni M. Exploiting the ensemble paradigm for stable feature selection:A case study on high dimensional genomic data. Information Fusion, 2017, 35(C): 132–147.
[doi:10.1016/j.inffus.2016.10.001] |
| [22] |
Saeys Y, Abeel T, Peer YVD. Robust feature selection using ensemble feature selection techniques. In: Proc. of the ECML/PKDD. 2008. 313-325. [doi: 10.1007/978-3-540-87481-2_21] |
| [23] |
Abeel T, Helleputte T, Peer YVD, Dupont P, Saeys Y. Robust biomarker identification for cancer diagnosis with ensemble feature selection methods. Bioinformatics, 2010, 26(3): 392–398.
[doi:10.1093/bioinformatics/btp630] |
| [24] |
Yang P, Ho JW, Yang YH, Zhou BB. Gene-Gene interaction filtering with ensemble of filters. Bmc Bioinformatics, 2011, 12(S1): S10.
[doi:10.1186/1471-2105-12-S1-S10] |
| [25] |
Rondina JM, Hahn T, Oliveira LD, Marquand A, Dresler T, Leitner T, Fallgatter AJ, Shawe-Taylor J, Mourao-Miranda J. SCoRS a method based on stability for feature selection and apping in neuroimaging. IEEE Trans. on Medical Imaging, 2014, 33(1): 85-98. [doi: 10.1109/TMI.2013.2281398] |
| [26] |
Kim HJ, Choi BS, Huh MY. Booster in high dimensional data classification. IEEE Trans. on Knowledge and Data Engineering, 2016, 28(1): 29-40. [doi: 10.1109/TKDE.2015.2458867] |
| [27] |
He ZY, Yu WC. Stable feature selection for biomarker discovery. Computational Biology and Chemistry, 2010, 34(4): 215–225.
[doi:10.1016/j.compbiolchem.2010.07.002] |
| [28] |
Kamker I, Gupta SK, Phung D, Venkatesh S. Stabilizing l1-norm prediction models by supervised feature grouping. Journal of Biomedical Informatics, 2016, 59(C): 149–168.
[doi:10.1016/j.jbi.2015.11.012] |
| [29] |
Moayedikia A, Ong KL, Boo YL, Yeoh WGS, Jensen R. Feature selection for high dimensional imbalanced class data using harmony search. Engineering Applications of Artificial Intelligence, 2017, 57(C): 38–49.
[doi:10.1016/j.engappai.2016.10.008] |
| [30] |
Fahad A, Tari Z, Khalil I, Almalawi A, Zomaya A. An optimal and stable feature selection approach for traffic classification based on multi criterion fusion. Future Generation Computer Systems, 2014, 36(7): 156–169.
[doi:10.1016/j.future.2013.09.015] |
| [31] |
Aldehim G, Wang WJ. Weighted heuristic ensemble of filters. In: Proc. of the SAI Intelligent Systems Conf. 2015. 609-615. [doi: 10.1109/IntelliSys.2015.7361203] |
| [32] |
Bolon-Canedo V, Sanchez-Marono N, Alonso-Betanzos A. Data classification using an ensemble of filters. Neurocomputing, 2014, 135: 13–20.
[doi:10.1016/j.neucom.2013.03.067] |
| [33] |
Lior R, Barak C. A methodology for improving the performance of non-ranker feature selection filters. Int'l Journal of Pattern Recognition and Artificial Intelligence, 2007, 21(5): 809–830.
[doi:10.1142/S0218001407005727] |
| [34] |
Yang F, Ma KZ. Robust feature selection for microarray data based on multi criterion fusion. IEEE/ACM Trans. on Computational Biology and Bioinformatics, 2011, 8(4): 1080-1092. [doi: 10.1109/TCBB.2010.103] |
| [35] |
Boucheham A, Batouche M. Massively parallel feature selection based on ensemble of filters and multiple robust consensus functions for cancer gene identification. In: Proc. of the Intelligent Systems in Science and Information. 2014. 93-108. [doi: 10.1007/978-3-319-14654-6_6] |
| [36] |
Dittman DJ, Khoshgoftaar TM, Wald R, Napolitano A. Comparing two new gene selection ensemble approaches with the commonly used approach. In: Proc. of the 11th Int'l Conf. on Machine Learning and Applications. 2012. 184-191. [doi: 10.1109/ICMLA.2012.175] |
| [37] |
Kuncheva L, Smith CJ, Syed Y, Phillips CO, Lewis KE. Evaluation of feature ranking ensembles for high dimensional biomedical data: A case study. In: Proc. of the IEEE Int'l Conf. on Data Mining Workshops. 2013. 49-56. [doi: 10.1109/ICDMW.2012.12] |
| [38] |
Loscalzo S, Yu L, Ding C. Consensus group stable feature selection. In: Proc. of the ACM Conf. on Knowledge Discovery and Data Mining. 2009. 567-575. [doi: 10.1145/1557019.1557084] |
| [39] |
Garcia-Torres M, Gomez-Vela F, Melian-Batista B, Moreno-Vega JM. High dimensional feature selection via feature grouping:A variable neighborhood search approach. Information Sciences, 2016, 326(C): 102–118.
[doi:10.1016/j.ins.2015.07.041] |
| [40] |
Yu L, Ding C, Loscalzo S. Stable feature selection via dense feature groups. In: Proc. of the 14th ACM Int'l Conf. on Knowledge Discovery and Data Mining. 2008. 803-811. [doi: 10.1145/1401890.1401986] |
| [41] |
Huang J, Horowitz JL, Ma SG. Asymptotic properties of bridge estimators in sparse high dimensional regression models. Annals of Statistics, 2008, 36(2): 587–613.
[doi:10.1214/009053607000000875] |
| [42] |
Zou H, Hastie T. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society, 2005, 67(2): 301–320.
[doi:10.1111/j.1467-9868.2005.00503.x] |
| [43] |
Gauraha N. Stability feature selection using cluster representative lasso. In: Proc. of the Int'l Conf. on Pattern Recognition Applications and Methods. 2016. 381-386. [doi: 10.5220/0005827003810386] |
| [44] |
Silva B, Marques N. Feature clustering with self-organizing maps and an application to financial time-series for portfolio selection. In: Proc. of the 6th Int'l Conf. on Neural Computation. 2010. 301-309. |
| [45] |
Wang LP, Chu F, Xie W. Accurate cancer classification using expressions of very few genes. IEEE/ACM Trans. on Computational Biology and Bioinformatics, 2007, 4(1): 40-53. [doi: 10.1109/TCBB.2007.1006] |
| [46] |
Dettling M, Buhlmann P. Finding predictive gene groups from microarray data. Journal of Multivariate Analysis, 2004, 90(1): 106–131.
[doi:10.1016/j.jmva.2004.02.012] |
| [47] |
Song QB, Ni JJ, Wang GT. A fast clustering based feature subset selection algorithm for high dimensional data. IEEE Trans. on Knowledge and Data Engineering, 2013, 25(1): 1-14. [doi: DOI:10.1109/TKDE.2011.181] |
| [48] |
Shu L, Ma TY, Latecki LJ. Stable feature selection with minimal independent dominating sets. In: Proc. of the ACM Int'l Conf. on Bioinformatics. 2013. 450-457. [doi: 10.1145/2506583.2506600] |
| [49] |
Beinrucker A, Dogan U, Blanchard G. Extensions of stability selection using subsamples of observations and covariates. Statistics and Computing, 2016, 26(5): 1059–1077.
[doi:10.1007/s11222-015-9589-y] |
| [50] |
Jerbi W, Brahim AB, Essoussi N. A hybrid embedded filter method for improving feature selection stability of random forests. In: Proc. of the 16th Int'l Conf. on Hybrid Intelligent Systems. 2016. 370-379. [doi: 10.1007/978-3-319-52941-7_37] |
| [51] |
Gabriel P, Belanche LA. Improved stability of feature selection by combining instance and feature weighting. In: Proc. of the Research and Development in Intelligent Systems XXXI. 2014. 35-49. [doi: 10.1007/978-3-319-12069-0_3] |
| [52] |
Zou Q, Zeng J, Cao L, Ji R. A novel features ranking metric with application to scalable visual and bioinformatics data classification. Neurocomputing, 2016, 173: 346–354.
[doi:10.1016/j.neucom.2014.12.123] |
| [53] |
Li Y Si J, Zhou GJ, Huang SS, Chen SC. FREL: A stable feature selection algorithm. IEEE Trans. on Neural Networks and Learning Systems, 2015, 26(7): 1388-1402. [doi: 10.1109/TNNLS.2014.2341627] |
| [54] |
Yan K, Zhang D. Feature selection and analysis on correlated gas sensor data with recursive feature elimination. Sensors and Actuators B Chemical, 2015, 212: 353–363.
[doi:10.1016/j.snb.2015.02.025] |
| [55] |
Lin XH, Wang XM, Xiao NY, Huang X, Wang J. A feature selection method based on feature grouping and genetic algorithm. In: Proc. of the Int'l Conf. on Intelligent Science and Big Data Engineering. 2015. 150-158. [doi: 10.1007/978-3-319-23862-3_15] |
| [56] |
Soufan O, Kleftogiannis D, Kalnis P, Bajic VB. DWFS:A wrapper feature selection tool based on a parallel genetic algorithm. Plos One, 2015, 10(2): e0117988.
[doi:10.1371/journal.pone.0117988] |
| [57] |
Liu QJ, Zhao ZM, Li YX, Yu XL. Ensemble feature selection method based on neighborhood information and pso algorithm. Acta Electronica Sinica, 2016, 44(4): 995–1002(in Chinese with English abstract).
[doi:10.3969/j.issn.0372-2112.2016.04.034] |
| [58] |
Xue B, Zhang MJ, Brownw WN, Yao X. A survey on evolutionary computation approaches to feature selection. IEEE Trans. on Evolutionary Computation, 2016, 20(4): 606-626. [doi: 10.1109/TEVC.2015.2504420] |
| [59] |
Jurman G, Merler S, Barla A, Paoli S, Galea A, Furlanello C. Algebraic stability indicators for ranked lists in molecular profiling. Bioinformatics, 2008, 24(2): 258–264.
[doi:10.1093/bioinformatics/btm550] |
| [60] |
Bloulesteix AL, Slawski M. Stability and aggregation of ranked gene lists. Briefings in Bioinformatics, 2009, 10(5): 556–568.
[doi:10.1093/bib/bbp034] |
| [61] |
Guzman-Martinez R, Alaiz-Rodriguez R. Feature selection stability assessment based on the Jensen-Shannon divergence. In: Proc. of the European Conf. on Machine Learning and Principles and Practice of Knowledge Discovery in Databases. 2011. 597-612. [doi: 10.1007/978-3-642-23780-5_48] |
| [62] |
Nogueria S, Brown G. Measuring the stability of feature selection with applications to ensemble methods. In: Proc. of the 12th Int'l Workshop on Multiple Classifier Systems. 2015. 135-146. [doi: 10.1007/978-3-319-20248-8_12] |
| [63] |
Kuncheva LI. A stability index for feature selection. In: Proc. of the 25th ACM Conf. on Int'l Multi-Conf. Artificial Intelligence and Applications. 2007. 390-395. |
| [64] |
Somol P, Novovicovaa J. Evaluating stability and comparing output of feature selectors that optimize feature subset cardinality. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2010, 32(11): 1921-1939. [doi: 10.1109/TPAMI.2010.34] |
| [65] |
Ning YP. Research on feature selection and stability analysis for high dimensionality small sample size data[MS. Thesis]. Xiamen: Xiamen University, 2014(in Chinese with English abstract). |
| [66] |
Ji JS. Feature selection and its stability for typical geoobjects of high resolution remote sensing image[MS. Thesis]. Shanghai: Shanghai Jiao Tong University, 2015(in Chinese with English abstract). |
| [67] |
Gulgenzen G, Cataltepe Z, Yu L. Stable and accurate feature selection. In: Proc. of the European Conf. on Machine Learning and Knowledge Discovery in Databases. 2009. 455-468. [doi: 10.1007/978-3-642-04180-8_47] |
| [68] |
Nogueira S, Brown G. Measuring the stability of feature selection. In: Proc. of the European Conf. on Machine Learning and Principles and Practice of Knowledge Discovery in Databases. 2016. 442-457. [doi: 10.1007/978-3-319-46227-1_28] |
| [69] |
Kamkar I, Gupta SK, Phung D, Venkatesh S. Stable feature selection for clinical prediction:Exploiting ICD tree structure using Tree-LASSO. Journal of Biomedical Informatics, 2015, 53: 277–290.
[doi:10.1016/j.jbi.2014.11.013] |
| [70] |
Drotar P, Smekal Z. Stability of feature selection algorithms and its influence on prediction accuracy in biomedical datasets. In: Proc. of the TENCON IEEE Region 10th Conf. 2014. 1-5. [doi: 10.1109/TENCON.2014.7022309] |
| [71] |
Wang H, Khoshgoftaar TM, Seliya N. On the stability of feature selection methods in software quality prediction:an empirical investigation. Int'l Journal of Software Engineering and Knowledge Engineering, 2015, 25(9n10): 1467–1490.
[doi:10.1142/S0218194015400288] |
| [72] |
Wang H, Khoshgoftaar T, Napolitano A. Stability of three forms of feature selection methods on software engineering data. In: Proc. of the Int'l Conf. on Software Engineering and Knowledge Engineering. 2015. 385-390. [doi: 10.18293/SEKE2015-198] |
| [73] |
Hassan SS, Ruusuvuori P, Latonen L, Huttunen H. Flow cytometry based classification in cancer research:A view on feature selection. Cancer Informatics, 2016, 14(5): 75.
[doi:10.4137/CIN.S30795] |
| [74] |
Wang HJ, Khoshgoftaar TM, Napolitano A. Stability of filter-and wrapper-based software metric selection techniques. In: Proc. of the IEEE Int'l Conf. on Information Reuse and Integration. 2015. 309-314. [doi: 10.1109/IRI.2014.7051905] |
| [75] |
Dessi N, Pes B. Similarity of feature selection methods:An empirical study across data intensive classification tasks. Expert Systems with Applications, 2015, 42: 4632–4642.
[doi:10.1016/j.eswa.2015.01.069] |
| [76] |
Dernoncourt D, Hanczar B, Zucker JD. Analysis of feature selection stability on high dimension and small sample data. Computational Statistics and Data Analysis, 2014, 71(C): 681–693.
[doi:10.1016/j.csda.2013.07.012] |
| [77] |
Tohka J, Moradi E, Huttunen H. Comparison of feature selection techniques in machine learning for anatomical brain MRI in dementia. Neuroinformatics, 2016, 14(3): 1–18.
[doi:10.1007/s12021-015-9292-3] |
| [78] |
Perthame E, Friguet C, Causeur D. Stability of feature selection in classification issues for high dimensional correlated data. Statistics and Computing, 2016, 26(4): 783–796.
[doi:10.1007/s11222-015-9569-2] |
| [79] |
Drotar P, Smekal Z. Comparison of stability measures for feature selection. In: Proc. of the IEEE 13th Int'l Symp. on Applied Machine Intelligence and Informatics. 2015. 71-75. [doi: 10.1109/SAMI.2015.7061849] |
| [57] |
刘全金, 赵志敏, 李颖新, 俞晓磊. 基于近邻信息和PSO算法的集成特征选取. 电子学报, 2016, 44(4): 995–1002.
[doi:10.3969/j.issn.0372-2112.2016.04.034]
|
| [65] |
宁永鹏. 高维小样本数据的特征选择研究及其稳定性分析[硕士学位论文]. 厦门: 厦门大学, 2014.
|
| [66] |
季金胜. 高分辨率遥感影像典型地物目标的特征选择及其稳定性研究[硕士学位论文]. 上海: 上海交通大学, 2015.
|



