The Chinese Meteorological Society
Article Information
- NAN, Sulan, Junli YANG, Yan BAO, et al., 2019.
- Simulation of the Northern and Southern Hemisphere Annular Modes by CAMS-CSM. 2019.
- J. Meteor. Res., 33(5): 934-948
- http://dx.doi.org/10.1007/s13351-019-8099-9
Article History
- Received October 10, 2018
- in final form May 17, 2019
2. National Meteorological Center, China Meteorological Administration, Beijing 100081;
3. Numerical Prediction Center, National Meteorological Center, China Meteorological Administration, Beijing 100081;
4. Binjiang College, Nanjing University of Information Science & Technology, Wuxi 214105
The dominant mode of the Northern Hemisphere (NH) wintertime sea level pressure (SLP) is characterized by a zonally symmetric and meridional seesaw pattern between the Arctic and the midlatitudes. The pattern is called the NH annular mode (NAM) or Arctic Oscillation (Thompson and Wallace, 1998). Meanwhile, an equivalent pattern in the Southern Hemisphere (SH) is presented by Gong and Wang (1998), which is called the SH annular mode (SAM) or Antarctic Oscillation. This mode is also characterized by a zonally symmetric structure between the Antarctic and the midlatitudes. Both the NAM and SAM are evident throughout the year in the troposphere, and they amplify with height up into the stratosphere in certain seasons (Baldwin and Dunkerton, 1999; Thompson and Wallace, 2000). The occurrence of NAM/SAM is related to the tropospheric internal dynamics and the downward propagation of disturbances from the stratosphere to the troposphere (Lorenz and Hartmann, 2001; Feldstein, 2003; Codron, 2005; Dai and Tan, 2017).
The NAM influences not only the climate variation in the Arctic and North Atlantic sector, but also the climate systems in East Asia, such as the Siberian high, Aleutian low, East Asian winter and summer monsoons (EAWM and EASM), air temperature in Siberia and East Asia, and summer precipitation over the Yangtze River region (Gong et al, 2002; Wu and Wang, 2002; Wu and Straus, 2004; Chen and Kang, 2006). As a dominant mode of the SH extratropical atmospheric circulation, the SAM affects not only the ocean–atmosphere–ice system of the SH, but also the climate variability in the NH (Ho et al., 2005; Sun et al., 2010; Liu et al., 2015). Meanwhile, the SAM is also related to the EAWM and EASM, spring dust weather, summer precipitation and air temperature, and winter air temperature in China (Nan and Li, 2003; Fan and Wang, 2004; Xue et al., 2004; Wu et al., 2009; Zheng et al., 2015). The ability of general circulation models (GCMs) in simulating the NAM/SAM variability is an important aspect in model evaluation.
Previous studies have examined the performance of the models that participate in the Coupled Model Intercomparison Project phases 3 and 5 (CMIP3 and CMIP5) in simulating the temporal variability and spatial pattern of the NAM and SAM and in projecting their future changes in the 21st century. Most CMIP3 and CMIP5 models capture the dipole structures of the NAM and SAM. Some CMIP5 models capture the recently observed positive trend of the SAM (Zheng et al., 2013), and some CMIP3 and CMIP5 models have projected significant positive SAM trends in the 21st century (Zhu and Wang, 2008; Zheng et al., 2013). The NAM shows a strengthening trend and obvious interdecadal variations in most CMIP5 models under the RCP4.5 and RCP8.5 scenarios (Zhang et al., 2017). The CMIP5 models show an improvement over CMIP3 in producing the trends and variations of the NAM (Zhu et al., 2013). Meanwhile, CMIP5 models also show an improvement over CMIP3 models in simulating the seesaw structure of the SAM and the recently observed positive SAM trend (Zheng et al., 2013). However, simulations of the intensity and center locations of the NAM and SAM are both model- and season-dependent (Zhu and Wang, 2008). Most models from CMIP5 overestimate the strength of the NAM pattern and show significant biases in the NAM’s vertical structure (Zuo et al., 2013). In addition, the performance of the models in simulating the interannual variability of the NAM and SAM is very poor, providing no indication of the true variability (Zhu and Wang, 2008).
Recently, a new climate system model (CSM) has been developed at the Chinese Academy of Meteorological Sciences (CASM), which is called CAMS-CSM. In this study, we assess the performance of CAMS-CSM in simulating the NAM’s and SAM’s spatial structures, the relationship of the NAM with East Asian climate, and the temporal variability of the SAM, using the ECMWF reanalysis data as the basis for the evaluation.
In Section 2, we introduce CAMS-CSM, as well as the reanalysis data and methods employed in our study. Section 3 examines the NAM’s horizontal and vertical structures, and its relationship with the East Asian winter climate as simulated by CAMS-CSM. Section 4 is similar to Section 3, but for the SAM spatial structures and its temporal variability. A summary and discussion are provided in Section 5.
2 Model, data, and methodsThe model used in this study is CAMS-CSM. It consists of a modified version of ECHAM5 (Roeckner et al., 2003) as its atmospheric component, MOM4 (Griffies et al., 2004) as its oceanic component, the Sea Ice Simula-tor (Winton, 2000) as its sea-ice component, and the Common Land Model (Dai et al., 2003) as its land surface component. The main modifications made to ECHAM5 are: (1) a two-step shape preserving advection scheme (TSPAS) for water vapor transport (Yu, 1994; Zhang et al., 2013); and (2) a correlated k-distribution scheme for radiation transfer parameterization (Zhang et al., 2006a, b). The model adopts a T106 resolution in the horizontal direction and 31 levels extending up to 10 hPa in the vertical direction. The model top is set in the lower stratosphere, thus the stratosphere is not well resolved in this model. CAMS-CSM exhibits good performance in simulating the climatological mean state and seasonal cycles of the major climate system quantities across the globe. A more detailed description of CAMS-CSM can be found in Rong et al. (2018). In the present study, the Atmospheric Model Intercomparison Project (AMIP) simulation of CAMS-CSM is used to evaluate the atmospheric model’s ability in simulating the NAM and SAM. The CMIP6 historical simulation (Eyring et al., 2016) forcing fields (i.e., greenhouse gases, ozone, aerosol, and total solar irradiance) are employed to run the model from 1978 to 2013, and the output data from 1979 to 2013 are used for the model evaluation.
For model validation, the monthly mean SLP, geopotential height, zonal and meridional winds from the ERA-Interim dataset of ECMWF are used (Simmons et al., 2007). The data are downloaded from https://apps.ecmwf.int/datasets/data/. The horizontal resolution of this dataset is 0.75 degree in both longitude and latitude.
The empirical orthogonal function (EOF) analysis with area weighting (by the square root of the cosine of latitude) is employed to distinguish the NAM and SAM modes, while regression analysis is utilized to investigate their vertical structures. Correlation analysis is performed to assess their relationship with climate variations in East Asia in the CAMS-CSM simulation results. Seasonal means are constructed from the monthly mean data for December–February (DJF: boreal winter or austral summer), March–May (MAM: boreal spring or austral autumn), June–August (JJA: boreal summer or austral winter), and September−November (SON: boreal autumn or austral spring). The Student’s t-test is adopted to assess the statistical significance of relationships. The normalized principal components of the leading EOF modes (EOF1) of SLP north/south of 20°N/20°S are defined as NAM/SAM indices. In this study, the mean meridional circulation is depicted by the mass streamfunction (Ma and Li, 2007), as defined by:
| $\psi = \mathop \int \nolimits \dfrac{{2\pi Rcos\phi }}{{\rm{g}}}\left[ v \right]{\rm d}p,$ | (1) |
where v is the meridional wind, R is the mean radius of the earth, p is the pressure, ϕ is the latitude, g is the acceleration of gravity, and [ ] represents zonal averaging.
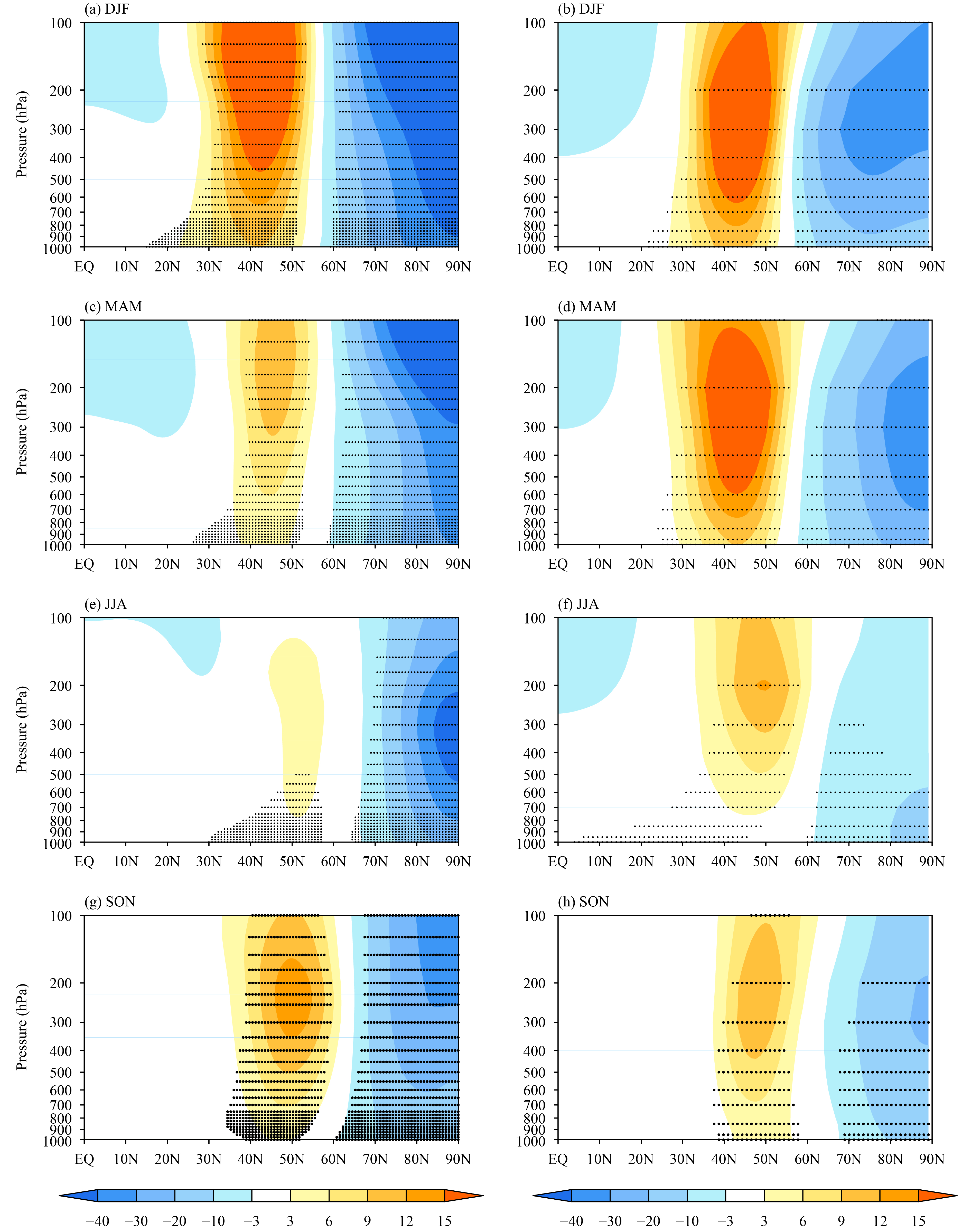
3 Spatial features of the NAM and its relation with East Asian winter climate 3.1 Spatial features 3.1.1 Horizontal structureTo examine CAMS-CSM’s simulation of the NAM’s spatial pattern, the EOF modes of SLP poleward of 20°N in all four seasons of 1979−2013 were calculated. As shown in Fig. 1, the leading modes (EOF1) in the four seasons account for 19.7%−33.8% of the total variance in ERA-Interim, and 18.0%−31.5% of the total variance in CAMS-CSM. The modes in DJF, MAM, and JJA are distinguishable in terms of the criterion of North et al. (1982). Comparing the observed and simulated results finds that CAMS-CSM is able to simulate the general features of the out-of-phase variations between the midlatitudes and the polar zones in all seasons. The locations of the three active centers, i.e., the polar zones, North Pacific, and North Atlantic at midlatitudes, are well captured. However, there are differences in the intensity and spatial distribution between the observation and simulation. Specifically, relative to the observations, the simulated negative values in the polar zone are bigger and broader, implying that CAMS-CSM produces a strong polar vortex. The simulated amplitude of the positive anomalies in the midlatitudes is also bigger, especially over North Pacific. These results indicate that the NAM in CAMS-CSM is stronger in intensity than observed. In JJA (Figs. 1e, f), the observed positive values of NAM over North America and North Atlantic are replaced by negative values in CAMS-CSM, which breaks the midlatitude zonal annular structure. In SON (Figs. 1g, h), the observed center of the negative values in the polar zone is located at the edge of Eurasia near 70°N. However, the negative values in CAMS-CSM extend toward two directions: one to the south of Greenland and the other to the midlatitudes of Eurasia. Thus, a big difference exists between the observed and simulated spatial distribution in JJA and SON.

|
| Figure 1 Leading EOF modes (EOF1) of SLP north of 20°N in (a, b) DJF (boreal winter); (c, d) MAM (boreal spring); (e, f) JJA (boreal summer); and (g, h) SON (boreal autumn) of 1979−2013 from (left panels) ERA-Interim and (right panels) CAMS-CSM. The percentage at the top right of each panel represents the variance contribution of the EOF mode. |
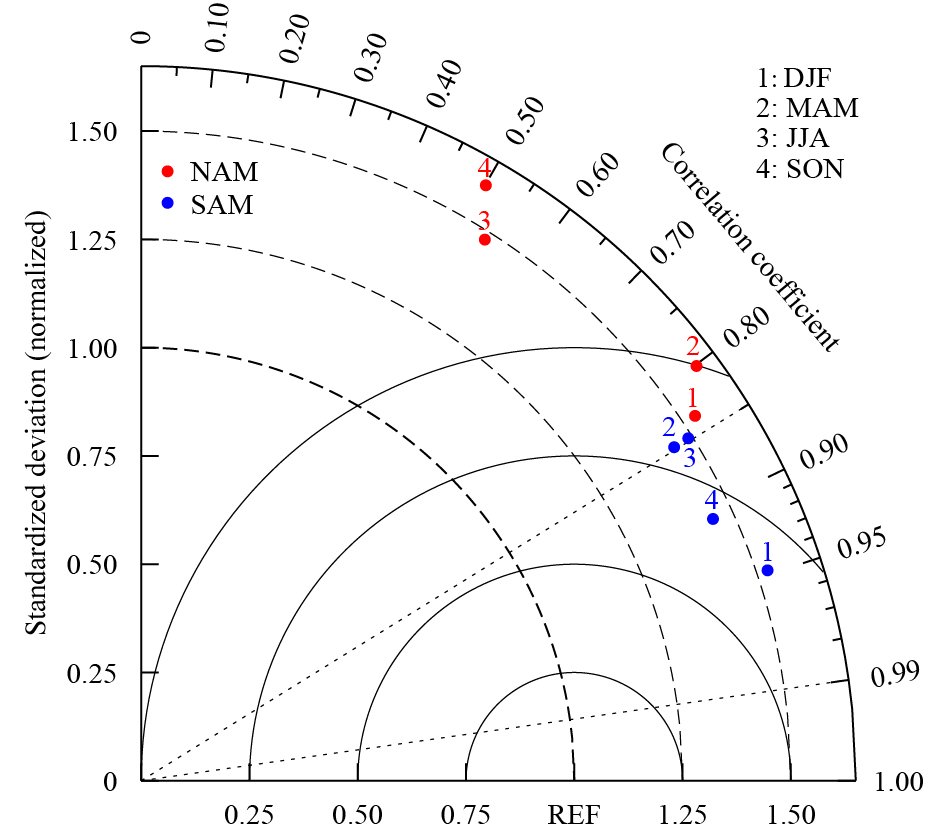
To quantify the integrated performance of CAMS-CSM in simulating the NAM, a Taylor diagram of the simulated EOF1 mode of SLP compared to the ERA-Interim data in all four seasons of 1979−2013 is shown in Fig. 2. The spatial correlation coefficients of the SLP EOF1 modes north of 20°N between CAMS-CSM and ERA-Interim are above 0.5 in all seasons, indicating a strong ability of CAMS-CSM in simulating the dipole pattern between the Arctic and northern midlatitudes. The root-mean-square errors in MAM and DJF between CAMS-CSM and the ERA-Interim/observation are less than 1, indicating that CAMS-CSM is relatively skillful in simulating the general horizontal patterns of the MAM and DJF NAM. In JJA and SON, the high root-mean-square errors are consistent with the big differences in the spatial distribution between ERA-Interim and CAMS-CSM in Fig. 1. The standardized deviation ratios of the NAM in CAMS-CSM relative to those in the observation are approximately 1.5, indicating that CAMS-CSM exaggerates the amplitude of the NAM and overestimates its intensity in all four seasons. This is in accordance with the results presented in Fig. 1. Zuo et al. (2013) also showed that most models from CMIP5 overestimate the intensity of the NAM patterns, especially in North Pacific.
|
| Figure 2 Taylor diagram of the SLP leading EOF modes (EOF1) in four seasons of 1979–2013 simulated by CAMS-CSM (denoted by color dots) compared with that in the ERA-Interim reanalysis data. REF indicates the reference value of 1.0; the radial distance from the model code point to the origin is the standardized deviation ratio of CAMS-CSM output relative to ERA-Interim; the cosine of the azimuthal angle of the model code point indicates the pattern correlation coefficient between the CAMS-CSM output and ERA-Interim; and the distance from the model code point to REF indicates the root-mean-square-error. |
The NAM exhibits a zonally symmetric and equivalent barotropic structure in the geopotential height and zonal wind fields from surface to the lower stratosphere (Thompson and Wallace, 1998). Accordingly, we further investigate the ability of CAMS-CSM in simulating the NAM’s vertical structure. Figure 3 shows the regression of zonally averaged geopotential height upon the NAM indices in all four seasons of 1979−2013. The results show that the equivalent barotropic structures can be seen in both ERA-Interim and CAMS-CSM, characterized by positive and negative values in the midlatitudes from 30° to 50°N and the polar cap region in the troposphere, respectively. Nevertheless, some differences exist in the centers of location between ERA-Interim and CAMS-CSM. For example, in MAM (Fig. 3c) and SON (Fig. 3g), the negative centers in the polar cap region are located in the upper troposphere in ERA-Interim; whereas the centers in CAMS-CSM are located in the mid–upper troposphere (Figs. 3d, h). The above results imply that CAMS-CSM is able to capture the equivalent barotropic structure of NAM in the geopotential height field from surface to the lower stratosphere, but the centers of location are not well simulated.
|
| Figure 3 Regression maps of the zonally averaged geopotential height (m) upon the NAM index in (a, b) DJF (boreal winter); (c, d) MAM (boreal spring); (e, f) JJA (boreal summer); and (g, h) SON (boreal autumn) of 1979−2013 from (left panels) ERA-Interim and (right panels) CAMS-CSM. Stippled areas are significant at the 95% confidence level with a Student’s t-test. |
The variability of the NAM reflects a meridional shift in the NH jet system. When the NAM is strong, the NH westerly jet shifts towards the Arctic. When the NAM is weak, the NH westerly jet shifts towards the equator. Figure 4 (see shadings) shows regression maps of the zonally averaged zonal winds on the NAM indices in all four seasons of 1979−2013. In both ERA-Interim and CAMS-CSM, there are negative values over the subtropical latitudes between 15° and 45°N, and positive values at the higher latitudes between 45° and 90°N in the troposphere. These results imply that CAMS-CSM can simulate the shift in the NH midlatitude westerly jet towards the Arctic in association with a positive phase of the NAM. However, the positive centers at higher latitudes in DJF (Fig. 4b) and MAM (Fig. 4d) in CAMS-CSM are located over 400–200 hPa, lower in altitude as compared to the centers of location near 100 hPa in the upper troposphere in ERA-Interim (Figs. 4a, c).

|
| Figure 4 Regression maps of the zonally averaged zonal wind (shaded; m s−1) and mass streamfunction (contours; 1010 kg s−1) upon the NAM index in (a, b) DJF (boreal winter); (c, d) MAM (boreal spring); (e, f) JJA (boreal summer); and (g, h) SON (boreal autumn) of 1979−2013 from (left panels) ERA-Interim and (right panels) CAMS-CSM. |
Li and Wang (2003) suggested that the NH Ferrel cell stands out as a dominant signal in the vertical circulation related to the NAM. Therefore, we further examine the simulation of CAMS-CSM in terms of the Ferrel cell. Figure 4 (contours) shows regression maps of the zonally averaged mass streamfunction upon the NAM indices in both ERA-Interim and CAMS-CSM. Negative values appear at mid−high latitudes in both ERA-Interim and CAMS-CSM, indicating a strengthening of the NH Ferrel cell in correspondence to a positive NAM phase. The result indicates that CAMS-CSM has captured the relationship between the NAM phase and NH Ferrel cell as observed in ERA-Interim.
3.2 Relationship with East Asian winter climateWu and Wang (2002) showed that the NAM can affect the EAWM and air temperature over East Asia. In view of the propagation of planetary waves, Chen and Kang (2006) proposed that the NAM can impact the Siberian high and Aleutian low, and then the East Asian trough, surface winds, and air temperature in the area from Northeast and North China to Siberia. These studies indicated that a positive phase of the NAM is accompanied by a weaker Siberian high and Aleutian low, a weaker EAWM, and higher air temperature in North and Northeast China. Now, the question is how well the relationship between the winter NAM and EAWM is simulated in the AMIP run of CAMS-CSM?
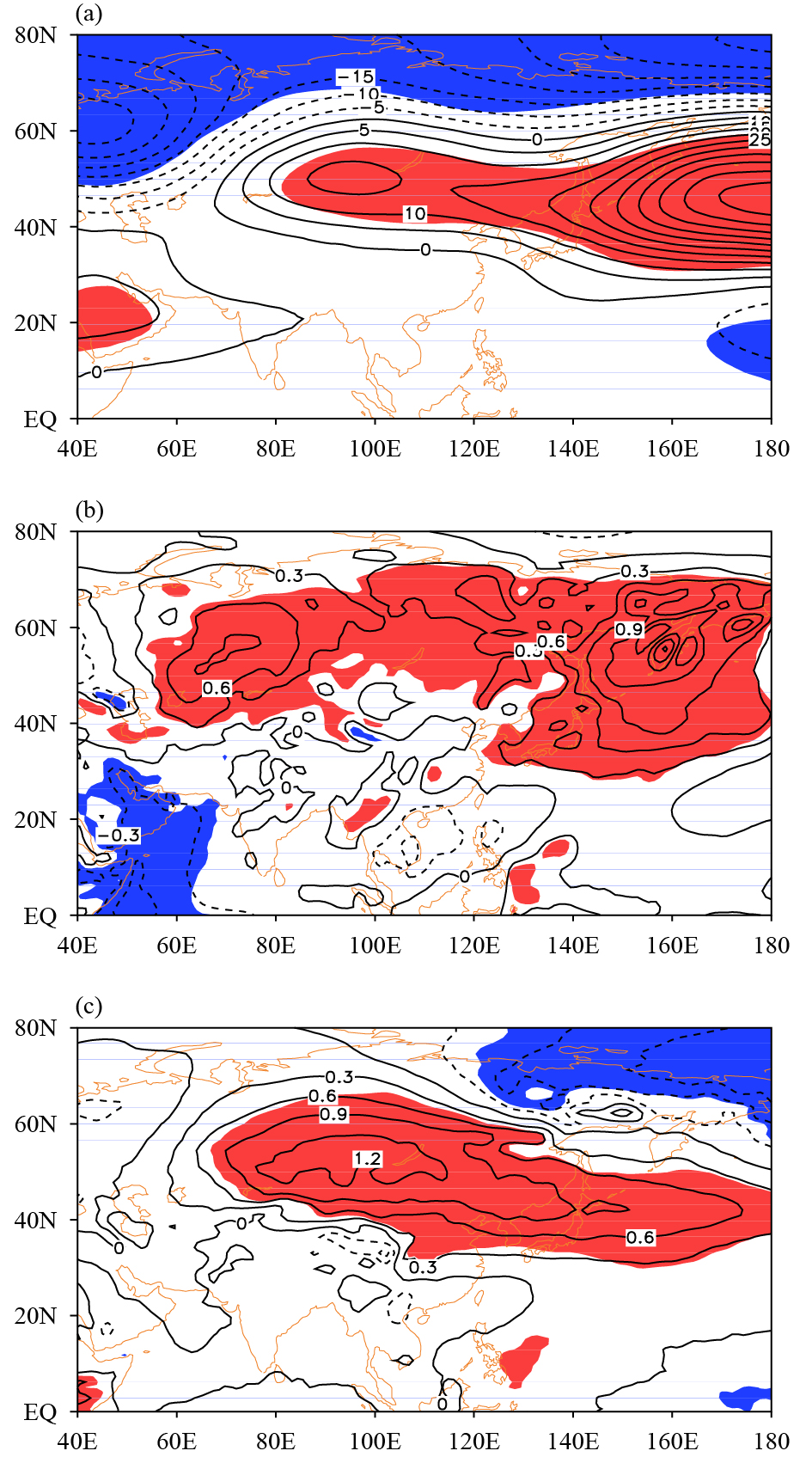
Figure 5a shows the regression of the 500-hPa geopotential height upon the DJF NAM index during 1979−2013 in CAMS-CSM. Positive values appear over the Asian region from Siberia to Lake Baikal and the western Pacific, implying a weakening of the East Asian trough. The result agrees with that of Chen and Kang (2006), and indicates that CAMS-CSM is capable to reproduce the observed relationship between the winter NAM and East Asian trough.
|
| Figure 5 Regression maps of the boreal winter (a) 500-hPa geopotential height (m), (b) 950-hPa meridional wind (m s−1), and (c) 950-hPa air temperature (°C) upon the boreal winter NAM index during 1979−2013 from CAMS-CSM. The red (positive values) and blue (negtive values) shaded areas are significant at the 95% confidence level with a Student’s t-test. |
Figure 5b shows the regression of the 950-hPa meridional wind field upon the DJF NAM index. Positive values occur from Siberia to Northeast Asia, including Northeast China, Korea, and Japan, indicating that a positive phase of the NAM is associated with anomalous southerly winds. Such anomalous southerly winds imply less cold airflow from high latitudes to East Asia, and then higher air temperature over East Asia. Figure 5c shows the regression of 950-hPa air temperature upon the DJF NAM index. Significantly positive values appear over the region from Siberia to East Asia, including Northeast China, North China, Korea, and Japan, indicating that high air temperature over East Asia is associated with the strong NAM. These results are consistent with the previous observation-based studies of Wu and Wang (2002) and Chen and Kang (2006).
In general, CAMS-CSM is able to simulate the relationship of the DJF NAM with air temperature over East Asia. The corresponding atmospheric circulation is also reproduced. That is, when the NAM is in a positive phase, the East Asian trough and the meridional wind weaken, which leads to less cold air from the high latitudes and higher air temperature over East Asia, including North and Northeast China.
4 Spatiotemporal features of the SAM 4.1 Spatial features 4.1.1 Horizontal structureSimilar to the NAM, the SAM is dominated by annular structures. Meanwhile, it also exhibits a zonally asymmetric feature (Zhang et al., 2018). Thus, we examine CAMS-CSM’s simulation of these features. Figure 6 shows the leading modes (EOF1) of SLP south of 20°S in ERA-Interim and CAMS-CSM. The leading modes in all four seasons during 1979−2013 account for 34.6%−42.5% of the total variance in ERA-Interim and 30.2%−47.6% of the total variance in CAMS-CSM, respectively. All of these modes are distinguishable in terms of the criterion of North et al. (1982). In all four seasons, SLP perturbations with opposite signs between the Antarctic and the midlatitudes are generally simulated in CAMS-CSM. In ERA-Interim, the leading EOF modes of SLP show a zonally asymmetric pattern in non-summer seasons (MAM, JJA, and SON). In these seasons, the positive values appear between 40° and 60°S, with the centers in the western Pacific, eastern Indian Ocean, and southern Atlantic. The negative values occur at the polar cap, and extend equatorward in the eastern Pacific. These observed features have also been described in previous studies (Fogt et al., 2012; Zhang et al., 2018). CAMS-CSM captures the equatorward extension of the negative anomalies in the eastern Pacific in MAM (Fig. 6d) and SON (Fig. 6h). In JJA (Figs. 6e, f), however, the negative extension equatorward from the polar cap in the southern Atlantic in CAMS-CSM is not observed in ERA-Interim. Meanwhile, CAMS-CSM has larger positive and negative values in the midlatitudes and at the polar cap, respectively, implying that CAMS-CSM overestimates the intensity of the SAM. In ERA-Interim, three positive centers appear in the midlatitudes of the SH in MAM (Fig. 6c), JJA (Fig. 6e), and SON (Fig. 6g). In CAMS-CSM, however, four positive centers in the midlatitudes of the SH are found in SON (Fig. 6h) and MAM (Fig. 6d), with three displaced centers compared to the observation and one more positive center in the eastern Pacific. Thus, CAMS-CSM shows some biases in the intensity and center location of the SAM pattern.

|
| Figure 6 Leading EOF modes (EOF1) of SLP south of 20°S in (a, b) DJF (austral summer); (c, d) MAM (austral autumn); (e, f) JJA (austral winter); and (g, h) SON (austral spring) of 1979−2013 from (left panels) ERA-Interim and (right panels) CAMS-CSM. The percentage at the top right of each panel represents the variance contribution of the EOF mode. |
As with the NAM, a Taylor diagram is plotted (Fig. 2) to compare the simulated SAM with that based on the ERA-Interim data. The spatial correlation coefficients between CAMS-CSM and ERA-Interim are above 0.8 in all seasons. Such high correlations suggest a good performance by CAMS-CSM in simulating the meridional dipole structure of the SAM patterns. The root-mean-square errors between CAMS-CSM and ERA-Interim are near 0.75, indicating that CAMS-CSM is relatively skillful in simulating the general horizontal distribution of the SAM. The standardized deviation ratios of the SAM in CAMS-CSM relative to that in ERA-Interim are approximately 1.5, indicating that CAMS-CSM exaggerates the amplitude of the SAM and overestimates its intensity in all four seasons. This is in agreement with the results presented in Fig. 6. Zheng et al. (2013) also pointed out that most CMIP5 models magnify the proportion of circulation variability related to the SAM. These results indicate that an overestimation of the SAM intensity is a common problem in state-of-the-art models.
4.1.2 Vertical structureThe SAM is characterized not only by a seesaw pattern of mass variability between the midlatitudes and the polar cap region, but also by a quasi-barotropic structure in the tropospheric geopotential height field. The regression of zonally averaged geopotential height upon the SAM indices in all four seasons of 1979−2013 is shown in Fig. 7. The polar cap region south of 60°S is covered by significant negative values, with the center in the upper troposphere, and the midlatitudes (30°−50°S) are dominated by significantly positive values throughout the whole troposphere, with the center in the mid−upper troposphere, in both ERA-Interim and CAMS-CSM. The similarity in general vertical structure between ERA-Interim and CAMS-CSM indicates that CAMS-CSM can capture the quasi-barotropic structure of the opposite variability of atmospheric mass between the midlatitudes and the south polar cap region.

|
| Figure 7 Regression maps of the zonally averaged geopotential height (m) upon the SAM index in (a, b) DJF (austral summer); (c, d) MAM (austral autumn); (e, f) JJA (austral winter); and (g, h) SON (austral spring) of 1979−2013 from (left panels) ERA-Interim and (right panels) CAMS-CSM. Stippled areas are significant at the 95% confidence level with a Student’s t-test. |
The variability of the SAM is also closely related to the meridional shift of the jet systems in the midlatitudes of the SH. Figure 8 shows regression maps of zonally averaged zonal wind upon the SAM indices in all four seasons of 1979−2013 (see the shadings). The negative and positive values of zonal mean wind appear from 15° to 40°S and from 45° to 70°S, respectively, in both CAMS-CSM and ERA-Interim, indicating that CAMS-CSM is able to reproduce the shift in the SH midlatitude westerly wind jet towards the Antarctic, in correspondence to a positive phase of the SAM.

|
| Figure 8 Regression maps of the zonally averaged zonal wind (shaded; m s−1) and mass streamfunction (contours; 1010 kg s−1) upon the SAM index in (a, b) DJF (austral summer); (c, d) MAM (austral autumn); (e, f) JJA (austral winter); and (g, h) SON (austral spring) of 1979−2013 from (left panels) ERA-Interim and (right panels) CAMS-CSM. |
Similar to the NAM, the SAM is related to the variability of the SH Ferrel cell (Li and Wang, 2003). Figure 8 shows the regression maps of mass streamfunction upon the SAM index (see the contours). It is seen that positive values appear from 45° to 70°S in both CAMS-CSM and ERA-Interim, implying an enhancement of the SH Ferrel cell in correspondence to a positive NAM phase. It is also apparent that the positive centers in CAMS-CSM are bigger than those in ERA-Interim, indicating that CAMS-CSM simulates a stronger SH Ferrel cell compared with ERA-Interim. The result is consistent with the overestimation of the SAM intensity by CAMS-CSM, as reported in Section 4.1.1.
4.2 Temporal variability of the SAMIn recent decades, the DJF SAM index presents a trend towards a positive phase in the twentieth century attributed to ozone depletion in Antarctica, and a less upward trend in the twenty-first century due to the recent ozone recovery (Polvani et al., 2011). The time series of DJF SAM index in CAMS-CSM during 1979−2013 is shown in Fig. 9a. It also presents a significant upward trend during 1979−2000 (above the 95% confidence level) and the less upward trend after 2000. This indicates that CAMS-CSM can capture the observed upward trend of the DJF SAM during the twentieth century. The SAM trend is largely attributable to the balancing effect of ozone and greenhouse gases (Jones and Widmann, 2004; McLandress et al., 2011; Polvani et al., 2011; Zheng et al., 2013). The simulation evaluated in the present study is the AMIP run, and its forcing (including greenhouse gases, ozone, etc.) is from the CMIP6 historical simulation (Eyring et al., 2016). Thus, the result indicates that CAMS-CSM can successfully simulate the balancing effect of ozone and greenhouse gases on the SAM trend. Some CMIP3 and CMIP5 models also perform well in simulating the SAM trend (Cai and Cowan, 2007; Fogt et al., 2009; Zheng et al., 2013).

|
| Figure 9 Time series of (a) DJF (austral summer) and (b) MAM (austral autumn) SAM index during 1979−2013 from ERA-Interim (black line) and CAMS-CSM (red line). |
Figure 9b shows the time series of the MAM SAM indices in CAMS-CSM and ERA-Interim. Both exhibit remarkable interannual variability. The correlation coefficient between them is 0.36, significant above the 95% confidence level. This result indicates that CAMS-CSM performs well in simulating the interannual variability of the MAM SAM index. Some CMIP5 models also present good performance in reproducing the interannual variations of the SAM (Zheng et al., 2013).
5 Summary and discussionA new coupled climate system model (CAMS-CSM) has recently been developed at the Chinese Academy of Meteorological Sciences. In this work, we have evaluated the ability of this model in simulating the spatial structures of the NAM and SAM, the relationship of the DJF NAM with East Asian climate, as well as the temporal variability of the SAM, when forced by observational SST and sea ice for the period 1978–2013.
The results indicate that CAMS-CSM is capable to well simulate the main horizontal and vertical characteristics of the NAM and SAM. It reproduces the zonally symmetric and out-of-phase variability of SLP between the midlatitudes and the polar zones. CAMS-CSM also reproduces the equivalent barotropic structure of the NAM/SAM. The meridional shift in the NH/SH jet system and the variabilities of the NH/SH Ferrel cell associated with the NAM/SAM anomalies can also be adequately simulated. The shift in the NH/SH midlatitude westerly jet towards the Arctic/Antarctic corresponds to a positive phase of the NAM/SAM. The NAM’s/SAM’s positive phases are also related to the enhancement of the NH/SH Ferrel cells.
CAMS-CSM reproduces the relationship of the DJF NAM with air temperature over East Asia. Meanwhile, the matching atmospheric circulations are also simulated. That is, when the NAM is in a positive phase, the East Asian trough weakens and the meridional wind weakens, which leads to less cold air from high latitudes and higher air temperature over East Asia.
CAMS-CSM can capture the upward trend of the DJF SAM index during 1979−2013 as that in ERA-Interim. Meanwhile, the CAMS-CSM AMIP run shows poor performance in simulating the NAM’s and SAM’s interannual variability except for the MAM SAM index. Using the monthly and seasonal data, we have calculated the correlation coefficients of the NAM/SAM indices bet-ween CAMS-CSM and observation. The results indicate that most of them are not statistically significant. The interannual variability of the NAM/SAM in AMIP results from the anomalous signals inside the atmosphere, and it is generally difficult to simulate the natural variability. Zhu and Wang (2008) also noted that the ability of the CMIP3 models in simulating the NAM’s and SAM’s interannual variability is low.
In general, the spatial correlation coefficients of the NAM/SAM between CAMS-CSM and the observation are found to be high. However, CAMS-CSM exaggerates the amplitude of the NAM/SAM and overestimates their intensities in all four seasons of 1979−2013. There are biases in their intensities and spatial distributions between CAMS-CSM and the observation. Previous studies presented that the NAM/SAM anomaly signals firstly appear in the stratosphere and then propagate downwards to the troposphere (Baldwin and Dunkerton, 1999; Christiansen, 2001; Thompson et al., 2005). The downward propagation is one possible mechanism underpinning the NAM/SAM pattern formation in the troposphere. Thus, the coupling between the stratosphere and the troposphere is crucial for the patterns of the NAM/SAM. At present, CAMS-CSM does not involve the process of stratospheric dynamics. This may be a reason behind the discrepancies in the NAM’s and SAM’s intensities and center locations between the model and observation. Meanwhile, some researchers have suggested that the NAM/SAM is a result of wave−mean flow interaction. Specifically, the wave−mean flow interaction is active in North Atlantic and North Pacific, coinciding with the action centers of the NAM (Zhao et al., 2012). Therefore, the CAMS-CSM’s simulation of the wave−mean flow interaction may be another reason for the discrepancy of the NAM’s and SAM’s intensities and center locations. Tackling these aspects of the issue constitutes the next step in the model’s development.
Acknowledgments. We thank the ECMWF for providing the ERA-Interim data.
| Baldwin, M. P., and T. J. Dunkerton, 1999: Propagation of the Arctic Oscillation from the stratosphere to the troposphere. J. Geophys. Res. Atmos., 104, 30,937–30,946. DOI:10.1029/1999JD900445 |
| Cai, W. J., and T. Cowan, 2007: Trends in Southern Hemisphere circulation in IPCC AR4 models over 1950−99: Ozone depletion versus greenhouse forcing. J. Climate, 20, 681–693. DOI:10.1175/JCLI4028.1 |
| Chen, W., and L. H. Kang, 2006: Linkage between the Arctic Oscillation and winter climate over East Asia on the interannual timescale: Roles of quasi-stationary planetary waves. Chinese J. Atmos. Sci., 30, 863–870. DOI:10.3878/j.issn.1006-9895.2006.05.15 |
| Christiansen, B., 2001: Downward propagation of zonal mean zonal wind anomalies from the stratosphere to the troposphere: Model and reanalysis. J. Geophys. Res. Atmos., 106, 27307–27322. DOI:10.1029/2000JD000214 |
| Codron, F., 2005: Relation between annular modes and the mean state: Southern Hemisphere summer. J. Climate, 18, 320–330. DOI:10.1175/JCLI-3255.1 |
| Dai, P. X., and B. K. Tan, 2017: The nature of the Arctic Oscillation and diversity of the extreme surface weather anomalies it generates. J. Climate, 30, 5563–5584. DOI:10.1175/JCLI-D-16-0467.1 |
| Dai, Y. J., X. B. Zeng, R. E. Dickinson, et al., 2003: The Common Land Model. Bull. Amer. Meteor. Soc., 84, 1013–1023. DOI:10.1175/BAMS-84-8-1013 |
| Eyring, V., S. Bony, G. A. Meehl, et al., 2016: Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev., 9, 1937–1958. DOI:10.5194/gmd-9-1937-2016 |
| Fan, K., and H. J. Wang, 2004: Antarctic Oscillation and the dust weather frequency in North China. Geophys. Res. Lett., 31, L10201. DOI:10.1029/2004GL019465 |
| Feldstein, S. B., 2003: The dynamics of NAO teleconnection pattern growth and decay. Quart. J. Roy. Meteor. Soc., 129, 901–924. DOI:10.1256/qj.02.76 |
| Fogt, R. L., J. Perlwitz, A. J. Monaghan, et al., 2009: Historical SAM variability. Part II: Twentieth-century variability and trends from reconstructions, observations, and the IPCC AR4 models. J. Climate, 22, 5346–5365. DOI:10.1175/2009JCLI2786.1 |
| Fogt, R. L., J. M. Jones, and J. Renwick, 2012: Seasonal zonal asymmetries in the southern annular mode and their impact on regional temperature anomalies. J. Climate, 25, 6253–6270. DOI:10.1175/JCLI-D-11-00474.1 |
| Gong, D. Y., and S. W. Wang, 1998: Antarctic Oscillation: Concept and applications. Chinese Sci. Bull., 43, 734–738. DOI:10.1007/BF02898949 |
| Gong, D. Y., J. H. Zhu, and S. W. Wang, 2002: Significant relationship between spring AO and the summer rainfall along the Yangtze River. Chinese Sci. Bull., 47, 948–951. DOI:10.1360/02tb9212 |
| Griffies, S. M., M. J. Harrison, P. C. Pacanowski, et al., 2004: A Technical Guide to MOM4. GFDL Ocean Group Technical Report No.5, Princeton, NJ, NOAA/Geophysical Fluid Dynamics Laboratory, 339 pp. |
| Ho, C. H., J. H. Kim, H. S. Kim, et al., 2005: Possible influence of the Antarctic Oscillation on tropical cyclone activity in the western North Pacific. J. Geophys. Res. Atmos., 110, D19104. DOI:10.1029/2005JD005766 |
| Jones, J. M., and M. Widmann, 2004: Early peak in Antarctic oscillation index. Nature, 432, 290–291. DOI:10.1038/432290b |
| Li, J. P., and J. X. L. Wang, 2003: A modified zonal index and its physical sense. Geophys. Res. Lett., 30, 34. DOI:10.1029/2003GL017441 |
| Liu, T., J. P. Li, and F. Zheng, 2015: Influence of the boreal autumn Southern Annular Mode on winter precipitation over land in the Northern Hemisphere. J. Climate, 28, 8825–8839. DOI:10.1175/JCLI-D-14-00704.1 |
| Lorenz, D. J., and D. L. Hartmann, 2001: Eddy−zonal flow feedback in the Southern Hemisphere. J. Atmos. Sci., 58, 3312–3327. DOI:10.1175/1520-0469(2001)058<3312:EZFFIT>2.0.CO;2 |
| Ma, J., and J. P. Li, 2007: Strengthening of the boreal winter Hadley circulation and its connection with ENSO. Prog. Nat. Sci., 17, 1327–1333. |
| McLandress, C., T. G. Shepherd, J. F. Scinocca, et al., 2011: Separating the dynamical effects of climate change and ozone depletion. Part II: Southern Hemisphere troposphere. J. Climate, 24, 1850–1868. DOI:10.1175/2010JCLI3958.1 |
| Nan, S. L., and J. P. Li, 2003: The relationship between the summer precipitation in the Yangtze River valley and the boreal spring Southern Hemisphere annular mode. Geophys. Res. Lett., 30, 2266. DOI:10.1029/2003GL018381 |
| North, G. R., T. L. Bell, R. F. Cahalan, et al., 1982: Sampling errors in the estimation of empirical orthogonal functions. Mon. Wea. Rev., 110, 699–706. DOI:10.1175/1520-0493(1982)110<0699:SEITEO>2.0.CO;2 |
| Polvani, L. M., D. W. Waugh, G. J. P. Correa, et al., 2011: Stratospheric ozone depletion: The main driver of twentieth-century atmospheric circulation changes in the Southern Hemisphere. J. Climate, 24, 795–812. DOI:10.1175/2010JCLI3772.1 |
| Roeckner, E., G. Bäuml, L. Bonaventura, et al., 2003: The Atmospheric General Circulation Model ECHAM5. Part I: Model Description. MPI Technical Report 349, Max Planck Institute for Meteorology, Hamburg, Germany, 127 pp. |
| Rong, X. Y., J. Li, H. M. Chen, et al., 2018: The CAMS climate system model and a basic evaluation of its climatology and climate variability simulation. J. Meteor. Res., 32, 839–861. DOI:10.1007/s13351-018-8058-x |
| Simmons, A., S. Uppala, D. Dee, et al., 2007: ERA-Interim: New ECMWF reanalysis products from 1989 onwards. ECMWF Newsletter, 110, 25–35. DOI:10.21957/pocnex23c6 |
| Sun, J. Q., H. J. Wang, and W. Yuan, 2010: Linkage of the boreal spring Antarctic Oscillation to the West African summer monsoon. J. Meteor. Soc. Japan, 88, 15–28. DOI:10.2151/jmsj.2010-102 |
| Thompson, D. W. J., and J. M. Wallace, 1998: The Arctic Oscillation signature in the wintertime geopotential height and temperature fields. Geophys. Res. Lett., 25, 1297–1300. DOI:10.1029/98GL00950 |
| Thompson, D. W. J., and J. M. Wallace, 2000: Annular modes in the extratropical circulation. Part I: Month-to-month variability. J. Climate, 13, 1000–1016. DOI:10.1175/1520-0442(2000)013<1000:AMITEC>2.0.CO;2 |
| Thompson, D. W. J., M. P. Baldwin, and S. Solomon, 2005: Stratosphere−troposphere coupling in the Southern Hemisphere. J. Atmos. Sci., 62, 708–715. DOI:10.1175/JAS-3321.1 |
| Winton, M., 2000: A reformulated three-layer sea ice model. J. Atmos. Oceanic Technol., 17, 525–531. DOI:10.1175/1520-0426(2000)017<0525:ARTLSI>2.0.CO;2 |
| Wu, B. Y., and J. Wang, 2002: Winter Arctic Oscillation, Siberian high and East Asian winter monsoon. Geophys. Res. Lett., 29, 1897. DOI:10.1029/2002GL015373 |
| Wu, Q. G., and D. M. Straus, 2004: AO, COWL, and observed climate trends. J. Climate, 17, 2139–2156. DOI:10.1175/1520-0442(2004)017<2139:ACAOCT>2.0.CO;2 |
| Wu, Z. W., J. P. Li, B. Wang, et al., 2009: Can the Southern Hemisphere annular mode affect China winter monsoon?. J. Geophys. Res. Atmos., 114, D11107. DOI:10.1029/2008JD011501 |
| Xue, F., H. J. Wang, and J. H. He, 2004: Interannual variability of Mascarene high and Australian high and their influences on East Asian summer monsoon. J. Meteor. Soc. Japan, 82, 1173–1186. DOI:10.2151/jmsj.2004.1173 |
| Yu, R. C., 1994: A two-step shape-preserving advection scheme. Adv. Atmos. Sci., 11, 479–490. DOI:10.1007/BF02658169 |
| Zhang, H., G. Y. Shi, T. Nakajima, et al., 2006a: The effects of the choice of the k-interval number on radiative calculations . J. Quant. Spectrosc. Radiat. Transf., 98, 31–43. DOI:10.1016/j.jqsrt.2005.05.090 |
| Zhang, H., T. Suzuki, T. Nakajima, et al., 2006b: Effects of band division on radiative calculations. Opt. Eng., 45, 016002. DOI:10.1117/1.2160521 |
| Zhang, Y., R. C. Yu, J. Li, et al., 2013: An implementation of a leaping-point two-step shape-preserving advection scheme in the high-resolution spherical latitude−longitude grid. Acta Meteor. Sinica., 71, 1089–1102. DOI:10.11676/qxxb2013.085 |
| Zhang, Y. R., L. P. Li, Z. H. Jin, et al., 2017: Simulation and projection of the Arctic Oscillation in winter based on CMIP5 models. Climatic Environ. Res., 22, 633–642. DOI:10.3878/j.issn.1006-9585.2017.17019 |
| Zhang, Z. R., P. Uotila, A. Stössel, et al., 2018: Seasonal Southern Hemisphere multi-variable reflection of the southern annular mode in atmosphere and ocean reanalyses. Climate Dyn., 50, 1451–1470. DOI:10.1007/s00382-017-3698-6 |
| Zhao, N., S. J. Liang, and Y. H. Ding, 2012: Coupling modes among action centers of wave−mean flow interaction and their association with the AO/NAM. J. Climate, 25, 447–458. DOI:10.1175/2011JCLI4240.1 |
| Zheng, F., J. P. Li, R. T. Clark, et al., 2013: Simulation and projection of the Southern Hemisphere annular mode in CMIP5 models. J. Climate, 26, 9860–9879. DOI:10.1175/JCLI-D-13-00204.1 |
| Zheng, F., J. P. Li, R. T. Clark, et al., 2015: Influence of the boreal spring Southern Annular Mode on summer surface air temperature over northeast China. Atmos. Sci. Lett., 16, 155–161. DOI:10.1002/asl2.541 |
| Zhu, X., W. J. Dong, and Y. Guo, 2013: Comparison of simulated winter and spring Arctic Oscillation variability by CMIP5 and CMIP3 coupled models. Progressus Inquisitiones De Mutatione Climatis, 9, 165–172. DOI:10.3969/j.issn.1673-1719.2013.03.002 |
| Zhu, Y. L., and H. J. Wang, 2010: The Arctic and Antarctic Oscillations in the IPCC AR4 coupled models. J. Meteor. Res., 24, 176–188. |
| Zuo, J. Q., W. J. Li, and H. L. Ren, 2013: Representation of the Arctic Oscillation in the CMIP5 models. Adv. Climate Change Res., 4, 242–249. DOI:10.3724/SP.J.1248.2013.242 |
 2019, Vol. 33
2019, Vol. 33


