The Chinese Meteorological Society
Article Information
- LI, Weiping, Yanwu ZHANG, Xueli SHI, et al., 2019.
- Development of Land Surface Model BCC_AVIM2.0 and Its Preliminary Performance in LS3MIP/CMIP6. 2019.
- J. Meteor. Res., 33(5): 851-869
- http://dx.doi.org/10.1007/s13351-019-9016-y
Article History
- Received March 18, 2019
- in final form May 7, 2019
2. CMA–NJU Joint Laboratory for Climate Prediction Studies, Nanjing University (NJU), Nanjing 210023, China;
3. Department of Atmospheric Sciences, Nanjing University, Nanjing 210023, China;
4. Department of Earth System Science, University of California, Irvine, Irvine, CA 92697-3100, USA;
5. Jiangsu Provincial Key Laboratory of Geographic Information Science and Technology, International Institute for Earth System Science, Nanjing University, Nanjing 210023, China;
6. Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
A land surface model (LSM) is an important tool to simulate the variations of earth surface conditions and to investigate the physical processes involved in land–atmosphere interactions. A variety of LSMs has been developed in the past decades, depicting various processes of land surface evaporation, snow cover, soil water freeze/thaw, vegetation growth, terrestrial carbon cycle, and so on (Sellers et al., 1996; Sun et al., 1999; Dai et al., 2003; Xue et al., 2003; Li et al., 2010; Bonan et al., 2011; Lawrence et al., 2011; Luo et al., 2017). Endeavors have been made at the Beijing Climate Center (BCC), China Meteorological Administration in recent years to develop a climate system model (CSM) with an integrated LSM to simulate the physical as well as biogeophysical processes of land surfaces.
The first version of the BCC Atmosphere–Vegetation Interaction Model (BCC_AVIM1.0) was based on the AVIM developed by Ji (1995) and Ji et al. (2008), which included three sub-modules simulating biogeophysical, ecophysiological, and soil carbon–nitrogen dynamical processes, and a modified biogeophysical framework with 10 soil layers and up to 5 snow layers [almost the same as that in the NCAR Community Land Model (CLM; Oleson et al., 2004)]. In BCC_AVIM1.0, the terrestrial carbon cycle was realized via a series of biochemical and physiological processes related to the photosynthesis and respiration of vegetation. There was a seasonally varying allocation of carbohydrates to leaves, stems, and roots as a function of the prognostic leaf area index (LAI). Carbon loss due to turnover and mortality of vegetation tissues and carbon dioxide release into the atmosphere from soil respiration was also taken into account. Plant litter on the ground surface and in the soil was theoretically divided into eight terrestrial carbon pools according to the timescale of carbon decomposition of each pool and the transfers between different pools based on the works of Parton et al. (1988) and Cao and Woodward (1998). BCC_AVIM1.0 has served as the land component of the BCC Climate System Model (BCC_CSM) and performed well in both operational seasonal climate prediction (Wu et al., 2014) and experiments of the Coupled Model Intercomparison Project Phase 5 (CMIP5; Arora et al., 2013; Su et al., 2013; Todd-Brown et al., 2013; Wu et al., 2013; Bao et al., 2014; Friedlingstein et al., 2014).
Like other current LSMs, BCC_AVIM1.0 has many deficiencies in its physical and biogeophysical parameterizations and consequent biases in its simulations. For example, BCC_AVIM1.0 underestimated the snow co-ver fraction of the Eurasian continent in winter (Xia and Wang, 2015). It produced earlier start and end dates for thaw (freeze) of soil ice (liquid water) over the Tibetan Plateau compared with the observations due to the unrealistic threshold temperature (i.e., 0°C) to initiate thaw (freeze) of soil ice (water) (Xia et al., 2011). Moreover, BCC_AVIM1.0 produced overestimation of land surface albedo (Zhou et al., 2018) and delayed vegetation phenology during the growing season. The aforementioned and other deficiencies of BCC_AVIM1.0 has motivated us to improve the parameterization schemes of relevant land surface processes.
After completion of the CMIP5 experiments, attempts were made to improve the parameterization schemes in BCC_AVIM1.0 related to snow cover, soil freeze/thaw processes, rice paddies, lakes with real depths in a snow–ice–water–soil framework, solar radiation transfer through vegetation canopies, and a prognostic phenology based on the carbon budget of a plant functional type (PFT). The above updates were implemented in BCC_AVIM2.0 and coupled to BCC_CSM2.0 for use in the ongoing CMIP6 project. This work gives a brief introduction to BCC_AVIM2.0 and its preliminary performance in the Land Surface, Snow and Soil Moisture Model Intercomparison Project (LS3MIP; van den Hurk et al., 2016).
The remainder of this paper is organized as follows. Section 2 describes the data and method that we have employed to evaluate BCC_AVIM. The updates of parameterizations in BCC_AVIM2.0 are presented in Section 3. Section 4 displays the performance of BCC_AVIM2.0 in LS3MIP. Finally, conclusions are given in Section 5.
2 Data and methods to evaluate BCC_AVIMThe observation datasets used in this study to validate the simulations of BCC_AVIM include: (1) site observations at Col de Porte, France (Morin et al., 2012), (2) site observations in Shouxian County of Anhui Province, China, (3) surface water temperature of the Great Lakes in North America on the daily analysis (on an approximately 1-km horizontal resolution) from NOAA satellite observations for 1995–2006 (ftp://coastwatch.glerl.noaa.gov/glsea), (4) LAI data derived from the Advanced Very High Resolution Radiometer (AVHRR) covering 1982 to 2010 (Myneni et al., 1997), (5) surface turbulent heat and carbon fluxes from the Global Biosphere–Atmosphere Flux (GBAF) dataset (upscaled from FLUXNET and satellite observations) spanning 1982 to 2008 (Jung et al., 2009, 2011), (6) above ground biomass from pan-tropical biomass (Avitabile et al., 2016) and the global biomass carbon dataset covering 1990 to 2010 (Saatchi et al., 2011), and (7) the surface radiation budget from the Cloud and Earth Radiant Energy System (CERES) from 2000 to 2010 (Kato et al., 2013).
In addition to the above observation datasets, the atmospheric forcing data at a specific site or at the global scale used to drive the LSM are also needed to evaluate the model simulations. The atmospheric forcing to drive BCC_AVIM2.0 in this study for the Great Lakes region and the entire globe is the Princeton global forcing dataset (Sheffield et al., 2006), which was developed for land surface and other terrestrial models, and for analyzing changes in near-surface climate. The dataset was based on 6-hourly surface climate data from the NCEP–NCAR reanalysis and was corrected for biases at diurnal, daily, and monthly timescales by using a variety of observation datasets. The data used in this study are on a 1-degree spatial resolution and a 3-h time step, and cover the pe-riod from 1948 to 2014. The Princeton global forcing dataset is among several options of atmospheric forcing for the ongoing LS3MIP of CMIP6.
BCC_AVIM2.0 was run offline at a crop field site in Shouxian County of Anhui Province, China for evaluation of surface heat fluxes over rice paddies, in Col de Porte, France for evaluation of snow albedo, around the Great Lakes region of North America for evaluation of lake surface temperature, and over the globe for evaluation of vegetation phenology.
In addition to the traditional validation of a LSM at a specific site, benchmarking has been widely used to assess the ability of climate models to capture the spatial and temporal variability of observations during the historical period. For the carbon cycle and terrestrial ecosystems, the design and development of an open-source community platform has been an important goal as part of the International Land Model Benchmarking (ILAMB) project. The ILAMB package was designed and developed as a diagnostic system that enables users to specify the models, benchmarks, and scoring metrics used to tailor the large amount of results to specific mo-del intercomparison projects. The ILAMB scoring system used information from three different aspects of climate, including the climate mean spatial pattern, the seasonal cycle, and the amplitude of interannual variability. A stable version of the ILAMB package was released in 2015 during the American Geophysical Union fall meeting (Mu et al., 2016; Mu and ILAMB team, 2019). The ILAMB package was used to evaluate the preliminary performance of BCC_AVIM2.0 in simulating global land surface energy budgets and their seasonal evolutions.
3 Updates of parameterization schemes in BCC_AVIM2.0 3.1 The lake with variable depth in a snow–ice–water–soil frameworkAs a specific nonvegetated underlying water body, a lake has been explicitly described in most LSMs to simulate thermal transfer within the water body and energy exchange between the lake surface and the overlying atmosphere, and related biogeochemical effects (Subin et al., 2012). With the increase of model horizontal resolution, the lake cover percentage in a model grid cell becomes larger and the climate impacts of lakes become more prominent, and more complicated and realistic processes describing the lake–atmosphere interactions need to be considered.
The lake module in BCC_AVIM1.0 is similar to that of NCAR CLM. It has 10 prescribed layers of water and a fixed depth of 50 m (Oleson et al., 2004); snow cover accumulation over the lake surface is much simplified and the soil beneath the lake water body is not considered. In BCC_AVIM2.0, we implemented the lake module of the Common Land Model (CoLM) of Dai et al. (2003) on the basis of previous works (Zeng et al., 2002; Subin et al., 2012). The main physical processes in the CoLM-lake module include the freeze/thaw at the surface of a lake body, snow accumulation over the frozen surface, eddy diffusion, heat exchange between the atmosphere and the lake surface, and heat exchange between the bottom water and the underlying soil layer.
In the CoLM-lake module, the lake surface roughness lengths for momentum (z0m), heat (z0h), and water vapor (z0q) under unfrozen conditions are parameterized as follows (Dai et al., 2018):
| $ {z_{0{\rm{m}}}} = \max\, (\frac{{0.1v}}{{{u_*}}},\,\,\,C\frac{{{u_*}^2}}{{\rm{g}}}) \geqslant {10^{ - 5}}{\rm{m}}, \quad\quad\quad\quad\quad\;\;\; $ | (1) |
| $ {z_{0{\rm{h}}}} = {z_{0{\rm{m}}}}\exp \left\{ { - \frac{{0.4}}{{0.713}}\left({4\sqrt {{{{R}}_0}} - 3.2} \right)} \right\} \geqslant {10^{ - 5}}{\rm{m}}, $ | (2) |
| $ {z_{0{\rm{q}}}} = {z_{0{\rm{m}}}}\exp \left\{ { - \frac{{0.4}}{{0.66}}\left({4\sqrt {{R_0}} - 4.2} \right)} \right\} \geqslant {10^{ - 5}}{\rm{m}},\;\; $ | (3) |
where
| $ v = {v_{0}} \,\, {\left({\frac{{{T_{\rm{g}}}}}{{{T_0}}}} \right)^{1.5}}\!\!\frac{{{P_0}}}{{{P_{{\rm{ref}}}}}}, $ | (4) |
in which v0 = 1.51 × 10−5 m2 s−1, T0 = 293.15 K, P0 = 1.013 × 105 Pa, and Pref is the air pressure at the atmospheric reference height. The effective Charnock coefficient C in Eq. (1) is calculated as:
| $ C = {C_{{\rm{min}}}} + \left({{C_{{\rm{max}}}} - {C_{{\rm{min}}}}{\rm{}}} \right)\exp \left[{ - \min \left({A,B} \right)} \right], $ | (5) |
| $ A = {\left({\frac{{F \cdot {\rm{g}}}}{{u^2}}} \right)^{1/3}}/{f_c}, $ | (6) |
| $ B = \varepsilon \frac{{\sqrt {d \cdot {\rm{g}}} }}{u}, $ | (7) |
where the maximum and minimum values of C are assumed to be Cmax = 0.11 and Cmin = 0.01, respectively; A and B represent restrictions from the wind-driving-waves length scale (F) and the lake depth (d), respectively; u (m s−1) is near surface atmospheric wind; and F depends on lake depth, which is assumed to be a constant of 100 for lakes shallower than 4 m and a constant 25 times the lake depth for those deeper than 4 m. The constant fc = 22; and
Offline simulations were conducted to compare the CoLM-lake of real depths in BCC_AVIM2.0 with the original water-only lake module of a fixed depth of 50 m in BCC_AVIM1.0. Figure 1 displays lake surface temperatures over the Great Lakes region in North America. Satellite observations show that the main body surface temperatures of the five lakes in January are above 0°C (Fig. 1a). The surface temperature of the northernmost Lake Superior ranges from 2 to 3°C; Lake Michigan to the south is relatively warmer, with surface temperature between 3 and 4°C; the surface temperature in the central part of Lake Huron and most of Lake Ontario is above 3°C; and the surface temperature of the southernmost yet shallowest Lake Erie is colder than 3°C. It is common to the five lakes that the central part of each lake is warmer than its outer parts in January, the margins of each lake freeze in winter, and the coverage of the frozen surface experiences interannual variability. In the simulation of BCC_AVIM1.0 (Fig. 1b), the surface temperatures of all five lakes are underestimated by as much as 6–8°C, e.g., Lake Superior, parts of Lake Michigan, and Lake Huron to the north of 44°N are colder than −6°C; temperatures increase southward of 44°N, yet the southern ends of Lake Michigan and Lake Erie are still colder than 2°C. In contrast, the surface temperature simulated by CoLM-lake in BCC_AVIM2.0 is much closer to the observations in both magnitude and spatial pattern, especially over Lake Ontario and the southern part of Lake Michigan (Fig. 1c). Lake Huron is approximately 1°C colder than the observations but the northernmost Lake Superior and the southernmost Lake Erie are approximately 2–3°C colder than the observations. The overall simulation of BCC_AVIM2.0 in January is statistically much better than that of BCC_AVIM1.0, with the spatial correlation coefficient between simulated and observed surface temperatures over the Great Lakes region being 0.21 for BCC_AVIM1.0 and 0.65 for BCC_AVIM2.0, and the root mean square error (RMSE) remarkably reduced from 10.3°C for BCC_AVIM1.0 to 1.8°C for BCC_AVIM2.0. The January cold bias in BCC_AVIM1.0 is possibly due to the quick freezing of surface water without considering the insulation of snow cover, and the alleviation of this cold bias in the lake surface temperature simulation of BCC_AVIM2.0 is partly due to the larger heat capacity of the entire water–soil system of CoLM-lake in BCC_AVIM2.0 than that from the water-only lake module in BCC_AVIM1.0.
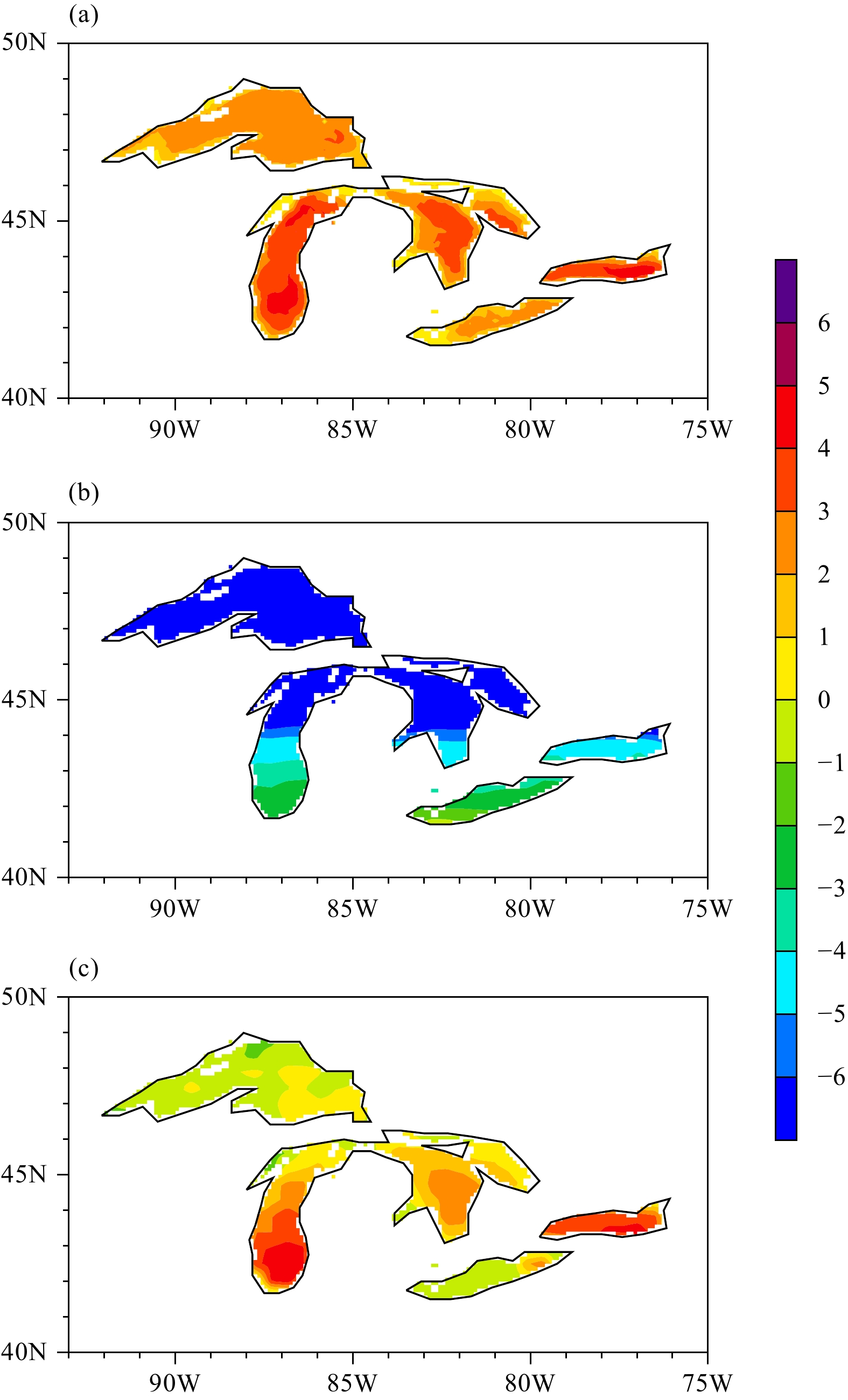
|
| Figure 1 January mean lake surface temperature over the Great Lakes region in North America derived from (a) AVHRR/NOAA satellite observation averaged for 1995–2006, (b) simulation of BCC_AVIM1.0, and (c) simulation of CoLM-Lake with real lake depths in BCC_AVIM2.0. |
The remarkable feature in observed lake surface temperature in July is the gradient distribution either within a specific lake or among different lakes (Fig. 2a). The northernmost Lake Superior is the coldest and the southernmost Lake Erie is the warmest. The northern part of Lake Superior is as cold as 9°C, and the southwestern part of the lake body becomes increasingly warmer as it becomes shallower. The surface temperature of Lake Michigan increases from approximately 17°C in the northern part to above 21°C in the southern end. The north central region of Lake Huron is approximately 14°C, and the southern end of Lake Huron and most of Lake Ontario are approximately 19°C, almost as warm as their counterpart of Lake Michigan located in the same latitudinal belt. The latitudinal gradient in surface temperature of Lake Erie is also obvious, ranging from 20°C in the northeastern part to 23°C in the southwestern end. Compared with the aforementioned observations, BCC_AVIM1.0 produces uniformly colder surface temperatures in the five lakes, except for the northern part of Lake Superior; the cold bias is approximately 6°C (16°C vs. 10°C) in northern Lake Michigan and approximately 9°C (20°C vs. 11°C) in southern Lake Michigan; and the cold bias in the BCC_AVIM1.0 simulation can be as large as 12°C (23°C vs. 11°C) in southern Lake Eire (Fig. 2b). The performance of BCC_AVIM2.0 (Fig. 2c) is much better than that of BCC_AVIM1.0. The overall spatial distribution of lake surface temperature is similar to observations but the magnitude is generally higher and the warm biases are larger at higher latitudes. The surface temperature of northern Lake Superior is approximately 8°C higher than that in the observations; the warm bias is approximately 6°C in northern Lake Huron; and the warm bias reduces to approximately 3°C in southern Lake Michigan. The summertime cold bias of surface temperature in BCC_AVIM1.0 simulation is associated with the strong heat diffusion from surface to deeper water layers; in contrast, the warm bias in BCC_AVIM2.0 is due to the relatively weak heat diffusion between vertical layers in the CoLM-lake module of BCC_AVIM2.0. Statistically, CoLM-lake in BCC_AVIM2.0 performs better than the lake module in BCC_AVIM1.0 in July, with the spatial correlation coefficient between the observed lake surface temperature and that simulated by BCC_AVIM1.0 over the Great Lakes region being 0.61 and that by BCC_AVIM2.0 being 0.75, and the RMSE reduced from 7.4°C for BCC_AVIM1.0 to 6.4°C for BCC_AVIM2.0.
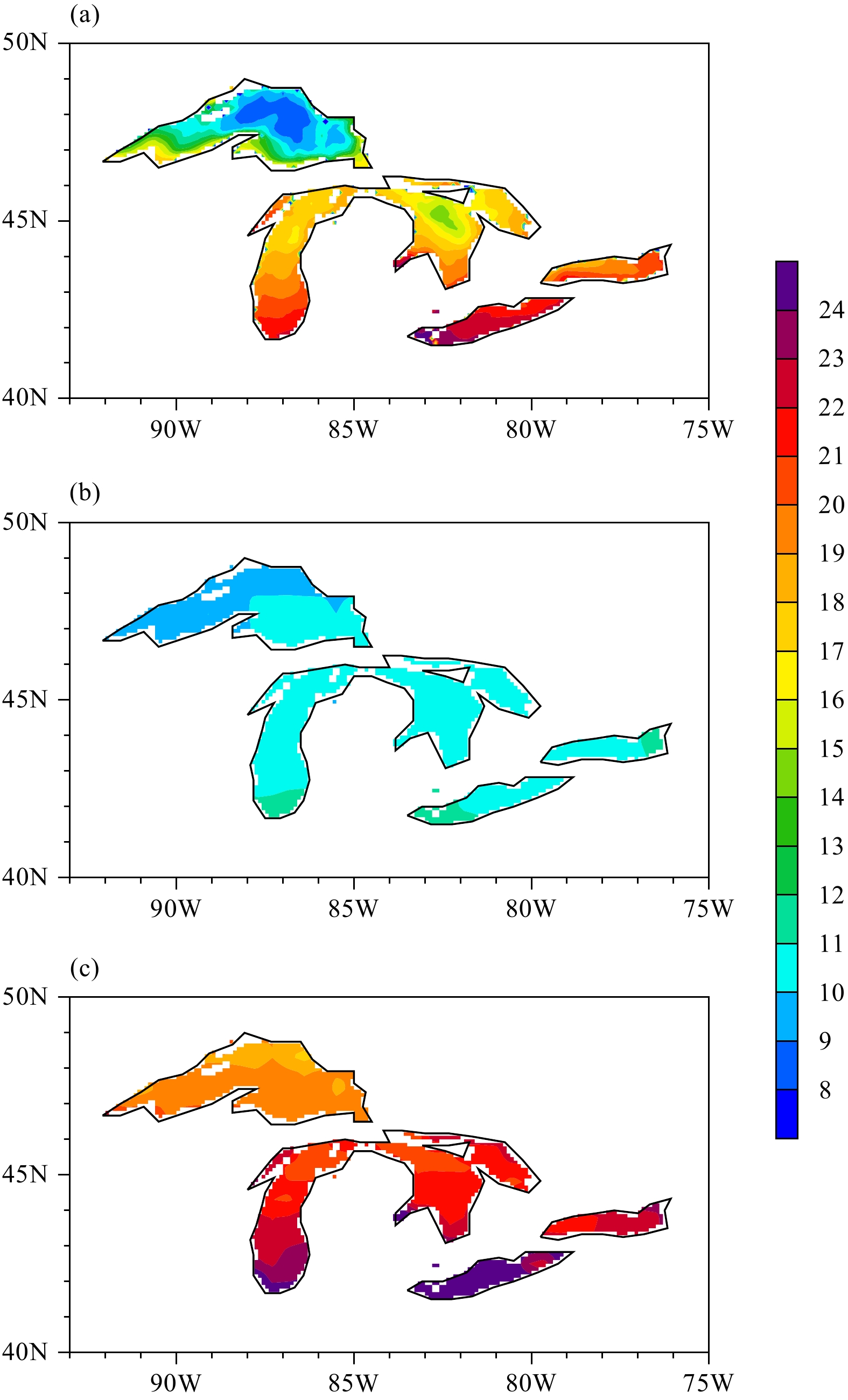
|
| Figure 2 As in Fig. 1, but for July. |
The interactions between agricultural land and overlying atmosphere play an important role, especially in paddy rice fields in eastern and southeastern parts of Asia, where surface latent heat flux (LHFX) values are relatively large. Using only one PFT to represent crop in BCC_AVIM1.0 undoubtedly underestimates surface evaporation over rice paddies where the ground is covered by water. A new scheme for rice paddy fields was developed in BCC_AVIM2.0 to incorporate the addition of surface water above soil, which is distinct from dry farmland; the energy flux stored in surface water is important to the energy balance and affects climate via heat and water fluxes at the canopy and water surface. The essential difference in the calculation of LHFX between this study and the original crop scheme in BCC_AVIM1.0 lies in that there is no limit in the evaporation from a rice paddy assumed to be a water body in BCC_AVIM2.0. The evaporation from rice paddies in BCC_AVIM2.0 comprises two parts: Ev from the rice canopy and Ew from the ground water body; and they are calculated as:
| $ {E_{\rm{v}}} = - {\rho _{{\rm{atm}}}}\frac{{\left({{q_{\rm{s}}} - q_{{\rm{sat}}}^{{T_{\rm{v}}}}} \right)}}{{{r_{{\rm{total}}}}}}, $ | (8) |
| $ {E_{\rm{w}}} = - {\rho _{{\rm{atm}}}}\frac{{\left({{q_{\rm{s}}} - {q_{\rm{w}}}} \right)}}{{{r_{{\rm{aw}}}}}}, $ | (9) |
where ρatm is the density of air (kg m−3); qs is the specific humidity of canopy air at the zero-plane displacement height (kg kg−1);
Figure 3 shows the seasonal evolution of daily mean SHFX and LHFX at a field station in Shouxian County of Anhui Province, China. In the observation, SHFX remains below 30 W m−2 almost year-round, except in June when it increases to above 60 W m−2. Surface LHFX is dominant during most of the year and is more than 30 W m−2 from March to November; two peaks of more than 130 W m−2 appear in Mayand July corresponding to the double growing seasons of rice in the midlatitudes of China. It is observed that the new scheme (Rice) in BCC_AVIM2.0 has simulated the seasonal variations of SHFX and LHFX more accurately than the old scheme (Crop) in BCC_AVIM1.0, both in magnitude and in the temporal evolution. Two peaks of LHFX simulated by the Rice scheme in May and July are associated with the growing seasons of rice and the consequent strong evapotranspiration; the dip in LHFX in June and the peak in SHFX around that period correspond to the harvest of rice and subsequent restricted evapotranspiration. Quantitatively, the RMSEs of SHFX simulation using the Crop and Rice schemes are 45.95 and 19.09 W m−2 respectively, and the RMSE of corresponding LHFX simulation is remarkably reduced from 46.10 to 16.83 W m−2. The improvements in the Rice scheme are due to increased evaporation from the water surface over rice paddies and the two growing seasons compared with relatively less evaporation over dry farmland and only one growing season in the old Crop scheme.

|
| Figure 3 Temporal evolution of (a) sensible heat flux (SHFX) and (b) latent heat flux (LHFX). Black circles: observations; blue curve: crop scheme in BCC_AVIM1.0; red curve: rice scheme in BCC_AVIM2.0. |
Snow cover fraction (SCF) is the percentage of a mo-del grid cell covered by snow. SCF is usually parameterized by the roughness length of the land surface and snow depth or snow water equivalence. SCF is generally underestimated in some LSMs in winter (Li et al., 2009; Xia and Wang, 2015), and the negative bias of SCF could be partly alleviated by using improved schemes (Niu and Yang, 2007). Meanwhile, SCF is overestimated in the regions with fluctuating topography such as southern Europe and in the areas around the Tibetan Plateau and the Mongolian Plateau (Li et al., 2009). An obvious defect in the previous SCF schemes is that the soil roughness length is assumed to be a global constant, although it should be location dependent (Yang et al., 1997). Considering the heterogeneous land surface and inhomogeneous precipitation, LSMs should take into account the subgrid variability of topography in a model grid cell to decrease the magnitude of SCF (Roesch et al., 2001). The SCF in BCC_AVIM2.0 is parameterized as:
| $ {F_{{\rm{sno}}}} = {\rm{tan}}h\left( {\frac{{{h_{{\rm{sno}}}}}}{{2.5{z_0}}}} \right).{\left( {\frac{{{h_{{\rm{sno}}}}}}{{{h_{{\rm{sno}}}} + \varepsilon + 0.0002{\sigma _z}}}} \right)^a}, $ | (10) |
where hsno is the snow depth (m); z0 is the roughness length of bare soil; σz (m) is the spatial variability of subgrid topography (i.e., the standard deviation of topographic height from the regional mean) in a grid cell of an LSM; ε is a minute constant (10−5) to avoid division by zero for totally flat and snow-free grid boxes; and the power exponent a is an adjustable constant smaller than 1 according to the spatial resolution of the model grid cell.
3.4 Snow aging and snow surface albedoIn current empirical parameterizations for snow surface albedo (SA), snow surface temperature is considered as an important and sometimes even the only dominant factor, and the distinct characteristics of snow aging at different stages of a snow season are neglected. However, analysis of observation data indicates that it is necessary to consider the different reduction rates of snow albedo in the accumulating and melting stages of a snow season. Snow albedo decreases more rapidly in the melting period than in the previous accumulating period (Aoki et al., 2003; Chen et al., 2014). Snow albedo in the melting stage of a snow season might be overestimated by previous schemes using a set of unified parameters throughout the entire snow season, which partly explains why the melting rate is weakened and the final ablation of the snow cover is delayed in BCC_AVIM1.0. The diffuse albedos of snow at different spectral bands are parameterized as those in Biosphere–Atmosphere Transfer Scheme (BATS; Dickinson et al., 1993):
| $ {\alpha_{{\rm{diff,vis}}}} = {\rm{ }}(1.0{\rm{ }}-{C_{{\rm{vis}}}} \cdot {F_{{\rm{age}}}}){\alpha_{{\rm{diff,vis}}0}}, $ | (11) |
| $ {\alpha_{{\rm{diff,nir}}}} = {\rm{ }}(1.0{\rm{ }}-{C_{{\rm{nir}}}} \cdot {F_{{\rm{age}}}}){\alpha_{{\rm{diff,nir}}0}}, $ | (12) |
where αdiff,vis and αdiff,nir are the diffuse albedos of snow at visible and near infrared wave bands, respectively; Cvis and Cnir are empirical constants that depict the albedo reduction with time; Fage is a snow aging parameter related to snow surface temperature and impurities; and αdiff,vis0 and αdiff,nir0 are the albedos of freshly fallen snow at visible and near infrared bands, respectively. The direct beam albedo of snow is the sum of the above diffuse albedo and the correction associated with solar zenith angle (Dickinson et al., 1993; Oleson et al., 2004).
In BCC_AVIM1.0, Cvis and Cnir are assumed to be constant (0.2 and 0.5 respectively) throughout the entire snow season, which weakens the snow aging effect during the melting stage and therefore overestimates snow albedo at that time. To better represent the reduction of snow albedo with elapsed time after a snowfall event, two sets of Cvis and Cnir are used before and after mid March to simply mimic the different snow aging effects for the accumulating and melting stages of a snow season in the Northern Hemisphere (NH) in BCC_AVIM2.0. The values of Cvis and Cnir are assumed to be 0.2 and 0.5 respectively for the snow accumulation period before mid March, and 0.3 and 0.65 for the snow melting stage afterwards. This revised scheme can partly alleviate the overestimation of snow albedo during boreal spring in BCC_AVIM1.0 as it keeps the SA of the previous accumulating period unchanged, thus shortening the snow season length by approximately 5 days, closer to the observations (Fig. 4).
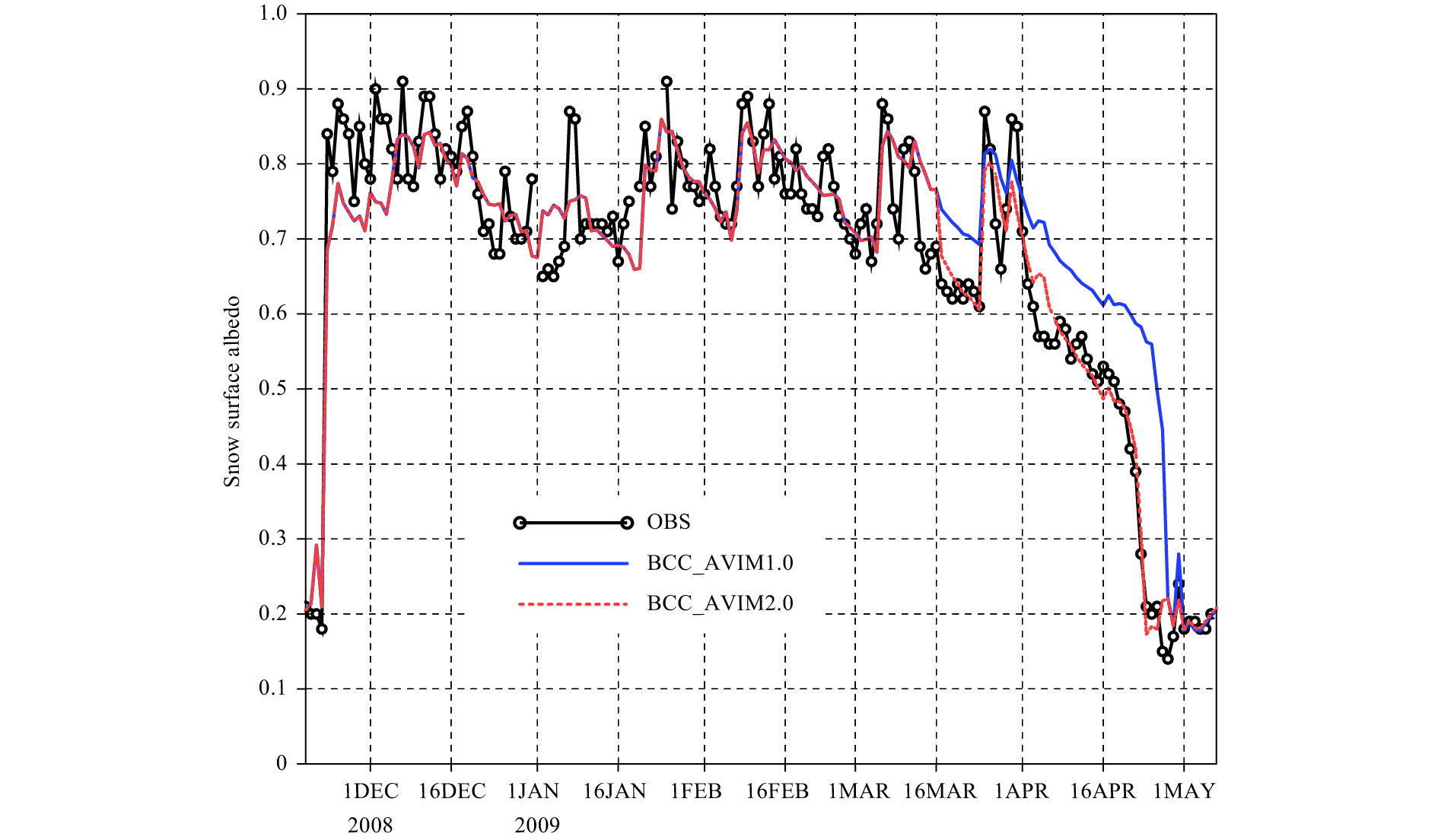
|
| Figure 4 Temporal evolution of snow surface albedo (SA) averaged over the 2008–09 snow season at the Col de Porte site in France. The black line with circles denotes observation (OBS), and the blue (red) curve denotes BCC_AVIM1.0 (BCC_AVIM2.0) simulation. |
Liquid water freezes when the soil temperature decreases to 0°C in BCC_AVIM1.0, and the soil temperature will remain at 0°C until all the liquid water has frozen. However, liquid water can coexist with ice in the real world when the soil temperature is below 0°C. The relationship between soil water content and soil temperature is determined by the inherent characteristics of soil hydraulics and the thermodynamic equilibrium between soil water potential and soil temperature. Therefore, the method to calculate the soil freeze/thaw critical temperature used by Li and Sun (2008) was adopted in BCC_AVIM2.0 to replace the unreasonable assumption used in BCC_AVIM1.0.
Soil water potential remains in equilibrium with the vapor pressure over soil ice when freezing occurs. Combining the relationship between soil water matrix potential ψ (mm) and soil temperature ψ(T) with the relationship between soil water matrix potential ψ (mm) and soil liquid water content ψ(θliq), the expression for the functional relation between the freeze/thaw threshold temperature of soil water (Tthre) and the soil liquid water content can be derived as:
| $ {T_{{\rm{thre}}}} = \dfrac{{{{10}^3}{L_{\rm{f}}} \cdot {T_{{\rm{frz}}}}}}{{{{10}^3}{L_{\rm{f}}} - {\psi _{{\rm{sat}}}}{{\left({\dfrac{{{\theta _{{\rm{liq}}}}}}{{{\theta _{{\rm{sat}}}}}}} \right)}^{ - b}} \cdot {\rm{g}}}}, $ | (13) |
where Lf is the latent heat of fusion (J kg−1); Tfrz is the freezing point of pure water (K); ψsat is the saturated soil matrix potential (mm), which is usually negative; θsat and θliq are soil porosity and the partial volume of liquid water, respectively; b is the Clapp–Hornberger parameter; and g is the gravitational acceleration (m s−2). The threshold temperature gradually rises as liquid water content increases but is always below the freezing point of pure water Tfrz. It can be deduced from Eq. (13) that under the same condition of soil liquid water content, the freeze/thaw threshold temperature for coarse sandy soil is higher than that for other kinds of soil with smaller soil particle size and relatively larger porosity. The absolute value of the saturated soil water potential of clayey soil is greater than that of sandy soil with the same liquid water content; the second term (with negative value) in the denominator is larger in magnitude for clayey soil, and the final value of Tthre is thus smaller for clayey soil. The underlying reason is that sandy soil has macropores that can be easily drained and the assembled water can easily freeze; therefore Tthre for sandy soil is higher than Tthre for clayey soil with a similar soil water content.
Validation of different parameterization schemes to simulate the seasonal freeze/thaw of soil water/ice shows that the temporal evolution of soil temperature is closer to observations by using Eq. (13) to initiate thaw in spring and freeze in autumn. After the melting of the seasonal frozen layer, the seasonal warming of soil temperature is delayed and is closer to observations compared with the old scheme (Xia et al., 2011). Considering that the Tthre to initiate thawing of soil ice is usually higher than that for the freezing of soil liquid water, for the sake of simplicity and for the time being, 0.5°C is added to Tthre to initiate thawing of soil ice in BCC_AVIM2.0.
Soil organic matter serves as an insulator for heat transfer through soil layers, and the soil solid heat capacity of organic matter is larger than that of mineral (Lawrence and Slater, 2008), both of which delay soil freeze/thaw processes. These factors will be considered in the future version of BCC_AVIM.
3.6 Prognostic phenology of vegetationThe phenology of a PFT in BCC_AVIM1.0 is empirically prescribed to ensure that the simulated seasonal evolution of LAI is in phase with the climatology derived from satellite observations (Ji, 1995). In other words, there is no interannual variation in leaf expansion and leaf fall dates for a PFT in BCC_AVIM1.0. To capture the interannual variation and long term trend in vegetation phenology, a prognostic phenology scheme based on the work of Arora and Boer (2005) is implemented in BCC_AVIM2.0. The phenology for deciduous ecosystems consists of four stages: the rapid expansion period of LAI indicating the start of a growing season, the normal growth period, the leaf fall period, and a dormant season without leaves. The herbaceous biomes experience three phonological stages during their growth in a year, which are the same as the first three phenology stages of the deciduous forests. Unlike deciduous forests, herbaceous ecosystems maintain leaves as long as the environmental and physiological conditions are met. The evergreen forests are always in a normal growth state. Maintenance respiration is separately calculated for leaves, stems, and roots, depending on the separate biomasses and a temperature dependent Q10 factor. Growth respiration for each biomass pool (leaf, stem, and root) is assumed to be a fixed percentage (25%) of the residual of gross primary productivity (GPP) minus maintenance respiration.
Allocation to and from the three vegetation biomass pools (leaf, stem, and root) leads to dynamic vegetation that in turn produces litter fall and ultimately transfers to soil organic carbon (SOC). The allocation of carbon to the three vegetation biomass pools depends on the light availability, water stress, and phenology stages of the canopy, and follows the formulations of Arora and Boer (2005). Most carbon assimilated in photosynthesis is allocated to the leaves during the leaf onset stage, carbon is allocated to the three vegetation carbon pools during the normal growth stage, and allocation to leaves stops during the leaf fall stage. The allocation of carbon to the vegetation biomass pools is constrained by the adverse effects of limited availability of light and water. Accordingly, the allocation in roots can help address the limited availability of water, whereas investments in stems tend to increase canopy access to light.
The carbon allocation process is constrained by two conditions. First, for the cold deciduous trees, almost all carbon is allocated to the leaves during leaf onset in order to maximize photosynthetic carbon gain. The second condition is to assure that the plant structure is preserved, which implies that sufficient root and stem biomass must be built up in advance to support the leaf biomass. The allocation of carbohydrates produced by photosynthesis to different biomass pools (leaf, stem, and root) is parameterized as follows:
| $ {\alpha _{{\rm{stem}}}} = \frac{{{\varepsilon _{{\rm{stem}}}} + \omega \left( {1 - L} \right)}}{{1 + \omega \left( {2 - L - W} \right)}}, \quad\quad\quad\quad\quad\quad\quad\; $ | (14) |
| $ {\alpha _{{\rm{root}}}} = \frac{{{\varepsilon _{{\rm{root}}}} + \omega {\rm{}}\left( {1 - W} \right)}}{{1 + \omega {\rm{}}\left( {2 - L - W} \right)}}, \quad\quad\quad\quad\quad\quad\quad\; $ | (15) |
| $ {\alpha _{{\rm{leaf}}}} = \frac{{{\varepsilon _{{\rm{leaf}}}}}}{{1 + \omega \left( {2 - L - W} \right)}} = 1 - {\alpha _{{\rm{stem}}}} - {\alpha _{{\rm{root}}}}, $ | (16) |
where ω, εleaf, εstem, and εroot are PFT-dependent constants for the sake of simplicity, and the parameters L and W are associated with LAI and soil moisture conditions respectively, as given by:
| $ \hspace{-39pt} L = {e^{ - K\cdot {\rm{LAI}}}}, $ | (17) |
| $ W = \mathop \sum \nolimits_{i = 1}^n {W_i} \cdot {\rm{Root}}{f_i}, $ | (18) |
where K is a PFT-dependent light extinction coefficient, Wi is the soil wetness, and Rootfi is the fraction of root distribution in the ith soil layer. It can be deduced from Eq. (16) that under the same soil moisture condition (W), a larger L is associated with a larger αleaf. The philosophy is that more carbohydrates are allocated to the canopy to increase LAI at the beginning of a growing season when LAI is small and the parameter L is relatively large, which favors photosynthesis and canopy growth and thus the increase of LAI.
The litter fall from leaves, stems, and roots is estimated as a function of temperature, water stress, and turnover rates. The turnover timescale for leaves is biome-dependent and varies from 0.75 yr for savanna to 2 yr for evergreen forests (Foley et al., 1996). The turn-over rates for stems vary from 2.5 yr for savanna to 50 yr for evergreen forests (Malhi et al., 2004), and for root turnover the rates are between 1 and 8 yr for different PFTs.
The timing of the LAI peak in a year depends on the seasonal evolution of photosynthesis of a specific PFT, which strongly influences the seasonal variation of turbulent heat exchanges between the land surface and the atmosphere. Figure 5 displays the geographical distribution of the climate mean calendar month when LAI reaches its annual maximum. The LAI peak timing derived from AVHRR data clearly displays the seasonal evolution of vegetation growth along the latitude belts, especially in the middle to high latitudes of the NH with four distinctive seasons (Fig. 5a). In North America, the earliest LAI peak occurs in the southern Great Plains of the US in May, LAI in northwestern US reaches its maximum in June, large areas spanning from central Canada northwestward to Alaska see maximum LAI in July, and most of the other parts of North America experience peak LAI in August, except that Mexico and the southeastern US see LAI peaks in September or October. In the Southern Hemisphere (SH), the timing of peak LAI is slightly heterogeneous. The central Amazon basin at approximately 10°S experiences its LAI peak in July, whereas the Conco basin at similar latitudes in Africa experiences peak LAI in November; the Brazilian Plateau to the southeast of the Amazon basin and most parts of the South African continent see peak LAI in February to March; and the southern end of South America to the south of 35°S see peak LAI in November.

|
| Figure 5 The timing of LAI peaks (month). (a) AVHRR, (b) BCC_AVIM1.0, and (c) BCC_AVIM2.0. |
The empirical phenology scheme in BCC_AVIM1.0 simulates an almost uniform timing of peak LAI: August in the NH and February in the SH, one month after the height of summer in both hemispheres, except for seve-ral regions at approximately 30°N (e.g., western and cen-tral part of the southern US, western Asia) with peak LAI in June–July, and in November in southern Australia (Fig. 5b). In contrast, BCC_AVIM2.0 performs better in simulating the geographical LAI peak timing, especially in the NH (Fig. 5c). The details of BCC_AVIM2.0 simulation in different continents are presented next.
In the North American continent, LAI reaches a maximum in June in the western and eastern parts of the US, while central US and central Canada see peak LAI in July, and most of the other parts of the North American continent from Alaska to eastern Canada experience the LAI peak in August to September. Generally, the timing of peak LAI in the BCC_AVIM2.0 simulation is approximately one month earlier than in the AVHRR data in the central and eastern US but one month later than in the AVHRR data in other parts of the North American continent to the north of approximately 50°N.
In the Eurasian continent, regions to the south of 60°N and to the west of 30°E see peak LAI in June, which is consistent with the AVHRR observations. Most of the midlatitude regions from 30°E to 90°E experience peak LAI in July, and the other parts of the Eurasian continent to the north of 40°N see peak LAI in August to September, one or two months later than in the AVHRR data. In contrast, the timing of peak LAI in the BCC_AVIM2.0 simulation is approximately one month earlier than in AVHRR observations in the southeastern parts of Asia; for example, eastern China experiences peak LAI in June–July, central and eastern India sees peak LAI in September.
In the SH, the timing of the LAI peak in April–May in the central Amazon basin is approximately two months earlier than in the observations. The LAI peak in January to February in the Brazilian Plateau is close to observations but the area coverage at approximately 40°S in South America with peak LAI in November expands more northward than in observations. In the South Afri-can continent, tropical forests in the Congo basin see peak LAI in December to January, and most of the other parts see LAI peaks in March to April, approximately one month later than in observations (Figs. 5a, c).
The improvement in vegetation phenology produces better simulation of LAI at the seasonal timescale. In the AVHRR observations, there are three latitudinal belts of LAI maxima associated with three integrated belts of the earth’s ecosystem. The northernmost belt corresponds to the boreal mixed forests in high latitudes of the NH. The central belt is related to the temperate zone forests in southeastern US and southeastern China, and the third belt is associated with tropical forests in the Amazon basin in South America, the Congo basin in central Africa, and the Maritime Continent in Southeast Asia (Figs. 6a1, b1). The LAI of tropical rainforests remains above 4 throughout the year. Boreal forests experience remarkable seasonal variation: LAI is less than 2 in boreal winter (December, January, and February, i.e., DJF) and can be more than 4 in boreal summer (June, July, and August, i.e., JJA). Both BCC_AVIM1.0 and BCC_AVIM2.0 capture the general pattern of LAI distribution in both seasons, although BCC_AVIM1.0 overestimates LAI in most parts of the summer hemisphere, i.e., positive biases in the NH in JJA and in the SH in DJF, except for patchy negative biases in central North America and central Europe in JJA (Figs. 6a2, b2). The above LAI biases in the BCC_AVIM1.0 simulation correspond to the unrealistic phenology in BCC_AVIM1.0 displayed in Fig. 5b and consequent GPP simulation biases (figure omitted). In contrast, LAI biases in the BCC_AVIM2.0 simulation are reduced to some extent (Figs. 6a3, b3), except for the overestimations of LAI in the northwestern Amazon basin, western central Africa, and southeastern mainland China in both JJA and DJF, which might be due to the too-large maximum rate of carbo-xylation prescribed for tropical and subtropical forests in BCC_AVIM2.0 and the consequent overestimation of GPP in the aforementioned regions, issues that need to be addressed by more sensitivity experiments in the future.
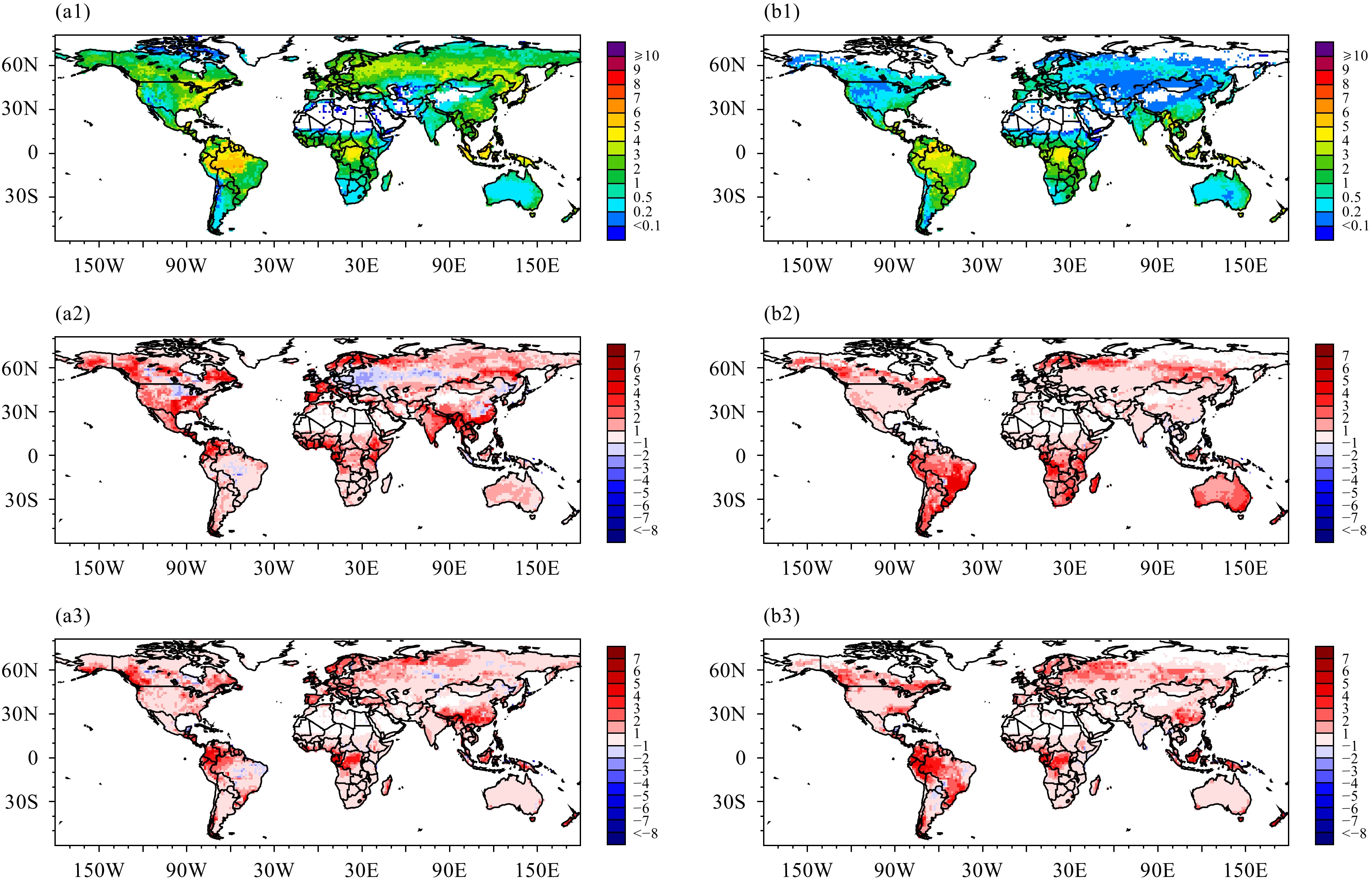
|
| Figure 6 Distributions of multi-year (1982–2008) seasonal mean LAI in (a1–a3) boreal summer (June, July, and August) and (b1–b3) boreal winter (December, January, Feburary). (a1, b1) AVHRR observations; (a2, b2) BCC_AVIM1.0 minus AVHRR; and (a3, b3) BCC_AVIM2.0 minus AVHRR. |
The two-stream scheme for calculating solar radiation transfer within a vegetation canopy in BCC_AVIM1.0 was originally developed by Dickinson (1983) and is widely used in LSMs. The four-stream radiation transfer module used in BCC_AVIM2.0 is based on the atmospheric radiation transfer theory (Liou, 1992), and it analytically solves a basic radiation transfer equation for the canopy, each parameter of which has its own geometry as well as specific leaf and canopy optical characteristics. The upward/downward radiation fluxes and canopy albedo calculated by the four-stream module are related to several factors such as the diffuse phase function, the area extinction coefficient, leaf reflectivity and transmissivity, LAI, and solar angle. Offline simulations show that the albedo of a vegetation canopy calculated by the four-stream module is lower than that calculated by the previous two-stream scheme. When coupled with the LSM BCC_AVIM2.0, the four-stream radiation transfer scheme produces lower albedos in mid–high latitudes but slightly higher albedos in most tropical dry land regions, which are closer to the observations (Zhou et al., 2018).
4 Performance of BCC_AVIM2.0 in LS3MIP/CMIP6The main purpose of LS3MIP is to provide a comprehensive assessment of land surface processes and associated feedbacks on climate variability and climate change and to diagnose systematic biases in the land component of current CSMs (van den Hurk et al., 2016). Two sets of experiments are designed for LS3MIP: the first addresses systematic biases of land surfaces in the offline mode and the second addresses land feedbacks attributed to snow cover and soil moisture in an integrated framework. LS3MIP has proposed several sets of atmospheric forcing data to drive LSMs in offline mode. The results of historical experiments with BCC_AVIM1.0 and BCC_AVIM2.0 driven by the Princeton global forcing dataset (Sheffield et al., 2006) are analyzed in this section under the framework of ILAMB (Mu et al., 2016), which focuses on land surface energy budgets and terrestrial carbon cycles at the seasonal timescale, especially the summer and winter seasons.
4.1 Net surface radiationAccording to the CERES data (Kato et al., 2013), the seasonal variation of net surface radiation (NSR; including both shortwave and longwave) strongly depends on the seasonal evolution of solar radiation, which peaks in summer and reaches its minimum in winter in both hemispheres. The tropics sees relatively strong year-round net radiation (Figs. 7a1, b1). Taking the summertime NH as an example (Fig. 7a1), the magnitude of NSR is above 90 W m−2 almost everywhere except in the Sahara desert in northern Africa, the Arabian Peninsula, and the Taklimakan desert in northwestern China. Most parts of mid- and high-latitude areas in the NH see more than 120 W m−2 of NSR; the southeastern part of the US even experiences more than 150 W m−2 of NSR in JJA. Generally, BCC_AVIM2.0 has reasonably captured the geographi-cal distribution and seasonal evolution of NSR (figure omitted), although the simulation biases are obvious in both summer and winter, especially in the SH (Figs. 7a2, b2). During the boreal JJA, negative biases of NSR in southern US and in the Sahel region are mainly associated with negative net longwave radiation biases (Figs. 7a2, a4). Patchy positive biases in the northern Eurasian continent, the Sahara desert of North Africa, and the Arabian Peninsula are associated with overestimation of net solar radiation in the above areas (Figs. 7a2, a3). The aforementioned underestimation (overestimation) of net shortwave radiation results from larger (smaller) SA simulation in relevant regions (figure omitted). In contrast to the above shortwave radiation-dominant cases, overestimation of NSR in the northeast part of the Eurasian continent in DJF is due to the positive net longwave radiation bias in the BCC_AVIM2.0 simulation in that area (Figs. 7b2, b4). Underestimations of DJF net shortwave radiation in BCC_AVIM2.0 simulations in the SH are responsible for the negative NSR biases, and negative biases of net longwave radiation in the southern American and southern African continents may have also made some contributions (Figs. 7b2–b4). The aforementioned systematic biases indicate that there is much room to improve BCC_AVIM2.0 to reasonably simulate the surface energy budget.

|
| Figure 7 Distributions of multi-year (2000–09) seasonal mean net surface radiation (NSR; W m−2) in (a1–a4) boreal summer and (b1–b4) boreal winter. (a1, b1) CERES (net radiation); (a2, b2) BCC_AVIM2.0 minus CERES (net radiation); (a3, b3) BCC_AVIM2.0 minus CERES (shortwave); (a4, b4) BCC_AVIM2.0 minus CERES (longwave). |
Land surface evaporation includes three parts: soil surface evaporation, evaporation from canopy intercepted precipitation, and vegetation transpiration through leaf pores (Lawrence et al., 2007). In addition to wind speed, the availability of net surface energy, soil water, and canopy-intercepted precipitation are among those factors that influence land evaporation. The LHFX magnitudes in the tropical areas remain more than 80 W m−2 year-round, and the NH experiences maximum LHFX in JJA, whereas LHFX peaks in DJF in the SH (Figs. 8a1, b1). There is an obvious northeastward gradient of LHFX in the Eurasian continent in JJA and DJF. In JJA, the magnitude of LHFX decreases from more than 80 W m−2 in western Europe to approximately 60–80 W m−2 in the central part and less than 60 W m−2 in the northeastern part of the Eurasian continent. LHFX can be more than 80 W m−2 in eastern Asia and as high as 100 W m−2 in southern Asia (Fig. 8a1). In DJF, most parts of the NH to the north of 50°N experience surface freezing, and the LHFX values in these regions are thus below 5 W m−2. In contrast, LHFX in the subtropical areas in South America and the African continent reach peaks as high as 100 W m−2 (Fig. 8b1). BCC_AVIM2.0 has captured the overall geographical distribution and seasonal evolution of LHFX, except for some magnitude difference from the GBAF observations (Figs. 8a2, b2). The systematic biases of the BCC_AVIM2.0 simulation in JJA are obvious. There are approximately 20-W m−2 underestimations of LHFX in eastern US, tropical South America, tropical Africa, and southeastern China. In contrast, approximately 20-W m−2 overestimations of LHFX exist in semiarid regions in the NH such as northern Canada, northern Sahel, the Tibetan Plateau, and the Mongolian plateau (Fig. 8a3). In DJF, the LHFX underestimations in tropical South America, tropical Africa, and South Asia are approximately 10–20 W m−2 (Fig. 8b3). The aforementioned underestimations in LHFX simulation in both JJA and DJF can be attributed to the negative biases in NSR shown in Figs. 7a2, b2, which indicates the dominance of available energy on land surface evaporation.

|
| Figure 8 Distributions of multi-year (1982–2008) seasonal mean seasonal mean LHFX (W m−2) in (a1–a3) boreal summer and (b1–b3) boreal winter. (a1, b1) GBAF observation, (a2, b2) BCC_AVIM2.0 simulation, and (a3, b3) BCC_AVIM2.0 minus GBAF. |
The surface SHFX indicates the land surface thermal status and directly affects the overlying atmospheric circulation. Generally, lower surface pressure and near surface cyclonic circulation usually occurs over warmer surfaces with relatively high SHFX, and vice versa. The seasonal variation of SHFX is remarkable in high latitudes to the north of 50°N. Taking the latitude belt of approximately 60°N as an example, SHFX reaches more than 40 W m−2 in JJA and decreases to less than 10 W m−2 and even below zero in DJF, which means that the land surface in high-latitude NH is a heat sink in boreal winter. This heat sink in DJF can extend southward to 50°N in North America and the Eurasian continent to the west of 90°E (Figs. 9a1, b1). BCC_AVIM2.0 can simulate the overall geographical distribution of SHFX, except for the more southward expansion (approximately 40°N) of low SHFX coverage in North America and the northern Eurasian continent to the west of 110°E during DJF (Fig. 9b2). In JJA, there are approximately 20-W m−2 overestimations of SHFX in the BCC_AVIM2.0 simulation in dry lands, such as the central part of North America, the Brazilian Plateau, the Arabian Peninsula, and the midlatitude belt from west Asia to Mongolian Plateau (Fig. 9a3). The positive biases of SHFX in the central part of North America and the Brazilian Plateau coincide with the underestimation of LHFX in these regions, which is a common deficiency in the simulation of arid and semi-arid land surface processes (Wang et al., 2017; Zhang et al., 2017). In DJF, there are approximately 10–20-W m−2 positive biases to the north of 60°N and negative biases in the midlatitudes of the NH between 30°N and 60°N (Fig. 9b3). The overestimation of SHFX by BCC_AVIM2.0 in the northeastern part of the Eurasian continent in DJF is probably due to the underestimation of SCF there in winter (figure omitted).
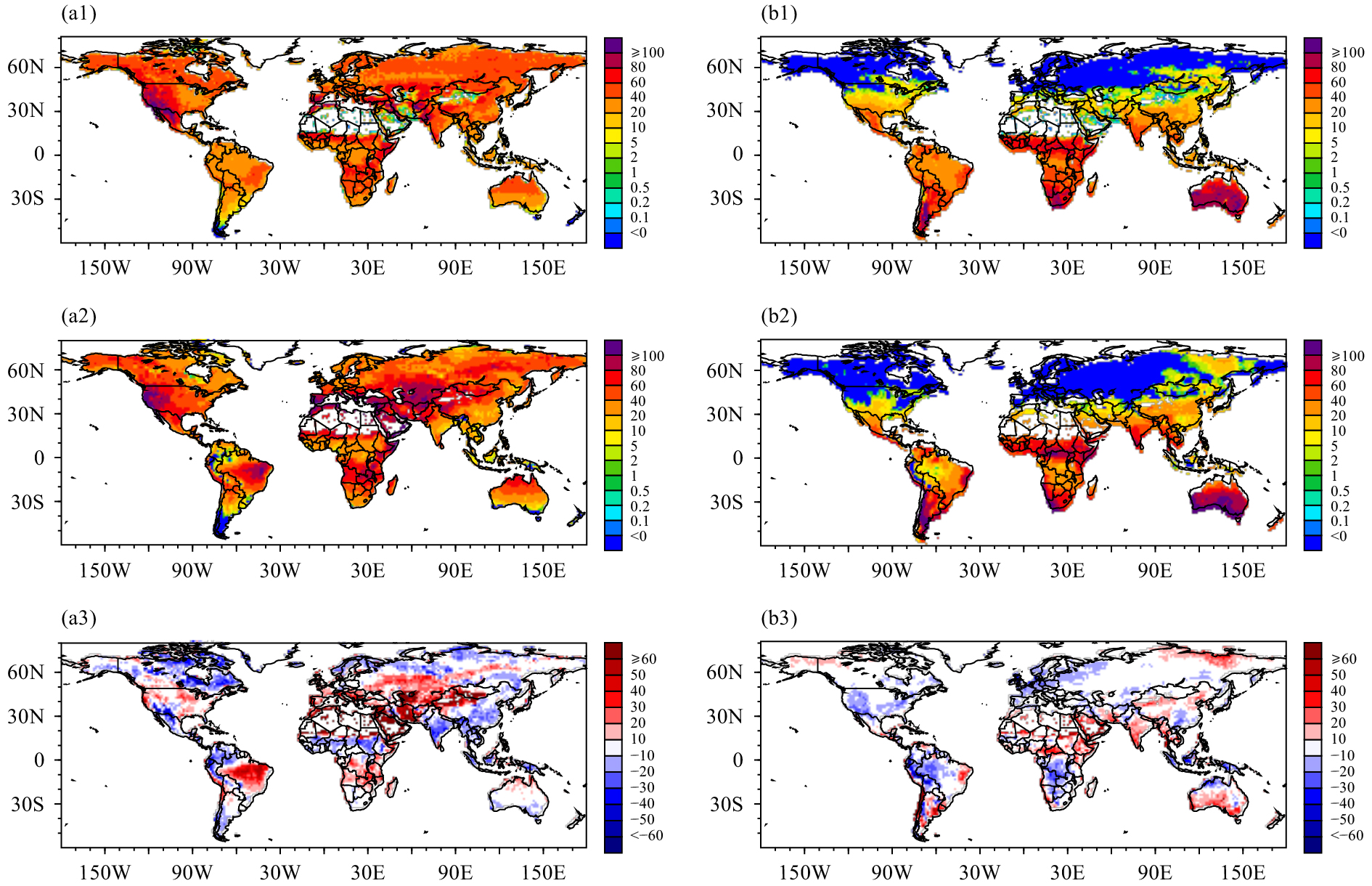
|
| Figure 9 As in Fig. 8, but for SHFX (W m−2). |
The simulations of BCC_AVIM1.0 and BCC_AVIM2.0 are compared in this section to check the overall impacts of the updates in parameterizations described in Section 3. The climatological annual cycles of regional averaged solar and surface fluxes (NSR, SHFX, and LHFX) and LAI are examined and analyzed, over the main body of the Eurasian continent (40°–70°N, 0°–140°E) and the South African continent (0°–35°S, 10°–40°E). These two domains are chosen as examples to represent the NH and SH, respectively.
Figure 10 shows the annual cycle for the Eurasian continent. NSR peaks in June in CERES observations, and both BCC_AVIM1.0 and BCC_AVIM2.0 simulations captured the seasonal cycle, except that the simulated NSRs are less than the observations by approximately 5–15 W m−2 from February to November. BCC_AVIM2.0 values are larger than BCC_AVIM1.0 and closer to CERES from June to October but BCC_AVIM1.0 performs better from February to May, although the difference between the two simulations is within 5 W m−2 (Fig. 10a). The underestimation of NSR in both simulations is due to more reflected shortwave radiation and more emitted longwave radiation than those in the observations (figure omitted); the contribution of longwave radiation is larger than that of shortwave radiation from March to October, especially in boreal spring. SHFX in BCC_AVIM1.0 is approximately 5 W m−2 smaller than GBAF observations from January to April, and SHFX in BCC_AVIM2.0 is smaller than GBAF by approximately 5–10 W m−2 from January to May. SHFXs in BCC_AVIM1.0 and BCC_AVIM2.0 are close to each other from June to December; they are nearly 7 W m−2 larger than GBAF from June to August but approximately 5 W m−2 smaller than GBAF from October to December (Fig. 10b). LHFX in BCC_AVIM2.0 is approximately 5 W m−2 larger than BCC_AVIM1.0 and is closer to GBAF from May to August (Fig. 10c). Further investigation indicates that this improvement in LHFX in BCC_AVIM2.0 is due to more transpiration through vegetation (figure omitted). LAI is larger in BCC_AVIM1.0 than in the AVHRR data by approximately 1 all year round, and the bias of LAI in BCC_AVIM1.0 can be as large as 2 in August when LAI peaks in BCC_AVIM1.0 (Fig. 5b). BCC_AVIM2.0 is better than BCC_AVIM1.0 in both the magnitude and phase of the seasonal evolution of LAI (Fig. 10d). In short, the seasonal cycle is better in BCC_AVIM2.0 due to the better representation of vegetation phenology.
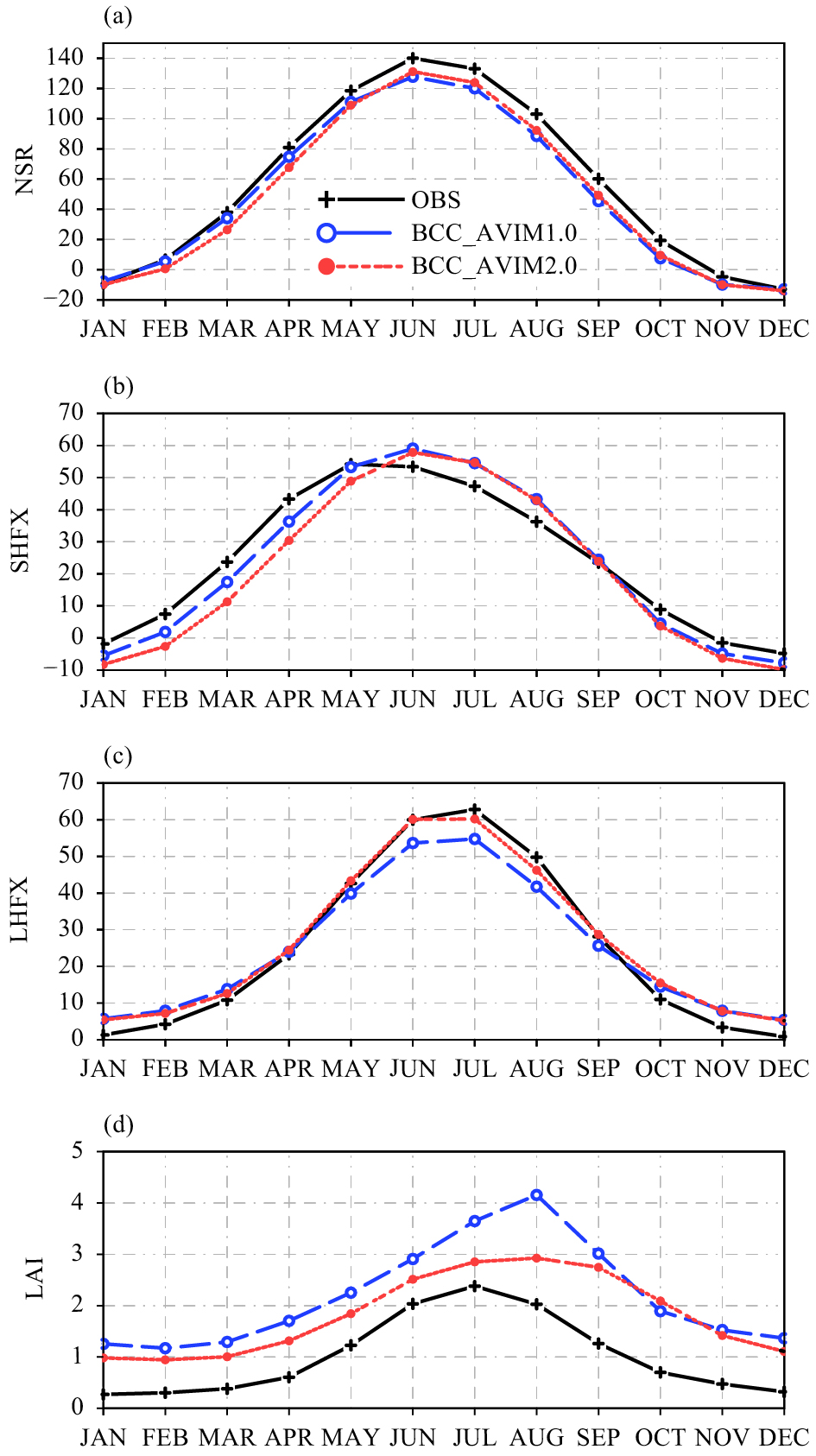
|
| Figure 10 Annual cycle of regional averaged (a) NSR, (b) SHFX, (c) LHFX, and (d) LAI over the main part of the Eurasian continent (40°–70°N, 0–140°E). Unit is W m−2 for energy fluxes in (a–c). |
The situation in the South African continent is shown in Fig. 11. NSR reaches a maximum of approximately 165 W m−2 in January and a minimum of approximately 75 W m−2 in July in CERES. Both BCC_AVIM1.0 and BCC_AVIM2.0 capture this seasonal evolution with year-round negative biases in both simulations. BCC_AVIM1.0 underestimates NSR by approximately 40 W m−2 in January and approximately 10 W m−2 in July. BCC_AVIM2.0 reduces this negative bias by approximately 5 W m−2 from February to September. The underestimation of NSR for the South African continent is due to more reflected shortwave radiation and more outgoing longwave radiation from the surface in both simulations (figure omitted). SHFX reaches a minimum (about 40 W m−2) in June and a maximum (about 67 W m−2) in October according to GBAF. BCC_AVIM1.0 underestimates SHFX by approximately 7 W m−2 from October to the following April, whereas SHFX in BCC_AVIM2.0 is larger than in BCC_AVIM1.0 year-round and closer to GBAF from October to the following April (Fig. 11b). However, this alleviation of negative SHFX bias in BCC_AVIM1.0 is at the cost of underestimation of LHFX by BCC_AVIM2.0 from January to April (Fig. 11c). The slight improvement in BCC_AVIM2.0 simulation of LHFX from May to October is associated with the better simulation of NSR during that period (Fig. 11a). LAI from AVHRR reaches a peak of approximately 2 in March. BCC_AVIM1.0 overestimates LAI by approximately 1 all year round, with a maximum near 5 in February; whereas BCC_AVIM2.0 captures the seasonal cycle of LAI evolution quite well, except for positive biases of approximately 0.5–1.0 from January to August (Fig. 11d). The maximum of LAI in the BCC_AVIM2.0 simulation from February to April is coincident with the LAI peak time over the South African continent shown in Fig. 5c. This indicates the advantage of the updated phenology scheme in BCC_AVIM2.0.
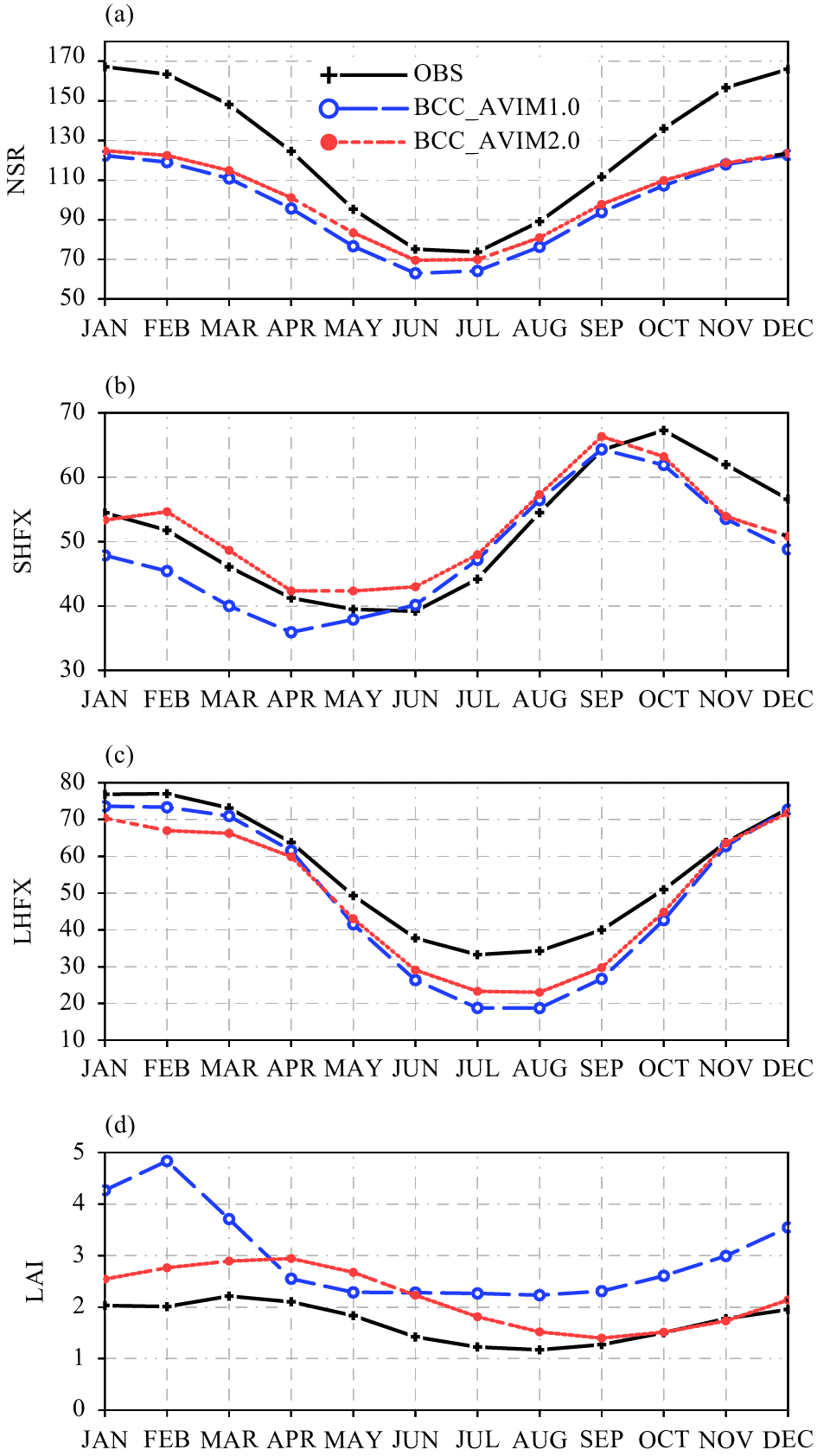
|
| Figure 11 As in Fig. 10, but over the South African continent (0–35°S, 10°–40°E). Unit is W m−2 for energy fluxes in (a–c). |
Statistics of the annual global land average of the aforementioned variables displayed in Table 1 also indicate improvements of BCC_AVIM2.0 simulations after the updates of the parameterizations. The global mean bias of NSR is reduced from −12.0 to −11.7 W m−2, and the RMSE drops from 20.6 to 19.0 W m−2. The bias of LHFX is reduced from 2.3 to −0.1 W m−2 and the RMSE is reduced from 15.4 to 14.3 W m−2. One exception is that the global mean SHFX bias is increased from 2.5 to 5.1 W m−2, whereas the RMSE is reduced from 18.4 to 17.0 W m−2. The bias of LAI is reduced from 0.89 to 0.75, and the RMSE is reduced from 1.46 to 1.27.
| BCC_AVIM1.0 | BCC_AVIM2.0 | |
| NSR | −12.0 (20.6) | −11.7 (19.0) |
| LHFX | 2.3 (15.4) | −0.1 (14.3) |
| SHFX | 2.5 (18.4) | 5.1 (17.0) |
| LAI | 0.89 (1.46) | 0.75 (1.27) |
The overall performance of BCC_AVIM1.0 and BCC_AVIM2.0 in simulating the global annual climatology of surface energy budgets, LAI, and variables associated with terrestrial carbon cycle is displayed in the Taylor diagram in Fig. 12. Both models perform well in simulating 9 variables with higher than 0.6 spatial correlations with the relevant observations [except for net ecosystem exchange (NEE) in the BCC_AVIM1.0 simulation], and 13 out of 18 standardized deviations fall approximately into the 0.5–1.5 range compared with the reference variability. Concerning spatial correlation, BCC_AVIM2.0 performs better than BCC_AVIM1.0 in simulating NEE, LAI, net surface radiation (NSR), SA, and SHFX, whereas BCC_AVIM1.0 performs slightly better in simulating GPP and respiration of ecosystem (RECO). It is noted that the two red circles representing the simulation performances of RECO and LAI in BCC_AVIM2.0 are very close to each other inFig. 12. With respect to standardized deviation, which indicates the spatial variability of each variable, BCC_AVIM2.0 performs better than BCC_AVIM1.0 and closer to the thick reference circular arc in the simulation of GPP, RECO, tropical biomass, NSR, and SA.

|
| Figure 12 Taylor diagram for the global annual climatology of gross primary productivity (gpp), respiration of ecosystem (reco), net ecosystem exchange of CO2 (nee), biomass, leaf area index (lai), land net surface radiation (nsr), surface albedo (sa), surface sensible heat flux (shfx), and surface latent heat flux (lhfx). The upper case suffix after each variable indicates the source of observation. The radial coordinate shows the standard deviation of the spatial pattern, normalized by the observed standard deviation. The azimuthal variable shows the correlation of the modeled spatial pattern with the observed spatial pattern. Analysis is for the entire globe (except that biomass is for tropi-cal areas). The BCC_AVIM2.0 and BCC_AVIM1.0 simulations are averaged over the same period as that for the relevant reference dataset. Crosses are for BCC_AVIM1.0 and circles for BCC_AVIM2.0. |
This paper has documented the updates in several land surfaces related parameterization schemes in the second version of the Beijing Climate Center Atmosphere–Vegetation Interaction Model (BCC_AVIM2.0). The updated parameterizations include those for lakes of variable depth in the framework of snow–ice–water–soil, evapotranspiration over rice paddies, snow cover fraction and snow surface albedo, threshold temperature to initiate freeze (thaw) of soil water (ice), prognostic vegetation phenology, and solar radiation transfer through the vegetation canopy. The performance of BCC_AVIM2.0 after the implementation of the revised parameterizations is evaluated with available observations.
The BCC_AVIM2.0 simulation of surface temperature of the Great Lakes region in North America is much improved, with lower RMSE and higher spatial correlation coefficients with observations, especially in wintertime. The cold bias in the BCC_AVIM1.0 simulation in January is possibly due to the relatively quick freezing of surface water without considering the insulation of snow cover. The alleviation of this cold bias in the simulation of BCC_AVIM2.0 is possibly due to the more efficient heat exchange in the vertical layers and larger heat capacity of the entire water–soil system of CoLM-lake in BCC_AVIM2.0 than in the water-only lake module in BCC_AVIM1.0.
Increased LHFX and reduced SHFX over rice paddies are closer to the observations in BCC_AVIM2.0 than in BCC_AVIM1.0. The increase of LHFX is due to enhanced ground water evaporation, and the decrease of SHFX is attributed to the redistribution of available NSR budget. It is inferred that the improvement in the seaso-nal evolutions of surface heat fluxes results from the revised rice phenology with two growing seasons in a year, which is closer to the midlatitude situation in China.
The two-stage snow albedo scheme in BCC_AVIM2.0 captures the different snow aging effects at the accumulation and melting periods of a snow season and decreases the overestimation of snow albedo during the snow melting period. This alleviates delay of final ablation of snow cover in boreal spring in the BCC_AVIM1.0 simulation, leading to improved simulation results.
The prognostic phenology scheme in BCC_AVIM2.0 can quite well reproduce the diversity of global timing of the LAI peak, especially the seasonal northeastward movement of the peak timing of vegetation growth in the Eurasian continent. Better simulation of LAI peak timing is favorable for the improvement in simulating land surface heat fluxes and land–atmosphere interactions. Therefore, it is beneficial to the simulation of the overlying atmospheric circulation, which will be validated in the future by running the coupled BCC_CSM with BCC_AVIM2.0 as its land component model.
Preliminary results of BCC_AVIM2.0 in the ongoing LS3MIP of CMIP6 show that it can reasonably capture the geographic distribution and seasonal evolution of surface energy fluxes. The overall performance of BCC_AVIM2.0 in simulation of the land surface energy budgets and terrestrial carbon cycle is better than that of BCC_AVIM1.0 in terms of geographical distribution and standardized deviations. The annual global land averaged biases and RMSEs of NSR, LHFX, and LAI are reduced after the updates of the parameterization schemes in BCC_AVIM2.0. The global mean RMSE of SHFX is also reduced whereas the bias of SHFX is increased.
The positive biases of SHFX in central North America and the Brazilian Plateau in the BCC_AVIM2.0 simulation in JJA are coincident with the underestimation of LHFX in these regions. The above overestimation of SHFX and underestimation of LHFX are associated with the positive biases in the surface temperature and the surface outgoing longwave radiation and thus the negative bias in NSR over these semiarid regions, which involves complicated interactions between surface energy budgets and the water cycle. This is an interesting topic that deserves further investigation.
Since there are uncertainties among different observational datasets and various atmospheric forcings to drive LSMs, it is necessary to employ alternative atmospheric forcings to run BCC_AVIM2.0 and evaluate the simulations against multi-source observations, which will provide new insights into land surface processes and enhance the understanding of the mechanisms involved in land–atmosphere interactions.
Acknowledgments. The authors thank Professor Shu-fen Sun of the Institute of Atmospheric Physics, Chinese Academy of Sciences for his constant support to the development of BCC_AVIM. We also thank the two reviewers for their valuable suggestions to improve the manuscript.
| Aoki, T., A. Hachikubo, and M. Hori, 2003: Effects of snow physical parameters on shortwave broadband albedos. J. Geophys. Res. Atmos., 108, 4616. DOI:10.1029/2003JD003506 |
| Arora, V. K., and G. J. Boer, 2005: A parameterization of leaf phenology for the terrestrial ecosystem component of climate models. Glob. Change Biol., 11, 39–59. DOI:10.1111/j.1365-2486.2004.00890.x |
| Arora, V. K., G. J. Boer, P. Friedlingstein, et al., 2013: Carbon–concentration and carbon–climate feedbacks in CMIP5 earth system models. J. Climate, 26, 5289–5314. DOI:10.1175/JCLI-D-12-00494.1 |
| Avitabile, V., M. Herold, G. B. M. Heuvelink, et al., 2016: An integrated pan-tropical biomass map using multiple reference datasets. Glob. Change Biol., 22, 1406–1420. DOI:10.1111/gcb.13139 |
| Bao, Y., Y. H. Gao, S. H. Lyu, et al., 2014: Evaluation of CMIP5 earth system models in reproducing leaf area index and vegetation cover over the Tibetan Plateau. J. Meteor. Res., 28, 1041–1060. DOI:10.1007/s13351-014-4023-5 |
| Bonan, G. B., P. J. Lawrence, K. W. Oleson, et al., 2011: Improving canopy processes in the community land model version 4 (CLM4) using global flux fields empirically inferred from fluxnet data. J. Geophys. Res. Biogeosci., 116, G02014. DOI:10.1029/2010JG001593 |
| Cao, M. K., and F. I. Woodward, 1998: Net primary and ecosystem production and carbon stocks of terrestrial ecosystems and their responses to climate change. Glob. Change Biol., 4, 185–198. DOI:10.1046/j.1365-2486.1998.00125.x |
| Chen, A. J., W. P. Li, W. J. Li, et al., 2014: An observational study of snow aging and the seasonal variation of snow albedo by using data from Col de Porte, France. Chinese Sci. Bull., 59, 4881–4889. DOI:10.1007/s11434-014-0429-9 |
| Dai, Y. J., X. B. Zeng, R. E. Dickinson, et al., 2003: The Common Land Model. Bull. Amer. Meteor. Soc., 84, 1013–1024. DOI:10.1175/BAMS-84-8-1013 |
| Dai, Y. J., N. Wei, A. J. Huang, et al., 2018: The lake scheme of the common land model and its performance evaluation. Chinese Sci. Bull., 63, 3002–3021. DOI:10.1360/N972018-00609 |
| Dickinson, R. E., 1983: Land surface processes and climate–surface albedos and energy balance. Adv. Geophys., 25, 305–353. DOI:10.1016/S0065-2687(08)60176-4 |
| Dickinson, R. E., A. Henderson-Sellers, and P. J. Kennedy, 1993: Biosphere–Atmosphere Transfer Scheme (BATS) Version 1e as Coupled to the NCAR Community Climate Model. NCAR Technical Note NCAR/TN-387+STR, National Center for Atmospheric Research, Boulder, CO, USA, 72 pp. |
| Foley, J. A., I. C. Prentice, N. Ramankutty, et al., 1996: An integrated biosphere model of land surface processes, terrestrial carbon balance, and vegetation dynamics. Glob. Biogeochem. Cycles, 10, 603–628. DOI:10.1029/96GB02692 |
| Friedlingstein, P., M. Meinshausen, V. K. Arora, et al., 2014: Uncertainties in CMIP5 climate projections due to carbon cycle feedbacks. J. Climate, 27, 511–526. DOI:10.1175/JCLI-D-12-00579.1 |
| Huang, A. N., Lazhu, J. B. Wang, et al., 2019: Evaluating and improving the performance of three 1-D lake models in a large deep lake of the central Tibetan Plateau. J. Geophys. Res. Atmos., 124, 3143–3167. DOI:10.1029/2018JD029610 |
| Ji, J. J., 1995: A climate–vegetation interaction model: Simulating physical and biological processes at the surface. J. Biogeogr., 22, 2063–2069. |
| Ji, J. J., M. Huang, and K. Li, 2008: Prediction of carbon exchange between China terrestrial ecosystem and atmosphere in 21st century. Sci. China Ser. D Earth Sci., 51, 885–898. DOI:10.1007/s11430-008-0039-y |
| Jung, M., M. Reichstein, and A. Bondeau, 2009: Towards global empirical upscaling of FLUXNET eddy covariance observations: Validation of a model tree ensemble approach using a biosphere model. Biogeosciences, 6, 2001–2013. DOI:10.5194/bg-6-2001-2009 |
| Jung, M., M. Reichstein, H. A. Margolis, et al., 2011: Global patterns of land–atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. Biogeosci., 116, G00J07. DOI:10.1029/2010JG001566 |
| Kato, S., N. G. Loeb, F. G. Rose, et al., 2013: Surface irradiances consistent with CERES-derived top-of-atmosphere shortwave and longwave irradiances. J. Climate, 26, 2719–2740. DOI:10.1175/JCLI-D-12-00436.1 |
| Lawrence, D. M., and A. G. Slater, 2008: Incorporating organic soil into a global climate model. Climate Dyn., 30, 145–160. DOI:10.1007/s00382-007-0278-1 |
| Lawrence, D. M., P. E. Thornton, K. W. Oleson, et al., 2007: The partitioning of evapotranspiration into transpiration, soil evaporation, and canopy evaporation in a GCM: Impacts on land–atmosphere interaction. J. Hydrometeor., 8, 862–880. DOI:10.1175/JHM596.1 |
| Lawrence, D. M., K. W. Oleson, M. G. Flanner, et al., 2011: Parameterization improvements and functional and structural advances in version 4 of the community land model. J. Adv. Model. Earth Syst., 3, M03001. DOI:10.1029/2011MS00045 |
| Li, Q., and S. F. Sun, 2008: Development of the universaland simplified soil model coupling heat and watertransport. Sci. China Ser. D Earth Sci., 51, 88–102. DOI:10.1007/s11430-007-0153-2 |
| Li, Q., S. F. Sun, and Y. K. Xue, 2010: Analyses and development of a hierarchy of frozen soil models for cold region study. J. Geophys. Res. Atmos., 115, D03107. DOI:10.1029/2009JD012530 |
| Li, W. P., X. Liu, S. P. Nie, et al., 2009: Comparative studies of snow cover parameterization schemes used in climate models. Adv. Earth Sci., 24, 512–522. DOI:10.11867/j.issn.1001-8166.2009.05.0512 |
| Liou, K. N., 1992: Radiation and Cloud Processes in the Atmosphere: Theory, Observation and Modeling. Oxford University Press, London, 487 pp. |
| Luo, S. Q., X. W. Fang, S. H. Lyu, et al., 2017: Improving CLM4.5 simulations of land–atmosphere exchange during freeze–thaw processes on the Tibetan Plateau. J. Meteor. Res., 31, 916–930. DOI:10.1007/s13351-017-6063-0 |
| Malhi, Y., T. R. Baker, O. L. Phillips, et al., 2004: The above-ground coarse wood productivity of 104 neotropical forestplots. Glob. Change Biol., 10, 563–591. DOI:10.1111/j.1529-8817.2003.00778.x |
| Morin, S., Y. Lejeune, B. Lesaffre, et al., 2012: An 18-yr long (1993–2011) snow and meteorological dataset from a mid-altitude mountain site (Col de Porte, France, 1325 m alt.) for driving and evaluating snowpack models. Earth Syst. Sci. Data, 4, 13–21. DOI:10.5194/essd-4-13-2012 |
| Mu, M. Q., F. Hoffman, D. Lawrence, et al., 2016: International Land Model Benchmarking (ILAMB) Package v001.00. Sponsored by the US DOE Office of Science (SC), Biologi-cal and Environmental Research (BER), doi: 10.18139/ILAMB.v001.00/1251597. Available at https://www.bgc-feedbacks.org/software/10.18139/ILAMB.v001.00/. |
| Mu, M. Q., and ILAMB team, 2019: Design and development of a community benchmark system for land surface models. Proc. International Workshop on Weather and Climate Variability and Their Mechanism, 7–9 August, Beijing, China, 337–356. |
| Myneni, R. B., R. Ramakrishna, R. Nemani, et al., 1997: Estimation of global leaf area index and absorbed Par using radiative transfer models. IEEE Trans. Geosci. Remote Sens., 35, 1380–1393. DOI:10.1109/36.649788 |
| Niu, G.-Y., and Z.-L. Yang, 2007: An observation-based formulation of snow cover fraction and its evaluation over large North American river basins. J. Geophys. Res. Atmos., 112, D21101. DOI:10.1029/2007JD008674 |
| Oleson, K. W., Y. J. Dai, G. Bonan, et al., 2004: Technical Description of the Community Land Model (CLM). NCAR Technical Note NCAR/TN-461+STR. National Center for Atmospheric Research, Boulder, CO, USA, 173 pp. |
| Parton, W. J., J. W. B. Stewart, and C. V. Cole, 1988: Dynamics of C, N, P and S in grassland soils: A model. Biogeochemistry, 5, 109–131. DOI:10.1007/BF02180320 |
| Roesch, A., M. Wild, H. Gilgen, et al., 2001: A new snow cover fraction parametrization for the ECHAM4 GCM. Climate Dyn., 17, 933–946. DOI:10.1007/s003820100153 |
| Saatchi, S. S., N. L. Harris, S. Brown, et al., 2011: Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA, 108, 9899–9904. DOI:10.1073/pnas.1019576108 |
| Sellers, P. J., D. A. Randall, G. J. Collatz, et al., 1996: A revised land surface parameterization (SiB2) for atmospheric GCMs. Part I: Model formulation. J. Climate, 9, 676–705. DOI:10.1175/1520-0442(1996)009<0676:ARLSPF>2.0.CO;2 |
| Sheffield, J., G. Goteti, and E. F. Wood, 2006: Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling. J. Climate, 19, 3088–3111. DOI:10.1175/JCLI3790.1 |
| Su, F. G., X. L. Duan, D. L. Chen, et al., 2013: Evaluation of the global climate models in the CMIP5 over the Tibetan Plateau. J. Climate, 26, 3187–3208. DOI:10.1175/JCLI-D-12-00321.1 |
| Subin, Z. M., W. J. Riley, and D. Mironov, 2012: An improved lake model for climate simulations: Model structure, evaluation, and sensitivity analyses in CESM1. J. Adv. Model. Earth Syst., 4, M02001. DOI:10.1029/2011MS000072 |
| Sun, S. F., J. M. Jin, and Y. K. Xue, 1999: A simple snow–atmosphere–soil transfer model. J. Geophys. Res. Atmos., 104, 19,587–19,597. DOI:10.1029/1999JD900305 |
| Todd-Brown, K. E. O., J. T. Randerson, W. M. Post, et al., 2013: Causes of variation in soil carbon simulations from CMIP5 earth system models and comparison with observations. Biogeosciences, 10, 1717–1736. DOI:10.5194/bg-10-1717-2013 |
| van den Hurk, B., H. Kim, G. Krinner, et al., 2016: LS3MIP (v1.0) contribution to CMIP6: The land surface, snow and soil moisture model intercomparison project—Aims, setup and expected outcome. Geosci. Model Dev., 9, 2809–2832. DOI:10.5194/gmd-9-2809-2016 |
| Wang, C., Z. G. Wei, Z. C. Li, et al., 2017: Testing and improving the performance of the Common Land Model: A case study for the Gobi landscape. J. Meteor. Res., 31, 625–632. DOI:10.1007/s13351-017-6080-z |
| Wu, T. W., L. C. Song, W. P. Li, et al., 2013: Global carbon budgets simulated by the Beijing Climate Center climate system model for the last century. J. Geophys. Res. Atmos., 118, 4326–4347. DOI:10.1002/jgrd.50320 |
| Wu, T. W., L. C. Song, W. P. Li, et al., 2014: An overview of BCC climate system model development and application for climate change studies. J. Meteor. Res., 28, 34–56. DOI:10.1007/s13351-014-3041-7 |
| Xia, K., and B. Wang, 2015: Evaluation and projection of snow cover fraction over Eurasia. Climatic Environ. Res., 20, 41–52. DOI:10.3878/j.issn.1006-9585.2014.13126 |
| Xia, K., Y. Luo, and W. P. Li, 2011: Simulation of freezing and melting of soil on the northeast Tibetan Plateau. Chinese Sci. Bull., 56, 2145–2155. DOI:10.1007/s11434-011-4542-8 |
| Xue, Y. K., S. F. Sun, D. S. Kahan, et al., 2003: Impact of parameterizations in snow physics and interface processes on the simulation of snow cover and runoff at several cold region sites. J. Geophy. Res. Atmos., 108, 8859. DOI:10.1029/2002JD003174 |
| Yang, Z.-L., R. E. Dickinson, A. Robock, et al., 1997: Validation of the snow submodel of the biosphere–atmosphere transfer scheme with Russian snow cover and meteorological observational data. J. Climate, 10, 353–373. DOI:10.1175/1520-0442(1997)010<0353:VOTSSO>2.0.CO;2 |
| Zeng, X. B., M. Shaikh, Y. J. Dai, et al., 2002: Coupling of the common land model to the NCAR community climate model. J. Climate, 15, 1832–1854. DOI:10.1175/1520-0442(2002)015<1832:COTCLM>2.0.CO;2 |
| Zhang, G., G. S. Zhou, and F. Chen, 2017: Analysis of parameter sensitivity on surface heat exchange in the Noah land surface model at a temperate desert steppe site in China. J. Meteor. Res., 31, 1167–1182. DOI:10.1007/s13351-017-7050-1 |
| Zhou, W. Y., Y. Luo, W. P. Li, et al., 2018: Comparative studies of different radiation schemes within vegetation in a land model. Chinese Sci. Bull., 63, 2772–2784. DOI:10.1360/N972018-00398 |
 2019, Vol. 33
2019, Vol. 33


