The Chinese Meteorological Society
Article Information
- TIAN, Baoqiang, and Ke FAN, 2019.
- Seasonal Climate Prediction Models for the Number of Landfalling Tropical Cyclones in China. 2019.
- J. Meteor. Res., 33(5): 837-850
- http://dx.doi.org/10.1007/s13351-019-8187-x
Article History
- Received November 28, 2018
- in final form May 15, 2019
2. Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Nanjing University of Information Science & Technology, Nanjing 210044;
3. University of Chinese Academy of Sciences, Beijing 100049
Tropical cyclones (TCs) are among the most destructive and deadly natural disasters in terms of the loss of human life and economic destruction. TCs that form over the South China Sea and western North Pacific (WNP) usually make landfall over East and Southeast Asia. Many studies have proved that the variation in WNP TC activity is associated with El Niño–Southern Oscillation (ENSO). Anomalies of the large-scale environment associated with the tropical Pacific sea surface temperature (SST) anomaly in different types of decaying El Niño events are responsible for remarkable anomalies of TC landfall (Ha and Zhong, 2014). In La Niña years, the increased frequency of TC landfall in the East Asian coast and decreased TC landfall frequency on the Indochina Peninsula were mainly due to the effect of ENSO on the mean WNP TC genesis position (Fudeyasu et al., 2006; Yonekura and Hall, 2014; Hong et al., 2016).
Considerable damage in terms of human life and property in coastal areas usually occurs around the period of landfalling TCs (LTCs). As such, there is growing concern about the prediction of LTCs. In South China, LTCs and their accompanying rainfall significantly modulate the spatial variation of the region’s typhoon season rainfall (Lee et al., 2010). Both statistical and dynamical models are used in typhoon forecasts. For instance, a higher-than-normal track density was successfully forecasted near Korea and Japan by the National Typhoon Center model (Kim et al., 2012). By using teleconnection patterns, a statistical model was built to predict the frequency of summer TCs that influence Taiwan (Choi et al., 2014). A seasonal prediction model for the number of TCs over East China was developed by using the Bayesian method (Ho et al., 2009). A genetic neural network model showed a higher prediction skill for the WNP TC intensity (Huang and Jin, 2013). Huang and Chan (2014) pointed out that the dynamical downscaling method for global forecast data was very effective in improving the forecasting skill for regional TC landfalls in most of the East Asian region. Three different dynamic initialization schemes for the TC prediction in numerical models were designed and evaluated on the basis of 120 real cases from both the North Atlantic and WNP basins from 2010 to 2011 (Hendricks et al., 2013). The predictability of WNP TCs using real-time global climate model predictions as boundary conditions for the Regional Climate Model version 3 was demonstrated by Au-Yeung and Chan (2012). Because of the homogeneity and consistency of TCs and climate data, and the deficiencies of climate models in simulating the TC climate, it is difficult to definitively explain the current relationship between the global warming and TC climate (Lei et al., 2009). Results show that interannual variations of cyclogenesis and TC tracks over the WNP are very obviously and closely associated with the thermal states of the western Pacific, especially the subsurface sea temperature of the western Pacific warm pool (Huang and Chen, 2007). Previous studies have indicated that the spring North Pacific Oscillation, Antarctic Oscillation, Siberian High, and North Pacific sea ice cover can be used as predictors for WNP typhoon frequency forecasts (Fan, 2007; Wang and Fan, 2007; Choi et al., 2010; Chen et al., 2015). Besides, variations in the number of LTCs are largely governed by those in the planetary-scale atmospheric circulations, which oscillate on various timescales (Chan et al., 2012).
In recent decades, the development in predicting the tracks of TCs is mainly due to the development of detection technologies and a deeper understanding of the physical mechanism related to TCs (Zhang et al., 2015). The number of LTCs has decreased but the numbers have barely changed for typhoons over the past 58 years (Yang et al., 2009). However, the accuracy of forecasts for the interannual variation of LTCs has not improved so rapidly. A statistical forecast model for the annual LTCs was developed based on five predictors associated with the tropical circulation over the WNP and high-latitude circulations in both hemispheres (Fan, 2009). The prediction of LTCs has always tended to concentrate on the number of LTCs in the whole typhoon season (from June to October). However, the relationship between the number of LTCs in summer [June–August (JJA)] and autumn [September–November (SON)] is not significant (Fig. 1). The temporal correlation coefficient (TCC) between them is only −0.18 during 1983–2017. The coastal region of China is affected by approximately 7 LTCs every year, 4.6 of which occur in summer.

|
| Figure 1 The number of LTCs in China during summer (JJA; red line) and autumn (SON; turquoise line) for 1983–2017. |
Therefore, the objective of this study is to develop a new hybrid statistical–dynamical prediction model for the number of LTCs that influence China in summer, based on the second version of the NCEP Climate Forecast System (CFSv2) during 1983–2017. The remainder of the paper is organized as follows: Section 2 introduces the data and methods used in this study. Section 3 discusses CFSv2’s prediction skill for the large-scale environmental circulation in summer associated with the number of LTCs. Section 4 describes the prediction model and its validation. Finally, the main conclusions and some further discussion are provided in Section 5.
2 Data and methodsThe data of the number of LTCs in China, which refer to the times of all TCs that have made landfall in China (Ying et al., 2014), are obtained from the National Climate Center of China and cover the period of 1951–2017. The monthly atmospheric reanalysis data (on a horizontal resolution of 2.5° × 2.5°) are obtained from the NCEP/NCAR of the US for 1948–2017 (Kalnay et al., 1996). The extended reconstructed SST data, version 3 (on a resolution of 2.0° × 2.0°), are derived from the NOAA of the US (Smith et al., 2008).
The NCEP CFSv2 seasonal hindcast dataset is used to evaluate the prediction skill with respect to the interann-ual variability of the large-scale environments that accompany LTCs in China. CFSv2 is a fully coupled operational dynamical seasonal prediction system (Saha et al., 2014). This version features upgrades to nearly all aspects of the data assimilation and forecast model components of the system. CFSv2 data are initiated every month with an integration period of nine months and comprise an ensemble of 24 members. The CFSv2 data in the summer (JJA) cover the period of 1982–2017, starting on 1 February, March, April, and May, respectively.
The year-to-year increment prediction method, which is also abbreviated as the DY method, is applied in establishing the prediction scheme of the number of LTCs. This method was proposed by (Fan et al., 2008). In this approach, the year-to-year increment of a variable is defined as the difference in a climate variable between the current and previous years. This method has two advantages. Firstly, the amplitude of the variable in the DY form is much larger than that of the variable itself. Signals of the predictors and predictand in the prediction model are both amplified. Secondly, the interdecadal component of the climate variable can be well reproduced in the DY method. The predicted variable is calculated by adding the predicted to the observation for the previous year that includes the real interdecadal component. The DY method has been used in improving the predictive skill for summer precipitation in the East Asian and western Pacific region (Wang and Fan, 2009; Liu et al., 2011), East Asian summer/winter monsoon in coupled models (Fan et al., 2012; Tian et al., 2018), and winter North Atlantic Oscillation (Tian and Fan, 2015; Fan et al., 2016). Most importantly, this method also shows high predictive skill for the Atlantic named-storm frequency, typhoon frequency over the WNP, and number of LTCs in China (Fan, 2009; Fan and Wang, 2009; Fan, 2010).
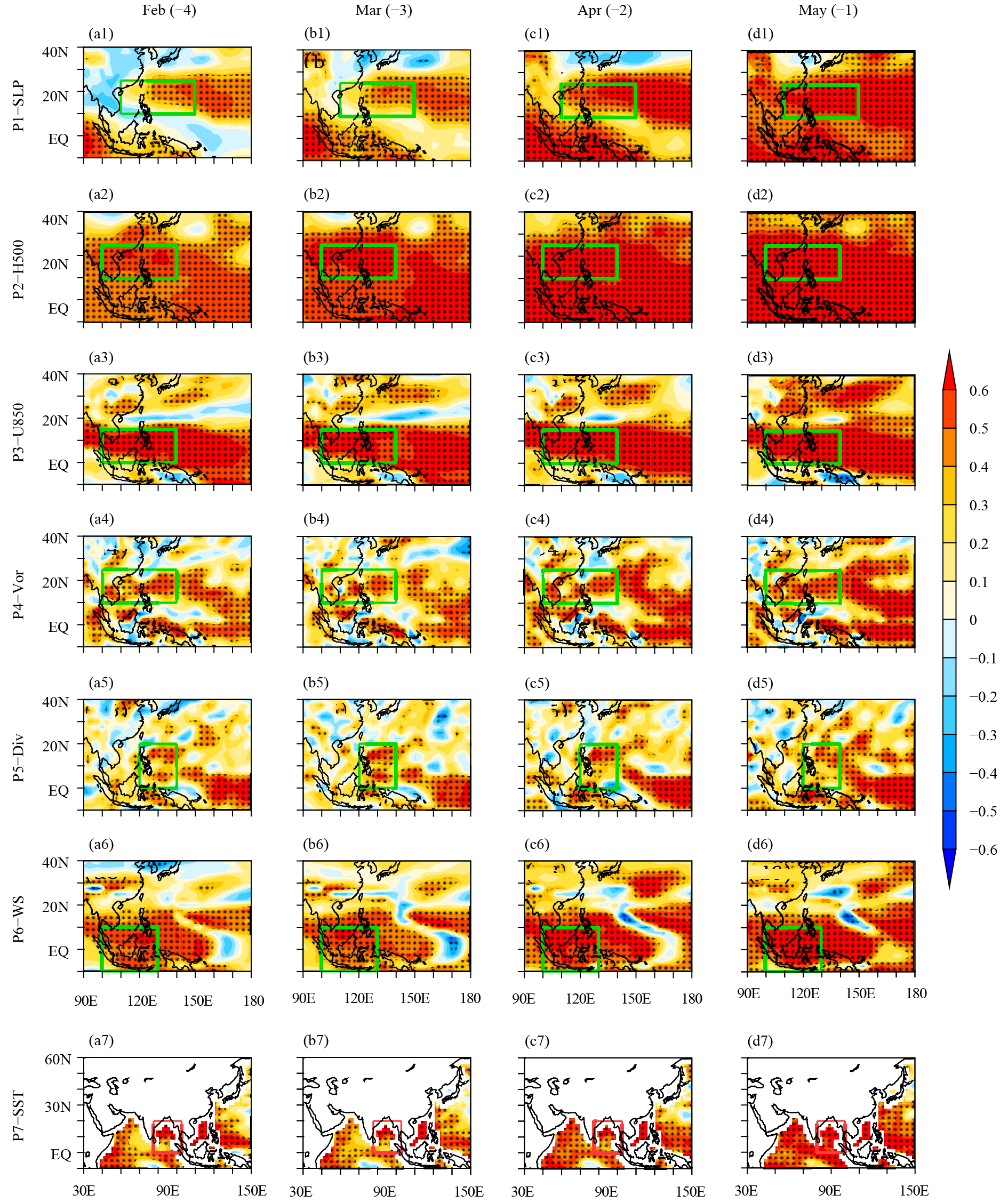
3 CFSv2 prediction skill for the large-scale environmental circulation associated with the number of LTCsPrevious studies have shown that the TC activity depends mainly on the conditions of the large-scale atmosphere–ocean interaction associated with regional changes in SST anomalies, vertical wind shear (WS), low-level relative vorticity, and extensions to the monsoon trough and western Pacific subtropical high (Chia and Ropelewski, 2002; Emanuel, 2003; Hendricks et al., 2013; Huang and Chan, 2014; Lok and Chan, 2018). In the present study, seven factors related to LTCs in China are identified, which can be divided into two groups: three steering factors [sea level pressure (SLP), 500-hPa geopotential height (H500), and zonal wind at 850 hPa (U850)] and four genesis factors [850-hPa relative vorticity (Vor), 200-hPa divergence (Div), 200–850-hPa vertical zonal WS, and SST].
To select a potential predictor in the forecast model, the prediction skill for summer environmental factors related to the number of LTCs using CFSv2 for the four initial months from February to May are evaluated in this section. Figure 2 shows the TCCs between the DY of the JJA number of LTCs and the observed and CFSv2-predicted large-scale summer environmental circulations in the four initial months from February to May during 1983–2017. The boxes in Fig. 2 represent the definition areas of seven potential prediction factors. The key areas defined by the seven potential predictors are: P1–SLP (10°–25°N, 110°–150°E), P2–H500 (10°–25°N, 100°–140°E), P3–U850 (0°–15°N, 100°–140°E), P4–Vor (10°–25°N, 100°–140°E), P5–Div (0°–20°N, 120°–140°E), P6–WS (10°S–10°N, 100°–130°E), and P7–SST (0°–20°N, 80°–100°E). The low-pressure anomaly in China’s coastal area (Figs. 2a1, a2) and the easterly anomaly of the Maritime Continent (Fig. 2a3) are favorable for LTCs in China. During the years with more LTCs in China, they are accompanied by the positive anomalous low-level relative vorticity in the South China Sea (Fig. 2a4), more anticyclonic high-level divergence, relatively strong WS in the Maritime Continent (Figs. 2a5, a6), and a cold SST anomaly (Fig. 2a7). For the 3-month lead (February), CFSv2 has low predictive skill in terms of the relationship between the DY of the JJA number of LTCs and the CFSv2-predicted predictors, except the divergence at 200 hPa (Figs. 2b1–b7). The TCC between the DY of the number of LTCs and P5–Div is 0.31, exceeding the 90% confidence level (Table 1). CFSv2 is able to make some skillful predictions with respect to the relationships between the number of LTCs and the predictors of P3–U850, P4–Vor, P5–Div, P6–WS, and P7–SST from March. For the 2- and 1-month leads (April and May), CFSv2 shows high skill in the relationships between the number of LTCs and the CFSv2-predicted potential predictors.

|
| Figure 2 TCCs between the DY of the JJA number of LTCs and the observed (a1–a7) and CFSv2-predicted JJA large-scale environmental conditions in the four initial months from February to May (b1–e7) during 1983–2017: sea level pressure (SLP; a1, b1, c1, d1, and e1), geopotential height at 500 hPa (H500; a2, b2, c2, d2, and e2), zonal wind at 850 hPa (U850; a3, b3, c3, d3, and e3), relative vorticity at 850 hPa (Vor; a4, b4, c4, d4, and e4), divergence at 200 hPa (Div; a5, b5, c5, d5, and e5), zonal wind shear at 200–850 hPa (WS; a6, b6, c6, d6, and e6), and sea surface temperature (SST; a7, b7, c7, d7, and e7). Dotted areas indicate the statistical significance at the 95% confidence level, as estimated by a local Student’s t-test. |
| TCC–NLTC | ACC–P | TCC–P | ||||||||||||
| Feb | Mar | Apr | May | Feb | Mar | Apr | May | Feb | Mar | Apr | May | |||
| P1–SLP | −0.05 | −0.23 | −0.36** | −0.41** | 0.25*** | 0.22** | 0.36** | 0.43*** | 0.34** | 0.38** | 0.56*** | 0.72*** | ||
| P2–H500 | −0.07 | −0.19 | −0.28* | −0.38** | 0.12 | 0.22** | 0.19* | 0.29* | 0.58*** | 0.66*** | 0.70*** | 0.81*** | ||
| P3–U850 | 0.23 | 0.35** | 0.35** | 0.38** | 0.24*** | 0.23*** | 0.31*** | 0.37*** | 0.70*** | 0.69*** | 0.73*** | 0.70*** | ||
| P4–Vor | 0.25 | 0.38** | 0.39** | 0.41** | 0.13 | 0.11 | 0.16* | 0.23** | 0.62*** | 0.60*** | 0.66*** | 0.66*** | ||
| P5–Div | 0.31* | 0.47*** | 0.39** | 0.47*** | 0.06 | 0.00 | 0.09 | 0.09 | 0.62*** | 0.55*** | 0.55*** | 0.60*** | ||
| P6–WS | 0.23 | 0.32* | 0.36** | 0.47*** | 0.30*** | 0.33*** | 0.36*** | 0.40*** | 0.54*** | 0.52*** | 0.62*** | 0.65*** | ||
| P7–SST | −0.27 | −0.37** | −0.36** | −0.46*** | 0.07 | 0.03 | 0.03 | 0.17* | 0.68*** | 0.66*** | 0.65*** | 0.74*** | ||
| Note: TCC–NLTC refers to the TCC between the DY of the number of LTCs and the potential single predictor. ACC–P represents the spatial ACC between the observed and predicted JJA large-scale atmospheric circulations in key areas. TCC–P means the TCC between the observed and predicted predictor. Triple, double, and single asterisks indicate the statistical significance at the 99%, 95%, and 90% confidence levels, respectively. | ||||||||||||||
The forecasting skill of CFSv2 in the four initial months is also assessed for the large-scale environmen-tal circulations associated with the JJA number of LTCs. Figure 3 shows TCCs between the observed and CFSv2-predicted JJA environmental factors at the 0- to 4-month leads associated with the number of LTCs during 1983–2017. Compared to the relationships between the DY of the number of LTCs and the predictors derived from CFSv2 in different initial months, CFSv2 shows high forecasting skill for the interannual variation of the environmental factor itself. The range of TCCs between the observed and predicted seven predictors is 0.34–0.70 at the 4-month lead, 0.38–0.69 at the 3-month lead, 0.56–0.73 at the 2-month lead, and 0.60–0.81 at the 1-month lead (Table 1). Based on the spatial anomaly correlation coefficients (ACCs) in key areas defined by the potential predictors, CFSv2 shows high predictive ability for P1–SLP, P3–U850, and P6–WS in February, with ACCs of 0.25, 0.24, and 0.30, all exceeding the 99% confidence level. For the 3- and 2-month leads, ACCs are significant for P1–SLP, P2–H500, P3–U850, and P6–WS. For all potential predictors apart from P5–Div, CFSv2 shows high skill in the spatial pattern at the 1-month lead.
|
| Figure 3 TCCs between the observed and CFSv2-predicted JJA large-scale environmental conditions in the four initial months from February to May during 1983–2017: SLP (a1, b1, c1, and d1), H500 (a2, b2, c2, and d2), U850 (a3, b3, c3, and d3), Vor (a4, b4, c4, and d4), Div (a5, b5, c5, and d5), WS (a6, b6, c6, and d6), and SST (a7, b7, c7, and d7). Dotted areas indicate the statistical significance at the 95% confidence level, as estimated by a local Student’s t-test. |
Although CFSv2 possesses the forecasting skill for the atmospheric circulation accompanying LTCs to some degree, the observed climate systems in the preceding seasons also play a vital role in predicting the number of LTCs. Previous studies have indicated that the influence of Southern Hemisphere circulation variability on large-scale environments and tropical convection in the subtropical Northern Hemisphere show a possible use of Antarctic Oscillation variation for the long-range forecasting of WNP TC activity (Ho et al., 2005).
In this study, a negative relationship is found between the number of LTCs and the preceding summer in the anomaly- and DY-form of SST in Southwest Indonesia (Fig. 4). The predictor x1 is defined as the regionally averaged DY of preceding-summer SST in Southwest Indonesia (14°S–0°, 90°–120°E). The TCC between the DY of the number of LTCs and the first predictor of the statistical prediction model is −0.34, exceeding the 95% confidence level estimated by a local Student’s t-test. TCCs between the predictor x1 and JJA SST are shown in Fig. 5a. It is found that the interannual JJA SST variability in Southwest Indonesia coincides with the interann-ual SST variability in the East Maritime Continent (EMC) and East Australia (EAU). The TCCs between the predictor x1 and the area-averaged SST in EMC (10°S–20°N, 130°–160°E) and EAU (40°–10°S, 150°E–150°W) are 0.64 and 0.68 respectively, exceeding the 99% confidence level. There is also a close relationship between the SST in EMC and EAU, with a TCC of 0.82. The SST signal in Southwest Indonesia can persist from summer to the following winter (Figs. 5a–c). The SST signal in EMC and EAU can persist for one year, subsequently affecting the number of LTCs in the following summer. But how does the JJA SST affect the number of LTCs in the following JJA? To answer this question, an EMC–EAU SST index (SSTI) is defined as the regionally averaged SST in EMC and EAU. The JJA EMC–EAU SST is not only closely related to the predic-tor x1, but also can last for one year. The JJA SST signal can be stored in EMC–EAU for one year, subsequently affecting the interannual variability of the number of LTCs in the following summer (Fig. 5). The teleconnection pattern from the mid–high latitudes of the Southern Hemisphere to WNP plays a key role in the linkage between the Antarctic Oscillation and TCs activity in WNP (Fan, 2007; Wang and Fan, 2007). Figure 6 shows the regression coefficients of the JJA SLP, relative vorticity at 850 hPa, geopotential height at 500 hPa, and horizontal wind at 850 hPa on the EMC–EAU SSTI in the preceding JJA. The SST in EMC–EAU increases in summer, which may lead to a negative SLP anomaly, low-level convergence over Indonesia, and divergence over the Philippines (Figs. 6a, b). The anomalous convection over the Maritime Continent may result in a strengthened WNP subtropical high in summer (Fig. 6c), contemporaneous with anomalous low-level southwesterly winds prevailing over eastern China (Fig. 6d). These conditions are unfavorable for LTCs over China.

|
| Figure 4 TCCs between the JJA number of LTCs and preceding summer SST during 1983–2017 in (a) anomaly- and (b) DY-form for the observation. The red box is the definition region (14°S–0°, 90°–120°E) of predictor x1. Dotted areas indicate the statistical significance at the 95% confidence level, as estimated by a local Student’s t-test. |

|
| Figure 5 TCCs between the predictor x1 and SST in the following seasons during 1983–2017: (a) JJA, (b) SON, (c) DJF, (d) MAM, and (e) the following JJA. Blue boxes are the definition regions of the predictor x1 (14°S–0°, 90°–120°E) and EMC–EAU (10°S–20°N, 130°–160°E; 40°–10°S, 150°E–150°W). Dotted areas indicate the statistical significance at the 95% confidence level, as estimated by a local Student’s t-test. |

|
| Figure 6 Regression coefficients of the (a) SLP, (b) Vor, (c) H500, and (d) horizontal wind at 850 hPa (UV850) on the EMC–EAU SSTI in JJA during 1983–2017. Dotted areas indicate the statistical significance at the 95% confidence level, as estimated by a local Student’st-test. |
Based on a statistical forecast model, a previous study proved that the preceding October SLP in southeastern Australia is an important factor for the number of LTCs (Fan, 2009). In this study, the preceding October SLP in South Australia is also found to be an important predic-tor in the prediction model for the number of LTCs. TCCs between the number of LTCs and the preceding October SLP during 1982–2016 in anomaly- and DY-form for the observation are shown in Fig. 7. Compared to the variables in anomaly-form, the negative correlation between the number of LTCs and South Australia SLP increases significantly in DY-form. The predictor x2 is defined as the area-averaged DY of SLP in the preceding October in South Australia (65°–45°S, 90°–160°E). The TCC between the number of LTCs and the second predictor is −0.48, exceeding the 99% confidence level. But how can the preceding October SLP in South Australia affect the number of LTCs in China? Previous studies have pointed out that the atmospheric circulations in the Southern Hemisphere are closely related to the TC activity over WNP (Ho et al., 2005; Sun et al., 2007; Wang and Fan, 2007). The boreal spring SST anomaly east of Australia may lead to simultaneous change in the tropical atmospheric circulation via the teleconnection wave train, and then affect the WNP TC activity (Zhou and Cui, 2011). Figure 8a shows the regressions of JJA vertical velocity in DY-form along 90°–150°E upon the JJA number of LTCs. When the summer number of LTCs is frequent, strong ascending motion appears over approximately 10°–25°N, which is conducive to TC genesis and landfall in China. As shown in Fig. 8b, the preceding October negative SLP anomaly in South Australia may weaken the ascending motion in WNP, which is detrimental to LTCs. The influence of Southern Hemisphere circulation variability on the large-scale environments and tropical convection in the subtropical Northern Hemisphere may be carried out by the teleconnection wave train.

|
| Figure 7 TCCs between the JJA number of LTCs and preceding October SLP during 1982–2016 in (a) anomaly- and (b) DY-form for the observation. The red box is the definition region (65°–45°S, 90°–160°E) of predictor x2. Dotted areas indicate the statistical significance at the 95% confidence level, as estimated by a local Student’s t-test. |

|
| Figure 8 Regressions of the JJA vertical velocity (10−3 Pa s−1) in DY-form along 90°–150°E upon the JJA number of (a) LTCs and (b) predictor x2 multiplied by −1.0. Dotted areas indicate the statistical significance at the 95% confidence level, as estimated by a local Student’s t-test. |
The preceding DJF SST in the Sea of Japan is also found to be a potential predictor for the number of LTCs in summer. The predictor x3 is defined as the area-averaged DY of DJF SST in the Sea of Japan (34°–44°N, 130°–150°E). Figure 9 shows TCCs between the JJA number of LTCs and the preceding winter SST during 1983–2017 in anomaly- and DY-form for the observation. The significant negative correlation between the number of JJA LTCs and the preceding winter SST exists only in DY-form. Previous studies have examined the impact of ENSO on LTCs along the coast of China (Wang and Chan, 2002; Liu and Chan, 2003; Wu et al., 2004; Fudeyasu et al., 2006). Seasonal variations of the LTC activity along the South China coast are closely related to the large-scale circulation accompanied with ENSO (Liu and Chan, 2003). The large-scale circulation anomalies associated with El Niño events result in the eastward shift in the mean TC genesis position, which will reduce the number of LTCs (Wu and Lau, 1992; Wang and Chan, 2002; Wu et al., 2004; Chen et al., 2006). The TC genesis location shifts eastward, which is not conducive to LTCs in China. There is a significant negative correlation between the predictor x3 and number of LTCs, with a TCC of −0.52. The TCC between the DY of the number of LTCs and DJF Niño-4 index is −0.33, exceeding the 95% confidence level estimated by a local Student’s t-test. Because the explained variance of the winter SST in the Sea of Japan is larger than that of the DJF Niño-4 index, the winter SST in the Sea of Japan is selected as a potential predictor in the prediction model. It is found that the significant relationship between the predictor x3 and Niño-4 index in DY-form continues from December to the following April (Fig. 10). The winter SST in the Sea of Japan may affect the number of LTCs via influencing the winter and spring ENSO, which in turn influences the interannual variation of the number of LTCs. As shown in Fig. 11a, the anomalous low-level divergence occurs over the Philippine Sea in summer, with anomalous cold DJF SST over the Niño-4 region. The suppressed ascending motion in the Maritime Continent may result in an enhancement and westward shift of the WNP subtropical high (Fig. 11b). As shown in Fig. 11c, during La Niña phases, an anomalous anticyclonic cell is situated over the South China Sea and westerlies tend to prevail between 20° and 30°N in WNP. In addition, there is a weak vertical WS in the Maritime Continent, accompanied by the anomalous cold DJF SST over the Niño-4 region (Fig. 11d). These conditions are unfavorable for LTCs over China.
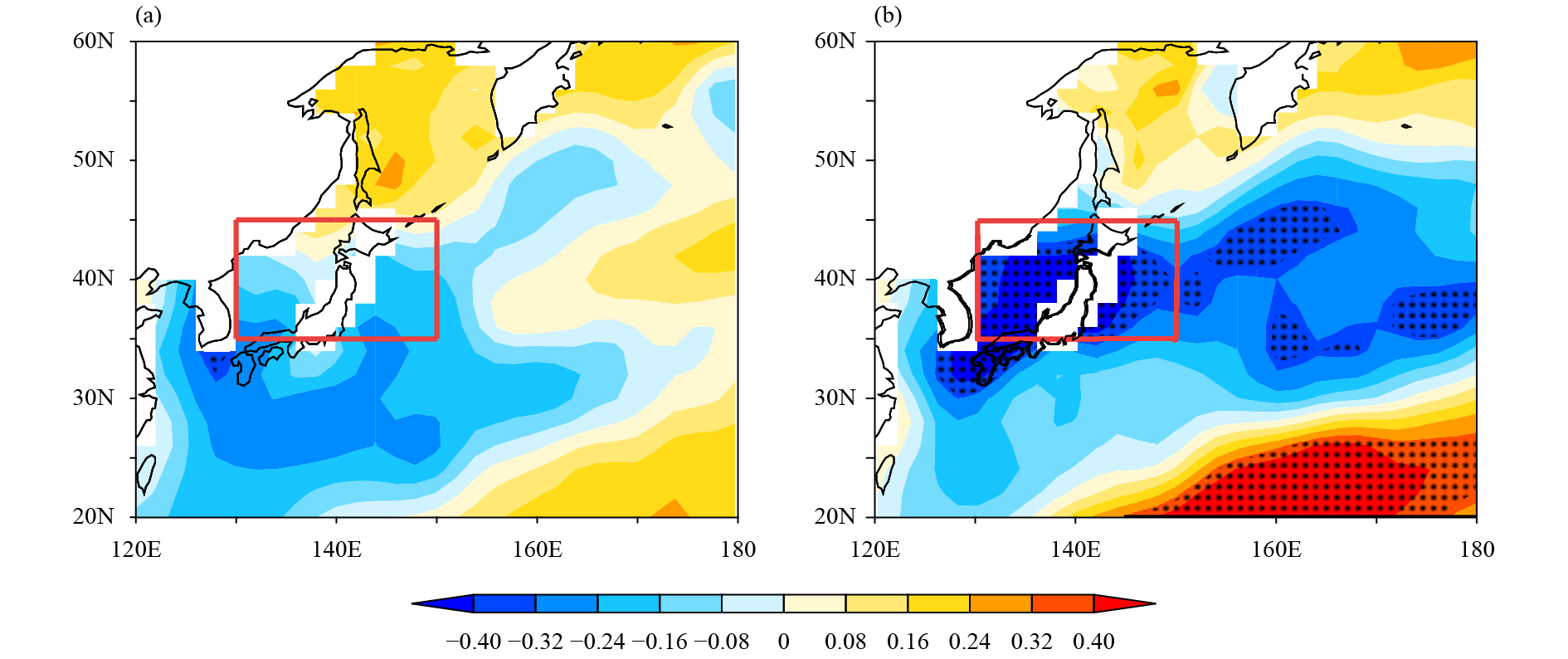
|
| Figure 9 TCCs between the JJA number of LTCs and preceding winter SST during 1983–2017 in (a) anomaly- and (b) DY-form for the observation. The red box is the definition region (34°–44°N, 130°–150°E) of predictor x3. Dotted areas indicate the statistical significance at the 95% confidence level, as estimated by a local Student’s t-test. |

|
| Figure 10 TCCs between the predictor x3 and monthly (December–August) Niño-4 index in DY-form. The blue line indicates the statistical significance at the 95% confidence level, as estimated by a local Student’s t-test. |
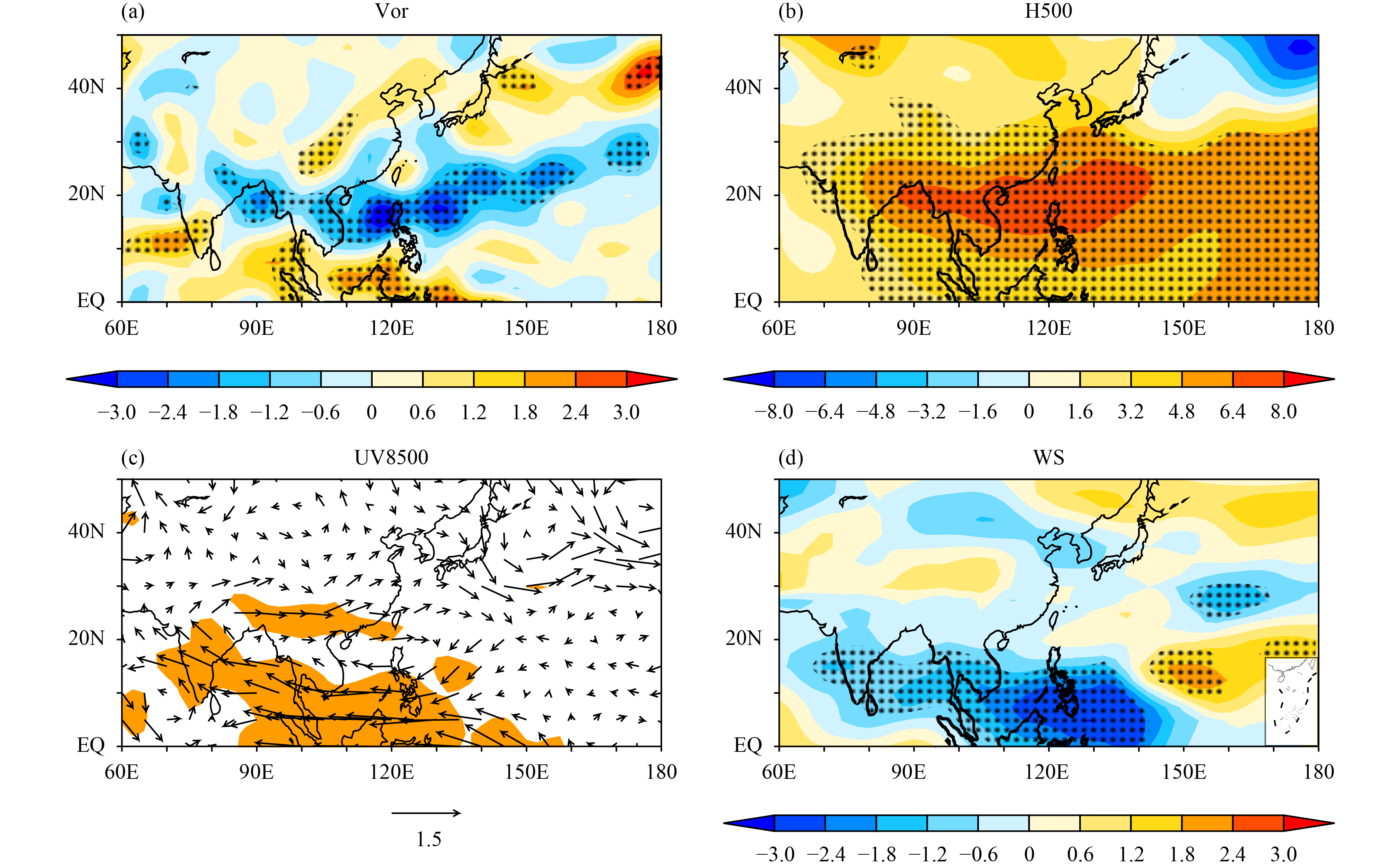
|
| Figure 11 Regression coefficients of (a) Vor, (b) H500, (c) UV850, and (d) WS on the DJF Niño-4 index. Dotted areas (a, b, and d) and shading (c) indicate the statistical significance at the 95% confidence level, as estimated by a local Student’s t-test. |
Based on the above research, a statistical model using three predictors is built by using the DY method. Cross-validation testing is used to evaluate the predictive skill of the forecast model (Michaelsen, 1987). The accuracy of the prediction model is quantitatively measured by using the TCC, mean absolute error (MAE), and mean-square skill score (MSSS). MSSS is defined by the following equation:
| $ {\rm{MSSS}} = 1 - \frac{{{\rm{MS}}{{\rm{E}}_P}}}{{{\rm{MS}}{{\rm{E}}_{\bar O}}}}, $ | (1) |
where MSE refers to the mean-squared error, P and O are the prediction and observation data respectively (Murphy, 1988). The MSSS is the most stringent of the three indicators.
The statistical prediction model is represented by Eqs. (2) and (3):
| $ \Delta {y_i} = {\rm{ }} - 0.71{x_1} - 1.11{x_2} - 1.31{x_3}, $ | (2) |
| $ {y_i} = \Delta {y_i} + {y_{i - 1}}, \quad\quad\quad\quad\quad\quad\quad\;\;$ | (3) |
where Δyi represents the DY of LTCs for one current year, yi-1 refers to the observed LTCs of the previous year, and yi refers to the predicted LTCs for one current year in the statistical prediction model. As shown in Fig. 12a, the predicted DY of the number of LTCs in the cross-validation tests agrees well with the observation during 1983–2017, with a TCC of 0.73. The predicted number of LTCs can be obtained by adding the predicted DY of the number of LTCs to the observed number of LTCs in the previous year (Fig. 12b). The TCC between them is 0.63, with an MAE of 1.18 and MSSS of −0.38. The years 1984, 1985, and 2014 are the three years during which the observed JJA number of LTCs falls outside the 95% predicted range.
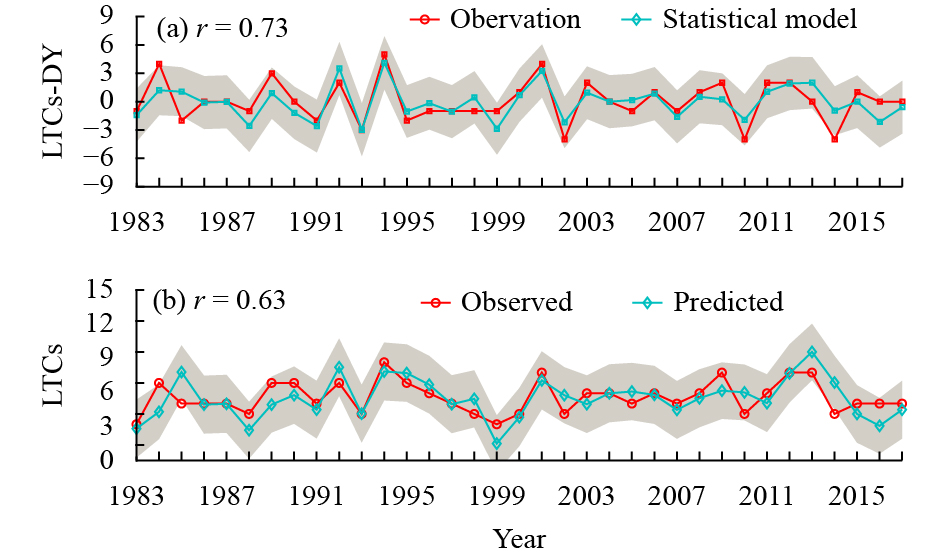
|
| Figure 12 (a) DY of the number of LTCs for the observation (red line) and statistical model (turquoise line) in the cross-validation during 1983–2017. (b) Predicted (turquoise line) and observed (red line) number of LTCs in the cross-validation during 1983–2017. The grey shading indicates the 95% prediction interval. |
Several studies have pointed out that the prediction ability of the hybrid statistical–dynamical model for TCs activity is not only higher than that of the statistical mo-del, but also higher than that of the dynamical model. (Wang et al., 2009; Kim and Webster, 2010; Vecchi et al., 2011). Based on the relationship between the number of LTCs and the physical significance of predictors, a hybrid statistical–dynamical model is constructed to predict the number of LTCs during the summer at 3- to 0-month leads from February to May. The model outputs used in the hybrid dynamical–statistical model are obtained from CFSv2. Predictors in the prediction models are selected based on correlations between the observed number of LTCs and the large-scale environmen-tal circulation. Because the seven predictors derived from CFSv2 for the four initial months are not independent of each other, only a single predictor is selected in the hybrid prediction model.
Table 2 shows the forecasting skill using the three statistical predictors and one CFSv2-predicted predictor for the four initial months from February to May. For the 4-month lead, TCCs for the seven predictors are 0.64 for P1–SLP, 0.61 for P2–H500, 0.71 for P3–U850 and P4–Vor, 0.70 for P5–Div, 0.69 for P6–WS, and 0.66 for P7–SST. Compared to the statistical prediction model, MAE is reduced by 0.4%–14.4%. For February, P4–Vor and P5–Div show the best skill, with an MSSS of 0.13 and 0.12 respectively. For the 3-month lead, the range of TCCs for the seven predictors is 0.62–0.73. MAE decreases by 4.2%–25.2%. The predictors P4–Vor and P5–Div also show the best forecasting skill among these predictors. For the 2-month lead, the predictors P1–SLP and P4–Vor show higher predictive ability than the other predictors, with an MSSS of 0.12 and 0.09 respectively. In May, both P1–SLP and P5–Div demonstrate considerable predictive skill for the JJA number of LTCs. For the 4-, 3-, and 2-month leads, the predictor P2–H500 shows the worst forecasting skill. In general, P4–Vor is a modest predictor, with the stable and good forecasting skill at all lead times.
| P1–SLP | P2–H500 | P3–U850 | P4–Vor | P5–Div | P6–WS | P7–SST | ||
| TCC | Feb | 0.64 | 0.61 | 0.71 | 0.71 | 0.70 | 0.69 | 0.66 |
| Mar | 0.65 | 0.62 | 0.73 | 0.72 | 0.70 | 0.69 | 0.68 | |
| Apr | 0.70 | 0.64 | 0.69 | 0.70 | 0.69 | 0.70 | 0.66 | |
| May | 0.70 | 0.66 | 0.66 | 0.68 | 0.70 | 0.69 | 0.66 | |
| MAE | Feb | 4.5% | 0.4% | 11.0% | 14.4% | 13.8% | 14.1% | 7.8% |
| Mar | 11.5% | 4.2% | 22.1% | 25.2% | 20.6% | 19.1% | 17.1% | |
| Apr | 16.7% | 4.8% | 13.7% | 17.2% | 11.6% | 14.3% | 6.4% | |
| May | 19.3% | 12.2% | 8.5% | 11.8% | 16.3% | 13.7% | 8.4% | |
| MSSS | Feb | −0.15 | −0.31 | 0.06 | 0.13 | 0.12 | 0.06 | −0.09 |
| Mar | −0.05 | −0.19 | 0.20 | 0.24 | 0.27 | 0.09 | 0.09 | |
| Apr | 0.12 | −0.10 | 0.01 | 0.09 | 0.03 | 0.07 | −0.07 | |
| May | 0.14 | 0.05 | −0.09 | 0.02 | 0.16 | 0.08 | −0.05 |
In addition, because LTCs are one of the most serious natural disasters, the need to well predict the number of LTCs over China is urgent. A summer climate consultation is held by the National Climate Center in March every year. Therefore, a real-time prediction model for the number of LTCs in summer is also constructed, based on the above research (Fig. 13). The real-time prediction model is established based on the three statistical predictors (x1, x2, and x3) and the CFSv2-predicted P4–Vor (x4) in JJA from February. The predicted JJA DY of the number of LTCs in the hybrid prediction model is obtained by Eq. (4) below:
|
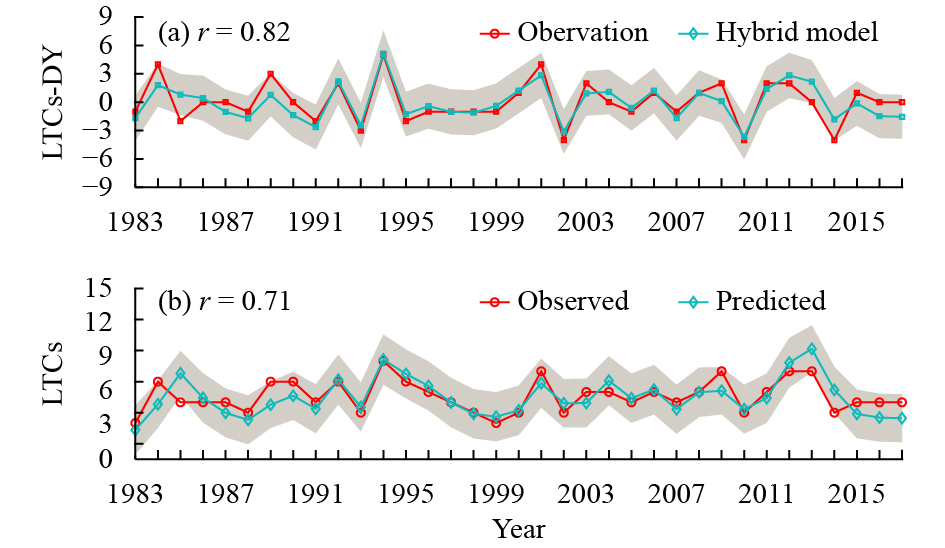
| Figure 13 DY of the number LTCs for the observation (red line) and hybrid model using three statistical predictors and the CFSv2-predicted relative vorticity at 850 hPa in February (turquoise line) in the cross-validation during 1983–2017. (b) Predicted (turquoise line) and observed (red line) number of LTCs in the cross-validation during 1983–2017. The grey shading is the 95% prediction interval. |
| $ \Delta {y_i} = {\rm{ }} - 0.67{x_1} - 1.46{x_2} - 1.19{x_3} + 0.81{x_4}. $ | (4) |
The TCC between the predicted JJA number of LTCs (DY of the number of LTCs) is 0.71 (0.82), exceeding the 99% confidence level. MAE decreases by 14.4%, and MSSS is 0.13. The real-time prediction model shows better prediction skill with respect to the JJA number of LTCs for 2014–17.
5 Conclusions and discussionIn this study, the prediction skill with regard to the summer environmental conditions related to the JJA number of LTCs is evaluated by using CFSv2 for the four initial months from February to May. Three steering factors (P1–SLP, P2–H500, and P3–U850) and four genesis factors (P4–Vor, P5–Div, P6–WS, and P7–SST) associated with LTCs in China are chosen. It is found that only P5–Div among the seven predictors is significantly related to the JJA number of LTCs from February. For the 3-month lead (March), CFSv2 is able to make some skillful predictions in terms of the relationships between the number of LTCs and the predictors of P3–U850, P4–Vor, P5–Div, P6–WS, and P7–SST. For the 2- and 1-month leads (April and May), CFSv2 shows high skill with respect to the relationships between the number of LTCs and the seven CFSv2-predicted potential predictors. In addition, the predictive ability of CFSv2 in the four initial months for the lager-scale environmental circulations associated with the number of LTCs is assessed. Compared to the relationships between the number of LTCs and the CFSv2-predicted predictors in different initial months, CFSv2 can successfully reproduce the relationships between the observed and CFSv2-predicted the interannual variation of environmental factors in key areas. The range of TCCs between the observed and predicted seven predictors is 0.34–0.70 at the 4-month lead, 0.38–0.69 at the 3-month lead, 0.56–0.73 at the 2-month lead, and 0.60–0.81 at the 1-month lead. Based on the ACCs in key areas defined by the potential predictor, CFSv2 shows high predictive ability for P1–SLP, P3–U850, and P6–WS in February, with ACCs of 0.25, 0.24, and 0.30, respectively, all exceeding the 99% confidence level. For the 3- and 2-month leads, ACCs are significant for P1–SLP, P2–H500, P3–U850, and P6–WS. For all potential predictors except P5-Div, CFSv2 shows high skill in terms of the spatial pattern at the 1-month lead.
Although CFSv2 possesses some prediction skill for the atmospheric circulation accompanying LTCs, the observed climate systems in the preceding seasons also play an important role in predicting the number of LTCs. The selected predictors in the preceding seasons for the prediction model are the previous boreal summer DY of SST in Southwest Indonesia, preceding October SLP in South Australia, and DY of DJF SST in the Sea of Japan. It is found that the interannual JJA SST variability in Southwest Indonesia coincides with the interannual SST variability in EMC and EAU. The SST signal in EMC and EAU can persist for one year, subsequently affecting the number of LTCs in the following summer. SST in EMC–EAU increases in summer, which may lead to a negative SLP anomaly, low-level convergence over Indonesia, and divergence over Philippines. The anomalous convection over the Maritime Continent may result in a strengthened WNP subtropical high in summer, contemporaneous with anomalous low-level southwesterly winds prevailing over eastern China. These conditions are unfavorable for LTCs over China. The SLP in the preceding October in South Australia is unfavorable for LTCs in China, via affecting the ascending motion appearing over approximately 10°–25°N. This process may be carried out by the teleconnection wave train. The preceding winter SST in the Sea of Japan may affect the number of LTCs via influencing the winter and spring ENSO, and then changing the interannual variation of the number of LTCs. Based on the three statistical predictors with physical processes, a statistical forecast model for the number of LTCs in China is established by using the multi-linear regression analysis method. The TCC between the observed and predicted number of LTCs (DY of the number of LTCs) during 1983–2017 is 0.63 (0.73), with an MAE of 1.18 and MSSS of −0.38.
As we know, the influence of the summer atmospheric circulation anomaly related to the JJA number of LTCs is not considered in the statistical model. Therefore, a new hybrid dynamical–statistical prediction model for predicting the JJA number of LTCs for 1983–2017 is built by using the DY method. Because the seven predictors derived from CFSv2 for the four initial months are not independent of each other, only a single predictor is selected in the hybrid prediction model. For the 4-, 3-, and 2-month leads, the predictor P2–H500 shows the worst forecasting skill among these factors. In general, P4–Vor is a modest predictor, with the stable and good forecasting skill at all lead times. In addition, because LTCs are one of the most serious natural disasters, predicting the number of LTCs over China successfully is an urgent matter. A summer climate consultation is held by the National Climate Center in March every year. Therefore, a real-time prediction model is established based on the three statistical predictors and the CFSv2-predicted P4–Vor for the 4-month lead. The TCC between the predicted JJA number of LTCs (DY of the number of LTCs) is 0.71 (0.82), with an MSSS of 0.13. Compared to the statistical model, MAE decreases by 14.4%. The real-time prediction model shows better forecasting skill in terms of the JJA number of LTCs for 2014–17. In order to improve the prediction skill of the all-year-round number of LTCs, we need to build a prediction model for the autumn number of LTCs in the future, through analyzing the physical mechanism related to TCs at this time of the year.
| Au-Yeung, A. Y. M., and J. C. L. Chan, 2012: Potential use of a regional climate model in seasonal tropical cyclone activity predictions in the western North Pacific. Climate Dyn., 39, 783–794. DOI:10.1007/s00382-011-1268-x |
| Chan, J. C. L., K. S. Liu, M. Xu, et al., 2012: Variations of frequency of landfalling typhoons in East China, 1450–1949. Int. J. Climatol., 32, 1946–1950. DOI:10.1002/joc.2410 |
| Chen, D., H. J. Wang, J. P. Liu, et al., 2015: Why the spring North Pacific Oscillation is a predictor of typhoon activity over the Western North Pacific. Int. J. Climatol., 35, 3353–3361. DOI:10.1002/joc.4213 |
| Chen, T. C., S. Y. Wang, and M. C. Yen, 2006: Interannual variation of the tropical cyclone activity over the western North Pacific. J. Climate, 19, 5709–5720. DOI:10.1175/JCLI3934.1 |
| Chia, H. H., and C. F. Ropelewski, 2002: The interannual variability in the genesis location of tropical cyclones in the Northwest Pacific. J. Climate, 15, 2934–2944. DOI:10.1175/1520-0442(2002)015<2934:TIVITG>2.0.CO;2 |
| Choi, K. S., J. Y. Moon, D. W. Kim, et al., 2010: Seasonal prediction of tropical cyclone genesis frequency over the western North Pacific using teleconnection patterns. Theor. Appl. Climatol., 100, 191–206. DOI:10.1007/s00704-009-0182-1 |
| Choi, K. S., C. C. Wu, and Y. Q. Wang, 2014: Seasonal prediction for tropical cyclone frequency around Taiwan using teleconnection patterns. Theor. Appl. Climatol., 116, 501–514. DOI:10.1007/s00704-013-0954-5 |
| Emanuel, K., 2003: Tropical cyclones. Annu. Rev. Earth Planet. Sci., 31, 75–104. DOI:10.1146/annurev.earth.31.100901.141259 |
| Fan, K., 2007: New predictors and a new prediction model for the typhoon frequency over western North Pacific. Sci. China Ser. D: Earth Sci., 50, 1417–1423. DOI:10.1007/s11430-007-0105-x |
| Fan, K., 2009: Seasonal forecast model for the number of tropical cyclones to make landfall in China. Atmos. Ocean. Sci. Lett., 2, 251–254. DOI:10.1080/16742834.2009.11446811 |
| Fan, K., 2010: A prediction model for Atlantic named storm frequency using a year-by-year increment approach. Wea. Forecasting, 25, 1842–1851. DOI:10.1175/2010WAF2222406.1 |
| Fan, K., and H. J. Wang, 2009: A new approach to forecasting typhoon frequency over the western North Pacific. Wea. Forecasting, 24, 974–986. DOI:10.1175/2009WAF2222194.1 |
| Fan, K., H. J. Wang, and Y. J. Choi, 2008: A physically-based statistical forecast model for the middle-lower reaches of the Yangtze River Valley summer rainfall. Chinese Sci. Bull., 53, 602–609. DOI:10.1007/s11434-008-0083-1 |
| Fan, K., Y. Liu, and H. P. Chen, 2012: Improving the prediction of the East Asian summer monsoon: New approaches. Wea. Forecasting, 27, 1017–1030. DOI:10.1175/WAF-D-11-00092.1 |
| Fan, K., B. Q. Tian, and H. J. Wang, 2016: New approaches for the skillful prediction of the winter North Atlantic Oscillation based on coupled dynamic climate models. Int. J. Climatol., 36, 82–94. DOI:10.1002/joc.4330 |
| Fudeyasu, H., S. Iizuka, and T. Matsuura, 2006: Impact of ENSO on landfall characteristics of tropical cyclones over the western North Pacific during the summer monsoon season. Geophys. Res. Lett., 33, L21815. DOI:10.1029/2006GL027449 |
| Ha, Y., and Z. Zhong, 2014: Features of tropical cyclone landfalls over East Asia corresponding to three types of Pacific warming decaying phase. Chinese Sci. Bull., 59, 4130–4136. DOI:10.1007/s11434-014-0582-1 |
| Hendricks, E. A., M. S. Peng, and T. Li, 2013: Evaluation of multiple dynamic initialization schemes for tropical cyclone prediction. Mon. Wea. Rev., 141, 4028–4048. DOI:10.1175/MWR-D-12-00329.1 |
| Ho, C. H., J. H. Kim, H. S. Kim, et al., 2005: Possible influence of the Antarctic Oscillation on tropical cyclone activity in the western North Pacific. J. Geophys. Res. Atmos., 110, D19104. DOI:10.1029/2005jd005766 |
| Ho, C.-H., H.-S. Kim, and P.-S. Chu, 2009: Seasonal prediction of tropical cyclone frequency over the East China Sea through a Bayesian Poisson-regression method. Asia-Pacific J. Atmos. Sci., 45, 45–54. |
| Hong, C.-C., Y.-K. Wu, and T. Li, 2016: Influence of climate regime shift on the interdecadal change in tropical cyclone activity over the Pacific Basin during the middle to late 1990s. Climate Dyn., 47, 2587–2600. DOI:10.1007/s00382-016-2986-x |
| Huang, R. H., and G. H. Chen, 2007: Research on interannual variations of tracks of tropical cyclones over Northwest Pacific and their physical mechanism. Acta Meteor. Sinica, 65, 683–694. DOI:10.11676/qxxb2007.064 |
| Huang, W. R., and J. C. L. Chan, 2014: Dynamical downscaling forecasts of Western North Pacific tropical cyclone genesis and landfall. Climate Dyn., 42, 2227–2237. DOI:10.1007/s00382-013-1747-3 |
| Huang, Y., and L. Jin, 2013: A prediction scheme with genetic neural network and Isomap algorithm for tropical cyclone intensity change over western North Pacific. Meteor. Atmos. Phys., 121, 143–152. DOI:10.1007/s00703-013-0263-7 |
| Kalnay, E., M. Kanamitsu, R. Kistler, et al., 1996: The NCEP/NCAR 40-year reanalysis project. Bull. Amer. Meteor. Soc., 77, 437–472. DOI:10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2 |
| Kim, H. M., and P. J. Webster, 2010: Extended-range seasonal hurricane forecasts for the North Atlantic with a hybrid dynamical-statistical model. Geophys. Res. Lett., 37, L21705. DOI:10.1029/2010GL044792 |
| Kim, J. H., C. H. Ho, H. S. Kim, et al., 2012: 2010 western North Pacific typhoon season: Seasonal overview and forecast using a track-pattern-based model. Wea. Forecasting, 27, 730–743. DOI:10.1175/WAF-D-11-00109.1 |
| Lee, M. H., C. H. Ho, and J. H. Kim, 2010: Influence of tropical cyclone landfalls on spatiotemporal variations in typhoon season rainfall over South China. Adv. Atmos. Sci., 27, 443–454. DOI:10.1007/s00376-009-9106-3 |
| Lei, X. T., M. Xu, and F. M. Ren, 2009: A review on the impacts of global warming on tropical cyclone activities. Acta Meteor. Sinica, 67, 679–688. DOI:10.11676/qxxb2009.068 |
| Liu, K. S., and J. C. L. Chan, 2003: Climatological characteristics and seasonal forecasting of tropical cyclones making landfall along the South China coast. Mon. Wea. Rev., 131, 1650–1662. DOI:10.1175//2554.1 |
| Liu, Y., K. Fan, and H. J. Wang, 2011: Statistical downscaling prediction of summer precipitation in southeastern China. Atmos. Ocean. Sci. Lett., 4, 173–180. DOI:10.1080/16742834.2011.11446925 |
| Lok, C. C. F., and J. C. L. Chan, 2018: Changes of tropical cyclone landfalls in South China throughout the twenty-first century. Climate Dyn., 51, 2467–2483. DOI:10.1007/s00382-017-4023-0 |
| Michaelsen, J., 1987: Cross-validation in statistical climate forecast models. J. Climate Appl. Meteor., 26, 1589–1600. DOI:10.1175/1520-0450(1987)026<1589:CVISCF>2.0.CO;2 |
| Murphy, A. H., 1988: Skill scores based on the mean square error and their relationships to the correlation coefficient. Mon. Wea. Rev., 116, 2417–2424. DOI:10.1175/1520-0493(1988)116<2417:SSBOTM>2.0.CO;2 |
| Saha, S., S. Moorthi, X. R. Wu, et al., 2014: The NCEP climate forecast system version 2. J. Climate, 27, 2185–2208. DOI:10.1175/JCLI-D-12-00823.1 |
| Smith, T. M., R. W. Reynolds, T. C. Peterson, et al., 2008: Improvements to NOAA’s historical merged land–ocean surface temperature analysis (1880–2006). J. Climate, 21, 2283–2296. DOI:10.1175/2007JCLI2100.1 |
| Sun, S. Q., G. Liu, and Q. Y. Zhang, 2007: The influence of the circulation anomalies in the Southern Hemisphere on the tropical cyclone frequency in summer over the western Pacific and its mechanism. Chinese J. Atmos. Sci., 31, 1189–1200. DOI:10.3878/j.issn.1006-9895.2007.06.14 |
| Tian, B. Q., and K. Fan, 2015: A skillful prediction model for winter NAO based on Atlantic sea surface temperature and Eurasian snow cover. Wea. Forecasting, 30, 197–205. DOI:10.1175/WAF-D-14-00100.1 |
| Tian, B. Q., K. Fan, and H. Q. Yang, 2018: East Asian winter monsoon forecasting schemes based on the NCEP’s climate forecast system. Climate Dyn., 51, 2793–2805. DOI:10.1007/s00382-017-4045-7 |
| Vecchi, G. A., M. Zhao, H. Wang, et al., 2011: Statistical–dynamical predictions of seasonal North Atlantic hurricane activity. Mon. Wea. Rev., 139, 1070–1082. DOI:10.1175/2010MWR3499.1 |
| Wang, B., and J. C. L. Chan, 2002: How strong ENSO events affect tropical storm activity over the western North Pacific. J. Climate, 15, 1643–1658. DOI:10.1175/1520-0442(2002)015<1643:HSEEAT>2.0.CO;2 |
| Wang, H., J. K. E. Schemm, A. Kumar, et al., 2009: A statistical forecast model for Atlantic seasonal hurricane activity based on the NCEP dynamical seasonal forecast. J. Climate, 22, 4481–4500. DOI:10.1175/2009JCLI2753.1 |
| Wang, H. J., and K. Fan, 2007: Relationship between the Antarctic oscillation in the western North Pacific typhoon frequency. Chinese Sci. Bull., 52, 561–565. DOI:10.1007/s11434-007-0040-4 |
| Wang, H. J., and K. Fan, 2009: A new scheme for improving the seasonal prediction of summer precipitation anomalies. Wea. Forecasting, 24, 548–554. DOI:10.1175/2008WAF2222171.1 |
| Wu, G. X., and N. C. Lau, 1992: A GCM simulation of the relationship between tropical-storm formation and ENSO. Mon. Wea. Rev., 120, 958–977. DOI:10.1175/1520-0493(1992)120<0958:AGSOTR>2.0.CO;2 |
| Wu, M. C., W. L. Chang, and W. M. Leung, 2004: Impacts of El Niño–Southern Oscillation events on tropical cyclone landfalling activity in the western North Pacific. J. Climate, 17, 1419–1428. DOI:10.1175/1520-0442(2004)017<1419:IOENOE>2.0.CO;2 |
| Yang, Y. H., M. Ying, and B. D. Chen, 2009: The climatic changes of landfall tropical cyclones in China over the past 58 years. Acta Meteor. Sinica, 67, 689–696. DOI:10.11676/qxxb2009.069 |
| Ying, M., W. Zhang, H. Yu, et al., 2014: An overview of the China meteorological administration tropical cyclone database. J. Atmos. Ocean. Technol., 31, 287–301. DOI:10.1175/JTECH-D-12-00119.1 |
| Yonekura, E., and T. M. Hall, 2014: ENSO effect on East Asian tropical cyclone landfall via changes in tracks and genesis in a statistical model. J. Appl. Meteor. Climatol., 53, 406–420. DOI:10.1175/JAMC-D-12-0240.1 |
| Zhang, W. J., Y. J. Zhang, D. Zheng, et al., 2015: Relationship between lightning activity and tropical cyclone intensity over the northwest Pacific. J. Geophys. Res. Atmos., 120, 4072–4089. DOI:10.1002/2014JD022334 |
| Zhou, B. T., and X. Cui, 2011: Sea surface temperature east of Australia: A predictor of tropical cyclone frequency over the western North Pacific?. Chinese Sci. Bull., 56, 196–201. DOI:10.1007/s11434-010-4157-5 |
 2019, Vol. 33
2019, Vol. 33


