The Chinese Meteorological Society
Article Information
- LI, Zhe, Qijun LIU, Zhanshan MA, et al., 2019.
- Simulation Study of Cloud Properties Affected by Heterogeneous Nucleation Using the GRAPES_SCM during the TWP-ICE Campaign. 2019.
- J. Meteor. Res., 33(4): 734-746
- http://dx.doi.org/10.1007/s13351-019-8203-1
Article History
- Received January 14, 2019
- in final form May 5, 2019
2. Numerical Weather Prediction Center of China Meteorological Administration, Beijing 100081;
3. College of Global Change and Earth System Science, Beijing Normal University, Beijing 100875
Monsoon is defined as a seasonal reversing wind with changes in precipitation (Ramage, 1971), and the term is used to refer to a rainy phase of a seasonally changing pattern with enhanced convective precipitation. Deep convective cloud plays a crucial role in both the radiative budget and the hydrological cycle. Deep convective cloud consists of a thick convective core with a large anvil. It is recognized that the large anvil cirrus layer of deep convective cloud can have considerable effect on the radiative budget. Anvil cirrus consists of very high cold cloud composed of ice crystals, and it is often formed in the outflow of deep convective cloud. The spatial extent of such cirrus can be two orders of magnitude greater than that of the parent deep convective cloud and it can persist for hours, even after the deep convective activity has decayed completely. Ice crystals in the cirrus both scatter incoming solar radiation, which cools the earth’s surface, and absorb infrared radiation from the ground. Such a balance is determined by the detailed microphysical structure of cirrus. Generally, deep convective cloud plays an important role in the radiation balance of the atmosphere and it dominates cloud radiative forcing in the tropics (Ramanathan et al., 1989; Harrison et al., 1990; Rossow and Schiffer, 1991;Hartmann et al., 1992). It is also recognized that deep convective cloud can redistribute heat and moisture both vertically and horizontally. Some of this redistribution is associated with the heavy precipitation of the thick convective core, which can cause localized surface damage. However, the redistribution of atmospheric heat and moisture is also determined to some extent by the microphysical structure of the cloud. Ice particles affect the precipitation of deep convective cloud because this type of precipitation is initiated by ice particles (Zhao et al., 2018). Previous study has shown that cirrus formed of large ice particles tends to precipitate out and dissipate, whereas cirrus composed of smaller ice particles persists longer (Jensen et al., 1996). Deep convective cloud is also the source of water vapor for the upper troposphere in the tropics, which contributes to the natural greenhouse effect in the atmosphere.
Two fundamental processes of ice formation exist in the atmosphere: homogeneous freezing and heterogeneous nucleation. Homogeneous freezing occurs in a supercooled liquid drop (e.g., aerosols or cloud droplets) without the assistance of ice nuclei (IN). In this study, homogeneous freezing is considered only in relation to cloud droplets. In numerical model simulation, parameterizations of homogeneous freezing usually set a threshold between −35 and −40°C below which all drops will freeze to solid particles. Heterogeneous nucleation facilitates ice formation with IN at temperatures higher than that of homogeneous freezing (Pruppacher and Klett, 1997, p287). Previous studies have confirmed that IN can affect some of the properties of deep convective cloud, e.g., ice water content and ice number concentration (van den Heever et al., 2006; Fan et al., 2009; Xie et al., 2013; Deng et al., 2018). The impact of IN on updrafts and precipitation remains largely uncertain because of the complicated ice-phased microphysical processes (Ekman et al., 2007; Hazra et al., 2016). The characteristics of IN can be expressed through different heterogeneous nucleation parameterizations. There are four known heterogeneous nucleation modes for ice formation in mixed-phased cloud: deposition nucleation, condensation freezing, contact freezing, and immersion freezing (Lamb and Verlinde, 2011). Laboratory experiments have shown that mineral dust, soot, biological, organic, and ammonium sulfate particles can all serves as efficient IN and that each species has its preferred onset condition (Hoose and Möhler, 2012; Du et al., 2017). Hence, for simplicity, model simulations often adjust the parameterizations of heterogeneous nucleation to represent the freezing efficiency of different IN. Simulations have shown that deposition nucleation/condensation freezing is efficient when the ambient temperature is below −10°C, while contact freezing is efficient when the temperature is above −15°C (Cotton et al., 1986). Simulation study has also highlighted that ice formation in convective cloud is dominated by homogeneous freezing and immersion freezing (Hiron and Flossmann, 2015). Moreover, other simulation studies have shown that deposition nucleation is the predominant mode for secondary ice formation (Diehl and Mitra, 2015).
Single-column models (SCMs) are constructed for the purposes of evaluating physical process parameterizations. An SCM represents a single grid box. Therefore, through use of the SCM, it can be reasonably straightforward both to compare how different physical schemes might respond to identical forcing and to provide evidence or justification for more expensive three-dimensional modeling tests. Large-scale forcing and the tendencies from other parameterizations are prescribed in the SCM. Therefore, the SCM can be used to evaluate unique parameterizations independently of other processes. Moreover, the SCM approach is conceptually simple, very quick to run, and it promotes less ambiguous interpretation of the derived results because it eliminates three-dimensional dynamical core feedbacks. Therefore, the SCM is a useful tool for investigating a particular parameterization. Previous studies have shown that an SCM is a simple and efficient tool for evaluating and developing physics parameterizations. Kennedy et al. (2010) used 3-yr surface and GOES data from the ARM SGP site to evaluate the NASA GISS SCM from January 1999 to December 2001. They concluded that the SCM could simulate most mid-level clouds; however, it overestimated low cloud by 4% and it underestimated total and high cloud by 7% and 15%, respectively. Mei et al. (2015) used the WRF-SCM to evaluate and compare two double-moment microphysics scheme and they analyzed the mechanism of ice production in detail. Gesso and Neggers (2018) studied the response of boundary layer cloud to climate change in the marine subtropical trade wind regime using an SCM. They reported that the cloud response to sea surface warming as produced by the SCM was found consistent with that of a general circulation model.
The purpose of this study was to investigate the effect of heterogeneous nucleation on monsoon precipitation using the Global/Regional Assimilation and PrEdiction System (GRAPES) SCM. The primary focus was on how the hydrometeor distribution, precipitation and radiation properties of deep convective cloud and the associated cirrus were affected by heterogeneous nucleation. The remainder of this paper is structured as follows. Section 2 introduces the case study, numerical model, and freezing process in the Liuma microphysics scheme considered in this investigation. Section 3 presents a comparison between observations and model simulations, as well as an analysis of the effect of heterogeneous nucleation on the microphysical and macrophysical properties of deep convective cloud and the associated cirrus. A discussion and the derived conclusions are provided in Section 4.
2 Case study and model description 2.1 Field campaignThe Tropical Warm Pool International Cloud Experiment (TWP-ICE) was conducted in January–February 2006 in Darwin under different atmospheric conditions during the northern Australian monsoon season. At the start of the experiment, the region experienced an active monsoon period. During 23–24 January, a strong mesoscale convective system passed through the domain, which was followed by a relatively suppressed monsoon period. A little rain occurred during 3–5 February, which was followed by a monsoon break period to the end of the field campaign. Full details of the meteorological conditions can be found in May et al. (2008). This study focused on the active monsoon period of 20–25 January and the suppressed monsoon period from 28 January to 2 February. The field campaign attempted to describe the development of tropical convective cloud and the associated cirrus cloud. Detailed observations of the cloud properties and the impact of the cloud on the local environment have been reported in previous studies (e.g., May et al., 2008; Wapler et al., 2010; Xie et al., 2010).
2.2 GRAPES_SCMGRAPES is a new generation of numerical weather prediction system, suitable for both global and regional numerical weather prediction, which has been developed by the China Meteorological Administration since 2000 (Chen et al., 2008; Xue and Chen, 2008; Ma et al., 2018). The GRAPES_SCM has been constructed for evaluating and developing the physics parameterizations of GRAPES. The GRAPES_SCM is adhered to the full model, which guarantees that the physical process parameterizations in both the full atmospheric model and the SCM are unified. By introducing new modules and options in the “namelist” in the GRAPES code, the SCM run is realized with a feasible treatment of observational data input as well as different configurations of physical processes. A diagram of the GRAPES_SCM integral is shown in Fig. 1. A detailed flow chart and the equations of the GRAPES_SCM can be seen in Yang and Shen (2011). Wang et al. (2013) used the GRAPES_SCM to evaluate cumulus parameterization schemes and to examine a new modified scheme, and they concluded that the modified scheme was more reasonable than the previous version. Li et al. (2018) adjusted the Liuma scheme using the GRAPES_SCM. Their results showed that the revised Liuma scheme had improved performance in simulating ice-phased hydrometeors, and that the simulated surface precipitation rate was much closer to the observations.

|
| Figure 1 Diagram of the GRAPES_SCM integral. |
Studies have shown that SCM solutions are sensitive to initial conditions because of the nonlinear nature of model physics (Cripe, 1998; Hack and Pedretti, 2000). Therefore, an ensemble methodology is necessary to represent the solution of a single model. In accordance with Davies (2009), this study ran key ensemble members (5th, 25th, 50th, 75th,and 95th) to obtain the best estimate simulation. The results presented in this paper are the means of those simulations. As also mentioned by Davies (2009), the simulations were initialized with observed temperature and moisture profiles from 19 January 2006. Temperature and moisture have only horizontal advective tendencies. The vertical terms are calculated by the model. There was no nudging of the temperature and moisture fields, and the simulation comprised a continuous simulation (no reinitialization) of the entire TWP-ICE period.
In this study, all settings and parameterization schemes other than the microphysical scheme were kept the same. The simulation center was located at Port Darwin (12.425°S, 130.891°E). The model had a fixed time-invariant sea surface temperature of 29°C and the interactive surface fluxes were calculated in the model. The time step of the simulation was 10 s (note that sub-stepping was used for fast processes such as sedimentation in the microphysics scheme). The model was run with the SAS cumulus scheme (Arakawa and Schubert, 1974), RRTMG scheme (Mlawer et al., 1997) for both longwave and shortwave radiation, and the slab scheme for the boundary layer (Blackadar, 1978).
2.3 Freezing processes in the Liuma microphysics schemeThe Liuma microphysics scheme is a two-moment mixed-phase scheme developed from the convective and stratus cloud model of Hu and Yan (1986) and Hu and He (1987). This scheme predicts the mass mixing ratios of cloud water, rain water, cloud ice, snow, and graupel, as well as the number concentrations of rain drops, cloud ice, snow, and graupel. The Liuma microphysics scheme is used for weather forecasting and scientific research (e.g., Liu et al., 2003; Zhang and Liu, 2006; Shi et al., 2015; Ma et al., 2018). Li et al. (2018, 2019) have tested the performance of the Liuma microphysics scheme in various models and they have improved its mixed-phased microphysical processes.
The initial version of the Liuma microphysics scheme (hereafter, Liuma_init) contains both homogeneous freezing and the three modes of heterogeneous nucleation (deposition nucleation, condensation freezing, and immersion freezing), following Hu and Yan (1986) and Reisner et al. (1998). A detailed calculation flowchart of the microphysical processes can be seen in Li et al. (2018). In this study, the equations of the number concentration production rate of homogeneous freezing and immersion freezing are described as a unified form based on the rain–graupel conversion from Reisner et al. (1998), as shown below:
| $ {N_{\rm fci}} = \left\{ {\begin{split} & 0.1 \exp [0.66(- T) - 1] \rho q_{\rm c}, \; 0 > T > - 40 {\text {\rm °C}} \\ & {1.0 \times 10^6 / {\Delta}t, \; T \leqslant - 40 {\text {\rm °C}}} \end{split} } \right., $ | (1) |
where Nfci (s−1) is the number concentration production rate, T (°C) is temperature, ρ (kg m−3) is air density, qc (kg kg−1) is the cloud water mixing ratio, and
Different parameterizations of deposition nucleation and condensation freezing were used to investigate how deep convective cloud and the associated cirrus are affected by heterogeneous nucleation. In recent research, the most widely adopted measurement-based deposition nucleation and condensation freezing parameterizations are from Meyers et al. (1992), DeMott et al. (2003), and Phillips et al. (2008); hereafter, denoted as Liuma_r1, Liuma_r2, and Liuma_r3, respectively. The equations of the number concentration production rate of the Liuma_init, Liuma_r1, Liuma_r2, and Liuma_r3 deposition nucleation and condensation freezing parameterizations are shown below:
| $ \!\!{N_{\rm f0}} = \left\{ {\begin{array}{*{20}{c}} {0.01 \exp \left[{0.6 \times \left({ - T} \right)} \right] {{\left({\dfrac{{{q_{\rm v}} - {q_{\rm vsi}}}}{{{q_{\rm vs}} - {q_{\rm vsi}}}}} \right)}^{4.5}}, \;\;\; T > - 26.5 {\text {\rm °C}}}\\ {0.01 \exp \left({0.6 \times 27.5} \right) {{\left({\dfrac{{{q_{\rm v}} - {q_{\rm vsi}}}}{{{q_{\rm vs}} - {q_{\rm vsi}}}}} \right)}^{4.5}},\;\;\; T \leqslant - 26.5 {\text {\rm °C}}} \end{array}} \right., \quad\quad\quad\quad\quad\quad $ | (2) |
| $ {N_{\rm f1}} = 1000 \exp \left({\min \left({57,\left({12.96 \left({\frac{{{q_{\rm v}}}}{{{q_{\rm vsi}}}} - 1} \right) - 0.639} \right)} \right)} \right), \;\;\; T \leqslant - 5 {\text {\rm °C},} \quad\quad\quad\quad\quad\!\! $ | (3) |
| $ \!\!\!\!\!\!\!\!\!{N_{\rm f2}} = 1000 \times 0.00446684 \exp \left({0.3108 \left({ - \max \left({ - 40,T} \right)} \right)} \right), \quad\quad\quad\quad\quad\quad\quad\;\;\; $ | (4) |
| $ \; {N_{\rm f3}} = \left\{ {\begin{array}{*{20}{c}} {1000 \exp \left({\min \left({57,\left({12.96 \left({\dfrac{{{q_{\rm v}}}}{{{q_{\rm vsi}}}} - 1} \right) - 0.639} \right)} \right)} \right), \;\;\; - 30 < T \leqslant - 5{\text {\rm °C}}}\\ {1000 \exp {{\left({\min \left({57,\left({12.96 \left({\dfrac{{{q_{\rm v}}}}{{{q_{\rm vsi}}}} - 1.1} \right)} \right)} \right)} \right)}^{0.3}}, \;\;\; T \leqslant - 30 \;{\rm or} \;T > - 5{\text {\rm °C}}} \end{array}} \right., $ | (5) |
where qv, qvs, and qvsi (kg kg−1) represent the water vapor mixing ratio of the environment and the saturation water vapor pressure over water and ice, respectively.
The saturation water vapor mixing ratio over water and ice can also be represented as a fractional function of saturation water vapor (es and esi) and pressure:
| $ {q_{\rm vs}} = \frac{{0.622 {e_{\rm s}}}}{{p - 0.378 {e_{\rm s}}}},\quad\quad\quad\quad\quad $ | (6) |
| $ {q_{\rm vsi}} = \frac{{0.622 {e_{\rm si}}}}{{p - 0.378 {e_{\rm si}}}}, \;\;\; T \leqslant 0{\text{°C}}, $ | (7) |
whereas saturation water vapor is related only to temperature:
| $ {e_{\rm s}} = \left\{ \begin{array}{l} 1000 \times 0.6112 \times \exp \left({\dfrac{{17.27 \times T}}{{T + 237.29}}} \right), \;\;\; T > 0 {\text{°C}}\\ 1000 \times0.6112 \times \exp \left({\dfrac{{17.67 \times T}}{{T + 243.5}}} \right), \;\;\; T \leqslant 0 {\text{°C}} \end{array} \right., $ | (8) |
| $ {\rm e_{si}} = 1000 \times 0.6112 \times \exp \left({\frac{{21.87 \times T}}{{T + 265.49}}} \right), \;\;\; T \leqslant 0{\text{°C}} . \quad\quad\quad\!\!\!\! $ | (9) |
The number concentration production rate of deposition nucleation/condensation freezing parameterizations under different water vapor mixing ratios is shown in Fig. 2. In general, the number concentration production rate increases significantly with decreasing temperature, but it increases smoothly with increases of pressure and water vapor mixing ratio. This is because, as already shown in Eqs. (1)–(8), the number concentration production rate is an exponential function of temperature and a fractional function of both pressure and water vapor mixing ratio. Thus, the number concentration production rate is much more sensitive to temperature than to pressure and water vapor mixing ratio. When the temperature is above −20°C, hardly any ice is formed under all parameterizations. The results from Liuma_init show that under a low water vapor mixing ratio (i.e., 0.2 g kg−1), the number concentration production rate increases from 1.0 kg−1 s−1 at around −40°C to more than 1 × 1010 kg−1 s−1 at around −60°C, as shown in Fig. 2a. Under a high water vapor mixing ratio (i.e., 1.0 g kg−1), such an increase occurs from around −20 to −40°C, as shown in Fig. 2i. The results from Liuma_r1–Liuma_r3 also show similar tendency. It should be noted that the number concentration production rate from Liuma_r2 does not change when the temperature is below −40°C (as shown in Figs. 2c, g, k) because of the limitation expressed in Eq. (3).

|
| Figure 2 Number concentration production rate (kg−1 s−1) of deposition nucleation/condensation freezing parameterizations. Left to right columns represent results of (a, e, i) Liuma_init, (b, f, j) Liuma_r1, (c, g, k) Liuma_r2, and (d, h, l) Liuma_r3, respectively; top to bottom panels represent environmental qv of 0.2, 0.5, and 1.0 g kg−1, respectively. Note the color bar is the logarithmic value of the production rate. |
It is also shown that different deposition nucleation/condensation freezing parameterizations have considerable effect on the number concentration production rate. Under a low water vapor mixing ratio, the number concentration production rate from Liuma_r1 increases sharply from around −40 to −50°C, and it can be as high as 1.0 × 1020 kg−1 s−1 at −50°C, as shown in Fig. 2b. This is much higher than the result from Liuma_init at the same temperature. The number concentration production rate from Liuma_r3 also increases sharply from around −40 to −50°C, and it can be as high as 1.0 × 1010 kg−1 s−1 at −50°C, as shown in Fig. 2d. Under a high water vapor mixing ratio, the number concentration production rate has the same tendency as under a low water vapor mixing ratio. The number concentration production rate from Liuma_r2 is relatively low in comparison with the other parameterizations, and it retains the highest value of frozen number concentration (1.0 × 105 kg−1 s−1) when the temperature is below −40°C.
3 Results 3.1 Comparison between observations and simulationsThe time evolutions of liquid-phased (sum of cloud water and rain) and ice-phased hydrometeor mixing ratios (sum of ice, snow, and graupel) from the CRM and simulation results from the SCM with Liuma_init are shown in Fig. 3. It should be noted that the observed hydrometeor mixing ratios are of poor quality. However, Varble et al. (2011) highlighted that the CRM results could reflect the convective precipitation process during the TWP-ICE. Therefore, this study opted to use the CRM results (Fridlind et al., 2010; Varble et al., 2011) as reference. As shown in Figs. 3a, c, the active monsoon period and the suppressed monsoon period are clearly separated. During 20–24 January, in the active monsoon period, the ice-phased hydrometeor mixing ratio is around 75–300 mg kg−1. The results from the CRM show that the cloud in this period is reasonably thick and that the deep convective core can extend up to 10 km. The thickest convective cloud appears on 24 January with a dense convective core up to 15 km. The results also show that the deep convective cloud precipitated heavily at this time, as shown in Fig. 3c. During the suppressed monsoon period, the total hydrometeor mixing ratio has two layers. The upper layer is around 15 km with an ice-phased hydrometeor mixing ratio of around 5 mg kg−1 (Fig. 3a), whereas the lower layer is below 10 km with an ice/liquid-phased hydrometeor mixing ratio of around 20–75 mg kg−1 (Figs. 3a, c) from 25 to 31 January. The results show that the deep convective cloud dissipates to shallow nonprecipitating cloud, and that the anvils remain at upper levels during this period. The results from the SCM with Liuma_init also simulate clearly the active and suppressed monsoon periods. During the active monsoon period, the ice-phased (liquid-phased) hydrometeor mixing ratio is lower (higher) than that of the CRM. The simulated cloud water from the SCM with Liuma_init is also thicker than the CRM, which shows the capability of Liuma_init to simulate supercooled water. During the suppressed monsoon period, the two-layered cloud structure is also captured, as shown in Figs. 3b, d. The liquid-phased hydrometeor mixing ratio is smaller than that of the CRM at this time. Both simulation results produce a 0°C layer at around 5-km height. The cloud top temperature can be as low as −80°C from the SCM with Liuma_init, and even colder from the CRM. In general, the results show that the SCM with Liuma_init is satisfactory in representing the findings of the TWP-ICE.
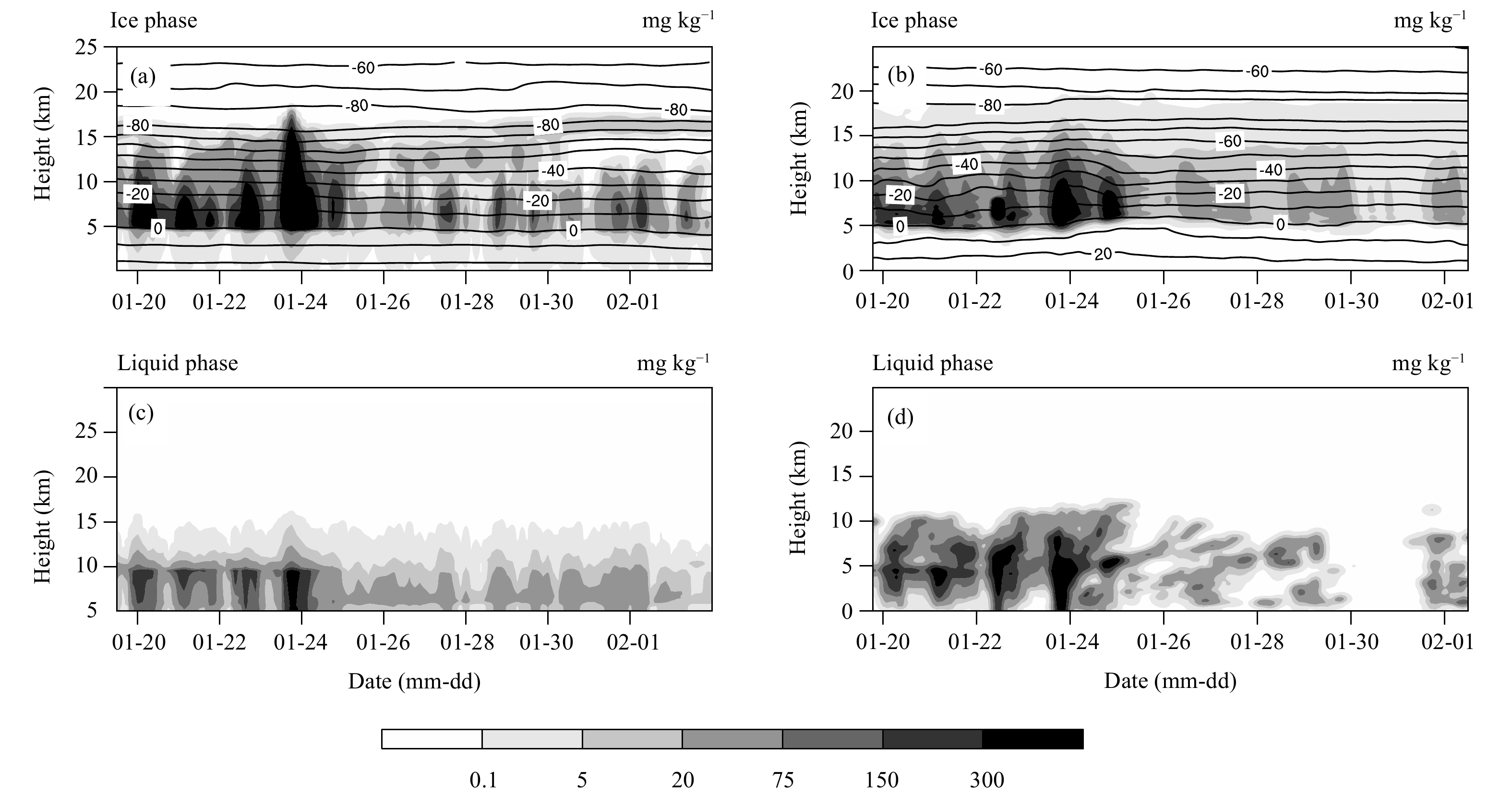
|
| Figure 3 Time evolutions of liquid-phased (sum of cloud water and rain) and ice-phased (sum of ice, snow, and graupel) hydrometeor mixing ratios (shaded) from (a, c) the CRM (https://www.arm.gov/research/campaigns/twp2006twp-ice#data) and (b, d) simulation results from the SCM with Liuma_init. Black contours indicate temperature. |
Figure 4 shows the time evolutions of surface precipitation rate, surface net shortwave radiation, and outgoing longwave radiation from observation and the simulation results from the SCM with Liuma_init from 19 January to 1 February. As shown in Fig. 4a, observed precipitation occurs during the active monsoon period with the highest precipitation rate of up to 8 mm h−1 on 4 January. This is consistent with the simulated deep convective cloud shown in Fig. 3. During the suppressed monsoon period, the surface precipitation rate is rather low. The results from the SCM with Liuma_init are very close to the observations. Radiation properties are affected strongly by cloud properties (e.g., Garrett and Zhao, 2006; Zhao and Garrett, 2015). For the surface net shortwave radiation, the liquid cloud is dense, which will decrease shortwave radiation efficiently. As shown in Fig. 4b, during the active monsoon period, the peak surface net downward radiation is much smaller than that of the suppressed monsoon period. This is because, compared with the suppressed monsoon period, the liquid cloud dominates during the active monsoon period and decreases the surface net shortwave radiation efficiently, especially around 24 January. The liquid-phased hydrometeor mixing ratio from the SCM with Liuma_init is higher than that of the CRM, and the surface net shortwave radiation is also smaller compared with the observations. During the suppressed monsoon period, the ice-phased hydrometeor mixing ratio from the SCM with Liuma_init is smaller than the CRM; thus, the surface net shortwave radiation is also higher compared with the observations. For the outgoing longwave radiation, the ice cloud is much colder than the surface and this will reduce outgoing longwave radiation considerably. The simulated outgoing longwave radiation is higher than that of the observations, possibly because of the lesser extent of the simulated ice cloud and the higher cloud top temperature (Figs. 3a, b). The difference in the effect of cloud properties on simulated and observed radiation properties has been discussed in the previous study (Mei et al., 2015).

|
| Figure 4 Time evolutions of (a) surface precipitation (rainrate; mm h−1), (b) surface net shortwave radiation (GSW; W m−2), and (c) outgoing longwave radiation (OLR; W m−2) from observation and the simulation results from the SCM with Liuma_init. Black lines represent the observation results and the blue lines represent the results from the SCM with Liuma_init. |
The time evolution of number concentration production rate of deposition nucleation/condensation freezing and homogeneous freezing/immersion freezing parameterizations is shown in Fig. 5. It can be seen that ice formation through deposition/condensation freezing and homogeneous freezing/immersion freezing occurs mostly at 8–15 km, where the temperature is below −20°C. The water vapor mixing ratio is up to 2.0 g kg−1 at around 8 km during the active monsoon period, but it decreases to 0.5 g kg−1 during the suppressed monsoon period.
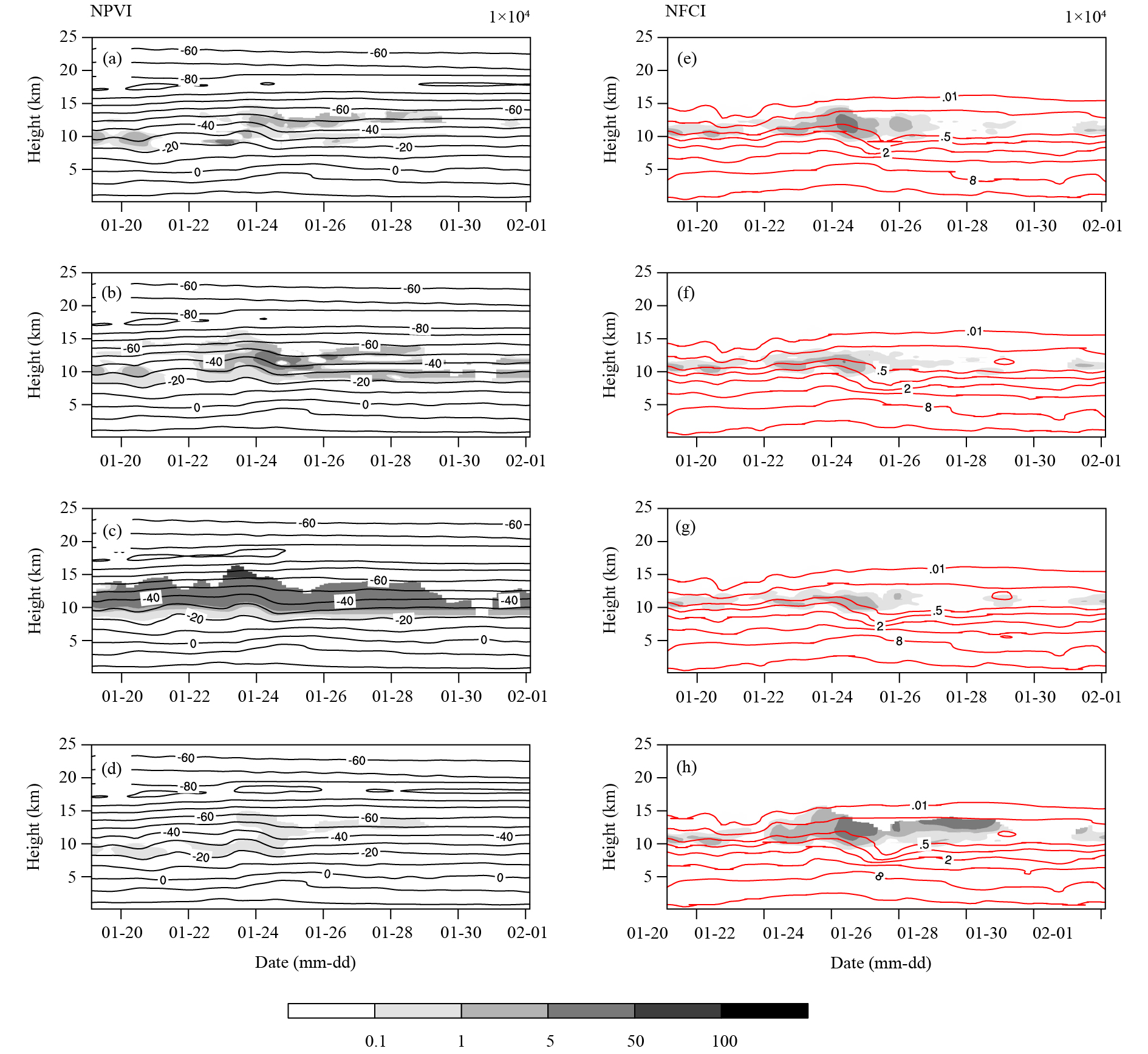
|
| Figure 5 Time evolutions of number concentration production rate of deposition nucleation/condensation freezing, homogeneous freezing/immersion freezing parameterizations, temperature and water vapor mixing ratio. Left and right columns represent number concentration production rates of (a–d) deposition/condensation freezing and (e–h) homogeneous/immersion freezing from the SCM with Liuma_init, Liuma_r1, Liuma_r2, and Liuma_r3 from top to bottom, respectively. Black contours are temperature and red contours are water vapor mixing ratio. |
As shown in Figs. 5a–d, the number concentration production rate varies significantly depending on the different deposition nucleation/condensation freezing parameterizations, which is consistent with Fig. 3. The number concentration production rate of deposition nucleation/condensation freezing from the SCM with Liuma_init and Liuma_r3 is around 0.1–1.0 unit, i.e., lower than that from the SCM with Liuma_r1 and Liuma_r2 (up to 50 units). This is because the number concentration production rate of deposition nucleation/condensation freezing is very sensitive to temperature from around −20 to −60°C, as illustrated in Fig. 3. Although the number concentration production rate of deposition nucleation/condensation freezing from the SCM with Liuma_r2 appears lower in Fig. 3, the noticeable (i.e., the highest rate in this situation) ice production from deposition nucleation/condensation freezing that begins at around −30°C at 10 km (~300 hPa), as shown in Fig. 5, is from Liuma_r2 rather than Liuma_r1 or the other parameterizations. This result raises questions over whether some high-efficiency IN could actually be as efficient in the real environment as found in the laboratory.
The results also indicate that ice formation through homogeneous freezing/immersion freezing can be very efficient in this case. The highest homogeneous freezing/immersion freezing number concentration production rate in all simulations is as high as 50 units during the active monsoon period. The number concentration production rate of homogeneous freezing/immersion freezing also varies considerably between the different simulations. Ice formation through homogeneous freezing/immersion freezing dominates the suppressed monsoon period in the simulations from the SCM with Liuma_init and Liuma_r3, when deposition nucleation/condensation freezing is reasonably low. Competition between deposition nucleation/condensation freezing and homogeneous freezing/immersion freezing is clearly captured in this study, which is consistent with the findings of previous study (Deng et al., 2018).
3.3 Cloud properties affected by heterogeneous nucleationThe hydrometeor mixing ratio of Liuma_init and Liuma_r1–Liuma_r3 is shown in Fig. 6. The results show that a change in heterogeneous nucleation can have slight effect on the distribution of hydrometeor mixing ratios. As shown in the panels of the top row, the ice mixing ratio is typically higher during the active monsoon period than the suppressed monsoon period. The ice mixing ratio is as high as 300 mg kg−1 in all simulations during the active monsoon period, whereas it is up to only 150 mg kg−1 during the suppressed monsoon period. The snow and graupel mixing ratios are concentrated during the active monsoon period. The snow mixing ratio from the SCM with Liuma_r2 is less than produced with the other parameterizations on 24 January, when convection is most active. The graupel mixing ratio in all parameterizations do not vary much. Consistent with Fig. 2, the cloud and rain mixing ratios are also concentrated during the active monsoon period with maximum values of 150–300 mg kg−1. The cloud mixing ratio from the SCM with Liuma_r3 is slightly higher than the other parameterizations, whereas the rain mixing ratio from the SCM with Liuma_r2 and Liuma_r3 is generally slightly higher than from the SCM with Liuma_init and Liuma_r1. It should be noted that the hydrometeor mixing ratios from different heterogeneous nucleation parameterizations also vary slightly on a daily basis.
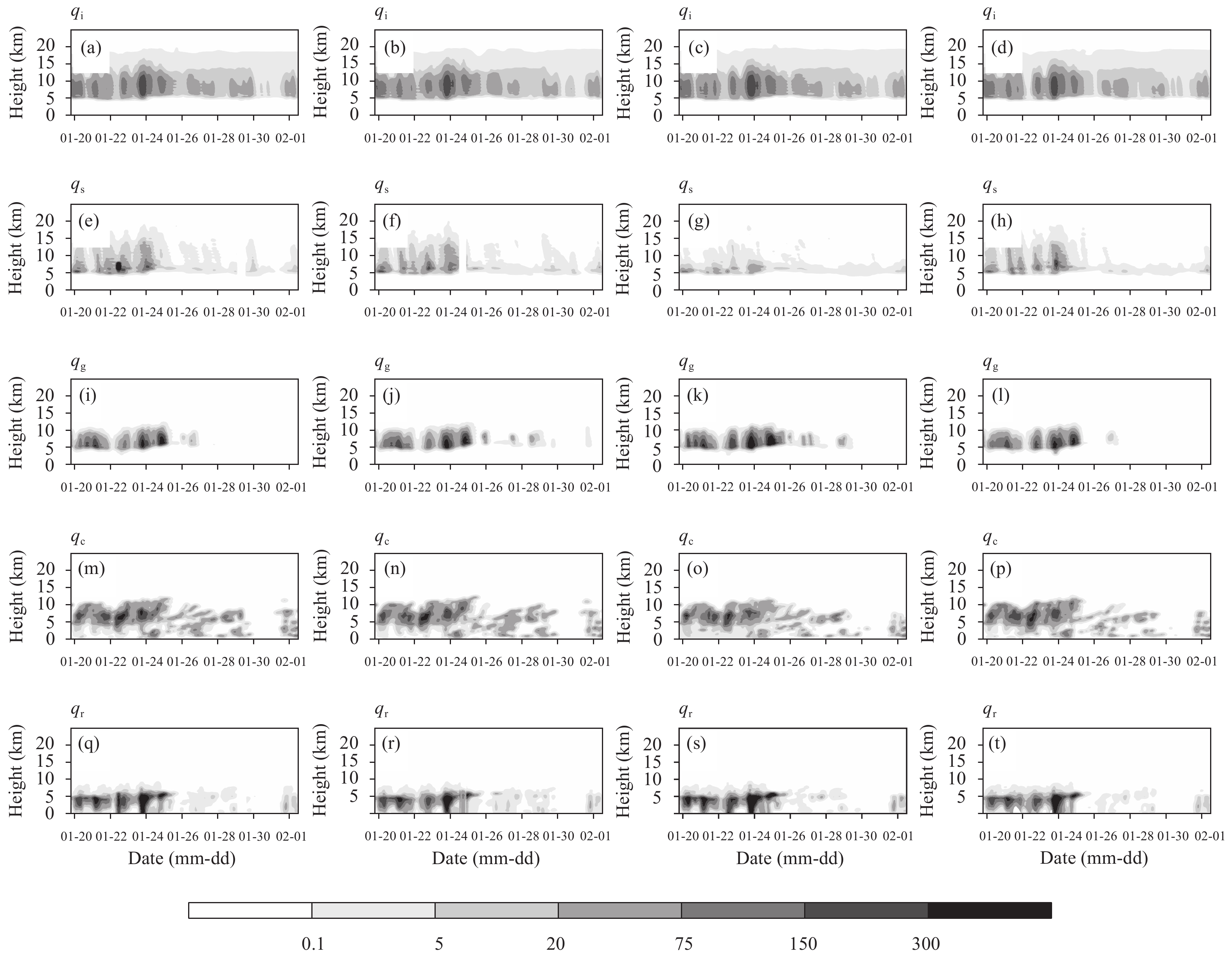
|
| Figure 6 Time evolutions of hydrometeor mixing ratio. Rows from top to bottom represent the hydrometeors of cloud ice (qi), snow (qs), graupel (qg), cloud water (qc), and rain (qr), respectively. Columns from left to right represent the results from the SCM with Liuma_init, Liuma_r1, Liuma_r2, and Liuma_r3, respectively. |
Consistent with Fig. 5, the results show that a change in heterogeneous nucleation has little effect on ice production. Thus, subsequent ice deposition growth and ice-related microphysical processes did not vary much. Therefore, although the distribution of hydrometeor mixing ratios is different when using different heterogeneous nucleation parameterizations, the macroscale properties of deep convective cloud and the associated cirrus might only be affected slightly by heterogeneous nucleation. In addition, the heat budget and the cloud water and ice tendencies attributable to the microphysics during the active monsoon period were investigated (figures omitted). The results show that a change in heterogeneous nucleation might have only slight effect on ice production. This finding is consistent with previous studies that have reported that IN concentration has little effect on deep convective cloud (Deng et al., 2018).
Figure 7 presents the same information as Fig. 4 but with the Liuma_r1–r3 schemes. As shown in Fig. 6a, all three simulations capture the active precipitating monsoon period and the nonprecipitating suppressed monsoon period clearly. The results also show that a change in heterogeneous nucleation can have a slight effect on surface precipitation rate and radiation properties. Consistent with Figs. 6q–t, higher rain mixing ratios (large particles in high hydrometeor mixing ratio region) lead to higher precipitation rate during the active monsoon per-iod. As for radiation properties, surface net downward radiation and outgoing longwave radiation vary slightly between different the heterogeneous nucleation parameterizations, which are due to the associated change of cloud properties. For example, the total hydrometeor mixing ratio from the SCM with Liuma_r2 is lowest on 22 January, which less shortwave radiation is reflected and there is the greatest surface net downward radiation, as shown in Fig. 7b. As for outgoing longwave radiation, during the suppressed monsoon period, the ice and snow mixing ratio from the SCM with Liuma_r2 is highest, which leads to the lowest outgoing longwave radiation during this period, as shown in Fig. 7c.

|
| Figure 7 As in Fig. 4, but with the revised Liuma schemes. Black lines represent results from observation and green/blue/red lines represent results from the SCM with Liuma_r1, Liuma_r2, and Liuma_r3, respectively. |
This study used the GRAPES_SCM to investigate the effect of heterogeneous nucleation on monsoon precipitation with deep convective cloud and associated cirrus in Darwin, Australia. The hydrometeor mixing ratio distributions, precipitation and radiation properties of the monsoon precipitation simulated with various heterogeneous nucleation parameterizations were compared with both observations and CRM results. The major findings of this study are noted as follows.
1) The results from the SCM with Liuma_init and Liuma_r1–Liuma_r3 all captured the active and suppressed monsoon periods observed during the TWP-ICE experiment. The simulated surface precipitation rate (8–11 mm h−1), radiation properties, and cloud hydrometeor mixing ratio distribution were close to both the observations and the CRM results.
2) Although the number concentration production rate of different deposition nucleation/condensation freezing parameterizations varied substantially (from 1.0 × 105 to 1.0 × 1020 kg−1 s−1) under the given temperature and water vapor mixing ratio, ice formation in deep convective cloud and the associated cirrus was affected only slightly by the deposition nucleation/condensation freezing parameterizations. These results agree well with previous studies (Li et al., 2013; Bi et al., 2018; Deng et al., 2018), which found that competition between heterogeneous nucleation and homogeneous freezing in deep convective cloud is highly important in determining the cloud microphysical properties, especially in the anvil region.
3) The precipitation and radiation properties of the studied case of monsoon precipitation were found affected slightly by heterogeneous nucleation because of the change of cloud properties. All simulations showed appropriate surface precipitation rates (up to 11 mm h−1) during the active monsoon period. During the suppressed monsoon period, higher simulated cloud top temperature might have caused the simulated outgoing longwave radiation to be higher than that of the observations.
Acknowledgments. We thank James Buxton MSc for editing the English text of this manuscript.
| Arakawa, A., and W. H. Schubert, 1974: Interaction of a cumulus cloud ensemble with the large-scale environment, Part I. J. Atmos. Sci., 31, 674–701. DOI:10.1175/1520-0469%281974%29031<0674%3AIOACCE>2.0.CO%3B2 |
| Bi, K., X. C. Ma, Y. B. Chen, et al., 2018: The observation of ice-nucleating particles active at temperatures above −15°C and its implication on ice formation in clouds. J. Meteor. Res., 32, 734–743. DOI:10.1007/s13351-018-7181-z |
| Blackadar, A. K., 1978: Modeling pollutant transfer during daytime convection. Preprints from Fourth Symposium on Turbulence, Diffusion, and Air Quality, Amer. Meteor. Soc., Reno, NV, 443–447. |
| Chen, D. H., J. S. Xue, X. S. Yang, et al., 2008: New generation of multi-scale NWP system (GRAPES): General scientific design. Chinese Sci. Bull., 53, 3433–3445. DOI:10.1007/s11434-008-0494-z |
| Cotton, W. R., G. J. Tripoli, R. M. Rauber, et al., 1986: Numerical simulation of the effects of varying ice crystal nucleation rates and aggregation processes on orographic snowfall. J. Climate Appl. Meteor., 25, 1658–1680. DOI:10.1175/1520-0450(1986)025<1658:NSOTEO>2.0.CO;2 |
| Cripe, D., 1998: Single-column modeling: Sensitivity to initial conditions and divergence forcing. Proceedings of the Seventh Atmospheric Radiation Measurement (ARM) Science Team Meeting, ARM, San Antonio, TX, 439–441. [Available on line at http://scholar.google.com/scholar?hl=en&q=Cripe%2C+D.%2C+1998%3A++Single-column+modeling%3A+Sensitivity+to+initial+conditions+and+divergence+forcing.+Proc.+Seventh+Atmospheric+Radiation+Measurement+%28ARM%29+Science+Team+Meeting%2C+San+Antonio%2C+TX%2C+ARM+Program%2C+439%E2%80%93441]. |
| Davies, L., 2009: TWP-ICE single column model case. [Available on line at http://users.monash.edu.au/~ladavies/SCM_TWP-ICEdoc.pdf]. |
| DeMott, P. J., K. Sassen, M. R. Poellot, et al., 2003: African dust aerosols as atmospheric ice nuclei. Geophys. Res. Lett., 30, 1732. DOI:10.1029/2003GL017410 |
| Deng, X., H. W. Xue, and Z. Y. Meng, 2018: The effect of ice nuclei on a deep convective cloud in South China. Atmos. Res., 206, 1–12. DOI:10.1016/j.atmosres.2018.02.013 |
| Diehl, K., and S. K. Mitra, 2015: New particle-dependent parameterizations of heterogeneous freezing processes: Sensitivity studies of convective clouds with an air parcel model. Atmos. Chem. Phys., 15, 12741–12763. DOI:10.5194/acp-15-12741-2015 |
| Du, C. H., T. van der Sar, T. X. Zhou, et al., 2017: Control and local measurement of the spin chemical potential in a magnetic insulator. Science, 357, 195–198. DOI:10.1126/science.aak9611 |
| Ekman, A. M. L., A. Engström, and C. Wang, 2007: The effect of aerosol composition and concentration on the development and anvil properties of a continental deep convective cloud. Quart. J. Roy. Meteor. Soc., 133, 1439–1452. DOI:10.1002/qj.108 |
| Fan, J. W., T. L. Yuan, J. M. Comstock, et al., 2009: Dominant role by vertical wind shear in regulating aerosol effects on deep convective clouds. J. Geophys. Res. Atmos., 114, D22206. DOI:10.1029/2009JD012352 |
| Fridlind, A., A. Ackerman, J. Petch, et al., 2010: ARM/GCSS/SPARC TWP-ICE CRM intercomparison study. NASA-TM-2010-215858, National Aeronautics and Space Administration, Greenbelt. [Available online at https://pubs.giss.nasa.gov/docs/2010/2010_Fridlind_fr08100v.pdf]. |
| Garrett, T. J., and C. F. Zhao, 2006: Increased Arctic cloud longwave emissivity associated with pollution from mid-latitudes. Nature, 440, 787–789. DOI:10.1038/nature04636 |
| Gesso, S. D., and R. A. J. Neggers, 2018: Can we use single-column models for understanding the boundary layer cloud-climate feedback?. J. Adv. Model. Earth Syst., 10, 245–261. DOI:10.1002/2017MS001113 |
| Hack, J. J., and J. A. Pedretti, 2000: Assessment of solution uncertainties in single-column modeling frameworks. J. Climate, 13, 352–365. DOI:10.1175/1520-0442(2000)013<0352:AOSUIS>2.0.CO;2 |
| Harrison, E. F., P. Minnis, B. R. Barkstrom, et al., 1990: Time dependence of the Earth’s radiation fields determined from ERBS and NOAA-9 satellites. Proceedings of SPIE Volume 1299, Long-Term Monitoring of the Earth’s Radiation Budget, SPIE, Orlando, FL, 222–230, doi: 10.1117/12.21380. |
| Hartmann, D. L., M. E. Ockert-Bell, and M. L. Michelsen, 1992: The effect of cloud type on Earth’s energy balance: Global analysis. J. Climate, 5, 1281–1304. DOI:10.1175/1520-0442(1992)005<1157:TEOCTO>2.0.CO;2 |
| Hazra, A., B. Padmakumari, R. S. Maheskumar, et al., 2016: The effect of mineral dust and soot aerosols on ice microphysics near the foothills of the Himalayas: A numerical investigation. Atmos. Res., 171, 41–55. DOI:10.1016/j.atmosres.2015.12.005 |
| Hiron, T., and A. I. Flossmann, 2015: A study of the role of the parameterization of heterogeneous ice nucleation for the modeling of microphysics and precipitation of a convective cloud. J. Atmos. Sci., 72, 3322–3339. DOI:10.1175/JAS-D-15-0026.1 |
| Hoose, C., and O. Möhler, 2012: Heterogeneous ice nucleation on atmospheric aerosols: a review of results from laboratory experiments. Atmos. Chem. Phys., 12, 9817–9854. DOI:10.5194/acp-12-9817-2012 |
| Hu, Z. J., and C. F. Yan, 1986: Numerical simulation of microphysical processes in stratiform clouds (I)—Microphysical model. J. Acad. Meteor. Sci., 1, 37–52. |
| Hu, Z. J., and G. F. He, 1987: Numerical simulation of microprocesses in cumulonimbus clouds. (I): Microphysical model. Acta Meteor. Sinica, 45, 467–484. DOI:10.11676/qxxb1987.060 |
| Jensen, E. J., O. B. Toon, L. Pfister, et al., 1996: Dehydration of the upper troposphere and lower stratosphere by subvisible cirrus clouds near the tropical tropopause. Geophys. Res. Lett., 23, 825–828. DOI:10.1029/96GL00722 |
| Kennedy, A. D., X. Q. Dong, B. K. Xi, et al., 2010: Evaluation of the NASA GISS single-column model simulated clouds using combined surface and satellite observations. J. Climate, 23, 5175–5192. DOI:10.1175/2010JCLI3353.1 |
| Lamb, D., and J. Verlinde, 2011: Physics and Chemistry of Clouds. Cambridge University Press, Cambridge, 584 pp. |
| Li, Z., H. W. Xue, and F. Yang, 2013: A modeling study of ice formation affected by aerosols. J. Geophys. Res. Atmos., 118, 11213–11227. DOI:10.1002/jgrd.50861 |
| Li, Z., Y. T. Zhang, Q. J. Liu, et al., 2018: A study of the influence of microphysical processes on Typhoon Nida (2016) using a new double-moment microphysics scheme in the wea-ther research and forecasting model. J. Trop. Meteor., 24, 123–130. DOI:10.16555/j.1006-8775.2018.02.001 |
| Li, Z., Z. S. Ma, Q. J. Liu, et al., 2019: The improvement of GRAPES double moment cloud scheme and case study of cloud precipitation. Part I: Modeling study of tropical convective cloud via GRAPES_SCM. Meteor. Mon., 45, 756–765. DOI:10.7519/j.issn.1000-0526 |
| Liu, Q. J., Z. J. Hu, and X. J. Zhou, 2003: Explicit cloud schemes of HLAFS and simulation of heavy rainfall and clouds. Part II: Simulation of heavy rainfall and clouds. J. Appl. Meteor. Sci., 14, 68–77. DOI:10.3969/j.issn.1001-7313.2003.z1.009 |
| Ma, Z. S., Q. J. Liu, C. F. Zhao, et al., 2018: Application and evaluation of an explicit prognostic cloud-cover scheme in GRAPES global forecast system. J. Adv. Model. Earth Syst., 10, 652–667. DOI:10.1002/2017MS001234 |
| May, P. T., J. H. Mather, G. Vaughan, et al., 2008: FIELD RESEARCH: Characterizing oceanic convective cloud systems. Bull. Amer. Meteor. Soc., 89, 153–155. DOI:10.1175/BAMS-89-2-153 |
| Mei, H. X., X. Y. Shen, and W. G. Wang, 2015: Evaluation and comparison of two double-moment bulk microphysics schemes using WRF single-column model. Plateau Meteor., 34, 890–909. DOI:10.7522/j.issn.1000-0534.2014.00113 |
| Meyers, M. P., P. J. DeMott, and W. R. Cotton, 1992: New primary ice-nucleation parameterizations in an explicit cloud model. J. Appl. Meteor., 31, 708–721. DOI:10.1175/1520-0450(1992)031<0708:NPINPI>2.0.CO;2 |
| Mlawer, E. J., S. J. Taubman, P. D. Brown, et al., 1997: Radiative transfer for inhomogeneous atmospheres: TMRR, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos., 102, 16663–16682. DOI:10.1029/97JD00237 |
| Phillips, V. T. J., P. J. Demott, and C. Andronache, 2008: An empirical parameterization of heterogeneous ice nucleation for multiple chemical species of aerosol. J. Atmos. Sci., 65, 2757–2783. DOI:10.1175/2007JAS2546.1 |
| Pruppacher, H. R., and J. D. Klett, 1997: Microphysics of Clouds and Precipitation. Kluwer Academic Press, Dordrecht, 954 pp. |
| Ramage, C. S., 1971: Monsoon Meteorology. Academic Press, New York, 296 pp. |
| Ramanathan, V., R. D. Cess, E. F. Harrison, et al., 1989: Cloud-radiative forcing and climate: Results from the earth radiation budget experiment. Science, 243, 57–63. DOI:10.1126/science.243.4887.57 |
| Reisner, J., R. M. Rasmussen, and R. T. Bruintjes, 1998: Explicit forecasting of supercooled liquid water in winter storms using the MM5 mesoscale model. Quart. J. Roy. Meteor. Soc., 124, 1071–1107. DOI:10.1002/qj.49712454804 |
| Rossow, W. B., and R. A. Schiffer, 1991: ISCCP cloud data products. Bull. Amer. Meteor. Soc., 72, 2–20. DOI:10.1175/1520-0477(1991)072<0002:ICDP>2.0.CO;2 |
| Shi, R. G., Q. J. Liu, and Z. S. Ma, 2015: Numerical simulation of aerosol effects on cloud and precipitation using GRAPES model. Meteor. Mon., 41, 272–285. DOI:10.7519/j.issn.1000-0526.2015.03.002 |
| van den Heever, S. C., G. G. Carrió, W. R. Cotton, et al., 2006: Impacts of nucleating aerosol on florida storms. Part I: Mesoscale simulations. J. Atmos. Sci., 63, 1752–1775. DOI:10.1175/JAS3713.1 |
| Varble, A., A. M. Fridlind, E. J. Zipser, et al., 2011: Evaluation of cloud-resolving model intercomparison simulations using TWP-ICE observations: Precipitation and cloud structure. J. Geophys. Res. Atmos., 116, D12206. DOI:10.1029/2010JD015180 |
| Wang, D. L., G. Q. Xu, and L. H. Jia, 2013: The evaluation of cumulus parameterization schemes in GRAPES model and its improved experiments. Meteor. Mon., 39, 166–179. DOI:10.7519/j.issn.1000-0526.2013.02.005 |
| Wapler, K., T. P. Lane, P. T. May, et al., 2010: Cloud-system-resolving model simulations of tropical cloud systems observed during the tropical warm pool-international cloud experiment. Mon. Wea. Rev., 138, 55–73. DOI:10.1175/2009MWR2993.1 |
| Xie, S. C., T. Hume, C. Jakob, et al., 2010: Observed large-scale structures and diabatic heating and drying profiles during TWP-ICE. J. Climate, 23, 57–79. DOI:10.1175/2009JCLI3071.1 |
| Xie, S. C., X. H. Liu, C. F. Zhao, et al., 2013: Sensitivity of CAM5-simulated arctic clouds and radiation to ice nucleation parameterization. J. Climate, 26, 5981–5999. DOI:10.1175/JCLI-D-12-00517.1 |
| Xue, J. S., and D. H. Chen, 2008: Scientific Design and Application of Numerical Forecasting System GRAPES. Science Press, Beijing, 383 pp. (in Chinese) |
| Yang, J. L., and X. S. Shen, 2011: The construction of SCM in GRAPES and its applications in two field experiment simulations. Adv. Atmos. Sci., 28, 534–550. DOI:10.1007/s00376-010-0062-8 |
| Zhang, J. C., and Q. J. Liu, 2006: Analysis of cloud schemes in simulation of short-term climatic process. Meteor. Mon., 32, 3–12. DOI:10.3969/j.issn.1000-0526.2006.07.001 |
| Zhao, C. F., and T. J. Garrett, 2015: Effects of Arctic haze on surface cloud radiative forcing. Geophys. Res. Lett., 42, 557–564. DOI:10.1002/2014GL062015 |
| Zhao, C. F., Y. L. Lin, F. Wu, et al., 2018: Enlarging rainfall area of tropical cyclones by atmospheric aerosols. Geophys. Res. Lett., 45, 8604–8611. DOI:10.1029/2018GL079427 |
 2019, Vol. 33
2019, Vol. 33


