The Chinese Meteorological Society
Article Information
- REN, Pengfei, Li GAO, Hong-Li REN, et al., 2019.
- Representation of the Madden–Julian Oscillation in CAMS-CSM. 2019.
- J. Meteor. Res., 33(4): 627-650
- http://dx.doi.org/10.1007/s13351-019-8118-x
Article History
- Received August 30, 2018
- in final form February 9, 2019
2. Numerical Prediction Center, National Meteorological Center, China Meteorological Administration, Beijing 100081;
3. Laboratory for Climate Studies & China Meteorological Administration–Nanjing University Joint Laboratory for Climate Prediction Studies, National Climate Center, China Meteorological Administration, Beijing 100081;
4. Department of Atmospheric Sciences, School of Environment Studies, China University of Geoscience, Wuhan 430074;
5. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, China Meteorological Administration, Beijing 100081;
6. Institute of Climate System (Polar Meteorology), Chinese Academy of Meteorological Sciences, China Meteorological Administration, Beijing 100081
The main features of the Madden–Julian Oscillation (MJO; Madden and Julian, 1971, 1972) include an eastward-/northward-propagating wave and planetary-scale circulation, with an eastward propagation speed of 5 m s−1 and a dominant period of 30–80 days. As the strongest low-frequency signal in the tropics, MJO has a significant impact on global weather and climate. For example, precipitation (Paegle et al., 2000; Bond and Vecchi, 2003; Barlow et al., 2005; Wheeler et al., 2009; Zhang et al., 2009), temperature (Jeong et al., 2005; Lin, 2015), the global monsoon system (Yasunari, 1979, 1980; Hendon and Liebmann, 1990; Sultan et al., 2003; Lorenz and Hartmann, 2006), tropical cyclone activity (Liebmann et al., 1994; Maloney and Hartmann, 2000; Bessafi and Wheeler, 2006; Klotzbach, 2010; Diamond and Renwick, 2015), and extreme weather events (Jones, 2000; Jones et al., 2004; Xavier et al., 2014; Hsu et al., 2016; Lee et al., 2017; Ren and Ren, 2017; Ren et al., 2018) in different regions and different seasons are all strongly modulated by MJO. As a bridge between deterministic weather forecasting and climate prediction, the MJO’s dominant low-frequency characteristics are considered to be a predictability resource at sub-seasonal timescales (Zhang, 2013), which is an important basis for the concept of “seamless prediction” (Hurrell et al., 2009; Brown et al., 2012).
A realistic MJO simulation is essential for the prediction at the sub-seasonal scale. There has been a significant improvement in the MJO prediction skill during the past decade by using more advanced, fully coupled dynamic climate models (Ren et al., 2015, 2016, 2017; Wu et al., 2016). However, the MJO prediction is still a challenge due to the elusive dynamic mechanisms behind its features (Jiang et al., 2015; Majda and Yang, 2016; Jiang, 2017). In general, the unrealistic features of MJO simulation are mainly reflected in its amplitude (Zhang et al., 2006; Hung et al., 2013; Zhao et al., 2014; Jiang et al., 2015; Ahn et al., 2017), dominant period (Zhang et al., 2006; Kim et al., 2009), eastward propagation (Zhao et al., 2014; Jiang et al., 2015; Jiang, 2017), and vertical tilting structure (Jiang et al., 2015). These MJO simulation biases are usually attributable to the resolution of the model (Hayashi and Golder, 1986; Slingo et al., 1996; Gualdi et al., 1997; Inness et al., 2001; Jia et al., 2008), convective parameterization (Slingo et al., 1996; Wang and Schlesinger, 1999; Maloney and Hartmann, 2001; Zhang and Mu, 2005), diabatic heating (Li et al., 2009), mean state (Slingo et al., 1996; Inness et al., 2003; Sperber et al., 2005; Ajayamohan and Goswami, 2007), and air–sea coupling (Wang and Xie, 1998; Kemball-Cook et al., 2002; Fu and Wang, 2004; Zheng et al., 2004; Sperber et al., 2005; Watterson and Syktus, 2007).
The US Climate Variability and Predictability Program (CLIVAR) developed a standardized diagnosis for MJO to compare simulation capabilities of different models (Waliser et al., 2009). We use this standard diagnosis to evaluate the performance of the Chinese Academy of Meteorological Sciences Climate System Model (CAMS-CSM) in simulating MJO, including the seasonality characteristics, geographical distribution of MJO in winter/summer, dominant wavenumber–frequency, propagation features, and coupling characteristics. The low-level convergence of moisture also plays an important part in the life cycle of MJO and generally promotes the growth of positive moisture anomalies east of the convection, thereby slowly moistening the atmosphere until it reaches a state that is again conducive to the development of convection (Maloney and Hartmann, 1998). The low-level convergence of moisture can therefore be considered as a prerequisite for deep convection in the troposphere (Kikuchi and Takayabu, 2004). The zonal asymmetry of this moisture anomaly mainly occurs in the planetary boundary layer (PBL; 1000–700 hPa), which destabilizes MJO convection and facilitates its eastward propagation (Hsu and Li, 2012; Jiang et al., 2015). Recent studies have shown that the northward propagation of MJO is accompanied by the low-level convergence of moisture ahead of the convection (Jiang et al., 2011; Neena et al., 2017). We also examine several key factors related to the eastward/northward propagation of MJO—including the vertical tilting structure of both moisture and wind and the PBL integral moisture budget—and suggest possible reasons for the detour of MJO over the Maritime Continent.
The paper is organized as follows. An introduction to the model simulations and validation data is given in Section 2. Section 3 presents the strategies and basic results of the MJO simulation. The possible effects of moisture processes on the eastward/northward propagation of MJO are described in Section 4. The summary and discussion are provided in Section 5.
2 Model simulations and validation data 2.1 CAMS-CSMWe evaluate the MJO simulation by using CAMS-CSM, which is a fully coupled model combining atmosphere, ocean, land, and sea ice components. The atmospheric component is ECHAM5 (version 5.4; Roeckner et al., 2003), which has a horizontal resolution of T106 (approximately 1.125°) and 31 vertical layers from the surface to 10 hPa. The oceanic component is the fourth edition of the Modular Ocean Model from Geophysical Fluid Dynamics Laboratory (Griffies et al., 2004). This model has 50 vertical levels with a global zonal resolution of 1°. The meridional resolution is 1/3° within the 10°S–10°N equatorial band, ranging to 1° at 30°S (30°N) with a nominal 1° resolution poleward of 60°N. The sea ice component is the Geophysical Fluid Dynamics Laboratory Sea Ice Simulator, and the land component is the Common Land Model (Dai et al., 2003). A detailed description of the CAMS-CSM model is given by Rong et al. (2018).
2.2 Observational dataWe use various observational data to evaluate the MJO simulation in the 23-yr run of CAMS-CSM, including the outgoing longwave radiation (OLR) from NOAA satellites (Liebmann and Smith, 1996) and daily reanalysis data from ERA-Interim (Dee et al., 2011) of wind speed and specific humidity. The pentad-mean Climate Prediction Center (CPC) Merged Analysis of Precipitation dataset (CMAP; Xie and Arkin, 1997) is also used.
All these observational datasets have a horizontal resolution of 2.5° × 2.5°. To facilitate the comparison of the model results with the observational data, corresponding data for the model were interpolated to obtain a resolution consistent with the observational data. The common period for all the observational datasets is 1981–2003. The summer season is defined as 1 May to 31 October and the winter season is from 1 November to 30 April of the following year.
3 Diagnostic strategy and basic resultsOur goal is to examine the primary features of MJO by using the two-level diagnostic strategies proposed by the CLIVAR MJOWG (MJO Working Group) (Waliser et al., 2009). When verifying the ability of CAMS-CSM to simulate MJO, the intraseasonal variability (ISV) signal is obtained by filtering out days 20–100 by using the Lanczos filter (Duchon, 1979). The daily climatological mean and seasonal cycle (first three annual harmonics) are subtracted before filtering.
3.1 Simulation of ISV characteristicsWe examine the ability of CAMS-CSM to simulate 20–100-day ISVs, including the seasonality characteristics, winter/summer regional dependence, dominant wavenumber–frequency, and propagation characteristics.
3.1.1 Examination of the seasonality of ISVIt is well known that the spatial distribution of ISVs shows a significant seasonality, that is, the winter ISV is mainly concentrated in the equatorial Indian Ocean and western Pacific and its positions are south of the equator, whereas the summer ISVs are mainly concentrated to the north of the equator, showing a clear tendency to migrate northward. This seasonal migration is not well represented in some models (Sperber, 2004; Zhang et al., 2006). Therefore, we first examine the ability of CAMS-CSM to simulate the seasonality of ISVs. The intraseasonal variance of precipitation and U850 of each calendar month averaged over the Indian Ocean (60°–130°E) and western Pacific (130°E–180°) show the seasonal variations in ISV as a function of time and latitude. The most salient feature in the observed seasonal cycle is the south–north migration of the ISV activity, which is reflected in the transitions between boreal winter and summer over both regions (Figs. 1a, c). Here, the ISV variance of precipitation and U850 is centered south of the equator in winter and moves northward to north of the equator in summer. Such a seasonal shift in the ISV variance can be well represented by the model (Figs. 1b, d), suggesting that the model gives a good simulation of the seasonality of ISVs. Given the clear seasonal difference in the distribution of ISVs, it is necessary to assess the ability of the model to simulate MJO signals in each season. We therefore evaluate the capability of the model to simulate MJO signals in both winter (November–April) and summer (May–October).
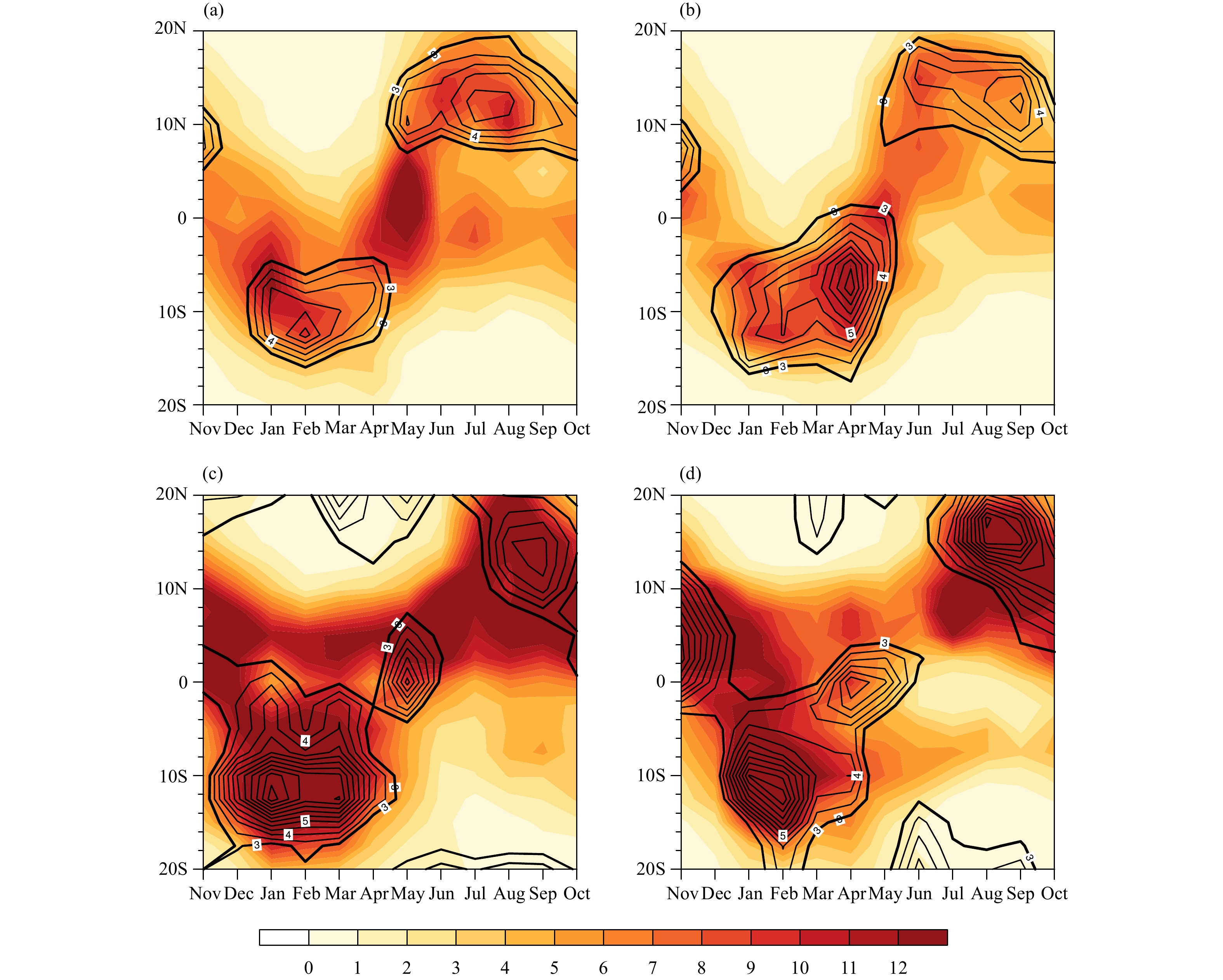
|
| Figure 1 Time–latitude cross-sections of the ISV variance of U850 (contours, interval: 0.5 m2 s−2; thick contours, 3 m2 s−2) and precipitation (shading; mm2 day−2) averaged over (a, b) the Indian Ocean (IO; 60°–130°E) and (c, d) western Pacific (WP; 130°E–180°) from (a, c) observation and (b, d) CAMS-CSM during 1981–2003. |
The spatial distribution and amplitude of the ISV activity are described by the ISV variances of precipitation and U850 during boreal winter (Fig. 2; contours) and summer (Fig. 3; contours). To relate the ISV activity to the corresponding background state, we also give the mean field distribution of precipitation and U850 (Figs. 2, 3; shading).

|
| Figure 2 (a, b) ISV variance of U850 (contours; interval: 2 m2 s−2) and mean of U850 (shading; m s−1) from (a) ERA-Interim and (b) CAMS-CSM; (c, d) ISV variance of precipitation (contours; interval: 8 mm2 day−2) and mean of precipitation (shading; mm day−1) from (c) CMAP and (d) CAMS-CSM for November–April during 1981–2003. |

|
| Figure 3 As in Fig. 2, but for May–October of 1981–2003. |
The strongest ISV of U850 in the observations is located in the south of the Maritime Continent, whereas the second value is located in the tropical western central Pacific and eastern Indian Ocean during boreal winter. Similarly, ISV of precipitation is concentrated in the equatorial eastern Indian Ocean and western Pacific. CAMS-CSM shows a good performance in representing the ISV variance of both U850 and precipitation, performing well for both the intensity center and amplitude. The model bias in ISV of precipitation is featured by a separation in western Pacific, with two centers on both sides of the equator. The model clearly simulates U850 better than precipitation during boreal winter, indicating that the coherence of precipitation and wind field in the model is slightly weaker than in the observations. No strong ISV signal was found over the Maritime Continent, tropical South America nor Africa, despite of the strong mean precipitation and U850 in these regions. Many previous studies have attempted to explain these features (Salby et al., 1994; Wang and Li, 1994; Maloney and Sobel, 2004; Zhang et al., 2006). It is probable that the land surface, especially complex terrains, affects the amount of energy absorbed by MJO from surface evaporation and moisture convergence. Locations of the largest ISV variance of U850 and precipitation move northward in boreal summer and these migrations are well captured by CAMS-CSM. Similarly, The model simulates U850 better than precipitation in boreal summer, and the main bias of precipitation is located in western Pacific, where the model overestimates ISV of precipitation in the North and South Pacific convergence zones.
Further investigation of the relationship between the ISV and background state indicated that there is a close relationship between the ISV variance and mean fields, that is, the ISV signal has a tendency to appear in the strong (weak) westerly (easterly) belts and in ocean areas with abundant precipitation. Both the observational data and model simulation have these characteristics, indicating that ISV has a strong dependence on the corresponding background, confirming the link between them (Slingo et al., 1996; Inness and Slingo, 2003). In other words, if a model does not simulate the distribution of climatic mean states well, its ability to simulate ISV signals may be weakened. Such a close relationship between the ISV and climatic mean state is highlighted in Fig. 4, which shows the difference between the model simulations and observations in Figs. 2, 3. The ISV signal is more likely to occur in the area of the westerly anomaly and for large values of precipitation. The CAMS-CSM simulation gives values for precipitation in the Northern Hemisphere intertropical convergence zone (ITCZ) and South Pacific convergence zone that are larger than the observational data, referred to as the double ITCZ phenomenon. The excessive precipitation in the model also leads to an overestimation of the amplitude of ISV, further confirming the dependence of ISV on the mean state.

|
| Figure 4 (a, b) The difference between CAMS-CSM and ERA-Interim for ISV variance of U850 (contours; interval: 1 m2 s−2) and mean of U850 (shading; m s−1); (c, d) the difference btween CAMS-CSM and CMAP for ISV variance of precipitation (contours; interval: 10 mm2 day−2) and mean of precipitation (shading; mm day−1) in (a, c) winter and (b, d) summer during 1981−2003. |
The spatiotemporal spectrum (Hayashi, 1979; Wheeler and Kiladis, 1999) emphasizes the existence of eastward-propagating signals on intraseasonal and planetary scales, which are fundamental features of MJO within the equatorial belt. Because the MJO signal is usually stronger and shows a more significant eastward propagation in boreal winter than in other seasons, our assessment focused on this period. Figure 5 shows the wavenumber–frequency spectra of the equatorial precipitation (Figs. 5a, b), OLR (Figs. 5c, d), and U850 (Figs. 5e, f) anomalies in boreal winter.

|
| Figure 5 Wavenumber–frequency spectra of the zonal mean of (a, b) precipitation, (c, d) OLR, and (e, f) U850 from (a) CMAP, (c) NOAA-OLR, (e) ERA-Interim, and (b, d, f) CAMS-CSM over the equatorial region (10°S–10°N) in winter during 1981–2003 with the climatological seasonal cycle subtracted from the simulation. The vertical dashed lines from left to right in each panel represent the periods of 80, 45, 30, and 20 days (80–20 days), respectively. The number on the top right of each panel indicates the ratio of eastward- to westward-propagation components (E/W ratio) of the MJO band. |
The east/west (E/W) ratio obtained by dividing the eastward-propagating component of the MJO band (days 30–80 and wavenumbers 1–3) by its westward-propagating component has been widely used in both observational (Zhang and Hendon, 1997) and modeling studies (Lin et al., 2006; Kim et al., 2009; Li et al., 2016; Ahn et al., 2017) to examine the robustness of the eastward propa-gation of MJO. It is applied in this study to test the performance and to give a quantitative evaluation of the model simulations.
In the observations, the spectral peaks of precipitation and OLR are concentrated in zonal wavenumbers 1–3 and timescale of the 30–80-day period, whereas the peak U850 is concentrated in wavenumber 1—that is, the zonal scale of U850 is larger than those of precipitation and OLR, which is in agreement with previous results (Zhang et al., 2006; Waliser et al., 2009; Li et al., 2016). In general, the model gives a reasonable simulation of the MJO spectrum band, on which the eastward-propagating power of precipitation, OLR, and U850 are much greater than that of the westward-propagating power. Compared with previous studies, this model gives an encouraging simulation of the spatiotemporal scale of MJO (Kim et al., 2009; Li et al., 2016; Ahn et al., 2017). However, although the model can simulate the main features of the MJO scale, such as the intraseasonal signal and eastward-propagating direction, there are still some systematic deviations. The model bias includes the following features. (1) The E/W ratio is weakened, and the precipitation, OLR, and U850 show a slight decrease in the ratio of eastward- to westward-propagating power, indicating that the MJO eastward-propagating features in the model are slightly weaker than those in the observational data. (2) Unrealistic low-frequency timescales with spectral peaks in the model shift to a lower frequency than the observed 30–80-day timescale. (3) There is more spreading of spectral peaks on the spatial scale. For example, the spectral peaks of precipitation and OLR are concentrated in wavenumbers 1–3 in the observational data, but extend to wavenumbers 4 and 5 in the model simulations. For U850, spectral peaks in the observation data are mainly concentrated in wavenumber 1, but the counterparts of the model can extend to wavenumbers 2 and 3.
3.1.4 Propagation characteristicsOne of the notable characteristics of MJO that is distinguished from other variabilities lies in its propagation features. During winter, this is mainly the eastward propagation, described in the spatiotemporal analysis of the spectrum, whereas in summer there is also significant northward propagation. This section presents the ability of CAMS-CSM to simulate the propagation characteristics of ISVs based on a lagged regression analysis. The spatial distributions of the regression coefficients are obtained by using filtered values for OLR and U850, and the OLR anomaly averaged over the Indian Ocean (5°S–5°N, 75°–85°E) and western Pacific (5°S–5°N, 130°–150°E). Figure 6 shows the time evolution of OLR and U850 along the equator for both observations and model simulations against the Indian Ocean and western Pacific base points in boreal winter. The main observational features show the eastward propagation in both OLR and U850, in which OLR is mainly confined to the Eastern Hemisphere with a propagation speed of 5–6 m s−1. In the Eastern Hemisphere, the propagation speed between U850 and OLR is equivalent, but after crossing the dateline, the eastward transmission of U850 is clearly accelerated. Signals of OLR and U850 show a 90° phase shift in the Indian Ocean, with the anomalous westerly wind lagging behind a negative OLR anomaly by about 5–7 days. When MJO enters the western Pacific region, the negative OLR anomaly is almost synchronized with U850, and the strongest convection is mainly controlled by westerly winds (Hendon and Salby, 1994; Zhang et al., 2006).

|
| Figure 6 Longitude–time evolutions of OLR (shading; W m−2) and U850 (contours; interval 0.2 m s−1) anomalies by lagged regression of ISV of OLR and U850 along the equatorial region (10°S–10°N) against (a, b) the Indian Ocean base point (5°S–5°N, 75°–85°E) and (c, d) western Pacific base point (5°S–5°N, 130°–150°E) from (a, c) observational data and (b, d) CAMS-CSM in winter during 1981–2003. The thick blue lines represent the eastward-propagating track of OLR, and their slopes are defined as the propagation speed with the value shown on the top right of each panel. |
CAMS-CSM can reproduce the typical features of the observed MJO propagation well. In the model, the eastward propagation of OLR and U850 in the Eastern Hemisphere are clear and the only difference is seen in the propagation speed. CAMS-CSM tends to produce a slower speed than the observational data, which is consistent with the results of the wavenumber–frequency spectrum in Fig. 5. The coherence of U850 and OLR is also simulated reasonably well in the model, where the lag effect in the Indian Ocean region and asymptotic synchronization in western Pacific between the westerly winds and OLR are captured well by the model.
MJO shows northward/northeastward propagation over the Indian summer monsoon region (Yasunari, 1979; Krishnamurti and Subrahmanyam, 1982; Lau and Chan, 1986; Annamalai and Sperber, 2005; Lee et al., 2013) and a northward/northwestward propagation over western North Pacific (Kemball-Cook and Wang, 2001) in boreal summer. Figure 7 shows the ability of the model to simulate the poleward propagation of MJO in these two regions. Using the results for the Indian Ocean base point (0°–10°N, 85°–90°E; Fig. 7a), both OLR and U850 show a significant northward propagation. The enhanced convective anomaly is first formed near the equator on day 0, and then propagates poleward from days 0 to 10 at the speed of 1.98 m s−1, reaching about 20°N. The convection around the equator in the Southern Hemisphere shows a southward trend, although this is not completely clear. Using the results for the western Pacific base point (0°–10°N, 135°–140°E; Fig. 7c), the northward propagation of OLR and U850 is as clear as that in the Indian Ocean, although the southern tropical band does not show any sign of southward propagation. Good coupling can be observed between the U850 and OLR results as the MJO convection propagates from 0° to 10°N. However, the center of U850 gradually detaches from the convection as it is further from the equatorial region. This may be why the MJO propagation slows down in this region and then gradually disappears.

|
| Figure 7 Latitude–time evolutions of OLR (shading; W m−2) and U850 (contours; interval 0.2 m s−1) anomalies against (a, b) the Indian Ocean base point (0°–10°N, 85°–90°E) and (c, d) western Pacific base point (0°–10°N, 135°–140°E) from (a, c) observational data and (b, d) CAMS-CSM in summer during 1981–2003. The regressed anomalies are averaged over 80°–100°E and 130°–150°E, respectively. The thick blue lines represent the northward-propagating track of OLR, and their slopes are defined as the propagation speed with the value shown on the top right of each panel. |
Unfortunately, the poleward propagation of MJO in these two regions is not well represented by the model. However, the simulation of northward propagation in the Indian Ocean is much better than the simulation in the western Pacific region. A more reasonable configuration between U850 and convection in the Indian Ocean may account for the better simulation of northward propagation in this region. The coupling between U850 and convection in the western Pacific region is not captured in the model. However, the ability of CAMS-CSM to simulate the northward propagation of MJO is better than simulations of CESM (Li et al., 2016), CCSM3, CGCM3.1 (T47), CGCM3.1 (T63), FGOALS-g1_0, GIS-AOM, and IPSL-CM4 models (Sperber and Annamalai, 2008), suggesting that the simulation of the northward propagation of MJO during summer is relatively difficult.
In conclusion, CAMS-CSM can successfully simulate the eastward propagation of MJO, but shows a weak simulation of the northward propagation of MJO during boreal summer. Comparing the two areas (the Indian Ocean and western Pacific), CAMS-CSM can simulate the northward propagation of MJO in the Indian Ocean, but the speed of northward propagation is slower than the observed propagation. The simulation of northward propagation of MJO in western Pacific is distorted, indicating that there is still much room for improvement in the model.
3.2 Coherent features of the MJOEvaluations discussed so far in this paper have focused on univariate ISVs, but classical MJO structures typically appear as interactions between the circulation and convective field, such as the configuration between upper/lower winds and convection. Therefore, this section focuses on these coherent features of MJO, especially the results of the multivariate combined empirical orthogonal function (MCEOF) analysis. The resulting principal components can be used to generate composites during the MJO life cycle, and the unfiltered principal components obtained by projecting the unfiltered anomaly data into the EOF mode can be used to verify whether the extracted MJO modes are physically meaningful and are distinct from noise (Subramanian et al., 2011).
3.2.1 Cross-spectra analysisCross-spectra analysis is applied to examine the coherence as well as phase lag between the circulation and convection (Fig. 8), which are presented separately for the symmetrical and asymmetrical components of each field (Wheeler and Kiladis, 1999; Hendon and Wheeler, 2008). We show a magnified display of the spectra of MJO band to highlight details in the MJO space–time scale.

|
| Figure 8 Cross-spectral analysis between U850 and OLR from (a–c) observational data and (d–f) CAMS-CSM during 1981–2003. Shadings and vectors indicate the square of the coherence and phase lag between U850 and OLR, respectively. The upward directed vector indicates a zero phase lag and increases in the clockwise direction. (a, d) and (b, e) The symmetrical components, and (c, f) the asymmetrical components of cross spectrum with details of the MJO band highlighted in (b, e) and (c, f). Spectra were computed for each latitude, for 256 consecutive days, overlapping two adjacent time periods by 206 days, and then averaged near the equatorial region (0°–10°N). The dispersion straight lines and curves superimposed on the graphs represent (n = –1) Kelvin, (n = 1) equatorial Rossby (ER), and (n = 1) inertia-gravity (IG) waves, corresponding to three equivalent depths h = 12, 25, and 50 m, respectively, from down to up in the shallow water equations. MJO is defined as a spectral component in the wavenumber range 1–3, with a period of 30–80 days, as indicated by the white dotted boxes. |
The symmetrical component is the first-order characteristics of the observed MJO. The most prominent feature in the observational data is the peak coherence of the 30–80-day period and wavenumbers 1–3 associated with MJO. For the MJO peak, the southwest-pointing vectors imply that positive westerly (easterly) anomalies lag the suppressed (enhanced) convection by about 235°. Another interpretation is that westerly (easterly) MJO wind anomalies lag the enhanced (suppressed) convection by about 1/8 cycle, or equivalently by about 5 days, which is consistent with previously reported results (Wheeler and Kiladis, 1999; Hendon and Wheeler, 2008; Subramanian et al., 2011; Li et al., 2016). Compared with the observational data, CAMS-CSM produces strong coherence in this low-frequency band and shows a similar phase lag relationship between U850 and OLR signals. However, for wavenumbers 1 and 2, the large value of the simulated peak shifts toward a lower frequency than the observational data with roughly an 80-day period. The coherence at wavenumbers 2 and 3 of the model is stronger than that for the observational data, indicating that the zonal scale is smaller than that for the observational data. However, the symmetrical part of the cross-spectrum may contain the equatorial Kelvin wave signal (Hendon and Wheeler, 2008).
To distinguish the signal of the MJO band from the Kelvin wave, the corresponding asymmetrical part of MJO band can exclude the signal of the linear Kelvin wave (Fig. 8). Both the observational data and model show large coherence values for the MJO band with a wavenumber of 1, indicating that this high coherence is a significant MJO behavior rather than a linear Kelvin wave. Similarly, a shift to a lower frequency of the coherent peak and stronger coherence at wavenumbers 2 and 3 than seen in the observational data also exist in the asymmetrical component. In addition, in the previous analysis of the eastward propagation (Fig. 6), we concluded that the propagation speed is slower in the model than that in the observational data. The cross-spectrum analysis shows that there is a weaker (stronger) Kelvin (Rossby) wave in the model than that in the observational data, which may explain the slower propagation in the model.
To sum up, the model gives a better simulation of the eastward propagation of MJO, and shows strong coherence with observations in the MJO space–time band. However, the simulated propagation is shifted toward a lower frequency, which implies a slower propagation speed than in the observed data, consistent with the results in Figs. 5, 6.
3.2.2 MJO mode from MCEOF analysisWheeler and Hendon (2004) invented the real-time multivariate MJO index by using MCEOF analysis to monitor and predict the MJO activity in real time, which was shown to effectively capture the salient features of MJO and is now widely used in MJO simulations (Kim et al., 2009; Waliser et al., 2009; Li et al., 2016). The index has no filtering variable (only the first three annual harmonics and interannual variability are removed) for real-time monitoring and prediction purposes in the study of Wheeler and Hendon (2004). However, in order to fully highlight the MJO band, we used the 20–100-day bandpass filtered data to facilitate the isolation of MJO modes, as in Waliser et al. (2009).
Figure 9 shows the meridional mean distribution of the 20–100-day OLR and 850- and 200-hPa zonal winds in the first two spatial modes derived from MCEOF analysis by using the observational data during 1981–2003 and performing the 23-yr run of CAMS-CSM over 15°S–15°N. EOF1 captures the enhanced convective activity over the eastern Indian Ocean and Maritime Continent in the observational data, whereas EOF2 captures the enhanced convection in the western/central Pacific Ocean and suppresses convection in the Indian Ocean. The first two modes together account for 43.8% of the filtered variance and are completely separated from the other modes based on criteria of North et al. (1982). The zonal winds in the upper (U200; blue line) and lower (U850; red line) troposphere are out of phase with each other. Specifically, the strong convection of EOF1 is located at 90° E and the corresponding high- and low-level winds are also inversed at the same longitude. For U850, the west (east) side of enhanced convection is the westerly (easterly) anomaly, so the dynamic field converges in the lower troposphere. By contrast, a westerly (easterly) anomaly of U200 occurs to the west (east) of the enhanced convection, accompanied by high-level divergence. As the convection moves eastward to the vicinity of 150°E (EOF2), the associated wind fields also move eastward to the adjacent area and maintain the baroclinic structure. The coupling between OLR and wind fields forms the most classic structure of MJO. Mode 2 from the observational data corresponds to mode 1 of the model.
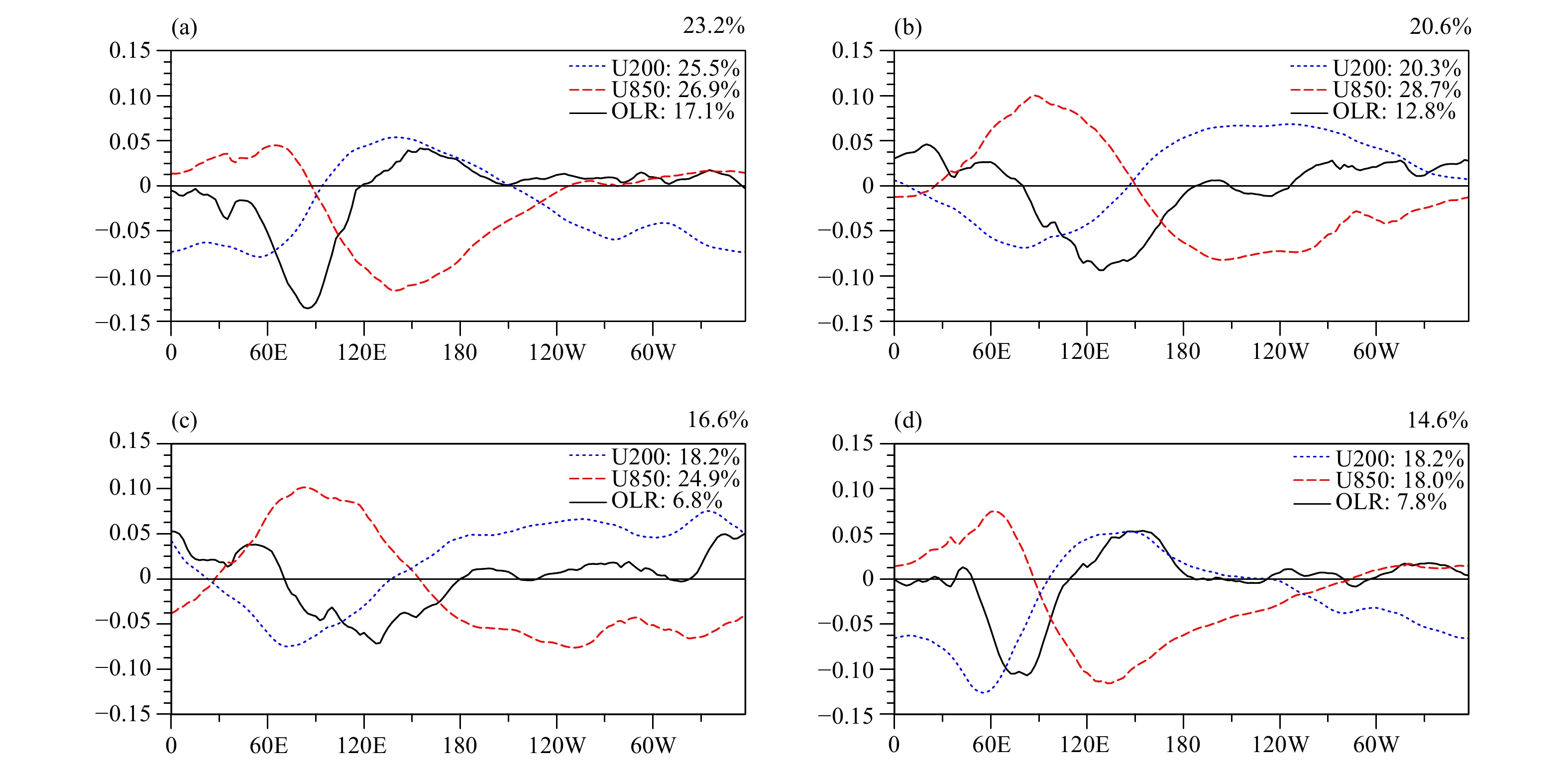
|
| Figure 9 The meridional mean distribution of the 20–100-day OLR (black solid line) and 850- (red dashed line) and 200-hPa (blue dotted line) zonal winds in the first two EOF modes: (a, c) EOF1 and (b, d) EOF 2 of MJO from (a, b) the observational data and (c, d) CAMS-CSM over 15°S–15°N for all season during 1981–2003. The percentage above each panel on the top right is the variance contribution of the EOF mode. The percentages in the upper right corner of each panel are the explained variance of each variable. The sign and order of each eigen mode in the model are adjusted to be similar to the observational data |
The fundamental features of MJO, including the location of enhanced convection and the maximum and minimum wind fields, are reasonably captured by CAMS-CSM. For example, convection is mainly confined to the Eastern Hemisphere, while the wind fields in the Western Hemisphere retain a large amplitude. The baroclinic structure between the upper and lower winds and their coupling to the convective field, such as the configuration of the upper and lower winds on both sides of the convection, are well simulated by the model. However, the overall variance accounted for by each EOF in the model is smaller than the variance in the observed fields because many climate models have smaller amounts of variance in the convective field than those in the observed field and calculation of the variance of individual fields occupied by EOF, especially for OLR, is recommended. The diagnosis of the explained variance of OLR in each EOF can provide a quantifiable measure for the ability of the model to faithfully simulate the strength of MJO (Waliser et al., 2009). The variance contribution of the filtered OLR is about 12%–18% in the observations, but only 6%–8% in the model, a significant reduction of about 50%. This means that the amplitude of OLR is greatly weakened in the model.
The lead–lag correlation between the time series of the first two principal components (PC) provides a measure of coherence for the eastward-propagating MJO (Fig. 10a). The lag time is the time that it takes for MJO to transition from the Indian Ocean to western Pacific (EOF1 to EOF2 in the observational data or EOF2 to EOF1 in the model) and it is equal to about one-fourth of the period of MJO. In the observational data, we found that the correlation coefficient of PC1 leading PC2 reached a maximum value of 0.77 on day −10 and reached a minimum value of −0.78 when PC1 lagged PC2 on day 10. This indicates that the dominant period is roughly 40 days in the observational data, which is consistent with previous studies (Sperber et al., 2005; Waliser et al., 2009; Subramanian et al., 2011). The model can grasp the lead–lag correlation between the first two principle components and show a roughly 40-day period similar to the observational data, with the absolute value of peak correlation coefficient > 0.6 occurring at ± 10-day lags in CAMS-CSM, which indicates that the model is good at simulating the eastward-propagating characteristics of MJO.
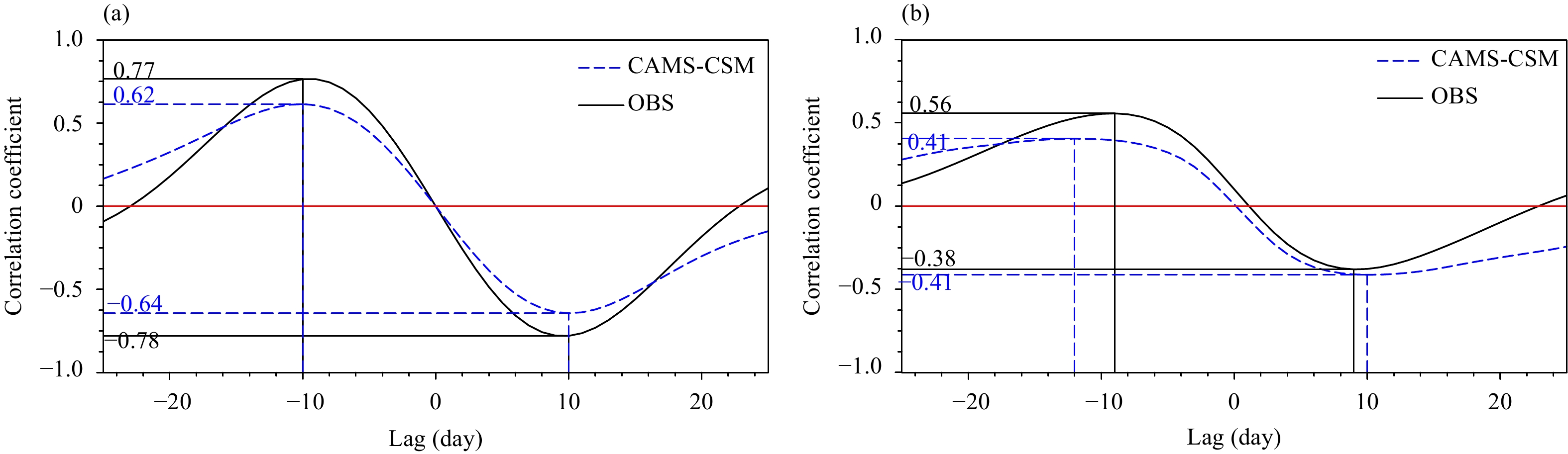
|
| Figure 10 (a) Lead–lag correlation coefficients between the first two principle components PC1 and PC2 from the observational data (black solid line) and CAMS-CSM (blue dashed line) by projecting (a) the filtered anomaly data and (b) the unfiltered anomaly data onto the eigenvector of the MCEOF |
This MCEOF analysis is based on filtered data, which contains some flaws, for example, it may misinterpret the red or white noise of the intraseasonal period as physically meaningful intraseasonal oscillations with a similar structure to the leading EOFs. Therefore, another crucial test of our results is needed to verify whether the two EOF modes derived from the MCEOF analysis are physically meaningful and distinct from noise. Figure 10b also shows the lead–lag correlation of the first two principle components formulated by projecting the unfiltered anomaly data onto the two leading EOFs. Use of unfiltered data has a benefit over use of filtered data as it examines the model’s ability to simulate intraseasonal signals. If a model simulation has a lower frequency variability than the observational data, as shown in Fig. 8, but with a similar spatial pattern to MJO, then this it will be seen in the lead–lag correlation using unfiltered data (Ahn et al., 2017). We can see that the peak correlation between the two principle components decreases sharply in both the observational data and model simulation relative to the results calculated by the filtered data. The dominant timescale of the intraseasonal signal in the model is also larger than that in the observational data, and the minimum and maximum lag coefficients appear on days 10 and −12, respectively. We can conclude from the lead–lag correlation analysis that the model can simulate the MJO timescale well, but on a lower frequency timescale than the observational data, which is in agreement with the results of Fig. 8.
We also investigated whether the extracted MJO modes are significantly distinct from noise by performing a power spectrum analysis of the unfiltered principle components (Fig. 11). If the power spectra for the unfiltered data exhibit statistically significant peaks on the MJO timescale, then the extracted EOFs can be assumed to represent meaningful MJO modes. For the first two principle components in the observations, the spectrum shows a prominent peak on the MJO timescale of 30–80 day, with the explained variances of about 52% and 46%, respectively. A similar peak at the 30–80-day period is also found in the model simulation, with the explained variances of about 37%–39% in both principle components. We also found that the spectral peaks in the MJO band in the model shift toward lower frequencies than those in the observational data.

|
| Figure 11 Time series spectrum of the first two principle components (a, c) PC1 and (b, d) PC2 (black solid line) of MJO from (a, b) the observational data and (c, d) CAMS-CSM by projecting unfiltered data onto the eigenvector of the MCEOFs. The percentage on the top right of each panel is the explained variance of the PC mode on the MJO time scale of 30–80-day. The red noise spectrum is denoted by the red dashed line with the upper limits of the 90% and 95% confidence interval denoted by the green dotted line and yellow dash-dotted line, respectively. |
Wheeler and Hendon (2004) showed that the leading EOFs are independent of the season. Therefore the life cycle of MJO can be obtained through composite analysis during boreal summer and winter and compared with the model simulations to assess the ability of the model to simulate the phase propagation structures of ISV (Figs. 12, 13). The composite is constructed by using only the days with (PC12 + PC22) > 1, when MJO is strongly activated.
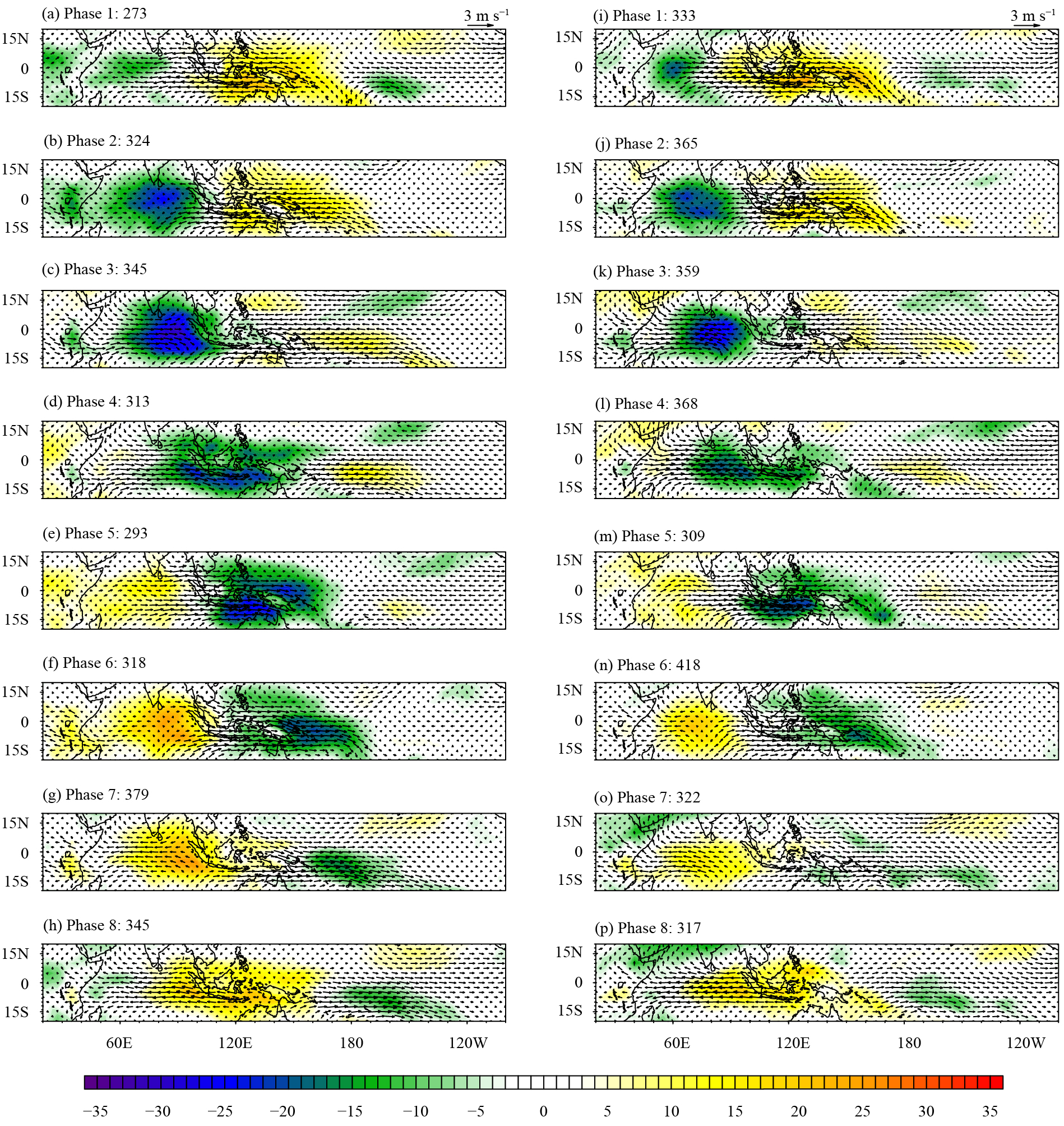
|
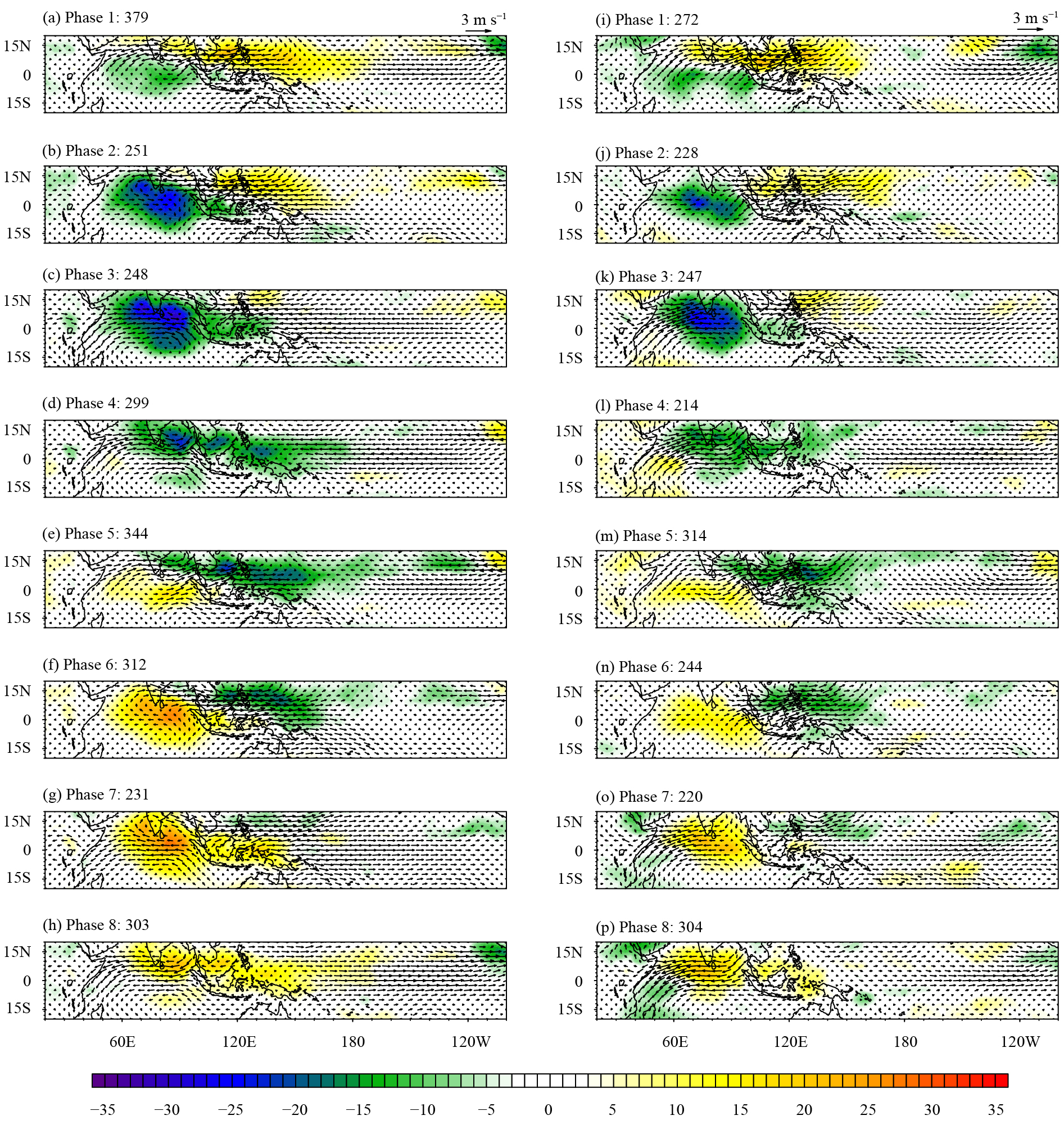
| Figure 12 Evolutions of the filtered OLR (shading; W m−2) and 850-hPa wind (vectors) with MJO phases 1–8 from (a−h) the observational data and (i−p) CAMS-CSM in boreal winter during 1981−2003. The number after each phase indicates the number of days used to generate the composite to the phase. The reference vector (3 m s−1) of the 850-hPa wind is indicated on the top right of left and right panels. |
|
| Figure 13 As in Fig. 12, but for boreal summer |
Observations in winter show that convection originally forms in the western Indian Ocean and is enhanced during the eastward propagation. Convection is weakened when crossing the Maritime Continent, after which it is strengthened again in the western Pacific region, then gradually weakens during further eastward propagation and disappears near the dateline. In general, the model produces a continuous propagation phase associated with MJO, which is similar to the phase distribution in the observational data. We also found that the model reasonably simulates the clear southward detour (Wu and Hsu, 2009), as documented in the observations when MJO passes through the Maritime Continent. CAMS-CSM shows a more organized pattern for OLR and more realistic detour-propagating components across the Maritime Continent than similar composites reported by Subramanian et al. (2011) for CCSM4 and Li et al. (2016) for CESM. Based on the results in Fig. 6, speed of the eastward propagation of convection in the model is slower than that in the observational data. We found a similar bias in the model simulation during the composite analysis of the MJO life cycle. The eastward propagation of convection in the model is slower than that in the observational data in phases 1–3 and then abruptly accelerates in phases 4–6, resulting in a more non-uniform phase speed in the model.
The eastward propagation of MJO in boreal summer is weakened in both the observational data and model, and is not as clear as in boreal winter. It is characterized by the northward propagation of OLR and U850, consistent with the results shown in Fig. 7. From the perspective of coupling between the wind and OLR, the northeasterly propagation is accompanied by the enhanced convection during phases 1–3 of MJO when it enters India and the Bay of Bengal. The convection and wind then spread to the northeast in the vicinity of the South China Sea and Philippine Sea during MJO phases 3–5. CAMS-CSM generally shows a good simulation of the phase propagation characteristics of MJO in boreal summer. However, similar to that in winter, the model’s bias is mainly reflected in the strength of convection, which is weaker in the model than that in the observational data.
4 Role of low-level moistening ahead of MJO convectionIn theoretical studies, the conditional instability of the second kind, namely the wave-CISK is considered to be the most important mechanism for maintaining MJO (Wang, 1988; Salby et al., 1994) and requires the presence of moisture in the PBL converging to the east of the area of deep convection. Many studies have documented the vertical structure of MJO (Sperber, 2003; Kiladis et al., 2005; Sperber et al., 2005; Kim et al., 2009; Jiang et al., 2011, 2015; Li et al., 2016), and the low-level convergence of moisture is considered to be a prerequisite of deep convection (Kikuchi and Takayabu, 2004). We therefore explored the moisture process, to which the propagation of MJO is closely related.
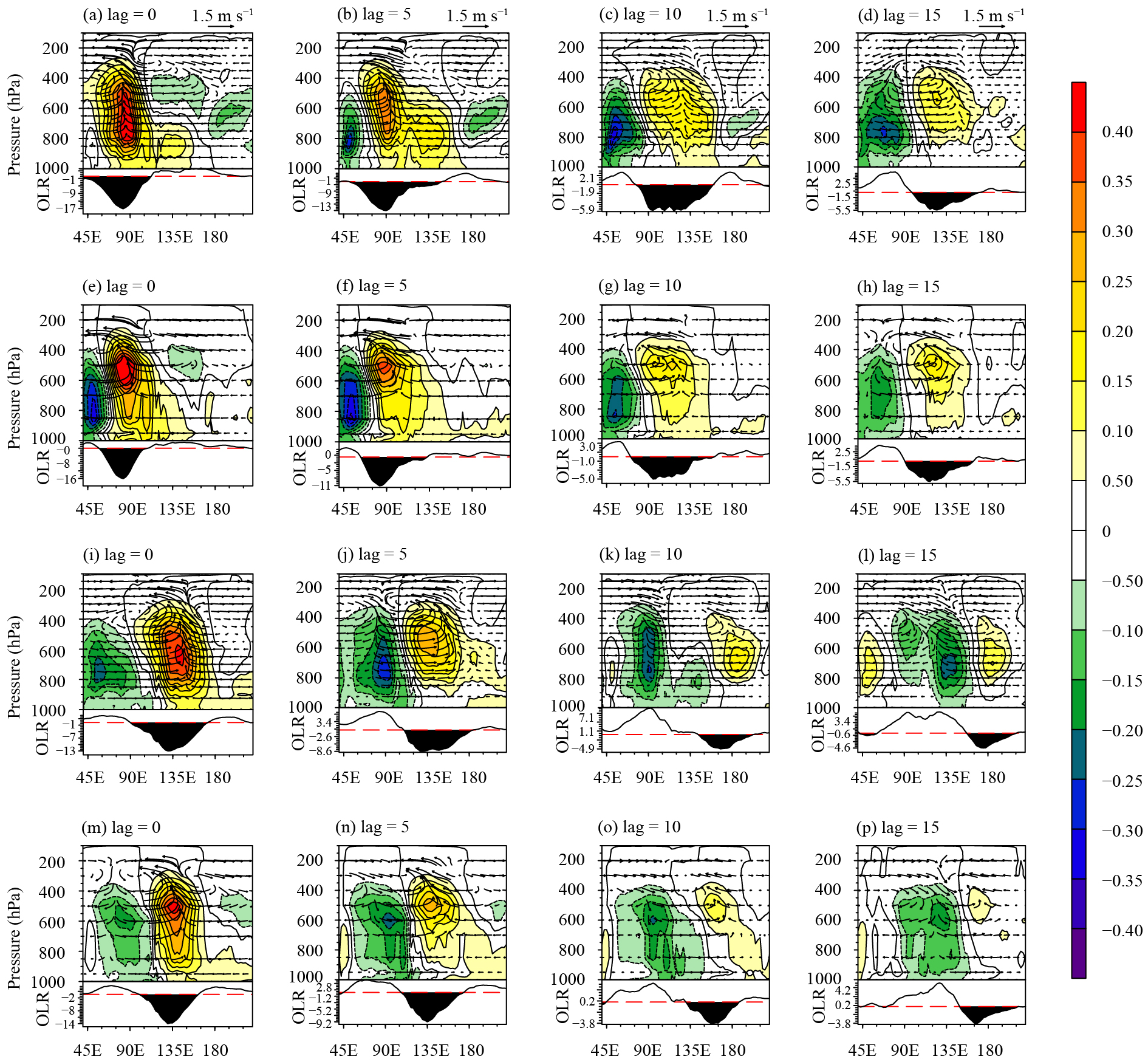
Figure 14 shows the vertical–longitudinal profiles of the zonal wind (U), vertical velocity (W), and specific humidity (Q) onto the 20–100-day filtered OLR averaged over the base points of the Indian Ocean (5°S–5°N, 75°–85°E) and western Pacific (5°S–5°N, 135°–140°E) based on lagged-regression analysis. It reveals the association between the vertical structure of the observed moisture content and MJO from the observational data and CAMS-CSM. Since the eastward propagation of MJO is more dominant in winter than that in summer (Figs. 12, 13), our analysis of the vertical structure for eastward propagation only focuses on boreal winter. Low-level moistening ahead of the convection can be clearly seen in both the observational data and model simulations during the evolution of propagation of MJO from the Indian Ocean to western Pacific based on the Indian Ocean base point (Figs. 14a–h). The vertical tilting structure of the U/W wind and top-heavy profile of Q are also well represented in CAMS-CSM. Correct simulation of the vertical structure of these variables is considered to be a key factor in simulating the eastward propagation of MJO (Jiang et al., 2015), which may explain why the MJO propagation can be simulated well in CAMS-CSM. Similar vertical tilting structures and a good model simulation can also be found for the western Pacific base point during the eastward propagation of MJO from western Pacific to the dateline (Figs. 14i–p).
|
| Figure 14 Vertical–longitudinal profiles of the lag-regressed zonal specific humidity (shading) and U/W wind (vectors) anomalies onto the 20–100-day OLR over (a–h) the Indian Ocean (5°S–5°N, 75°–85°E) and (i–p) western Pacific (5°S–5°N, 135°–140°E) base points from (a–d, i–l) the observational data and (e–h, m–p) CAMS-CSM. The lag days of 0, 5, 10, and 15 are indicated from the left to right panels sequentially. The OLR anomaly (W m–2) below each plot shows the active area of convection. All variables are averaged over the region 10°S–10°N when regressed over the Indian Ocean and western Pacific base points, respectively. |
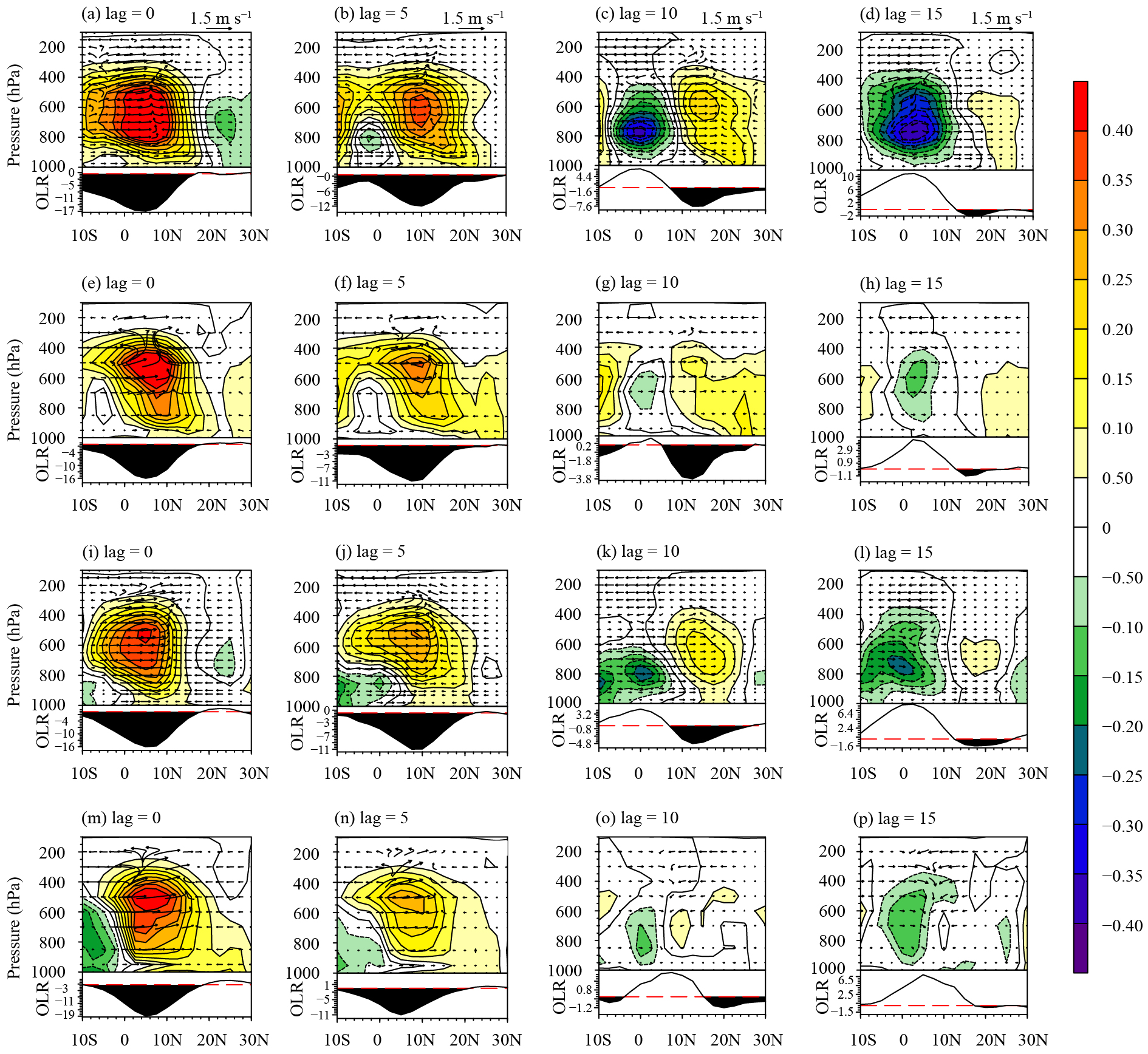
Northward propagation is also noticeable in MJO, especially during boreal summer (Fig. 7). CAMS-CSM shows the northward propagation of MJO based on the Indian Ocean base point, but has difficulty in simulating the slow and continuous propagation of the western Pacific base point. Different capabilities in simulating the northward propagation between the Indian Ocean and western Pacific base points provide an opportunity to illustrate the key physical processes associated with MJO. Figure 15 shows the vertical structures of MJO during its northward propagation. A low-level moistening ahead of convection occurs when MJO propagates north from the equator to near 20°N based on the Indian Ocean base point during lag days 0–15 (Figs. 15a–h). In addition, a clear southward tilt with height is observed in the U/W wind with a westerly (easterly) anomaly on the south (north) side of the convective center. Meridional shear of the zonal wind produces a positive vorticity in front of the convection, resulting in the low-level convergence of moisture, which in turn provides favorable conditions for the northward propagation of MJO. Comparing the simulation results of CAMS-CSM with the observational data, we find that the vertical structures of Q and U/W winds are well represented in the model. A previously reported study has shown that the exact representation of vertical structures in the Q field plays a key part in the ability of the model to simulate the northward propagation of MJO (Neena et al., 2017). In view of the successful simulation of the vertical structure of MJO by using the Indian Ocean base point of CAMS-CSM, the model also shows a good performance in simulating the northward propagation of MJO in the Indian Ocean region (Figs. 7a, b). A much poorer structure is simulated in CAMS-CSM for the western Pacific base point (Figs. 15i–p). Specifically, the simulated Q and U/W winds in the model precede convection much more than those in the observational data during the lag days 0–5, which agrees well with the faster propagation seen in Figs. 7c, d. After lag day 10, the near-disappearance of the convergence of moisture in the model is not conducive to the further northward propagation of MJO, which leads to the poor simulation of northward propagation in western Pacific (Figs. 7c, d).
|
| Figure 15 As in Fig. 14, but for vertical–latitudinal profile of lag-regressed meridional specific humidity (shading) and U/W wind (vectors) anomalies. |
Figure 14 shows that low-level moisture anomalies usually precede convection in the Indian Ocean and western Pacific, but are usually in phase in the mid- to upper-troposphere. Therefore, the preceding effect of low-level moisture anomalies provides a potential instability layer on the east side of convection, which in turn promotes the eastward propagation of MJO (Hsu and Li, 2012, Adames et al., 2016). We can find the phenomenon known as the MJO detour (Kim et al., 2017) in the life cycle of MJO (Fig. 12), which is characterized by stronger convection in Sumatra, Java, and southern Timor Sea than elsewhere in Indonesia. Successful simulation of the MJO detour in CAMS-CSM provides a good opportunity for us to understand the interaction between the MJO and Maritime Continent. We analyzed the budget of the integral moisture in PBL of the observational data and model to further examine the physical processes of moistening ahead of convection, which is of great significance in understanding the eastward propagation, especially the detour characteristics of MJO, and in improving the model capability to simulate MJO.
The intraseasonal, vertically integrated specific humidity budget can be expressed as
| $ \frac{{\partial {{\left\langle q \right\rangle }^\prime }}}{{\partial t}} = - {\left\langle { { V} \cdot \nabla q} \right\rangle ^\prime } - {\left\langle {\omega \frac{{\partial q}}{{\partial p}}} \right\rangle ^\prime } - \frac{{{{Q}_2}'}}{L}, $ |
where q (g kg−1) is the specific humidity;
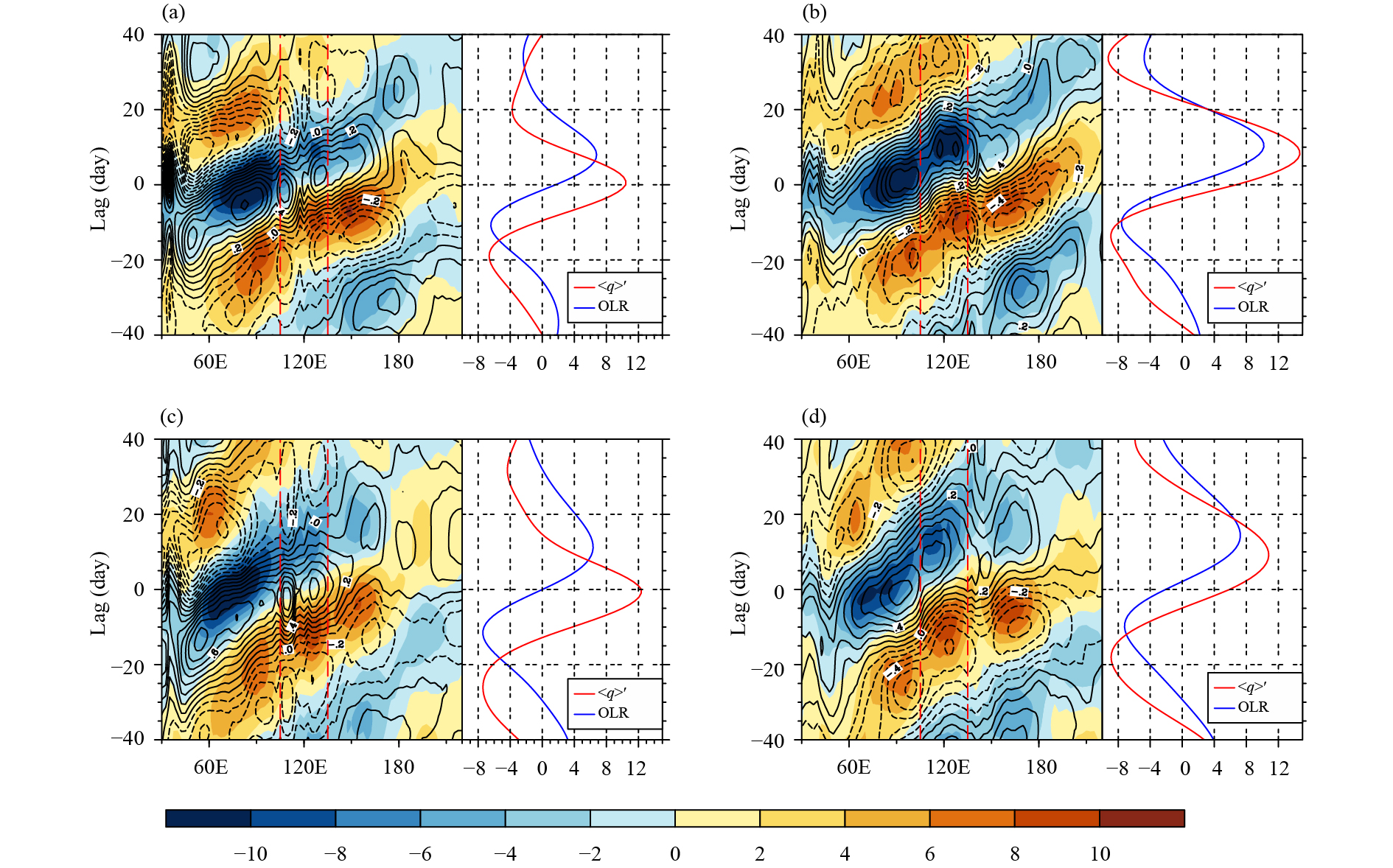
Figure 16 shows the lagged regression of the convection and PBL integral (1000–700 hPa) moisture anomalies based on PC1 (model PC2) calculated from Fig. 9. Good coupling between OLR and moisture can be found in both the model and observational data, with the low-level moisture converging ahead of the convection by 0–10 days. As the enhanced convective anomaly propagates toward the Maritime Continent, these areas experience a transition to an enhanced condition in both latitude bands (lag days −15 to 5). Amplitude of the shift is markedly different between the two latitude bands and shows a much stronger transition in the southern Maritime Continent (sMC; 15°–5°S) than that in the central Maritime Continent (cMC; 5°S–5°N). A much slower eastward propagation was found in CAMS-CSM than that in the observational data, with the transition from abnormally dry to wet conditions lasting for about 30 days (lag days −20 to 10). Similar to the observational data, the charging process for PBL moisture in CAMS-CSM is also stronger in sMC than that in cMC, corresponding to a more favorable conditions for development of deep convection in sMC than in cMC. The Maritime Continent therefore undergoes a charging process ahead of convection in both the observational data (lag days −15 to 5) and CAMS-CSM (lag days −20 to 10), and the transition in sMC is stronger than that in cMC.
|
| Figure 16 Longitude–lag of OLR (shading; W m−2) and PBL integrated specific humidity (contours; interval 0.1 kg m−2) anomalies onto PC1 calculated in Fig. 9 for (a, c) the equatorial band (cMC; 5°S–5°N) and (b, d) southern tropical band (sMC; 15°–5°S) from (a, b) the observational data and (c, d) CAMS-CSM. OLR (W m−2; blue solid lines) and PBL integrated specific humidity (<q>'; 0.1 kg m−2; red solid lines) anomalies averaged over the Maritime Continent (105°–135°E; vertical red dashed lines) are shown on the right-hand side of each panel |
To address the question of what processes are responsible for the marked contrast during the suppressed–active transition over the Maritime Continent, we examine the PBL integrated moisture budget of MJO during the charging period (Fig. 17). The total tendency of moistening in the observational data and model is greater in sMC than that in cMC, and the largest positive contribution of the difference in moistening comes from the zonal advection of moisture convergence. This is the same as the results from the model. Our budget analysis shows that the zonal moisture advection plays a primary part in the MJO detour. The largest positive contribution of the moistening ahead of convection in the cMC region is the vertical advection of moisture. CAMS-CSM is unable to simulate this factor, and the maximum positive contribution is the meridional advection of moisture. The largest difference between sMC and cMC is the relative contribution of the vertical advection of moisture, which tends to contribute negatively to the low-level moistening in both the observational data and model over the sMC region. In general, the model successfully shows the moistening ahead of the MJO convection, which is reflected in the total tendency of the PBL integral moisture anomalies and relative contribution of each term, especially the zonal advection of moisture convergence, which is related to the MJO detour. Based on the results of the PBL integrated moisture budget of MJO in both the observational data and model, we conclude that the advection of low-level zonal moisture makes the dominant contribution to the difference in moistening between sMC and cMC regions, which may result in the MJO detour over the Maritime Continent.

|
| Figure 17 Relative contribution of PBL integrated (1000–700 hPa) intraseasonal moisture budget terms during the charging period averaged over the Maritime Continent (105°–135°E) for the near-equatorial band (cMC; 5°S–5°N; red bars) and southern tropical band (sMC; 15°–5°S; blue bars) from (a) the observational data and (b) CAMS-CSM. The intraseasonal integrated specific humidity (<q>'t) includes the terms of zonal moisture advection (Uadv), meridional moisture advection (Vadv), vertical moisture advection (Wadv), and moisture loss (gain) due to the condensational heating (−Q2'/L). |
MJO has an important influence on the global weather and climate. The simulation of MJO is important in helping us to understand the mechanism of this oscillation and to predict its modulation of both the weather and climate. Climate models are continuously increasing in resolution and improving their ability to solve the physical processes that cause and contribute to ISV. However, many climate models are still unable to accurately represent the basic characteristics of MJO. We evaluated the performance of the 23-yr run of CAMS-CSM to reproduce the main features of MJO based on the diagnostic results established by MJOWG.
We examine the ability of CAMS-CSM to simulate the 20–100-day ISVs, including the seasonality characteristics, regional dependence in winter and summer, wavenumber–frequency, and propagation characteristics. It is found that CAMS-CSM can produce a good simulation of the seasonality characteristics of ISV of precipitation and U850. In view of the seasonal differences in the distribution of ISV, we further assess the model’s ability to simulate the regional dependence of ISVs in winter and summer. In general, the regional centers, distribution characteristics, and amplitude of ISV of precipitation and U850 are well represented by the model in both winter and summer. The model simulation of U850 is better than that of precipitation, and the model bias in simulating precipitation is concentrated in western Pacific, showing a double ITCZ structure. ISV signals often occur in a strong westerly wind, a weak easterly wind, and where there is abundant precipitation over the ocean. The double ITCZ bias embodied in the model, which is characterized by excessive precipitation over the Northern Hemisphere ITCZ and South Pacific convergence zone, also leads to overestimate of the amplitude of ISV precipitation in this region, further confirming the dependence of the ISV signal on climatic mean state. Thus a realistic mean state of precipitation in a model is required to give a realistic simulation of MJO.
Wavenumber–frequency spectral analysis is applied to the anomalies in precipitation, OLR, and U850 during boreal winter. The results show that the model gives a good simulation of the dominant frequency (30–80 days) of MJO and wavenumbers 1–3 in the zonal direction. Although the model can show the main characteristics of MJO scales, such as the intraseasonal signals and eastward propagation, there are some systematic deviations. The model bias is mainly manifested in a weaker eastward propagation, lower frequency peak spectra, and smaller zonal scales. Based on the lagged regression method, the ability of the model to simulate the eastward propagation of MJO in winter and its northward propagation in summer is evaluated. The results indicate that the model can simulate the eastward propagation of ISV of OLR and U850 in winter well, but the speed of propagation is slower than that seen in the observational data. The model simulates the northward propagation of MJO in summer moderately well, indicating that there is still room for improvement.
We also evaluate the ability of the model to simulate the coupling feature of MJO and analyze the cross-spectra between OLR and U850 in both the observational dataset and model. The results demonstrate that the model simulation can capture the eastward propagation of MJO, but the spectrum shifts toward lower frequencies and becomes less coherent than the observational data. Furthermore, the MCEOF method is applied to evaluate the ability of the model to simulate MJO. The baroclinic structure of the wind field and coupling characteristics between the wind field and OLR are simulated well in the model, but OLR is weaker than that in the observational data with a smaller explained variance. From the lead–lag correlation analysis of the principle components obtained by MCEOF, we conclude that the model successfully simulates the MJO timescale, proving that it is physically meaningful. In addition, we can obtain the life cycle of MJO through composite analysis by using the principle component obtained by MCEOF. In general, CAMS-CSM generates a realistic succession of MJO phases, close to those from the observational data. However, the eastward propagation of convection is slower during phases 1–3 of MJO than that in the observational data. It then suddenly accelerates in phases 4–6, resulting in a more uneven phase speed in the model.
Moreover, we analyze and evaluate the impact of the moisture process on the eastward/northward propagation of MJO. Through composite analysis of the vertical structure of moisture content, it is found that the low-level moisture anomaly shows a pronounced tilting structure during the life cycle of MJO, which is well represented by the model, again showing the excellent simulation of MJO by the model. Budget analysis of the integral moisture anomaly shows that the dominant contribution of the MJO detour comes from the zonal advection of moisture convergence. CAMS-CSM successfully simulates this moisture charging process and thus can better reproduce the MJO detour during eastward propagation.
As an important factor affecting the global weather and climate, MJO can be considered as a link between weather forecasting and seasonal predictions and can be used as a major resource in extended-range forecasting. Despite of the fact that considerable progress has been achieved in recent decades in the development of climate and weather forecasting models, MJO is still poorly simulated in state-of-art models. Great challenges in the MJO simulation and prediction suggest that our knowledge of the fundamental physics and maintenance mechanism of MJO is still both inadequate and ambiguous. In particular, the propagation of MJO through the Maritime Continent has become a major challenge in current climate models due to its complex topographical distribution. Therefore, a detailed understanding and accurate simulation of the complex processes of interactions between the MJO and Maritime Continent are essential in successful mid-range weather forecasting. More sensitivity experiments are needed to diagnose the connection between the Maritime Continent and MJO to illustrate the influence of the terrain of the Maritime Continent on MJO. This will be the direction explored in our future work.
Acknowledgments. The authors thank the Chinese Academy of Meteorological Sciences for providing the model data. The authors also thank the two reviewers for their constructive comments on this paper.
| Adames, Á. F., J. M. Wallace, and J. M. Monteiro, 2016: Seasonality of the structure and propagation characteristics of the MJO. J. Atmos. Sci., 73, 3511–3526. DOI:10.1175/jas-d-15-0232.1 |
| Ahn, M. S., D. Kim, K. R. Sperber, et al., 2017: MJO simulation in CMIP5 climate models: MJO skill metrics and process-oriented diagnosis. Climate Dyn., 49, 4023–4045. DOI:10.1007/s00382-017-3558-4 |
| Ajayamohan, R. S., and B. N. Goswami, 2007: Dependence of simulation of boreal summer tropical intraseasonal oscillations on the simulation of seasonal mean. J. Atmos. Sci., 64, 460–478. DOI:10.1175/jas3844.1 |
| Annamalai, H., and K. R. Sperber, 2005: Regional heat sources and the active and break phases of boreal summer intraseasonal (30–50 day) variability. J. Atmos. Sci., 62, 2726–2748. DOI:10.1175/jas3504.1 |
| Barlow, M., M. Wheeler, B. Lyon, et al., 2005: Modulation of daily precipitation over Southwest Asia by the Madden–Julian Oscillation. Mon. Wea. Rev., 133, 3579–3594. DOI:10.1175/Mwr3026.1 |
| Bessafi, M., and M. C. Wheeler, 2006: Modulation of south Indian Ocean tropical cyclones by the Madden–Julian Oscillation and convectively coupled equatorial waves. Mon. Wea. Rev., 134, 638–656. DOI:10.1175/mwr3087.1 |
| Bond, N. A., and G. A. Vecchi, 2003: The influence of the Madden–Julian Oscillation on precipitation in Oregon and Washington. Wea. Forecasting, 18, 600–613. DOI:10.1175/1520-0434(2003)018<0600:tiotmo>2.0.co;2 |
| Brown, A., S. Milton, M. Cullen, et al., 2012: Unified modeling and prediction of weather and climate: A 25-year journey. Bull. Amer. Meteor. Soc., 93, 1865–1877. DOI:10.1175/bams-d-12-00018.1 |
| Dai, Y. J., X. B. Zeng, R. E. Dickinson, et al., 2003: The common land model. Bull. Amer. Meteor. Soc., 84, 1013–1024. DOI:10.1175/bams-84-8-1013 |
| Dee, D. P., S. M. Uppala, A. J. Simmons, et al., 2011: The ERA-interim reanalysis: Configuration and performance of the data assimilation system. Quart. J. Roy. Meteor. Soc., 137, 553–597. DOI:10.1002/qj.828 |
| Diamond, H. J., and J. A. Renwick, 2015: The climatological relationship between tropical cyclones in the southwest pacific and the Madden–Julian Oscillation. Int. J. Climatol., 35, 676–686. DOI:10.1002/joc.4012 |
| Duchon, C. E., 1979: Lanczos filtering in one and two dimensions. J. Appl. Meteor., 18, 1016–1022. DOI:10.1175/1520-0450(1979)018<1016:lfioat>2.0.co;2 |
| Fu, X. H., and B. Wang, 2004: Differences of boreal summer intraseasonal oscillations simulated in an atmosphere–ocean coupled model and an atmosphere-only model. J. Climate, 17, 1263–1271. DOI:10.1175/1520-0442(2004)017<1263:dobsio>2.0.co;2 |
| Gualdi, S., A. Navarra, and H. Von Storch, 1997: Tropical intraseasonal oscillation appearing in operational analyses and in a family of general circulation models. J. Atmos. Sci., 54, 1185–1202. DOI:10.1175/1520-0469(1997)054<1185:TIOAIO>2.0.CO;2 |
| Griffies, S. M., M. J. Harrison, R. C. Pacanowski, et al., 2004: A Technical Guide to MOM4. GFDL Ocean Group Technical Report No. 5, NOAA/Geophysical Fluid Dynamics Laboratory, Princeton NJ, 339 pp. |
| Hayashi, Y., 1979: A generalized method of resolving transient disturbances into standing and traveling waves by space–time spectral analysis. J. Atmos. Sci., 36, 1017–1029. DOI:10.1175/1520-0469(1979)036<1017:agmort>2.0.co;2 |
| Hayashi, Y., and D. G. Golder, 1986: Tropical intraseasonal oscilations appearing in a GFDL general circulation model and FGGE data. Part I: Phase propagation. J. Atmos. Sci., 43, 3058–3067. DOI:10.1175/1520-0469(1986)043<3058:TIOAIA>2.0.CO;2 |
| Hendon, H. H., and B. Liebmann, 1990: The intraseasonal (30–50 day) oscillation of the Australian summer monsoon. J. Atmos. Sci., 47, 2909–2924. DOI:10.1175/1520-0469(1990)047<2909:tidoot>2.0.co;2 |
| Hendon, H. H., and M. L. Salby, 1994: The life cycle of the Madden–Julian Oscillation. J. Atmos. Sci., 51, 2225–2237. DOI:10.1175/1520-0469(1994)051<2225:tlcotm>2.0.co;2 |
| Hendon, H. H., and M. C. Wheeler, 2008: Some space–time spectral analyses of tropical convection and planetary-scale waves. J. Atmos. Sci., 65, 2936–2948. DOI:10.1175/2008jas2675.1 |
| Hsu, P.-C., and T. Li, 2012: Role of the boundary layer moisture asymmetry in causing the eastward propagation of the Madden–Julian Oscillation. J. Climate, 25, 4914–4931. DOI:10.1175/jcli-d-11-00310.1 |
| Hsu, P.-C., J.-Y. Lee, and K.-J. Ha, 2016: Influence of boreal summer intraseasonal oscillation on rainfall extremes in southern China. Int. J. Climatol., 36, 1403–1412. DOI:10.1002/joc.4433 |
| Hung, M.-P., J.-L. Lin, W. Q. Wang, et al., 2013: MJO and convectively coupled equatorial waves simulated by CMIP5 climate models. J. Climate, 26, 6185–6214. DOI:10.1175/jcli-d-12-00541.1 |
| Hurrell, J., G. A. Meehl, D. Bader, et al., 2009: A unified modeling approach to climate system prediction. Bull. Amer. Meteor. Soc., 90, 1819–1832. DOI:10.1175/2009bams2752.1 |
| Inness, P. M., and J. M. Slingo, 2003: Simulation of the Madden–Julian Oscillation in a coupled general circulation model. Part I: Comparison with observations and an atmosphere-only GCM. J. Climate, 16, 345–364. DOI:10.1175/1520-0442(2003)016<0345:sotmjo>2.0.co;2 |
| Inness, P. M., J. M. Slingo, S. J. Woolnough, et al., 2001: Organization of tropical convection in a GCM with varying vertical resolution; implications for the simulation of the Madden–Julian Oscillation. Climate Dyn., 17, 777–793. DOI:10.1007/s003820000148 |
| Inness, P. M., J. M. Slingo, E. Guilyardi, et al., 2003: Simulation of the Madden–Julian Oscillation in a coupled general circulation model. Part II: The role of the basic state. J. Climate, 16, 365–382. DOI:10.1175/1520-0442(2003)016<0365:sotmjo>2.0.co;2 |
| Jeong, J.-H., C.-H. Ho, B.-M. Kim, et al., 2005: Influence of the Madden–Julian Oscillation on wintertime surface air temperature and cold surges in East Asia. J. Geophys. Res. Atmos., 110, D11104. DOI:10.1029/2004jd005408 |
| Jia, X. L., C. Y. Li, J. Ling, et al., 2008: Impacts of a GCM’s resolution on MJO simulation. Adv. Atmos. Sci., 25(1), 139–156. DOI:10.1007/s00376-008-0139-9 |
| Jiang, X. A., 2017: Key processes for the eastward propagation of the Madden–Julian Oscillation based on multimodel simulations. J. Geophys. Res. Atmos., 122, 755–770. DOI:10.1002/2016jd025955 |
| Jiang, X. A., D. E. Waliser, J.-L. Li, et al., 2011: Vertical cloud structures of the boreal summer intraseasonal variability based on CloudSat observations and ERA-interim reanalysis. Climate Dyn., 36, 2219–2232. DOI:10.1007/s00382-010-0853-8 |
| Jiang, X. A., D. E. Waliser, P. K. Xavier, et al., 2015: Vertical structure and physical processes of the Madden–Julian Oscillation: Exploring key model physics in climate simulations. J. Geophys. Res. Atmos., 120, 4718–4748. DOI:10.1002/2014jd022375 |
| Jones, C., 2000: Occurrence of extreme precipitation events in California and relationships with the Madden–Julian Oscillation. J. Climate, 13, 3576–3587. DOI:10.1175/1520-0442(2000)013<3576:ooepei>2.0.co;2 |
| Jones, C., D. E. Waliser, K. M. Lau, et al., 2004: Global occurrences of extreme precipitation and the Madden–Julian Oscillation: Observations and predictability. J. Climate, 17, 4575–4589. DOI:10.1175/3238.1 |
| Kemball-Cook, S., and B. Wang, 2001: Equatorial waves and air–sea interaction in the boreal summer intraseasonal oscillation. J. Climate, 14, 2923–2942. DOI:10.1175/1520-0442(2001)014<2923:ewaasi>2.0.co;2 |
| Kemball-Cook, S., B. Wang, and X. H. Fu, 2002: Simulation of the intraseasonal oscillation in the ECHAM-4 model: The impact of coupling with an ocean model. J. Atmos. Sci., 59, 1433–1453. DOI:10.1175/1520-0469(2002)059<1433:sotioi>2.0.co;2 |
| Kikuchi, K., and Y. N. Takayabu, 2004: The development of organized convection associated with the MJO during TOGA COARE IOP: Trimodal characteristics. Geophys. Res. Lett., 31, L10101. DOI:10.1029/2004gl019601 |
| Kiladis, G. N., K. H. Straub, and P. T. Haertel, 2005: Zonal and vertical structure of the Madden–Julian Oscillation. J. Atmos. Sci., 62, 2790–2809. DOI:10.1175/jas3520.1 |
| Kim, D., H. Kim, and M.-I. Lee, 2017: Why does the MJO detour the maritime continent during austral summer?. Geophys. Res. Lett., 44, 2579–2587. DOI:10.1002/2017gl072643 |
| Kim, D., K. Sperber, W. Stern, et al., 2009: Application of MJO simulation diagnostics to climate models. J. Climate, 22, 6413–6436. DOI:10.1175/2009jcli3063.1 |
| Klotzbach, P. J., 2010: On the Madden–Julian Oscillation–Atlantic hurricane relationship. J. Climate, 23, 282–293. DOI:10.1175/2009jcli2978.1 |
| Krishnamurti, T. N., and D. Subrahmanyam, 1982: The 30–50 day mode at 850 mb during MONEX. J. Atmos. Sci., 39, 2088–2095. DOI:10.1175/1520-0469(1982)039<2088:tdmamd>2.0.co;2 |
| Lau, K.-M., and P. H. Chan, 1986: Aspects of the 40–50 day oscillation during the northern summer as inferred from outgoing longwave radiation. Mon. Wea. Rev., 114, 1354–1367. DOI:10.1175/1520-0493(1986)114<1354:aotdod>2.0.co;2 |
| Lee, J.-Y., B. Wang, M. C. Wheeler, et al., 2013: Real-time multivariate indices for the boreal summer intraseasonal oscillation over the Asian summer monsoon region. Climate Dyn., 40, 493–509. DOI:10.1007/s00382-012-1544-4 |
| Lee, S.-S., J.-Y. Moon, B. Wang, et al., 2017: Subseasonal prediction of extreme precipitation over Asia: Boreal summer intraseasonal oscillation perspective. J. Climate, 30, 2849–2865. DOI:10.1175/jcli-d-16-0206.1 |
| Li, C. Y., X. L. Jia, J. Ling, et al., 2009: Sensitivity of MJO simulations to diabatic heating profiles. Climate Dyn., 32, 167–187. DOI:10.1007/s00382-008-0455-x |
| Li, X. J., Y. M. Tang, L. Zhou, et al., 2016: Assessment of Madden–Julian oscillation simulations with various configurations of CESM. Climate Dyn., 47, 2667–2690. DOI:10.1007/s00382-016-2991-0 |
| Liebmann, B., and C. A. Smith, 1996: Description of a complete (interpolated) outgoing longwave radiation dataset. Bull. Amer. Meteor. Soc., 77, 1275–1277. |
| Liebmann, B., H. H. Hendon, and J. D. Glick, 1994: The relationship between tropical cyclones of the western pacific and Indian oceans and the Madden–Julian Oscillation. J. Meteor. Soc. Japan, 72, 401–412. DOI:10.2151/jmsj1965.72.3_401 |
| Lin, H., 2015: Subseasonal variability of North American wintertime surface air temperature. Climate Dyn., 45, 1137–1155. DOI:10.1007/s00382-014-2363-6 |
| Lin, J.-L., G. N. Kiladis, B. E. Mapes, et al., 2006: Tropical intraseasonal variability in 14 IPCC AR4 climate models. Part I: Convective signals. J. Climate, 19, 2665–2690. DOI:10.1175/jcli3735.1 |
| Lorenz, D. J., and D. L. Hartmann, 2006: The effect of the MJO on the North American monsoon. J. Climate, 19, 333–343. DOI:10.1175/jcli3684.1 |
| Madden, R. A., and P. R. Julian, 1971: Detection of a 40–50 day oscillation in the zonal wind in the tropical pacific. J. Atmos. Sci., 28, 702–708. DOI:10.1175/1520-0469(1971)028<0702:doadoi>2.0.co;2 |
| Madden, R. A., and P. R. Julian, 1972: Description of global-scale circulation cells in the tropics with a 40–50 day period. J. Atmos. Sci., 29, 1109–1123. DOI:10.1175/1520-0469(1972)029<1109:dogscc>2.0.co;2 |
| Majda, A. J., and Q. Yang, 2016: A multiscale model for the intraseasonal impact of the diurnal cycle over the maritime continent on the Madden–Julian Oscillation. J. Atmos. Sci., 73, 579–604. DOI:10.1175/jas-d-15-0158.1 |
| Maloney, E. D., and D. L. Hartmann, 1998: Frictional moisture convergence in a composite life cycle of the Madden–Julian Oscillation. J. Climate, 11, 2387–2403. DOI:10.1175/1520-0442(1998)011<2387:fmciac>2.0.co;2 |
| Maloney, E. D., and D. L. Hartmann, 2000: Modulation of eastern North Pacific hurricanes by the Madden–Julian Oscillation. J. Climate, 13, 1451–1460. DOI:10.1175/1520-0442(2000)013<1451:moenph>2.0.co;2 |
| Maloney, E. D., and D. L. Hartmann, 2001: The sensitivity of intraseasonal variability in the NCAR CCM3 to changes in convective parameterization. J. Climate, 14, 2015–2034. DOI:10.1175/1520-0442(2001)014<2015:tsoivi>2.0.co;2 |
| Maloney, E. D., and A. H. Sobel, 2004: Surface fluxes and ocean coupling in the tropical intraseasonal oscillation. J. Climate, 17, 4368–4386. DOI:10.1175/jcli-3212.1 |
| Neena, J. M., D. Waliser, and X. N. Jiang, 2017: Model performance metrics and process diagnostics for boreal summer intraseasonal variability. Climate Dyn., 48, 1661–1683. DOI:10.1007/s00382-016-3166-8 |
| North, G. R., T. L., Bell, R. F. Cahalan, et al., 1982: Sampling errors in the estimation of empirical orthogonal functions. Mon. Wea. Rev., 110, 699–706. DOI:10.1175/1520-0493(1982)110<0699:SEITEO>2.0.CO;2 |
| Paegle, J. N., L. A. Byerle, and K. C. Mo, 2000: Intraseasonal modulation of South American summer precipitation. Mon. Wea. Rev., 128, 837–850. DOI:10.1175/1520-0493(2000)128<0837:imosas>2.0.co;2 |
| Ren, H.-L., and P. F. Ren, 2017: Impact of Madden–Julian Oscillation upon winter extreme rainfall in Southern China: Observations and predictability in CFSv2. Atmosphere, 8, 192. DOI:10.3390/atmos8100192 |
| Ren H. L., J. Wu, C. B. Zhao, et al., 2015: Progresses of MJO prediction researches and developments. J. Appl. Meteor. Sci., 26, 658–668. |
| Ren, H.-L., J. Wu, C.-B. Zhao, et al., 2016: MJO ensemble prediction in BCC-CSM1.1(m) using different initialization schemes. Atmos. Oceanic Sci. Lett., 9, 60–65. DOI:10.1080/16742834.2015.1116217 |
| Ren, H.-L., F. F. Jin, L. C. Song, et al., 2017: Prediction of primary climate variability modes at the Beijing Climate Center. J. Meteor. Res., 31, 204–223. DOI:10.1007/s13351-017-6097-3 |
| Ren, P. F., H.-L. Ren, J.-X. Fu, et al., 2018: Impact of boreal summer intraseasonal oscillation on rainfall extremes in southeastern China and its predictability in CFSv2. J. Geophys. Res. Atmos., 123, 4423–4442. DOI:10.1029/2017JD028043 |
| Roeckner, E., G. Bäuml, L. Bonaventura, et al., 2003: The Atmospheric General Circulation Model ECHAM5. Part I: Model Description. MPI-Report 349, Max Planck Institute for Meteorology, Hamburg, Germany, 127 pp. |
| Rong, X. Y., J. Li, H. M. Chen, et al., 2018: The CAMS climate system model and a basic evaluation of its climatology and climate variability simulation. J. Meteor. Res., 32, 839–861. DOI:10.1007/s13351-018-8058-x |
| Salby, M. L., R. R. Garcia, and H. H. Hendon, 1994: Planetary-scale circulations in the presence of climatological and wave-induced heating. J. Atmos. Sci., 51, 2344–2367. DOI:10.1175/1520-0469(1994)051<2344:pscitp>2.0.co;2 |
| Slingo, J. M., K. R. Sperber, J. S. Boyle, et al., 1996: Intraseasonal oscillations in 15 atmospheric general circulation models: Results from an AMIP diagnostic subproject. Climate Dyn., 12, 325–357. DOI:10.1007/bf00231106 |
| Sperber, K. R., 2003: Propagation and the vertical structure of the Madden–Julian Oscillation. Mon. Wea. Rev., 131, 3018–3037. DOI:10.1175/1520-0493(2003)131<3018:patvso>2.0.co;2 |
| Sperber, K. R., 2004: Madden–Julian variability in NCAR CAM2.0 and CCSM2.0. Climate Dyn., 23, 259–278. DOI:10.1007/s00382-004-0447-4 |
| Sperber, K. R., and H. Annamalai, 2008: Coupled model simulations of boreal summer intraseasonal (30–50 day) variability, Part 1: Systematic errors and caution on use of metrics. Climate Dyn., 31, 345–372. DOI:10.1007/s00382-008-0367-9 |
| Sperber, K. R., S. Gualdi, S. Legutke, et al., 2005: The Madden–Julian Oscillation in ECHAM4 coupled and uncoupled gene-ral circulation models. Climate Dyn., 25, 117–140. DOI:10.1007/s00382-005-0026-3 |
| Subramanian, A. C., M. Jochum, A. J. Miller, et al., 2011: The Madden–Julian oscillation in CCSM4. J. Climate, 24, 6261–6282. DOI:10.1175/jcli-d-11-00031.1 |
| Sultan, B., S. Janicot, and A. Diedhiou, 2003: The West African monsoon dynamics. Part I: Documentation of intraseasonal variability. J. Climate, 16, 3389–3406. DOI:10.1175/1520-0442(2003)016<3389:twamdp>2.0.co;2 |
| Waliser, D., K. Sperber, H. Hendon, et al., 2009: MJO simulation diagnostics. J. Climate, 22, 3006–3030. DOI:10.1175/2008jcli2731.1 |
| Wang, B., 1988: Dynamics of tropical low-frequency waves: An analysis of the moist Kelvin wave. J. Atmos. Sci., 45, 2051–2065. DOI:10.1175/1520-0469(1988)045<2051:dotlfw>2.0.co;2 |
| Wang, B., and T. M. Li, 1994: Convective interaction with boundary-layer dynamics in the development of a tropical intraseasonal system. J. Atmos. Sci., 51, 1386–1400. DOI:10.1175/1520-0469(1994)051<1386:ciwbld>2.0.co;2 |
| Wang, B., and X. S. Xie, 1998: Coupled modes of the warm pool climate system. Part I: The role of air–sea interaction in maintaining Madden–Julian Oscillation. J. Climate, 11, 2116–2135. DOI:10.1175/1520-0442-11.8.2116 |
| Wang, W. Q., and M. E. Schlesinger, 1999: The dependence on convection parameterization of the tropical intraseasonal oscillation simulated by the UIUC 11-layer atmospheric GCM. J. Climate, 12, 1423–1457. DOI:10.1175/1520-0442(1999)012<1423:TDOCPO>2.0.CO;2 |
| Watterson, I. G., and J. Syktus, 2007: The influence of air–sea interaction on the Madden–Julian Oscillation: The role of the seasonal mean state. Climate Dyn., 28, 703–722. DOI:10.1007/s00382-006-0206-9 |
| Wheeler, M., and G. N. Kiladis, 1999: Convectively coupled equatorial waves: Analysis of clouds and temperature in the wavenumber–frequency domain. J. Atmos. Sci., 56, 374–399. DOI:10.1175/1520-0469(1999)056<0374:CCEWAO>2.0.CO;2 |
| Wheeler, M. C., and H. H. Hendon, 2004: An all-season real-time multivariate MJO index: Development of an index for monitoring and prediction. Mon. Wea. Rev., 132, 1917–1932. DOI:10.1175/1520-0493(2004)132<1917:Aarmmi>2.0.Co;2 |
| Wheeler, M. C., H. H. Hendon, S. Cleland, et al., 2009: Impacts of the Madden–Julian Oscillation on Australian rainfall and circulation. J. Climate, 22, 1482–1498. DOI:10.1175/2008jcli2595.1 |
| Wu, C.-H., and H.-H. Hsu, 2009: Topographic influence on the MJO in the maritime continent. J. Climate, 22, 5433–5448. DOI:10.1175/2009jcli2825.1 |
| Wu, J., H.-L. Ren, J. Q. Zuo, et al., 2016: MJO prediction skill, predictability, and teleconnection impacts in the Beijing Climate Center atmospheric general circulation model. Dyn. Atmos. Oceans, 75, 78–90. DOI:10.1016/j.dynatmoce.2016.06.001 |
| Xavier, P., R. Rahmat, W. K. Cheong, et al., 2014: Influence of Madden–Julian Oscillation on Southeast Asia rainfall extremes: Observations and predictability. Geophys. Res. Lett., 41, 4406–4412. DOI:10.1002/2014gl060241 |
| Xie, P. P., and P. A. Arkin, 1997: Global precipitation: A 17-year monthly analysis based on gauge observations, satellite estimates, and numerical model outputs. Bull. Amer. Meteor. Soc., 78, 2539–2558. DOI:10.1175/1520-0477(1997)078<2539:gpayma>2.0.co;2 |
| Yasunari, T., 1979: Cloudiness fluctuations associated with the Northern Hemisphere summer monsoon. J. Meteor. Soc. Japan, 57, 227–242. DOI:10.2151/jmsj1965.57.3_227 |
| Yasunari, T., 1980: A quasi-stationary appearance of 30 to 40 day period in the cloudiness fluctuations during the summer monsoon over India. J. Meteor. Soc. Japan, 58, 225–229. DOI:10.2151/jmsj1965.58.3_225 |
| Zhang, C. D., 2013: Madden–Julian Oscillation: Bridging weather and climate. Bull. Amer. Meteor. Soc., 94, 1849–1870. DOI:10.1175/Bams-D-12-00026.1 |
| Zhang, C. D., and H. H. Hendon, 1997: Propagating and standing components of the intraseasonal oscillation in tropical convection. J. Atmos. Sci., 54, 741–752. DOI:10.1175/1520-0469(1997)054<0741:pascot>2.0.co;2 |
| Zhang, C. D., M. Dong, S. Gualdi, et al., 2006: Simulations of the Madden–Julian Oscillation in four pairs of coupled and uncoupled global models. Climate Dyn., 27, 573–592. DOI:10.1007/s00382-006-0148-2 |
| Zhang, G. J., and M. Q. Mu, 2005: Simulation of the Madden–Julian Oscillation in the NCAR CCM3 using a revised Zhang–McFarlane convection parameterization scheme. J. Climate, 18, 4046–4064. DOI:10.1175/jcli3508.1 |
| Zhang, L., B. Z. Wang, and Q. C. Zeng, 2009: Impact of the Madden–Julian Oscillation on summer rainfall in Southeast China. J. Climate, 22, 201–216. DOI:10.1175/2008jcli1959.1 |
| Zhao, C. B., T. J. Zhou, L. C. Song, et al., 2014: The boreal summer intraseasonal oscillation simulated by four Chinese AGCMs participating in the CMIP5 project. Adv. Atmos. Sci., 31, 1167–1180. DOI:10.1007/s00376-014-3211-7 |
| Zheng, Y., D. E. Waliser, W. F. Stern, et al., 2004: The role of coupled sea surface temperatures in the simulation of the tropical intraseasonal oscillation. J. Climate, 17, 4109–4134. DOI:10.1175/jcli3202.1 |
 2019, Vol. 33
2019, Vol. 33


