The Chinese Meteorological Society
Article Information
- CAO, Bangjun, Fuping MAO, Shuwen ZHANG, et al., 2019.
- Assessing the Performance of Separate Bias Kalman Filter in Correcting the Model Bias for Estimation of Soil Moisture Profiles. 2019.
- J. Meteor. Res., 33(3): 519-527
- http://dx.doi.org/10.1007/s13351-019-8057-6
Article History
- Received April 8, 2018
- in final form January 23, 2019
2. Key Laboratory for Semi-Arid Climate Change of the Ministry of Education, College of Atmospheric Sciences, Lanzhou University, Lanzhou 730000;
3. No. 2 Qishan Road, Mount Wuyi 354301;
4. Moji Co. Ltd., Beijing 100016
Soil moisture plays an important role in the land–atmosphere interaction and links with the water, energy, and carbon exchanges between the land and atmosphere. Having precise soil moisture measurements may be beneficial for a more accurate forecast of the temperature and precipitation. Due to limited soil moisture measurements available, the soil moisture initialization in a forecast model is generally made by assimilating indirect observations such as active and passive remote sensing measurements (Reichle and Koster, 2004; Zhang et al., 2005, 2010, 2011, 2013). The data assimilation is done by using the three-dimensional variational (3DVAR) framework, extended Kalman filter (EKF), ensemble Kalman filter (EnKF), and so on (Evensen, 1994; Anderson and Anderson, 1999; Reichle et al., 2001; Walker et al., 2002; Montzka et al., 2011; Yan et al., 2015). The assimilated observations include the site observation (Seuffert et al., 2003) and remote sensing observation from the Soil Moisture and Ocean Salinity (SMOS) satellite and the Soil Moisture Active Passive (SMAP) mission (Yang et al., 2007; Montzka et al., 2012). However, difficulties still exist; for example, how the model bias is properly addressed in a data assimilation system?
A fundamental assumption in the EnKF assimilation theory is that both observations and model predictions are free of bias, only in the presence of random and zero-mean errors. However, the error in a land surface model (LSM) forecasts caused by the inaccurate meteorological forcing, simplified representations of the land surface process, and uncertainties in soil parameters, is not well represented by random noise (Hamill et al., 2001; Reichle et al., 2001; Reichle and Koster, 2004; Walker and Houser, 2004; Crow et al., 2005; Hamill and Whitaker, 2005). Satellite observations of soil moisture contain the instrument-dependent biases, and approximations in the radiative transfer equation cause complex and state-dependent systematic errors. To reduce the impact of the biases in model forecasts and observations on the estimation of soil moisture, bias correction for EnKF is necessary (Reichle and Koster, 2004). If the observation bias has been removed or does not exist, the general methodology for the model bias correction is to update the bias with the model state variables during each data assimilation cycle. It includes the state augmentation method and the Kalman filter (SepKF) method (Friedland, 1969; Dee and Da Silva, 1998; Drécourt and Madsen, 2002; Drécourt et al., 2006). The state augmentation method is to add uncertain parameters representing model error terms into the original model state, and update the state and bias parameters at the same time (Jazwinski, 1970). Since the model bias could not be exactly known, different types of bias models have been proposed and tested. For example, Reichle and Koster (2004) assumed that the error in the LSM is a first order Markov process. On the other hand, the SepKF method updates the state and bias separately. De Lannoy et al. (2007) evaluated the SepKF’s performance by assimilating soil moisture measurements respectively at a single layer and at all layers with the Community Land Model (CLM), and found improved analysis of soil moisture than the standard Kalman filter without the bias correction on the basis of EnKF. The SepKF method has been extended to more general conditions and nonlinear models (Kollat et al., 2008, 2011; Pauwels and De Lannoy, 2015).
Up to now, few studies have been carried out on the impact of different types of model bias on the estimation of soil moisture profiles with SepKF. In this paper, we firstly assess the improvement of soil moisture profiles with and without implementation of the bias filter by using two types of bias models in an observing system simulation experiment (OSSE); secondly, the performance of SepKF with and without the bias filter is evaluated in assimilating the real near-surface observations for the estimation of soil moisture profiles.
2 Model description and assimilation methods 2.1 LSMThe community Noah LSM with multiparameterization options (Noah-MP) was used (Niu et al., 2011). Noah-MP is a fully augmented Noah LSM version with multiple options for the key land–atmosphere interaction process. Some improved biophysical realism (land memory processes) has been added, including the separate vegetation canopy and ground temperature, a multi-layer snowpack, an unconfined aquifer model for groundwater dynamics, and an interactive vegetation canopy layer.
The model state includes the soil moisture and soil temperature in four layers, skin temperature (bare soil or vegetation), canopy water storage, and a variety of storage variables related to snow processes (Niu et al., 2011). Noah-MP has been validated over a variety of underlying surfaces and climate regimes (Cai et al., 2014). The 2-m depth of soil is divided into 4 layers at the depths of 0.10, 0.40, 1.0, and 2.0 m. The parameterization scheme includes the Ball–Berry stamatal resistance scheme (Ball et al., 1987), soil resistance scheme (Sakaguchi and Zeng, 2009), and Monin–Obukhov surface transfer coefficient scheme. Surface albedo is diagnosed from the surface solar radiation budget.
2.2 Assimilation methods 2.2.1 EnKFThe procedure in EnKF includes three steps: first, an initial ensemble is generated; second, the forecast covariance is calculated between the state variables and measurement predictions; finally, each ensemble forecast member is updated at the measurement time.
In a pure Monte Carlo implementation, the i-th analysis member xia(t) is obtained by using a randomly perturbed vector of new observations yio and a member of a corresponding ensemble of background estimates xif(t) as in Eq. (1) (Zhang et al., 2010):
| $ {{x}}_i^{\rm a}{\rm{(}}t{\rm{) = }}{{x}}_i^{\rm f}{\rm{(}}t{\rm{) + }}{{K}}[{{y}}_i^{\rm o} - H{{x}}_i^{\rm f}{\rm{(}}t{\rm{)]}},\;\;\;\;\;\;\;\;\;\;\;\;i = {\rm{ }}1,{\rm{ }}2,{\rm{ }} \ldots ,N. $ | (1) |
The Kalman gain K is defined as:
| ${{K}} = {{{P}}^{\rm{f}}}{H^{\rm{T}}}{(H{{{P}}^{\rm{f}}}{H^{\rm{T}}} + {{R}})^{ - 1}}, $ | (2) |
where
| $ \hspace{-38pt} {{{P}}^{\rm f}}{H^{\rm{T}}} = \frac{1}{{N - 1}}\sum\limits_{i = 1}^N {({{x}}_i^{\rm f} - \overline {{{x}}_{}^{\rm f}})} {(H{{x}}_i^{\rm f} - \overline {H{{x}}_{}^{\rm f}})^{\rm{T}}}, $ | (3) |
| $\!\!\! \!\!\!\!\! \!\!\!\!\! H{{{P}}^{\rm f}}{H^{\rm{T}}} = \frac{1}{{N - 1}}\sum\limits_{i = 1}^N {(H{{x}}_i^{\rm f} - \overline {H{{x}}_{}^{\rm f}})} {(H{{x}}_i^{\rm f} - \overline {H{{x}}_{}^{\rm f}})^{\rm{T}}}, $ | (4) |
| $ \hspace{-144pt} \overline {{{{x}}^{\rm f}}} = \frac{1}{N}\sum\limits_{i = 1}^N {{{x}}_i^{\rm f}} , $ | (5) |
where H is the forward observation operator, superscript T is the matrix transpose, Pf is the background error covariance, and R is observation error covariance.
2.2.2 Separate bias Kalman filter (SepKF) with complete feedbacksSepKF is implemented in two steps: first, a standard EnKF is used to derive a bias-blind state estimate (stage 1, hereafter named state filter); and second, a bias filter similar to that in Dee and Da Silva (1998; hereafter DD98) is used to estimate the bias (stage 2).
As in DD98, a forecast model M is used to transport the i-th unbiased estimation of the state member
| $ {{x}}_i^{\rm f}(t + 1) = M[{\tilde { x}}_i^{\rm a}(t)],\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = {\rm{ }}1,{\rm{ }}2,{\rm{ }} \cdots , N, $ | (6) |
and an unbiased analysis member
| $ \begin{align} {\tilde { x}}{_i^{\rm a}}(t) = & \left({{{x}}_i^{\rm f}(t) - {{{b}}^{\rm a}}(t)} \right) + {{K}}\left[ {{{y}}_i^{\rm o} - H\left({{{x}}_i^{\rm f}(t) - {{{b}}^{\rm a}}(t)} \right)} \right], \\ i = & {\rm{ }}1,{\rm{ }}2,{\rm{ }} \cdots , N, \end{align}$ | (7) |
where ba(t) is a bias vector at analysis time t; the state Kalman gain K is calculated by using the same procedure as in Section 2.2.1.
Different from DD98, we use a persistence model for the bias propagation:
| ${{{b}}^{\rm f}}{\rm{(}}t{\rm{ + 1) = }}{{{b}}^{\rm a}}(t),$ | (8) |
and the bias analysis is given by:
| $ - {{{b}}^{\rm a}}{\rm{(}}t{\rm{) = }} - {{{b}}^{\rm f}}{\rm{(}}t{\rm{) + }}{{L}}[{{d}}{\rm{(}}t{\rm{) + }}H{{{b}}^{\rm f}}{\rm{(}}t)], $ | (9) |
where the innovation vector
As in DD98, Kalman gain for the bias filter L is easily calculated by:
| ${{L}} = \lambda {{{P}}^{\rm f}}{H^{\rm{T}}}{\left[ {H{{{P}}^{\rm f}}{H^{\rm{T}}} + {{R}}} \right]^{ - 1}}, $ | (10) |
where the free parameter λ is determined empirically.
3 Experimental setup 3.1 Setup of an OSSEIn OSSE, the atmosphere forcing data, soil and plant parameters are obtained by measurements at Bondville observation station (40.01°N, 88.37°W), which is located in a flat field with the soil texture of silt loam over Great Plains of North America (Meyers and Hollinger, 2004; Brunsell et al., 2011). The land cover is grassland,and the measurements were performed from 10 May to 8 August 1998.
Considering that the modeled soil moisture in deep soil layers takes a long time to reach a hydraulic balance, the Noah-MP simulation is spun up for three years, forced by cycling the same observations in 1998. The final spunup results are chosen as a true state, whereas the “observations” in OSSE are obtained by adding random errors with the specified statistics into the true state (Fig.1).

|
| Figure 1 Flowchart in OSSE. |
An ensemble with 40 members is adopted in EnKF and is much larger than the model state with only 4-layer soil moisture forecasts. To reflect errors from different sources as many as possible, initial soil moisture and plant and soil parameters are all perturbed according to possible uncertainties in these variables (Table 1; Zhou et al., 2006; Zhang et al., 2010).
| Variable | Nominal value | Uncertainty in replicates |
| Humidity; solar radiation; wind speed;
wind direction |
Observations | Temporally uncorrelated multiplicative uniform noise: relative humidity: U (0.9, 1.1), solar radiation: U (0.9, 1.1), wind speed: U (0.7, 1.3), wind direction: U (0.7, 1.3) |
| Air temperature | Temporally uncorrelated additive uniform noise: U (–4, 4) | |
| Precipitation | Temporally uncorrelated multiplicative lognormal noise with a mean of 1.0 and a standard deviation equal to 35% of the nominal value | |
| Leaf area index (LAI) | Multiplicative uniform noise U (0.85, 1.15) for the LAI without change with time
(i.e., static) |
|
| Initial soil moisture | 0.25 cm3 cm–3 | Vertically uncorrelated additive zero-mean Gaussian noise with the variance of 0.12 |
| Soil moisture observation | Simulated true value | Temporally uncorrelated additive zero-mean Gaussian noise with the variance of 0.052 |
The assimilated observations are only near-surface soil moisture observations. Assimilating the observations is carried out every six hours and further tests with other time intervals is presented in Section 4.1. Two kinds of bias models are investigated: one is persistent with a consistent bias at each soil layers to represent a fixed systematic model error, and the other is drifting to reflect the variation of meteorological forcings, defined by:
| $b(t) = A[\alpha + \sin (\frac{{2\pi }}{T}t + \beta)],$ | (11) |
where b(t) is the model bias at time t with the same unit as the model state, A is the amplitude, T is the period,
Setup of all experiments including specifications of the key parameters is listed in Tables 2, 3. To quantitatively compare estimations by different approaches, root mean square error (RMSE) and mean absolute error (MAE) are computed as follows:
| Experiment | Bias (cm3 cm–3) | Bias correction | λ (–) | b0 (cm3 cm–3) | Observation error (cm3 cm–3) |
| EnKF-C1 | 0.01 | No | – | – | 0.01 |
| EnKF-C2 | 0.03 | No | – | – | 0.01 |
| SepKF-C1 | 0.01 | Yes | 0.2 | 0.005 | 0.01 |
| SepKF-C2 | 0.03 | Yes | 0.2 | 0.005 | 0.01 |
| SepKF-C1A | 0.01 | Yes | 0.8 | 0.005 | 0.01 |
| SepKF-C2A | 0.03 | Yes | 0.8 | 0.005 | 0.01 |
| Experiment | Bias correction | T (day) | A (cm3 cm–3) | λ (–) | b0 (cm3 cm–3) | Observation error (cm3 cm–3) |
| EnKF-S1 | No | 48 | 0.03 | – | – | 0.01 |
| EnKF-S2 | No | 6 | 0.03 | – | – | 0.01 |
| SepKF-S1 | Yes | 48 | 0.03 | 0.2 | 0.005 | 0.01 |
| SepKF-S2 | Yes | 6 | 0.03 | 0.2 | 0.005 | 0.01 |
| SepKF-S1A | Yes | 48 | 0.03 | 0.8 | 0.005 | 0.01 |
| SepKF-S2A | Yes | 6 | 0.03 | 0.8 | 0.005 | 0.01 |
| ${\rm{RMSE = [}}{M_t^{ - 1}}\sum\limits_{i = 1}^{M_t} {{{(f - \tilde f)}^2}} {{\rm{]}}^{1/2}}, $ | (12) |
| $\hspace{-30pt} {\rm{MAE = }}{M_t^{ - 1}}\sum\limits_{i = 1}^{M_t} {\left| {f - \tilde f} \right|} , $ | (13) |
where Mt is the number of verification times, f is the state estimate, and
| $ \begin{aligned} {\rm{PRI}} = & {\rm {[RMSE }}\left( {{\rm{Openloop}}} \right){\rm{ \,-\, RMSE }}\left( {{\rm{DA}}} \right)]/ \\ & {\rm{ RMSE }}\left( {{\rm{Openloop}}} \right){\rm{ \times 100 \text% }}, \end{aligned} $ | (14) |
where RMSE(Openloop) is the RMSE of soil moisture profiles in the openloop simulation, and RMSE(DA) is the RMSE in the data assimilation experiment.
3.2 Data and field description in real experimentObservation data from 1 to 30 August 2009 at the Semi-Arid Climate and Environment Research Observatory (SACOL) are used in the real experiment. SACOL is located in Yuzhong Campus of Lanzhou University (35.94°N, 104.13°E) with an elevation of 1965.8 m (Huang et al., 2008). The soil is mainly quaternary aeolian loess with the soil type of sierozem. The surface is covered mainly by short grass with species ofstipa bungeana, artemisia frigida, and leymus secalinu.
There is a 32-m observation tower at SACOL. Wind speed, temperature, and relative humidity observation instruments are installed at the 1-, 2-, 4-, 8-, 12-, 16-, and 32-m heights, respectively. The surface radiation flux measurement includes the outgoing and incoming longwave radiation. The measurement of soil temperature and soil moisture is at the depths of 5, 10, 20, 40, and 80 cm. In addition, the surface pressure, surface temperature, and soil heat flux are also measured. All the above data are collected every 30 minutes.
4 Results 4.1 Constant biasFigure 2 shows the soil moisture estimations at the 2nd, 3rd, and 4th layers in SepKF-C1. For comparison, the estimations with no bias corrections are also shown. In SepKF-C1, the soil moisture estimations quickly approach the true values with the cycling update and then maintain around, and the estimations at the two shallow layers (i.e., the 2nd and 3rd layers) are more accurate. In EnKF-C1, the estimations slowly arrive at the truth, but then gradually depart from the truth, showing the large impact of the bias on estimating the soil moisture if the bias is not corrected in the cycling update.
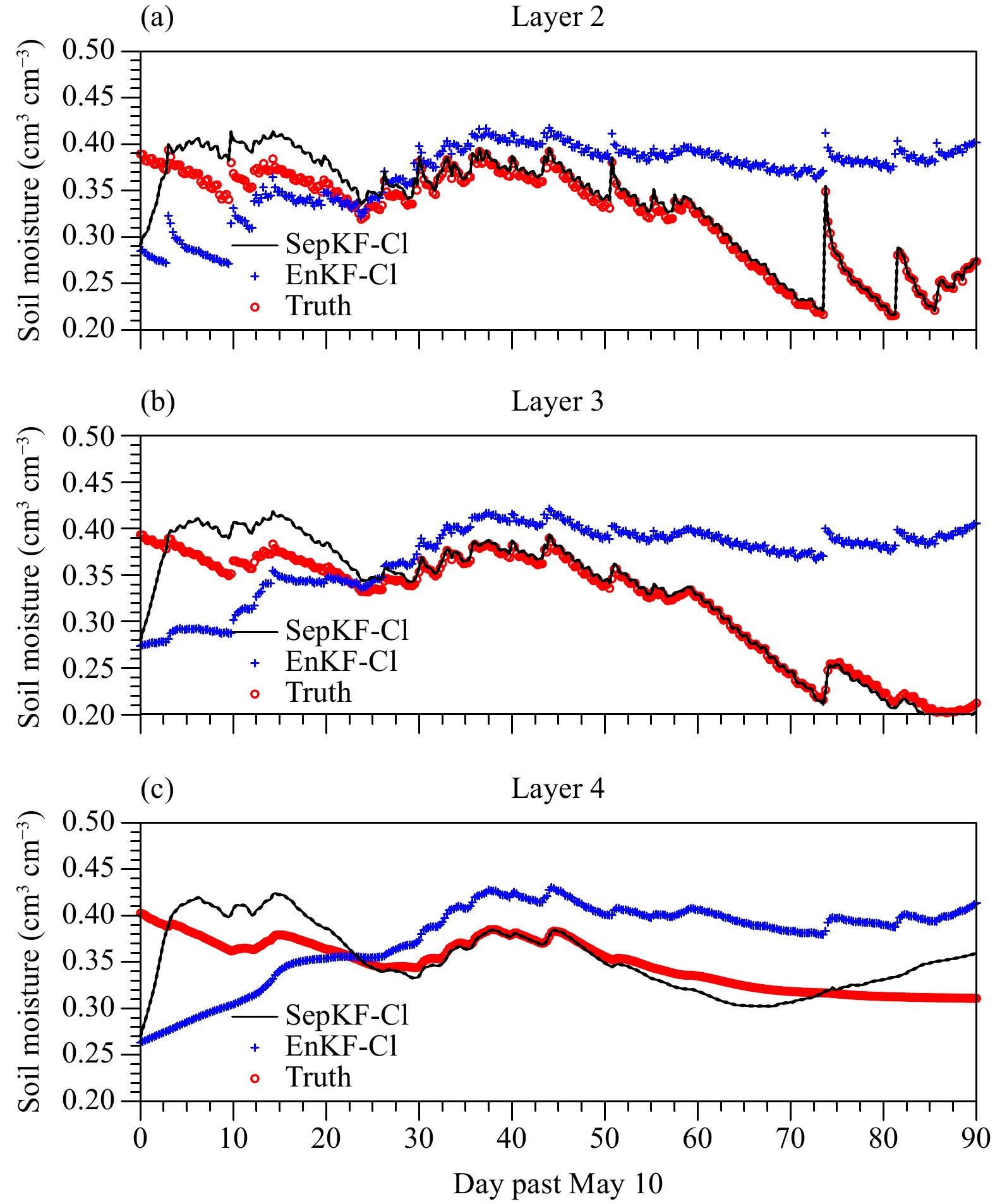
|
| Figure 2 Comparison of the soil moisture estimation in SepKF-C1 and EnKF-C1 with the truth at the (a) 2nd, (b) 3rd, and (c) 4th layers with the bias of 0.01 cm3 cm–3. |
To comprehensively compare the performance during the whole time window of data assimilation, RMSE of the soil moisture estimation and the estimated bias are listed in Table 4. If the model bias exists, SepKF produces better soil moisture estimation than EnKF with no bias correction although the bias is not completely corrected; with the increasing model bias, the error in soil moisture estimation in each layer with SepKF increases, but it is still smaller than that with EnKF with no bias correction (Table 5).
| Experiment | Soil moisture estimation | Bias estimation | |||||||
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 1 | Layer 2 | Layer 3 | Layer 4 | ||
| EnKF-C1 | 0.023 | 0.037 | 0.103 | 0.074 | – | – | – | – | |
| SepKF-C1 | 0.012 | 0.016 | 0.017 | 0.019 | 0.012 | 0.014 | 0.019 | 0.021 | |
| SepKF-C1A | 0.019 | 0.021 | 0.033 | 0.039 | 0.012 | 0.021 | 0.024 | 0.026 | |
| EnKF-C2 | 0.043 | 0.057 | 0.133 | 0.104 | – | – | – | – | |
| SepKF-C2 | 0.018 | 0.021 | 0.025 | 0.028 | 0.019 | 0.023 | 0.028 | 0.035 | |
| SepKF-C2A | 0.032 | 0.036 | 0.069 | 0.072 | 0.022 | 0.029 | 0.033 | 0.036 | |
| Experiment | Layer 1 | Layer 2 | Layer 3 | Layer 4 |
| EnKF-C1 | 54.0 | 53.8 | 14.2 | 50.7 |
| SepKF-C1 | 76.0 | 80.0 | 85.8 | 87.3 |
| SepKF-C1A | 62.0 | 73.8 | 72.5 | 74.0 |
| EnKF-C2 | 14.0 | 28.8 | –10.8 | 30.7 |
| SepKF-C2 | 64.0 | 73.8 | 79.2 | 81.3 |
| SepKF-C2A | 36.0 | 55.0 | 42.5 | 52.0 |
To investigate the effect of the parameter λ on the bias correction, λ = 0.2 and 0.8 are tested (Fig. 3). Compared to λ = 0.2, the convergence speed of the estimated bias with λ = 0.8 is faster due to more observation information absorbed, but the fluctuation of the estimated bias is much larger. Using a large parameter λ at the early stage of assimilation to increase the convergence speed, and then using a small parameter λ at the later stage to reduce noise in the bias estimation, are suggested.

|
| Figure 3 Comparison with the true value of the bias estimation using SepKF respectively with λ = 0.2 and 0.8. |
To assess the impact of the time interval in the experiments, three additional assimilation experiments are carried out, respectively, with the intervals of 24, 48, and 96 h, and RMSEs of the soil moisture estimations at the four layers during the assimilation period are listed in Table 6. RMSE at the 6-h time interval is the smallest at all layers among all assimilation intervals. For example, RMSE increases from 0.019 cm3 cm–3 at the 6-h assimilation interval to 0.074 cm3 cm–3 at the 96-h assimilation interval at the fourth layer, but the RMSE difference of the estimations for different time intervals is not large at the two shallow layers. RMSE increases with the increase of depth for all time intervals, showing that the deeper the soil layer is, the more difficult the soil moisture estimation is.
| Time interval (h) | Layer 1 | Layer 2 | Layer 3 | Layer 4 |
| 6 | 0.012 | 0.016 | 0.017 | 0.019 |
| 24 | 0.015 | 0.018 | 0.021 | 0.025 |
| 48 | 0.018 | 0.021 | 0.027 | 0.029 |
| 96 | 0.023 | 0.037 | 0.054 | 0.074 |
Unlike the atmospheric state variables, soil moisture shows a very slow diurnal variation at the shallow layer only and it almost does not vary at the deep layers without rainfall (Fig. 4), suggesting that it does not change drastically even using more frequent assimilating intervals such as once every six hours. Under this condition, the update does not need much time to finish. This is because magnitudes of the covariance are very small, especially those between the near surface and deep layers. Nonetheless, it will significantly improve the soil moisture estimation, especially at the deep layer.

|
| Figure 4 The soil moisture estimated by SepKF-C1 with the assimilation intervals of 6 h (dot line), 24 h (star line), 48 h (short-dashed line), and 96 h (long-dashed line), respectively. |
To simulate a near real condition, a sinusoidal model bias is used. For a 48-day period, variations of the model bias and soil moisture estimations at the 2nd, 3rd, and 4th layers are plotted in Fig. 5, including the estimations with EnKF for comparison. Since SepKF can correct the model bias with the cycling assimilation, especially the phase change, the soil moisture estimation with SepKF-S1 is much consistent with the true value while that with EnKF does not.
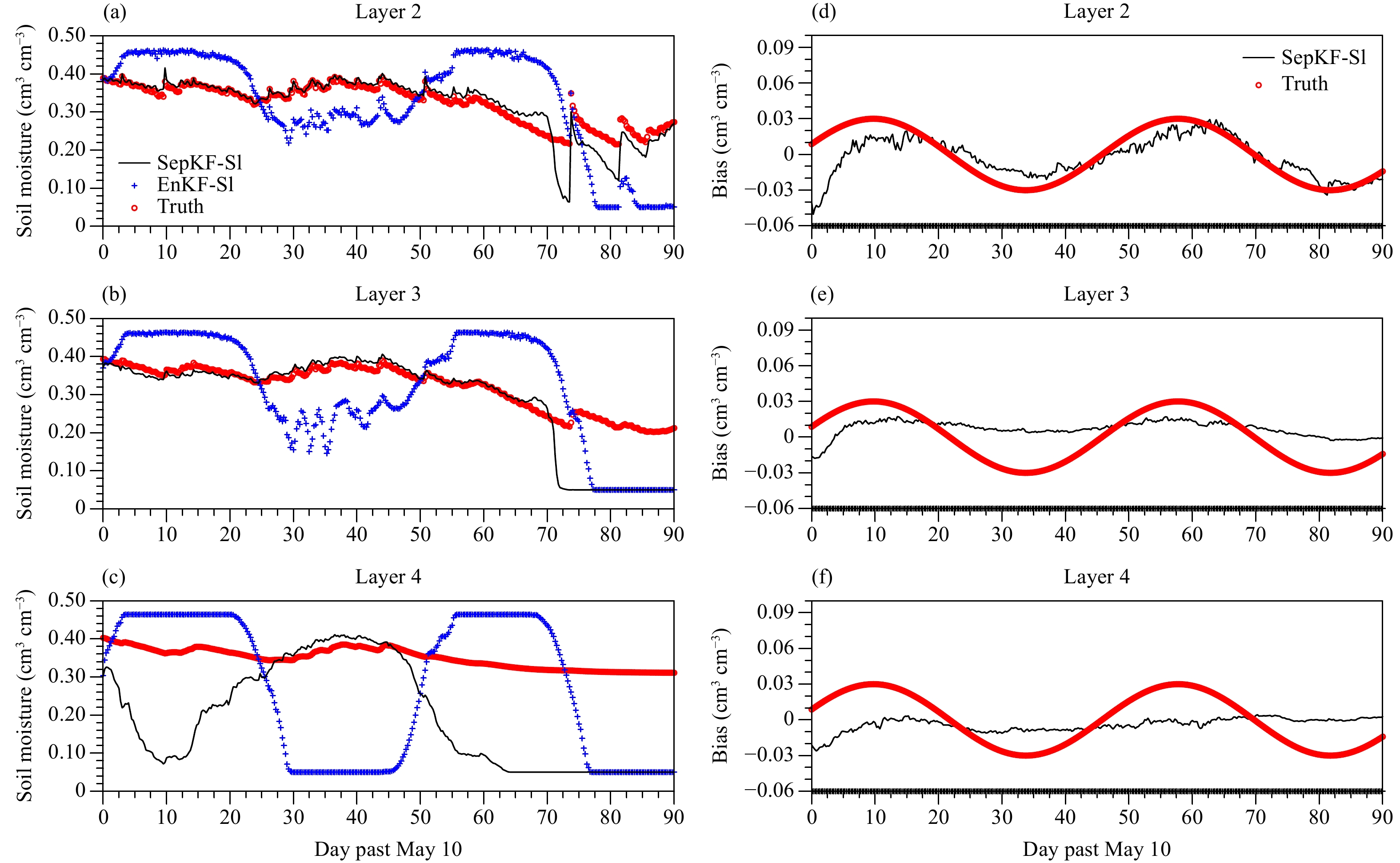
|
| Figure 5 Comparison of the soil moisture estimation in EnKF-S1 and SepKF-S1 with the truth by using the sinusoidal model bias with T = 48 days and λ = 0.2 at the (a) 2nd, (b) 3rd, and (c) 4th layers. The bias estimation in SepKF-S1 are also compared to the truth at the (d) 2nd, (e) 3rd, and (f) 4th layers. |
If the temporal variability of the model bias increases within the period of six days, the error in the soil moisture estimation in SepKF-S2 also increases although it is still more consistent with the truth compared to EnKF-S2. Similarly, the model bias in SepKF-S2 is not well corrected compared with the low temporal variability of the model bias although the phase change has been better estimated (Fig. 6).
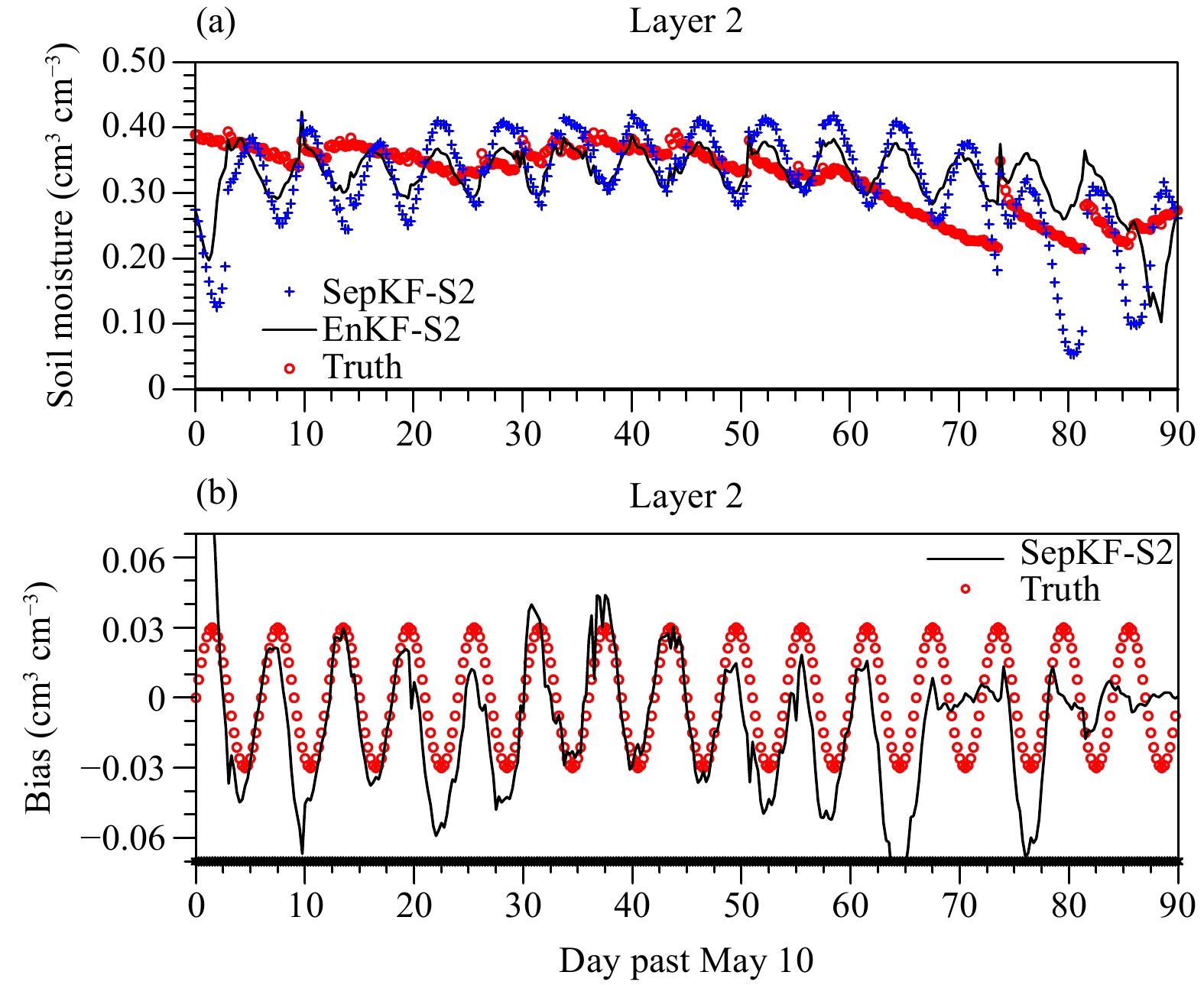
|
| Figure 6 (a) The 2nd-layer soil moisture estimation by SepKF-S2 with T = 6 days and λ = 0.2, and EnKF-S2 compared with the truth; (b) the 2nd-layer bias estimation with SepKF-S2 compared with the truth. |
RMSE between the soil moisture estimation with SepKF or EnKF and true value within the 90-day assimilation window is listed in Table 7. First, RMSE for the soil moisture estimation is analyzed. For EnKF, RMSE increases with depth and further does with the temporal variability of the model bias becoming quick. For SepKF, RMSE is very small for the low temporal variability of the bias with a reduction of 62.0%, 68.8%, 71.7%, and 76.7%, respectively, from the 1st to 4th layers; but for the high temporal variability, RMSE increases but is still smaller with a reduction of 10.0%, 18.8%, 36.7%, and 41.3% in comparison with Openloop (Table 8).
| State | Bias | ||||||||
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 1 | Layer 2 | Layer 3 | Layer 4 | ||
| EnKF_S1 | 0.042 | 0.063 | 0.084 | 0.132 | – | – | – | – | |
| SepKF_S1 | 0.019 | 0.025 | 0.034 | 0.035 | 0.004 | 0.015 | 0.021 | 0.025 | |
| SepKF_S1A | 0.033 | 0.044 | 0.052 | 0.065 | 0.015 | 0.023 | 0.025 | 0.035 | |
| EnKF_S2 | 0.074 | 0.093 | 0.112 | 0.134 | – | – | – | – | |
| SepKF_S2 | 0.045 | 0.065 | 0.076 | 0.088 | 0.015 | 0.026 | 0.032 | 0.034 | |
| SepKF_S2A | 0.023 | 0.025 | 0.030 | 0.035 | 0.002 | 0.012 | 0.017 | 0.029 | |
| Experiment | Layer 1 | Layer 2 | Layer 3 | Layer 4 |
| EnKF_S1 | 16.0 | 21.3 | 30.0 | 12.0 |
| SepKF_S1 | 62.0 | 68.8 | 71.7 | 76.7 |
| SepKF_S1A | 34.0 | 45.0 | 56.7 | 56.7 |
| EnKF_S2 | –48.0 | –16.3 | 6.7 | 10.7 |
| SepKF_S2 | 10.0 | 18.8 | 36.7 | 41.3 |
| SepKF_S2A | 54.0 | 68.8 | 75.0 | 76.7 |
Second, the bias estimation is investigated. For the low temporal variability of the bias, except for the first soil layer, the bias is not well estimated with a relative error even larger than 50%, and slightly becomes better if the smaller λ is used (i.e., 0.2 rather than 0.8). For the high temporal variability of the bias, RMSE of the bias estimation increases for the smallerλ (0.2) in comparison with the low temporal variability and becomes smaller for the larger λ (0.8). Therefore, it is suggested that a large (small) λ should be used for the high (low) temporal variability of the model bias.
4.3 A real observation assimilation experimentTo evaluate the performance of SepKF in the real situation, assimilating point-scale observations on the natural grass terrain over Northwest China was performed with an updating frequency of once every six hours. Based on the results in OSSE, λ was set to 0.2 in the first 15-day assimilation period and decreased to 0.1 in the later 15-day period. The initial model bias b0 is set to 0.001 cm3 cm–3. The observation error is 0.01 cm3 cm–3. The perturbation scheme is the same as that in OSSE. RMSE and MAE are also used to assess the performance by different approaches.
The soil moisture estimation at the two middle layers during the final 30 days is plotted in Fig. 7. For comparison, the ensemble forecast (Openloop), observation (Obs), and estimation with EnKF without the bias correction (EnKF) are also shown. The soil moisture estimation with EnKF at all layers is closer to the observations than that from Openloop. SepKF further improves the soil moisture estimation, especially at the third layer. For the whole assimilation period, RMSE is the largest at all layers in Openloop and smallest with SepKF (Table 9). For example, RMSE of the soil moisture estimation relative to EnKF has a reduction of 40.4% and 13.5% with Openloop, respectively, at layers 2 and 3, while that with SepKF reduces 51.9% and 71.2% (Table 10).

|
| Figure 7 Comparison of the soil moisture estimation by Openloop (star line), EnKF (cross line), and SepKF (solid line) with observations (circle line) at the (a) layer 2 and (b) layer 3 during the final 30 days at SACOL. |
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | |
| EnKF | 52.6 | 40.4 | 13.5 | 16.7 |
| SepKF | 63.2 | 51.9 | 71.2 | 33.3 |
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | |
| Openloop | 0.038 | 0.052 | 0.104 | 0.060 |
| EnKF | 0.018 | 0.031 | 0.093 | 0.051 |
| SepKF | 0.014 | 0.025 | 0.032 | 0.042 |
The performance of a separate bias Kalman filter (SepKF) in correcting the model bias to improve the soil moisture profile estimation is evaluated by assimilating the near-surface soil moisture into Noah-MP. First, an observing system simulation experiment (OSSE) is carried out, where two bias models with a constant and sinusoidal function are tested. Second, a real assimilation experiment is carried out with the point-scale observations at SACOL over Northwest China.
In OSSE, SepKF improves the soil moisture estimation, especially at the shallow layers compared with EnKF without the bias correction. Improvement of the estimation is limited by the amplitude and the temporal variability of the model bias. For example, if the amplitude or temporal variability is increased, the improvement will reduce.
Sensitivity tests show that SepKF is affected by the tuning parameter λ (i.e., the ratio of the bias error covariance matrix to forecast error covariance matrix). It is suggested that a large (small) λ should be used if the temporal variability of the model bias is high (low). Not only has the soil moisture in OSSE been better estimated, SepKF also improves the soil moisture profile in assimilating the real observations at SACOL over Northwest China over both EnKF without the bias correction and Openloop.
Finally, in this paper, SepKF is evaluated only with measurements at a point location for two weeks, so it needs further evaluation over a large enough area for a longer period in the future. In addition, further study is also necessary over different land surfaces and land uses, such as the frozen soil, wetland, cropland, and forestland.
Acknowledgments. Datasets used in this paper were kindly provided by the Semi-Arid Climate and Environment Observatory of Lanzhou University. See their website http://climate.lzu.edu.cn/data/index.asp for details.
| Anderson, J. L., and S. L. Anderson, 1999: A Monte Carlo implementation of the nonlinear filtering problem to produce ensemble assimilations and forecasts. Mon. Wea. Rev., 127, 2741–2758. DOI:10.1175/1520-0493(1999)127<2741:AMCIOT>2.0.CO;2 |
| Ball, J. T., I. E. Woodrow, and J. A. Berry, 1987: A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions. Progress in Photosynthesis Research, J. Biggins, Ed., Springer, Dordrecht, 221–224, doi: 10.1007/978-94-017-0519-6_48. |
| Brunsell, N. A., S. J. Schymanski, and A. Kleidon, 2011: Quantifying the thermodynamic entropy budget of the land surface: Is this useful?. Earth Syst. Dyn., 2, 87–103. DOI:10.5194/esd-2-87-2011 |
| Cai, X. T., Z. L. Yang, C. H. David, et al., 2014: Hydrological evaluation of the Noah-MP land surface model for the Mississippi River Basin. J. Geophys. Res. Atmos., 119, 23–38. DOI:10.1002/2013JD020792 |
| Crow, W. T., R. D. Koster, R. H. Reichle, et al., 2005: Relevance of time-varying and time-invariant retrieval error sources on the utility of spaceborne soil moisture products. Geophys. Res. Lett., 32, L24405. DOI:10.1029/2005GL024889 |
| De Lannoy, G. J. M., R. H. Reichle, P. R. Houser, et al., 2007: Correcting for forecast bias in soil moisture assimilation with the ensemble Kalman filter. Water Resour. Res., 43, W09410. DOI:10.1029/2006WR005449 |
| Dee, D. P., and A. M. Da Silva, 1998: Data assimilation in the presence of forecast bias. Quart. J. Roy. Meteor. Soc., 124, 269–295. DOI:10.1002/qj.49712454512 |
| Drécourt, J. P., and H. Madsen, 2002: Uncertainty estimation in groundwater modelling using Kalman filtering. Proceedings of the 4th International Conference on Calibration and Reliability in Groundwater Modelling, Acta Universitatis Carolinae, Prague, Czech Republic, 306–309. |
| Drécourt, J. P., H. Madsen, and D. Rosbjerg, 2006: Bias aware Kalman filters: Comparison and improvements. Adv. Water Resour., 29, 707–718. DOI:10.1016/j.advwatres.2005.07.006 |
| Evensen, G., 1994: Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Oceans, 99, 10,143–10,162. DOI:10.1029/94JC00572 |
| Friedland, B., 1969: Treatment of bias in recursive filtering. IEEE Trans. Autom. Control, 14, 359–367. DOI:10.1109/TAC.1969.1099223 |
| Hamill, T. M., and J. S. Whitaker, 2005: Accounting for the error due to unresolved scales in ensemble data assimilation: A comparison of different approaches. Mon. Wea. Rev., 133, 3132–3147. DOI:10.1175/MWR3020.1 |
| Hamill, T. M., J. S. Whitaker, and C. Snyder, 2001: Distance-dependent filtering of background error covariance estimates in an ensemble Kalman filter. Mon. Wea. Rev., 129, 2776–2790. DOI:10.1175/1520-0493(2001)129<2776:DDFOBE>2.0.CO;2 |
| Huang, J. P., W. Zhang, J. Q. Zuo, et al., 2008: An overview of the semi-arid climate and environment research observatory over the Loess Plateau. Adv. Atmos. Sci., 25, 906. DOI:10.1007/s00376-008-0906-7 |
| Jazwinski, A. H., 1970: Stochastic Processes and Filtering Theory. Academic Press, New York, 1–103. |
| Kollat, J. B., P. M. Reed, and D. M. Rizzo, 2008: Addressing model bias and uncertainty in three dimensional groundwater transport forecasts for a physical aquifer experiment. Geophys. Res. Lett., 35, L17402. DOI:10.1029/2008GL035021 |
| Kollat, J. B., P. M. Reed, and R. M. Maxwell, 2011: Many-objective groundwater monitoring network design using bias-aware ensemble Kalman filtering, evolutionary optimization, and visual analytics. Water Resour. Res., 47, W02529. DOI:10.1029/2010WR009194 |
| Meyers, T. P., and S. E. Hollinger, 2004: An assessment of storage terms in the surface energy balance of maize and soybean. Agric. For. Meteor., 125, 105–115. DOI:10.1016/j.agrformet.2004.03.001 |
| Montzka, C., H. Moradkhani, L. Weihermüller, et al., 2011: Hydraulic parameter estimation by remotely-sensed top soil moisture observations with the particle filter. J. Hydrol., 399, 410–421. DOI:10.1016/j.jhydrol.2011.01.020 |
| Montzka, C., V. R. N. Pauwels, H. J .H. Franssen, et al., 2012: Multivariate and multiscale data assimilation in terrestrial systems: A review. Sensors, 12, 16291–16333. DOI:10.3390/s121216291 |
| Niu, G. Y., Z. L. Yang, K. E. Mitchell, et al., 2011: The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos., 116, D12109. DOI:10.1029/2010JD015139 |
| Pauwels, V. R. N., and G. J. M. De Lannoy, 2015: Error covariance calculation for forecast bias estimation in hydrologic data assimilation. Adv. Water Resour., 86, 284–296. DOI:10.1016/j.advwatres.2015.05.013 |
| Reichle, R. H., and R. D. Koster, 2004: Bias reduction in short records of satellite soil moisture. Geophys. Res. Lett., 31, L19501. DOI:10.1029/2004GL020938 |
| Reichle, R. H., D. Entekhabi, and D. B. McLaughlin, 2001: Downscaling of radio brightness measurements for soil moisture estimation: A four-dimensional variational data assimilation approach. Water Resour. Res., 37, 2353–2364. DOI:10.1029/2001WR000475 |
| Sakaguchi, K., and K. B. Zeng, 2009: Effects of soil wetness, plant litter, and under-canopy atmospheric stability on ground evaporation in the Community Land Model (CLM3.5). J. Geophys. Res. Atmos., 114, D01107. DOI:10.1029/2008JD010834 |
| Seuffert, G., H. Wilker, P. Viterbo, et al., 2003: Soil moisture analysis combining screen-level parameters and microwave brightness temperature: A test with field data. Geophys. Res. Lett., 30, 1498. DOI:10.1029/2003GL017128 |
| Walker, J. P., and P. R. Houser, 2004: Requirements of a global near-surface soil moisture satellite mission: Accuracy, repeat time, and spatial resolution. Adv. Water Resour., 27, 785–801. DOI:10.1016/j.advwatres.2004.05.006 |
| Walker, J. P., G. R. Willgoose, and J. D. Kalma, 2002: Three-dimensional soil moisture profile retrieval by assimilation of near-surface measurements: Simplified Kalman filter covariance forecasting and field application. Water Resour. Res., 38, 1301. DOI:10.1029/2002WR001545 |
| Yan, H. X., C. M. DeChant, and H. Moradkhani, 2015: Improving soil moisture profile prediction with the particle filter-Markov chain Monte Carlo method. IEEE Trans. Geosci. Remote Sens., 53, 6134–6147. DOI:10.1109/TGRS.2015.2432067 |
| Yang, K., T. Watanabe, T. Koike, et al., 2007: Auto-calibration system developed to assimilate AMSR-E data into a land surface model for estimating soil moisture and the surface energy budget. J. Meteor. Soc. Japan, 85A, 229–242. DOI:10.2151/jmsj.85A.229 |
| Zhang, F., C. Snyder, and J. Z. Sun, 2004: Impacts of initial estimate and observation availability on convective-scale data assimilation with an ensemble Kalman filter. Mon. Wea. Rev., 132, 1238–1253. DOI:10.1175/1520-0493(2004)132<1238:IOIEAO>2.0.CO;2 |
| Zhang, S. W., H. R. Li, W. D. Zhang, et al., 2005: Estimating the soil moisture profile by assimilating near-surface observations with the ensemble Kalman filter (EnKF). Adv. Atmos. Sci., 22, 936–945. DOI:10.1007/BF02918692 |
| Zhang, S. W., X. B. Zeng, W. D. Zhang, et al., 2010: Revising the ensemble-based Kalman filter covariance for the retrieval of deep-layer soil moisture. J. Hydrometeorol., 11, 219–227. DOI:10.1175/2009JHM1146.1 |
| Zhang, S. W., D. Q. Li, and C. J. Qiu, 2011: A multimodel ensemble-based Kalman filter for the retrieval of soil moisture profiles. Adv. Atmos. Sci., 28, 195–206. DOI:10.1007/s00376-010-9200-6 |
| Zhang, S. W., Y. H. Liu, and W. D. Zhang, 2013: Ensemble square root filter assimilation of near-surface soil moisture and reference-level observations into a coupled land surface-boundary layer model. Acta Meteor. Sinica, 27, 541–555. DOI:10.1007/s13351-013-0402-6 |
| Zhou, Y. H., D. McLaughlin, and D. Entekhabi, 2006: Assessing the performance of the ensemble Kalman filter for land surface data assimilation. Mon. Wea. Rev., 134, 2128–2142. DOI:10.1175/MWR3153.1 |
 2019, Vol. 33
2019, Vol. 33


