1 Introduction

It is well known that the Tibetan Plateau (TP) has a significant impact on precipitation in eastern, southern, and even northern China (Tao and Ding, 1981; Chen and Dell’osso, 1984; Yasunari and Miwa, 2006). The causes and mechanisms of the influence of the TP on China’s precipitation have received considerable attention during the past decades, and fruitful research results have been achieved. As an elevated heat source, the TP can form unique weather systems (such as the TP low vortex and shear line) due to its unique dynamic and thermal effects. These weather systems are the main sources of precipitation over the plateau, and their development and eastward propagation often bring severe weather processes to the downstream areas (Wang and Orlanski, 1987; Wu et al., 2013; Xiang et al., 2013; Zheng et al., 2013; Chen et al., 2015; Cheng et al., 2016; Ni et al., 2017; Wang and Liu, 2017). For example, the Yangtze River basin experienced record-breaking heavy rainfall and floods in summer 1998. According to Shi et al. (2000), most of the heavy rain was caused by the low vortices or shear lines that developed and propagated eastward from the TP. In addition, the TP is an active area of mesoscale convective clouds (Wang et al., 1993; Jiang et al., 1996; Yasunari and Miwa, 2006; Li et al., 2008). Vigorous convective clouds often develop and propagate eastward under suitable circulation conditions, leading to heavy rainfall in the middle and lower reaches of the Yangtze River (Zhuo et al., 2002; Guo et al., 2003; Fu et al., 2011).

The TP is a huge heat source in summer. The eastern China is located in the East Asian monsoon region and usually suffers from frequent floods during summer. Therefore, the research on the impact of the TP on precipitation in eastern China is mostly concentrated in summer. Despite this, considerable attention has been paid to the influence of the TP on winter precipitation in China. In the beginning of 2008, southern China suffered from the most severe and long-persisting snowstorm in the past 50 years. The disaster lasted for more than 20 days, and up to 20 provinces (autonomous regions and municipalities) were affected to varying degrees. As of 24 February 2008, 129 people died from the disaster, and 1.66 million people were resettled in emergency. The direct economic loss was as high as 151.65 billion yuan (Tao and Wei, 2008). Tao and Wei (2008) pointed out that the extreme winter storm disaster mainly included four stages of heavy snowfall and freezing precipitation: 10–14, 18–22, 25–29 January, and 30 January–2 February. The anomalous atmospheric circulation in Eurasia was the main cause of this incident. Ding et al. (2008) reported that the extreme winter storm disaster was the result of multiple factors cooperating and superimposing at the same time and over the same area: the strong La Niña event provided a climate background for the invasion of cold air, the sustained anomalous circulation over Eurasia directly led to the occurrence of heavy snow, and the northward movement of the warm and humid airstream in the Bay of Bengal and the South China Sea was a necessary condition for the formation and persistence of the rain and snow. In addition, meteorologists also explored the relationship between this event and the western Pacific subtropical high (Shi et al., 2008; Wen et al., 2009; Zhou et al., 2009), East Asian winter monsoon (Gu et al., 2008), East Asian jet stream (Liao and Zhang, 2013; Zhang and Zhang, 2013; Zuo et al., 2017), South China quasi-stationary front (Tao et al., 2008), and the TP. With numerical models, Bao et al. (2010) and Li et al. (2011) found that the warming of the TP was conducive to the development and enhancement of the southern branch trough, which in turn facilitated the transport of moist air to southern China. Tao and Wei (2008) found that during the extreme winter storm disaster, strong potential vorticity (PV) from the west side of the plateau in the upper layer constantly moved to the stationary front over southern China, inducing the frontogenesis of the stationary front and leading to severe precipitation over southern China. Sun and Zhao (2010) also showed similar findings. They pointed out that after 18 January 2008, the convective systems over the TP became extremely active and frequently moved eastward. The last three synoptic episodes in the four rainy and snowy weather processes over southern China were accompanied by the eastward movement of the convective clouds originated from the TP. Sun and Zhao (2008) pointed out that there were three eastward movements of the plateau convections during the third rainy and snowy weather process, which caused the severest damages. It seems that there is a close relationship between the TP and the occurrence of the extreme winter storm disaster over southern China in 2008. Then, the reason why the convection over the plateau was extremely active during the extreme winter storm disaster becomes an important question.

In order to answer the above question, the concept of PV is introduced in this study. PV can better indicate the characteristics and evolution of large-scale atmospheric motion (Hoskins et al., 1985; Hoskins, 1997; Huo et al., 1999; Griffiths et al., 2000; Bracegirdle and Gray, 2009). It has been widely used in weather analysis and research. In general, PV increases with latitude and height, and its value is very low in the lower troposphere, especially near the surface. That is why most studies focus on PV anomalies in high latitudes and upper troposphere. With the continuous application and development of the PV theory, some studies (Held and Schneider, 1999; Koh and Plumb, 2004; Schneider, 2005; Egger et al., 2015) demonstrated that the PV in the free atmosphere is closely linked to the surface PV generation. The surface generated PV can be transported into the free atmosphere, affecting the PV in the free atmosphere. Shaw (1930) and Hoskins (1991) divided the atmosphere into overworld, middleworld, and underworld according to the distribution of the isentropic surfaces in the atmosphere. The isentropic surfaces above the tropical tropopause constitute the overworld; the isentropic surfaces below the tropical tropopause and not intersecting with the ground constitute the middleworld; and the underworld is composed of all isentropic surfaces that intersect with the ground surface. According to the PV theorem (Haynes and McIntyre, 1987), there is no net PV budget on the entire isentropic surfaces in the overworld and the middleworld. But there is PV generation in the underworld. Hoskins (1991) studied the PV budget in the underworld. From the perspective of long-term climatic average, the PV anomaly caused by frictional effect should be offset by the PV anomaly caused by diabatic heating. Under this constraint, the surface diabatic cooling should be generated over the area controlled by the low-level westerly in the Southern Hemisphere. Schneider et al. (2003) defined the “generalized PV” as the sum of the traditional PV and the surface generated PV. Based on the definition, they showed a theoretical and simulative result that a wake vortex can form on the lee side of a mountain in weakly dissipative flows. However, because the distribution of meteorological elements in the boundary layer is more complicated than that in the free atmosphere, and the description of meteorological elements near the surface is too rough in the reanalysis data, the generation and influence of surface PV generation have not been thoroughly explored and understood.

The purpose of this study is to analyze the relationship between surface PV density (PVD) forcing and surface PV generation. From a case study of the extreme winter storm disaster over southern China in early 2008, the influence of surface PV generation over the eastern flank of the TP and its eastward propagation on the precipitation in the downstream area is investigated, which reveals a new mechanism concerning the TP effect on the severe weather in eastern China.

2 Principles and data 2.1 PV and PVD in different coordinate systems

A general form of PV (P) defined by Ertel (1942) is: $P = \alpha {{{\xi}} _{\rm{a}}} \cdot \nabla \theta $ , where α is the specific volume of the air parcel, ${{{\xi}} _{\rm{a}}}$ is the three-dimensional absolute vorticity vector, and θ is the potential temperature. The PV equation proposed by Ertel (1942) is in the form

$ \dfrac{{{\rm{d}}P}}{{{\rm{d}}t}} = \alpha \left({{{{\xi}} _{\rm{a}}} \cdot \nabla \dot \theta + \nabla \times {{F}} \cdot \nabla \theta } \right), $

(1)

where $\dot \theta $ is the diabatic heating $\left({\dot \theta = \dfrac{{{\rm{d}}\theta }}{{{\rm{d}}t}}} \right)$ ; ${{F}}$ is the three-dimensional frictional acceleration, where the zonal and meridional components are expressed as ${F_x} = \alpha \dfrac{{\partial {\tau _x}}}{{\partial z}}$ and ${F_y} = \alpha \dfrac{{\partial {\tau _y}}}{{\partial z}}$ , respectively; τ_x and τ_y are the zonal and meridional surface wind stresses, respectively; and their calculation formulas are ${\tau _x} = \rho {C_{\rm{D}}}\left| {{V}} \right|u$ and τ_y = ρC_D|V|v, where ρ is the density of the air parcel, C_D is a non-dimensional drag coefficient assumed to be 2 × 10^–3, and $\left| {{V}} \right| = \sqrt {{u^2} + {v^2}} $ is wind speed at 10 m. In the calculation, the height of the friction layer is taken as 1000 m, so Δz is equal to 1000 m in calculating the momentum friction.

By introducing the notion of PVD (W), we obtain

$ W = \rho P = {{{\xi}} _{\rm a}} \cdot \nabla \theta . $

(2)

According to Haynes and McIntyre (1987), W is the total PV per unit volume and is referred to as the PVD in this study (Schneider et al., 2003). Substituting Eqs. (2) into (1) and applying the continuity equation, we have

$ \begin{aligned} \dfrac{{{\rm d}P}}{{{\rm d}t}} =& \alpha \dfrac{{{\rm d}W}}{{{\rm d}t}} + W\dfrac{{{\rm d}\alpha }}{{{\rm d}t}} = \alpha \left({\dfrac{{{\rm d}W}}{{{\rm d}t}} + W\nabla \cdot {V}} \right)\\ = & \alpha \left({{{\xi }_{\rm{a}}} \cdot \nabla \dot \theta + \nabla \times {F} \cdot \nabla \theta } \right). \end{aligned}$

(3)

By eliminating α from both sides of Eq. (3), the PVD equation can be obtained, after arranging terms, as:

$ \dfrac{{{\rm d}W}}{{{\rm d}t}} = - W\nabla \cdot {V} + {{\xi }_{\rm{a}}} \cdot \nabla \dot \theta + \nabla \times {F} \cdot \nabla \theta . $

(4)

The above equation shows that in the Cartesian coordinate system, the rate of change of PVD following the air motion is given by the sum of the three terms on the right, i.e., the divergence term, the diabatic term, and the frictional term. Compared with the PV equation [Eq. (1)], which states that PV is conserved assuming a frictionless and adiabatic flow, PVD is not conserved and the concentration or dilution of PVD by the divergence field will cause the change of PVD.

Further simplifying Eq. (4) and applying the vector operation relationship $\nabla \cdot \left({\varPhi {A}} \right) = \varPhi \nabla \cdot {A} + {A} \cdot \nabla \varPhi $ , the local change equation of the PVD can be obtained

$ \dfrac{{\partial W}}{{\partial t}} = - \nabla \cdot \left({W{V} - \theta \nabla \times {F} - {{\xi }_{\rm a}}\dot \theta } \right). $

(5)

The above equation indicates that the evolution of the local PVD is determined by the three terms on the right, namely, the divergence term of the PVD flux, frictional term, and diabatic heating term.

Since the expression of PV (P) is different under different coordinate systems, the expression of PVD (W) and its equation are also different in different coordinate systems. Because the isentropic coordinate system and the isobaric coordinate system are two commonly used coordinate systems in PV analysis, the following will focus on the forms of the PVD (W) and its equations in these two coordinate systems.

In the isentropic coordinate system, PV can be expressed as $P = \dfrac{{{{\xi }_{\rm{a}}} \cdot \nabla \theta }}{{{\rm{\rho }}_\theta }}$ , where ${{\rm{\rho }} _\theta } = - \dfrac{1}{g}\dfrac{{{\rm d}p}}{{{\rm d}\theta }}$ is the “density” in (x, y, θ) space (Holton, 2004). Introducing the PVD (W =ρ_θP), then the following relationship exists in the isentropic coordinate system: $W = {{\xi }_{\rm{a}}} \cdot \nabla \theta = {{\xi }_{\rm{a}}} \cdot {k} = f + {\zeta _\theta }$ , indicating that the PVD is numerically equal to the isentropic absolute vorticity in the isentropic coordinate system (Rossby, 1940; Hoskins et al., 1985; Haynes and McIntyre, 1987). Similarly, by using this relationship and the continuous equation in the isentropic coordinate system, the equation of the PVD in the isentropic coordinate system can be obtained,

$ \dfrac{{\partial W}}{{\partial t}} = - {\nabla _\theta } \cdot \left[ {\left({f + {\zeta _\theta }} \right){V} - {F} \times {k} + \dot \theta \dfrac{{\partial {V}}}{{\partial \theta }} \times {k}} \right], $

(6)

where in the isentropic coordinate system, the vertical component ( $ - \dfrac{\partial }{{\partial \theta }}\left[ {\left({f + {{\rm{\zeta }}_\theta }} \right)\dot \theta } \right]$ ) of the divergence term of PVD flux [ $ - \nabla \cdot \left({W{V}} \right)$ ] and the vertical component ( $\dfrac{\partial }{{\partial \theta }}\left[ {\left({f + {{\rm{\zeta }}_\theta }} \right)\dot \theta } \right]$ ) of the diabatic heating term [ $\nabla \cdot \left({{{\xi }_{\rm a}}\dot \theta } \right)$ ] are just offset, and the friction term $\nabla \times {F} \cdot \nabla \theta = \nabla \times {F} \cdot {k} = $ $ {\nabla _{\rm{\theta }}} \cdot \left({{F} \times {k}} \right)$ . Therefore, the evolution of the local PVD follows a horizontal motion on an isentropic surface. Equation (6) shows that in the isentropic coordinate system, the local variation of the PVD is related to the horizontal convergence or divergence of the PVD flux, the frictional effect, and the diabatic heating along the isentropic surface.

The isobaric coordinate system is widely used in synoptic analysis. An infinitesimal control volume in isobaric coordinate with cross-sectional area δA and vertical extent δp has a mass: ${\rm{\delta }}M = \rho_z{\rm{\delta }} z{\rm{\delta }}A = \left({ - \dfrac{{\delta p}}{g}} \right){\rm{\delta }}A = $ ${\rho _{p}}\left({ - {\rm{\delta }}p} \right){\rm{\delta }}A $ . Therefore, the “density” in (x, y, p) space is ρ_p = – ρ_z $\dfrac{{{\rm d}z}}{{{\rm d}p}} $ = g^–1, and the expressions of the PV (P) and PVD (W) in the isobaric coordinate system are

$ \left\{ {\begin{array}{*{20}{c}} {{P_p} = - g{{\xi }_{{\rm a}p}} \cdot {\nabla _p}\theta = - g\left[ {{k} \times \dfrac{{\partial {{V}_{\rm h}}}}{{\partial p}} \cdot {\nabla _{p{\rm h}}}\theta + \left({f + {\zeta _p}} \right)\dfrac{{\partial \theta }}{{\partial p}}} \right]}\\ \!\!\!\!\!\!{{W_p} = - {{\xi }_{{\rm a}p}} \cdot {\nabla _p}\theta = - \left[ {{k} \times \dfrac{{\partial {{V}_{\rm h}}}}{{\partial p}} \cdot {\nabla _{p{\rm h}}}\theta + \left({f + {\zeta _p}} \right)\dfrac{{\partial \theta }}{{\partial p}}} \right]} \end{array}} \right.. $

By comparing PV and PVD in the isobaric coordinate system, it can be found that, unlike in the isentropic coordinates, PV and PVD in the isobaric coordinate system are the same except for a factor g. PVD retains the dynamic and thermal properties of PV. Similarly, the local variation equation of PVD in the isobaric coordinate system can be obtained as follows,

$ \dfrac{{\partial W}}{{\partial t}} = - {V} \cdot {\nabla _p}W - {{\xi }_{{\rm a}p}} \cdot {\nabla _p}\dot \theta - {\nabla _p}\theta \cdot {\nabla _p} \times {F}. $

(8)

The above equation shows that in the isobaric coordinate system, the local variation of the PVD is related to the PVD advection, diabatic heating, and frictional effects. In the case of an adiabatic and frictionless flow, Eq. (8) is reduced to $\dfrac{{\partial W}}{{\partial t}} + { V} \cdot \nabla W = \dfrac{{dW}}{{dt}} = 0$ , indicating that the PVD is conserved following the flow motion. Like that PV is conserved following a horizontal motion on an isentropic surface with the absence of the diabatic heating and friction, PVD is conserved following a horizontal motion on an isobaric surface when the vertical velocity equals zero (ω = dp/dt = 0), which means that PVD-analysis in isobaric coordinate can be used to reveal the dynamic and thermal features of the atmospheric circulation following the quasi-horizontal motions. However, when considering a high-impact synoptic process, with vertical velocity developing rapidly, it is necessary to diagnose the effect of the air ascending motion.

2.2 Relationship between surface PV generation and PVD

Integrating Eq. (6) over an isentropic surface θ_s and employing Gauss’s theorem for the integration of the divergence of the PVD flux lead to

$ \begin{aligned} & \dfrac{\partial }{{\partial t}}\int_S {\sigma P{\rm{d}}s} = \dfrac{\partial }{{\partial t}}\int_S {W{\rm{d}}s} \\ & = - \oint_\varGamma {\left[ {\left({f + {\zeta _\theta }} \right){V} - {F} \times {k} + \dot \theta \dfrac{{\partial {V}}}{{\partial \theta }} \times {k}} \right] \cdot {n}{\rm{d}}l}, \end{aligned} $

(9)

whereσ = ρ_θ, S is the total area of the isentropic surface θ_s for the integration, Γ is the boundary of the θ_s surface intersecting with the ground surface, dl is the unit increment of the boundary Γ, which is positive when the linear integration takes an anticlockwise path, and n is a unit vector perpendicular to dl and oriented to its right side. For an isentropic layer with unit thickness (dθ = 1) and centered at the θ_s surface, the above equation defines the relationship between PV generation and PVD, i.e., the mass weighted PV increment of the isentropic layer is related to the distributions of PVD flux, friction, and diabatic heating along the boundary of the isentropic layer. For the isentropic surfaces in the overworld and the middleworld, since the isentropic surface does not intersect with the ground, there is no boundary (Γ→0) and the integral result must be zero. That is, the PV is conserved on these isentropic surfaces. However, the integral result in the underworld is related to the magnitude of the PVD transport, friction, and diabatic heating at the boundary. As a result, there will be PV generation at the boundary of the isentropic surface. In addition, Eq. (9) also shows that the change of the PVD on the boundary of the isentropic surface can intrude into the isentropic surface by the convergence or divergence of the PVD flux, and then influence the interior circulation.

By dividing the boundary Γ into N equal segments ( $\varGamma = \sum\nolimits_{n = 1}^N {{\varGamma _n}} $ ), Eq. (9) is transformed into

$ \dfrac{\partial }{{\partial t}}\int_S {W{\rm{d}}s} = \sum\nolimits_{n = 1}^N {\int_{{\varGamma _n}} {A{\rm{d}}l} } , $

(10)

where $A = - \left[( {f + {\zeta _\theta }){V} - {F} \times {k} + \dot \theta \dfrac{{\partial {V}}}{{\partial \theta }} \times {k}} \right]\cdot{n}$ represents the normal component of the PVD flux along the isentropic surface boundary. Under the framework of the geostrophic balance, $\dfrac{{\partial {V}}}{{\partial \theta }} = - \dfrac{R}{{fp}}\dfrac{{\partial p}}{{\partial \theta }}{k} \times \nabla T$ . Therefore, the contribution of surface heating to A can be expressed as

$ {A_{{Q}}} = - \left({\dot \theta \dfrac{{\partial {V}}}{{\partial \theta }} \times {k}} \right) \cdot {n} = - \dfrac{g}{{f{\theta _z}}}\dfrac{{\dot \theta }}{\theta }{\theta _n}, $

(11)

where θ_z is the static stability, and θ_n is the surface potential temperature gradient, indicating the baroclinicity. Equations (10) and (11) then show that in the areas where the surface baroclinicity is stronger, there is more contribution of surface diabatic heating to the surface PV generation.

Suppose that at one moment, the lowest isentropic surface intersecting with the ground is θ_l, and the top isentropic surface is θ_M, then the total surface PV generation at that moment can be obtained by spatial integration of Eq. (10) from θ_l to θ_M

$ \begin{aligned} & {{G}_{\rm{total}}}\left({{\theta }_{1}}, {{\theta }_{\rm M}} \right)=\int_{{{\theta }_{1}}}^{{{\theta }_{\rm M}}}{\left[ \dfrac{\partial }{\partial t}\int_{S}{W{\rm{d}}s} \right]{\rm{d}}\theta } \\ & = \sum\nolimits_{n=1}^{N}{\int_{{{\theta }_{1}}}^{{{\theta }_{\rm M}}}{\left[ \int_{{{\varGamma }_{n}}}{A{\rm{d}}l} \right]{\rm{d}}\theta }}=\dfrac{\partial }{\partial t}\iiint_{V}{P{\rm{d}}m}, \end{aligned}$

(12)

where dm = ρ_θdxdydθ. Since the isentropic surfaces intersecting with the ground always change with time, G_total is a function of time. It can be seen from Eqs. (10)–(12) that the larger the value of A, the larger the value of G_total, indicating that the total amount of surface PV generation is related to the PVD flux, and frictional and diabatic heating effects at the isentropic surface boundary. In addition, the total amount of surface PV generation is also related to the distribution of the surface potential temperature (A_Q) in the integral region. The denser the surface potential temperature in the integral region (the larger the θ_n), the larger the value of A, and the more the surface PV generation.

2.3 Data

The data used in this study are 3-h averaged data in January and February 1980–2017 from MERRA-2 (the second Modern-Era Retrospective Analysis for Research and Applications) reanalysis dataset (Gelaro et al., 2017), provided by NASA Global Modeling and Assimilation Office. Three collections of the dataset are used here, including the basic assimilated meteorological fields on both pressure levels (“inst3_3d_asm_Np” also known as “M2I3NPASM”) and model levels (“tavg3_3d_asm_Nv” also known as “M2T3NVASM”), as well as the single-level atmospheric state variables (“tavg1_2d_slv_Nx” also known as “M2T1NXSLV”).

According to Sun and Zhao (2010), after 18 January, the convective systems over the TP became extremely active and frequently moved eastward. In order to highlight the role of surface PVD forcing over the TP, the extreme winter freezing rain/snow storm disaster from 18 January to 2 February 2008 is selected for this study and the time period is defined as the “storm period” in the following context. By comparing the difference of various fields during the storm period with the climatology from January to February over 1980–2017, the impact of surface PVD forcing over the TP on the extreme winter freezing rain/snow storm disaster is explored.

According to the surface PV generation theory introduced in Section 2.2, the isentropic coordinate system has a great advantage for PV and PVD analyses. However, it is difficult to calculate the surface PV and PVD in the isentropic coordinate system, which is mainly related to the complex distribution of the isentropic surfaces in the boundary layer. For example, due to the strong heating and cooling effects on the TP surface, the distribution of isentropic surfaces near the TP surface is usually tilted; the turbulent mixing in the boundary layer sometimes forms a constant flux layer near the ground surface, and the isentropic surface is almost perpendicular to the ground surface; in some areas, there is an unstable hydrostatic stratification ( $\dfrac{\partial \theta }{\partial z} < 0$ ), which disables the PVD diagnosis. In addition, since the isentropic surfaces intersect with the ground suface, when calculating the forcing terms on the right hand side of Eq. (6) at an isentropic surface boundary, it is necessary to use both surface data and isentropic surface data. Since most of the reanalysis data only have a few typical levels of isentropic surfaces, plenty of interpolations are needed, which may introduce inestimable errors. The same problem exists with the Cartesian coordinate system and the isobaric coordinate system. In order to avoid the introduction of errors, the forms of PV, PVD, and PVD equation are transformed to the σ–p coordinate system, so that each term in the PVD tendency equation can be directly calculated by using the data at model levels from MERRA-2. After obtaining the PVD tendency at each model level, the PVD tendency in other coordinate systems can be obtained by coordinate transformation. The forms of PV, PVD, and PVD equation in the σ–p coordinate system are

$ \left\{ \begin{matrix} P=-\dfrac{g}{{{p}_{\rm s}}}{{{\xi}}_{{\rm a}\sigma }}\cdot {{\nabla }_{\sigma }}\theta =-\dfrac{g}{{{p}_{\rm s}}}\left[ {k}\times \dfrac{\partial {{{V}}_{\rm h}}}{\partial \sigma }\cdot {{\nabla }_{\sigma {\rm h}}}\theta +\left(f+{{\zeta }_{\sigma }} \right)\dfrac{\partial \theta }{\partial \sigma } \right] \\ \!\!\!\!\!\!\!\!\! \!\!\!\!\!\!\! W=-{{\xi}_{{\rm a} \sigma }}\cdot {{\nabla }_{\sigma }}\theta =-\left[ {k}\times \dfrac{\partial {{{V}}_{\rm h}}}{\partial \sigma }\cdot {{\nabla }_{\sigma {\rm h}}}\theta +\left(f+{{\zeta }_{\sigma }} \right)\dfrac{\partial \theta }{\partial \sigma } \right] \\ \!\!\!\!\!\!\!\!\! \!\!\!\!\!\!\! \!\!\!\!\!\!\! \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \!\!\!\!\!\!\! \!\!\!\!\!\!\! \!\!\!\!\!\!\! \!\!\!\!\!\!\! \dfrac{\partial W}{\partial t}={{\nabla }_{\sigma }}\cdot \left(-W{V}+\theta \nabla \times {F}+{{\xi}_{{\rm a}\sigma }}\dot{\theta } \right) \\ \end{matrix} \right., $

(13)

where p_s is the surface pressure, and ${\nabla _{\rm{\sigma }}}$ is the three-dimensional gradient operator in the σ–p coordinate system: ${\nabla _{\rm{\sigma }}} = \dfrac{\partial }{{\partial x}}{i} + \dfrac{\partial }{{\partial y}}{j} + \dfrac{\partial }{{\partial \sigma }}{k}$ .

3 Impact of surface PVD forcing on the extreme winter storm disaster over southern China in early 2008

Figure 1 shows the evolution of the PVD, the zonal PVD advection on the 305-K isentropic surface, and the 6-h accumulative precipitation averaged over 28°–34°N from 1 January to 5 February 2008. It seems that there was a boundary at about 103°E over eastern TP. Negative PVD was mainly located in the region to the west of 103°E, while positive PVD was located in the region to the east of 103°E, indicating that eastern TP might play a certain regulatory role in the distribution of the PVD. Positive PVD centers were mainly located along 105°E. Negative zonal PVD advection was distributed in the region to the west of 105°E, and positive zonal PVD advection prevailed in the region to the east of 105°E (Fig. 1b), indicating that the PVD propagated eastward with time. At the beginning of January, the positive and negative PVDs alternated. The zonal advection of positive PVD was relatively weak. From 10 January, the intensity and duration of the positive PVD over the eastern TP were strengthened and PVD continued to propagate downstream. With the continuous eastward propagation of the positive PVD forcing, the four major precipitation processes over southern China during the extreme winter storm disaster are clearly displayed, which are 10–14, 18–20, 25–29 January, and 30 January–2 February, respectively. The last three epi-sodes were accompanied by strong zonal advection of positive PVD, indicating that certain relationship existed between the occurrence of the precipitation over southern China and the eastward propagation of the PVD over the eastern TP. After 18 January, positive PVD maintained over eastern TP. The intensity of the positive PVD was stronger than that over 10–14 January. This distribution corresponded well to the findings of Sun and Zhao (2010) that the convective system over the plateau was anomalously active after 18 January.

In order to investigate the relationship of PVD anomaly between the plateau and southern China, Fig. 2 shows the vertical distribution of PVD averaged over 30°–36°N, 110°–120°E during 1980–2017 and the storm period. It can be seen that the PVD during 1980–2017 was very small in the middle and lower troposphere (Fig. 2a). A high PVD center was located near 700 hPa over eastern TP, with an intensity of about 0.6 × 10^–7 K m s kg^–1. Affected by the high PVD center and the westerly wind, the PVD between 850 and 600 hPa in the downstream area was relatively large, resulting in a relatively strong PVD distribution over the southern part of eastern China (25°–35°N, 110°–120°E) (Fig. 2b). This feature was particularly evident during the storm period (Figs. 2c, d). The PVD center near the TP was significantly enhanced, and the intensity reached 1.2 × 10^–7 K m s kg^–1 or so. The PVD between 850 and 500 hPa in the downstream area was also strengthened. Over southern China near 30°–35°N, a large PVD center was located between 850 and 500 hPa. Up-sliding southerly wind prevailed in the region to the south of 35°N, and descending northerly wind dominated in the region to the north of 35°N. During the extreme winter storm disaster, there was a significant positive PVD anomaly center near 600 hPa over eastern TP (Fig. 2e). The intensity of the anomalous PVD center gradually weakened eastward. The anomalous cyclonic circulation accompanied by the positive PVD anomaly caused significant anomalous ascending air in the middle and lower troposphere in the region to the east of 110°E, which explained the activity of the convective systems near the plateau after 18 January from the perspective of PVD forcing. The positive PVD anomaly center reached the maximum at 33°N and 700–600 hPa (Fig. 2f), and extended towards the low-level to the low-latitude region of southern China, corresponding to the quasi-stationary frontal region over southern China. Abnormal southerly wind and anomalous ascending air occupied the whole lower troposphere over southern China, which was beneficial to transport more warm and moist air to southern China. To the south of the positive PVD anomaly center, there was a significant negative PVD anomaly region located above 700 hPa near 25°N.

It can be seen from the PVD equation in the isobaric coordinate system [Eq. (8)] that the local tendency of the PVD is related to the PVD advection, diabatic heating, and frictional effects. As shown in Fig. 1, the eastward propagation of PVD from the TP will inevitably increase the local PVD over southern China. In addition, the release of a large amount of latent heating over the precipitation area during the storm period will also inevitably lead to changes of PVD. Then, what is the main cause of the positive PVD anomaly in the middle and lower troposphere over southern China as shown in Fig. 2f?

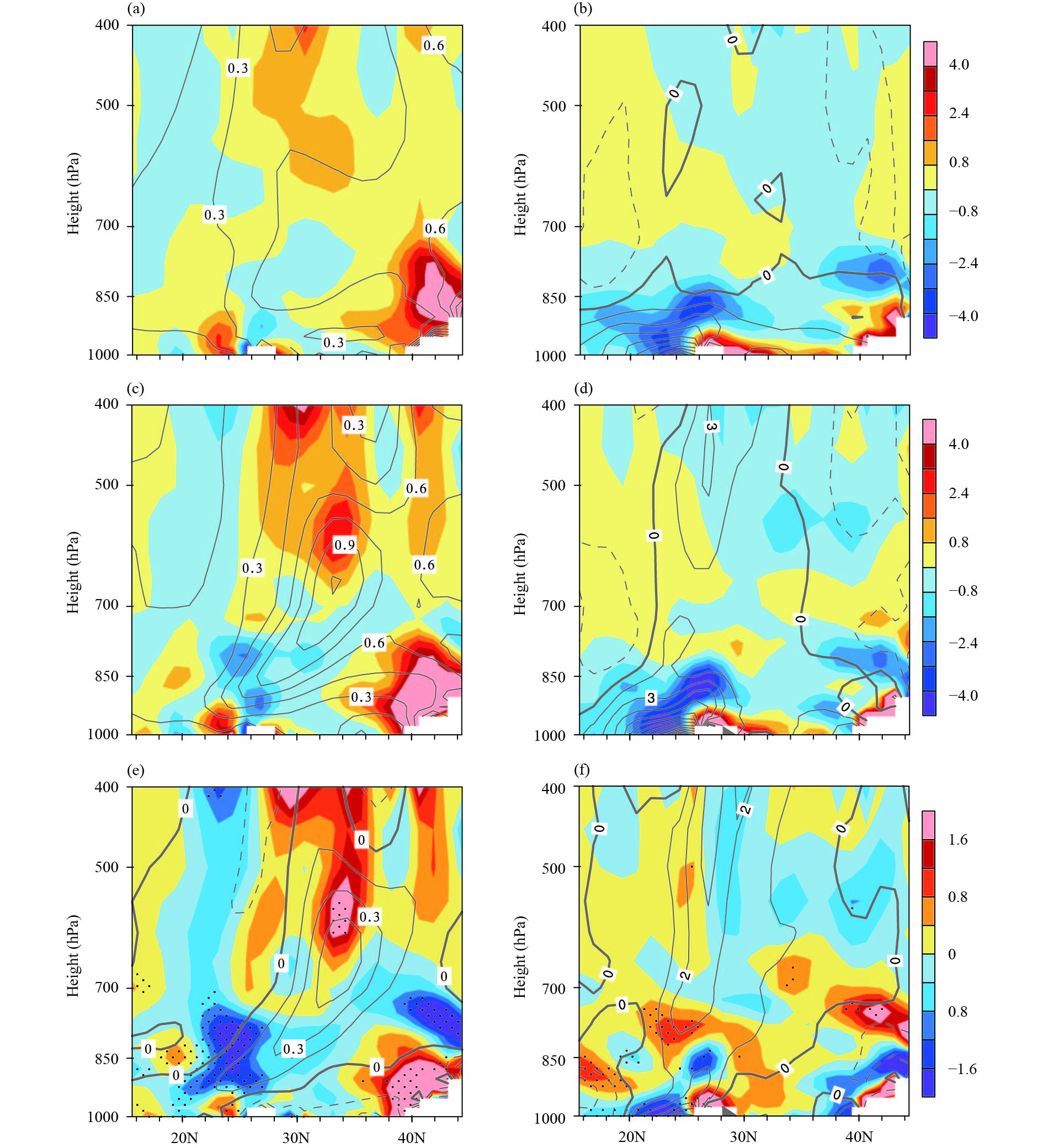
Figure 3 shows the vertical distribution of PVD advection term and the diabatic heating term calculated from the PVD equation [Eq. (8)] in isobaric coordinate system. Since the frictional effect in the free atmosphere is small, the contribution of the frictional term is ignored here. It can be seen that the distributions of PVD advection were similar during 1980–2017 (Fig. 3a) and the extreme winter storm disaster period (Fig. 3c). For both periods, a negative PVD advection center was located below 700 hPa, while a positive PVD advection center was located above 700 hPa near 30°N. However, the intensity of the positive and negative PVD advection centers during the storm period was greater than that of the climatology. During the storm period, the positive PVD advection near 30°N had two centers. One was located between 700 and 500 hPa and the other was located above 500 hPa (Fig. 3c). Compared with the climatology, these two positive PVD centers still existed during the storm period (Fig. 3e). The positive PVD advection center between 700 and 500 hPa corresponded to the eastward propagation of the PVD forcing originated from eastern TP, contributing significantly to the positive PVD anomaly in the middle and lower troposphere over southern China during the storm period. On the other hand, the PVD advection center above 500 hPa corresponded to the transport of PVD in the upper troposphere. Accompanied by the strengthening of the positive PVD advection at the middle and upper levels during the storm period, the negative PVD advection at 850 hPa near 25°N was also enhanced (Fig. 3e).

The distribution of the diabatic heating term also exhibited similar characteristics during 1980–2017 and the storm period, except that its intensity during the storm period was greater than the climatology. Diabatic heating dominated below 850 hPa during 1980–2017 (Fig. 3b). The strongest diabatic heating center was located near the South China Sea and southern China coastal areas. The diabatic heating in the lower troposphere decreased with height, corresponding to the formation of negative PVD. Diabatic cooling occupied above 850 hPa. But the intensity was relatively weak, corresponding to weak PVD production. During the storm period (Figs. 3d, f), the diabatic heating in the whole troposphere was enhanced over southern China. Due to the release of latent heating over the precipitation area, the diabatic heating rate in the middle and upper troposphere between 25° and 30°N was significantly increased. A positive PVD anomaly center appeared below the anomalous diabatic heating center (Fig. 3f). In addition, the enhancement of the diabatic heating rate in the region bounded by 20° and 27°N near the surface caused the strengthening of negative PVD anomaly near the surface south of 25°N.

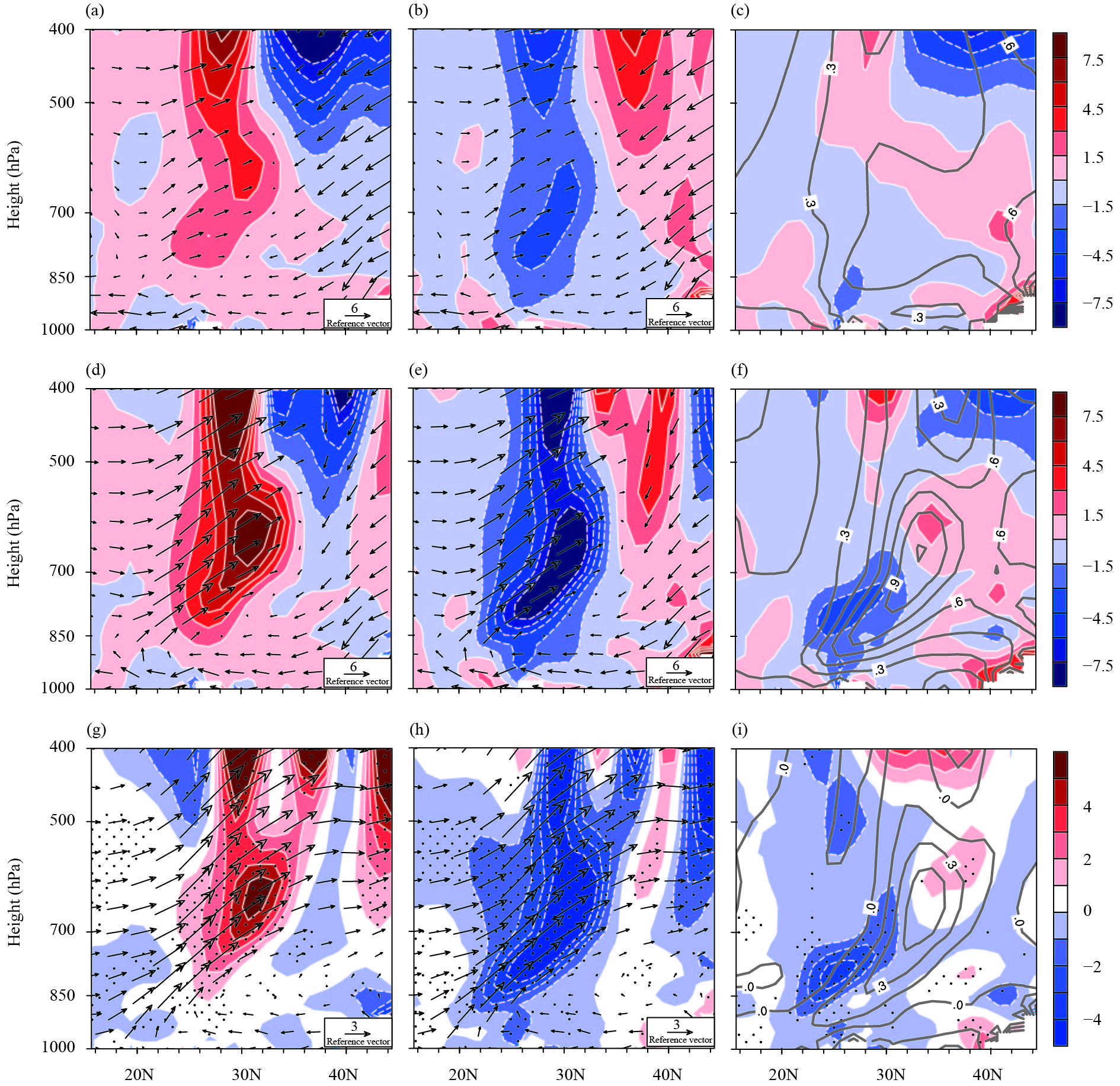
The above analysis demonstrates that the positive PVD anomaly near 700 hPa along 33°N shown in Fig. 2f was mainly caused by the PVD advection. Further analysis of the zonal and meridional PVD advection (Fig. 4) shows that the positive PVD advection was mainly related to the zonal PVD advection. A remarkable positive zonal PVD advection center was located in the upper troposphere near 30°N during 1980–2017 (Fig. 4a), which extended downward to 850 hPa. During the storm period (Fig. 4d), the positive zonal PVD advection center was greatly enhanced in the upper and middle troposphere. A strong positive zonal PVD advection center formed within 700–500 hPa near 30°N. The difference of zonal PVD advection between the two periods (Fig. 4g) shows that the enhancement of the positive zonal PVD advection in the upper and middle troposphere was separated. The strengthening of the zonal PVD advection above 500 hPa was related to the PVD advection in the upper troposphere, while the enhancement of the zonal PVD advection in the middle troposphere corresponded to the eastward propagation of PVD originated from eastern TP. The distribution of the meridional PVD advection was almost opposite to the distribution of the zonal PVD advection. The negative meridional PVD advection almost dominated the whole troposphere over southern China (Figs. 4b, e). The negative meridional PVD advection also had two centers in the upper and middle troposphere, which were located above 500 hPa and around 700 hPa. Interestingly, the intensity and location of the negative meridional PVD advection above 700 hPa were substantially equal to those of the positive zonal PVD advection, while the negative meridional PVD advection within 700–850 hPa was slightly stronger than the positive zonal PVD advection (Figs. 4c, f, i). Then, what is the role of these positive and negative PVD advection configurations in the formation of the extreme winter storm disaster?

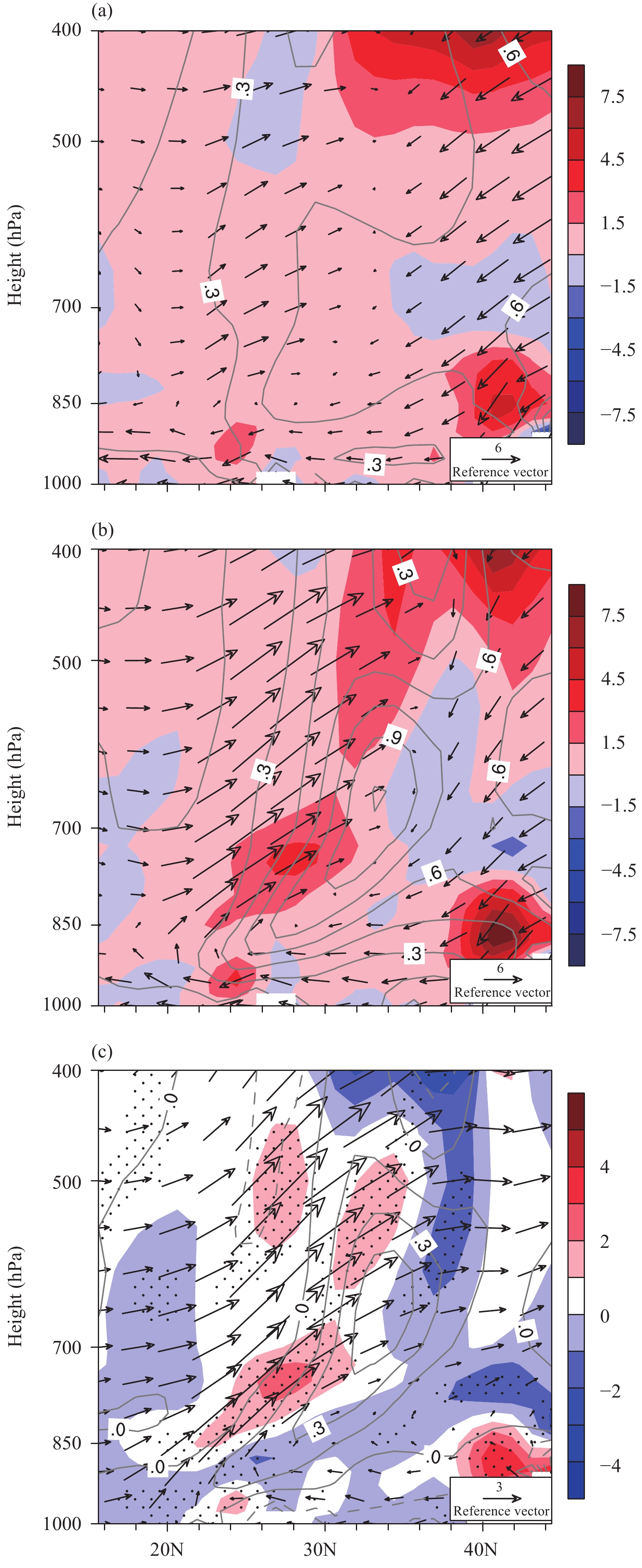
Figures 2d and 2f show that during the storm period, the ascending air in the middle and lower troposphere over southern China was significantly enhanced. Further exploration of the effect of ascending air on the evolution of the PVD (Fig. 5) shows that compared with the zonal and meridional PVD advections, the vertical PVD advection was relatively weak during both the climatological and the storm periods (Figs. 5a, b). Positive vertical PVD advection dominated almost the whole troposphere during 1980–2017 (Fig. 5a). The positive PVD advection caused by the ascending air during the storm period increased significantly between 850 and 700 hPa near 22°–30°N (Figs. 5b, c). The intensity of the positive vertical PVD advection was slightly weaker than that of the horizontal PVD advection (Figs. 4f, i), resulting in a negative distribution of the total PVD advection in this region (Figs. 3c, e). In addition, the positive vertical PVD advection between 650 and 500 hPa near 32°N was also strengthened. This positive vertical PVD advection, together with the positive horizontal PVD advection (Figs. 4f, i) produced a positive PVD advection between 700 and 500 hPa (Fig. 3c) and positive PVD advection anomalies (Fig. 3e). Therefore, it can be seen that in the isobaric PVD analysis of a severe weather process with the significant development of the ascending air, not only the horizontal PVD advection should be taken into consideration, but also the vertical PVD advection must be analyzed.

The above analysis indicates that during the storm period, the PVD between 700 and 500 hPa over southern China was significantly increased, which was beneficial to the increasing of the cyclonic circulation and the development of the ascending air. The enhancement of the PVD was closely related to the zonal PVD advection. In addition, the vertical velocity also contributed positively to the increasing of the PVD. The zonal PVD advection can be traced back to the eastward propagation of the PVD over eastern TP. Therefore, the extreme winter storm disaster over southern China was closely related to the surface PVD anomaly over eastern TP. In the following analysis, we attempt to answer the following questions: Why does the surface PVD increase over eastern TP? How does the eastward propagation of the PVD affect the precipitation over southern China?

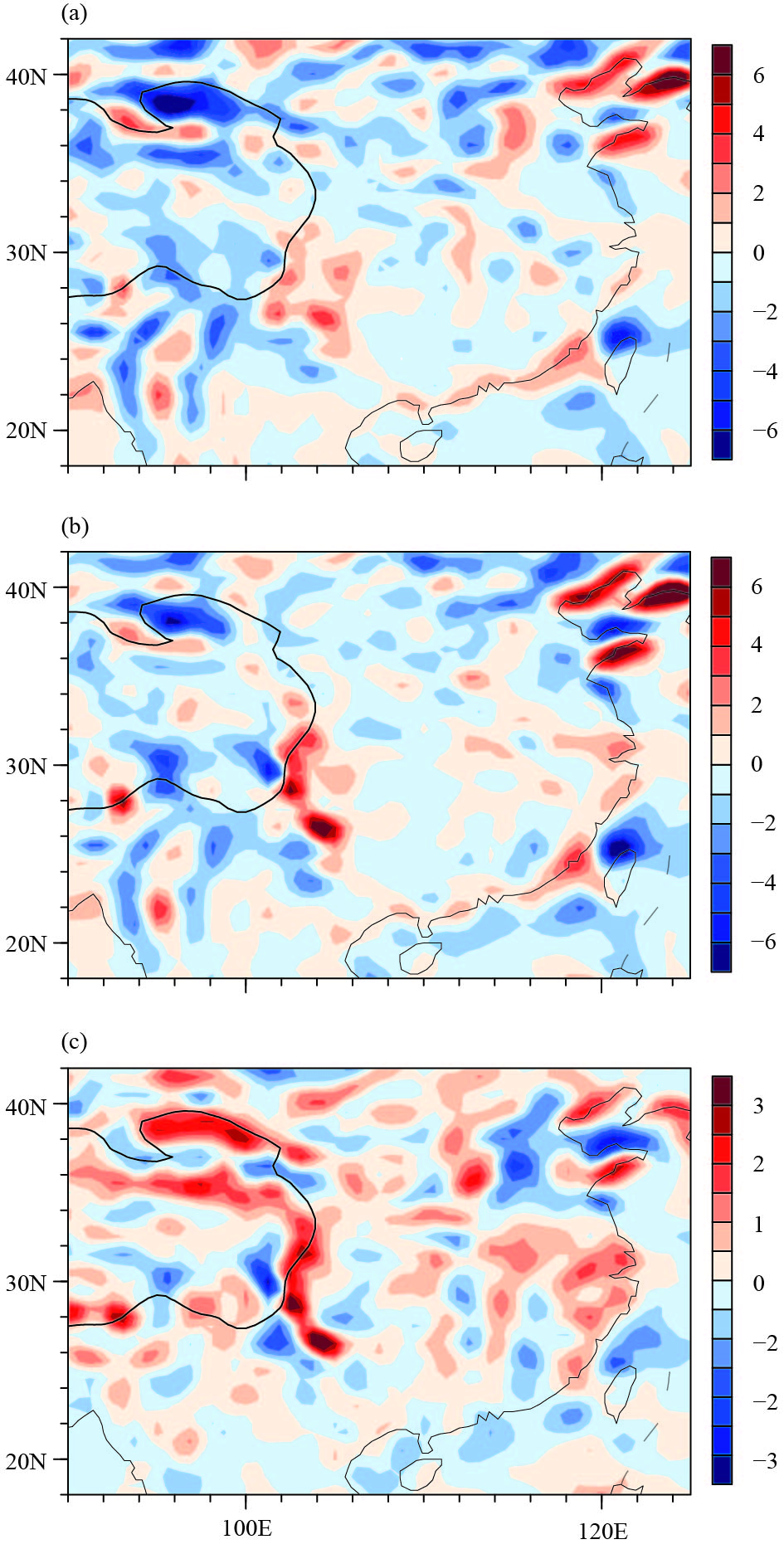
4 PVD forcing and its impact on the extreme winter storm

Figure 6 shows the distributions of surface PVD tendency during 1980–2017 and the storm period. It can be seen that the distributions of PVD tendency were rather messy. The PVD tendency along the coast and over the TP was relatively large. These are areas where the distribution of surface potential temperature was usually relatively dense. According to Eq. (12), these are key areas of surface PV generation. Compared with the climatology, positive PVD tendency anomalies were located over the northern and eastern TP and eastern coastal area during the storm period (Fig. 6c). Among them, the positive PVD tendency anomaly over the TP was greater than that in other regions. The TP is located in the upstream of the extreme winter storm disaster area. The positive PVD tendency anomaly, which was at an altitude of about 3000 m, could be transported into the interior of the isentropic surfaces in the middle troposphere, making the TP a source of PVD forcing. This explains why the negative PVD was located in the region to the west of 103°E and the positive PVD to the east over the eastern plateau as shown in Fig. 1.

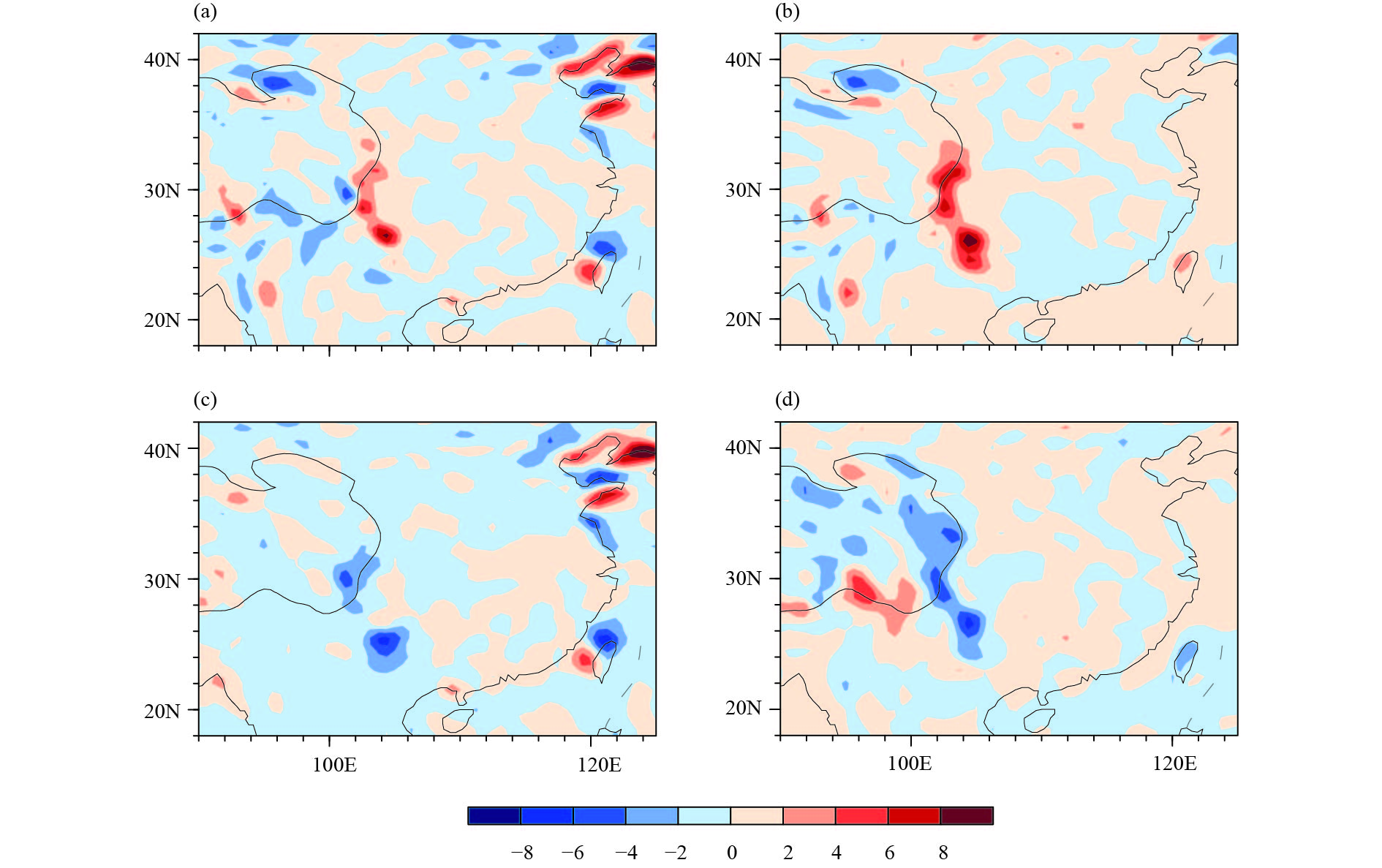
Further investigation of the role of dynamic and thermal factors in surface PVD tendency anomaly (Fig. 7) demonstrates that the convergence and divergence term of the PVD flux contributed most to the total surface PVD tendency (Fig. 7b), particularly for eastern TP, where this term was the only contributor to the positive PVD anomaly. The diabatic heating term was relatively weak (Fig. 7c), but it was important over the coastal areas of southern China. In addition, the southern slope of the TP also had strong positive PVD anomaly produced by diabatic heating. Frictional term was the weakest among the three terms (Fig. 7d) and contributed little to the overall surface PVD anomaly.

The convergence/divergence term of the PVD flux can be divided into the air convergence/divergence term and the PVD advection term: $ - \nabla \cdot \left({W{V}} \right) = $ $ - W\nabla \cdot {V} - {V} \cdot \nabla W $ . Comparing the contributions of these two terms (Fig. 8) reveals that the air convergence/divergence term contributed most to the positive PVD tendency over eastern TP (Fig. 8b). That was mainly due to the strong convergence of the surface air (Fig. 8d), while the PVD advection term had negative contribution in this area (Fig. 8c). The distribution of PVD tendency in coastal areas was mainly controlled by the PVD advection term (Fig. 8c).

The above analysis shows that due to the strong surface air convergence over the eastern plateau during the storm period, positive PVD forcing enhanced on the surface of eastern TP, which was conducive to the enhancement of cyclonic circulation and the development of convection system in the plateau. Due to the high terrain of TP, the positive PVD forcing can propagate downstream under the effect of westerly wind in the middle and lower troposphere. Then, how does the eastward propagation of the PVD forcing cause the precipitation over southern China?

As mentioned above, in the isentropic coordinate system, the PVD is essentially the isentropic absolute vorticity; while in the isobaric coordinate system, the PVD retains the dynamic and thermal properties of the PV. Therefore, in these two coordinate systems, the eastward propagation of the PVD is inevitably accompanied by the eastward propagation of the absolute vorticity. Hence, positive absolute vorticity advection appeared in the middle and upper troposphere over southern China during the storm period (Fig. 9a). According to the previous analysis, the appearance of positive absolute vorticity advection below 500 hPa was related to the enhancement and eastward propagation of surface PVD over eastern TP. The absolute vorticity advection in the middle troposphere was slightly smaller than that in the upper troposphere. With the increasing of positive absolute vorticity advection, the cyclonic circulation increased over southern China, which was beneficial to the development of low-level convergence and southerly wind near 30°N. In addition, the spatial distribution of relative vorticity over southern China during the storm period was represented by 28°N as a boundary (Fig. 9b), with positive relative vorticity to its north and negative relative vorticity to its south. Strong westerly wind was located between the positive and negative relative vorticity areas. Since the positive relative vorticity center was located north of 30°N, the occurrence of low-level southerly wind was conducive to the enhancement of negative meridional absolute vorticity advection to the south of 30°N (Figs. 4, 9a). Thus, similar to the PVD advection configuration shown in Fig. 4, the large-scale circulation background in which the absolute vorticity advection increased with height over southern China favored the development of the ascending air. The development of the ascending air further strengthened the low-level convergence and southerly wind, which continuously strengthened the negative meridional absolute vorticity advection. Consequently, the circulation background in which the absolute vorticity advection increased with height was further enhanced. Under such a background, the ascending air and the low-level convergence were continuously strengthened, promoting the occurrence of the extreme precipitation over southern China.

Figure 9 also shows that in the south of the Huaihe River during the storm period, the northerly wind with cold advection occupied below 850 hPa, while southerly wind with warm advection dominated above 850 hPa. The distribution of temperature (Fig. 9b) shows that the near-surface temperature over southern China was relatively low during the storm period. The 0°C isotherm was located near 27°N, which was about 10° southward than the 0°C isotherm in the climatology. The warm and humid airflow in the lower troposphere between 24° and 32°N caused higher temperature between 850 and 700 hPa, which was about 3 K higher than that between 950 and 900 hPa, forming an inversion layer. This temperature distribution in the lower troposphere was conducive to the formation of snowfall and freezing rain over southern China.

5 Summary and discussion

Based on the PV theory, the relationship between surface PV generation and PVD forcing has been analyzed in details in this study. By using MERRA-2 reanalysis data, the mechanism for the enhancement of surface PVD forcing over the TP and its eastward propagation, as well as the induced precipitation in the downstream area of the TP are explored. The main conclusions are summarized as follows.

Air convergence or divergence, diabatic heating, and frictional forcing are sources or sinks of atmospheric PVD. In an adiabatic and frictionless flow, the PV is conserved, but the PVD is not. Air convergence or divergence can generate PVD. When an isobaric coordinate system is adopted, the PVD is conserved. The PVD retains the dynamic and thermal properties of the PV. However, in the isentropic coordinate system, the PVD is in essence the isentropic absolute vorticity.

The surface air convergence over the eastern TP can generate positive PVD forcing. Due to the high altitude of the plateau, the isentropic surfaces intersect with the plateau’s surface, making it the source of surface PVD forcing. It is easy for the positive PVD forcing to propagate downstream along westerly flow, and then affect the weather in the downstream area.

Along with the eastward propagation of the positive PVD forcing originated from eastern TP, the absolute vorticity in the middle troposphere increases and the cyclonic circulation strengthens over southern China, which is beneficial to the development of low-level convergence and southerly wind. The latter can bring abundant moist air from the south. In addition, the emergence of low-level southerly wind is also conducive to the enhancement of negative meridional absolute vorticity advection. Thus, a large-scale circulation background is formed, in which the absolute vorticity advection increases with the increasing height. This favors the development of ascending air. Because of the remarkable development of the ascending air during the severe weather process, analysis of the vertical PVD transport must be included. The development of the ascending air can further strengthen the low-level convergence and southerly wind. As a result, the negative meridional absolute vorticity advection in the lower troposphere is continuously strengthened, and the circulation background in which the absolute vorticity advection increases with height is also further strengthened. Under such a background, the ascending airflow continues to develop and enhance, promoting the occurrence of the extreme precipitation over southern China.

From the perspective of data analysis, this study proposes a new mechanism for the impact of the TP on the occurrence of the extreme winter storm disaster over southern China in early 2008. The near-surface atmospheric convergence over eastern TP is beneficial to the increasing of surface positive PVD forcing. The generated surface PVD forcing then propagates eastward, and leads to the precipitation over the downstream area. The related numerical simulation study is given by Yu et al. (2019) and their results support our findings.

This study did not consider the impacts of friction. Since the height of the boundary layer over the plateau is higher than that over the plain area (Li and Xu, 2005), and the drag coefficient is also large (Li et al., 2001), the influence of friction within the boundary layer over the TP on PV behaviour can be important. Further investigation is needed for the accurate calculation of the frictional impact.

Acknowledgment. The authors thank the Global Modeling and Assimilation Office (GMAO) and GES DISC for providing the MERRA-2 data.