The Chinese Meteorological Society
Article Information
- HU, Juyang, Shihao TANG, Hailei LIU, et al., 2019.
- An Operational Precipitable Water Vapor Retrieval Algorithm for Fengyun-2F/VISSR Using a Modified Three-Band Physical Split-Window Method . 2019.
- J. Meteor. Res., 33(2): 276-288
- http://dx.doi.org/10.1007/s13351-019-8111-4
Article History
- Received July 18, 2018
- in final form December 21, 2018
2. Key Laboratory of Atmospheric Sounding, Chengdu University of Information Technology, Chengdu 610225
Fengyun-2 (FY-2), the Chinese first-generation geostationary (GEO) meteorological satellite series, is managed and operated by the National Satellite Meteorological Center, China Meteorological Administration (NSMC/CMA). Seven FY-2 series GEO satellites (from FY-2A to FY-2G) have been launched successfully and collected data for more than 20 successive years. FY-2E, FY-2F, and FY-2G, located at 86.5°, 112°, and 105°E, respectively, remained in space and were active until the end of 2017. The unique Visible and Infrared Spin-Scan Radiometer (VISSR) aboard FY-2 has five installed channels, from visible (VIS, 0.66 μm) to thermal infrared (IR, 12.0 μm) wavelengths, with spatial resolutions of 1.25 km (VIS) or 5.0 km (IR) (Hu et al., 2013). The VISSR imager normally provides full-disk observations every 60 min; this maneuver is enhanced to 30 min during the rainy season from May to September. The current two-satellite constellation function as back-ups for each other, and this can also increase the full-disk observation frequency to 15 min. Besides this traditional observation mode, FY-2F also has a fast target-area scanning function that focuses on a local area of interest every 6 min. Real-time FY-2 observation data with a high spatiotemporal resolution are always used when estimating or retrieving important atmospheric and environmental parameters (Guo et al., 2014; Hu et al., 2008), including precipitable water vapor (PWV).
PWV is generally defined as the total atmospheric water vapor contained in a vertical column of a cross-sectional unit of area extending from the earth’s surface to the top of the atmosphere. Long-term and continuous PWV data can make good contribution to regional climate analyses in energy budgets and hydrological cycles (Trenberth et al., 2009). High frequency PWV or other weather products from the GEO satellites can also be applied in real-time monitoring and nowcasting of mesoscale weather conditions such as typhoons, heavy rainfall, and strong convective weather (Min and Zhang, 2014; Min et al., 2017). Moreover, as an important atmospheric correction parameter, PWV can directly improve the precision of land surface temperature estimates from FY-2/VISSR thermal infrared data (Labbi and Mokhnache, 2015).
However, due to a lack of near infrared or microwave observations, the FY-2/VISSR PWV retrieval algorithm can only use thermal infrared observation data. According to many previous studies (Dalu, 1986; Jedlovec, 1990; Ottle et al., 1997; Czajkowski et al., 2002), physical split-window (PSW) algorithm for PWV product retrieval performed as well or better than other thermal infrared retrieval techniques (Suggs et al., 1998). The PSW technique has been chosen and already implemented in the current FY-2 operational system (Shi, 2005). However, Min et al. (2015) found that the relative errors of the PWV measurements made over the Tibetan Plateau using theFY-2E/VISSR were up to 780.45% in the dry months compared to PWV data from radiosondes. This result showed clearly that the current quality of FY-2/VISSR PWV product needs improvements for dry conditions.
The PSW technique and other thermal infrared PWV retrieval algorithms all use the differential water vapor absorption of split-window channels (Kleespies and McMillin 1990), referring to the pair of channels at 11.0 and 12.0 μm. For dry atmospheric conditions, the accuracy of PWV could easily be influenced by uncertainties in surface emissivity (Sun et al., 2013), instrument noise, and calibration errors (Liu et al., 2017). Retrieved by the same PSW algorithm, PWV products of FY-2/VISSR and FY-3/VIRR (visible and infrared radiometer) have good agreement with radiosonde data for most cases but tend to overestimate the PWV values at lower humidity levels (Hu et al., 2017; Shi et al., 2018). FY-2/VISSR carries a 6.9-μm channel whose spectral response functions cover a wide water vapor absorption region (Hu et al., 2013). This channel is more sensitive to water vapor than split-window channels. In addition, the radiances observed from space by this band are primarily from the emissive energy within 250–500 hPa of the upper troposphere (Steranka et al., 1973). This means that the measured radiances are closely associated with middle to upper tropospheric moisture content (Muller and Fuelberg, 1990). Furthermore, this band can provide extra data on atmospheric temperature if there is enough moisture in the atmosphere (Seemann et al., 2003; Tang and Li, 2008). Overall, the sensitivities of this band imply that it could potentially have an effect on improving the accuracy of PWV retrieval. Zhu et al. (1998) attempted to retrieve PWV using the split-window and water vapor channel brightness temperatures from the Geostationary Meteorological Satellite (GMS-5), based on statistical regression techniques. However, the final results did not show a significant improvement over the split-window technique. Liu et al. (2017) presented an improved PSW technique by adding water vapor channel observations and achieved more accurate PWVs using either FY-2G/VISSR or moderate-resolution imaging spectroradiometer (MODIS)/Terra data.
Therefore, the primary objective of this investigation is to develop an effective and robust operational PWV algorithm for FY-2F/VISSR data, through modifying the improved three-band PSW technique (Liu et al., 2017). The new operational algorithm will be able to significantly enhance the quality of FY-2F/VISSR PWV products compared to the current operational products, especially in dry atmospheric conditions. Section 2 of this paper briefly describes the dataset used in this study. Section 3 introduces the atmospheric water vapor sensitivity experiment for three FY-2F/VISSR channels, the original operational PWV inversion method, and the new operational PWV inversion method. Validations for the new FY-2F PWV products are shown in Section 4. Finally, the conclusions are drawn in Section 5.
2 Data sources 2.1 FY-2F/VISSRFY-2F, the first satellite in Group-3 of the FY-2 series of GEO meteorological satellites, was successfully launched in January 2012. One of most the significant improvements inFY-2F, compared to the other FY-2 satellites, is its fast target-area scanning function. With the ability to be flexible and frequently observe regions of interest, the measurements from FY-2F can be better applied to real-time monitoring and nowcasting of mesoscale severe weather. The five spectral channels on FY-2F/VISSR include a visible channel, two split-window channels, a water vapor channel, and a mid-infrared channel. Detailed instrument specifications ofFY-2F/VISSR are listed in Table 1.
| Band | Bandwidth (μm) | Spatial resolution (km) | Sensitivity/signal-to-noise ratio | Dynamic range |
| VIS | 0.55–0.75 | 1.25 | ≥ 2 (albedo = 1%) | 0%–98% |
| IR1 | 10.3–11.3 | 5 | 0.2–0.4 K@300 K | 180–330 K |
| IR2 | 11.5–12.5 | 5 | 0.2–0.4 K@300 K | 180–330 K |
| WV | 6.3–7.6 | 5 | 0.3–0.6 K@260 K | 190–300 K |
| IR3 | 3.5–4.0 | 5 | 0.3–0.6 K@300 K | 220–340 K |
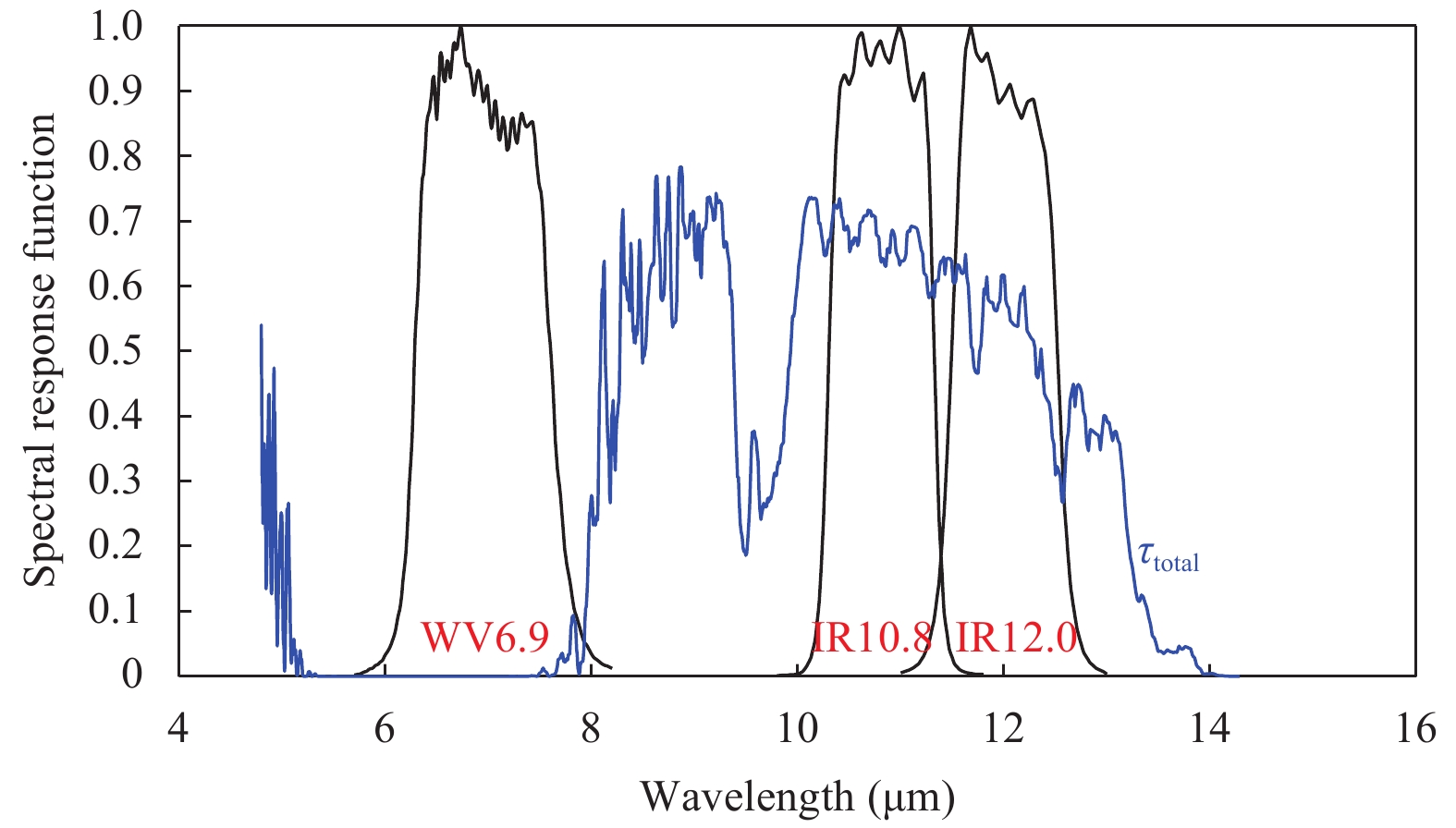
Figure 1 shows the spectral response functions of three single channels (WV6.9, IR10.8, and IR12.0) of FY-2F/VISSR and a typical atmospheric transmissivity spectrum line simulated by using a midlatitude summer atmosphere profile based on the MODerate resolution atmospheric TRANsmission (MODTRAN) 4.0 radiative transfer model. It is clear that bands IR10.8 and IR12.0 are located at atmospheric absorption window regions with high atmospheric transmissivity, and the WV6.9 band covers a water vapor absorption region. The FY-2F/VISSR data used in this study are L1b radiance data, L2 cloud detect products, and geographical information based on measurements taken at 0000 UTC January–December 2016, and are downloaded for free via the Fengyun Satellite Data Archiving and Order Center (http://satellite.nsmc.org.cn).
|
| Figure 1 Spectral response functions (black lines) of the WV6.9, IR10.8, and IR12.0 channels of the FY-2F/VISSR. A typical atmospheric transmissivity spectrum line (blue) is simulated by using midlatitude summer atmosphere profile based on the MODTRAN 4.0 radiative transfer model. WV6.9, IR10.8, and IR12.0 represent the channels with the mid-wavelengths of 6.9, 10.8, and 12.0 μm, respectively. |
The T639L60 (T639) model is an operational global medium-term numerical weather prediction (NWP) model developed by the CMA. Its horizontal resolution is 30 km with 60 vertical layers, up to 0.1 hPa. The operational data interval is 3 h, and forecast predictability time is 240 h (Chang, 2015). These can be freely downloaded from the Data Archiving and Order Center of National Meteorological Center (NMC) at the CMA (http://nwpc.nmc.cn/sites/main/index.htm).
Four atmospheric variables in T639 are used to retrieve PWV in this study: temperature profile (T), humidity profile (Q), surface temperature (Ts), and surface pressure (ps). As the first-guess environmental fields used in the PWV algorithm, the variables from the T639 NWP data should be temporally and spatially interpolated to match the scale of the observation times and the fixed GEO-locations of every imaging pixel in the FY-2/VISSR L1b data. All four variables were interpolated into the FY-2F/VISSR grid. Vertically, the T and Q profiles will be interpolated into the standard atmospheric pressure layers of the radiative transfer model.
2.3 RadiosondesTo validate the retrieved PWV products, the radiosonde data available for free download from the University of Wyoming (http://weather.uwyo.edu/upperair/sounding.html) are used as the truth data. These vertical profiles were retrieved from different types of radiosondes and models launched in temperate, tropical, desert, and subtropical atmospheric conditions (Julien et al., 2015). In this investigation, 452 radiosonde sites located in FY-2F/VISSR disk are chosen, as shown in Fig. 2. The distribution in Fig. 2 demonstrates that radiosonde data include samples from over land and sea in the Northern and Southern Hemispheres. The PWV is derived from the radiosondes by integrating the humidity from the surface to the top of the sounding profile and eliminating samples with negative values.

|
| Figure 2 Locations of the radiosonde (circles) used to validate the results of this study. |
To analyze the sensitivities of the split-window and water vapor channel observations to PWV, numerical radiative transfer simulations are performed by using six typical atmospheric profiles from MODTRAN V4.0 model (Berk et al., 1999): tropical (TRO), midlatitude summer (MLS), midlatitude winter (MLW), sub-Arctic summer (SAS), sub-Arctic winter (SAW), and 1976 United States standard atmospheres (1976US).
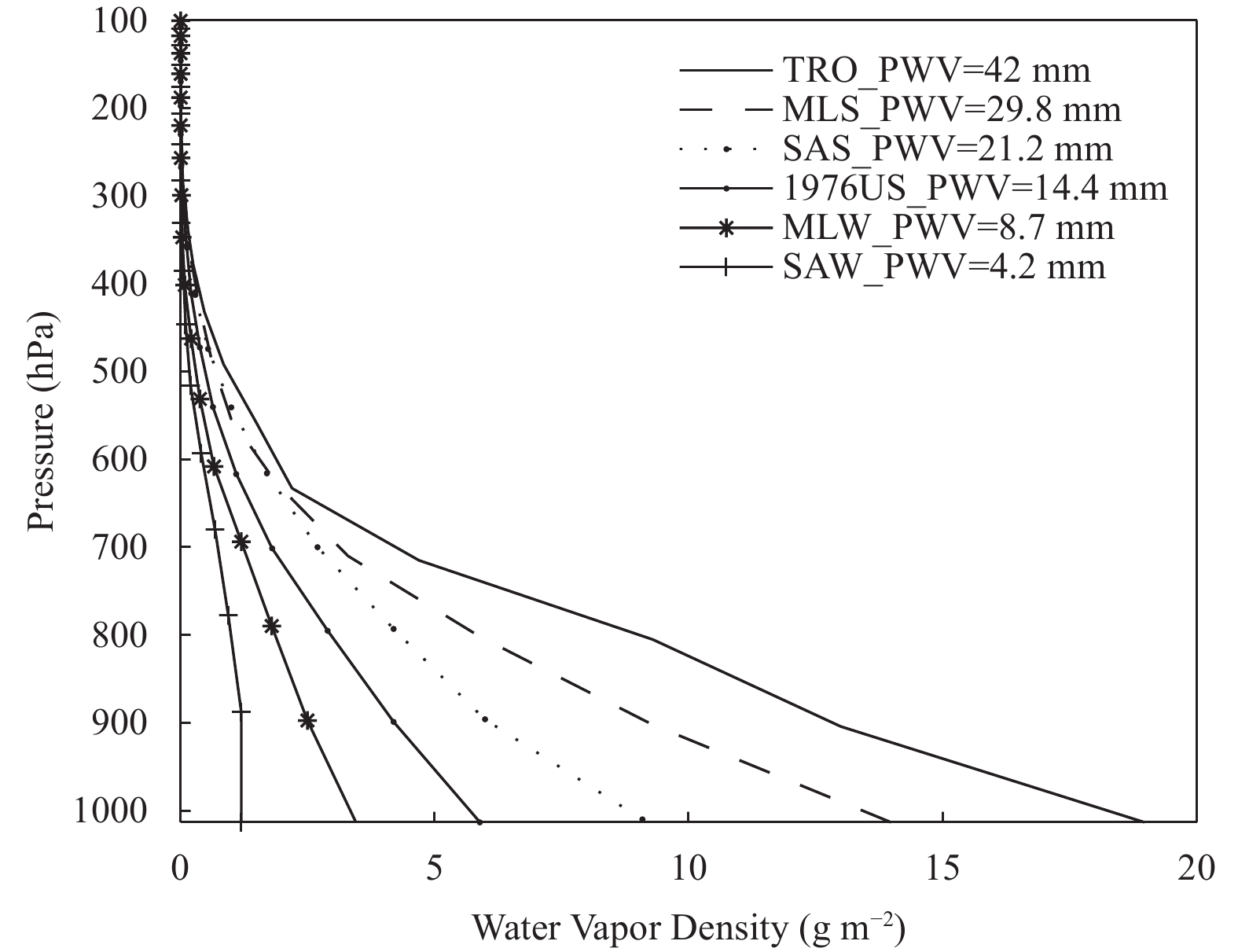
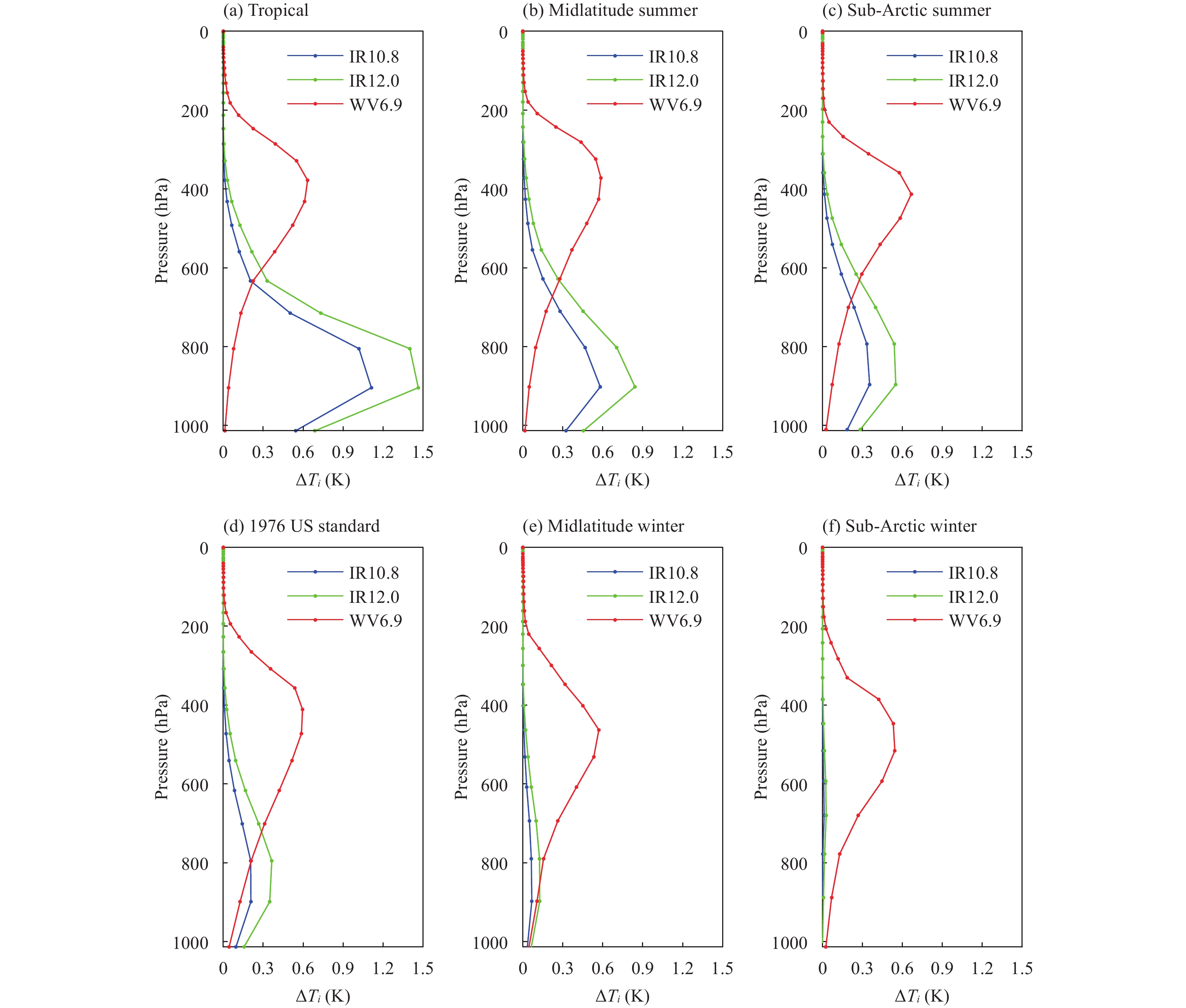
These six typical atmospheric profiles all include 33 layers from 0 to 100 km above sea level, and their water vapor density profiles are shown in Fig. 3. Every point in Fig. 4 refers to the change of brightness temperature (ΔTi) caused by reducing 50% of the humidity at the specific layer of every atmospheric profile. As theorized, the WV6.9 channel shows more sensitivity to water vapor at 300–500 hPa, while the water vapor sensitive layers for IR10.8 and IR12.0 are below 600 hPa. In addition, as Guillory et al. (1993) concluded, it is clear that the water vapor can be routinely measured and retrieved up to approximately 300 hPa using only two FY-2F IR split-window channels but also that it will become very difficult to measure or retrieve water vapor at higher altitudes. Therefore, the WV6.9 channel could provide a supplement for retrieving water vapor in the higher layers.
|
| Figure 3 Distributions of the following six typical atmospheric profiles: TRO (tropical), MLS (midlatitude summer), MLW (midlatitude winter), SAS (sub-Arctic summer), SAW (sub-Arctic winter), and 1976US (1976 United States standard). |
|
| Figure 4 The differences in the brightness temperature (ΔTi) of three FY-2F/VISSR channels [IR10.8 (blue lines), IR12.0 (green lines), and WV6.9 (red lines)] between six original/typical and humidity-changed atmospheric profiles: (a) tropical, (b) midlatitude summer, (c) sub-Arctic summer, (d) 1976 US standard, (e) midlatitude winter, and (f) sub-Arctic winter. |
Figures 4a–d also show that IR10.8 and IR12.0 are sensitive to water vapor changes in TRO, MLS, SAS, and 1976US atmospheres, but only very slightly so for MLW and SAW atmospheres (Figs. 4e, f). Meanwhile, the sensitivities of WV6.9 to water vapor are significant in the six typical atmospheric profiles. As shown in Fig. 3, the PWV values of SAW, MLW, 1976US, SAS, MLS, and TRO are 4.2, 8.7, 14.4, 21.2, 29.8, and 42 mm, respectively. Therefore, WV6.9 is necessary to retrieve water vapor in drier atmosphere or to enhance the accuracy of PWV products.
3.2 The original operational PWV inversion method based on the traditional PSW algorithmThe PSW method was first developed by Jedlovec (1987) to retrieve PWV from the split-window channels of the Multispectral Atmospheric Mapping Sensor using the constraints of the radiative transfer equation (Guillory et al., 1993). This technique has already been widely used to retrieve PWV for data from many satellites (Haines et al., 2004; Shi and Xie, 2005; Zheng et al., 2010), and it is also the operational algorithm for the PWV of FY-2/VISSR data (Xu et al., 2008). The retrieval equations are derived from the simplified radiative transfer equations, which assume a non-scattering, plane-parallel, cloud-free atmosphere, and an emissivity of unity. The detailed derivation of the PSW method is given in Suggs et al. (1998). The derived equations used to calculate the perturbations of skin temperature (δTs) and the departures of total PWV (δU) from a mean of first-guess state and can be written as follows:
| ${{\delta }}{T_{{\rm{IR}}1}} = \delta {T_ {\rm{s}}}{C_{{\rm{IR}}1}} + \left( {\frac{{\delta U}}{{{U_0}}}} \right){D_{{\rm{IR}}1}},$ | (1) |
| ${{\delta }}{T_{{\rm{IR}}2}} = \delta {T_ {\rm{s}}}{C_{{\rm{IR}}2}} + \left( {\frac{{\delta U}}{{{U_0}}}} \right){D_{{\rm{IR}}2}},$ | (2) |
where the subscripts IR1 and IR2 represent two particular split-window channels and water vapor channel, respectively; U0 and Ts are the first-guess PWV and skin temperature, and the related perturbation terms of δU and δTs are unknown; and δTIR1 and δTIR2 are the perturbations of the brightness temperature of the two channels contributed by the perturbations in skin temperature and PWV. The coefficients C and D are defined as follows:
| ${C_{{\rm{IR}}1}} = {\tau _{{\rm{sIR}}1}}\left( {\frac{{\partial {B_{{\rm{IR}}1}}\left( {{T_{{\rm{IR}}1}}} \right)}}{{\partial {T_ {\rm{s}}}}}} \right){\left( {\frac{{\partial {B_{{\rm{IR}}1}}\left( {{T_{{\rm{IR}}1}}} \right)}}{{\partial {T_{{\rm{IR}}1}}}}} \right)^{ - 1}},\!\!\!\!\!\!\!\!\quad\quad\quad$ | (3) |
| ${C_{{\rm{IR}}2}} = {\tau _{{\rm{sIR}}2}}\left( {\frac{{\partial {B_{{\rm{IR}}2}}\left( {{T_{{\rm{IR}}2}}} \right)}}{{\partial {T_ {\rm{s}}}}}} \right){\left( {\frac{{\partial {B_{{\rm{IR}}2}}\left( {{T_{{\rm{IR}}2}}} \right)}}{{\partial {T_{{\rm{IR}}2}}}}} \right)^{ - 1}},\!\!\!\!\!\!\!\!\quad\quad\quad$ | (4) |
| ${D_{{\rm{IR}}1}} = \mathop \int \limits_0^{{ p_ {\rm{s}}}} U\left( p \right)\frac{{\partial {\tau _{{\rm{IR}}1}}}}{{\partial U}}{\left( {\frac{{\partial {B_{{\rm{IR}}1}}\left( {{T_{{\rm{IR}}1}}} \right)}}{{\partial {T_{{\rm{IR}}1}}}}} \right)^{ - 1}}{\rm{d}}{B_{{\rm{IR}}1}}\left( {{T_ {\rm{p}}}} \right),$ | (5) |
| ${D_{{\rm{IR}}2}} = \mathop \int \limits_0^{{ p_ {\rm{s}}}} U\left( p \right)\frac{{\partial {\tau _{{\rm{IR}}2}}}}{{\partial U}}{\left( {\frac{{\partial {B_{{\rm{IR}}2}}\left( {{T_{{\rm{IR}}2}}} \right)}}{{\partial {T_{{\rm{IR}}2}}}}} \right)^{ - 1}}{\rm{d}}{B_{{\rm{IR}}2}}\left( {{T_ {\rm{p}}}} \right),$ | (6) |
where τ is the atmospheric transmittance; B is the Planck function radiance; T and p are the temperature and pressure, respectively; and the subscripts s and p represent the surface pressure and specific pressure, respectively.
With a priori information on the first-guess temperature, humidity and pressure profiles, surface temperature, and surface pressure, typical radiative transfer models [e.g., MODTRAN, the Radiative Transfer for Television Operational Vertical (RTTOV), or the Community Radiative Transfer Model (CRTM) from the U.S. Joint Center for Satellite Data Assimilation] can be used to simulate the atmospheric transmittance and radiance. The first-guess temperature profile should be the same as or very close to the observed profile (Suggs et al., 1998).
In the operational PWV retrieval program, to ensure the first-guess parameters obtained timely and conveniently, only T639 data (see Section 2.2) can be used as first-guess data. At the same time, to meet the needs of rapid transmittance and radiance simulations, RTTOV was preferred as the radiative transfer model. Four variables from the matched T639 data referred to in Section 2.2 combined with the FY-2F/VISSR cloud detection products, land–sea mask, and viewing geometry data, are all put into the RTTOV model (Saunders, 2002), which has been used widely in satellite data assimilation and retrieval. Once the atmospheric transmittances and other parameters in Eqs. (3)–(6) have been calculated by RTTOV, the coefficients C and D can be obtained. Preparations are then made to calculate the differences between the brightness temperatures simulated by RTTOV and recorded in the FY-2F/VISSR L1b files. Based on the coefficients (C and D) and the brightness temperature differences of two split-window channels, the related perturbation term δU can be calculated through Eqs. (1) and (2). Finally, as first-guess PWVs are obtained from the T639 humidity profiles, the PWV can be retrieved by using Eq. (7).
| $U = {U_0} + \delta U.$ | (7) |
In theory, the effects of surface heterogeneity (Coret et al., 2004) and multiple scattering are very difficult to eliminate in simulations through radiative transfer models and satellite calibrations under large satellite view zenith angles. Therefore, only absolutely clear pixels with a satellite view zenith angle smaller than 70° can be included in the FY-2F/VISSR PWV calculations.
3.3 The new operational PWV inversion method based on the modified three-band PSW algorithmRecently, Liu et al. (2017) proposed an improved PSW algorithm by adding a water vapor channel to the traditional PSW retrieval technique. In this method, δU is calculated by using Eqs. (1), (2), and (8). The first-guess parameters and radiative transfer model used in their study for PWV retrieving from FY-2G/VISSR are the ERA-Interim data and MODTRAN, respectively. The corresponding flowchart is shown in Fig. 5 of Liu et al. (2017). They proved that this approach can reduce PWV retrieval errors caused by uncertainties in the surface emissivity, first-guess field data, instrument noise, and calibration error. This significantly enhances the accuracy of PWV retrieved under dry atmospheric conditions (PWV < 2 cm).
| ${{\delta }}{T_ {\rm{WV}}} = \delta {T_ {\rm{s}}}{C_ {\rm{WV}}} + \left( {\frac{{\delta U}}{{{U_0}}}} \right){D_ {\rm{WV}}}, \!\!\!\!\quad\quad\quad\quad\quad\quad\quad\quad\quad$ | (8) |
| $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{C_ {\rm{WV}}} = {\tau _ {\rm{sWV}}}\left( {\frac{{\partial {B_ {\rm{WV}}}\left( {{T_ {\rm{WV}}}} \right)}}{{\partial {T_ {\rm{s}}}}}} \right){\left( {\frac{{\partial {B_ {\rm{WV}}}\left( {{T_ {\rm{WV}}}} \right)}}{{\partial {T_ {\rm{WV}}}}}} \right)^{ - 1}}, $ | (9) |
| ${D_ {\rm{WV}}} = \mathop \int \limits_0^{{p_ {\rm{s}}}} U\left( p \right)\frac{{\partial {\tau _ {\rm{WV}}}}}{{\partial U}}{\left( {\frac{{\partial {B_ {\rm{WV}}}\left( {{T_ {\rm{WV}}}} \right)}}{{\partial {T_ {\rm{WV}}}}}} \right)^{ - 1}}{\rm{d}}{B_ {\rm{WV}}}\left( {{T_ {\rm{p}}}} \right),$ | (10) |
where δTWV is the perturbation of the brightness temperature of the water vapor channel contributed by the perturbations in skin temperature and PWV; CWV and DWV are coefficients of water vapor channel.
To improve the accuracy of FY-2F/VISSR operational PWV products under dry atmospheric conditions, we tried to use the improved PSW algorithm instead of the traditional PSW algorithm. When producing the operational products, as described in Section 3.2, T639 data and RTTOV are selected as first-guess data and the radiative transfer model, respectively.
The improved PSW algorithm, the same as traditional PSW algorithm, depends on the assumption of the same moisture structure in vertical between the first-guess and observed moisture profiles. Therefore, the ratio of the departure [δU(p)] to the first-guess water vapor content [U0(p)] for every pressure layer is equal to the ratio of the whole column (
| $\frac{{{{\delta U}}\left( {{p}} \right)}}{{{{{U}}_0}\left( {{p}} \right)}} = \frac{{{{\delta U}}}}{{{{{U}}_0}}} = {\rm{constant}}.$ | (11) |
In the two-band algorithm, the water vapor sensitive layers of two split-window channels are both the lower layers of the atmosphere (Fig. 4), which contain the majority of the water vapor of the atmospheric column. Therefore, the above assumption for the two-band algorithm is reasonable. However, as shown in Fig. 4, the water vapor sensitive layers of the water vapor channel, which are the upper layers of the atmosphere, are different from the two split-window channels. Therefore, the above assumption for the three-band algorithm may affect the accuracy of the inversions. Moreover, as the analysis in Liu et al. (2017) showed, the three-band algorithm is more sensitive to water vapor vertical distribution uncertainties of first-guess data, especially at high PWV values. Unfortunately, the precision of T639 data in upper layers is sometimes lower than in lower layers (Chang, 2015). The ratio of the departure to the first-guess water vapor content in the upper layer is different from the ratio of the whole column. It can be inferred that the assumption described in Eq. (11) is better to be modified for water vapor channel in the three-band FY-2F/VISSR operational algorithm.
We add a new coefficient of A in Eq. (11) to represent an average ratio, in spite of the fact that the ratio
| $\frac{{{{\delta U}}\left( {{{p'}}} \right)}}{{{{{U}}_0}\left( {{{p'}}} \right)}} = {{A}}\frac{{{{\delta U}}}}{{{{{U}}_0}}},$ | (12) |
where p' represents the atmospheric pressure of water vapor sensitive layer of the water vapor channel; A is a coefficient (or weighting factor) determined by the relationship between the differences of moisture structure in the upper and whole layers. As a result, the corresponding formulas for FY-2F/VISSR WV channel [Eq. (8)] can be written as:
| ${{\delta }}{T_ {\rm{WV}}} = \delta {T_ {\rm{s}}}{C_ {\rm{WV}}} + \left( {A\frac{{\delta U}}{{{U_0}}}} \right){D_ {\rm{WV}}}.$ | (13) |
Equation (13) is used by the modified three-band PSW algorithm together with Eqs. (1)–(2) to calculate the related water vapor perturbation δU. In this algorithm, the determination of A is an important part and should be accomplished through more detailed physical derivations and other further studies. In this study, a sensitivity analysis was conducted to determine the optimal value of coefficient A forFY-2Foperational PWV retrieval. With the same input data introduced in Section 3.2, adding FY-2F water vapor channel observations, we retrieved 40 groups of PWVs at 0000 UTC January–March 2016 under 40 values of A from 1 to 40. These PWVs were evaluated by spatial-temporal matched radiosonde data (see Section 2.3). Figure 5 shows the RMSEs (root mean square errors) of the PWVs retrieved by using the modified three-band PSW algorithm under corresponding values of A. The results showed that the coefficient A = 10 will result in an optimumFY-2F/VISSR PWV retrieval. Hence, we chose 10 as the value of coefficient A in FY-2F/VISSR new operational PWV calculations.

|
| Figure 5 The RMSEs of FY-2F/VISSR PWVs retrieved by the modified three-band PSW algorithm under different A values (To show the trend more clearly, this figure only shows RMSEs under A of 3–40). |
To better validate the new FY-2F/VISSR PWV products, we estimated the PWV values at 0000 UTC for 366 days in 2016 over the 452 selected radiosonde stations referred to in Section 2.3. Meanwhile, the current operational FY-2F/VISSR PWV values retrieved by using traditional two-band PSW algorithm are also validated by using these matched radiosonde data. Figure 6 shows the precision evaluation results of the operational PWV (Fig. 6a), the PWV retrieved by using the improved three-band PSW algorithm from Liu et al. (2017) (Fig. 6b), and the PWV retrieved based the modified three-band PSW algorithm (Fig. 6c). All 37,137 matched samples are presented here based on scatterplots and probability distribution functions (PDFs), which can depict the difference in the distribution of the PWV products clearly.

|
| Figure 6 Scatterplots for (a1, b1, c1) retrieved precipitable water vapor (PWV) values versus radiosonde PWV values (the black line represents the 1:1 line and the red line is the line fitted based on all the matched points) and (a2, b2, c2) the probability distribution functions of the difference between the retrieved PWV and radiosonde PWV. (a1, a2) The operational PWV retrieved by using the traditional two-band PSW algorithm; (b1, b2) the PWV retrieved by using the improved three-band PSW algorithm from Liu et al. (2017); and (c1, c2) the PWV retrieved by using the modified three-band PSW algorithm. |
From Fig. 6a, we find that the scatters are closer to the 1:1 line when the PWV values for the radiosondes are larger than 20 mm. On the other hand, the deviations of the operational PWVs become very large when the radiosonde PWVs are lower than 15 mm. As shown in Fig. 6a, the operational PWVs have a mean bias of 12.67 mm, an RMSE of 29.35 mm, and a correlation coefficient of 0.23. In Fig. 6b, the distribution of the scatter is symmetrical centered around the 1:1 line without an obvious bias; the mean bias, RMSE, and correlation coefficient for PWVs retrieved by using the improved three-band PSW algorithm are 0.11 mm, 6.36 mm, and 0.94, respectively. Compared to the results in Fig. 6b, the scatters in Fig. 6c are much more focused around the 1:1 line, and the PDF also exhibits a much higher and narrower distribution. The PWVs retrieved with the modified three-band PSW algorithm have a mean bias of 0.28 mm, an RMSE of 4.53 mm, and a correlation coefficient of 0.969.
It is very clear that the precisions of the PWV products gradually increase from Figs. 6a–c. The improved three-band PSW algorithm from Liu et al. (2017) performs better than the traditional two-band PSW algorithm for retrieving FY-2F/VISSR operational PWV product when the PWV is smaller than 20 mm. This significant enhancement is a direct contribution of the supplementary water vapor information observed by the water vapor channel. However, the improved three-band PSW algorithm also shows some shortages in the retrieving relatively larger PWV due to the use of the same scale for the water vapor and split-window channels. Introducing a new scale into the water vapor channel in Eq. (13), limits the influence caused by the deviations of actual water vapor from first-guess values in upper layers, so that the values of the PWVs retrieved the modified three-band PSW algorithm present the best accuracy.
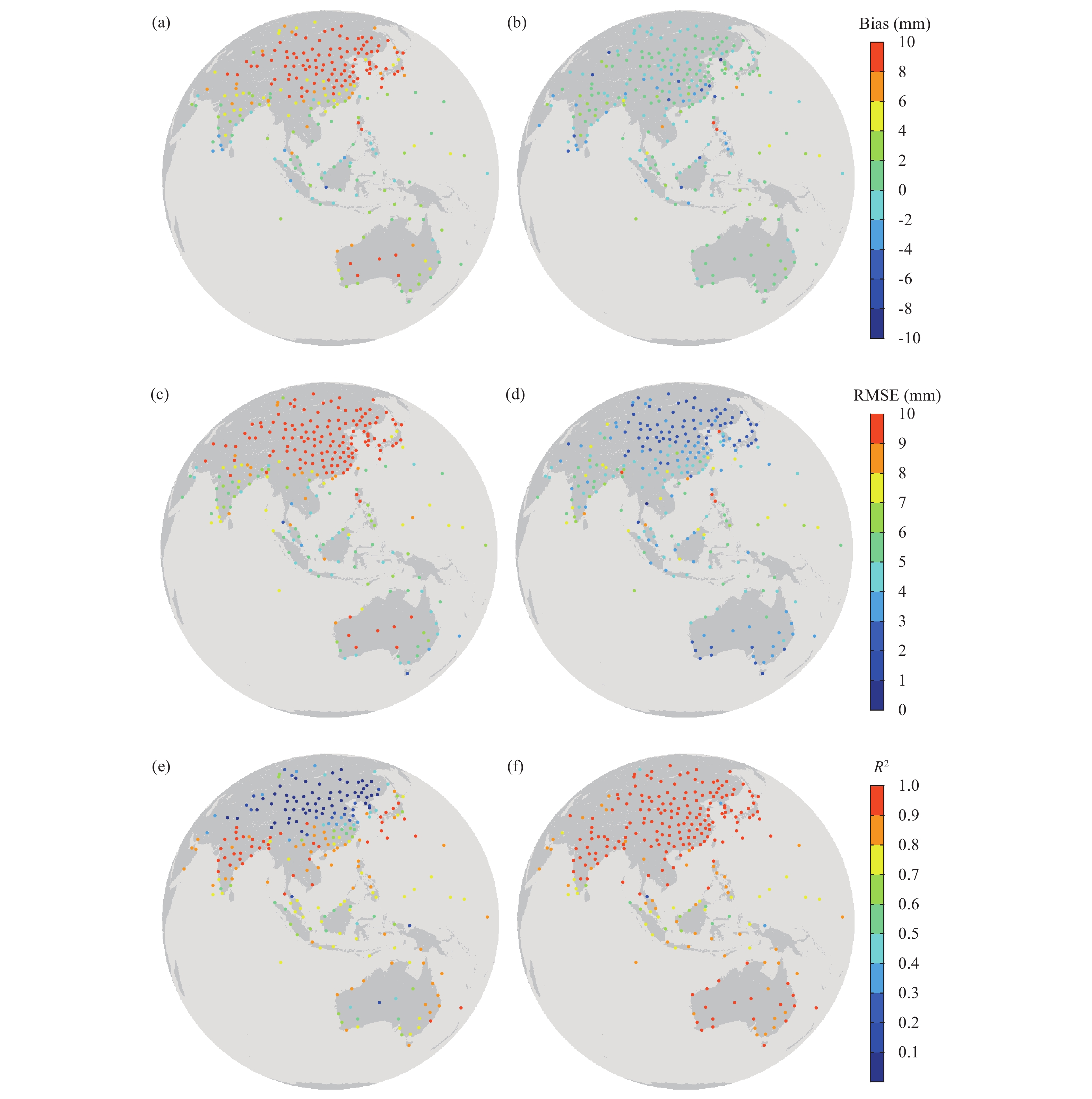
Comparing with the radiosonde PWV at each site, Fig. 7 shows the distributions of the mean biases, RMSEs, and correlation coefficients of two kinds of FY-2F/VISSR PWV retrieved by the traditional two-band PSW algorithm and the modified three-band PSW algorithm, respectively. Figures 7a and 7b show the results of the mean biases of the PWV at each site. There are wet biases at most sites when the two-band PSW algorithm is used. The biases at the lower latitudes (near the equator) vary from –4 to 4 mm. These are significantly lower than those at the middle and high latitudes in the Northern and Southern Hemispheres, which can be up to 10 mm. This finding reveals that the biases increase as the latitude moving from the equator to Polar regions. However, for the PWVs based on the modified three-band PSW algorithm (Fig. 7b), the biases vary from –4 to 4 mm at sites either near the equator or at middle and high latitudes without any obvious latitudinal patterns. The distribution of atmospheric water vapor, which is dominated by latitude, topographical features, and monsoon, shows a significant decrease as latitude increases. The RMSEs of the PWV based on the two-band algorithm (Fig. 7c) are higher in middle and high latitudes (up to 10 mm) and lower near the equator (~5 mm). Meanwhile, the RMSEs of the PWV values from the modified three-band method are about 5 mm for sites near the equator and within 2 mm in high latitudes near the poles (Fig. 7d). As the latitudes increase, the RMSEs of two kinds of PWVs change in the opposite directions. As shown in Figs. 7e, f, the correlation coefficients for the two-band PWV at sites in the higher northern latitudes are mostly less than 0.2, while most of those for the modified three-band PWV at these sites are above 0.9. For the sites near the equator, the correlation coefficients between the two kinds of FY-2F PWV value are between 0.4 and 0.8. These findings show that the modified three-band PWV is more consistent with the radiosonde PWV than the two-band PWV.
|
| Figure 7 The bias (top panels), RMSE (middle panels), and correlation coefficient (bottom panels) between the PWV retrieved from the radiosonde stations and estimated from FY-2F/VISSR using the traditional two-band PSW algorithm (left-hand columns) and the modified three-band PSW algorithm (right-hand columns). |
This shows that PWV retrieved by using the modified three-band PSW algorithm has a better agreement with the PWV values measured by radiosondes. For the relatively lower PWV conditions or drier atmospheres (such as those in the middle and high latitudes), especially, the accuracy of the modified three-band PSW algorithm is much higher than the current operational two-band PWV algorithm. The modified three-band PSW algorithm also shows a slightly higher RMSE near the quator. This finding is attributed mainly to higher and more frequent cloud cover in this region (Sassen et al., 2008), which is very difficult to determine by using satellite imaging measurements. Additionally, as shown by the red or deep blue points in Fig. 7b or red points in Fig. 7d, the PWVs with large biases and RMSEs are influenced by low precision of first-guess data. The accuracy of the modified three-band PSW algorithm is associated with the precision of first-guess data, which is the same as other first-guess dependence PWV estimated algorithms (Knabb and Fuelberg, 1997).
Figure 8 presents the zonal and seasonal mean precision comparisons between the two-band and the modified three-band PWVs. Owing to the lack of sites at the region from 60° to 90°S, we do not show the results in this region. Figure 8a indicates that the zonal mean radiosonde PWV values decrease with increasing latitude. The annual mean PWV values at five typical regions from north to south are 8.5, 13.45, 36.1, 36.17, and 15.19 mm, respectively, implying a slightly lower annual mean PWVs of zonal belts in the Northern Hemisphere than in the Southern Hemisphere with corresponding latitudes. The two probable causes for the differences between the Northern/Southern Hemispheres are: (1) more sea sites can be found in the Southern Hemisphere and (2) the Tibetan Plateau located at 25°–40°N in the Northern Hemisphere. Furthermore, the three north zonal belts showed the same seasonal PWV variation trends. However, we could not find an obvious seasonal variation over the two zonal belts in the Southern Hemisphere. No matter when and where, the PWV differences between the values from the modified three-band algorithm and radiosondes are much smaller than these from the two-band algorithm.
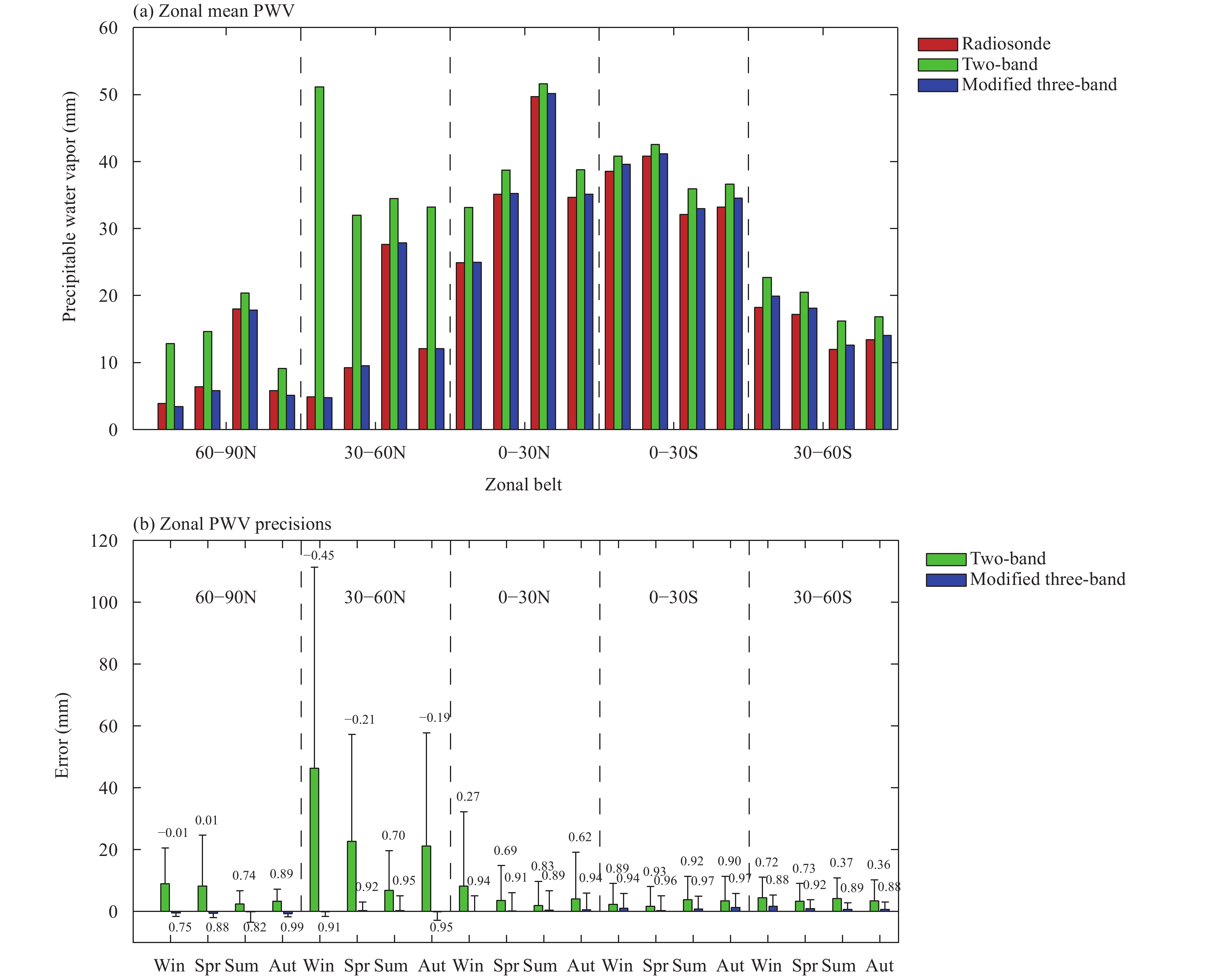
|
| Figure 8 Comparisons of zonal mean PWVs between the two-band PSW (green) and the modified three-band PSW (blue) results. (a) Zonal mean PWV and (b) its precision. Four groups of belts in both (a) and (b) refer to four seasons [Win: winter (December, January, and February); Spr: spring (March, April, and May); Sum: summer (June, July, and August); Aut: autumn (September, October, and November)]. The boxes, bars, and numbers above the bars in (b) are mean biases, RMSEs, and correlation coefficients, respectively. |
The zonal and seasonal mean biases, RMSEs, and correlation coefficients of two retrieved PWVs are also presented in Fig. 8b. Apparently, the two-band algorithm always overestimates the PWV values. In winter, spring, and autumn within 30°–90°N, when the mean radiosonde PWV values are lower than 15 mm, the two-band algorithm overestimates the PWV values by factors of 0.56 to 9.49 times higher than the radiosonde PWVs. In contrast, the accuracies in other seasons and other belts with higher PWV values are much better. Moreover, the two-band algorithm showed the worst performance in the belt of 30°–60°N. Especially in the winter season, the mean bias, RMSE, and correlation coefficient are 46.28 mm, 65.10 mm, and –0.45, respectively. This was mainly caused by the poor results at the Tibetan Plateau sites in this belt. This finding indicates that not only in drier conditions but also in a complicated topography area like plateau, the PWV accuracy from the two-band algorithm significantly decreases. On the other hand, the modified three-band PWVs show better consistency with radiosonde PWVs in any belt and season than the two-band PWVs. In contrast, in two belts (30°–60°N and 60°–90°N), the modified three-band algorithm slightly underestimated the PWV values by the factors of 0.001 to 0.12 times lower than the radiosonde PWVs. In other belts and seasons, the PWV values were slightly overestimated by this algorithm.
5 ConclusionsThe aim of the study was to develop a robust and operational precipitable water vapor retrieval scheme that could significantly improve the qualities of current FY-2/VISSR PWV products in dry atmospheres. Considering the sensitivity of FY-2F/VISSR channels to water vapor, the improved three-band PSW algorithm based on information from the water vapor channel combined with that from split-window channels is more precise and robust than the traditional two-band PWV methods, especially under conditions where the air is drier. Considering the quality of the NWP data used in the FY-2 operational system, we modified the previous improved three-band PSW algorithm by adding a scale (the ratio of A) for water vapor channel, which directly reduced the weighting of this channel in the PWV retrieval. The value of A was determined through sensitivity studies.
The accuracy of the PWV retrieved by this modified three-band PSW algorithm and operational PWV retrieved by the traditional two-band PSW algorithm were evaluated by using ground-based radiosonde PWV observations. The results demonstrated that the modified three-band algorithm can obtain more accurate PWV values, with a mean bias of 0.28 mm, an RMSE of 4.53 mm, and a correlation coefficient of 0.969, while the correspond parameters for the PWV retrieved by using the two-band algorithm are 12.67 mm, 29.35 mm, and 0.23. At the moister sites near the equator, the results of the two kinds of algorithms exhibit a similar PWV retrieval precision with the bias varying from –4 to 4 mm, an RMSE of 5 mm, and a correlation coefficient between 0.4 and 0.8. Meanwhile, at sites in the middle or high latitudes with relatively lower air water vapor content, the terrible precisions of PWV values based on the two-band algorithms can be improved obviously using the modified three-band PSW algorithm. It reduces the biases from 10 mm to ± 4 mm, reduces the RMSEs from 10 to 2 mm, and increases the correlation coefficients from 0.2 to 0.9. Besides, the zonal and seasonal precision comparisons of the two algorithms indicated that the modified three-band PSW algorithm improves the performance of the traditional two-band PSW algorithm in drier conditions and plateau areas. Moreover, the accuracy differences between five belts and four seasons for the modified three-band PWV were far less than for the two-band PWV.
Therefore, the modified three-band PSW algorithm proposed in this study has a remarkable advantage compared to the current operational two-band algorithm, in low PWV values retrievals. It could directly improve the quality of the current FY-2/VISSR PWV products and can even be applied to data from other satellite imagers, such as the VISSR aboard the Geostationary Operational Environmental Satellites (GOES) and the Spinning Enhanced Visible and Infrared Imager aboard Meteosat Second Generation (MSG) satellites, which have one or more water vapor channel and split-window channels.
Furthermore, the scale in Eq. (13) is determined jointly by the spectral ranges of the water vapor channel and the accuracy of the first-guess humidity profile vertical structures. In future studies, a more objective and reproducible method should be developed to determine this value. We will also try to retrieve and improve the real-time FY GEO PWV products based on the new version of the RTTOV model and new numerical weather forecasting data.
Acknowledgments. The authors wish to thank the University of Wyoming for providing the radiosonde data. We also thank the anonymous reviewers for thoughtful suggestions and comments.
| Berk, A., G. P. Anderson, P. K. Acharya, et al., 1999: Modtran4 User’s Manual. Air Force Research Laboratory, Space Vehicles Directorate, AIR FORCE MATERIEL COMMAND, Hanscom AFB, MA 01731-3010, 99 pp. |
| Chang, F., 2015: Comparison of T639 numerical forecast and actual sounding data. Mod. Agric. Sci. Technol., 2, 252–254,257. |
| Coret, L., X. Briottet, Y. H. Kerr, et al., 2004: Simulation study of view angle effects on thermal infrared measurements over heterogeneous surfaces. IEEE Trans. Geosci. Remote Sens., 42, 664–672. DOI:10.1109/tgrs.2003.819443 |
| Czajkowski, K. P., S. N. Goward, D. Shirey, et al., 2002: Thermal remote sensing of near-surface water vapor. Remote Sens. Environ., 79, 253–265. DOI:10.1016/S0034-4257(01)00277-2 |
| Dalu, G., 1986: Satellite remote sensing of atmospheric water vapour. Int. J. Remote Sens., 7, 1089–1097. DOI:10.1080/01431168608948911 |
| Guillory, A. R., G. J. Jedlovec, and H. E. Fuelberg, 1993: A technique for deriving column-integrated water content using VAS split-window data. J. Appl. Meteor., 32, 1226–1241. DOI:10.1175/1520-0450(1993)032<1226:ATFDCI>2.0.CO;2 |
| Guo, Z., Y. H. Chen, M. M. Cheng, et al., 2014: Near-surface air temperature retrieval from Chinese Geostationary FengYun Meteorological Satellite (FY-2C) data. Int. J. Remote Sens., 35, 3892–3914. DOI:10.1080/01431161.2014.919674 |
| Haines, S. L., G. J. Jedlovec, and R. L. Suggs, 2004: The GOES Product Generation System. NASA/TM-2004-213286, NASA, Huntsville, Alabama, 64 pp. |
| Hu, J. Y., S. H. Tang, H. L. Liu, et al., 2017: Production and validation of FY-3C VIRR total precipitable water products. J. Remote Sens., 21, 842–852. DOI:10.11834/jrs.20176350 |
| Hu, X., N. M. Lu, T. Niu, and P. Zhang, 2008: Operational retrie-val of Asian sand and dust storm from FY-2C geostationarymeteorological satellite and its application to real time fore-cast in Asia. Atmos. Chem. Phys., 8, 1649–1659. DOI:10.5194/acp-8-1649-2008 |
| Hu, X. Q., N. Xu, F. Z. Weng, et al., 2013: Long-term monit-oring and correction of FY-2 infrared channel calibration us-ing AIRS and IASI. IEEE Trans. Geosci. Remote Sens., 51, 5008–5018. DOI:10.1109/TGRS.2013.2275871 |
| Jedlovec, G. J., 1987: Determination of atmospheric moisture structure from high resolution MAMS radiance data. Ph.D. dissertation, University of Wisconsin, Madison, 187 pp |
| Jedlovec, G. J., 1990: Precipitable water estimation from high-resolution split window radiance measurement. J. Appl. Meteor., 29, 863–877. DOI:10.1175/1520-0450(1990)029<0863:PWEFHR>2.0.CO;2 |
| Julien, Y., J. A. Sobrino, C. Mattar, et al., 2015: Near-real-time estimation of water vapor column from MSG-SEVIRI thermal infrared bands: Implications for land surface temperature retrieval. IEEE Trans. Geosci. Remote Sens., 53, 4231–4237. DOI:10.1109/tgrs.2015.2393378 |
| Kleespies, T. J., and L. M. McMillin, 1990: Retrieval of precipitable water from observations in the split window over varying surface temperatures. J. Appl. Meteor., 29, 851–862. DOI:10.1175/1520-0450(1990)029<0851:ROPWFO>2.0.CO;2 |
| Knabb, R. D., and H. E. Fuelberg, 1997: A comparison of the first-guess dependence of precipitable water estimates from three techniques using GOES data. J. Appl. Meteor., 36, 417–427. DOI:10.1175/1520-0450(1997)036<0417:ACOTFG>2.0.CO;2 |
| Labbi, A., and A. Mokhnache, 2015: Estimating of total atmospheric water vapor content from MSG1-SEVIRI Observations. Atmos. Meas. Tech. Discuss., 8, 8903–8923. DOI:10.5194/amtd-8-8903-2015 |
| Liu, H. L., S. H. Tang, J. Y. Hu, et al., 2017: An improved physi-cal split-window algorithm for precipitable water vapor retrieval exploiting the water vapor channel observations. Remote Sens. Environ., 194, 366–378. DOI:10.1016/j.rse.2017.03.031 |
| Min, M., and Z. B. Zhang, 2014: On the influence of cloud fraction diurnal cycle and sub-grid cloud optical thickness variability on all-sky direct aerosol radiative forcing. J. Quant. Spectrosc. Radiat. Transfer, 142, 25–36. DOI:10.1016/j.jqsrt.2014.03.014 |
| Min, M., C. Q. Wu, C. Li, et al., 2017: Developing the science product algorithm testbed for Chinese next-generation geostationary meteorological satellites: FengYun-4 series. J. Meteor. Res., 31, 708–719. DOI:10.1007/s13351-017-6161-z |
| Min, W. B., B. Li, J. Peng, et al., 2015: Evaluation of total precipitable water derived from FY-2E satellite data over the southeast of Tibetan Plateau and its adjacent areas. Resour. Environ. Yangtze Basin, 24, 625–631. |
| Muller, B. M., and H. E. Fuelberg, 1990: A simulation and diagnostic study of water vapor image dry bands. Mon. Wea. Rev., 118, 705–722. DOI:10.1175/1520-0493(1990)118<0705:ASADSO>2.0.CO;2 |
| Ottle, C., S. Outalha, C. Francois, et al., 1997: Estimation of total atmospheric water vapor content from split-window radiance measurements. Remote Sens. Environ., 61, 410. DOI:10.1016/S0034-4257(97)00055-2 |
| Sassen, K., Z. E. Wang, and D. Liu, 2008: Global distribution of cirrus clouds from CloudSat/CloudʜAerosol Lidar and Infrared Pathfinder Satellite Observations (CALIPSO) measurements. J. Geophys. Res. Atmos., 113, D00A12. DOI:10.1029/2008JD009972 |
| Saunders, R., 2002: RTTOV-7 Users Guide. Met Office, London, 21 pp. Available at https://nwpsaf.eu/oldsite/deliverables/rtm/rttov7_ug.pdf. |
| Seemann, S. W., J. Li, L. E. Gumley, et al., 2003: Operational retrieval of atmospheric temperature, moisture, and ozone from MODIS infrared radiances. Proceedings of SPIE 4895, Applications with Weather Satellites, SPIE, Hangzhou, China, 168–176, doi: 10.1117/12.466686. |
| Shi, C. X., and Z. H. Xie, 2005: Operational method of total precipitable water retrieved from satellite multi-channels’ infrared data. Journal of Infrared and Millimeter Waves, 24, 304–308. DOI:10.3321/j.issn:1001-9014.2005.04.015 |
| Shi, F. L., J. Y. Xin, L. K. Yang, et al., 2018: The first validation of the precipitable water vapor of multisensor satellites over the typical regions in China. Remote Sens. Environ., 206, 107–122. DOI:10.1016/j.rse.2017.12.022 |
| Steranka, J., L. J. Allison, and V. V. Salomonson, 1973: Application of Nimbus 4 THIR 6.7 μm observations to regional and global moisutre and wind field analyses. J. Appl. Meteor., 12, 386–395. DOI:10.1175/1520-0450(1973)012<0386:aontot>2.0.co;2 |
| Suggs, R. J., G. J. Jedlovec, and A. R. Guillory, 1998: Retrieval of geophysical parameters from GOES: Evaluation of a split-window technique. J. Appl. Meteor., 37, 1205–1227. DOI:10.1175/1520-0450(1998)037<1205:ROGPFG>2.0.CO;2 |
| Sun, D. L., Y. Y. Yu, L. Fang, et al., 2013: Toward an operational land surface temperature algorithm for GOES. J. Appl. Meteor. Climatol., 52, 1974–1986. DOI:10.1175/JAMC-D-12-0132.1 |
| Tang, B. H., and Z.-L. Li, 2008: Estimation of instantaneous net surface longwave radiation from MODIS cloud-free data. Remote Sens. Environ., 112, 3482–3492. DOI:10.1016/j.rse.2008.04.004 |
| Trenberth, K. E., J. T. Fasullo, and J. Kiehl, 2009: Earth’s global energy budget. Bull. Amer. Meteor. Soc., 90, 311–324. DOI:10.1175/2008BAMS2634.1 |
| Xu, J. M., W. J. Zhang, J. Yang, et al., 2008: Fengyun-2 Satellite Operational Products and Data Formats Practical Handbook. China Meteorological Press, Beijing, 67–71. (in Chinese) |
| Zheng, J., C. X. Shi, Q. F. Lu, et al., 2010: Evaluation of total precipitable water over East Asia from FY-3A/VIRR infrared radiances. Atmos. Oceanic Sci. Lett., 3, 93–99. DOI:10.1080/16742834.2010.11446853 |
| Zhu, Y. J., W. B. Li, and Y. Chen, 1998: Study of total precipitable water by GMS-5. Quart. J. Appl. Meteor., 9, 8–14. |
 2019, Vol. 33
2019, Vol. 33


