
The Chinese Meteorological Society
Article Information
- ZHANG, Feimin, Zhaoxia PU, and Chenghai WANG, 2019.
- Impacts of Soil Moisture on the Numerical Simulation of a Post-Landfall Storm. 2019.
- J. Meteor. Res., 33(2): 206-218
- http://dx.doi.org/10.1007/s13351-019-8002-8
Article History
- Received January 10, 2018
- in final form December 17, 2018
2. Department of Atmospheric Sciences, University of Utah, Salt Lake City, UT 84112, USA
Over tropical and subtropical latitudes, tropical cyclones are one of the most significant weather-related threats to shore- and sea-based locations. Accurate prediction of the track, intensity, and structure of a hurricane during landfall and its further evolution over land is a great challenge for Numerical Weather Prediction (NWP).
Apart from the common decay processes a hurricane undergoes when it interacts with the land surface, in some extreme cases, such as Hurricanes Carla (1961), David (1979), and Danny (1997), and Tropical Storms Fran (1996), Danny (1997), Erin (2007), Fay (2008), and Bill (2015), the storm survives for a longer time and even undergoes reintensification, or “agukabams” (from the aboriginal root words “agu” meaning land, and “kabam” meaning storm; Emanuel et al. 2008). Previous studies (Hart and Evans, 2001; Jones et al., 2003; Arndt et al., 2009) have revealed that the maintenance and intensification of post-landfall tropical cyclones might be strongly related to the inland baroclinic zone, ambient environmental conditions, and moist soil surface. Compared to other landfalling hurricanes that undergo a normal and continuous decay process, the evolution of extreme hurricanes over land is more difficult to predict and might cause more casualties and property loss (Arndt et al., 2009). These have not been investigated in many previous studies.
Among the factors that influence hurricane development and maintenance, energy supplied through surface enthalpy fluxes (sum of surface sensible heat and latent heat fluxes) that are parameterized by land surface models is essential (Tuleya, 1994). Based on a simple land surface model, Emanuel et al. (2008) suggested that warm-core cyclones can indeed intensify when the underlying soil is sufficiently warm and wet. Besides, when storms are sufficiently isolated from their oceanic moisture source, the rainfall that they produce is insufficient to keep the soil wet enough to transfer significant quantities of heat, and the storms then decay rapidly. Sensitivity studies by Evans et al. (2011) with the Weather Research and Forecasting (WRF) model investigated the impacts of different soil moisture signals on the evolution of Tropical Storm Erin (2007). The results showed that soil moisture content was important to the development of this storm over land. Specifically, increasing soil moisture could increase moisture and instability in the boundary layer, thus significantly affecting the storm’s thermodynamic environment. In addition, the variation in soil moisture contributed by the storm’s rainfall has no obvious influence on the simulation of the storm’s evolution over land. The results from Bozeman et al. (2012) and Kishtawal et al. (2012) also showed that forecasts of landfalling hurricanes are sensitive to the land surface scheme, as well as the soil state. Although the above studies highlight the important influence of soil moisture on landfalling hurricanes, it is still unclear to what degree and by what mechanism soil moisture influences landfalling hurricanes and their evolution over land.
Soil moisture is an important component of land surface processes and their parameterization. It can significantly affect surface sensible and latent heat fluxes due to its impacts on the calculation of surface energy balance (Eltahir, 1998; Koster et al., 2009). Previous studies (e.g., Eltahir, 1998; Zheng and Eltahir, 1998; Findell and Eltahir, 2003) highlighted the important effects of soil moisture on local convection. Eltahir (1998) proposed a hypothesis regarding the role of soil moisture conditions in land–atmosphere interactions. Namely, there is a positive feedback mechanism between soil moisture and rainfall because wet soil tends to enhance surface net radiation, resulting in enhanced surface enthalpy fluxes from the land surface to the boundary layer. A further study by Findell and Eltahir (2003) investigated the influence of soil moisture on the development and triggering of local convection. The results indicated that convection can be triggered by either dry or wet soil, which is closely related to the evolution of the boundary layer influenced by soil moisture. Moreover, other studies (e.g., Lanicci et al., 1987; Beljaars et al., 1996; Betts et al., 1996) have also acknowledged a linkage that relates boundary layer processes to soil moisture and the evolution of baroclinic zones, drylines, and precipitating systems. In other words, the feedback of soil moisture to local convection can be either positive or negative and is largely dependent on boundary layer processes.
As an important linkage between the land/ocean surface and atmosphere, vertical mixing in the Planetary Boundary Layer (PBL), which is strongly influenced by thermal conditions over the land/ocean surface, has a great impact on the feedback of momentum, moisture, and heat between the surface and the atmosphere. Previous studies (e.g., Braun and Tao, 2000; Smith, 2003; Zhang et al., 2015, 2017; Zhang and Pu, 2017) have also revealed that vertical mixing in the PBL is a key factor that modulates the hurricane evolution over both ocean and land. So far, to the best of our knowledge, the role of boundary layer vertical mixing in the feedback of soil moisture on the landfall of a tropical storm and its further evolution over land has rarely been documented in the literature. Recent studies (e.g., Emanuel et al., 2008; Evans et al., 2011) have indicated that soil moisture variation modified by a storm’s rainfall is not a key factor influencing the storm’s track and intensity, since the rainfall produced by the post-landfall storm is insufficient to keep the soil wet enough to transfer significant quantities of heat from the land surface. This suggests that the evolution of landfalling hurricanes could be significantly sensitive to the soil moisture state before their landfall. Since the thermal conditions of the land surface, which are directly influenced by soil moisture, could significantly affect vertical mixing in the PBL, a disturbance of soil moisture before a hurricane’s landfall could significantly affect the simulation of the landfalling hurricane and its further evolution over land. Thus, this study will attempt to examine and extend earlier research by analyzing the response of boundary layer vertical mixing to the change of soil moisture and its further influence on a post-landfall Tropical Storm Bill (2015) and its evolution over land, through numerical sensitivity simulations.
The paper is divided into the following sections: Section 2 briefly describes the tropical storm case and data. The HWRF model, land surface schemes, and experiment design are discussed in Section 3. Section 4 compares the simulation results of each experiment. The impacts of soil moisture and its associated mechanisms on the simulations are diagnosed and illustrated in Section 5. A discussion and concluding remarks are provided in Section 6.
2 Description of tropical storm case and dataTropical Storm Bill made landfall at 1645 UTC 16 June 2015 with maximum winds of 50 kt [1 knot (kt) = 0.5144 m s–1]. Bill’s remnant low survived for the next several days over land during its interaction with midlatitude westerlies. It produced heavy rain, flooding, and tornadoes over the central Great Plains. The low ultimately dissipated after 0000 UTC 21 June over the mountainous terrain of central West Virginia. The overall lifespan of Tropical Storm Bill after its landfall was about 103 h, which is much longer than normal decay cases such as Hurricanes Dennis, Katrina, and Rita in 2005. The simulation period in this study covers the evolution of Tropical Storm Bill from about 17 h before its landfall through its whole lifespan over land, namely, from 0000 UTC 16 to 0000 UTC 21 June 2015. The NCEP Global Forecasting System (GFS) Final analysis (FNL) data (1° × 1°) are used for the initial and boundary conditions.
The National Hurricane Center (NHC) best-track data and precipitation analysis from the NCEP Climatology Calibrated Precipitation Analysis (CCPA) reanalysis (Hou et al., 2014) are used to validate the simulation results. In addition, phase 2 of the North American Land Data Assimilation System (NLDAS2) datasets, which includes the NOAH land surface model (Chen and Dudhia, 2001), executed in an uncoupled mode in a 1° × 1° grid, and soil moisture anomaly from the Climate Prediction Center (CPC), are used as a reference to compare the uncertainties and discrepancies of the initial soil moisture in FNL data.
3 Description of the HWRF model, land surface scheme, and experimentsThe HWRF model (Gopalakrishnan et al., 2013) has been an NCEP operational hurricane forecast system since 2007. It has also been a popular and reliable model in hurricane research in recent years (e.g., Zhang et al., 2015, 2017; Pu et al., 2016). At the beginning of this research, the HWRF research (community) version released from the Developmental Testbed Center (DTC) at the NCAR was version 3.6a (Tallapragada et al., 2014). The HWRF system adopted the Non-hydrostatic Mesoscale Model (NMM) dynamic core (Janjic et al., 2010) with a two-way interactive, movable, triple-nested grid procedure. The three domains have grid resolutions of 27, 9, and 3 km and cover areas of roughly 80° × 80°, 12° × 12°, and 7.1° × 7.1°, respectively. The atmospheric model in the HWRF system employs a suite of advanced physics developed for tropical cyclone applications, such as the Ferrier microphysics scheme (Ferrier et al., 2002), the simplified Arakawa–Schubert (SAS) deep convection scheme (Pan and Wu, 1995), the Geophysical Fluid Dynamics Laboratory (GFDL) longwave and shortwave radiation schemes (Schwarzkopf and Fels, 1991), the GFDL surface layer scheme (Sirutis and Miyakoda, 1990), the GFDL SLAB land surface model (Tuleya, 1994), and the NCEP Global Forecast System (GFS) PBL parameterization (Gopalakrishnan et al., 2011).
The SLAB model, which is the default land surface scheme in HWRF 3.6a, is a simple model that predicts surface temperature only (Deardorff, 1978; Tuleya, 1994), based on the surface energy balance (SEB):
| $ \frac{{\partial {T_{\rm{s}}}}}{{\partial t}} = \frac{{ - \sigma T_{\rm{s}}^4 - {\rm SH} - {\rm LH} + \left({S + F\!\! \downarrow } \right)}}{{{\rho _{\rm{s}}}{c_{\rm{s}}}d}} - c\left({{T_{\rm{s}}} - {T_{\rm{sref}}}} \right), $ | (1) |
where
| $ \;\; d = {\left({\frac{{\lambda k}}{{{\rho _{\rm{s}}}{c_{\rm{s}}}\pi }}} \right)^{\frac{1}{2}}}, \quad\quad\quad\quad\quad\quad\quad$ | (2) |
| $ \quad\quad\quad\quad\quad\quad {\rm SH} = \rho {c_{p}}{c_{\rm{h}}}U\left({{T_{\rm{s}}} - {T_{\rm{a}}}} \right), \quad\quad\quad\quad\quad\;\; $ | (3) |
| $ {\rm LH} = M\rho {L_{\rm{v}}}{c_{\rm{h}}}U\left({{q_{\rm{s}}} - {q_{\rm{a}}}} \right), \quad\quad$ | (4) |
| $\quad\quad c = \frac{{2\pi }}{\lambda }, \;\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad $ | (5) |
where Ts is the temperature of the ground surface; Tsref is the soil temperature at the lower boundary; Ta is the low-level air temperature;
When this land surface model is activated, soil moisture and soil temperature are regarded as invariant during model forecasts, with initial values based on the GFS analysis (e.g., FNL). Although soil moisture is invariant during the whole period of the model integration, the effect of soil moisture on land surface process such as surface temperature is still included in SLAB scheme through its impact on thermal conductivity, which in turn could affect surface enthalpy fluxes. For instance, in Eq. (1), ρscs is the soil heat capacity, k is the soil thermal conductivity, and these quantities become different with the change of initial soil moisture (see the original code in HWRF3.6a, such as “module_sf_slab.F”, “LANDUSE.TBL”, and “module_physics_init.F”), namely, the increase of initial soil moisture as done in this study will change the initial status and property of soil heat capacity and soil thermal conductivity, thereby influencing the simulation of surface temperature. This is similar to the model used by Emanuel et al. (2008). In other words, SLAB scheme accounts the effects of soil moisture on land surface process such as surface temperature and could still adequately simulate the thermal evolution that is similar to a more complicated multiple-level land model, as indicated by Deardorff (1978). The results of Tuleya (1994) also showed that this scheme is capable of well representing the evolution of the landfalling hurricane simulation.
To examine the uncertainties in initial soil moisture, Fig. 1 compares soil moisture at the initial simulation time (0000 UTC 16 June 2015, before the landfall of Tropical Storm Bill) between the soil moisture anomaly from CPC and the volumetric fractional soil moisture content from FNL and the NLDAS2-NOAH analysis. The results from the CPC (Fig. 1a) clearly show a positive soil moisture anomaly over Texas, Oklahoma, and western Arkansas and Louisiana. The results from Figs. 1b and 1c also show that soil moisture in NLDAS2-NOAH is significantly higher than that in FNL over these areas, suggesting that FNL data might underestimate soil moisture, and FNL does not capture the positive soil moisture anomaly as shown by the CPC (Fig. 1a). Further comparisons based on soil moisture in different land surface models of the Global Land Data Assimilation System (GLDAS) show that soil moisture from different land surface models or analysis datasets is very different (figure omitted), indicating that the soil moisture state is highly model-dependent (Koster et al., 2009) and uncertain. Meanwhile, similarities are also revealed in the GLDAS data products regarding the variability in spatial soil moisture—namely, a soil moisture anomaly is clearly shown over Texas, Oklahoma, and the Great Plains, similar to the results from the CPC. In contrast, soil moisture in FNL (Fig. 1c) has no obvious spatial anomalies.

|
| Figure 1 (a) Soil moisture anomaly from CPC (courtesy of CPC); volumetric fractional 0–10-cm soil moisture content (%) from (b) NLDAS2-NOAH and (c) FNL. The valid time is 0000 UTC 16 June 2015, and the black box denotes the key region of the soil moisture anomaly. |
Based on the comparison in Fig. 1, it is apparent that the positive soil moisture anomaly is not well represented by FNL before the storm’s landfall, suggesting that FNL data might underestimate soil moisture at the initial simulation time. In order to investigate the impacts of soil moisture before a tropical storm’s landfall on the evolution of the storm after its landfall, sensitivity experiments are conducted by perturbing the soil moisture input to the SLAB model. In particular, the following two experiments are performed:
(1) SLAB: FNL data are used to drive HWRF directly, and the initial soil moisture comes from FNL data directly.
(2) SLAB_SM: same as SLAB, but initial soil moisture in FNL data is increased by roughly a factor of two in the key region of Bill’s evolution after its landfall (i.e., the area inside the bold black box in Fig. 1). Note that the change of initial soil moisture is done before the landfall of Tropical Storm Bill (2015).
4 Simulation resultsFigure 2 compares the simulated storm track against observations from the National Hurricane Center (NHC) best track from 0000 UTC 16 to 0000 UTC 21 June 2015. The simulated storm centers are determined by the GFDL best-tracker module in the HWRF model (Tallapragada et al., 2014). The results show that both experiments portray the direction of the storm’s movement well. The great differences in the storm track simulation between SLAB and SLAB_SM occur mainly after the storm recurves into the midlatitude westerlies. In particular, the SLAB_SM storm moves eastward for a longer distance than the SLAB storm, and the track even extends over the ocean, implying that the increase in soil moisture before storm’s landfall tends to make the storm move faster and thus has negative impacts on the storm track simulation.

|
| Figure 2 Comparison of storm track positions between NHC best-track and different simulation experiments at 6-h intervals from 0000 UTC 16 to 0000 UTC 21 June 2015. The shaded contours indicate terrain height (m). |
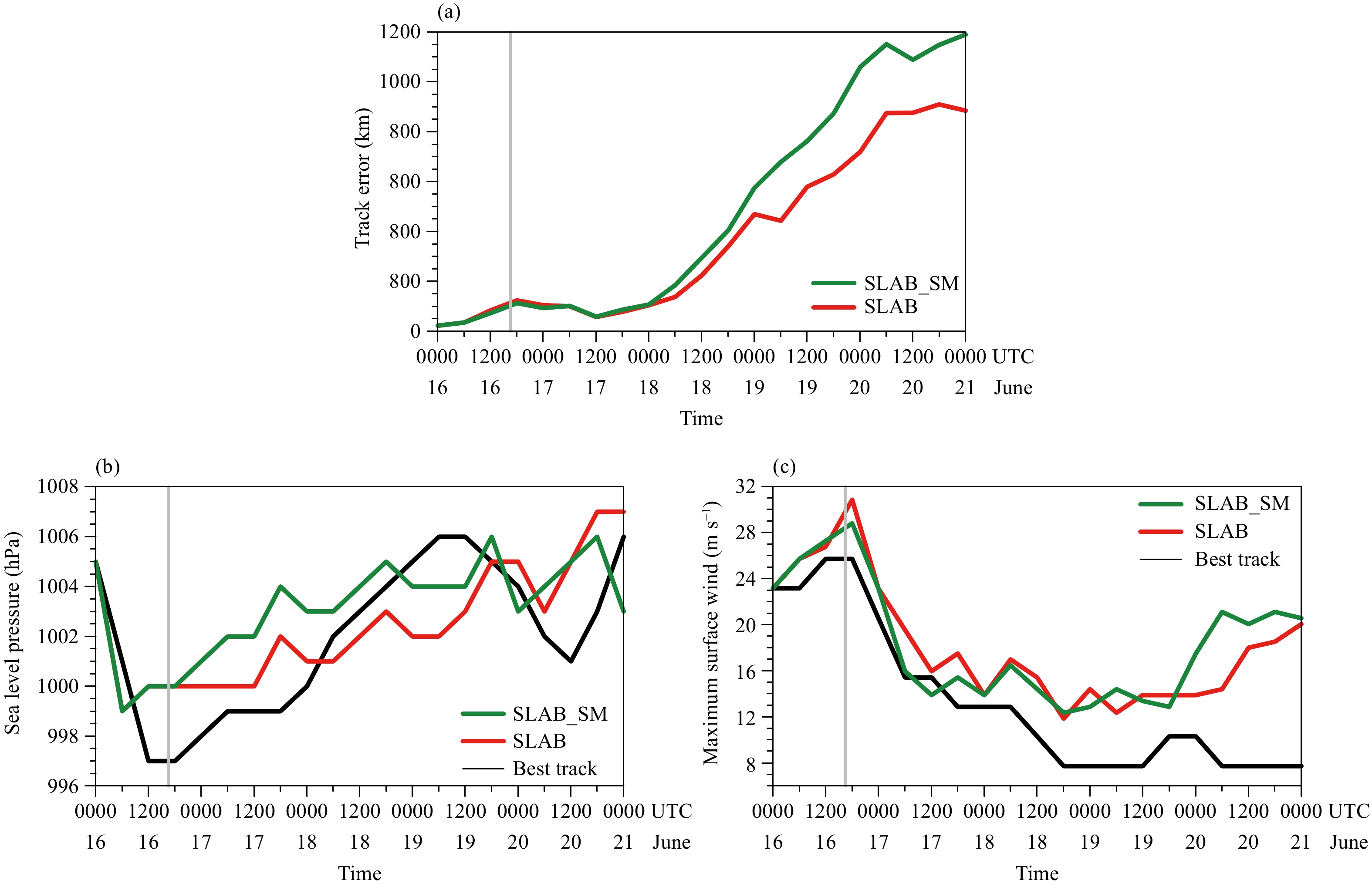
Figure 3 compares the HWRF simulations of track errors and intensity with the NHC best-track data in different experiments. Figure 3a indicates that the simulated track error is smaller in SLAB than in SLAB_SM, especially from 0000 UTC 18 June 2015 to the end of the simulation, in agreement with the analysis in Fig. 2. The intensity simulation in Figs. 3b and 3c shows that during the early phase of landfall, until 0000 UTC 18 June 2015, when the storm has not yet recurved into the midlatitude westerlies, the storm intensity, measured by its minimum sea level pressure, is underestimated by the two experiments. Specifically, SLAB_SM produces a weaker storm than SLAB in most of the simulation, indicating that the increase in soil moisture before storm’s landfall tends to weaken the storm intensity after its landfall and further evolution over land.
|
| Figure 3 Time series of (a) track errors (km) and intensity in terms of (b) minimum central sea level pressure (hPa) and (c) maximum surface wind speed (m s–1) at 6-h intervals against NHC best-track data from different experiments. The solid gray line denotes the storm’s approximate landfall time. |
Figure 4 shows a sample of the accumulated precipitation distribution for Tropical Storm Bill from 0600 UTC 18 to 0000 UTC 21 June 2015, compared with precipitation analysis from the NCEP CCPA reanalysis. The results show that the overestimated precipitation over the central Great Plains produced by SLAB is remedied by SLAB_SM, mainly because the weaker storm with SLAB_SM is closer to observations during this period (Fig. 3).

|
| Figure 4 Accumulated precipitation (mm) over the Great Plains, valid from 0600 UTC 18 to 0000 UTC 21 June 2015. (a) CCPA, (b) SLAB, and (c) SLAB_SM. |
Overall, compared to SLAB experiment, increasing soil moisture before storm’s landfall in SLAB_SM tends to weaken the storm intensity and leads to increased simulation error in the storm track, as well as a weaker precipitation simulation over the central Great Plains due to the weakened storm.
5 Vortex structures and environmental conditionsThe results above show that SLAB_SM produces a worse storm track simulation than SLAB, and the simulated track error between SLAB and SLAB_SM is small early in the integration but becomes significant after the storm recurves into the midlatitude westerlies. To investigate the reason for the difference in the storm track simulation between the two experiments, we compare two experiments regarding steering winds. The steering winds have a great effect on a storm’s motion and are commonly used to determine the influence of environmental flows, such as the subtropical high, monsoon trough, and other synoptic upper-level troughs or ridges on the storm’s track (Fig. 5). As defined by Wu and Kurihara (1996), the steering wind at each pressure level is the averaged wind field over the secondary domain (a 10° × 10° box around the storm center).

|
| Figure 5 The evolution of steering wind (m s–1) at different pressure levels with forecast time from SLAB (shaded) and the difference in steering wind (m s–1) between SLAB_SM and SLAB (SLAB_SM minus SLAB; contours and vectors). The solid and dashed white lines represent the approximate landfall time and the transition time when the storm recurves into midlatitude westerlies, respectively. |
The results show that the eastward steering wind simulated by SLAB_SM is much stronger than that by SLAB, especially after the storm recurves into the midlatitude westerlies. Thus, the eastward movement of the simulated storm over the Great Plains is expected to be faster in SLAB_SM than that in SLAB.
To obtain insight into the process associated with the influence of soil moisture on the structures of tropical storm evolution, further diagnosis is conducted. It has been recognized that surface enthalpy flux and boundary layer vertical mixing are important to the simulation of a tropical storm’s landfall and its further evolution over land (Tuleya, 1994; Zhang et al., 2017; Zhang and Pu, 2017). Therefore, their related variables are analyzed.
Figure 6 compares the Hovmöller diagrams of azimuthally averaged surface sensible heat flux (SHF), surface latent heat flux (LHF), and boundary layer vertical mixing at 950 hPa in each experiment. It shows that the two simulations differ from each other in both the storm and its environment. Within the storm boundary layer, it is obvious that boundary layer vertical mixing, as well as the associated negative SHFs, is much stronger in SLAB_SM than in SLAB during the storm’s landfall before 1200 UTC 19 June 2015. According to recent studies by Zhang et al. (2017) and Zhang and Pu (2017), stronger vertical mixing within the hurricane boundary layer leads to a rapid decay of landfalling hurricanes because it tends to destroy the turbulent kinetic energy in the hurricane boundary layer and stabilizes this layer, thus limiting the storm’s maintenance over land. As a result, the simulated storm over land with SLAB_SM is accordingly weaker than that with SLAB. In the environment outside the storm (e.g., 300–600 km), the diurnal variation of SHF and LHF is much weaker in SLAB_SM than in SLAB. In particular, SLAB_SM produces weaker SHF, LHF and boundary layer vertical mixing than SLAB during the daytime. Such quantities, however, are comparable in the two schemes during the nighttime.

|
| Figure 6 Hovmöller diagram of azimuthally averaged (a, d) surface sensible heat flux (SHF; W m–2), (b, e) surface latent heat flux (LHF; W m–2), and (c, f) vertical eddy diffusivity for momentum in the PBL (Km; m2 s–1) at 950 hPa during the evolution of Tropical Storm Bill from ocean to land throughout the period of numerical simulations (from 0000 UTC 16 June to 0000 UTC 21 June 2015). (a-c) SLAB and (d-f) SLAB_SM. The solid black lines in each panel represent the approximate landfall time. |
Previous studies (e.g., Shen et al., 1986; Rossow et al., 2016) have indicated that the evolution of a weather system is strongly affected by surface diabatic heating during the daytime. Besides, the results in Fig. 6 also indicate that surface diabatic heating and boundary layer vertical mixing in the environment outside the storm are both significant during the daytime. Therefore, the 42-h forecast, which represents not only the daytime (~ noon, LST) but also the time when the storm is located near the center of the black box in Fig. 1, is selected to further illustrate the impacts of soil moisture on surface diabatic heating and boundary layer vertical mixing in the storm environment, as well as the their possible relations with storm’s evolution over land.
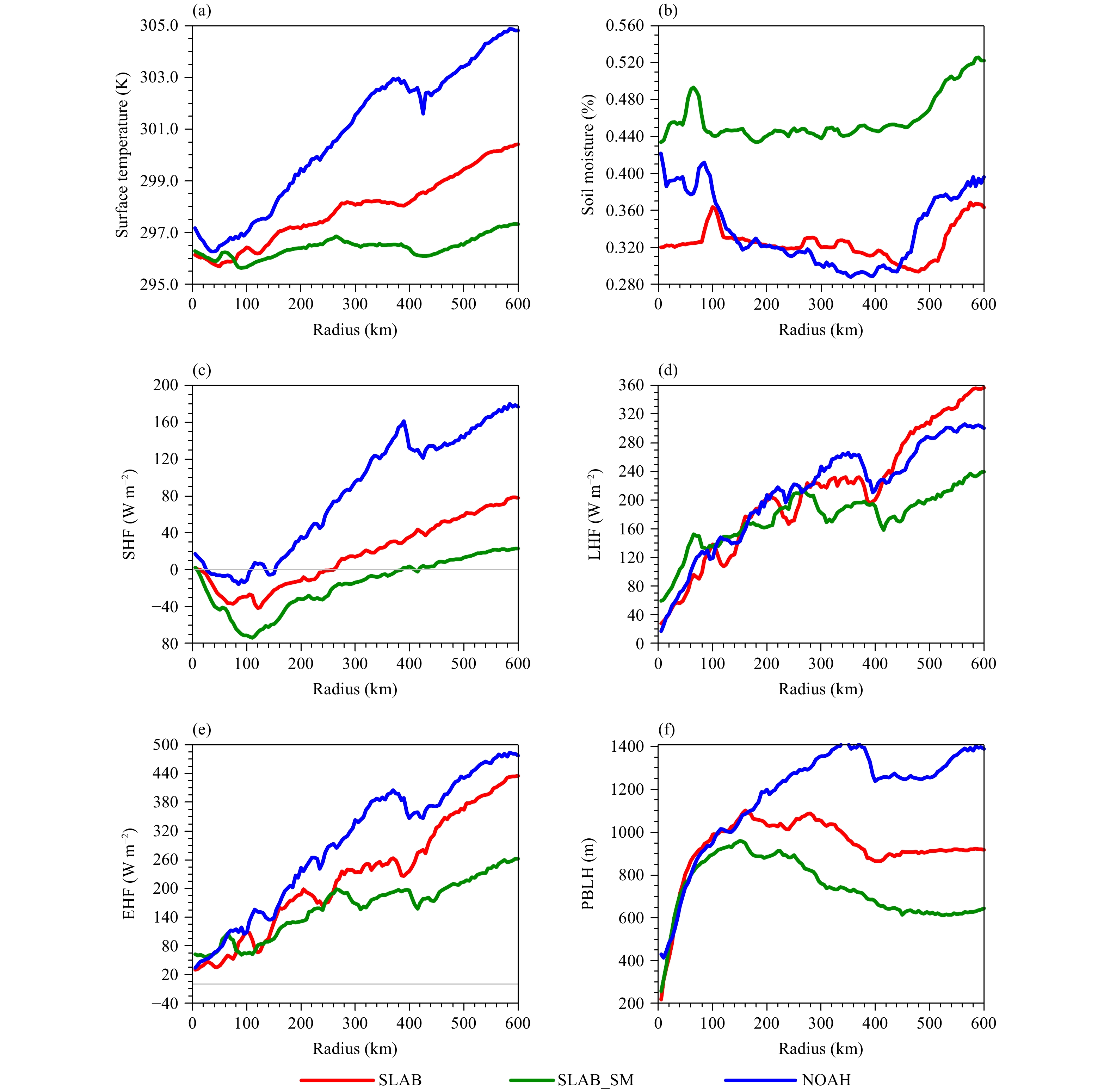
Figure 7 compares the azimuthally averaged surface temperature, soil moisture, SHF, LHF, surface enthalpy flux (EHF, henceforth), and boundary layer height (PBLH, defined with the critical Richardson method; Troen and Mahrt, 1986) at the 42-h forecast. The results show that the increased soil moisture inside and outside the storm in SLAB_SM experiment (Fig. 7b) tends to cool the land surface (Fig. 7a), especially in the environment outside the storm. Besides, SHF, LHF, EHF, and PBLH over the storm environment are all weaker in SLAB_SM than in SLAB, suggesting that the increase in soil moisture tends to weaken surface diabatic heating over the storm environment and is not conducive to the storm’s maintenance over land. Inside the storm, although LHF (Fig. 7d) in SLAB_SM is stronger than in SLAB, SHF deceases at the same time in SLAB_SM. Consequently, the surface enthalpy fluxes (Fig. 7e) and PBLH (Fig. 7f) have no obvious differences inside the storm, indicating that the increase in soil moisture has no significant impacts on the transport of the total heat and moisture fluxes from the land surface into the boundary layer within the storm.
|
| Figure 7 Azimuthally averaged (a) surface temperature (K), (b) volumetric fractional 0–10-cm soil moisture content (%), and surface fluxes (W m–2) in terms of (c) SHF, (d) LHF, (e) EHF, and (f) PBLH (m) valid at the 42-h forecast (daytime). |
Figure 8 compares the azimuthally averaged radial wind and tangential wind below 300 hPa at the 42-h forecast. The results show that SLAB_SM produces much weaker tangential winds than SLAB. SLAB_SM also produces weaker inflow and outflow than SLAB. For instance, outflow with a magnitude of 1.0 is shown in SLAB but disappears completely in SLAB_SM. Gopalakrishnan et al. (2013) indicated that the weaker forcing related to gradient wind imbalance within a storm can weaken the inflow winds near the eyewall region. This corresponds well with our results, in which the increased soil moisture in SLAB_SM produces weaker inflow winds (Fig. 8b) than SLAB, and thus the forcing related to gradient wind imbalance could be weaker in SLAB_SM compared to SLAB. The results in Fig. 8 also indicate that the storm’s symmetrical structure in SLAB_SM is worse because of the much weaker tangential wind, suggesting that the weaker storm produced by SLAB_SM could be easily modulated by midlatitude synoptic environment flows, compared to SLAB. As a result, the larger simulation error of the storm track, especially after the storm recurves into the midlatitude westerlies, is produced in SLAB_SM (shown in Figs. 2, 3a).

|
| Figure 8 Azimuthally averaged radial wind (contours; m s–1) and tangential wind (shaded; m s–1) below 300 hPa during the evolution of the storm over land at the 42-h forecast (daytime). (a) SLAB, (b) SLAB_SM, and (c) NOAH. |
To further illustrate the influence of the weakened surface diabatic heating over the storm environment, azimuthally averaged equivalent potential temperature (θe) and boundary layer vertical mixing is diagnosed in Fig. 9. The results show that over the storm environment (300–600 km), vertical mixings in the PBL are comparable in the two experiments; θe is weaker in SLAB_SM than in SLAB, especially in the lower boundary layer. Combined with the results of Fig. 7, it is clear that increasing soil moisture over the storm environment weakens surface diabatic heating effects and tends to strengthen dry, cold air over the storm’s environment boundary layer, which is conducive to the decay of the storm over land.

|
| Figure 9 As in Fig. 8, but for equivalent potential temperature (θe; K, contour line) and boundary layer vertical mixing (Km; m2 s–1, shaded color). |
It should be noted that the SLAB model has considered for the influences of the change of soil moisture on other land surface variables, such as surface temperature and enthalpy fluxes, through its impact on thermal conductivity. However, soil moisture and soil temperature are not directly coupled together, compared to other sophisticated land surface model such as NOAH and CLM, in which soil temperature is a function of soil moisture [e.g., see Eq. (1) in Chen and Dudhia (2001)]. To further understand the impacts of soil moisture on storm’s structures after its landfall, an additional simulation is conducted with the NOAH land surface model and compared with the SLAB. In addition, it is found that the perturbed soil moisture at the initial time in NOAH will rapidly spin down and the soil moisture will be quickly adjusted back to original climatology status once model integration starts, due to lack of land surface data assimilation. Since land surface data assimilation is beyond the scope of this study, we do not include the simulation with the NOAH land surface model with perturbed soil moisture.
Comparison results between simulations with SLAB and NOAH land surface models are shown in Figs. 7–9. Figure 7 indicates that there is an evident discrepancy between simulations with two schemes in both the storm and its environment. Inside the storm (e.g., 0–100 km from the storm center), NOAH produces larger soil moisture than SLAB but smaller soil moisture than SLAB_SM. Meanwhile, soil temperature, SHFs, LHFs, and PBLH are comparable in all three experiments. Over the storm environment, NOAH produces strongest SHFs, EHFs, and PBLH, followed by SLAB and SLAB_SM. Although the simulated soil moisture in NOAH is smaller (e.g., 300–450 km) and larger (e.g., 450–600 km) than in SLAB, respectively; the simulated LHFs, however, present an opposite variation features in the two schemes. Figure 8 shows that tangential and radial winds produced by NOAH are weaker than these by SLAB, but stronger than these by SLAB_SM. The results could be closely related to the stronger boundary layer vertical mixing inside the storm (e.g., 0–100 km) in SLAB_SM, followed by NOAH and SLAB as shown in Fig. 9. Further comparisons in Fig. 9 indicate that boundary layer vertical mixing over the storm environment is much stronger in NOAH than that in SLAB and SLAB_SM. This could be directly attributed to the response of boundary layer vertical mixing to the near-surface atmospheric conditions, as suggested by the parameterization of Km [see Eq. (1) in Troen and Mahrt (1986)]. In other words, the much stronger surface temperature in NOAH over the storm environment tends to heat up and form an unstable near-surface atmosphere, leading to the rapid increase of vertical mixing in the PBL. Combined with the stronger surface enthalpy fluxes, θe over the storm environment is strengthened in NOAH.
Furthermore, the storm intensity regarding tangential and radial winds, the warm inner core is strongest in SLAB, followed by NOAH and SLAB_SM. Soil moisture and boundary layer vertical mixing and their variations within the storm are similar and are strongest in SLAB_SM, followed by NOAH and SLAB. The variations of soil moisture and boundary layer vertical mixing over the storm environment are not consistent, while the latter presents a significant response to near-surface atmospheric stability (surface temperature). Surface diabatic heating effects over the storm environment are strongest in NOAH, followed by SLAB and SLAB_SM. Therefore, comparison results for this case with different experiments consistently indicate that inside the storm, the larger soil moisture corresponds to a stronger boundary layer vertical mixing, which is conducive to the decay of storm and has a negative impact on storm evolution. Over the environment outside the storm, surface diabatic heating effects also contribute to the storm intensity, but their impacts are not so significant as boundary layer vertical mixing inside the storm. In other words, the storm evolution after its landfall depends more on boundary layer vertical mixing within the storm, compared to surface diabatic heating effects in the environment outside the storm.
6 Concluding remarks and discussionThe sensitivity experiments in this study highlight the influence of soil moisture uncertainty before the storm’s landfall on the evolution of landfalling hurricanes and provide useful insights into the processes associated with the influence of soil moisture on tropical storm forecasts over land. The results found that the perturbed (increased) soil moisture before the storm’s landfall produces a weaker storm after its landfall. Further investigations indicate that the increase in soil moisture inside the storm corresponds to a strengthened vertical mixing within the storm boundary layer, which is conducive to the decay of storm and has negative impacts on storm evolution. The stronger surface diabatic heating effects over the environment outside the storm also contribute to the storm evolution after its landfall, but their impacts are not so significant as boundary layer vertical mixing inside the storm.
Besides, the major findings mentioned above, the analysis in this study also implies that uncertainty in surface temperature simulations, in addition to soil moisture, could be the key factor influencing the simulation of Tropical Storm Bill (2015) after landfall and its further evolution over land since they are important to surface diabatic heating effects. Since the land is usually covered by clouds during a hurricane’s landfall, which inhibits downward shortwave radiation, variation in surface temperature might be strongly related to the heat transfer potential within the soil layer, as highlighted by Tuleya (1994) and Emanuel et al. (2008). Obviously, the uncertainties of heat transfer within the soil are closely related to the uncertainties of the parameterization of soil heat capacity and conductivity, as well as predefined soil and vegetation properties (Horváth et al., 2009; Breuer et al., 2012). Therefore, the parameterization of heat transfer potential within the soil layer needs to be further investigated in a future study.
The results from this study indicate the significant impacts of soil moisture on the evolution of landfalling hurricanes. Incorrect soil moisture can cause significant error in the numerical prediction of landfalling hurricanes. However, soil moisture perturbations are subjectively based on analysis differences, the increase of soil moisture with SLAB is done in the whole integration time for both the storm and its environment, and only one case is included. Meanwhile, it is found that the perturbed initial soil moisture in NOAH will rapidly spin down and the soil moisture will be quickly adjusted back to its original climatology status once model integration starts. Moreover, compared to the simulation results with NOAH, we also noticed that the SLAB scheme used in this study might eliminate possible feedback between the land surface and the post-landfall storm since soil moisture and temperature beneath and around the storm should vary as the storm evolves over land. The interactive (mutual feedback) of soil moisture and temperature is also important to the simulation results. Future work should emphasize surface and soil moisture data assimilation techniques (Pu et al., 2013; Li and Pu, 2018) with the more sophisticated land surface model, as well as more cases, to produce more robust results.
Acknowledgments. This study is initially conducted when the first author (FZ) visited the University of Utah. The research was supported by National Science Foundation Award #AGS-1243027 (ZP and FZ). High-performance computing support from Yellowstone (ark:/85065/d7wd3xhc), provided by NCAR’s Computational and Information Systems Laboratory (CISL) and the Center for High-Performance Computing (CHPC) at the University of Utah, is greatly appreciated. Authors also thank the Development Testbed Center (DTC) at the National Center for Atmospheric Research (NCAR) for their efforts to make the community research version of the HWRF model available on a public website. The first and third authors (FZ and CW) were alsosupported by the National Natural Science Foundation of China (41805032), and the Fundamental Research Funds of the Central Universities (lzujbky-2017-71).
Two anonymous reviewers are appreciated for their constructive comments that are very helpful for improving the manuscript.
| Arndt, D. S., J. B. Basara, R. A. McPherson, et al., 2009: Observations of the overland reintensification of tropical storm Erin (2007). Bull. Amer. Meteor. Soc., 90, 1079–1093. DOI:10.1175/2009BAMS2644.1 |
| Beljaars, A. C. M., P. Viterbo, M. J. Miller, et al., 1996: The anomalous rainfall over the United States during July 1993: Sensitivity to land surface parameterization and soil moisture anomalies. Mon. Wea. Rev., 124, 362–383. DOI:10.1175/1520-0493(1996)124<0362:TAROTU>2.0.CO;2 |
| Betts, A. K., J. H. Ball, A. Beljaars, et al., 1996: The land surface–atmosphere interaction: A review based on observational and global modeling perspectives. J. Geophys. Res. Atmos., 101, 7209–7225. DOI:10.1029/95JD02135 |
| Bozeman, M. L., D. Niyogi, S. Gopalakrishnan, et al., 2012: An HWRF-based ensemble assessment of the land surface feedback on the post-landfall intensification of Tropical Storm Fay (2008). Nat. Hazards, 63, 1543–1571. DOI:10.1007/s11069-011-9841-5 |
| Braun, S. A., and W. K. Tao, 2000: Sensitivity of high-resolution simulations of Hurricane Bob (1991) to planetary boundary layer parameterizations. Mon. Wea. Rev., 128, 3941–3961. DOI:10.1175/1520-0493(2000)129<3941:SOHRSO>2.0.CO;2 |
| Breuer, H., F. Ács, B. Laza, et al., 2012: Sensitivity of MM5-simulated planetary boundary layer height to soil dataset: comparison of soil and atmospheric effects. Theor. Appl. Climatol., 109, 577–590. DOI:10.1007/s00704-012-0597-y |
| Chen, F., and J. Dudhia, 2001: Coupling an advanced land surface–hydrology model with the Penn State–NCAR MM5 modeling system. Part I: Model description and implementation. Mon. Wea. Rev., 129, 569–585. DOI:10.1175/1520-0493(2001)129<0569:CAALSH>2.0.CO;2 |
| Deardorff, J. W., 1978: Efficient prediction of ground surface temperature and moisture, with inclusion of a layer of vegetation. J. Geophys. Res. Oceans, 83, 1889–1903. DOI:10.1029/JC083iC04p01889 |
| Eltahir, E. A. B., 1998: A soil moisture-rainfall feedback mechanism: 1. Theory and observations. Water Resour. Res., 34, 765–776. DOI:10.1029/97WR03499 |
| Emanuel, K., J. Callaghan, and P. Otto, 2008: A hypothesis for the redevelopment of warm-core cyclones over northern Australia. Mon. Wea. Rev., 136, 3863–3872. DOI:10.1175/2008MWR2409.1 |
| Evans, C., R. S. Schumacher, and T. J. Jr. Galarneau, 2011: Sensitivity in the overland reintensification of Tropical Cyclone Erin (2007) to near-surface soil moisture characteristics. Mon. Wea. Rev., 139, 3848–3870. DOI:10.1175/2011MWR3593.1 |
| Ferrier, B. S., Y. Jin, Y. Lin, et al., 2002: Implementation of a new grid-scale cloud and precipitation scheme in the NCEP Eta model. 19th Conference on Weather Analysis and Forecasting/15th Conference on Numerical Weather Prediction. American Meteorological Society, San Antonio, TX. |
| Findell, K. L., and E. A. B. Eltahir, 2003: Atmospheric controls on soil moisture-boundary layer interactions. Part I: Framework development. J. Hydrometeorol., 4, 552–569. DOI:10.1175/1525-7541(2003)004<0552:ACOSML>2.0.CO;2 |
| Gopalakrishnan, S. G., F. Jr. Marks, X. J. Zhang, et al., 2011: The experimental HWRF system: A study on the influence of horizontal resolution on the structure and intensity changes in tropical cyclones using an idealized framework. Mon. Wea. Rev., 139, 1762–1784. DOI:10.1175/2010MWR3535.1 |
| Gopalakrishnan, S. G., F. Jr. Marks, J. A. Zhang, et al., 2013: A study of the impacts of vertical diffusion on the structure and intensity of the tropical cyclones using the high-resolution HWRF system. J. Atmos. Sci., 70, 524–541. DOI:10.1175/JAS-D-11-0340.1 |
| Hart, R. E., and J. L. Evans, 2001: A climatology of the extratropical transition of Atlantic tropical cyclones. J. Climate, 14, 546–564. DOI:10.1175/1520-0442(2001)014<0546:ACOTET>2.0.CO;2 |
| Horváth, Á., F. Ács, and H. Breuer, 2009: On the relationship between soil, vegetation and severe convective storms: Hungarian case studies. Atmos. Res., 93, 66–81. DOI:10.1016/j.atmosres.2008.10.007 |
| Hou, D. C., M. Charles, Y. Luo, et al., 2014: Climatology-calibrated precipitation analysis at fine scales: Statistical adjustment of stage IV toward CPC gauge-based analysis. J. Hydrometeorol., 15, 2542–2557. DOI:10.1175/JHM-D-11-0140.1 |
| Janjic, Z. I., R. Gall, and M. E. Pyle, 2010: Scientific documentation for the NMM solver. NCAR Tech. Note NCAR/TN-4771STR, NCAR, 53 pp, doi: 10.5065/D6MW2F3Z. |
| Jones, S. C., P. A. Harr, J. Abraham, et al., 2003: The extratropical transition of tropical cyclones: Forecast challenges, current understanding, and future directions. Wea. Forecasting, 18, 1052–1092. DOI:10.1175/1520-0434(2003)018<1052:TETOTC>2.0.CO;2 |
| Kishtawal, C. M., D. Niyogi, A. Kumar, et al., 2012: Sensitivity of inland decay of North Atlantic tropical cyclones to soil parameters. Nat. Hazards, 63, 1527–1542. DOI:10.1007/s11069-011-0015-2 |
| Koster, R. D., Z. C. Guo, R. Q. Yang, et al., 2009: On the nature of soil moisture in land surface models. J. Climate, 22, 4322–4335. DOI:10.1175/2009JCLI2832.1 |
| Kurihara, Y., and R. E. Tuleya, 1974: Structure of a tropical cyclone developed in a three-dimensional numerical simulation model. J. Atmos. Sci., 31, 893–919. DOI:10.1175/1520-0469(1974)031<0893:SOATCD>2.0.CO;2 |
| Lanicci, J. M., T. N. Carlson, and T. T. Warner, 1987: Sensitivity of the Great Plains severe-storm environment to soil-moisture distribution. Mon. Wea. Rev., 115, 2660–2673. DOI:10.1175/1520-0493(1987)115<2660:SOTGPS>2.0.CO;2 |
| Lin, L-F, and Z. Pu, 2018: Characteristics of Background Error Covariance of Soil Moisture and Atmospheric States in Strongly Coupled Land–Atmosphere Data Assimilation. J. Appl. Meteorol. Climatol., 57, 2507–2529. |
| Pan, H.-L., and J.-S. Wu, 1995: Implementing a mass flux convection parameterization package for the NMC medium-range forecast model. NMC Office Note 409. U.S. National Center for Environmental Prediction, Washington, DC, 40 pp. |
| Pu, Z., H. Zhang, and J. A. Anderson, 2013: Ensemble Kalman filter assimilation of near-surface observations over complex terrain: Comparison with 3DVAR for short-range forecasts. Tellus A, 65, 19620. |
| Pu, Z., S. X. Zhang, M. J. Tong, et al., 2016: Influence of the self-consistent regional ensemble background error covariance on hurricane inner-core data assimilation with the GSI-based hybrid system for HWRF. J. Atmos. Sci., 73, 4911–4925. DOI:10.1175/JAS-D-16-0017.1 |
| Rossow, W. B., Y. C. Zhang, and G. Tselioudis, 2016: Atmospheric diabatic heating in different weather states and the general circulation. J. Climate, 29, 1059–1065. DOI:10.1175/JCLI-D-15-0760.1 |
| Schwarzkopf, M. D., and S. Fels, 1991: The simplified exchange method revisited: An accurate, rapid method for computation of infrared cooling rates and fluxes. J. Geophys. Res. Atmos., 96, 9075–9096. DOI:10.1029/89JD01598 |
| Shen, R. J., E. R. Reiter, and J. F. Bresch, 1986: Some aspects of the effects of sensible heating on the development of summer weather systems over the Tibetan Plateau. J. Atmos. Sci., 43, 2241–2260. DOI:10.1175/1520-0469(1986)043<2241:SAOTEO>2.0.CO;2 |
| Sirutis, J. J., and K. Miyakoda, 1990: Subgrid scale physics in 1-month forecasts. Part I: Experiment with four parameterization packages. Mon. Wea. Rev., 118, 1043–1064. DOI:10.1175/1520-0493(1990)118<1043:SSPIMF>2.0.CO;2 |
| Smith, R. K., 2003: A simple model of the hurricane boundary layer. Quart. J. Roy. Meteor. Soc., 129, 1007–1027. DOI:10.1256/qj.01.197 |
| Tallapragada, V., L. Bernardet, M. K. Biswas, et al., 2014: Hurricane Weather Research and Forecasting (HWRF) Model: 2014 Scientific Documentation. NCAR HWRF Development Testbed Center Tech. Rep., 99 pp. |
| Troen, I. B., and L. Mahrt, 1986: A simple model of the atmospheric boundary layer; sensitivity to surface evaporation. Bound.-Layer Meteor., 37, 129–148. DOI:10.1007/BF00122760 |
| Tuleya, R. E., 1994: Tropical storm development and decay: Sensitivity to surface boundary conditions. Mon. Wea. Rev., 122, 291–304. DOI:10.1175/1520-0493(1994)122<0291:TSDADS>2.0.CO;2 |
| Wu, C.-C., and Y. Kurihara, 1996: A numerical study of the feedback mechanisms of hurricane–environment interaction on hurricane movement from the potential vorticity perspective. J. Atmos. Sci., 53, 2264–2282. DOI:10.1175/1520-0469(1996)053<2264:ANSOTF>2.0.CO;2 |
| Zhang, F. M., and Z. X. Pu, 2017: Effects of vertical eddy diffusivity parameterization on the evolution of landfalling hurricanes. J. Atmos. Sci., 74, 1879–1905. DOI:10.1175/JAS-D-16-0214.1 |
| Zhang, F. M., Z. X. Pu, and C. H. Wang, 2017: Effects of boundary layer vertical mixing on the evolution of hurricanes over land. Mon. Wea. Rev., 145, 2343–2361. DOI:10.1175/MWR-D-16-0421.1 |
| Zhang, J. A., D. S. Nolan, R. F. Rogers, et al., 2015: Evaluating the impact of improvements in the boundary layer parameterization on hurricane intensity and structure forecasts in HWRF. Mon. Wea. Rev., 143, 3136–3155. DOI:10.1175/MWR-D-14-00339.1 |
| Zheng, X. Y., and E. A. B. Eltahir, 1998: A soil moisture–rainfall feedback mechanism: 2. Numerical experiments. Water Resour. Res., 34, 777–785. DOI:10.1029/97WR03497 |
 2019, Vol. 33
2019, Vol. 33


