The Chinese Meteorological Society
Article Information
- YUAN, Meng, and Wei ZHONG, 2019.
- Detecting Intensity Evolution of the Western North Pacific Super Typhoons in 2016 Using the Deviation Angle Variance Technique with FY Data. 2019.
- J. Meteor. Res., 33(1): 104-114
- http://dx.doi.org/10.1007/s13351-019-8064-7
Article History
- Received April 16, 2018
- in final form September 27, 2018
The western North Pacific (WNP) is one of the basins with the most frequent tropical cyclogenesis (Tang et al., 2012). The genesis and development of tropical cyclones (TCs) have an adverse impact on maritime activities. Therefore, it is imperative to strengthen research on the evolution of TC intensity and structure during TC’s whole lifecycle as this would improve the prediction capability for TCs in the WNP.
A TC system generally generates and develops over the open ocean, where conventional measurements are sparse. As a consequence, satellite-based data (both visible and infrared) are the most effective sources for tracking the development of maritime TCs (Piñeros et al., 2010). The most popular method for analysis of TCs based on satellite images is the Dvorak technique (DT), which was proposed in the 1970s. This method compares the similarity of clouds that are analyzed with a series of standard cloud patterns using the infrared and visible images (Dvorak, 1975, 1984). However, this method is subjective, time-intensive and requires a complex set of rules for estimation of TC intensity. Velden et al. (1998, 2006) introduced an empirically determined look-up table to the original DT, which became known as the objective Dvorak technique (ODT). This technique estimates the TC intensity by measuring the differences in brightness temperature between the eye and its surroundings. Olander and Velden (2007) refined the approach by proposing the advanced Dvorak technique (AODT), which integrated radical modifications to the ODT and used regression equations to estimate the TC intensity. When the TC has not yet reached tropical storm (TS) intensity, the intensity is estimated by analyzing the shape and curvature of the spiral cloud bands. This enables application of the method to the entire lifecycle of the TC (Olander and Velden, 2007). In addition, some other methods exploiting numerical weather pro-ducts to predict the tropical cyclogenesis and TC intensity have also been reported. However, it has been proved difficult to distinguish TC systems that have developed from disorganized cloud clusters using the afore-mentioned methods, as many of the methods are applicable only to cloud systems that show clear spiral bands (Brueske and Velden, 2003; Liu et al., 2007).
To overcome the limitations of the previous subjective analysis methods, Piñeros et al. (2011) proposed an objective method, the deviation angle variance technique (DAV-T), for obtaining the shape and dynamic characteristics of TCs using infrared images. When a TC system has developed and strengthened from disorganized clouds, the structure becomes increasingly axisymmetric. The DAV-T enables quantification of the TC axisymmetry by calculating the gradient of the brightness temperatures for the infrared images. The results show that this method is effective throughout the TC lifecycle, which includes its genesis, development, maturity, and dissipation. The DAV values are used to quantify the axisymmetry, and the organization of the TC systems can be linked with the TC intensity; further, the maximum surface wind speed (Vmax) may be indirectly estimated from the DAV values (Piñeros et al., 2008, 2009). Piñeros et al. (2011) applied this approach to TC systems that were generated during the hurricane seasons from 2004 to 2009 in North Atlantic (NA). The root mean square errors (RMSEs) between the Vmax fitted by the DAV values and the Vmax recorded by the best-track data of the US National Hurricane Center (NHC) were between 6.7 and 7.7 m s–1. Ritchie et al. (2014) applied the DAV-T to the TC intensity estimation in North Pacific (NP) from 2007 to 2011. A variety of satellite data sources (GEOS-E, GEOS-W, MTSAT, etc.) were used in their study. Considering the differences of the TCs between eastern North Pacific (ENP) and WNP, different calculation parameters were used for these regions. It was found that, the RMSEs of TC intensity estimation by the DAV-T were 6.6–7.8 m s–1 for individual years in the WNP compared with the best-track data of the Joint Typhoon Warning Center (JTWC), and they were 4.8–8.6 m s–1 in the ENP compared with the best-track data of the NHC (Ritchie et al., 2014). In addition, the DAV-T shows great potential in identification of the tropical cyclogenesis (Kofron et al., 2009; Piñeros et al., 2010; Rodríguez-Herrera et al., 2015; Wood et al., 2015).
However, as the DAV-T is an emerging technique, further research concerning its application and physical significance is needed; in particular, it is critical to understand how DAV values characterize the TC axisymmetry. Accordingly, the analyses of DAV distributions during the entire lifecycle of multiple TC cases and the relationship between the DAV distributions and the evolution of TC structure and intensity are needed. In addition, verification of the DAV-T using data sources from Chinese installations (such as the FY series meteorological satellites) is both necessary and possible, enabling establishment of an objective monitoring and forecasting system for TCs based on independent data sources in China.
2 Data and methods 2.1 DataAs a result of satellite debugging, regional encrypted observation or other tasks, observations made by using a single satellite to detect the TC activities in the WNP region, or a part of it, during a given period, are inevitably incomplete. Therefore, the main observations in this paper were obtained from FY-2F, and the missing data were supplemented from FY-2G. The sub-satellite points of FY-2F and FY-2G were located at 112° and 105°E, respectively. Considering the consistency of the two satellites, coverage of the remote data was integrated over 0°–40°N, 100°–160°E. The longwave (10.7μm) infrared brightness temperatures derived from the satellites were used. The temporal and spatial resolutions of the data were once per hour and 0.05° per pixel (about 5 km per pixel), respectively. It was found that appropriate reduction of the spatial resolution of the data had little effect on the calculated results, but significantly reduced the calculation time (Piñeros et al., 2011). Consequently, the research data were resampled to 0.1° per pixel (about 10 km per pixel) to improve the calculation efficiency.
The conventional data in this study include the BestTrack data from the China Meteorological Administration (CMA-BestTrack) and the Final Operational Global Analysis (FNL) data provided by the NCEP of US. The CMA-BestTrack data, updated every 6 h, were used to analyze the TC position, intensity, and life stages. The FNL data used for the diagnosis and analysis of TC physical fields also have a 6-h temporal resolution, consistent with that of the CMA-BestTrack; and the FNL data are on a horizontal resolution of 1° × 1°.
To cover the complete TC lifecycle, TC cases that reached super typhoon intensity in 2016 (except for the cases of Typhoons Chaba and Songda, whose activity areas were beyond the coverage of the FY-2F and FY-2G satellites) were analyzed. Therefore, the research survey involved seven super typhoons: Nepartak, Lionrock, Meranti, Megi, Sarika, Haima, and Nock-ten. The TCs were divided into seven different intensity levels according to the Chinese National Standard for Grading of Tropical Cyclones. Among the CMA-BestTrack data, there were 47 moments for tropical depression (TD, 10.8–17.1 m s–1), 47 moments for tropical storm (TS, 17.2–24.4 m s–1), 25 moments for severe tropical storm (STS, 24.5–32.6 m s–1), 37 moments for typhoon (TY, 32.7–41.4 m s–1), 39 moments for severe typhoon (STY, 41.5–50.9 m s–1), 42 moments for super typhoon (SuperTY, ≥ 51.0 m s–1), and 8 moments for TCs that were weaker than tropical depressions (WTD, < 10.8 m s –1). Overall, 1330 h of satellite infrared images was collected for research on the super typhoons.
2.2 MethodsAccording to observational research, TC genesis and intensification may be interpreted from satellite imagery of the concentration and closure of the disorganized cloud clusters, while termination corresponds to the dissipation of axisymmetric cloud bands over land or cooler oceans (Fritz, 1962; Hubert and Timchalk, 1969; Dvorak, 1975). It has also been shown that the gradient directions of the brightness temperature (TBB) in TCs tend to point to the warm center. The stronger the TC intensity, the more closely the TBB gradient directions approach the ideal convergent shape. Therefore, it is possible to locate the TC and estimate TC intensity by quantifying its axi-symmetric features using infrared images.
The DAV-T that determines the TC axisymmetry by DAV was first proposed by Piñeros et al. (2008, 2009). The Typhoon Nepartak’s infrared image at 1200 UTC 6 July (Fig. 1a) is now taken as an example. First, the gradient of the infrared image at every pixel should be calculated; next, a reference point Or should be chosen. Then, the deviation angle θi between the infrared gradient vector and the radial line whose direction points to the reference point from the pixel (Fig. 1b) should be measured. This process should be repeated for every pixel within a certain calculated radius (R). Next, the distribution of the deviation angles is plotted (Fig. 1c) and the DAV of the reference point Or is defined as the variance of that distribution. The more closely θi approaches 0°, the smaller is the variance (i.e., the DAV value) within the calculation area, indicating that strong convective cloud clusters are more axisymmetric with respect to the selected reference center. Thus, when the TC center is determined, a DAV value can be calculated to characterize the TC axisymmetry by using the TC center as the reference point. Therefore, the DAV value is very sensitive to the selection of the reference center position. However, it is difficult to accurately determine the TC center in actual observations, especially for real-time monitoring and early warning. To overcome this problem, the calculation is repeated by using every pixel in turn as the reference point and where each point would correspond to a DAV value. Then, a DAV map can be created by plotting back all DAV values into their reference point locations (Fig. 1d); the low-DAV areas correspond to regions with strong circular or annular convective clouds while the location of the minimum DAV (or map minimum value: MMV) of a TC system corresponds to its TC center. Further, the MMV indicates the best axisymmetric level of the TC system. Thus, information about the TC center and intensity can be analyzed and determined by using the DAV-T.
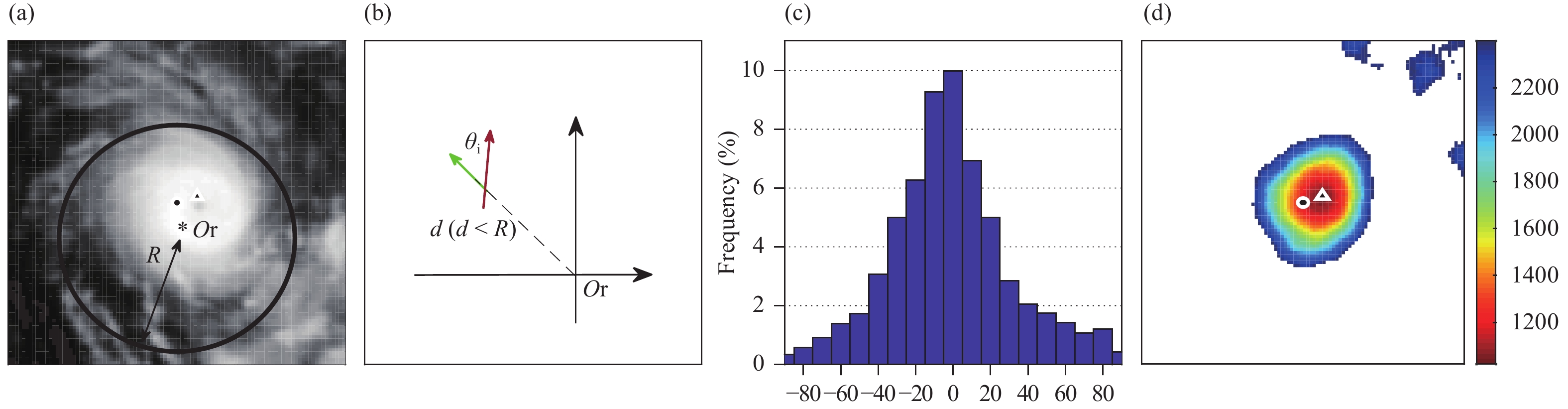
|
| Figure 1 Schematic of DAV-T. (a) The Nepartak infrared image (shading; K) at 1200 UTC 6 July. (b) Schematic of deviation angle (degree) calculation. (c) Deviation angle frequency distribution at the reference point Or. (d) DAV map (shading; deg2). In (a), the symbol “●” represents the TC center recorded by CMA-BestTrack dataset; “▲” indicates the MMV location; “*” is the position of the reference point Or; and R is the calculation radius. In (b), the red arrow represents the direction of the brightness temperature gradient; the green arrow represents the radial line, which is derived from Or; and θi is the deviation angle between the two directions. |
In this section, two representative examples of Super Typhoons Lionrock and Meranti are used to explore the evolution characteristics of the DAV distribution at different TC evolutional periods. According to the CMA-BestTrack data, Lionrock reached TD intensity in the WNP at 1800 UTC 17 August and landed in eastern Japan at 0800 UTC 30 August, forming an extratropical cyclone 10 h later. The genesis latitude was 33.1°N, which is the northernmost point for TC formations since 1977. In the early stages, Lionrock’s intensity initially weakened because of cold eddies, but then moved southward under the influence of Typhoons Kompasu and Mindulle, and its intensity continued to increase. Finally controlled by a subtropical high, it made landfall in Japan. The super typhoon was characterized by a high genesis latitude, a complicated path, and a long duration at low intensity. In the case of Typhoon Meranti, it lasted 8 days from its genesis at 0900 UTC 9 September to its dissipation at 0600 UTC 17 September. At the peak of its development, the minimum pressure (pmin) in the center was 890 hPa, which was the lowest ever observed. The trajectory of Meranti was stable. It had been moving steadily northwestwards since its formation at a speed of 20–25 m s–1 until it landed in China at 1700 UTC 14 September; then, it started moving northward. The typhoon was characterized by a strong intensity, a stable path, and a long duration after landfall.
3.1 DAV distribution characteristicsThis section examines the relationship between the DAV distribution and the TC structure at different stages using NCEP reanalysis data. Severe comparative analyses were performed between different TC periods. From the CMA-BestTrack dataset, Lionrock reached TD intensity initially at 1800 UTC 17 August (Figs. 2a, b). It can be observed from the infrared image that the TC cloud was semi-closed in the southeast quadrant of the circulation center, and the structure of the TC clouds was clearly asymmetric. The area of deep convective clouds and the low-DAV area were basically coincident; and there was a relatively long distance between the MMV location and the TC center. Compared to 1800 UTC 17 August, the intensity of deep convection (TBBmin) at 1800 UTC 22 August was comparable, but the structure of the clouds was more organized (Figs. 2c, d). This made the distribution of low-DAV areas more regular, and the relative distance between the TC center and the MMV location became smaller. However, the MMVs for the two time periods were roughly equivalent. Meranti reached its maximum intensity at 1200 UTC 13 September (Figs. 2e, f), and had the appearance of closed eyewalls. The low-DAV area presented a regular disc-shaped distribution. Meanwhile, the MMV was as low as 950 deg2, and its position was very close to the TC center, even closer to the eye. Meranti landed at 0600 UTC 15 August, and its intensity weakened rapidly thereafter. According to the infrared image (Figs. 2g, h), a wide range of clouds were distributed in the northeast direction from the TC center. The low-DAV area appeared as a band-like distribution extending from the circulation center to the northeast. In addition, the MMV drastically increased to 1894 deg2, and its position was biased northeastward, which was consistent with the cloud distribution.
The above analysis shows that deep convection of the TC had a significant impact on the DAV distribution, especially when the cloud structure was unclosed. This caused the MMV locations to deviate from the actual TC center and move towards where the convection was strong. However, when the TC intensity was strong, the clouds tended to be more axisymmetric and the distribution of the low-DAV zone tended to be more regular, leading to smaller MMV values and relative distances. Therefore, both the MMV and its location can be used as a reference to determine the TC intensity.
3.2 MMV characteristicsWe compared the TC paths that were recorded by the CMA-BestTrack dataset with the trajectories of their MMV locations that were calculated from the infrared images at each time point (Figs. 3a, b). It was found that there was a good correspondence between them regardless of whether it was Meranti that had a relatively stable moving direction and speed, or Lionrock that exhibited a serpentine-type route with variable velocity. However, the deviations for Meranti were smaller than those for Lionrock, especially in the early stages. To explore the relationship between the TC centers and the MMV locations, the relative distances between the two were calculated. The lifecycle of Lionrock was affected by many weather systems, and the intensity dropped rapidly during the dissipation period (turned into an extratropical cyclone from STS directly). This resulted in fluctuations in the relative distances, especially in the final stage when the relative distances showed increasing fluctuations. For Typhoon Meranti, the changes of relative distances were much more stable than for Lionrock. However, due to the influence of topography, the curvature of its path was tortuous, and its intensity weakened after landfall, which led to a significant increase in relative distances. From the evolutions of the relative distances during the TC’s lifecycle (Figs. 3c, d), it can be deduced that the relative distances were small when the TC intensities were strong. In addition, moments with larger relative distances were concentrated in the periods when the TC was in its genesis or dissipation. The RMSEs of relative distances during the entire lifecycle of Lionrock and Meranti were 103.8 and 191.7 km, respectively. However, when the samples whose intensities were below TD were removed, the RMSE values of relative distances decreased to 85.7 and 76.2 km, respectively.

|
| Figure 3 (a) Paths of TC centers and MMV locations for Lionrock and (b) changes of relative distances (km) in the lifecycle of Lionrock. (c, d) Same as (a, b) but for Meranti. The blue (purple) line in (a, c) represents the path of TC centers recorded by the CMA-BestTrack dataset (satellite data); the black line in (b, d) represents the path for MMV locations; and the bigger blue dots in (b, d) represent moments with relative distances greater than 200 km. |
Given that the MMVs may be calculated from the hourly infrared images and that the data for CMA-BestTrack dataset were recorded every 6 h, the temporal resolutions between the two data sources were different. Thus, the high-frequency characteristics of the MMVs are not well reflected in the conventional data. However, the high-frequency signal of the MMVs mainly included noise as well as the instantaneous convection changes in the TC circulation, which had little effect on the TC intensity (Piñeros et al., 2011). Therefore, a Chebyshev filter (low-pass) with cutoff frequency of 0.1π rad/sample was used to reduce the MMV high-frequency oscillations to match the CMA-BestTrack dataset. From the perspective of the characteristics of the TC intensity (Fig. 4), Lionrock had a long genesis but a short dissipation. During the development to maturity, the intensity alternated between a maintenance level and reinforcement, and even decreased in a short period of time. These features of MMVs showed high-frequency fluctuations and a large amplitude of oscillation. In contrast, the changes for Meranti’s intensity were a typical “V (inverted V)” distribution. The process from reaching the TD intensity to maturity was very rapid, lasting only 3 days, and the intensity stabilized rapidly after landfall. Thus, the high-frequency fluctuations of Meranti’s MMVs were much weaker. Overall, the trend of the MMVs was opposite to that of the maximum surface wind speed (Vmax) and was coincident with the minimum pressure of the TC center (pmin).

|
| Figure 4 Changes in Vmax and pmin during the lifecycles of (a) Lionrock and (b) Meranti, and changes in (c) Lionrock’s MMVs and (d) Meranti’s MMVs. The green line represents the change in Vmax (m s–1) and MMV (deg2) before filtering; the blue line represents the change in pmin (hPa) and the filtered MMV (deg2). |
This section describes the correlation between the MMVs (both before and after filtering) and the TC intensities (Vmax and pmin). All results were significant at the 99% confidence level (Fig. 5), and strong correlations were observed between the MMVs and the intensity dataset for all samples except Lionrock. In particular, the correlation coefficient between Megi’s MMV sequence before (after) filtering and pmin was 0.89 (0.91), and the correlation coefficient with Vmax was –0.92 (–0.94). Clearly, the correlation coefficient (absolute value) between the filtered MMVs and the TC intensities is much higher than that before filtering; further, the correlation between the MMVs and Vmax was stronger than that between the MMVs and pmin. These results indicated that the MMVs corresponded better to the TC intensities after filtering out the high-frequency fluctuations, and that the MMVs showed more information about the wind field than the pressure field. Therefore, the TC intensity can be indirectly estimated by establishing mathematical models between the filtered MMVs andVmax.

|
| Figure 5 Correlation coefficients for MMVs and TC intensities. Orange (yellow) color represents the correlation coefficient between the before (after) filtering MMVs (deg2) and pmin (hPa); blue (cyan) color represents the correlation coefficient between the before (after) filtering MMVs (deg2) and Vmax (m s–1). |
All filtered MMVs were classified according to the TC intensity recorded in the CMA-BestTrack dataset (Fig. 6a). It can be seen from the box-plot that the distribution of the MMVs were scattered when the TC intensity was weak. When the TC intensity became enhanced, the MMVs tended to decrease and become more and more concentrated. The medians of the MMVs were reduced by more than 200 deg2 for the processes whereby the TC intensity was transformed from WTD to TD and from TD to TS. The decrease of the medians of the MMVs was also clear given the fact that the TC intensity turned from TS to STS and from SYT to SuperTY. However, there was not much difference in the medians of the MMVs when the TC intensity changed from STS to TY and from TY to STY. Those distribution characteristics of the MMVs and the TC intensities can be fitted by a sigmoid function (Fig. 6b). In addition, the temporal scales of the CMA-BestTrack dataset and the MMVs were different, because the former contained larger-scale information compared to the latter. This complicated the correlation analysis between the two datasets. To overcome this problem, only the medians of all the MMVs associated with a single intensity were chosen as the fitting data for regression analysis (Piñeros et al., 2011). The sigmoid equation is described as follows:
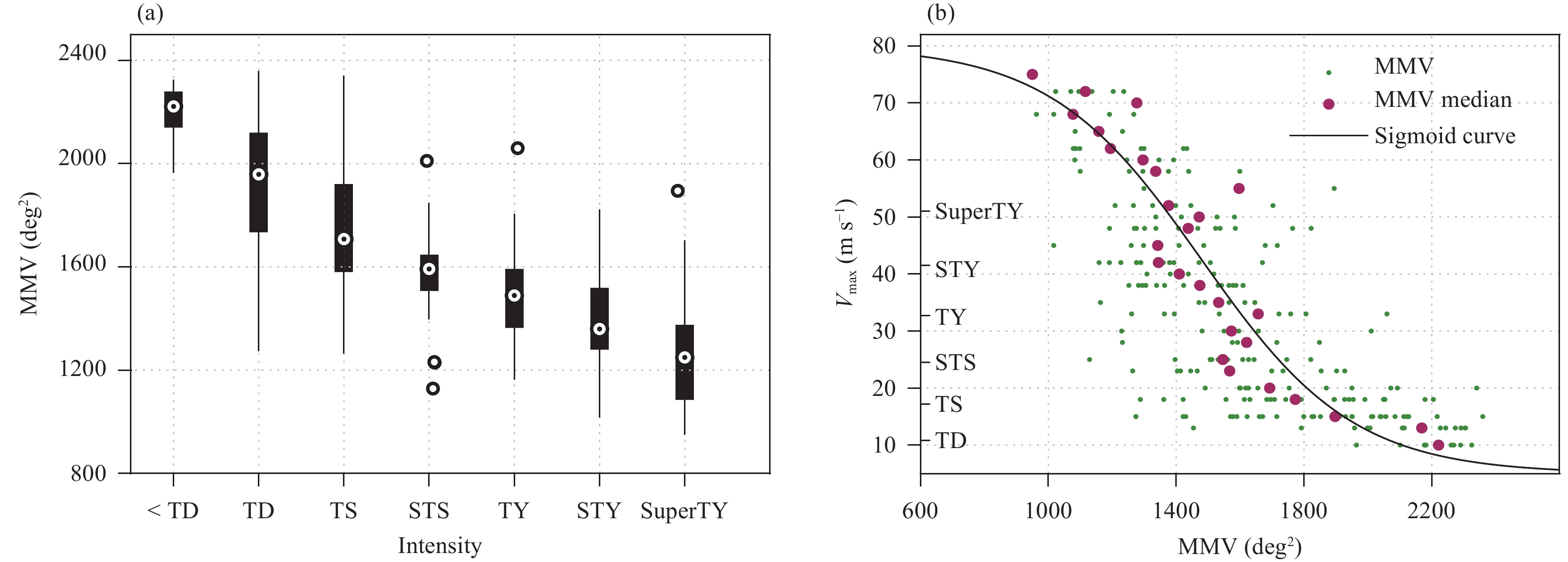
|
| Figure 6 Relationship between the MMVs and the TC intensities. (a) Boxplot of MMVs for different TC intensities. In each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentile, respectively. The whiskers extend to the most extreme data points excluding outliers, and the outliers are plotted individually using the “o” symbol. (b) The relationship between the MMVs and Vmax. The black line is the sigmoid curve, the green points are the MMVs at all of the CMA-BestTrack moments, and the purple points represent the MMV medians for each TC intensity. |
| ${\overline v_{{\rm max}}} = \frac{{{I_{\rm max}} - {I_{\rm min}}}}{{1 + {\rm exp}[\alpha ({\sigma ^2} - \beta)]}} + {I_{\rm min}}, $ | (1) |
where
Based on the regression model, the estimated MMVs and the confidence interval for each intensity bin can be calculated (Table 1). Then, those fitted data can be used as threshold to determine the TC intensity, and thus help improve the ability to predict TC damage. However, it should be noted that the lower the adopted MMV threshold was, the higher the accuracy of the TC identification (true positive rate) and the higher the false negative rate would be. In contrast, when the adopted MMV threshold was high, the false negative rate would be lower, but the false alarm rate (false positive rate) would increase at the same time (Wood et al., 2015). Clearly, this aspect is very important for the monitoring and prediction of TCs.
| TC intensity | TD | TS | STS | TY | STY | SuperTY |
| Estimated MMV
95% CI |
2127 | 1751 | 1615 | 1513 | 1421 | 1324 |
| 1971–2352 | 1661–1873 | 1549–1700 | 1465–1569 | 1389–1453 | 1309–1329 |
Considering that the water vapor condition is insufficient in the early stages of a TC and the TC would be greatly affected by the topography after landfall, the characteristics of a TC in weak-intensity periods would be significantly different from those in the other periods. When samples that below the TD (including TD) intensity were excluded, the RMS error of relative distances dropped dramatically compared to that for the complete lifecycle. In particular, in the cases of Meranti, which was of long duration after landfall, and Sarika, which had multiple landfalls, the RMS errors of relative distances decreased by 115.5 and 69.5 km, respectively (Table 2). Overall, there was a strong consistency between the MMV locations and the CMA-BestTrack dataset.
| Relative distance (km) | Nepartak | Lionrock | Meranti | Megi | Sarika | Haima | Nock-ten | All TCs | |
| Minimum | 16.7 | 7.5 | 7.7 | 17.0 | 7.7 | 17.4 | 17.1 | —— | |
| Median | ≥ TS intensity | 73.2 | 44.5 | 54.0 | 52.6 | 54.3 | 81.1 | 44.6 | 56.5 |
| Lifecycle | 97.0 | 50.0 | 77.8 | 62.1 | 84.9 | 84.6 | 55.6 | 73.8 | |
| RMS | ≥ TS intensity | 126.8 | 85.7 | 76.2 | 74.6 | 90.1 | 101.7 | 97.3 | 95.0 |
| Lifecycle | 127.4 | 103.8 | 191.7 | 133.0 | 159.6 | 124.6 | 145.6 | 140.3 | |
It can be seen that the range of relative distance distribution gradually becomes concentrated for an increase in the TC intensity (Fig. 7a). Further, the relative distance distribution in the TC weak-intensity periods was very scattered, resulting in the correlation coefficient (–0.48) being not very large. However, when the TC reached the TD intensity, the relative distance dramatically decreased; when the TC reached the TS intensity, the relative distance became very concentrated compared to the previously dispersed distribution. In the meantime, TD is the intensity at which a TC alert needs to be given, and TS is the intensity at which a TC should be graded. These findings show that the relative distance is a good indicator of the TC genesis. Similar to the analysis of the relationship between the MMVs and the TC intensities, only the median of the relative distances corresponding to a single intensity was selected as the fitting data for regression analysis. From the distribution of scatter plots, it was appropriate to use an inverse function as the regression model (Fig. 7b). The inverse function is described as follows:
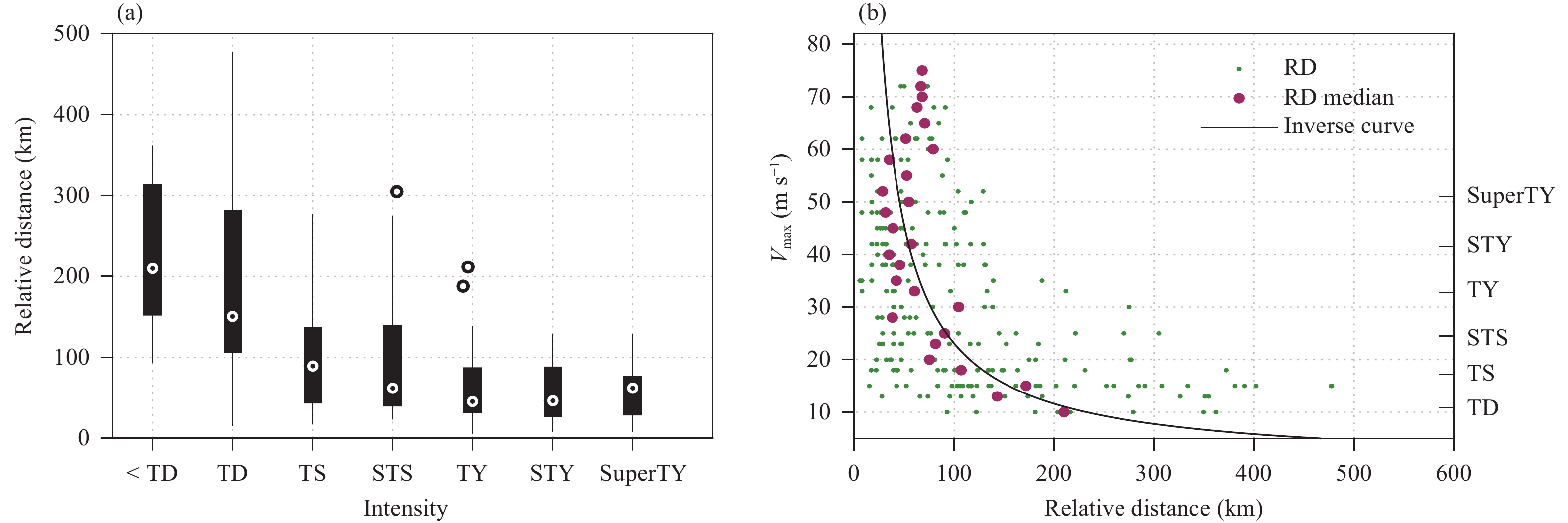
|
| Figure 7 As in Fig. 6, except for relative distances. The black line in (b) represents an inverse function curve. |
| $ \overline v_ {{{\rm max}}} = \frac{a}{{{R_{\rm d}} + b}},$ | (2) |
where
In the present work, the FY-2F and FY-2G infrared satellite data were used to study the complete lifecycle of seven super typhoons in 2016 based on the perspective of TC axisymmetry using DAV-T. The results showed that the characteristics of the DAV distribution have important implications for the TC structure and intensity. In addition, mathematical models were used to quantitatively analyze the relationship between the MMVs (or their locations) and the TC intensities (or TC centers). The main findings are as follows.
(1) The DAV distribution showed significant differences for different stages of the TC systems. For TCs that were in their weak-intensity periods, the DAV values tended to be higher overall and the low-DAV areas were more irregular; conversely, for TCs that were in their strong-intensity periods, the TCs always corresponded to lower DAV values and the much regular low-DAV regions. Thus, the MMV, which is the minimum value in the low-DAV area, enables quantification of the axisymmetry of the TC clouds and may serve as an important basis for analyzing the distribution and organization of strong convection within the TC.
(2) There was a good correlation between the MMVs and the TC intensities (Vmax or pmin). However, due to the influence of noise and small-scale background fields, certain high-frequency fluctuations may occur in the MMV sequence, especially for TC systems, which exhibit complicated development processes. Thus, the correlation between the TC intensities and the filtered MMV sequence was better than for the original MMV signals. In addition, it was found from statistical analysis that the MMVs decrease the most in going from WTD to TD and from TD to TS. This indicates that the TC cloud structure did change significantly during its genesis and dissipation. Therefore, MMVs may be used to estimate the TC intensity and to characterize tropical cyclogenesis.
(3) The MMV locations matched the TC centers well, but the relative distances between the two varied for the different TC stages. It was found that the relative distances were usually small during the development and maturation of the TC, while they were relatively large during the TC genesis and dissipation. The studies have shown that when the cloud clusters of the TC system are closed, the MMV position can specify the location of the eye. However, when the clouds showed clear non-closed features, the MMV locations always appeared in the most vigorous areas of local convection. Therefore, the MMVs would always lie in one of the cloud clusters that make up the TC system during the TC genesis and dissipation. Relative distances were greatly affected by the changes of the TC intensity in the weak-intensity periods, but when the TC had a stable morphological structure, the relative distances decreased slowly with increase of the TC intensity. Therefore, the relative distances may be used as an auxiliary reference to estimate the TC intensity.
In the statistical analysis, the CMA-BestTrack dataset was made the default for the objective data. However, the CMA-BestTrack dataset itself has uncertainty. Knaff et al. (2010) found that the errors of the CMA-BestTrack data are a function of the TC intensity. In addition, Torn and Snyder (2012) found that, in the CMA-BestTrack dataset, the TC position uncertainty decreased as the TC became more intense. Similarly, the RMSEs of the TC intensity tended to be larger for more intense TCs. Clearly, this uncertainty has a certain influence on the real errors between the estimated values and the objective values. According to the analysis of many samples, estimated TC positions seem to be more reasonable when compared to the CMA-BestTrack dataset (e.g., Fig. 2e, the TC position recorded by the CMA-BestTrack dataset is not located in the eye). This seems to indicate that the differences between the TC positions that are estimated by DAV-T and the objective values of TC are not large from a statistical standpoint. It is, however, hard to judge whether the uncertainty of the TC intensity results in an increase or decrease in real errors. This requires further investigation.

|
| Figure 2 Comparison of infrared images, meteorological fields, and DAV distributions for Lionrock and Meranti at specific times: (a, b) for Lionrock (TD) at 1800 UTC 17 August; (c, d) for Lionrock (STS) at 1800 UTC 22August; (e, f) for Meranti (STY) at 1200 UTC 13 September; and (g, h) for Meranti (STS) after landfall at 0600 UTC 15 September 15. (a, c, e) Infrared image (shading; K), 500-hPa geopotential height (contour; dagpm), and 10-m wind (vector; m s–1); and (b, d, f) DAV (shading; deg2) and 850-hPa relative vorticity (contour; 10–6 s–1). The symbol “●” represents the typhoon center from CMA-BestTrack data and “▲” represents the MMV location. |
Future work should also include diagnosis and statistical analysis based on examination of the development process for additional TCs in the WNP. In addition, the choice of the calculation radius will have an important influence on the quantification process of the TC system axisymmetry. Thus, it will be necessary to perform a sensitivity experiment on the calculation radius of the DAV-T to determine the optimal value based on independent data from China. Consequently, the effects of different calculation radii on the DAV distribution need to be addressed.
Acknowledgments. The FY satellite images were down-loaded from the National Satellite Meteorological Center of China Meteorological Administration (http://www.nsmc.org.cn/en/NSMC/Home/Index.html). CMA-BestTrack data were obtained from the Shanghai Typhoon Institute of China Meteorological Administration (http://www.typhoon.org.cn/). FNL data were obtained from the NCEP of US (https://rda.ucar.edu/datasets/ds083.2/#!access).
| Berg, R. J., and L. A. Avila, 2011: Atlantic hurricane season of 2009. Mon. Wea. Rev., 139, 1049–1069. DOI:10.1175/2010MWR3476.1 |
| Beven II, J. L., L. A. Avila, E. S. Blake, et al., 2008: Atlantic hurricane season of 2005. Mon. Wea. Rev., 136, 1109–1173. DOI:10.1175/2007MWR2074.1 |
| Brueske, K. F., and C. S. Velden, 2003: Satellite-based tropical cyclone intensity estimation using the NOAA-KLM series advanced microwave sounding unit (AMSU). Mon. Wea. Rev., 131, 687–697. DOI:10.1175/1520-0493(2003)131<0687:SBTCIE>2.0.CO;2 |
| Dvorak, V. F., 1975: Tropical cyclone intensity analysis and forecasting from satellite imagery. Mon. Wea. Rev., 103, 420–430. DOI:10.1175/1520-0493(1975)103<0420:TCIAAF>2.0.CO;2 |
| Dvorak, V. F., 1984: Tropical Cyclone Intensity Analysis Using Satellite Data. NOAA Tech. Rep., 47 pp. |
| Fritz, S., 1962: Satellite pictures and the origin of hurricane Anna. Mon. Wea. Rev., 90, 507–513. DOI:10.1175/1520-0493(1962)090<0507:SPATOO>2.0.CO;2 |
| Hubert, L. F., and A. Timchalk, 1969: Estimating hurricane wind speeds from satellite pictures. Mon. Wea. Rev., 97, 382–383. DOI:10.1175/1520-0493(1969)097<0382:EHWSFS>2.3.CO;2 |
| Klein, P. M., P. A. Harr, and R. L. Elsberry, 2000: Extratropical transition of western North Pacific tropical cyclones: An overview and conceptual model of the transformation stage. Wea. Forecasting, 15, 373–395. DOI:10.1175/1520-0434(2000)015<0373:ETOWNP>2.0.CO;2 |
| Knaff, J. A., D. P. Brown, J. Courtney, et al., 2010: An evaluation of Dvorak technique–based tropical cyclone intensity estimates. Wea. Forecasting, 25, 1362–1379. DOI:10.1175/2010WAF2222375.1 |
| Knaff, J. A., T. A. Cram, A. B. Schumacher, et al., 2008: Objective identification of annular hurricanes. Wea. Forecasting, 23, 17–28. DOI:10.1175/2007WAF2007031.1 |
| Kofron, D. E., M. F. Piñeros, E. A. Ritchie, et al., 2009: Defining the lifecycle of the extratropical transition of tropical cyclones using the deviation angle variance technique for remotely-sensed imagery. Proceedings of the 13th Conference on Mesoscale Processes, Amer. Meteor. Soc., Salt Lake City. |
| Liu, Z., X. Wang, W. B. Li, et al., 2007: Progresses in estimation of tropical cyclone intensity with Dvorak technique. Meteor. Sci. Technol., 35, 453–457. DOI:10.3969/j.issn.1671-6345.2007.04.001 |
| Olander, T. L., and C. S. Velden, 2007: The advanced Dvorak technique: Continued development of an objective scheme to estimate tropical cyclone intensity using geostationary infrared satellite imagery. Wea. Forecasting, 22, 287–298. DOI:10.1175/WAF975.1 |
| Piñeros, M. F., 2009: Objective measures of tropical cyclone intensity and formation from satellite infrared imagery. Ph.D. dissertation, Dept. of Optical Science, University of Arizona, USA, 124 pp. |
| Piñeros, M. F., E. A. Ritchie, and J. S. Tyo, 2008: Objective measures of tropical cyclone structure and intensity change from remotely sensed infrared image data. IEEE Trans. Geosci. Remote Sens., 46, 3574–3580. DOI:10.1109/TGRS.2008.2000819 |
| Piñeros, M. F., E. A. Ritchie, and J. S. Tyo, 2010: Detecting tropical cyclone genesis from remotely sensed infrared image data. IEEE Geosci. Remote Sens. Lett., 7, 826–830. DOI:10.1109/LGRS.2010.2048694 |
| Piñeros, M. F., E. A. Ritchie, and J. S. Tyo, 2011: Estimating tropical cyclone intensity from infrared image data. Wea. Forecasting, 26, 690–698. DOI:10.1175/WAF-D-10-05062.1 |
| Ritchie, E. A., K. M. Wood, O. G. Rodríguez-Herrera, et al., 2014: Satellite-derived tropical cyclone intensity in the North Pacific Ocean using the deviation-angle variance technique. Wea. Forecasting, 29, 505–516. DOI:10.1175/WAF-D-13-00133.1 |
| Rodríguez-Herrera, O. G., K. M. Wood, K. P. Dolling, et al., 2015: Automatic tracking of pregenesis tropical disturbances within the deviation angle variance system. IEEE Geosci. Remote Sens. Lett., 12, 254–258. DOI:10.1109/LGRS.2014.2334561 |
| Tang, L. L., D. Y. Hu, and X. J. Li, 2012: Spatiotemporal characteristics of tropical cyclone activities in northwestern Pacific from 1951 to 2006. J. Nat. Disast., 21, 31–38. DOI:10.13577/j.jnd.2012.0105 |
| Torn, R. D., and C. Snyder, 2012: Uncertainty of tropical cyclone best-track information. Wea. Forecasting, 27, 715–729. DOI:10.1175/WAF-D-11-00085.1 |
| Velden, C. S., T. L. Olander, and R. M. Zehr, 1998: Development of an objective scheme to estimate tropical cyclone intensity from digital geostationary satellite infrared imagery. Wea. Forecasting, 13, 172–186. DOI:10.1175/1520-0434(1998)013<0172:DOAOST>2.0.CO;2 |
| Velden, C. S., B. Harper, F. Wells, et al., 2006: The Dvorak tropical cyclone intensity estimation technique: A satellite-based method that has endured for over 30 years. Bull. Amer. Meteor. Soc., 87, 1195–1210. DOI:10.1175/BAMS-87-9-1195 |
| Wood, K. M., O. G. Rodríguez-Herrera, E. A. Ritchie, et al., 2015: Tropical cyclogenesis detection in the North Pacific using the deviation angle variance technique. Wea. Forecasting, 30, 1663–1672. DOI:10.1175/WAF-D-14-00113.1 |
 2019, Vol. 33
2019, Vol. 33


