The Chinese Meteorological Society
Article Information
- QI, Yanjun, Renhe ZHANG, Xinyao RONG, et al., 2019.
- Boreal Summer Intraseasonal Oscillation in the Asian–Pacific Monsoon Region Simulated in CAMS-CSM. 2019.
- J. Meteor. Res., 33(1): 66-79
- http://dx.doi.org/10.1007/s13351-019-8080-7
Article History
- Received May 8, 2018
- in final form November 5, 2018
2. Institute of Atmospheric Sciences, Fudan University, Shanghai 200438
The dominant mode of the intraseasonal atmospheric circulation and convective precipitation in the tropics in boreal winter is the Madden–Julian oscillation (MJO; Madden and Julian, 1971, 1972) and that in boreal summer is the intraseasonal oscillation (ISO; Yasunari, 1979; Lau and Chan, 1986; Wang and Rui, 1990). These two phenomena are featured with eastward/northward pro-pagation of convection and precipitation across the equatorial Indian and western/central Pacific oceans. The boreal summer ISO (BSISO) is more complicated compared to the MJO in terms of the activity center, frequency, and propagation (see review papers of the MJO/BSISO in Lau and Waliser, 2005; Zhang, 2005; Lee et al., 2013; Li, 2014; Li et al., 2014).
Currently, more attention is paid to the performance of numerical models in simulating the atmospheric intra-seasonal variability. Accurate modeling and prediction of the MJO/BSISO may help improve the climate prediction on seasonal-to-interannual timescales, and bridge the gap between weather forecast and seasonal prediction (Waliser et al., 2003a; Zhang, 2013; Ren et al., 2016; Li W. et al., 2018). Unfortunately, most general circulation models (GCMs) have great difficulty in simulating the propagation characteristics of the tropical intraseasonal oscillation correctly during the last decades (Slingo et al., 1996; Wu et al., 2002, Waliser et al., 2003b). Although there is a notable improvement in simulating the MJO/BSISO in recent studies, the MJO simulation is still a big challenge in the current state-of-the-art GCMs. As such, a global model evaluation project on vertical structure and physical processes of the MJO was carried out (Jiang et al., 2015), with the goal to reduce the deficiencies in representing the MJO in GCMs. Based on the climate simulations of this project, Jiang et al. (2015) concluded that the systematic MJO eastward propagation is only reasonably simulated in roughly 8 out of total 27 GCM simulations. In the BSISO evaluation, which is also based on the results from the climate simulation of the global circulation multi-model project, Neena et al. (2017) demonstrated that many of the GCMs, which are able to capture BSISO eastward propagation, also show good fidelity in simulating BSISO northward propagation. However, the simulation of the physical process of vertical structure associated with the northward propagating BSISO remains challenging. Hsu and Li (2012) emphasized the importance of the zonal asymmetry of boundary layer perturbation moisture in favoring the eastward-propagation of MJO. The vertical moist static energy (MSE) plays a critical role in driving the eastward propagation of the wintertime MJO (Wang L. et al., 2017, 2018). Wang and Lee (2017) proposed that the cause of diverse zonal propagation of MJO in the GCMs may be attributed to the intrinsic linkage between MJO propagation and structural asymmetry in the interactions among convective heating, moisture, equatorial wave, and boundary layer dynamics.
The simulation of MJO/BSISO is sensitive to the mo-del convective parameterization choice (Slingo et al., 1996; Wang and Schlesinger, 1999; Jia et al., 2010; Ling et al., 2013). Previous modeling studies have shown that the air–sea coupled models can reproduce more realistic atmospheric intraseasonal oscillation compared to the atmosphere-only model (Fu and Wang, 2004; Lin et al., 2011). The role of air–sea interaction on the ISO is well demonstrated in some theoretical models (Wang and Xie, 1998; Liu and Wang, 2013; Jiang et al., 2015). Flatau et al. (1997) formulated an empirical relationship between wind speed and sea surface temperature (SST) tendency, and then applied this relationship in a global circulation model to examine the impact of SST feedback. They concluded that the convection-generated SST gradient plays a critical role in development of MJO and propagation of cloud cluster. Waliser et al. (1999) showed that air–sea coupling improves the simulation of MJO when using a GCM coupled with an ocean mixed layer. The improvement includes increased MJO variability, a closer match of period of oscillation with observations, reduced eastward-propagation phase speed in the eastern hemisphere, and an enhanced MJO signal occurring in the December–May period.
Numerous studies of the ISO with different versions of the European Centre/Hamburg model (ECHAM) have been performed. Gualdi et al. (1997) and Gualdi and Navarra (1998) analyzed the MJO in a series of ECHAM model experiments. They found that ECHAM3 gave a more realistic distribution of MJO convection than ECHAM2, suggesting that the improvement was due to a better representation of convection in the Tiedtke convective parameterization scheme. The updated version of ECHAM shows better skill in simulating eastward propagation of MJO and northward propagation of BSISO (Gualdi et al., 1999; Sperber et al., 2005; Neena et al., 2017).
In analyzing the outputs of ECHAM4 and its coupled version with the University of Hawaii 2.5 layer intermediate ocean model, Kemball-Cook et al. (2002) showed that upon coupling, pronounced northward propagation of convection and circulation anomalies appear as in the observations in May–June over the Indian Ocean. The improvement is attributed to the increased low-level convergence into the positive SST anomaly ahead of the convective anomaly. The coupled modeling study by Fu and Wang (2004) further demonstrated that the air–sea interaction significantly enhances the northward propagation of ISO compared to the atmosphere-only runs. They pointed out that the coupled and atmosphere-only runs are fundamentally different in simulating the BSISO. In the uncoupled run, the convection and SST anomalies are nearly in phase, while in the coupled run the convection and SST have structures similar to the observations. The observed positive SST anomaly ahead of the convection enhances the northward propagation of the ISO. The processes by which the SST anomalies organize convection may include destabilization of the moist Rossby waves or local adjustment of the atmospheric convection to the SST anomalies [see Wang (2005) for a review about the effects of air–sea coupling on the BSISO].
In addition to the impact of the atmosphere–ocean interaction on enhancing MJO or BSISO, a realistic simulation of the mean state in the coupled model appears to be necessary (Hendon, 2000; Fu and Wang, 2001; Kemball-Cook et al., 2002; Sperber et al., 2005; Benedict et al., 2014). Inness et al. (2003) demonstrated that even in the presence of air–sea interaction, a well-simulated basic state is crucial for the ISO simulation.
Recently, a new coupled climate system model (CSM) has been developed at the Chinese Academy of Meteorological Sciences (CAMS) by employing several start-of-the-art model components. This newly developed coupled model has demonstrated its ability to capture some prominent modes of climate variability, such as winter MJO, the El Niño–Southern Oscillation (ENSO), East Asian summer monsoon (EASM), and the Pacific Decadal Oscillation (PDO) (Rong et al., 2018). The model also displays a promising capability in simulating the EASM variability and the ENSO–EASM relationship (Rong et al., 2018). By running the climate model of CAMS-CSM in the weather forecast mode, Li J. et al. (2018) evaluated the performance of CAMS-CSM in simulating spatiotemporal distributions of rainfall and related synoptic circulations, concluding that the CAMS-CSM has the ability to simulate severe extreme events.
The aim of this work is to investigate how well the CAMS-CSM reproduces the characteristics of BSISO in the Asian–Pacific summer monsoon region. Our preliminary evaluation begins with simulation of the mean state and some basic features of BSISO, including variance, periodicity, and propagation. A suite of dynamics-oriented diagnostic metrics has been developed and applied to evaluate the simulation of vertical structure and physical processes associated with MJO/BSISO in CAMS-CSM, as in other GCMs (Jiang et al., 2015; Neena et al., 2017; Wang B. et al., 2018). The manuscript is organized as follows. Description of the model and analysis method is presented in Section 2. In Section 3, we show simulations of the mean state, including the annual cycle and seasonal mean, and the vertical shear of zonal wind, which reflects the strength of the large-scale Asian summer monsoon. In Section 4, we discuss the intensity and propagation of the BSISO over the Asian summer monsoon region in the model. In Section 5, we focus on the zonal propagation along the equator and the meridional propagation over the Indian summer monsoon sector and the South China Sea (SCS)–western North Pacific (WNP) region. The main results and discussion are provided in Section 6.
2 Model and analysis methodThe atmospheric component of the CAMS-CSM is the ECHAM5 AGCM, which is documented in detail in Roeckner et al. (2003). It has a horizontal resolution of T106, with 31 vertical levels extending from surface to 10 hPa. The mass flux scheme of Tiedtke (1989) for cumulus convective parameterization is used with modification for penetrative convection (Nordeng, 1994). For detailed description of the radiative scheme, land surface scheme, cloud and vertical diffusion solution in this model, one is referred to Roeckner et al. (2003).
The ocean component of the CAMS-CSM coupled model is the Geophysical Fluid Dynamics Laboratory (GFDL) Modular Ocean Model version 4 (MOM4) (Griffies et al., 2004). The spatial domain is quasi global excluding the Arctic region, extending from 74°S to 64°N. The zonal resolution is 1°; and the meridional resolution is 1/3° between 10°S and 10°N, linearly increasing to 1° poleward of 30°S and 30°N. There are 50 layers in the vertical, with 23 layers in the upper 230 m. In the control experiment, the model is integrated for 23 yr with the atmosphere and ocean being coupled once per hour. More details of the CAMS-CSM atmosphere–ocean coup-ling process can be found inRong et al. (2018).
In this paper, we present the results obtained from a 23-yr coupled integration. The May–October period is considered as representing the boreal summer season, and all the analyses associated with BSISO are performed over this season.
To examine the model reliability for large-scale circulation simulation, we compare the results against the NCEP–NCAR reanalysis dataset. The Climate Prediction Center (CPC) Merged Analysis of Precipitation data (CMAP) are also used to evaluate the model capability in precipitation simulation. The daily averaged outgoing longwave radiation (OLR) data from the NOAA of US are employed as a proxy for convection. To be consistent with the model simulation, the observational datasets are also taken from 1979 to 2001 (23 yr).
A band-pass filter is used to extract the intraseasonal signal. The standard deviation of the filtered precipitation is used to assess the BSISO intensity. To quantitatively measure the intensity, propagation, and frequency of the BSISO, wavenumber–frequency analysis is performed in this study. The wavenumber–frequency analysis transforms a time series from spatial–temporal domain to a wavenumber–frequency domain (Hayashi, 1982). The wavenumber–frequency analysis is often adopted to describe the wave properties of the BSISO (Salby and Hendon, 1994; Hendon et al., 1999; Wheeler and Kiladis, 1999; Fu and Wang, 2004; Qi et al., 2008; Ji et al., 2014; Cao et al., 2015).
3 Simulation of tropical mean stateIn the coupled model, a realistic basic mean state is at least as important as the air–sea interaction in terms of simulating the intraseasonal oscillation (Sperber et al., 2005). An accurate simulation of seasonal mean state in precipitation and vertical wind shear in summer determines a proper propagation of the BSISO in the model (Hendon, 2000; Kemball-Cook et al., 2002, Inness et al., 2003). Earlier studies (e.g., Ajayamohan and Goswami, 2007; Sperber and Annamalai, 2008; Sabeerali et al., 2013) suggested that a better representation of the BSISO associated with the Asian–Pacific summer monsoon in a model depends on how well the model simulates the seasonal mean precipitation over this region. Therefore, we first carry out an examination of the capability of the CAMS-CSM in simulating the annual cycle and the climatological summer mean of the precipitation field.
3.1 Annual cycleThe monthly mean precipitation from CMAP (taken as observation) and the CAMS-CSM are presented in Figs. 1a and 1b, respectively. The climatological annual cycle of precipitation shows that the maximum precipitation is located in the equator or south of the equator particularly in the eastern equatorial Indian Ocean (EEIO), maritime continent, and the western equatorial Pacific in boreal winter. The zonal precipitation belt moves northward off the equator during the seasonal transition. The intertropical convergence zone (ITCZ) represented by the convective precipitation shifts to the north of the equator from boreal winter to summer in the Asian–Pacific monsoon region (Fig. 1a). The intensified precipitation in boreal summer is mainly located in the eastern Arabian Sea, Bay of Bengal, SCS, and the region eastern to the Philippines along 15°N (Fig. 2). The EEIO and the region eastern to the maritime continent are also large-value precipitation centers. The precipitation shows a strong annual cycle in terms of both strength and latitudinal position. The features of monthly mean precipitation patterns in the model (Fig. 1b) match the observation closely (Fig. 1a), except that the precipitation strength over the Asian–Pacific summer monsoon domain is overestimated.
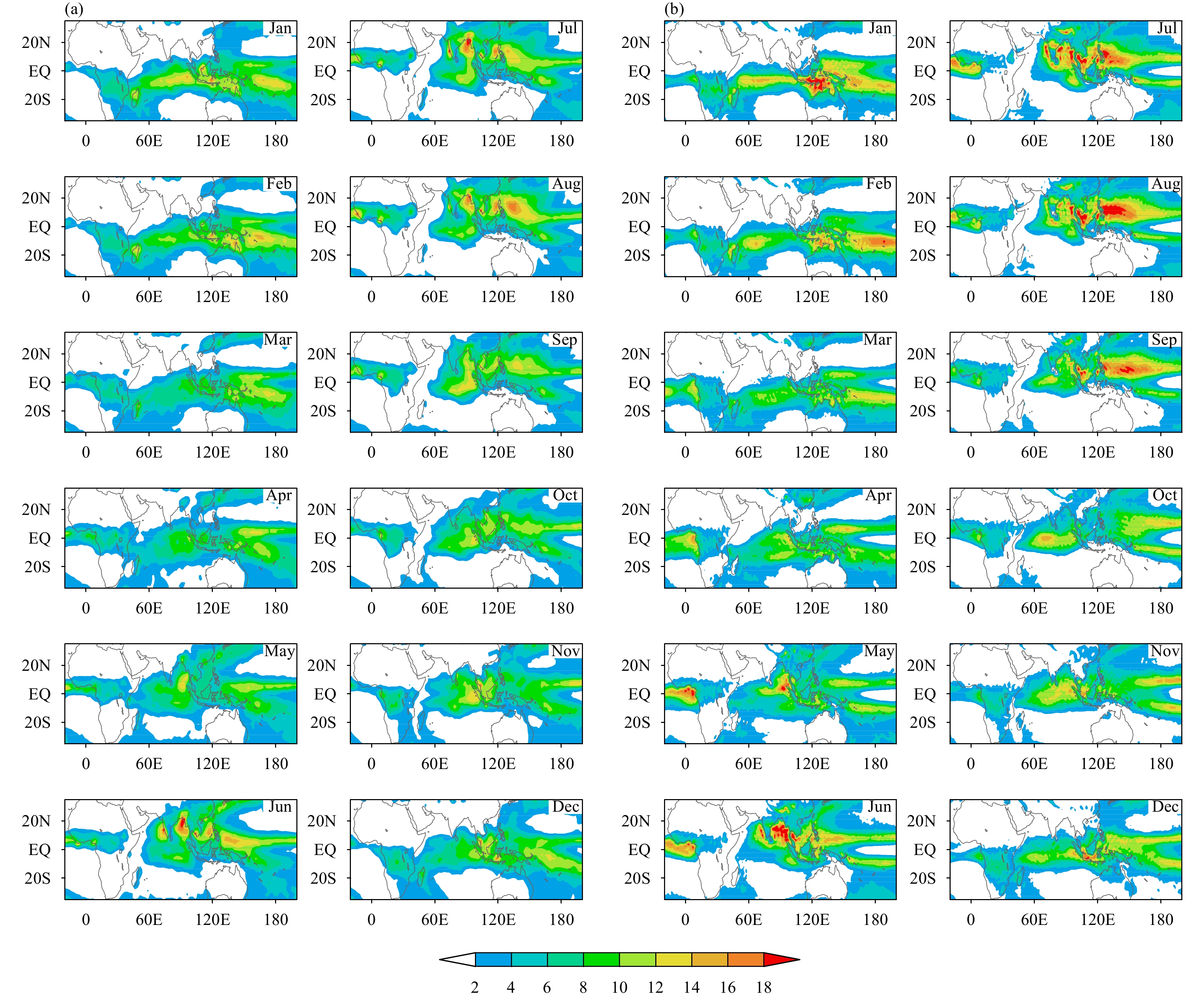
|
| Figure 1 Distributions of monthly mean precipitation (mm day–1) from (a) CMAP and (b) CAMS-CSM. |
In terms of seasonal mean precipitation, the patterns in the model match the observation well. For example, the maximum centers of simulated summer mean precipitation are very close to those of the CMAP, except for the overall larger intensity of simulated precipitation over the Asian–Pacific summer monsoon domain. Similar to most other models, the CAMS-CSM tends to simulate double ITCZs, with an excessive convective precipitation band south of the equatorial western Pacific (Fig. 2b). The root mean square error (RMSE) is computed, which indicates the biases of precipitation simulation with respect to the observation, as shown in Fig. 3. The large RMSEs appear over eastern Himalayas, southern Indo–China Peninsula, EEIO, SCS, and WNP (Fig. 3), which are consistent with the results of Neena et al. (2017).
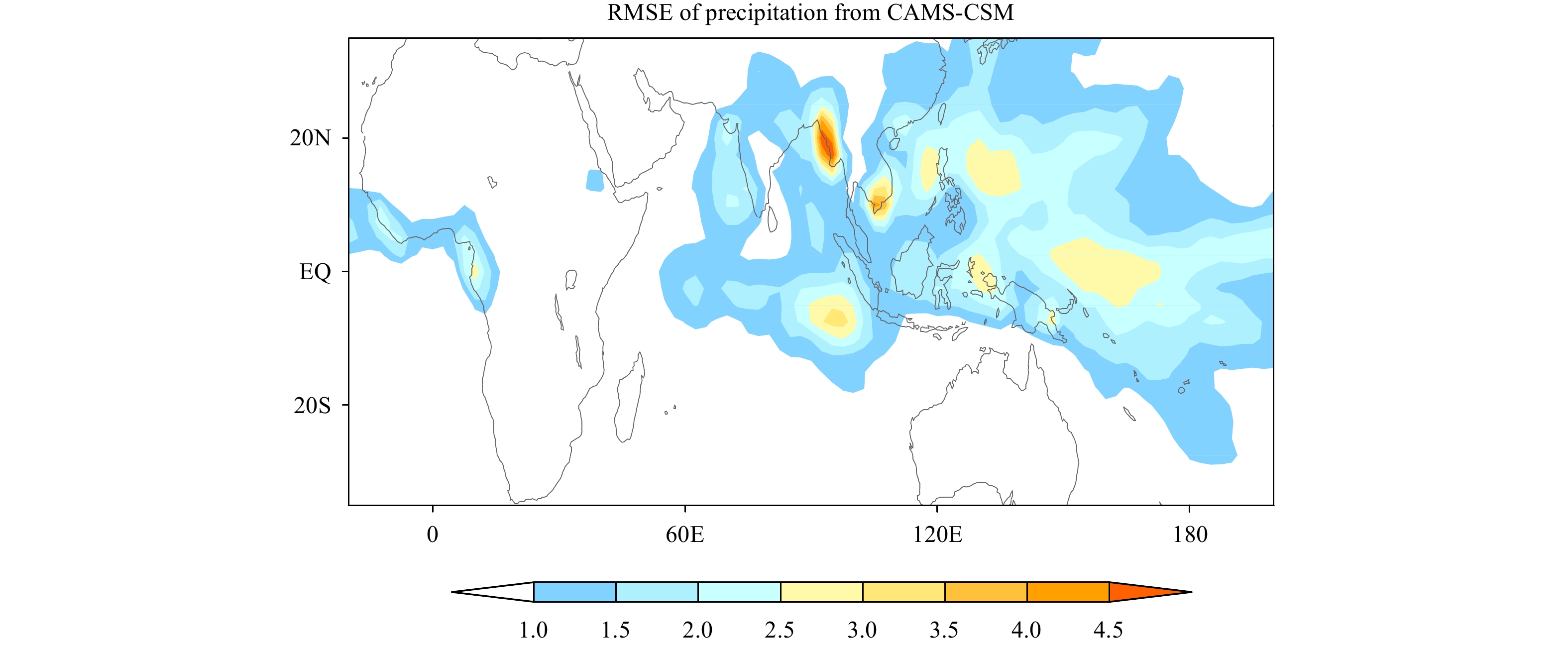
|
| Figure 3 Root mean square error of precipitation (mm day–1) with respect to CMAP observation during June–August. |
In addition to the mean state of precipitation, the background vertical shear of the zonal mean flow also plays an important role in the amplification and northward pro-pagation of the BSISO in the Indian Ocean (Jiang et al., 2004; DeMott et al., 2013; Liu et al., 2015). The basic zonal flow may also influence the interaction between the extra-tropics and the tropics, which may be important as a forcing mechanism for the ISO (Hsu et al., 1990). The vertical shear, which is defined as the difference between 850- and 200-hPa zonal winds (Webster and Yang, 1992), reflects the strength of the South Asian summer monsoon, and may form a favorable condition for the development of the BSISO in the tropics. Figure 4 shows that the large-scale vertical easterly wind shear dominates the region latitudinally from 10°S to 30°N and longitudinally extending along 10°N from Africa to the WNP, with an maximum of 35 m s–1. The model well simulates the change of the zonal wind direction vertically from the lower to the upper troposphere in the Asian monsoon region, which exhibits a baroclinic structure (Fig. 4b). The overall simulation of the vertical zonal wind shear by the CAMS-CSM agrees well with the observation over most of the South Asian monsoon region, although its magnitude is not as large over the western Indian Ocean as in the observation. An exception is seen in the monsoon region between 10°N and the equator, where the vertical wind shear is deficient. The failure in simulating the vertical wind shear in this region could be one cause for the reduced BSISO amplitude in the model based on earlier studies, which again emphasizes the importance of mean vertical wind shear and low-level zo-nal wind in the development of the BSISO as in previous studies (e.g., Wang and Xie, 1996, 1997; Kemball-Cook et al., 2002; Inness et al., 2003; Jiang et al., 2004).

|
| Figure 4 Seasonal (JJA) mean zonal wind vertical shear (u850 – u200; m s–1) from (a) NCEP and (b) CAMS-CSM. |
The standard deviation of 20–50-day rainfall anomalies is used to measure the intensity of BSISO. Figure 5 displays the 23-yr averaged BSISO intensity for June–August in CMAP and CAMS-CSM. Similar to the results of Ajayamohan and Goswami (2007) and Sperber and Annamalai (2008), the spatial pattern of BSISO intensity closely follows that of the maximum summer mean precipitation regions (Figs. 5, 2). The active centers of BSISO are significantly distributed in the north of the equator in the Asian–Pacific monsoon region. The largest amplitude BSISO region is located between 10° and 20°N over the eastern Arabian Sea and the Bay of Bengal, SCS, and the Philippine Sea (Fig. 5a). Another active center of BSISO is found over the EEIO. Previous studies showed that the northward movement of these variability centers of BSISO is associated with the active/break cycle of summer monsoons in South Asia and Southeast Asia during boreal summer.
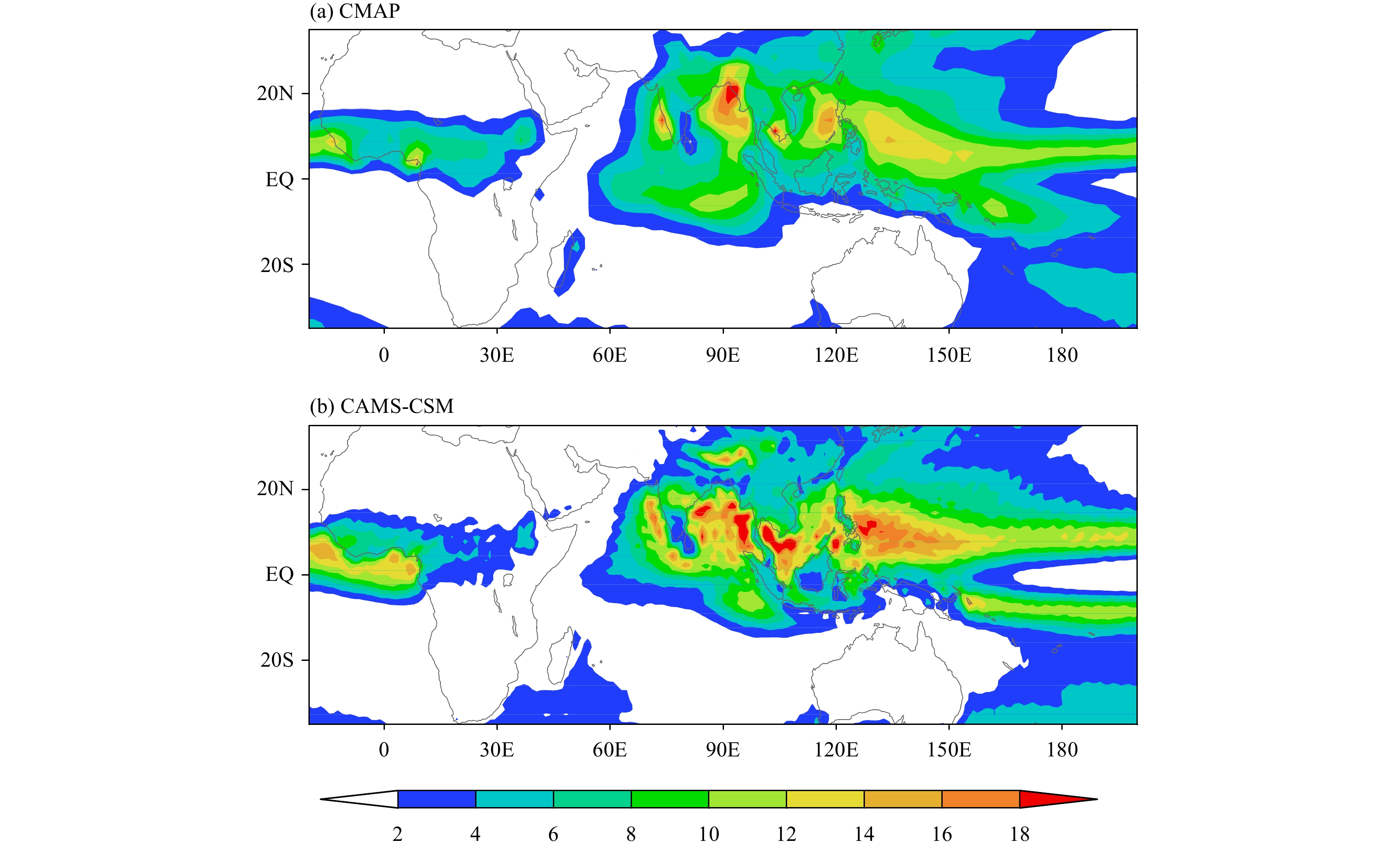
|
| Figure 2 Seasonal (JJA) mean precipitation (mm day–1) from (a) CMAP and (b) CAMS-CSM. |
The simulated position of BSISO variability center is consistent with the observation, except for the variability center over the EEIO. The variability centers of BSISO are mainly in the latitudinal zone between 10° and 20°N from the eastern Arabian Sea and Bay of Bengal to the SCS and the Philippine Sea. But the intensity of BSISO tends to be stronger over the Bay of Bengal and weaker over the SCS. In addition, the active center of BSISO in the EEIO is not well reproduced in the model, and the BSISO center is exaggerated in the south to the Indian subcontinent (Fig. 5b).
4.2 Propagation of BSISO in monsoon regionsFigure 5 shows that the tropical Indian Ocean and WNP are the regions for enhanced BSISO variability. The BSISO is normally featured by the northward movement from the equator to the South Asian monsoon region in the EEIO and from the tropics to the SCS and WNP, representing its close association with the weather and sub-seasonal to seasonal climate variability in South Asia and Southeast Asia.
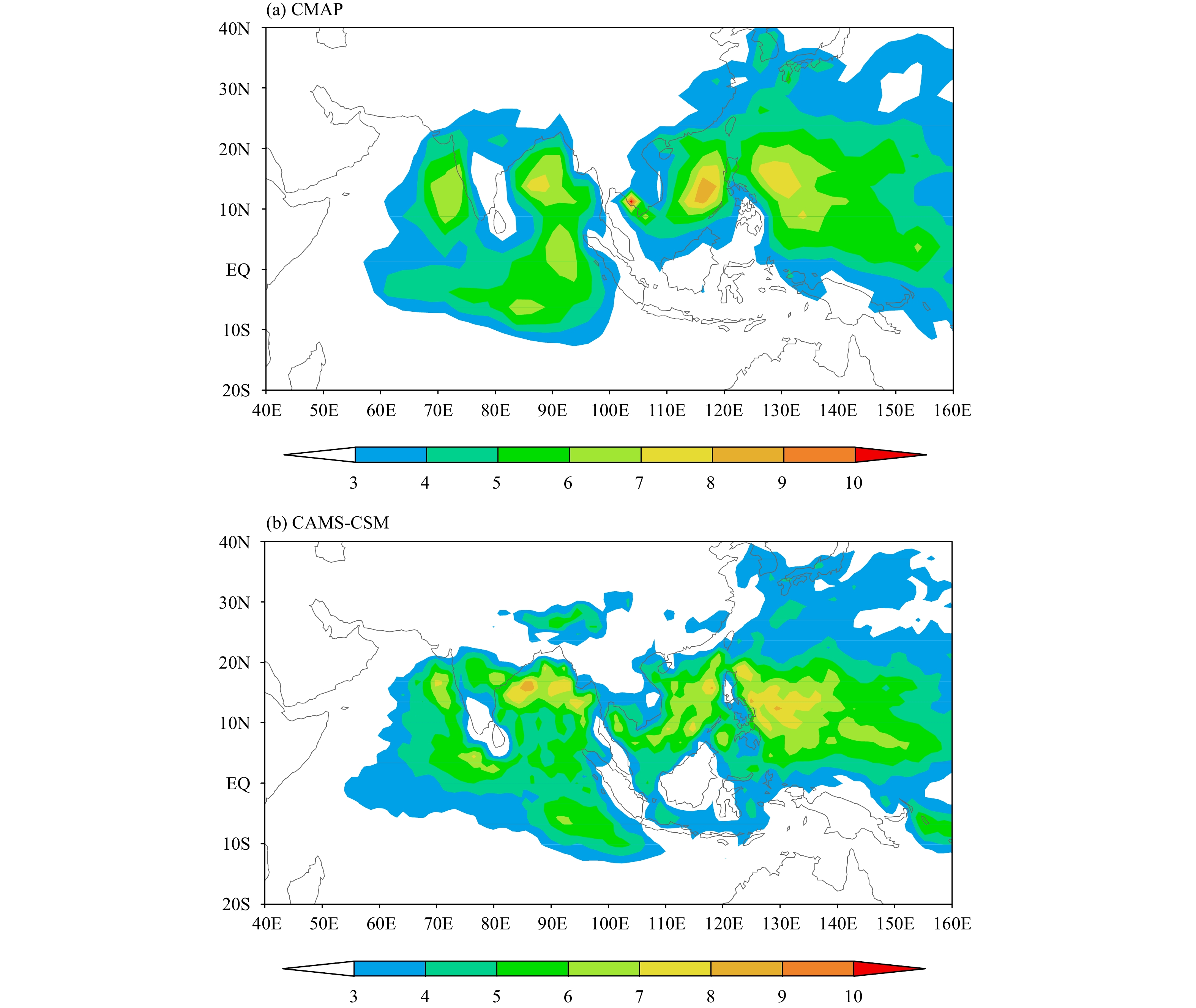
|
| Figure 5 The 23-yr averaged ISO intensity (mm day–1) in the boreal summer from (a) CMAP and (b) CAMS-CSM. |
To examine the performance of CAMS-CSM in capturing meridional propagation features of BSISO in the Asian–Pacific monsoon region, we follow the way as in DeMott et al. (2013) to llustrate the northward propagation of BSISO. The meridional propagation of BSISO in nature episodes is illustrated in Figs. 6, 7. Figure 6 displays the time series of 20–50-day filtered precipitation anomalies as a function of latitude for three years of CMAP data and three years of CAMS-CSM output over the Indian summer monsoon sector. The selected years with different disturbances of BSISO are chosen to illustrate the interannual variations of BSISO in this region: the events exhibiting systematic northward propagation from the equator to 20°N in both CMAP and model results (Figs. 6a, d), the events with coexisting southward- and northward-propagating disturbances (Figs. 6b, e), and the non-organized meridional propagating episodic events (Figs. 6c, f). The Hovmöller diagrams demonstrate the capability of CAMS-CSM in reproducing the episodic nature of meridional propagation of BSISO over the Indian monsoon region, which reflects the inter-annual variability of propagation of BSISO.

|
| Figure 6 Hovmöller diagrams of the 20–50-day filtered precipitation rate (mm day–1) averaged over the Indian summer monsoon region (75°–100°E) from (a–c) CMAP and (d–f) CAMS-CSM. |
In addition to the eastern Indian Ocean, the broad region from the SCS and Philippine Sea to the WNP is also dominated by significant northward migration of BSISO. In the SCS–WNP domain, the CAMS-CSM simulation shows that anomalous ISO precipitation propagates northward to the north of 20°N in June–July, but the propagation is deficient in late summer after August (Fig. 7), which is similar to the results in Kemball-Cook and Wang (2001). This implies that the BSISO experiences a seasonal variation over the western Pacific summer monsoon region. The amplitudes of BSISO in Indian Ocean show relatively large values in the model compared to the observation. In contrast, the feature of meridional propagation in the western Pacific Ocean is more reasonably captured by the model (Figs. 6, 7).

|
| Figure 7 Hovmöller diagrams of 20–50-day filtered precipitation rate (mm day–1) averaged over the SCS–WNP region (110°–140°E) from (a) CMAP and (b) CAMS-CSM. |
The wavenumber–frequency analysis is used to quan-tify the intensity, frequency, and propagation characteristic of ISO (Salby and Hendon, 1994; Hendon et al., 1999; Wheeler and Kiladis, 1999; Teng and Wang, 2003, Fu and Wang, 2004; Lin and Li, 2008; Qi et al., 2008). The analysis is extended from a global domain to a finite domain of (30°S–30°N, 40°E–180°) in this study. This is because the BSISO is effectively trapped in the northern summer monsoon region by the lower-boundary conditions (such as SST, land and ocean surface moisture distributions, and so on), and the mean monsoon flows (Wang and Xie, 1997). Detailed regional characteristics of BSISO can be zoomed in by using the finite domain wavenumber–frequency analysis.
5.1 Eastward propagationDuring boreal summer, the MJO disturbances weaken significantly, and the variability centers in convection of BSISO move to the Northern Hemisphere. Figure 8 shows the wavenumber–frequency analysis of observed and simulated convection (represented by OLR) associated with zonal propagating disturbances of BSISO. Although the MJO substantially weakens in summer, the 23-yr mean spectrum of observed OLR shows that it is dominated by a prominent eastward propagation with wavenumber-1 spanning from 40°E to 180° (Fig. 8a). The eastward propagating BSISO, with the maximum spectrum of about 270 (W m–2)2, has a dominant period between 20 and 50 days and the peak closer to 30 days.

|
| Figure 8 The 23-yr mean wavenumber–frequency spectra for zonal propagation of OLR in boreal summer along the equator (5°S–5°N) from (a) observation and (b) CAMS-CSM. Contour interval is 30 (W m–2)2. |
The eastward wavenumber-1 propagation is well reproduced by the coupled CAMS-CSM (Fig. 8b). The periodicity of the simulated BSISO disturbances is consistent with the observed dominant period. But the intensity of the eastward propagating disturbances exhibits a smaller amplitude, with its maximum being 240 (W m–2)2, compared to the observation. Also note that the westward propagating BSISO is distinctly larger than that in the observation. In addition, the variance of 20–50-day OLR is mainly concentrated on wavenumbers 1–3 in the model in both eastward and westward propagations, whereas the variance of observed 20–50-day OLR is primary centered on wavenumbers 1–2 (Figs. 8a, b).
As a function of latitude and period, from the wavenumber–frequency analysis, Fig. 9 shows the strength of zonal propagation of convection for wavenumber-1. The wavenumber-1 corresponds to a wavelength of 140° in longitude spanning over 40°E and 180°. In Fig. 9a, the BSISO is featured by wavenumber-1 with a period of 20–50 days, which exhibits eastward propagation along the equator and westward propagation off the equator between 10° and 20°N, which is the domi-nant mode in the WNP during boreal summer. But the eastward propagation is still the most significant mode in the tropics.
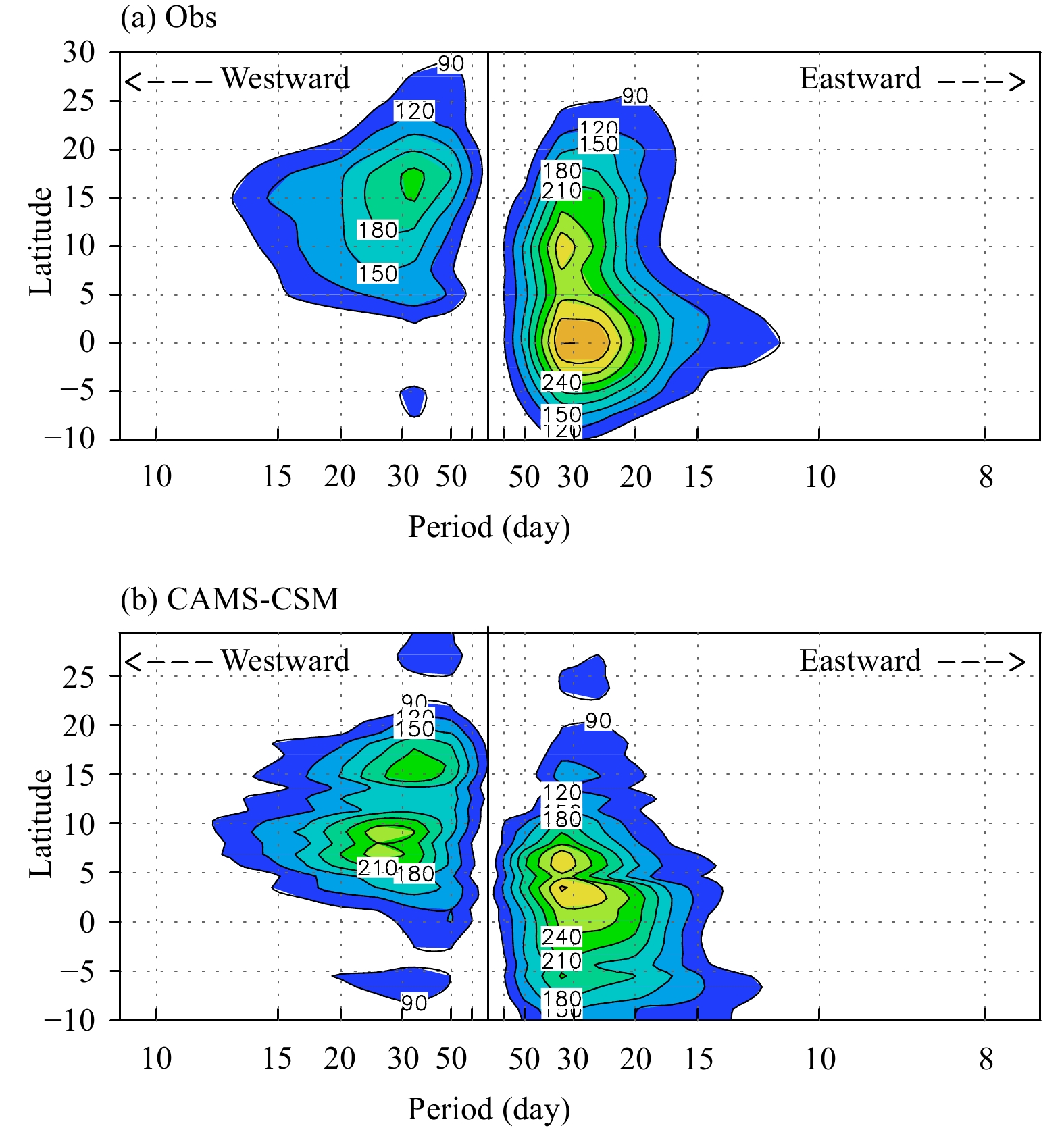
|
| Figure 9 The 23-yr mean wavenumber–frequency spectra for zonal propagating wavenumber-1 of OLR over 40°E–180° in boreal summer for (a) observation and (b) CAMS-CSM. Contour interval is 30 (W m–2)2. |
In the CAMS-CSM simulation, the periodicities of both the eastward and westward propagations are all on the 15–50-day band, which is the dominant mode in the observation (Fig. 9b). The simulated intensity of eastward propagation is weaker, and the maximum spectrum is located north of the equator around 5°N instead of at the equator as in the observation. Compared to the observation, the CAMS-CSM does not produce the convection with a period of about 45 days that propagates eastward along 10°N; moreover, the westward propagation is much stronger in the off-equatorial region along 5°–10°N (Fig. 9b).
5.2 Northward propagationA prominent feature of BSISO in the Asian summer monsoon region is its northward propagation in the In-dian Ocean and in the SCS to the western Pacific. The active to break cycles of the Asian summer monsoon in both South Asia and Southeast Asia are modulated frequently by the northward propagating BSISO from the tropics. The maximum northward propagating spectrum of OLR is indeed located in those areas within the Asian–Pacific summer monsoon region (Fig. 10a). The northward propagation in the Indian Ocean is significantly stronger than that in the SCS or the western Pacific. Compared to the observation, the intensity of northward propagation in the simulation is apparently weaker; meanwhile, the simulated southward component is overestimated (Fig. 10b).
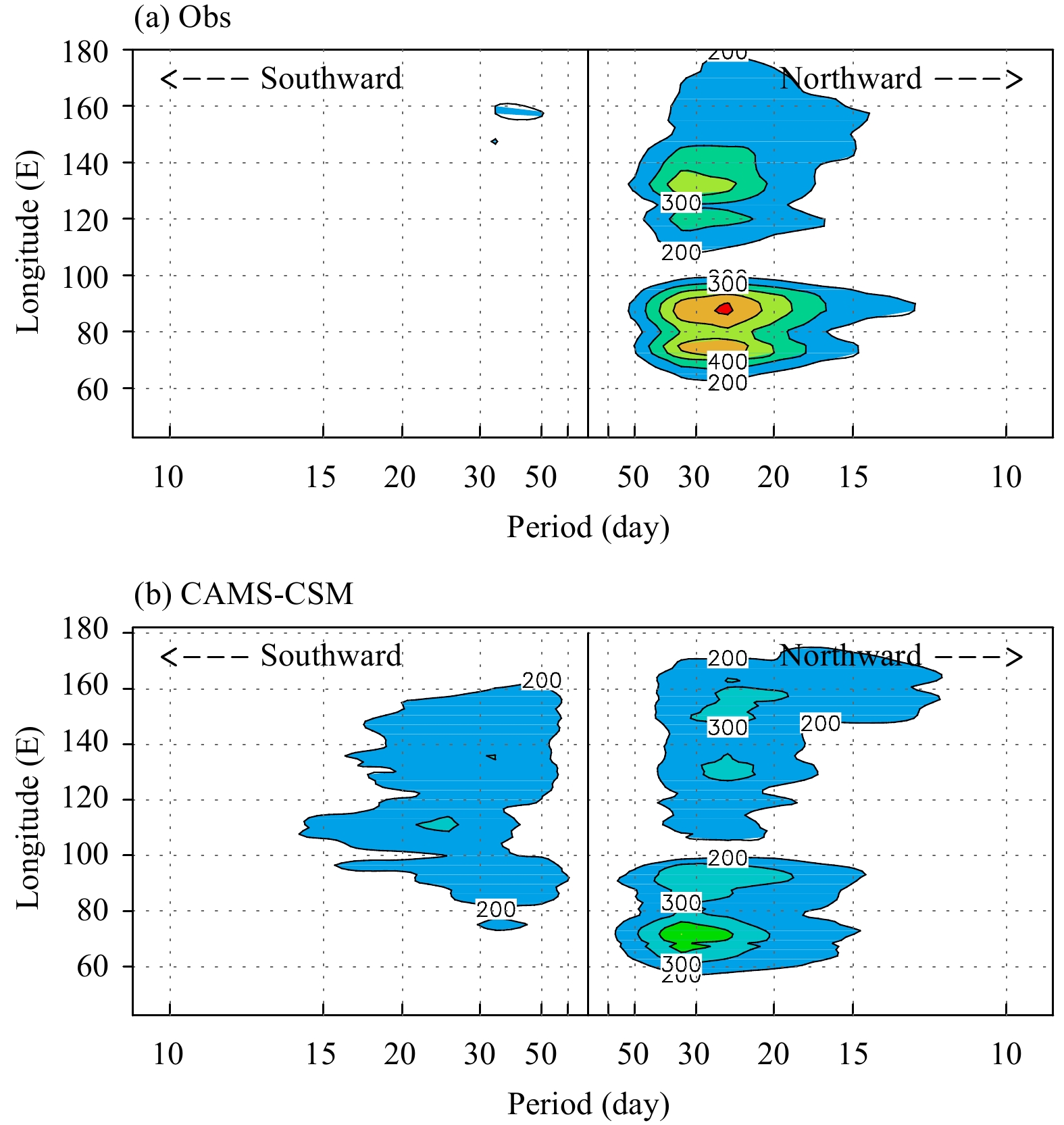
|
| Figure 10 The 23-yr mean wavenumber–frequency spectra for meridional propagating wavenumber-1 of OLR over 30°S–30°N in boreal summer for (a) observation and (b) CAMS-CSM. Contour interval is 100 (W m–2)2. |
To further show the propagating properties of BSISO, the wavenumber–frequency analysis is applied to the regions of the Indian Ocean and the western Pacific, respectively. Both regions are well-known for monsoon activities during boreal summer. Figure 11 presents the northward and southward propagations of BSISO over the Bay of Bengal between 85° and 95°E. The northward propagating BSISO in the observed OLR has a maximum variance of about 500 (W m–2)2, apparently dwarfing its southward counterpart (Fig. 11a). The strongest northward convective perturbation is featured by wavenumber-1 with a peak period of about 30 days. The northward propagation of meridional wavenumber-1 of observed OLR in the Indian Ocean is much stronger than the eastward propagation of zonal wavenumber-1 of OLR along the equator (Figs. 11a vs. 8a). This may be due to the fact that the eastward propagating BSISO along the equator dramatically weakens in summer.
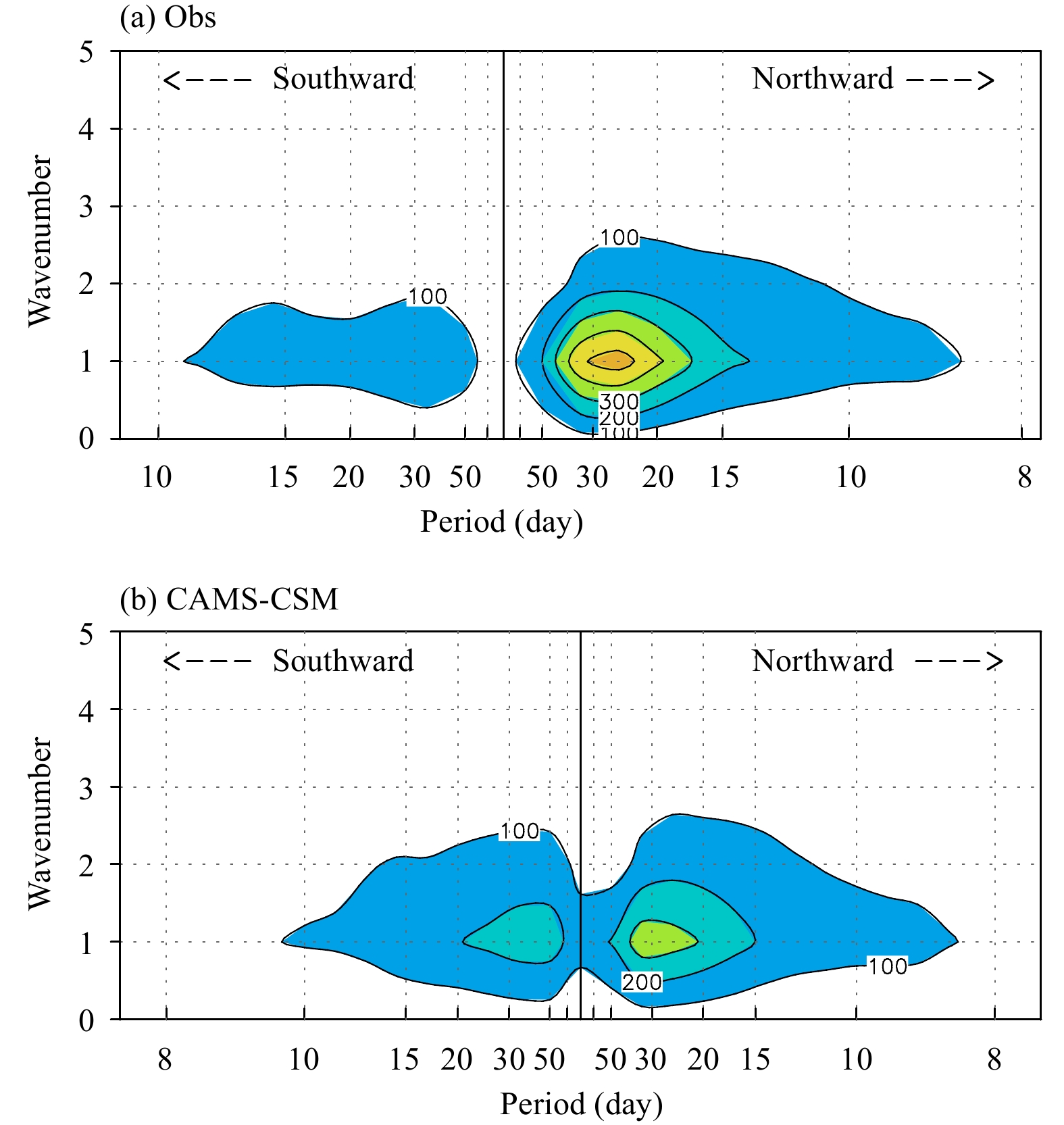
|
| Figure 11 The 23-yr mean wavenumber–frequency spectra for meridional propagation of OLR in boreal summer over the Bay of Bengal (85°–95°E) for (a) observation and (b) CAMS-CSM. Contour interval is 100 (W m–2)2. |
The simulated northward propagating BSISO in the Bay of Bengal presents the similar dominant mode with a meridional wavenumber-1 and 20–50-day period, compared to the observation (Fig. 11b). The BSISO intensity in meridional propagation, however, shows much more difference from the observation. The maximum spectrum in this case is only about 300 (W m–2)2 (Fig. 11b), which is about 40% smaller than that in the observation. Meanwhile, the southward propagating component from the model is much stronger than the observed.
In another significant northward propagating region of BSISO, namely, the SCS and the WNP sector, the wavenumber–frequency analysis exhibits similar result as shown inFig. 11. In the SCS and WNP region, the simulated northward propagating BSISO is weaker and the southward component is much stronger than those in the observation (Fig. 12).
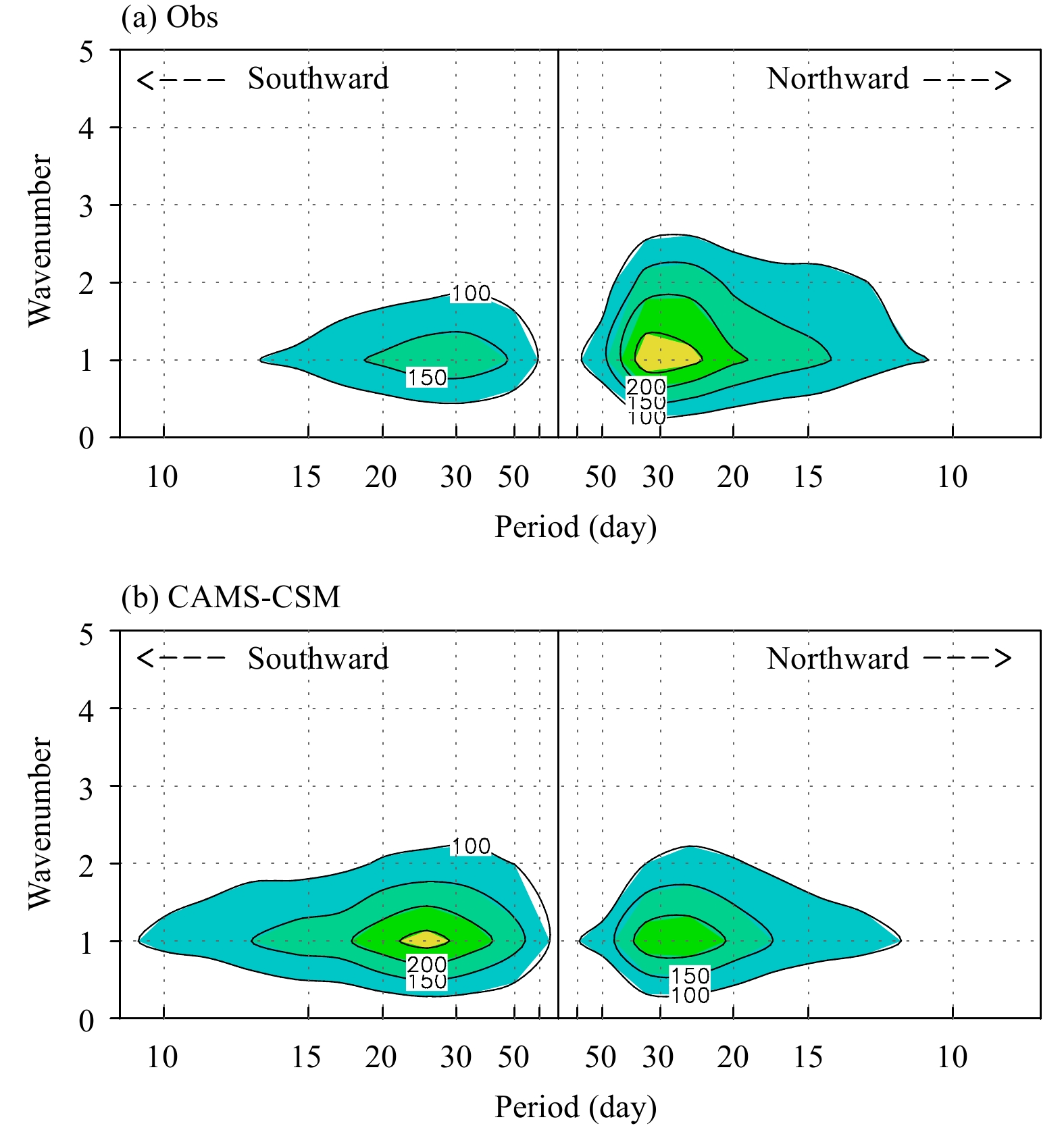
|
| Figure 12 The 23-yr mean wavenumber–frequency spectra for meridional propagation of OLR in boreal summer over 110°–120°E for (a) observation and (b) CAMS-CSM. Contour interval is 50 (W m–2)2. |
For meridional propagations of BSISO in both northward and southward directions in the eastern Indian Ocean and in the SCS and WNP region, the simulated northward propagating BSISO is significantly weaker while southward propagating BSISO is stronger than those in the observation.
6 Summary and discussionThe purpose of this study is to evaluate the performance of the newly developed model CAMS-CSM, with a focus on its simulation of the BSISO. Our preliminary assessment of the characteristics of the simulated BSISO, as well as the simulated annual cycle and summer mean state, is presented.
The CAMS-CSM simulation of the annual cycle and seasonal mean in precipitation is realistic, and the maximum center of precipitation is also in agreement with the observation. But, like most other models, CAMS-CSM tends to simulate double ITCZs, with an excess of the precipitation belt south of the equatorial western Pacific. In terms of the vertical shear of large-scale zonal wind, the CAMS-CSM well simulates the baroclinic structure of zonal wind in the Asian–Pacific summer monsoon region, except that the strength of the vertical shear is relatively weaker compared to the observation and the vertical shear is deficient along the EEIO.
The variability centers of simulated BSISO are mainly located between 10° and 20°N from the eastern Arabian Sea, Bay of Bengal, to the SCS, and the Philippine Sea. But the intensity of simulated BSISO tends to be stronger over the Bay of Bengal and weaker over the SCS. Besides, the active center of observed BSISO in the EEIO is not well reproduced, and the BSISO center in the model is exaggerated south of the India subcontinent.
In the Hovmöller diagram that illustrates meridional propagation of BSISO, three episodes in the nature of BSISO anomalous precipitation are examined and compared between the observation and model output, respectively. It is shown that the northward and southward propagation and non-meridional propagation events of BSISO over the Indian monsoon domain are captured in individual years by the CAMS-CSM, suggesting that the interannual variability of BSISO propagation is reproduced well by the model. According to the proposed mechanism for the BSISO northward propagation in the Indian Ocean by Jiang et al. (2004), the internal atmospheric dynamics is essential in causing the northward propagation of BSISO. In this regard, the physical processes involved in wind convergence and moisture–convection feedback need to be further investigated.
The assessment of BSISO properties by the wavenumber–frequency analysis indicates that the newly developed climate system model by the CAMS is able to reproduce the characteristics of BSISO. The eastward propagating wavenumber-1 BSISO along the equator with a dominant period of 20–50 days is well simulated. But the strength of the eastward propagation of BSISO tends to be weaker in the model. Meanwhile, the westward component in the model is stronger than that in the observation. The simulated northward propagation of ISO in the Asian–Pacific summer monsoon region is more realistic in contrast. In the famous Indian and SCS summer monsoon regions, the meridional wave numbers and periodicities are all in agreement with the observations, except that the intensity of northward propagating BSISO is underestimated. The southward component tends to be overestimated in both the Indian and SCS monsoon regions. In summary, both the overall magnitude of BSISO convection in eastward propagation along the equator and northward propagation in the In-dian and SCS summer monsoon sectors are underestimated in the model, suggesting that the origins of eastward and northward propagation of BSISO convection are not well reproduced and the physical processes responsible for the eastward and northward propagation need to be better understood. Based on previous studies, the BSISO originates from complex interactions among many physical processes with different forcing factors involved, which may include air–sea interaction and internal atmospheric dynamics related to vertical wind shear and moisture asymmetry (Kemball-Cook and Wang, 2001; Fu and Wang, 2004; Jiang et al., 2004; Hsu and Li, 2012; Liu and Wang, 2017). Accurate modeling of BSISO needs a better understanding of the relevant physical mechanisms as well as improved physical parameterization schemes for cumulus convection, flux adjustment, moisture budget and cycle, and so on. The mathematical descriptions of these interactive parameterizations are crucial in simulating the BSISO realistically. As such, more detailed diagnostics and analysis as well as the experiments that aim at simulating the evolutionary and structural characteristics of the eastward and northward propagations of BSISO by the CAMS-CSM are required in future investigations.
In this study, we focus on the climatological features of BSISO in the Asian–Pacific summer monsoon region. It is well known that the BSISO has significant interannual variations over the tropics and monsoon regions (Wang et al., 2006; Hsu et al., 2018). The interannual and seasonal variations of BSISO intensity and its northward propagation directly affect rainfall variability over the monsoon regions over the Indian Ocean, the SCS, and western Pacific (Teng and Wang, 2003; Qi et al., 2008, 2013; Hsu and Yang, 2016). How does the CAMS-CSM perform in terms of the SST relationship with the ISO on the interannual timescale is our ongoing research.
| Ajayamohan, R. S., and B. N. Goswami, 2007: Dependence of simulation of boreal summer tropical intraseasonal oscillations on the simulation of seasonal mean. J. Atmos. Sci., 64, 460–478. DOI:10.1175/JAS3844.1 |
| Benedict, J. J., E. D. Maloney, A. H. Sobel, et al., 2014: Gross moist stability and MJO simulation skill in three full-physics GCMs. J. Atmos. Sci., 71, 3327–3349. DOI:10.1175/JAS-D-13-0240.1 |
| Cao, J., B. Wang, B. Xiang, et al., 2015: Major modes of short-term climate variability in the newly developed NUIST Earth System Model (NESM). Adv. Atmos. Sci., 32, 585–600. DOI:10.1007/s00376-014-4200-6 |
| DeMott, C. A., C. Stan, and D. A. Randall, 2013: Northward propagation mechanisms of the boreal summer intraseasonal oscillation in the ERA-Interim and SP-CCSM. J. Climate, 26, 1973–1992. DOI:10.1175/JCLI-D-12-00191.1 |
| Flatau, M., P. J. Flatau, P. Phoebus, et al., 1997: The feedback between equatorial convection and local radiative and evaporative processes: The implications for intraseasonal oscillations. J. Atmos. Sci., 54, 2373–2386. DOI:10.1175/1520-0469(1997)054<2373:TFBECA>2.0.CO;2 |
| Fu, X. H., and B. Wang, 2001: A coupled modeling study of the seasonal cycle of the Pacific cold tongue. Part I: Simulation and sensitivity experiments. J. Climate, 14, 765–779. DOI:10.1175/1520-0442(2001)014<0765:ACMSOT>2.0.CO;2 |
| Fu, X. H., and B. Wang, 2004: Differences of boreal summer intraseasonal oscillations simulated in an atmosphere–ocean coupled model and an atmosphere-only model. J. Climate, 17, 1263–1271. DOI:10.1175/1520-0442(2004)017<1263:DOBSIO>2.0.CO;2 |
| Griffies, S. M., M. J. Harrison, P. C. Pacanowski, et al., 2004: A Technical Guide to MOM4. GFDL Ocean Group Technical Report No. 5, 339 pp. |
| Gualdi, S., and A. Navarra, 1998: A study of the seasonal variability of the tropical intraseasonal oscillation. Global Atmos. Ocean Syst., 6, 337–372. |
| Gualdi, S., A. Navarra, and H. von Storch, 1997: Tropical intraseasonal oscillation appearing in operational analyses and in a family of general circulation models. J. Atmos Sci., 54, 1185–1202. DOI:10.1175/1520-0469(1997)054<1185:TIOAIO>2.0.CO;2 |
| Gualdi, S., A. Navarra, and M. Fischer, 1999: The tropical intraseasonal oscillation in a coupled ocean–atmosphere gene-ral circulation model. Geophys. Res. Lett., 26, 2973–2976. DOI:10.1029/1999GL010414 |
| Hayashi, Y., 1982: Space–time spectral analysis and its applications to atmospheric waves. J. Meteor. Soc. Japan, 60, 156–171. DOI:10.2151/jmsj1965.60.1_156 |
| Hendon, H. H., 2000: Impact of air–sea coupling on the Madden-Julian Oscillation in a general circulation model. J. Atmos. Sci., 57, 3939–3952. DOI:10.1175/1520-0469(2001)058<3939:IOASCO>2.0.CO;2 |
| Hendon, H. H, C. D. Zhang, and J. D. Glick, 1999: Interannual variation of the Madden–Julian Oscillation during austral summer. J. Climate, 12, 2538–2550. DOI:10.1175/1520-0442(1999)012<2538:IVOTMJ>2.0.CO;2 |
| Hsu, H.-H., B. J. Hoskins, and F.-F. Jin, 1990: The 1985/86 intraseasonal oscillation and the role of the extratropics. J. Atmos. Sci., 47, 823–839. DOI:10.1175/1520-0469(1990)047<0823:TIOATR>2.0.CO;2 |
| Hsu, P.-C., and T. Li, 2012: Role of the boundary layer moisture asymmetry in causing the eastward propagation of the Madden–Julian oscillation. J. Climate, 25, 4914–4931. DOI:10.1175/JCLI-D-11-00310.1 |
| Hsu, P.-C., and Y. Yang, 2016: Contribution of atmospheric internal processes to the interannual variability of the South Asian summer monsoon. Int. J. Climatol., 36, 2917–2930. DOI:10.1002/joc.4528 |
| Hsu, P.-C., Z. Fu, and T. Xiao, 2018: Energetic processes regulating the strength of MJO circulation over the Maritime continent during two types of El Niño. Atmos. Ocean. Sci. Lett., 11, 112–119. DOI:10.1080/16742834.2018.1399049 |
| Inness, P. M., J. M. Slingo, E. Guilyardi, et al., 2003: Simulation of the Madden–Julian oscillation in a coupled general circulation model. Part II: The role of the basic state. J. Climate, 16, 365–382. DOI:10.1175/1520-0442(2003)016<0365:SOTMJO>2.0.CO;2 |
| Ji, D., L. Wang, J. Feng, et al., 2014: Description and basic evaluation of BNU-ESM version 1. Geosci. Model Dev. Discuss., 7, 1601–1647. DOI:10.5194/gmdd-7-1601-2014 |
| Jia, X. L., C. Y. Li, N. F. Zhou, et al., 2010: The MJO in an AGCM with three different cumulus parameterization schemes. Dyn. Atmos. Oceans, 49, 141–163. DOI:10.1016/j.dynatmoce.2009.02.003 |
| Jiang, X., T. Li, and B. Wang, 2004: Structures and mechanisms of the northward propagating boreal summer intraseasonal oscillation. J. Climate, 17, 1022–1039. DOI:10.1175/1520-0442(2004)017<1022:SAMOTN>2.0.CO;2 |
| Jiang, X., D. E. Waliser, P. K. Xavier, et al., 2015: Vertical structure and physical processes of the Madden–Julian oscillation: Exploring key model physics in climate simulations. J. Geophys. Res. Atmos., 120, 4718–4748. DOI:10.1002/2014JD022375 |
| Kemball-Cook, S., and B. Wang, 2001: Equatorial waves and air–sea interaction in the boreal summer intraseasonal oscillation. J. Climate, 14, 2923–2942. DOI:10.1175/1520-0442(2001)014<2923:EWAASI>2.0.CO;2 |
| Kemball-Cook, S., B. Wang, and X. Fu, 2002: Simulation of the intraseasonal oscillation in the ECHAM-4 Model: The impact of coupling with an ocean model. J. Atmos. Sci., 59, 1433–1453. DOI:10.1175/1520-0469(2002)059<1433:SOTIOI>2.0.CO;2 |
| Lau, K.-M., and P. H. Chan, 1986: Aspects of the 40–50 day oscillation during the northern summer as inferred from outgoing longwave radiation. Mon. Wea. Rev., 114, 1354–1367. DOI:10.1175/1520-0493(1986)114<1354:AOTDOD>2.0.CO;2 |
| Lau, W. K. M., and D. E. Waliser, 2005: Intraseasonal Variabi-lity in the Atmosphere–Ocean Climate System. Springer, Heidelberg, Germany, 474 pp. |
| Lee, J.-Y., B. Wang, M. C. Wheeler, et al., 2013: Real-time multivariate indices for the boreal summer intraseasonal oscillation over the Asian summer monsoon region. Climate Dyn., 40, 493–509. DOI:10.1007/s00382-012-1544-4 |
| Li, C. Y., J. Ling, J. Song, et al., 2014: Research progress in China on the tropical atmospheric intraseasonal oscillation. J. Meteor. Res., 28, 671–692. DOI:10.1007/s13351-014-4015-5 |
| Li, J., H. M. Chen, X. Y. Rong, et al., 2018: How well can a climate model simulate an extreme precipitation event: A case study using the Transpose-AMIP experiment. J. Climate, 31, 6543–6556. DOI:10.1175/JCLI-D-17-0801.1 |
| Li, T., 2014: Recent advance in understanding the dynamics of the Madden–Julian oscillation. J. Meteor. Res., 28, 1–33. DOI:10.1007/s13351-014-3087-6 |
| Li, W., Y. J. Zhu, X. Q. Zhou, et al., 2018: Evaluating the MJO prediction skill from different configurations of NCEP GEFS extended forecast. Climate Dyn.. DOI:10.1007/s00382-018-4423-9 |
| Lin, A. L., and T. Li, 2008: Energy spectrum characteristics of boreal summer intraseasonal oscillations: Climatology and variations during the ENSO developing and decaying phases. J. Climate, 21, 6304–6320. DOI:10.1175/2008JCLI2331.1 |
| Lin, A. L., T. Li, X. H. Fu, et al., 2011: Effects of air–sea coupling on the boreal summer intraseasonal oscillations over the tropical Indian Ocean. Climate Dyn., 37, 2303–2322. DOI:10.1007/s00382-010-0943-7 |
| Ling, J., C. D. Zhang, and P. Bechtold, 2013: Large-scale distinctions between MJO and non-MJO convective initiation over the tropical Indian Ocean. J. Atmos. Sci., 70, 2696–2712. DOI:10.1175/JAS-D-13-029.1 |
| Liu, F., and B. Wang, 2013: An air–sea coupled skeleton model for the Madden–Julian oscillation. J. Atmos. Sci., 70, 3147–3156. DOI:10.1175/JAS-D-12-0348.1 |
| Liu, F., and B. Wang, 2017: Effects of moisture feedback in a frictional coupled Kelvin–Rossby wave model and implication in the Madden–Julian oscillation dynamics. Climate Dyn., 48, 513–522. DOI:10.1007/s00382-016-3090-y |
| Liu, F., B. Wang, and I.-S. Kang, 2015: Roles of barotropic convective momentum transport in the intraseasonal oscillation. J. Climate, 28, 4908–4920. DOI:10.1175/JCLI-D-14-00575.1 |
| Madden, R. A., and P. R. Julian, 1971: Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific. J. Atmos. Sci., 28, 702–708. DOI:10.1175/1520-0469(1971)028<0702:DOADOI>2.0.CO;2 |
| Madden, R. A., and P. R. Julian, 1972: Description of global-scale circulation cells in the tropics with a 40–50 day period. J. Atmos. Sci., 29, 1109–1123. DOI:10.1175/1520-0469(1972)029<1109:DOGSCC>2.0.CO;2 |
| Neena, J. M., D. Waliser, and X. Jiang, 2017: Model performance metrics and process diagnostics for boreal summer intraseasonal variability. Climate Dyn., 48, 1661–1683. DOI:10.1007/s00382-016-3166-8 |
| Nordeng, T. E., 1994: Extended Versions of the Convective Parameterization Scheme at ECMWF and Their Impact on the Mean and Transient Activity of the Model in the Tropics. Technical Memorandum 206, ECMWF, Reading, UK. 41 pp. |
| Qi, Y. J., R. H. Zhang, T. Li, et al., 2008: Interactions between the summer mean monsoon and the intraseasonal oscillation in the Indian monsoon region. Geophys. Res. Lett., 35, L17704. DOI:10.1029/2008GL034517 |
| Qi, Y. J., R. H. Zhang, P. Zhao, et al., 2013: Comparison of the structure and evolution of intraseasonal oscillations before and after onset of the Asian summer monsoon. Acta Meteor. Sinica, 27, 684–700. DOI:10.1007/s13351-013-0511-2 |
| Ren, H.-L., J. Wu, C.-B. Zhao, et al., 2016: MJO ensemble prediction in BCC-CSM1.1(m) using different initialization schemes. Atmos. Ocean. Sci. Lett., 9, 60–65. DOI:10.1080/16742834.2015.1116217 |
| Roeckner, E., G. Bäuml, L. Bonaventura, et al., 2003: The Atmos-pheric General Circulation Model ECHAM 5. Part I: Model Description. Rep. No. 349, Max-Planck-Institut für Meteorologie, Hamburg, Germany, 127 pp. |
| Rong, X. Y., J. Li, H. M. Chen, et al., 2018: The CAMS climate system model and a basic evaluation of its climatology and climate variability simulation. J. Meteor. Res., 32, 839–861. DOI:10.1007/s13351-018-8058-x |
| Sabeerali, C. T., A. Ramu Dandi, A. Dhakate, et al., 2013: Simulation of boreal summer intraseasonal oscillations in the latest CMIP5 coupled GCMs. J. Geophys. Res. Atmos., 118, 4401–4420. DOI:10.1002/jgrd.50403 |
| Salby, M. L., and H. H. Hendon, 1994: Intraseasonal behavior of clouds, temperature, and motion in the tropics. J. Atmos. Sci., 51, 2207–2224. DOI:10.1175/1520-0469(1994)051<2207:IBOCTA>2.0.CO;2 |
| Slingo, J. M., K. R. Sperber, J. S. Boyle, et al., 1996: Intraseaso-nal oscillations in 15 atmospheric general circulation models: Results from an AMIP diagnostic subproject. Climate Dyn., 12, 325–357. DOI:10.1007/BF00231106 |
| Sperber, K. R., and H. Annamalai, 2008: Coupled model simulations of boreal summer intraseasonal (30–50 day) variability, Part 1: Systematic errors and caution on use of metrics. Climate Dyn., 31, 345–372. DOI:10.1007/s00382-008-0367-9 |
| Sperber, K. R., S. Gualdi, S. Legutke, et al., 2005: The Madden–Julian oscillation in ECHAM4 coupled and uncoupled general circulation models. Climate Dyn., 25, 117–140. DOI:10.1007/s00382-005-0026-3 |
| Teng, H. Y., and B. Wang, 2003: Interannual variations of the boreal summer intraseasonal oscillation in the Asian–Pacific region. J. Climate, 16, 3572–3584. DOI:10.1175/1520-0442(2003)016<3572:IVOTBS>2.0.CO;2 |
| Tiedtke, M., 1989: A comprehensive mass flux scheme for cumulus parameterization in large-scale models. Mon. Wea. Rev., 117, 1779–1800. DOI:10.1175/1520-0493(1989)117<1779:ACMFSF>2.0.CO;2 |
| Waliser, D. E., 2006: Intraseasonal variability. The Asian Monsoon, B. Wang, Ed., Springer, Berlin, 203–257. |
| Waliser, D. E., K. M. Lau, and J.-H. Kim, 1999: The influence of coupled sea surface temperatures on the Madden–Julian Oscillation: A model perturbation experiment. J. Atmos. Sci., 56, 333–358. DOI:10.1175/1520-0469(1999)056<0333:TIOCSS>2.0.CO;2 |
| Waliser, D. E., K. M. Lau, W. Stern, et al., 2003a: Potential predictability of the Madden–Julian Oscillation. Bull. Amer. Meteor. Soc., 84, 33–50. DOI:10.1175/BAMS-84-1-33 |
| Waliser, D. E., K. Jin, I.-S. Kang, et al., 2003b: AGCM simulations of intraseasonal variability associated with the Asian summer monsoon. Climate Dyn., 21, 423–446. DOI:10.1007/s00382-003-0337-1 |
| Wang, B., 2005: Theory. Chapter 10 in Intraseasonal variability in the Atmosphere–Ocean Climate System, K. M. Lau and D. E. Waliser, eds, Springer and Praxis, Chichester, UK, 307–351. |
| Wang, B., and H. Rui, 1990: Synoptic climatology of transient tropical intraseasonal convection anomalies: 1975–1985. Meteor. Atmos. Phys., 44, 43–61. DOI:10.1007/BF01026810 |
| Wang, B., and X. S. Xie, 1996: Low-frequency equatorial waves in vertically sheared zonal flow. Part I: Stable waves. J. Atmos. Sci., 53, 449–467. DOI:10.1175/1520-0469(1996)053<0449:LFEWIV>2.0.CO;2 |
| Wang, B., and X. S. Xie, 1997: A model for the boreal summer intraseasonal oscillations. J. Atmos. Sci., 54, 72–86. DOI:10.1175/1520-0469(1997)054<0072:AMFTBS>2.0.CO;2 |
| Wang, B., and X. S. Xie, 1998: Coupled modes of the warm pool climate system. Part I: The role of air–sea interaction in maintaining Madden–Julian oscillation. J. Climate, 11, 2116–2135. DOI:10.1175/1520-0442-11.8.2116 |
| Wang, B., and S.-S. Lee, 2017: MJO propagation shaped by zonal asymmetric structures: Results from 24 GCM simulations. J. Climate, 30, 7933–7952. DOI:10.1175/JCLI-D-16-0873.1 |
| Wang, B., P. Webster, K. Kikuchi, et al., 2006: Boreal summer quasi-monthly oscillation in the global tropics. Climate Dyn., 27, 661–675. DOI:10.1007/s00382-006-0163-3 |
| Wang, B., S.-S. Lee, D. E. Waliser, et al., 2018: Dynamics-oriented diagnostics for the Madden–Julian Oscillation. J. Climate, 31, 3117–3135. DOI:10.1175/JCLI-D-17-0332.1 |
| Wang, L., T. Li, E. Maloney, et al., 2017: Fundamental causes of propagating and non-propagating MJOs in MJOTF/GASS models. J. Climate, 30, 3743–3769. DOI:10.1175/JCLI-D-16-0765.1 |
| Wang, L., T. Li, and T. Nasuno, 2018: Impact of Rossby and Kelvin wave components on MJO eastward propagation. J. Climate, 31, 6913–6931. DOI:10.1175/JCLI-D-17-0749.1 |
| Wang, W. Q., and M. E. Schlesinger, 1999: The dependence on convection parameterization of the tropical intraseasonal oscillation simulated by the UIUC 11-layer atmospheric GCM. J. Climate, 12, 1423–1457. DOI:10.1175/1520-0442(1999)012<1423:TDOCPO>2.0.CO;2 |
| Webster, P. J., and S. Yang, 1992: Monsoon and ENSO: Selectively interactive systems. Quart. J. Roy. Meteor. Soc., 118, 877–926. DOI:10.1002/qj.49711850705 |
| Wheeler, M., and G. N. Kiladis, 1999: Convectively coupled equatorial waves: Analysis of clouds and temperature in the wavenumber–frequency domain. J. Atmos. Sci., 56, 374–399. DOI:10.1175/1520-0469(1999)056<0374:CCEWAO>2.0.CO;2 |
| Wu, M. L. C., S. Schubert, I.-S. Kang, et al., 2002: Forced and free intraseasonal variability over the South Asian monsoon region simulated by 10 AGCMs. J. Climate, 15, 2862–2880. DOI:10.1175/1520-0442(2002)015<2862:FAFIVO>2.0.CO;2 |
| Yasunari, T., 1979: Cloudiness fluctuations associated with the Northern Hemisphere summer monsoon. J. Meteor. Soc. Japan, 57, 227–242. DOI:10.2151/jmsj1965.57.3_227 |
| Zhang, C. D., 2005: Madden–Julian oscillation. Rev. Geophys., 43, RG2003. DOI:10.1029/2004RG000158 |
| Zhang, C. D., 2013: Madden–Julian oscillation: Bridging weather and climate. Bull. Amer. Meteor. Soc., 94, 1849–1870. DOI:10.1175/BAMS-D-12-00026.1 |
 2019, Vol. 33
2019, Vol. 33


