The Chinese Meteorological Society
Article Information
- CHEN, Xiaolong, Zhun GUO, Tianjun ZHOU, et al., 2019.
- Climate Sensitivity and Feedbacks of a New Coupled Model CAMS-CSM to Idealized CO2 Forcing: A Comparison with CMIP5 Models . 2019.
- J. Meteor. Res., 33(1): 31-45
- http://dx.doi.org/10.1007/s13351-019-8074-5
Article History
- Received May 23, 2018
- in final form November 27, 2018
2. Climate Change Research Center, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
3. University of the Chinese Academy of Sciences, Beijing 100049;
4. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, China Meteorological Administration, Beijing 100081
Climate sensitivity is the core concept in climate change research, measuring how sensitive a climate system is to external forcing of doubled CO2 concentration (Stocker et al., 2013). There are two terms of climate sensitivity widely used in different stages of climate change. One is called equilibrium climate sensitivity (ECS), defined as the global mean surface temperature (GMST) response to a doubled CO2 concentration relative to the pre-industrial level when climate state reaches to a new equilibrium (Flato et al., 2013). The other is called transient climate response (TCR), defined as GMST change relative to the pre-industrial level at the time when CO2 concentration is doubled in an idealized scenario that CO2 increases 1% per year (Flato et al., 2013). The ECS deals with equilibrium change where every part of climate system has adjusted to the doubled CO2 forcing and will not change any more, whereas the TCR regards transient state in which climate change still continues, for example, ongoing warming in the deep ocean (Li et al., 2013). Hence, the ECS is only determined by climate feedbacks whereas the TCR is additionally affected by ocean heat uptake (OHU) efficiency (Zhou and Chen, 2015).
In terms of surface temperature response, there are a lot of climate feedbacks that dampen or amplify the initial forcing at the top of the atmosphere (TOA) and in turn alter the temperature response (Roe, 2009). To keep a climate system stable under an external perturbation, net climate feedback should be negative to avoid runaway warming. Besides the well-known negative Planck feedback and positive water vapor feedback (Held and Soden, 2000; Randall et al., 2007), cloud feedback is one of the most complex processes because it is determined by a variety of macro and micro parameters, such as cloud macro proprieties (i.e. cloud fraction, cloud top height, water mixing ratio, and three-dimensional structures), cloud particle size and phases, etc. (Boucher et al., 2013). As change in one cloud feature may affect both longwave and shortwave radiation and bring about both positive and negative feedbacks at the same time (Stephens, 2005), the net effect of cloud processes is still ambiguous (Stocker et al., 2013; Ceppi et al., 2017).
In the past 40 years, a large uncertainty in ECS estimation always exists in studies using either climate models or observational data (Charney et al., 1979; Vial et al., 2013; Cox et al., 2018). The latest possible range suggested by the Intergovernmental Panel on Climate Change (IPCC) Fifth Assessment Report (AR5) is 1.5–4.5 K, identical with the Charney sensitivity obtained in 1979 (Charney et al., 1979). The ECS and its uncertainty are mainly determined by climate feedbacks. Among all the feedbacks, cloud feedback is the major source of uncertainty, especially the cloud shortwave feedback associated with response of tropical and subtropical low cloud (Sherwood et al., 2014; Ceppi et al., 2017). Much of the uncertainty in cloud feedback in general circulation models (GCMs) comes from parameterizations for sub-grid processes, which can affect boundary-layer cloud (Bretherton, 2015). Reponses of strength of the inversion capping the planetary boundary layer (PBL) and sea surface temperature (SST) are found to be two major factors for uncertainty in marine low cloud simulation, in which the SST term dominates (Qu et al., 2014). Uncertainty in low-cloud feedback is also found to be related to strength of convective mixing between the lower and middle tropical troposphere, hence controlling the spread in ECS (Sherwood et al., 2014).
Recently, a new climate system model (CSM) is developed by Chinese Academy of Meteorological Sciences (CAMS). The CAMS-CSM is established by widely used and evaluated component models, with several modifications to improve model performance especially in the East Asian region (Li et al., 2018; Rong et al., 2018). Climatological mean states, seasonal cycles, and major climate variability modes including Madden–Julian Oscillation and El Niño–Southern Oscillation are well reproduced (Rong et al., 2018). Nevertheless, the climate sensitivity and feedbacks in this model remain unknown and need to be clarified, especially its differences from other models, given large uncertainty in cloud feedback. In this study, we find that the CAMS-CSM model has a relatively low ECS compared with multi-model results from the Coupled Model Intercomparison Project phase 5 (CMIP5; Taylor et al., 2012), caused by an unusually strong negative cloud shortwave feedback. Weaker static stability over the Indo-Pacific Ocean in pre-industrial simulation is found as a key factor which promotes circulation convergence and low-cloud formation under warming, providing a new insight in constraining the uncertainty in cloud shortwave feedback.
The remainder of this paper is organized as follows. Section 2 describes the CAMS-CSM model and experiment used for analysis. Methods to estimate climate sensitivity and feedbacks are introduced in Section 3. Section 4 shows the major results, followed by conclusions and discussion in Section 5.
2 Model, data, and experimentThe CAMS-CSM is a fully coupled GCM with four components: atmosphere, ocean, land, and sea ice. The atmosphere component is a modified version of the atmospheric general circulation model ECHAM5 (v5.4) from the Max-Planck-Institute for Meteorology (Roeckner et al., 2003). The modifications include dynamic core and physical processes, such as using a two-step shape preserving advection scheme for passive tracer transport (Yu, 1994) and a k-distribution scheme for radiation transfer parameterization (Zhang et al., 2006a, b). Other details in the ECHAM5 model could be referred to Roeckner et al. (2003). Atmosphere resolution is T106L31, a horizontal resolution of about 1° with 31 vertical layers from the surface to 10 hPa. The ocean component is the Modular Ocean Model version 4 (MOM4) from the Geophysical Fluid Dynamic Laboratory (GFDL). A tripolar grid is used in MOM4 with two northern poles placed over North America and Eurasia (Murray, 1996). The zonal resolution is 1° globally and the meridional resolution is 1/3° within 10°S–10°N gradually increasing to 1° at 30°S (N). There are 50 vertical layers with 23 equidistant layers above 230 m. The sea ice component is the Sea Ice Simulator from GFDL (Winton, 2000) and the land component is the Common Land Model (CoLM; Dai et al., 2003). The four components are interacted through Flexible Modeling System (FMS) coupler. More details in CAMS-CSM are referred to Rong et al. (2018).
Three benchmark experiments are used in this study: 1) a pre-industrial control simulation (piControl) in which any forcing agent has no interannual variability and long-term trend, 2) a simulation forced by abruptly quadrupled CO2 (abrupt4×CO2), and 3) a simulation forced by CO2 increasing 1% per year (1pctCO2). The control simulation reached a quasi-equilibrium state after 500-yr integration (Rong et al. 2018). In the last 290 years of piControl run (model years 2140–2429) for analysis (Fig. 1), global mean surface air temperature (GMST) and net radiation at the TOA are 13.6°C and 1.19 W m–2 (downward) for mean state, 0.07°C (100 yr)–1 and –0.08 W m–2 (100 yr)–1 for trend, respectively. The GMST still has a slightly positive trend because of the unbalanced incoming energy at the TOA. The latter two simulations are branch experiments that are initialized from piControl in 1 January in model years 2145 and 2245, respectively, and then continuously integrated for 150 yr (Fig. 1).

|
| Figure 1 Time series of (a) net radiation at the TOA (W m–2) and (b) surface air temperature (°C) in the pre-industrial control simulation (piControl; thick gray line) of CAMS-CSM, and under two idealized CO2 forcing scenarios, i.e., CO2 concentration abruptly quadrupled (abrupt4×CO2; black line) or increasing 1% per year (1pctCO2; thin gray line). |
Longwave/shortwave radiation at the TOA and surface air temperature are used to estimate climate sensitivity and feedback (see Section 3). These radiations in both all-sky and clear-sky conditions are used to yield cloud radiation effect (CRE). In addition, other variables such as three-dimensional cloud fraction (CF), water vapor, vertical p-velocity, surface temperature, surface latent heat, and cloud water path are used to analyze important physical processes related to feedbacks. For comparing with multi-model results, climate sensitivity and feedbacks of 24 CMIP5 models are calculated in the same manner (Table 1). Annual mean of all data is calculated for analysis.
3 MethodsAs documented in many previous literatures (e.g., Hansen et al., 1984; Gregory et al., 2002; Roe, 2009; Vial et al., 2013; Zhou and Chen, 2015), the principle of estimating climate sensitivity is based on energy conservation. Specifically, it is a zero-dimensional relation between net radiation at the TOA (N), forcing (F), net feedback (λ), and GMST response (
| $N = F + \lambda T'.$ | (1) |
For simplicity, λ is assumed as a negative constant whereas the others can vary with time. With a constant forcing F exerted by some forcing agents, such as greenhouse gases, the outgoing radiation will eventually compensate the forcing, that is N = 0, and a new equilibrium is reached. According to the definition, at an equilibrium state under a forcing of doubled CO2 concentration (F2×), the ECS can be estimated by
| ${\rm{ECS}} = {F_{2 \times }}/\left( { - \lambda } \right).$ | (2) |
Estimating F and λ in Eq. (1) is the core issue in calculating climate sensitivity. To reduce impact of climate drift, all changes in forced simulations are calculated by subtracting those in the piControl run during the same range of model years (Fig. 1).
3.1 The Gregory-style regression for ECS estimationIntegrating coupled climate model under CO2 doubling until a new equilibrium to obtain the ECS needs huge computational cost. In practice, a simple approach to estimate ECS using transient response to a constant forcing in fully coupled GCM was proposed by Gregory et al. (2004). The abrupt4×CO2 experiment is ad hoc designed for this approach, in which CO2 concentration keeps constant at a quadrupling level relative to the pre-industrial. A standard least-square regression is applied on N against
The net radiation N at the TOA can be further decomposed into clear-sky/cloud (CS/CL) and longwave/shortwave (LW/SW) components, that is
| $\begin{array}{l} {N_ {\rm{LWCS}}} + {N_ {\rm{SWCS}}} + {N_ {\rm{LWCL}}} + {N_ {\rm{SWCL}}}\\ = {F_ {\rm{LWCS}}} + {F_ {\rm{SWCS}}} + {F_ {\rm{LWCL}}} + {F_ {\rm{SWCL}}} \\ \;\;\;\; + \left( {{\lambda _ {\rm{LWCS}}} + {\lambda _ {\rm{SWCS}}} + {\lambda _ {\rm{LWCL}}} + {\lambda _ {\rm{SWCL}}}} \right)T'. \end{array}$ | (3) |
Thus, corresponding components contributing to the feedback and forcing can be obtained by applying the Gregory-style regression on each component individually (Gregory and Webb, 2008). Here, changes in CRE per K warming are used to estimate cloud feedbacks (Soden et al., 2004), that is the so-called “CRE feedback”. Moreover, the clear-sky longwave at the TOA (NLWCS) can be decomposed into one part emitted by the surface (NLWS) and the other part blocked by the atmosphere (NLWA), as well as the corresponding feedback λLWS and λLWA (Chen et al., 2014).
3.2 Alternative estimation of feedback from 1pctCO2 experimentFor 1pctCO2 experiment, CO2 concentration increases 1% per year, beginning at the pre-industrial level. The parameter F of Eq. (1) in this scenario varying with time can be calculated as following equation.
| $F\left( t \right) = {F_{2 \times }}\frac{{\ln {1.01}}}{{\ln 2 }}t,$ | (4) |
where F2× is estimated by using the Gregory-style regression in the abrutp4×CO2 experiment as described in Subsection 3.1. Then, based on Eq. (1), N – F regressed against
Following the definition of TCR, its value can be directly derived from averaging GMST changes in the 1pctCO2 experiment around the 70th model year when CO2 concentration is doubled. We use a 20-yr average, that is, during the 60–79th model years, to estimate TCR, following the practice in IPCC AR5 (Flato et al., 2013).
The net radiation at the TOA is nearly equal to the heat absorbed by oceans, since heat capacities of atmosphere and soil are negligible compared with sea water. Under linear increasing CO2 forcing in the 1pctCO2 experiment [Eq. (4)], both N and
| $N \cong \kappa T',$ | (5) |
where κ is called the efficiency of OHU with the same dimension as climate feedback, and it can be estimated from the linear-fitting slope by regressing N against
Based on the Gregory-style regression, we obtain the quadrupled CO2 forcing F4× in CAMS-CSM about 8.44 W m–2 and the equilibrium GMST response ΔTeqm around 4.55 K (Fig. 2a). Then, for doubled CO2 concentration, F2× and ECS are estimated by half of the above values, i.e., 4.22 W m–2 and 2.27 K, respectively. Net climate feedback λ, the slope of fitting line, is about –1.85 W m–2 K–1 (Fig. 2a). An alternative estimation of λ based on the 1pctCO2 experiment (see Subsection 3.2) yields –1.89 W m–2 K–1 (Fig. 2b). The consistent results under distinct CO2 forcing scenarios show robustness of the regression method based on Eq. (1). Compared with the MME of CMIP5 models (Table 1), despite larger F2× of CAMS-CSM model (4.22 vs. 3.39 W m–2), the ECS is about 1.1 K smaller than the CMIP5 MME (2.27 vs. 3.36 K), because the negative λ is much stronger (–1.85 vs. –1.06 W m–2 K–1) in CAMS-CSM.

|
| Figure 2 (a) Gregory-style regression to estimate effective radiative forcing F4× of quadrupled CO2 (y-axis intercept; W m–2), equilibrium surface temperature change ΔTeqm (i.e., 2×ECS, x-axis intercept; K), and climate feedback λ (slope; W m–2 K–1) under constant forcing of quadrupled CO2 (abrupt4×CO2), using least square method based on Eq. (1). (b) Alternative method to estimate climate feedback λ′ (slope; W m–2 K–1) in transient climate response to 1pctCO2, using least square method based on Eq. (1). |
Thus, CAMS-CSM model has a relatively low ECS, which is close to the lower bound of 5%–95% ranges of probability distribution function (Fig. 3a) based on the CMIP5 results (Table 1). The strongly negative λ in CAMS-CSM is located outside of the 5%–95% ranges, far away from the lower bound (Fig. 3c) whereas F2× is almost at the upper bound (Fig. 3b). The unusually negative feedback in CAMS-CSM reduces the radiative imbalance at the TOA caused by the CO2 forcing so effectively that surface air temperature response

|
| Figure 3 Probability density distributions of (a) ECS (red) and TCR (blue) (K), (b) effective radiative forcing (ERF; W m–2), (c) climate feedback λ (W m–2 K–1), and (d) ocean heat uptake efficiency κ (W m–2 K–1) derived from 24 CMIP5 models (Table 1). Median (50%) and range between 5% and 95% percentiles (shading and values in parentheses) for each parameter are labeled. Corresponding values in CAMS-CSM model for corresponding parameter are marked by dashed lines. |
In contrast to ECS, the estimated value of TCR is about 1.64 K in CAMS-CSM (Table 1; Fig. 3a), close to but slightly less than that in the CMIP5 MME (1.88 K). Since there is a positive correlation between ECS and TCR (Flato et al., 2013), why does not the TCR in CAMS-CSM seem so low as the ECS compared with the CMIP5 MME? Except climate feedbacks, OHU also plays an important role in transient response. Based on Eq. (5), we estimate the OHU efficiency κ by about 0.32 W m–2 K–1 in CAMS-CSM, which is less than the CMIP5 MME (0.48 W m–2 K–1) and close to the lower bound of 5%–95% ranges across the CMIP5 models (Fig. 3d). A low κ means relatively more heat is stored in surface or subsurface rather than absorbed by the deep ocean, which favors more surface warming at transient state. Hence, although negative climate feedback is extraordinarily strong in CAMS-CSM, the TCR is not too low due to compensation of the low OHU efficiency.
| Model | ERF (F2×) | ECS | λ | TCR | κ | λLWCS | λLWS | λLWA | λSWCS | λLWCL | λSWCL | λCL |
| ACCESS1-0 | 2.91 | 3.88 | –0.75 | 1.98 | 0.46 | –1.64 | –5.36 | 3.72 | 0.78 | 0.09 | 0.01 | 0.11 |
| ACCESS1-3 | 2.86 | 3.56 | –0.80 | 1.65 | 0.53 | –1.84 | –5.42 | 3.58 | 0.77 | –0.12 | 0.39 | 0.27 |
| BCC-CSM1-1 | 3.18 | 2.84 | –1.12 | 1.76 | 0.35 | –1.90 | –5.26 | 3.35 | 0.84 | 0.22 | –0.27 | –0.06 |
| BCC-CSM1-1-m | 3.56 | 2.83 | –1.26 | 2.23 | 0.27 | –1.98 | –5.43 | 3.46 | 0.68 | 0.13 | –0.09 | 0.04 |
| BNU-ESM | 3.73 | 4.04 | –0.92 | 2.64 | 0.41 | –1.74 | –7.15 | 5.42 | 1.08 | 0.17 | –0.44 | –0.27 |
| CanESM2 | 3.81 | 3.70 | –1.03 | 2.41 | 0.38 | –1.88 | –5.50 | 3.62 | 0.73 | 0.45 | –0.33 | 0.12 |
| CCSM4 | 3.62 | 2.90 | –1.25 | 1.76 | 0.46 | –1.95 | –5.30 | 3.34 | 0.87 | 0.05 | –0.22 | –0.17 |
| CNRM-CM5 | 3.68 | 3.26 | –1.13 | 2.08 | 0.43 | –1.74 | –5.34 | 3.60 | 0.80 | 0.10 | –0.29 | –0.19 |
| CSIRO-Mk3-6-0 | 2.56 | 4.10 | –0.62 | 1.78 | 0.50 | –1.70 | –5.41 | 3.70 | 0.84 | –0.23 | 0.47 | 0.24 |
| FGOALS-g2 | 2.90 | 3.34 | –0.87 | 1.36 | 0.98 | –1.73 | –5.33 | 3.59 | 0.89 | 0.17 | –0.19 | –0.02 |
| FGOALS-s2 | 3.79 | 4.20 | –0.90 | 2.42 | 0.54 | –1.45 | –5.18 | 3.73 | 1.01 | 0.10 | –0.57 | –0.46 |
| GFDL-CM3 | 2.97 | 3.99 | –0.74 | 1.95 | 0.43 | –1.94 | –5.41 | 3.47 | 0.69 | –0.06 | 0.57 | 0.51 |
| GISS-E2-H | 3.68 | 2.36 | –1.56 | 1.74 | 0.41 | –1.66 | –5.27 | 3.61 | 0.54 | 0.29 | –0.72 | –0.43 |
| GISS-E2-R | 3.76 | 2.11 | –1.78 | 1.45 | 0.60 | –1.66 | –5.29 | 3.63 | 0.37 | 0.33 | –0.82 | –0.49 |
| HadGEM2-ES | 2.89 | 4.63 | –0.62 | 2.50 | 0.37 | –1.66 | –5.36 | 3.70 | 0.67 | 0.11 | 0.26 | 0.37 |
| INMCM4 | 3.02 | 2.06 | –1.46 | 1.29 | 0.51 | –1.98 | –5.19 | 3.21 | 0.69 | –0.03 | –0.14 | –0.17 |
| IPSL-CM5A-LR | 3.07 | 4.15 | –0.74 | 2.04 | 0.45 | –1.98 | –5.41 | 3.42 | 0.53 | 0.09 | 0.62 | 0.71 |
| IPSL-CM5B-LR | 2.63 | 2.61 | –1.01 | 1.48 | 0.38 | –1.89 | –5.25 | 3.37 | 0.58 | 0.00 | 0.30 | 0.30 |
| MIROC5 | 4.10 | 2.73 | –1.50 | 1.51 | 0.62 | –1.86 | –5.48 | 3.62 | 0.83 | –0.04 | –0.44 | –0.47 |
| MIROC-ESM | 4.24 | 4.68 | –0.91 | 2.16 | 0.54 | –1.93 | –5.66 | 3.73 | 0.83 | 0.03 | 0.16 | 0.19 |
| MPI-ESM-LR | 4.06 | 3.64 | –1.11 | 2.05 | 0.41 | –1.79 | –5.30 | 3.50 | 0.69 | 0.17 | –0.18 | –0.01 |
| MPI-ESM-MR | 4.04 | 3.47 | –1.16 | 2.04 | 0.43 | –1.85 | –5.32 | 3.48 | 0.64 | 0.12 | –0.08 | 0.04 |
| MRI-CGCM3 | 3.10 | 2.64 | –1.17 | 1.56 | 0.37 | –1.98 | –5.39 | 3.40 | 0.86 | –0.19 | 0.14 | –0.05 |
| NorESM1-M | 3.10 | 2.80 | –1.10 | 1.39 | 0.56 | –1.86 | –5.24 | 3.38 | 0.84 | 0.06 | –0.14 | –0.09 |
| MME | 3.39 | 3.36 | –1.06 | 1.88 | 0.48 | –1.82 | –5.43 | 3.61 | 0.75 | 0.08 | –0.08 | 0.00 |
| Std Dev | 0.49 | 0.75 | 0.30 | 0.38 | 0.13 | 0.14 | 0.37 | 0.40 | 0.15 | 0.15 | 0.38 | 0.30 |
| CAMS-CSM | 4.22 | 2.27 | –1.85 | 1.64 | 0.32 | –1.66 | –5.34 | 3.68 | 0.57 | 0.25 | –1.01 | –0.77 |
In the above subsection, net climate feedback in CAMS-CSM is found extremely negative compared with the CMIP5 models (Fig. 3c), which physical process is responsible for such a strong negative feedback? To answer this question, we decompose the net climate feedback into clear-sky/cloud and longwave/shortwave components, i.e., clear-sky longwave feedback (λLWCS), clear-sky shortwave feedback (λSWCS), cloud longwave feedback (λLWCL), and cloud shortwave feedback (λSWCL). To separate contributions of longwave from atmospheric blocking and surface emitting, λLWCS is further decomposed into atmospheric longwave feedback (λLWA) and surface longwave feedback (λLWS), respectively.
Figure 4 shows geographical patterns of corresponding feedback components in CAMS-CSM and their global mean values. The net feedback λNet in CAMS-CSM is negative throughout nearly the globe, especially in the Indo-Pacific and subpolar regions (Fig. 4a). Large positive λSWCS, also called albedo feedback, is concentrated in the Arctic and Antarctic (Fig. 4b), reflecting the warming effect of sea ice melting (Chen et al., 2014). Loss of sea ice with response to global warming in the polar regions in turn increases the shortwave absorbed by the surface. The parameter λLWCS (–1.66 W m–2 K–1) is the most important negative feedback (Fig. 4d) contributing to λNet to keep climate system stable after such a strong external perturbation (e.g., quadrupled CO2). The pattern of λLWCS results from offsetting between two large but opposite feedbacks, i.e., negative λLWS and positive λLWA (Figs. 4f, h). The former is response of surface longwave emission following the Stefan–Boltzmann law, also known as Planck feedback. The latter is similar to the water vapor–lapse rate feedback, i.e., the net longwave effect of changes in water vapor and temperature profile. As the greenhouse effect of water vapor dominates, λLWA is positive throughout the world (Fig. 4h). Because the negative λLWS is generally stronger than positive λLWA, the net effect is negative in most regions (Fig. 4d). An exception in CAMS-CSM is the positive λLWCS in the equatorial western Pacific, which is dominated by λLWA, indicating a very strong greenhouse effect of water vapor in that region.

|
| Figure 4 Geographical distributions of (a) net climate feedback and (b–h) corresponding components (W m–2 K–1) in CAMS-CSM model. (g) Net cloud feedback is sum of (c) cloud longwave feedback and (e) cloud shortwave feedback. (h) Atmosphere longwave feedback is (d) clear-sky longwave feedback minus (f) surface longwave feedback. The patterns are derived from regressing (a–e) radiative responses at the TOA or (f) emitted longwave by surface onto global mean surface temperature change in abrupt4×CO2 experiment. Values at the top-right corner are global mean, which is definitely the same as those in Fig. 5. Dotted shadings denote areas exceeding the 95% confidence level. |
Clouds can both reflect solar radiation into space and block longwave from surface, despite the two sides varying with different microphysical features. Hence, the patterns of λLWCL and λSWCL look similar but opposite to each other in a large-scale perspective (Figs. 4c, e). However, net cloud feedback λCL in CAMS-CSM (Fig. 4g) is dominated by λSWCL (Fig. 4e), evidently negative in the equatorial western Pacific and Atlantic, Arctic, and subpolar regions of the Southern Ocean. In fact, the spatial distribution of λNet is determined by λCL with a global pattern correlation coefficient of 0.75.
As shown in Fig. 5, by comparing the feedback components of CAMS-CSM with the CMIP5 counterparts, we find that, except for λSWCL, the results of CAMS-CSM are close to the CMIP5 MME. However, much stronger negative λSWCL (–1.01 W m–2 K–1) in CAMS-CSM than that in the CMIP5 MME (–0.08 W m–2 K–1) leads to the exceptional net feedback as shown in Fig. 3c. The spatial differences of feedback components in CAMS-CSM from the CMIP5 MME are shown in Fig. 6. Consistent with Fig. 5, biases of λLWCS, λSWCS, and λLWCL are relatively small (Figs. 6b, d, f), in which λLWCS (0.16 W m–2 K–1) and λSWCS (–0.18 W m–2 K–1) largely cancel out (Figs. 6b, d). In contrast, negative bias of λSWCL (–0.93 W m–2 K–1) is prominent over the tropical Indo-Pacific (Fig. 6h) with a center in the equatorial western Pacific, overwhelming the small positive bias in λLWCL (0.16 W m–2 K–1) (Fig. 6f). Therefore, too strong negative λSWCL of CAMS-CSM explains its relatively low ECS. The next question is that physical process should be responsible for such a negative cloud shortwave feedback.
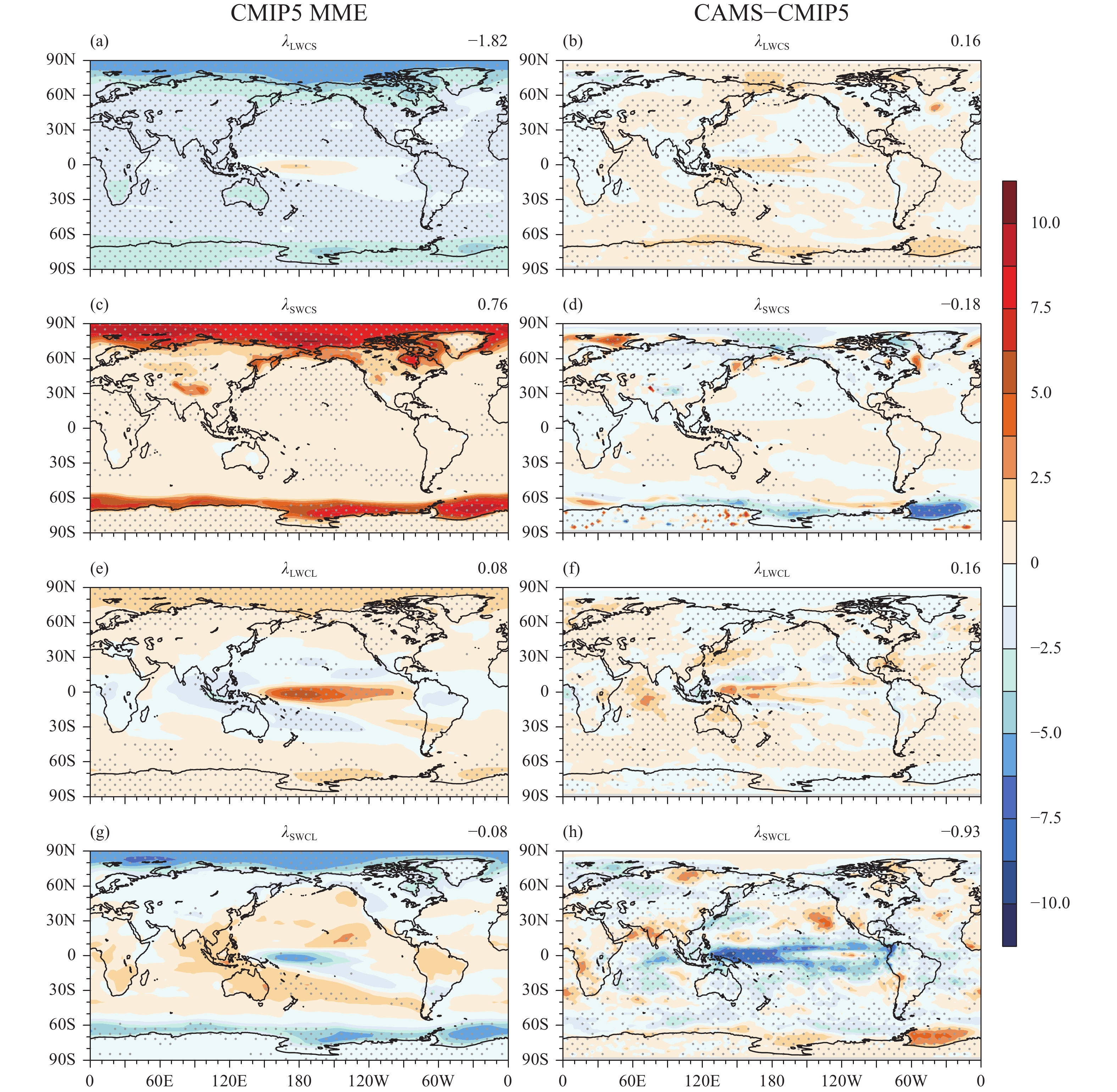
|
| Figure 6 Geographical distributions of feedback components (W m–2 K–1) in CMIP5 MME (left) and differences between CAMS-CSM and CMIP5 (right). (a, b) Clear-sky longwave feedback, (c, d) clear-sky shortwave feedback, (e, h) cloud longwave feedback, and (g, h) cloud shortwave feedback. Values at the top-right corner are global mean. Dotted shadings denote areas exceeding the 95% confidence level. |

|
| Figure 5 Comparison of net climate feedback λNet and its decompositions (λLWCS, λSWCS, λLWCL, λSWCL, λLWS, and λLWA; W m–2 K–1) between CAMS-CSM and CMIP5 models. |
Cloud shortwave feedback is related to changes in cloud optical depth, which are highly related to cloud amount (fractional coverage), liquid water content, and particle concentration number (Roeckner et al., 1987; Zelinka et al., 2012; Ceppi et al., 2016). If cloud fraction and liquid cloud water could increase with temperature, more solar radiation would be reflected back to space due to the increased cloud albedo, hence cooling the surface. As shown in Fig. 7, both the responses of cloud fraction and cloud liquid water path over the equatorial western Pacific and Intertropical Convergence Zone (ITCZ) in CAMS-CSM are evidently larger than those in the CMIP5 MME (Figs. 7e, f). In particular, the anomalous pattern of liquid cloud water response (Fig. 7f) is coincident with the negative bias in λSWCL in CAMS-CSM (Fig. 6h). The double-ITCZ-like anomalies in cloud responses are probably related to the evident double-ITCZ bias in CAMS-CSM (Rong et al., 2018).

|
| Figure 7 Geographical distributions of total cloud fraction (left; % K–1) and cloud water path (right; kg m –2 K–1) responses to 1-K global mean warming in abrupt4×CO2 experiment in (a, b) CAMS-CSM, (c, d) CMIP5 MME, and (e, f) their differences. Dotted shadings denote areas exceeding the 95% confidence level. |
The vertical profile of cloud fraction is shown to examine at which level the cloud response mainly contributes to the increasing cloud liquid water over the tropical Indo-Pacific domain (Figs. 8a, e). In the piControl simulation, clouds at nearly all levels in CAMS-CSM are less than those in the CMIP5 MME, especially few low clouds in the PBL (below 850 hPa; Fig. 8a). In contrast, forced by quadrupled CO2, low clouds below 700 hPa in CAMS-CSM extraordinarily increase with warming, whereas decreases are seen in the CMIP5 MME (Fig. 8e). Further, we find that response of low clouds between 925 and 700 hPa to global mean warming is correlated with λSWCL across the CMIP5 models (Fig. 9a). Their correlation coefficient is about –0.54, exceeding the 95% confidence level. Using this relation, 0.54 % K–1 of low clouds increasing in CAMS-CSM can explain –0.89 W m–2 K–1 of λSWCL that is nearly 90% of the total amount (–1.01 W m–2 K–1). Hence, the huge increase in low clouds over the tropical Indo-Pacific region in CAMS-CSM plays a critical role in its unusually negative λSWCL.

|
| Figure 8 Vertical profiles of cloud fraction (a, e; %), p-velocity (b, f; 10–3 Pa s–1), specific humidity (c, g; g kg–1), and relative humidity (d, h; %) over the tropical Indo-Pacific region (10°S–10°N, 70°E–90°W) in piControl simulation (top) and changes scaled by global mean surface warming in abrupt4×CO2 simulation (bottom). Dashed lines denote CAMS-CSM model and solid lines denote CMIP5 ensemble mean. Grey shadings denote ± 1σ across CMIP5 models. |
To understand so strong response of low clouds to warming in CAMS-CSM, the profiles of vertical motion (ω), specific humidity (q), and relative humidity (RH) over the tropical Indo-Pacific are analyzed. The increase of low clouds in CAMS-CSM well corresponds to dramatically enhanced vertical motion (Fig. 8f) and increased water vapor (Fig. 8g) at the same levels. Both the convection and moisture get much larger under warming than those in the CMIP5 MME while the mean states in piControl simulations are similar (Figs. 8b, c). The profile shape of ω response in CAMS-CSM (Fig. 8f) is similar to its climatology (Fig. 8b), which indicates enhanced convergence (divergence) in lower (upper) troposphere, whereas ω in the CMIP5 MME is intensified moderately at each level that means few changes in low-level convergence. Consequently, compared with the CMIP5 MME, more water vapor in CAMS-CSM is transported from the surface to lower troposphere by enhanced convergence, leading to dramatic increase in relative humidity below 500 hPa (Fig. 8h). In CAMS-CSM, the cloud is diagnosed on the basis of relative humidity introduced by Slingo (1987). In this scheme, cloud occurs where the relative humidity exceeds the prescribed threshold, which is 85% at the top of the PBL and even smaller over the PBL when penetrative convection happens. As prominent response of relative humidity in the lower troposphere in CAMS-CSM (larger than 2% K–1; Fig. 8h), it is not surprising that low-level cloud and cloud water can increase so rapidly (Figs. 7h, 8e). Furthermore, more liquid low cloud in the warmer climate, which is composed of many small droplets, leads to a stronger reflection of incoming solar flux, as well as a stronger negative λSWCL.
The uncertainty of λSWCL may be rooted in the spread of pre-industrial simulation. The CMIP5 models show a close relationship between their λSWCL and static stability in the PBL (temperature difference between 850 and 925 hPa) over the tropical Indo-Pacific (Fig. 9b), with a high correlation coefficient of 0.69. It indicates that stronger static stability in the tropical PBL nowadays may lead to more positive λSWCL under CO2 forcing in future, and vice versa. This relation can also explain λSWCL by –0.69 W m–2 K–1 in CAMS-CSM. It is reasonable that weak static stability is easier to trigger convection under a warmer world, so enhanced convergence in less stable PBL can be expected in the lower troposphere, as shown by CAMS-CSM (Fig. 8f). We find that correlation coefficient between the pre-industrial static stability and low-cloud response over the Indo-Pacific in abrupt4×CO2 experiment is about –0.56 across the CMIP5 models (figure omitted). The central Pacific PBL becomes even more unstable with warming in CAMS-CSM than that in the CMIP5 MME (Figs. 10a, b), which could contribute to the negative λSWCL that cannot be explained by the pre-industrial stability alone (Fig. 9b).

|
| Figure 10 Geographical distributions of responses to 1-K global mean warming in abrupt4×CO2 experiment in CMIP5 MME (left) and differences between CAMS-CSM and CMIP5 MME (right) for (a, b) temperature difference between 850 and 925 hPa (K K–1), (c, d) SST (K K–1), (e, f) latent heat (W m–2 K–1), and (g, h) relative humidity at 850 hPa (% K–1). Dotted shadings denote areas exceeding the 95% confidence level. |

|
| Figure 9 Intermodel relationships between shortwave cloud feedback λSWCL (W m–2 K–1) and (a) low-cloud fraction (925–700 hPa) response to global mean surface warming (% K–1) over the tropical Indo-Pacific region (10°S–10°N, 70°E–90°W) in abrupt4×CO2 simulation, (b) climatological boundary layer static stability (temperature difference between 850 and 925 hPa; K) in piControl simulation. Values at top-left corner are correlation coefficients. Corresponding results from CAMS-CSM (black circle) and least square fitting across only CMIP5 models (black line) are also shown. |
As another important condition for low-cloud formation, moisture increases so intensively in response to surface warming in CAMS-CSM (Fig. 8f), but why? The enhanced vertical moisture transport is part of the answer. But if there is no sufficient moisture supplied from the surface, strong convection will dry the lower troposphere by ventilating to higher level (Rieck et al., 2012). In CAMS-CSM, the tropical Pacific SSTs warm more than those in the CMIP5 MME in abrupt4×CO2 simulation (Figs. 10c, d). Corresponding to the SST anomalies, evaporations from the surface, shown by upward latent heat flux in Fig. 10f, also increase, keeping a highly humid PBL under warming in CAMS-CSM (Fig. 10h). The patterns of SST, evaporation, and relative humidity at 850 hPa in response to warming are quite similar in the tropical Pacific basin, indicating a close relation between the local surface warming and moisture supply to the lower troposphere.
Based on the above analysis, the warmer tropical SST and consequential enhanced evaporation in CAMS-CSM provide sufficient moisture to the PBL. Weak static stability in the PBL makes circulation convergence happen easily that enhances moisture transport upward to lower troposphere. These conditions promote more low-cloud formation, leading to intensified negative λSWCL and eventually the lower ECS.
5 Conclusions and discussionTo understand basic response features of the CAMS-CSM model under global warming, the climate sensitivity and climate feedbacks are analyzed based on benchmark sensitivity experiments under idealized CO2 forcing, and compared with CMIP5 multi-model results. By intercomparison across various models, we aim to shed light on understanding and constraining uncertainties in cloud feedback and climate sensitivity. Main conclusions are summarized as below.
(1) Based on Gregory-style regression, the estimated ECS and TCR of CAMS-CSM are 2.27 and 1.88 K, respectively. The ECS is near the lower bound of 5%–95% ranges across CMIP5 models due to an extraordinarily negative climate feedback (–1.85 W m–2 K–1), which is an outlier compared with the CMIP5 results. Nevertheless, the TCR is closer to the CMIP5 median because of an evidently low ocean heat uptake efficiency (0.32 W m–2 K–1), which partly compensates the negative feedback.
(2) By decomposing the net feedback into clear-sky/cloud, longwave/shortwave components, we find that the exceptional net feedback in CAMS-CSM results from an unusually negative cloud shortwave feedback (λSWCL). Except that, all the other feedback components in CAMS-CSM are close to the CMIP5 MME. In terms of geographical distribution, the negative biases of λSWCL in CAMS-CSM are mainly over the tropical Indo-Pacific Ocean.
(3) The low-cloud response between 925 and 700 hPa to surface warming can explain about 90% of λSWCL in CAMS-CSM. The dramatically warming in the tropical Pacific contributes to intensification of local evaporation and water vapor in the PBL. Weak static stability in the tropical PBL promotes circulation convergence, vertical moisture transport, growing in relative humidity and finally leading to increase of low cloud. Therefore, with tropics getting warmer and moistened, increased cloud liquid water over the climatological convective regions thickens cloud optical depth and amplifies cloud albedo, ultimately contributing to the unusually negative cloud shortwave feedback and the low ECS in CAMS-CSM.
The ECS is estimated based on the Gregory-style regression that relies on transient response under constant forcing. Hence, the OHU at transient state may also partly contribute to the ECS estimation although conceptually the ECS does not depend on the OHU. Despite of more cloud increasing in the tropical Pacific under warming (Fig. 7e), the SSTs is much warmer in CAMS-CSM compared with the CMIP5 MME (Fig. 10d), possibly resulting from the low OHU efficiency (Fig. 3d). It implies that the OHU may influence climate feedbacks (e.g., cloud feedback, water vapor feedback) and then the ECS by modulating regional SST responses.
Although the ECS in this study is assumed to be constant, it has been found to be increasing with warming (Meraner et al., 2013; Knutti et al., 2017). We estimated the ECS by changing length of data that starts with the first 20 years and gradually increases to 150 yr by appending the next 10 years. The obtained 14 ECS values range from 2.20 to 2.27 K, increasing with more data used (larger warming), consistent with the previous studies. However, the differences among these ECS can be negligible since the ratio of standard deviation to mean is just 1%. Moreover, using the total 150-yr data is reasonable as it contains cumulative effects of responses on different time scales.
This study provides a new insight in understanding the model spread in cloud shortwave feedback. Static stability in the tropical PBL and related low-cloud response can explain a large part of the uncertainty in cloud shortwave feedback, which is a potential constraint on the uncertainty in climate sensitivity. Less stable PBL tends to induce stronger convection under warming, in favor of low-cloud formation. The CAMS-CSM is an extreme example to clearly show how the mechanism works. The relatively low ECS in CAMS-CSM could affect long-term climate change simulation. For instance, the simulated 20th century global warming may be lower than the observation. The exaggerated low-cloud response in CAMS-CSM may also impact monsoon projection through changing the tropical energy budget and circulation. As shown in this study, the biases in response to warming could partly be traced back to the pre-industrial simulation. The pre-industrial PBL clouds are nearly missing in CAMS-CSM (Fig. 8a). For its extremely important role on large-scale circulation, this bias needs to be improved in the near future.
Acknowledgments . We acknowledge the climate modeling groups (listed in Table 1) for making their model outputs available (www.ipcc-data.org/sim/gcm_monthly/AR5/Reference-Archive.html), and the World Climate Research Program’s (WCRP’s) Working Group on Coupled Modeling (WGCM) for coordinating the CMIP5 project.
| Andrews, T., J. M. Gregory, M. J. Webb, et al., 2012: Forcing, feedbacks and climate sensitivity in CMIP5 coupled atmosphere–ocean climate models. Geophys. Res. Lett., 39, L09712. DOI:10.1029/2012GL051607 |
| Boucher, O., D. Randall, P. Artaxo, et al., 2013: Clouds and aerosols. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, T. F. Stocker, D. H. Qin, G. K. Plattner, et al., Eds., Cambridge University Press, Cambridge, United Kingdom and New York, USA, 1535 pp. |
| Bretherton, C. S., 2015: Insights into low-latitude cloud feedbacks from high-resolution models. Philos. Trans. Roy. Soc. A: Math., Phys. Eng. Sci., 373, 20140415. DOI:10.1098/rsta.2014.0415 |
| Ceppi, P., D. L. Hartmann, and M. J. Webb, 2016: Mechanisms of the negative shortwave cloud feedback in middle to high latitudes. J. Climate, 29, 139–157. DOI:10.1175/JCLI-D-15-0327.1 |
| Ceppi, P., F. Brient, M. D. Zelinka, et al., 2017: Cloud feedback mechanisms and their representation in global climate models. WIREs Climate Change, 8, e465. DOI:10.1002/wcc.465 |
| Charney, J. G., A. Arakawa, D. J. Baker, et al., 1979: Carbon Dioxide and Climate: A Scientific Assessment. Report of an Ad Hoc Study Group on Carbon Dioxide and Climate. National Academy of Sciences Press, Washington D.C., 22 pp, doi: 10.17226/12181. |
| Chen, X. L., T. J. Zhou, and Z. Guo, 2014: Climate sensitivities of two versions of FGOALS model to idealized radiative forcing. Sci. China Earth Sci., 57, 1363–1373. DOI:10.1007/s11430-013-4692-4 |
| Cox, P. M., C. Huntingford, and M. S. Williamson, 2018: Emergent constraint on equilibrium climate sensitivity from global temperature variability. Nature, 553, 319–322. DOI:10.1038/nature25450 |
| Dai, Y. J., X. B. Zeng, R. E. Dickinson, et al., 2003: The common land model. Bull. Amer. Meteor. Soc., 84, 1013–1024. DOI:10.1175/BAMS-84-8-1013 |
| Flato, G., J. Marotzke, B. Abiodun, et al., 2013: Evaluation of climate models. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, T. F. Stocker, D. H. Qin, G. K. Plattner, et al., Eds., Cambridge University Press, Cambridge, United Kingdom and New York, USA, 1535 pp. |
| Gregory, J., and M. Webb, 2008: Tropospheric adjustment induces a cloud component in CO2 forcing . J. Climate, 21, 58–71. DOI:10.1175/2007JCLI1834.1 |
| Gregory, J. M., R. J. Stouffer, S. C. B. Raper, et al., 2002: An observationally based estimate of the climate sensitivity. J. Climate, 15, 3117–3121. DOI:10.1175/1520-0442(2002)015<3117:AOBEOT>2.0.CO;2 |
| Gregory, J. M., W. J. Ingram, M. A. Palmer, et al., 2004: A new method for diagnosing radiative forcing and climate sensitivity. Geophys. Res. Lett., 31, L03205. DOI:10.1029/2003GL018747 |
| Hansen, J., A. Lacis, D. Rind, et al., 1984: Climate sensitivity: Analysis of feedback mechanisms. Climate Processes and Climate Sensitivity, J. E. Hansen, and T. Takahashi, Eds., American Geophysical Union, Washington D.C., 130–163. |
| Held, I. M., and B. J. Soden, 2000: Water vapor feedback and global warming. Annu. Rev. Energy Environ., 25, 441–475. DOI:10.1146/annurev.energy.25.1.441 |
| Knutti, R., M. A. A. Rugenstein, and G. C. Hegerl, 2017: Beyond equilibrium climate sensitivity. Nat. Geosci., 10, 727–736. DOI:10.1038/ngeo3017 |
| Li, C., J. S. Von Storch, and J. Marotzke, 2013: Deep-ocean heat uptake and equilibrium climate response. Climate Dyn., 40, 1071–1086. DOI:10.1007/s00382-012-1350-z |
| Li, J., H. M. Chen, X. Y. Rong, et al., 2018: How well can a climate model simulate an extreme precipitation event: A case study using the Transpose-AMIP experiment. J. Climate, 31, 6543–6556. DOI:10.1175/JCLI-D-17-0801.1 |
| Meraner, K., T. Mauritsen, and A. Voigt, 2013: Robust increase in equilibrium climate sensitivity under global warming. Geophys. Res. Lett., 40, 5944–5948. DOI:10.1002/2013GL058118 |
| Murray, R. J., 1996: Explicit generation of orthogonal grids for ocean models. J. Comput. Phys., 126, 251–273. DOI:10.1006/jcph.1996.0136 |
| Myhre, G., E. J. Highwood, K. P. Shine, et al., 1998: New estimates of radiative forcing due to well mixed greenhouse gases. Geophys. Res. Lett., 25, 2715–2718. DOI:10.1029/98GL01908 |
| Qu, X., A. Hall, S. A. Klein, et al., 2014: On the spread of changes in marine low cloud cover in climate model simulations of the 21st century. Climate Dyn., 42, 2603–2626. DOI:10.1007/s00382-013-1945-z |
| Randall, D. A., R. A. Wood, S. Bony, et al., 2007: Climate models and their evaluation. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, S. Solomon, D. H. Qin, M. Manning, et al., Eds., Cambridge University Press, Cambridge, United Kingdom and New York, USA, 996 pp. |
| Rieck, M., L. Nuijens, and B. Stevens, 2012: Marine boundary layer cloud feedbacks in a constant relative humidity atmosphere. J. Atmos. Sci., 69, 2538–2550. DOI:10.1175/JAS-D-11-0203.1 |
| Roe, G., 2009: Feedbacks, timescales, and seeing red. Annu. Rev. Earth Planet Sci., 37, 93–115. DOI:10.1146/annurev.earth.061008.134734 |
| Roeckner, E., U. Schlese, J. Biercamp, et al., 1987: Cloud optical depth feedbacks and climate modelling. Nature, 329, 138–140. DOI:10.1038/329138a0 |
| Roeckner, E., G. Bäuml, L. Bonaventura, et al., 2003: The Atmospheric General Circulation Model ECHAM5. Part I: Model Description. Report No. 349, Max Planck Institute for Meteorology, Hamburg, Germany, 127 pp. |
| Rong, X. Y., J. Li, H. M. Chen, et al., 2018: The CAMS Climate System Model and a basic evaluation of its climatology and climate variability simulation. J. Meteor. Res., 32, 839–861. DOI:10.1007/s13351-018-8058-x |
| Sherwood, S. C., S. Bony, and J. L. Dufresne, 2014: Spread in model climate sensitivity traced to atmospheric convective mixing. Nature, 505, 37–42. DOI:10.1038/nature12829 |
| Slingo, J. M., 1987: The development and verification of a cloud prediction scheme for the ECMWF model. Quart. J. Roy. Meteor. Soc., 113, 899–927. DOI:10.1002/qj.49711347710 |
| Soden, B. J., A. J. Broccoli, and R. S. Hemler, 2004: On the use of cloud forcing to estimate cloud feedback. J. Climate, 17, 3661–3665. DOI:10.1175/1520-0442(2004)017<3661:OTUOCF>2.0.CO;2 |
| Stephens, G. L., 2005: Cloud feedbacks in the climate system: A critical review. J. Climate, 18, 237–273. DOI:10.1175/JCLI-3243.1 |
| Stocker, T. F., D. H. Qin, G. K. Plattner, et al., 2013: Technical summary. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, T. F. Stocker, D. H. Qin, G. K. Plattner, et al., Eds., Cambridge University Press, Cambridge, United Kingdom and New York, USA, 1535 pp. |
| Taylor, K. E., R. J. Stouffer, and G. A. Meehl, 2012: An overview of CMIP5 and the experiment design. Bull. Amer. Meteor. Soc., 93, 485–498. DOI:10.1175/BAMS-D-11-00094.1 |
| Vial, J., J. L. Dufresne, and S. Bony, 2013: On the interpretation of inter-model spread in CMIP5 climate sensitivity estimates. Climate Dyn., 41, 3339–3362. DOI:10.1007/s00382-013-1725-9 |
| Winton, M., 2000: A reformulated three-layer sea ice model. J. Atmos. Oceanic Technol., 17, 525–531. DOI:10.1175/1520-0426(2000)017<0525:ARTLSI>2.0.CO;2 |
| Yu, R. C., 1994: A two-step shape-preserving advection scheme. Adv. Atmos. Sci., 11, 479–490. DOI:10.1007/BF02658169 |
| Zelinka, M. D., S. A. Klein, and D. L. Hartmann, 2012: Computing and partitioning cloud feedbacks using cloud property histograms. Part II: Attribution to changes in cloud amount, altitude, and optical depth. J. Climate, 25, 3736–3754. DOI:10.1175/JCLI-D-11-00249.1 |
| Zhang, H., G. Y. Shi, T. Nakajima, et al, 2006a: The effects of the choice of the k-interval number on radiative calculations . J. Quant. Spectros. Radiat. Trans., 98, 31–43. DOI:10.1016/j.jqsrt.2005.05.090 |
| Zhang, H., T. Suzuki, T. Nakajima, et al., 2006b: Effects of band division on radiative calculations. Opt. Eng., 45, 016002. DOI:10.1117/1.2160521 |
| Zhou, T. J., and X. L. Chen, 2015: Uncertainty in the 2°C warming threshold related to climate sensitivity and climate feedback. J. Meteor. Res., 29, 884–895. DOI:10.1007/s13351-015-5036-4 |
 2019, Vol. 33
2019, Vol. 33


