The Chinese Meteorological Society
Article Information
- TAO, Wei, Xuexing QIU, Ruijiao WU, et al., 2019.
- Role of Differences in Surface Diurnal–Nocturnal Thermodynamics over Complex Terrain in a Squall Line Process. 2019.
- J. Meteor. Res., 33(1): 1-17
- http://dx.doi.org/10.1007/s13351-019-8052-y
Article History
- Received April 8, 2018
- in final form September 24, 2018
Squall lines are strong convective systems that often cause disasters in China. A key difficulty in forecasting squall lines is the interaction between mesoscale convective systems (MCSs) and the surface conditions (Clark et al., 2004; Frame and Markowski, 2006; Wolters et al., 2010; Oberthaler and Markowski, 2013; Peters and Hohenegger, 2017). Specifically, the terrain in the Yangtze–Huaihe River region (YHR) is complex and includes the Dabie Mountain, the Wannan Mountains, the middle-to-lower reaches of the Yangtze River, and many lakes and rivers. Diurnal–nocturnal thermodynamic differences (DNTDs) are distinct among the various surface conditions, which affect atmospheric temperature and humidity triggering deep convection, and thus the DNTDs complicate the squall line processes in this region (Tawfik and Dirmeyer, 2014; Peters and Hohenegger, 2017). Therefore, further study of the impact of surface DNTDs is important for improved forecasting of squall lines.
The development mechanism for squall lines has been studied from various aspects. In the initial stage, the high Convective Available Potential Energy (CAPE) (Parker and Johnson, 2000; Weckwerth, 2000), low Level of Free Convection (LFC) (Parker and Johnson, 2004), and less stability (Takemi, 2007) may lead to intense scattered deep convection, which then results in precipitation dri-ven downdrafts and formation of cold pools. Afterwards, the cold pools merge and the convective cells organize into MCSs such as squall lines (Chen and Wang, 2012). Alfaro and Khairoutdinov (2015) suggested that the CAPE attained by both low and mid troposphere determined the morphology of the squall lines. As they mature, some squall lines develop bowing structures with rear inflow and embedded bookend vortices (Weisman, 1993; Wheatley and Trapp, 2008). Meng et al. (2012) investigated a squall line in southern China and revealed that the rear inflow and bookend vortices could reinforce each other. Alfaro (2017) proposed the layer-lifting model of convection (LLMC), which illustrates that the more strongly sheared environment leads to greater inflow of unstable air as a fraction of the total storm-relative inflow, thus producing more latent heating. Such a process primarily determines deep convection. Most of the afore-mentioned studies investigated squall lines that were free of external influences such as topography. However, terrain forcing cannot be neglected in the case of some squall lines.
Surface conditions are important for the triggering and growth of severe convective systems. For example, the blocking and uplifting effects of mountains help to form boundary-layer convergence zones (Weckwerth et al., 2014; Zhang et al., 2016), where heavy precipitation usually occurs (Rudari et al., 2004; Barthlott and Kirshbaum, 2013; Sever and Lin, 2017). Frame and Markowski (2006) documented a discretely propagating squall line as it passed an idealized mountain ridge, and found that wind gusts were likely to arise on the lee side and at the top of the high ridge. According to an idealized model by Sun and Ogura (1979), a surface temperature gradient could trigger instability and initiate convection. Peters and Hohenegger (2017) applied the unified ICOsahedral Nonhydrostatic modeling system (ICON) in an idealized setting to reveal that a higher surface temperature results in an earlier secondary convection initial time, which suggests a more rapid preconditioning of the atmosphe-ric column toward the occurrence of deep convection. Schlemmer and Hohengger (2014) pointed out that low-level moist patches promote wider clouds and prolong the peak time of precipitation. Some squall line sensitivity tests found that soil moisture gradients can have profound influences on the propagation of the precipitation associated with West African squall lines (Clark et al., 2004; Wolters et al., 2010). In eastern China, researchers have shown that surface sensible heat flux could enhance low-level turbulent mixing, while the surface latent heat flux could increase moisture levels in the boundary layer and establish favorable atmospheric conditions for convection (Cai and Pan, 2010; Shen et al., 2016).
In addition, the above thermodynamic conditions for daytime and nighttime are distinct, and the resultant convection varies with time and region. Research has shown that squall lines are more likely to cross the Appalachian Mountains in the US during the day because of higher instability and lower convective inhibition induced by so-lar radiation (Letkewicz and Parker, 2010). However, squall lines in the Great Plains of the US are active at night because of the nocturnal jet supporting the squall line organization and longevity (French and Parker, 2010). Meng et al. (2013) studied the diurnal variation of squall lines in China and found that those squall lines on the north side of the Yangtze River peaked in the early afternoon, showing the peak period to be distinct from their counterparts in southern China and the US Great Plains, where the peak periods usually happen in early morning and late evening (Parker and Johnson, 2000; Jirak et al., 2003).
However, the underlying mechanisms for the differences between diurnal and nocturnal squall lines remain unclear, especially for cases where the squall lines encounter complex terrain. In this simulation study, a squall line that occurred at night over the YHR (a region with mountains, plains, and lakes, as shown in Fig. 1b) was forced to pass the same region in the afternoon through a sensitivity test. Comparison of the actual scenario and the test reveals how the surface thermodynamic diurnal variation impacts on the development of the squall line. The squall line investigated in this study occurred on 30 July 2014 and caused wind gusts as strong as 19.2 m s–1 and heavy rainfall with a maximum precipitation rate of 56.6 mm h–1. Chen et al. (2016) improved the simulation of this squall line by assimilating surface observations and radar data through a four-dimensional variational Doppler radar analysis system. We will further quantify how disasters in this region change (e.g., the intensities and locations of wind gusts and precipitation) due to the DNTDs of the mountain and water surfaces and explore the underlying physical mechanisms.
2 Design of modeling experimentsTo simulate the squall line and conduct the sensitivity experiment, the Weather Research and Forecasting (WRF) model Version 3.8 (Skamarock et al., 2008; NCAR, 2016) was used. The initial and boundary conditions were driven by the NCEP Final Operational Global Analysis data (NCEP-FNL) with a grid spacing of 1° × 1° at 6 h intervals. The model top was at 50 hPa, and we used 35 vertical levels with spacings of 100–2000 m from the lowest to the highest layer. Specifically, there were 10 levels within the boundary layer (from the surface to 850 hPa).The three nested domains (d01, d02, and d03) with two-way nesting schemes are shown inFig. 1. The horizontal grid spacing was 27, 9, and 3 km for d01, d02, and d03, respectively. We focused on domain d03, which covers the YHR and has incorporated Chaohu Lake and the Dabie and Wannan Mountains.
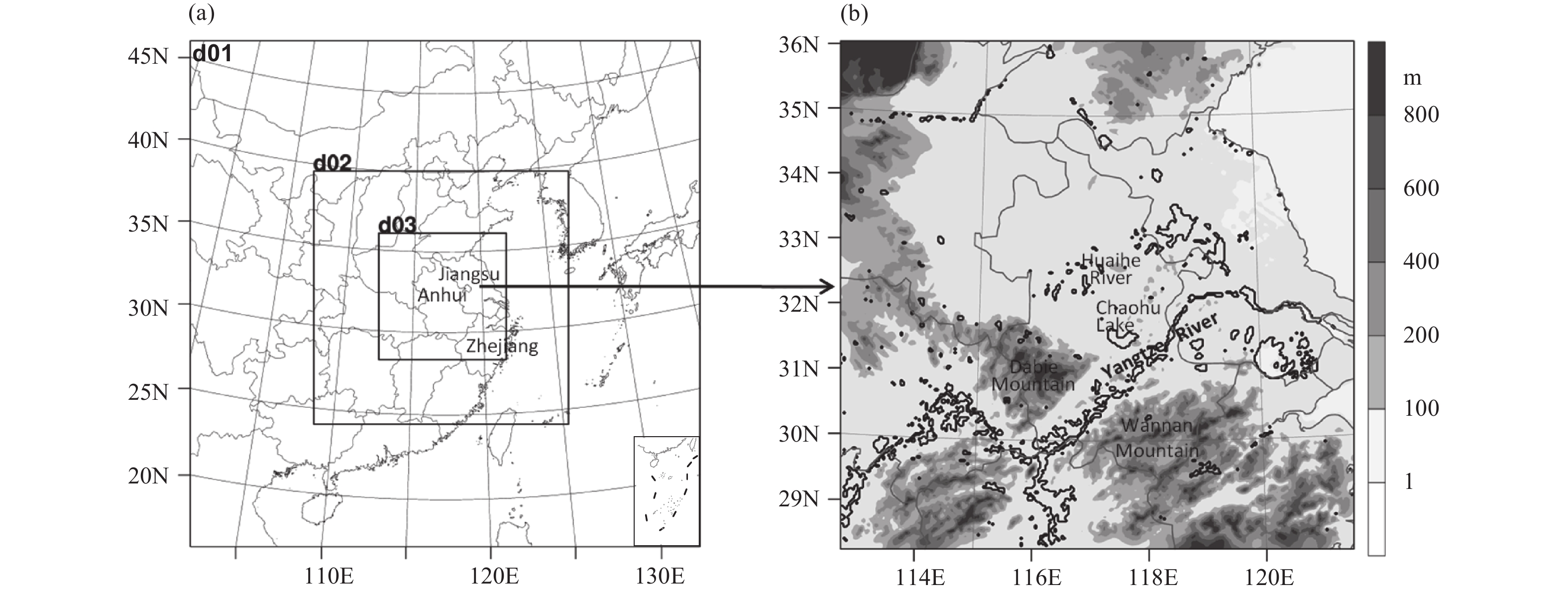
|
| Figure 1 (a) The three WRF domains (denoted by d01, d02, and d03) used in this study. (b) Terrain height of d03 (thick black lines indicate lakes and rivers). |
One of the fundamental limitations for simulation of severe convective systems is the inaccuracy of the initial state (Schenkman et al., 2011). Suffering from coarse temporal (6 h) and spatial (1 degree) resolutions, the glo-bal model NCEP-FNL is unable to probe the variation of hydrometeors and the airflow structure inside mesoscale systems (Kalnay et al., 1996; NCEP et al., 2000). Therefore, the model was initialized by using ensemble Kalman filter (EnKF) analysis (Zhang et al., 2006; Meng and Zhang, 2008a, b) that assimilated the radar radial velocity, Global Positioning System (GPS) water vapor, 2-m temperature, humidity, and 10-m wind from the China national standard surface stations. The radars, located in Hefei and Nanjing (as shown by the black stars in Fig. 4), have a detection radius of 230 km and a resolution of 3 km. The locations of 18 GPS stations and 381 national surface stations are shown in Fig. S1 (see online supplemental material). Based on previous modeling studies (Qiu and Zhang, 2016), EnKF was employed in this work. The EnKF system had 32 members and the initial ensemble perturbations were derived from the NCEP background error covariance (CV3), which estimated the differences of 24- and 48-h GFS forecasts over a period of 1 yr through using the National Meteorological Center (NMC) method (Parrish and Derber, 1992; Barker et al., 2004). The ensemble system was initialized at 0000 UTC 30 July and the cycled EnKF assimilation was performed once an hour during 0600–1200 UTC 30 July. The EnKF analysis at 1200 UTC was regarded as the initial and boundary conditions for the 6-h single deterministic WRF forecast that was used to simulate the squall line in this study.
Furthermore, atmospheric profiles play an important role in the initiation and persistence of convection, and knowledge of the true state of the humidity profiles is particularly important for accurately simulating mesoscale weather systems (Takemi, 2007; Zheng et al., 2013). One flexible method is to adjust the vertical distribution factors of water vapor according to the observation data. Therefore, radar observation was used to optimize the initial humidity conditions. Similar to Hu et al. (2006) whose simulation assumed that the atmosphere over the precipitation area should follow the principle of wet-adiabatic expansion, the relative humidity in this study was set as saturated in those regions where the composite radar reflectivity exceeded 30 dBZ.
The WRF physics included the WSM6 microphysics (Hong et al., 2004), CAM longwave and shortwave radiation (Collins et al., 2004), YSU PBL scheme (Noh et al., 2003), Monin–Obukhov surface layer scheme (Janjić, 1994), and the Noah land surface model (Chen and Dudhia, 2001). In addition, the Kain–Fritsch cumulus parameterization (Kain, 2004) was employed in the two coarser domains (d01 and d02), but was turned off in d03.
To investigate the impact of the surface DNTDs on the squall line development, experiments that comprised one control experiment named CTRL and a sensitivity experiment named SW (shortwave radiation) were conducted. CTRL was the deterministic WRF hindcast for the squall line during 1200–1800 UTC 30 July 2014 [i.e., from 2000 local time (LT) 30 July to 0200 LT 31 July]. SW was set up with the same model configuration and initial and boundary conditions as CTRL, but the simulation period was changed to 0300–0900 UTC (i.e., 1100–1700 LT) on 30 July, when the surface experienced the maximum solar radiation. SW differed from CTRL in terms of the downward shortwave radiation from the model top, which was in the range of 1000–1100 W m–2 in SW and was absent in CTRL (Fig. 2).

|
| Figure 2 Mean downward solar radiation on the model top during the simulation period in (a) CTRL and (b) SW. |
The squall line was observed in the evening of 30 July 2014 and was influenced by several synoptic systems. As shown in Fig. 3, a 500-hPa trough extended from northern China to the Huaihe river area at 1400 UTC 30 July and contributed to the development of convection over the YHR through upper-level positive vorticity advection. Meanwhile, tropical storm Nakri was situated to the east of the South China Sea, and the easterly wind on its northern boundary not only transported warm air to the YHR, but also provided an eastward vertical wind shear favorable for updraft development (Weisman et al., 1988). The subtropical high, which is defined by the 588-dgpm isoline, was cut off by the upper-level trough and Nakri. The descending air to the north of the subtropical high ridge generated a warm dry region near the east coast of China around 30°N. In addition, a southwest air stream could be identified over southern China at 850 hPa, and this also resulted in the advection of warm and moist air. As shown by the satellite infrared image in Fig. 3, a baroclinic leaf extended along the east side of the upper-level trough to the north of the Yangtze River. A mass of convective clouds was situated to the south of this baroclinic leaf, which is indicative of the squall line system discussed in this study.
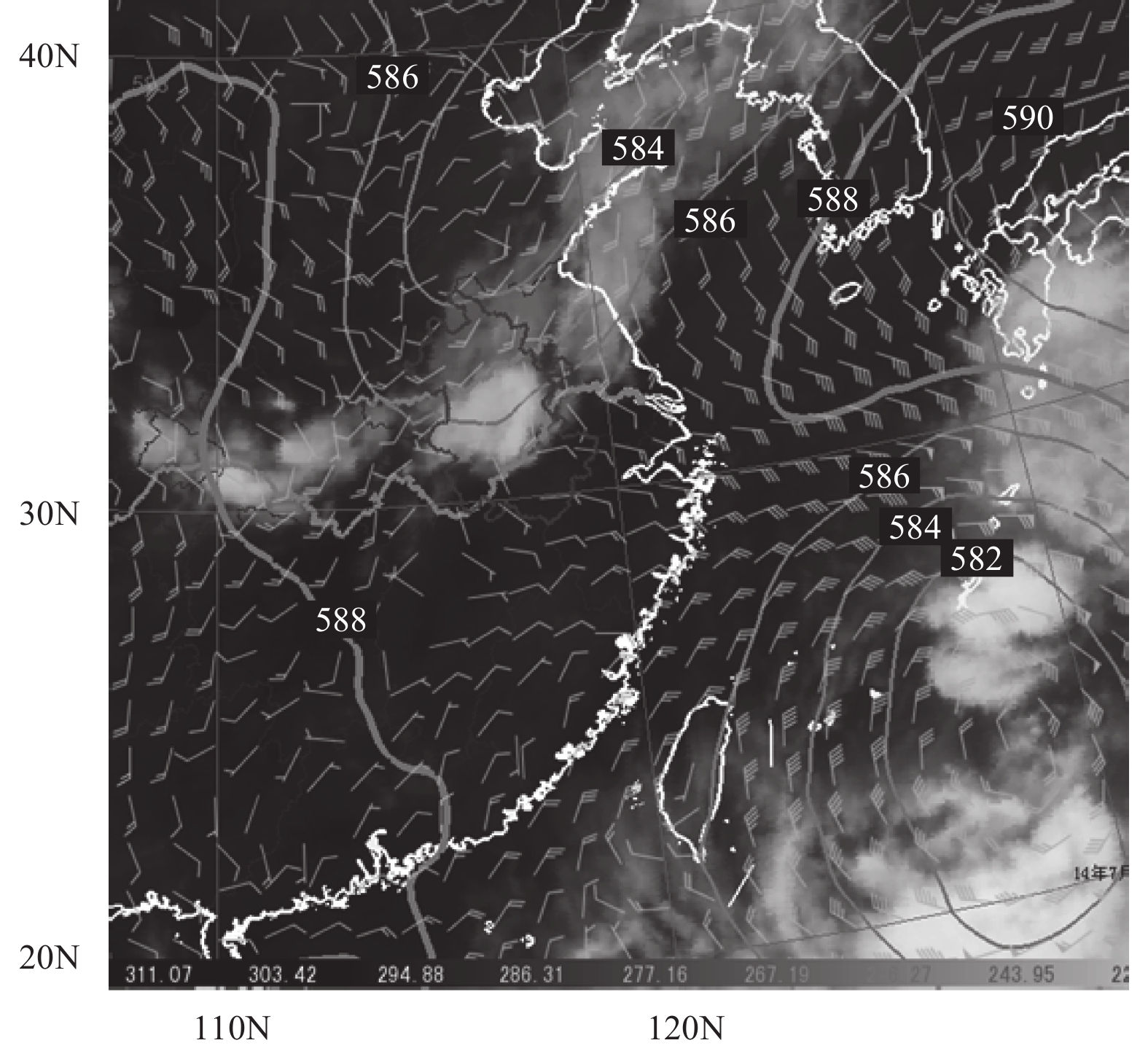
|
| Figure 3 Infrared imagery from FY-2E at 1500 UTC (filled color), superposed by 500-hPa geopotential height (contours) and 850-hPa wind field (wind barbs) at 1400 UTC 30 July 2014. |
The squall line evolution is depicted by the WRF simulated radar reflectivity (Fig. 4), the precipitation (Fig. 5), and the gale (Fig. 6). The simulated radar reflectivity was verified against the composite radar reflectivity based on two operational radars located in Hefei and Nanjing, respectively (locations are indicated by the black stars in Figs. 4a–c). The precipitation and gale were compared with the observed hourly rainfall and maximum wind from 975 automatic weather stations. At 1300 UTC, both the simulation and observation showed three northeast–southwest-oriented quasi-linear MCSs, accompanied by a rainbelt around 31°–33°N and 115°–117°N (marked as A, B, and C inFigs. 4a, d; 5a, d). The precipitation rate was 1–20 mm h–1 at most stations during 1200–1300 UTC, while 8 stations in belt C experienced short-term heavy rainfall, with the precipitation rate exceeding 30 mm h–1. Meanwhile, a gale of 8–14 m s–1 could be identified in the MCSs region in both observation and simulation, although the simulated wind speed was about 2 m s–1 weaker (Figs. 6a, d). As the whole system approached Chaohu Lake at 1500 UTC, MCSs A and B dissipated while MCS C generated a new bow-shaped squall line east of Chaohu Lake (Fig. 4b). The squall line was roughly 300 km long with a maximum reflectivity greater than 55 dBZ. This squall line was the one focused on herein; it was also evident at a similar location in the CTRL simulation, although in this case the stratiform region west of Chaohu Lake was weaker (Figs. 4b, e). The squall line generated a rainbelt to the north of Chaohu Lake, with a maximum hourly rainfall of around 40 mm h–1 (Figs. 5b, e). Meanwhile, a gale of 10–14 m s–1 occurred between Chaohu Lake and the Yangtze River in the actual observation and in CTRL (Figs. 6b, e). Two hours later, the CTRL simulated squall line moved to the eastern boundary of Anhui Province, producing precipitation of 10–30 mm h–1 and a gale of 8–14 m s–1, which agreed with the observations (Figs. 4c, f; 5c, f; 6c, f). Afterwards, the squall line began to decay. Because the CTRL simulation generally reproduced the intensity, scale, and location of the observed squall line, and the associated rainfall and gales, the model can be used with confidence in the following sensitivity experiment.

|
| Figure 5 Observed accumulated precipitation at (a) 2100–2200 and (b) 2300–2400 LT 30 July, and (c) 0000–0100 LT 31 July; (d–f) are as (a–c), but from the CTRL simulation. The slant-line regions and thick black lines are the same as inFig. 4. |

|
| Figure 6 Observed maximum wind speed at (a) 2100–2200 and (b) 2300–2400 LT 30 July, and (c) 0000–0100 LT 31 July; (d–f) are as (a–c), but from the CTRL simulation. The slant-line regions and thick black lines are the same as in Fig. 4. |
To show the differences in squall line performance between day and night, the SW sensitivity experiment was conducted. In CTRL the simulated squall line matured at night as in the actual scenario, whereas in SW the squall line was forced to occur at daytime during 1100–1700 LT on 30 July. To explore how the near-surface DNTDs impact on the development of the squall line, the modeling results from CTRL and SW were compared.
3.2.1 Accumulated precipitation and strong windsWe selected accumulated precipitation and gales to highlight the differences between CTRL and SW. Although both experiments exhibit a meridional rainbelt in the middle–eastern region of Anhui Province, in SW the precipitation region extends farther south to the Wannan Mountains. During the 2–6-h forecast period, the CTRL maximum accumulated precipitation exceeds 70 mm on the northern side of the Yangtze River, whereas in SW the heavy precipitation occurs on both sides of the Yangtze River (Figs. 7a, b). Along with precipitation, strong winds are constrained to the north of the Yangtze River in CTRL, with a maximum wind speed of around 14 m s–1. In SW, strong wind gusts spread more widely in the YHR, and the maximum wind speed exceeds 17 m s–1, especially between the Yangtze River and the Wannan Mountains, while in the case of CTRL, gusts in this region are absent (Figs. 7c, d).
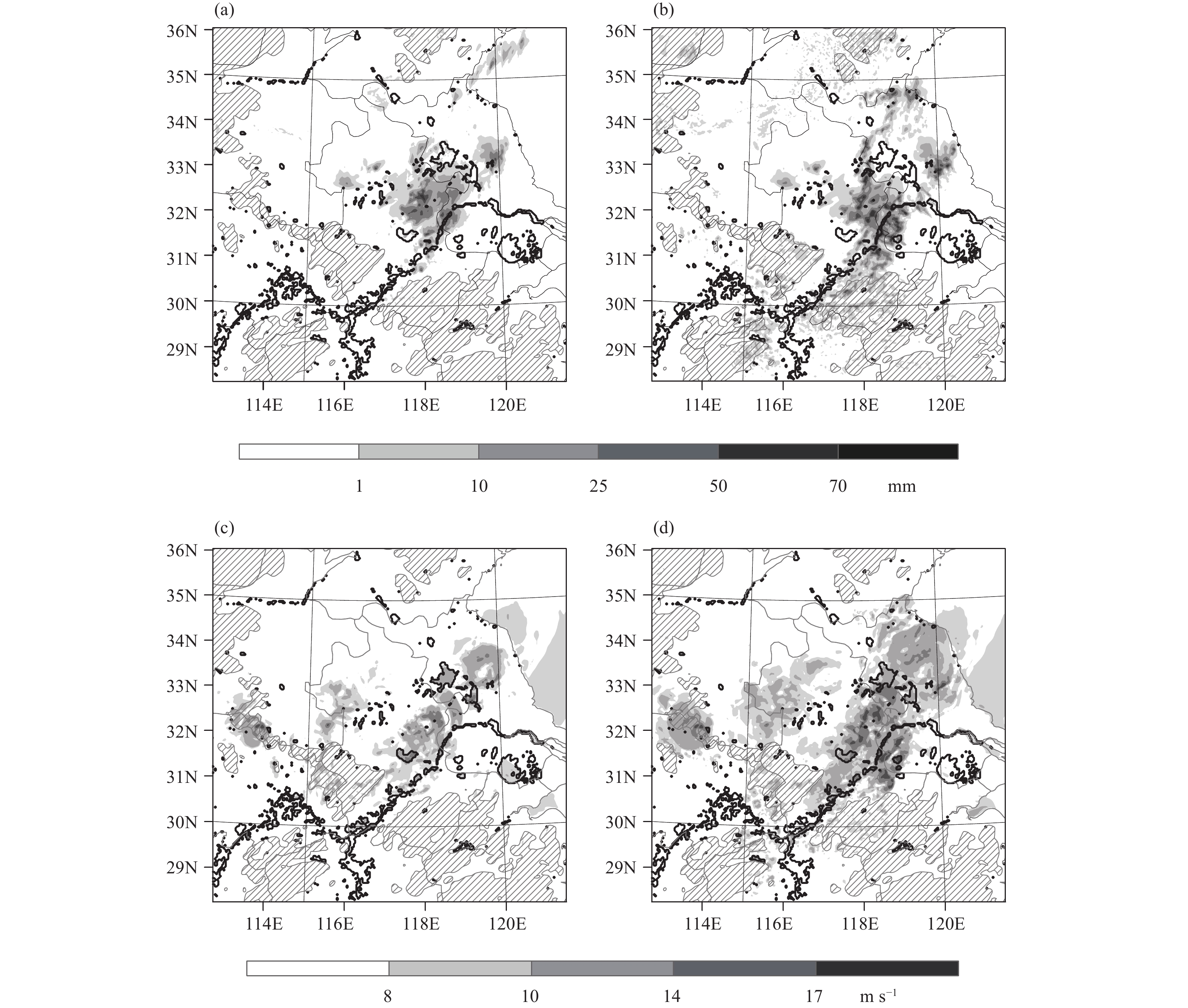
|
| Figure 7 (a, b) Accumulated rainfall and (c, d) maximum wind speed during 2–6-h forecast period for (a, c) CTRL and (b, d) SW. The slant-line regions and thick black lines are the same as inFig. 4. |
On the whole, compared with the nighttime scenario in CTRL, the intense precipitation and wind gusts tend to expand southward if the squall line matures during the day. The underlying mechanism for this is discussed in Section 3.2.2.
3.2.2 Thermodynamics associated with CTRL and SWGiven that the difference in external forcing between CTRL and SW lies in the shortwave radiation whose effects are most prominent near the surface, we first analyzed the surface heat flux. In CTRL, the surface sensible heat flux is between −30 and 10 W m–2, indicating that the heat flux is moderate at night (Fig. 8a). During the day, the land surface under a clear sky warms up rapidly, but water surface and regions blocked by convective clouds remain cold (Figs. 8b, 4e). Such radiative effects are similar to “anvil shading” as studied by Oberthaler and Markowski (2013). Therefore, in SW, the sensible heat flux exceeds 100 W m–2 over most of the land surface but is less than 10 W m–2 over water surfaces and for those regions under convective clouds. The distinctive surface heating effect during the day sets favorable baroclinic conditions for squall line development. In CTRL, the latent heat flux is weak and can be identified only over water surfaces and under precipitation systems, indicating that evaporation is moderate during the night (Fig. 8c). In SW, the magnitude of the latent heat flux in lakes and precipitation regions is the same as that in CTRL, but it exceeds 450 W m–2 over the land surface because the higher temperature induces stronger evaporation there (Fig. 8d). Clark et al. (2004) proposed that the rainfall of the squall lines in semi-arid regions is very sensitive to the surface heat and moisture fluxes. In the present study, the warm moist region ahead of the cold pool contributes to a lower LFC that further strengthens convective systems during the day.

|
| Figure 8 Surface (a, b) sensible and (c, d) latent heat fluxes at 3-h forecast time in (a, c) CTRL and (b, d) SW. |

|
| Figure 4 Observed radar reflectivity at (a) 2100 and (b) 2300 LT 30 July, and (c) 0100 LT 31 July; (d–f) are as (a–c) but from the CTRL simulation. The black stars represent the location of radars: the west one is Hefei and the east one is Nanjing. The regions covered with slant lines represent the terrain height of 200 m, and thick black lines represent rivers and lakes. |
A comparison of the thermal and humidity conditions for CTRL and SW is presented in Fig. 9, where 850 and 975 hPa were chosen to represent the lower-troposphere levels and the near-surface, respectively. Although the CTRL and SW have similar distributions of potential temperature at 850 hPa (Figs. 9a, e, i, m), SW shows a distinct thermal gradient along the Yangtze at 975 hPa. In the 3-h forecast, SW is generally warmer, especially between the Yangtze and the Wannan Mountains (30.5°–31.5°N, 118°–120°E) where the SW potential temperature is around 308 K, 2–4 K higher than that in CTRL. The CTRL and SW temperatures are of the same magnitude (approximately 302 K) in the cold pool around Chaohu Lake, which is determined by the evaporatively driven downdrafts originating from the mid troposphere (Takemi, 2007; Schlemmer and Hohenegger, 2014; Alfaro and Khairoutdinov, 2015; Peters and Hohenegger, 2017). Therefore, the SW squall line exhibits a much stronger temperature gradient along the Yangtze River (Figs. 9b, f). Two hours later, the SW cold pool expands to the Yangtze around 119°E, with the minimum potential temperature decreasing to 298 K. Meanwhile, the environment under the clear sky is especially warm to the east of 119°E, the potential temperature difference between the two sides of the squall line reaches 8 K in SW but it is less than 4 K in CTRL (Figs. 9j, n). Such a warm surface also indicates a high lapse rate, which may contribute to a strengthening of the cold pool and gales (Takemi, 2007; Alfaro and Khairoutdinov, 2015). The squall line humidity structure is presented by the water vapor mixing ratio (the two right-hand most columns in Fig. 9). Both CTRL and SW show dry air masses northwest of Chaohu Lake and east of 120°E; these areas are associated with the intrusion of cold dry air in the upper-level trough and the downdraft in the subtropical high, respectively. The environment is very humid along the Yangtze and its southern side, where the mixing ratio is slightly higher in SW compared to CTRL (Figs. 9d, h). On the whole, the near-surface is sensitive to solar radiation, which enhances the buoyancy of layer-lifting convection, thermal gradient, and moisture along and to the south of the Yangtze River. According to Benjamin’s theory (1968), the squall line is a kind of density current, the confrontation of the cold dry and warm humid environments strengthens the cold pool, and thus benefits the intensification of the squall line in a southern direction.

|
| Figure 9 CTRL simulated (a, b) potential temperature and (c, d) water vapor mixing ratio on (a, c) 850 and (b, d) 975 hPa at 3-h forecast time; (e–h) as (a–d) but for SW; (i–l) as (a–d) but at 5-h forecast time; (m–p) as (i–l) but for SW. |
We applied the “Heated Condensation Framework” (HCF; Tawfik and Dirmeyer, 2014) to quantify the favorable atmospheric condition for the deep convection initiation. The framework defines two variables: buoyant condensation level (BCL) and the surface potential temperature deficit (θdef) to reach saturation at BCL. The BCL in CTRL and SW are around the same altitude (1.5–1.8 km at 3-h forecast time and 2.2–2.6 km at 5-h forecast time, as shown inTable 1), indicating that their mid-level thermal and humidity conditions are similar (Fig. 9). The value of θdef is 1–2 K in SW and 9–10 K in CTRL, and the difference is even larger in the southern region (Table 1). A large θdef indicates that much more boundary layer heating and moistening are required for CTRL to promote convection. In contrast, convection is more likely to be triggered in the southern part of SW, and thus the squall line shows discrete propagation in a southerly direction (Peters and Hohenegger, 2017).
The squall line thermodynamics were further quantified by calculating the intensity and height of the cold pool and the vertical wind shear (Table 1). Benjamin (1968) defined the moving velocity of the density current as:
| $c_{}^2 = \frac{{2gH\left({{\rho _{\rm h}} - {\rho _{\rm l}}} \right)}}{{{\rho _{\rm l}}}},$ | (1) |
where ρh and ρl are the density of the heavier and lighter air, respectively; H is the height of the density current. However, air density cannot be output directly from the numerical model. Therefore, similar to Meng et al. (2012), Eq. (1) is transformed to:
| ${c^2} = - \int_{z = 0}^{z = H} {[({\theta_{\rm t}} - {\theta_{\rm s}}) /{\theta _{\rm s}} - {q_{\rm ct}}]}{\rm d}z,$ | (2) |
where c is also considered as the cold pool intensity;
| ${\rm Fr} = \frac{c}{{\sqrt {\left({g'H} \right)} }} = \frac{c}{{\sqrt {\left({\dfrac{{\theta _{\rm v}'}}{{{\theta _{\rm s}}}}gH} \right)} }}.$ | (3) |
In addition, we also calculated the maximum vertical wind shear
In the 3-h forecast fields, the 850-hPa virtual potential temperature and wind fields are similar in CTRL and SW, showing a cold trough in northern Anhui (Figs. 10a, d). At 975 hPa, the cold pool temperatures of CTRL and SW are of the same magnitude, but the SW virtual potential temperature ahead of the squall line is 3–6 K higher than that in CTRL, meaning that the SW squall line has a larger temperature gradient and more unstable air (Figs. 10b, e). To explore the thermodynamic structure in detail, two vertical cross- sections were selected at lines AB and CD in Figs. 10c, f. The two lines represent the northern and southern parts of the squall line, respectively. Along AB, the robust temperature gradient extends from the surface to 700 hPa (Figs. 11a, c), indicating that the cold pool depth (H) is around 3 km in the northern part of the squall line (Table 1). It is shallower in the southern part, being 2.4 km in SW and 1.8 km in CTRL. The larger Fr also reflects a shallower density current depth and a weaker thermal contrast in the south, especially for CTRL. Comparison between SW and CTRL reveals that the pre-squall line region below 800 hPa is notably warmer in the day time (Figs. 11a–d), and thus the SW cold pool intensity is about 5 m s–1 higher in the northern part and 13 m s–1 higher in the southern part than CTRL. Such a strong and deep cold pool generates robust Downward Convective Available Potential Energy (DCAPE), which would enhance wind gusts. Accompanying this, the warm section ahead of the squall line exhibits a high CAPE and favors stronger updrafts and heavier precipitation (Tawkif and Dirmeyer, 2014; Peters and Hohenegger, 2017). The evaporative cooling and the precipitation drag force also intensify the cold pool and the downdraft (Figs. 11a–d), which in turn favors convective cloud development (Schlemmer and Hohenegger, 2014). Meanwhile, the vertical wind shear and
| Forecast | CTRL | SW | |||||
| hour (h) | North | South | North | South | |||
| BCL (km) | 3 | 1.8 | 1.7 | 1.6 | 1.5 | ||
| 5 | 2.5 | 2.6 | 2.2 | 2.2 | |||
| θdef (K) | 3 | 10.05 | 9.55 | 1.60 | 0.73 | ||
| 5 | 12.72 | 13.55 | 2.64 | 2.13 | |||
| c (m s–1) | 3 | 43.3 | 23.6 | 48.5 | 36.6 | ||
| 5 | 2.8 | N/A | 42.6 | 37.2 | |||
| H (km) | 3 | 2.8 | 1.8 | 3.3 | 2.4 | ||
| 5 | 0.3 | N/A | 3.2 | 3.2 | |||
| Fr | 3 | 1.06 | 1.33 | 1.01 | 1.14 | ||
| 5 | 0.96 | N/A | 1.02 | 1.01 | |||
| Δumax (m s–1) | 3 | 17.2 | 12.8 | 17.7 | 12.9 | ||
| 5 | 3.5 | N/A | 17.3 | 16.6 | |||
| c/Δumax | 3 | 2.5 | 1.8 | 2.8 | 2.7 | ||
| 5 | 0.8 | N/A | 2.4 | 2.2 | |||
In the 5-h forecast fields, the squall line and the associated near-surface temperature gradient in CTRL are moderate and constrained to the north of the Yangtze, whereas the radar reflectivity and cold pool in SW are stronger and broader, expanding southeastward and governing the Yangtze River (Figs. 10g–l; 11e–h). The cold pool intensity decays to 2.8 m s–1 with its height around 0.3 km in the northern part of the squall line in CTRL, and it almost disappears in the southern part. Consequently, the vertical motion and associated heavy precipitation decay in CTRL (Fig. 11f). By contrast, the cold pool is still strong in both the northern and southern parts of the squall line in SW, with an intensity of around 40 m s–1 and a height of 3.2 km. The Froude number is close to 1, indicating that the squall line maintains critical density current flow and deep lifting occurs at the boundary between the cold pool and warm air. As a result, convective precipitation in SW is robust in both the northern and southern cross-sections and extends to the south of the Yangtze (Figs. 10i, l). The precipitation also intensifies the cold pool and the downward motion. When the strong downdrafts touch the surface, the resultant divergence pushes the gust front as far as 40 km from the convection center (Figs. 11g, h). The above analysis illustrates that the squall line, especially its southern part, tends to decay in the 5-h forecast at night, but its strength could be maintained and it even extends southward during the day, because of the strong cold pool and vertical wind shear. The enhanced surface heat flux induced by solar radiation plays a key role as shown by the strongest difference of θdef between SW and CTRL.

|
| Figure 11 Vertical cross-sections along lines (a, c, e, g) AB and (b, d, f, h) CD in Fig. 10c of virtual potential temperature (color shaded), potential temperature (black solid contours), total mixing ratio of all condensation (black dashed contours), and wind (arrows) along the cross-section at (a–d) 3- and (e–h) 5-h forecast times from (a, b, e, f) CTRL and (c, d, g, h) SW. |

|
| Figure 10 CTRL simulated (a, b) virtual potential temperature (color shaded) at 850 and 975 hPa; (c) radar reflectivity at 3-h forecast time; (d–f) as (a–c) but for SW; (g–i) as (a–c) but at 5-h forecast time; (j–l) as (g–i) but for SW. In (c, f, i, l), AB and CD are two dashed cross-section lines. Along each line, letter T denotes a small box area (in gray; zoom in to see; containing 7 × 7 model points on a 3-km resolution) used for calculation of Eqs. (2) and (3). So does letter S. The outmost rectangular with solid purple lines is referred to as the purple box in Fig. 12. |
Accompanied by the cold pool and downdrafts, the SW near-surface meso-high and divergence also shift southward, with its center at around 31°30′N (Figs. 12a, c). Under the influence of the strong divergence and pressure-gradient force around the meso-high, the southward outflow can reach the Wannan Mountains. Meanwhile, the mountain slope is warmed up faster by the so-lar radiation than the valley region, thereby a low-pres-sure perturbation is created around the mountain tops, which drives a valley breeze (Fig. 12d). During the day, this upslope wind and valley breeze promote convection on the windward slope (Fig. 12d), allowing the squall line to elongate to as far as the Wannan Mountains. By contrast, in CTRL, the meso-high is located around 32°30′N and the associated outflow is too far away from the mountainous terrain to interact with it (Figs. 12a, b). The down slope wind induced by the mountain breeze during the night also suppresses convection in the Wannan Mountains. As a result, the squall line is restricted to the north side of the Yangtze River at night.

|
| Figure 12 CTRL simulated (a) sea level pressure (color shaded) and 10-m wind (wind barbs) in the purple box of Fig. 10i at 5-h forecast time; (b) vertical cross-section along the thick blue line in (a) for pressure perturbation (color shaded) and wind (vectors) along the cross-section. Panels (c, d) are as (a, b) but for SW. |
A squall line, which occurred on 30 July 2014 in the YHR and was initialized by an EnKF analysis, has been simulated with the WRF model. To investigate the impact of surface DNTDs on the development of the squall line, we conducted sensitivity experiments by forcing the squall line to pass the YHR in daytime and nighttime, respectively. To sum up, a conceptual model is given to illustrate the different squall line evolutions during the diurnal and nocturnal times (Fig. 13).

|
| Figure 13 Conceptual models of squall line development during (left) day and (right) night. The sun and moon indicate day and night, respectively; clouds denote convective cells; brown lines denote gust fronts; and black arrows denote horizontal winds and vertical motions. Green–blue areas represent cold regions (green region warmer than blue region). Yellow–red areas represent warm regions (red region warmer than yellow region), and purple areas under the clouds are the cold pools (the darker, the colder). |
During the daytime, the southeastern region ahead of the squall line is warmed up rapidly by solar radiation under the clear sky near the subtropical high (red region in Fig. 13). Meanwhile, the western and northern regions of the squall line and the water surface are cold, with their temperatures being of similar magnitudes to those at night. The former region is cooled by the cloud associated with the upper-level trough (Fig. 3), and the latter could be explained by its thermal attribution, which warms up slowly. Accordingly, the temperature gradient in the southern part during the day is considerably larger than that at night. By applying HCF, it is possible to quantify the precondition of the squall line, which reveals that such high low-level baroclinity and surface fluxes prompt a more rapid conditioning towards deep convection. In turn, the evaporative cooling of the heavier precipitation enhances the cold pool, which also extends southward and further intensifies the convection (as shown by the higher convective cloud in Fig. 13). The southward outflow from the cold pool could couple with the valley breeze of the Wannan Mountains that is induced by the warmer mountain tops. The upslope wind generates new convection cells on the northern slopes of the Wannan Mountains, and therefore, the squall line and resultant heavy precipitation and wind gusts are able to intensify in a southward direction.
During the nighttime, the areas to the south of the Yangtze River are colder than during the daytime, whereby a weaker low-level temperature gradient results in weaker convection, a cold pool, and divergence in the south. In addition, the Wannan Mountains are governed by downslope winds. Finally, the southern part of the convection is suppressed, and the squall line exists mainly to the north of the Yangtze. The distinct squall line performance during the day and night further confirms the idealized study of Peters and Hohenegger (2017), which shows that the diurnal evolution of the surface condition provides sufficient forcing to advance the occurrence of convection initiation.
Squall lines in the US and southern China tend to arise early in the morning and late in the evening, whereas they peak in the afternoon in the YHR (Meng et al., 2013). The conceptual model presented here may shed some new light on the underlying mechanisms. Similar to the present case, a large proportion of the squall lines in the YHR occur ahead of the upper-level long wave trough and to the west of the subtropical high. Coupled with strong solar radiation, such a scenario could amp-lify the temperature gradient between the warm land surface and the cold water surfaces in Chaohu Lake and the Yangtze River region as well as the valley breeze around the Wannan Mountains. Such low-level baroclinity benefits convection with precipitation and condensation occuring with the upward flow. As the rain falls, evaporation produces the cold pool and the downburst enhances the gale, thereby the squall line tends to show a southward extension. Comprehensive investigation of additional cases is advocated to gain a systematic understanding of squall line DNTDs in the YHR.
Acknowledgments. We wish to thank Editor Huqiang Zhang and the two anonymous reviewers for their very careful reviews and constructive comments, which have greatly improved both content and presentation of this paper. Wei Tao thanks Dingling Zhong for her assistance with Fig. 13.
| Alfaro, D. A., 2017: Low-tropospheric shear in the structure of squall lines: Impacts on latent heating under layer-lifting ascent. J. Atmos. Sci., 74, 229–248. DOI:10.1175/JAS-D-16-0168.1 |
| Alfaro, D. A., and M. Khairoutdinov, 2015: Thermodynamic constraints on the morphology of simulated midlatitude squall lines. J. Atmos. Sci., 72, 3116–3137. DOI:10.1175/JAS-D-14-0295.1 |
| Barker, D. M., W. Huang, Y. R. Guo, et al., 2004: A three-dimensional variational data assimilation system for MM5: Implementation and initial results. Mon. Wea. Rev., 132, 897–914. DOI:10.1175/1520-0493(2004)132<0897:ATVDAS>2.0.CO;2 |
| Barthlott, C., and D. J. Kirshbaum, 2013: Sensitivity of deep convection to terrain forcing over Mediterranean islands. Quart. J. Roy. Meteor. Soc., 139, 1762–1779. DOI:10.1002/qj.2089 |
| Benjamin, T. B., 1968: Gravity currents and related phenomena. J. Fluid Mech., 31, 209–248. DOI:10.1017/S0022112068000133 |
| Cai, F., and Y. N. Pan, 2010: A numerical simulation study of surface flux impacts on the development of a squall line. J. Trop. Meteor., 26, 105–110. DOI:10.3969/j.issn.1004-4965.2010.01.016 |
| Chen, F., and J. Dudhia, 2001: Coupling an advanced land surface-hydrology model with the Penn State–NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Wea. Rev., 129, 569–585. DOI:10.1175/1520-0493(2001)129<0569:CAALSH>2.0.CO;2 |
| Chen, M. X., and Y. C. Wang, 2012: Numerical simulation study of interactional effects of the low-level vertical wind shear with the cold pool on a squall line evolution in North China. Acta Meteor. Sinica, 70, 371–386. DOI:10.11676/qxxb2012.033 |
| Chen, X. C., K. Zhao, J. Z. Sun, et al., 2016: Assimilating surface observations in a four-dimensional variational Doppler radar data assimilation system to improve the analysis and forecast of a squall line case. Adv. Atmos. Sci., 33, 1106–1119. DOI:10.1007/s00376-016-5290-0 |
| Clark, D. B., C. M. Taylor, and A. J. Thorpe, 2004: Feedback between the land surface and rainfall at convective length scales. J. Hydrometeor., 5, 625–639. DOI:10.1175/1525-7541(2004)005<0625:FBTLSA>2.0.CO;2 |
| Collins, W. D., P. J. Rasch, B. A. Boville, et al., 2004: Description of the NCAR Community Atmosphere Model (CAM 3.0). NCAR Technical Note NCAR/TN-464+STR. Boulder, 1–214, doi: 10.5065/D63N21CH. |
| Frame, J., and P. Markowski, 2006: The interaction of simulated squall lines with idealized mountain ridges. Mon. Wea. Rev., 134, 1919–1941. DOI:10.1175/MWR3157.1 |
| French, A. J., and M. D. Parker, 2010: The response of simulated nocturnal convective systems to a developing low-level jet. J. Atmos. Sci., 67, 3384–3408. DOI:10.1175/2010JAS3329.1 |
| Hong, S. Y., J. Dudhia, and S. H. Chen, 2004: A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Wea. Rev., 132, 103–120. DOI:10.1175/1520-0493(2004)132<0103:ARATIM>2.0.CO;2 |
| Hu, M., M. Xue, and K. Brewster, 2006: 3DVAR and cloud analysis with WSR-88D Level-II data for the prediction of the Fort Worth, Texas, tornadic thunderstorms. Part I: Cloud analysis and its impact. Mon. Wea. Rev., 134, 675–698. DOI:10.1175/MWR3092.1 |
| Janjić, Z. I., 1994: The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon. Wea. Rev., 122, 927–945. DOI:10.1175/1520-0493(1994)122<0927:TSMECM>2.0.CO;2 |
| Jirak, I. L., W. R. Cotton, and R. L. McAnelly, 2003: Satellite and radar survey of mesoscale convective system development. Mon. Wea. Rev., 131, 2428–2449. DOI:10.1175/1520-0493(2003)131<2428:SARSOM>2.0.CO;2 |
| Kain, J. S., 2004: The Kain-Fritsch convective parameterization: An update. J. Appl. Meteor., 43, 170–181. DOI:10.1175/1520-0450(2004)043<0170:TKCPAU>2.0.CO;2 |
| Kalnay, E., M. Kanamitsu, R. Kistler, et al., 1996: The NCEP/NCAR 40-year reanalysis project. Bull. Amer. Meteor. Soc., 77, 437–472. DOI:10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2 |
| Letkewicz, C. E., and M. D. Parker, 2010: Forecasting the maintenance of mesoscale convective systems crossing the Appalachian Mountains. Wea. Forecasting, 25, 1179–1195. DOI:10.1175/2010WAF2222379.1 |
| Meng, Z. Y., and F. Q. Zhang, 2008a: Tests of an ensemble Kalman filter for mesoscale and regional-scale data assimilation. Part III: Comparison with 3DVAR in a real-data case study. Mon. Wea. Rev., 136, 522–540. DOI:10.1175/2007MWR2106.1 |
| Meng, Z. Y., and F. Q. Zhang, 2008b: Tests of an ensemble Kalman filter for mesoscale and regional-scale data assimilation. Part IV: Comparison with 3DVAR in a month-long experiment. Mon. Wea. Rev., 136, 3671–3682. DOI:10.1175/2008MWR2270.1 |
| Meng, Z. Y., F. Q. Zhang, P. Markowski, et al., 2012: A modeling study on the development of a bowing structure and associated rear inflow within a squall line over south China. J. Atmos. Sci., 69, 1182–1207. DOI:10.1175/JAS-D-11-0121.1 |
| Meng, Z. Y., D. C. Yan, and Y. J. Zhang, 2013: General features of squall lines in East China. Mon. Wea. Rev., 141, 1629–1647. DOI:10.1175/MWR-D-12-00208.1 |
| Moncrieff, M. W., and C. H. Liu, 1999: Convection initiation by density currents: Role of convergence, shear, and dynamical organization. Mon. Wea. Rev., 127, 2455–2464. DOI:10.1175/1520-0493(1999)127<2455:CIBDCR>2.0.CO;2 |
| National Centers for Environmental Prediction (NCEP), National Weather Service (NWS), NOAA, et al., 2000: NCEP FNL Operational Model Global Tropospheric Analyses, Continuing from July 1999. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. Available online at 10.5065/D6M043C6. Accessed on 25 June 2017. |
| NCAR, 2016: User’s Guide for the Advanced Research WRF (ARW) Modeling System Version 3.8. National Center for Atmospheric Research, 434 pp. Available online at www2.mmm.ucar.edu/wrf/users/docs/user_guide_V3.8/contents.html. |
| Noh, Y., W. G. Cheon, S. Y. Hong, et al., 2003: Improvement of the K-profile model for the planetary boundary layer based on large eddy simulation data. Bound-Layer Meteor., 107, 401–427. DOI:10.1023/A:1022146015946 |
| Oberthaler, A. J., and P. M. Markowski, 2013: A numerical simulation study of the effects of anvil shading on quasi-linear convective systems. J. Atmos. Sci., 70, 767–793. DOI:10.1175/JAS-D-12-0123.1 |
| Parker, M. D., and R. H. Johnson, 2000: Organizational modes of midlatitude mesoscale convective systems. Mon. Wea. Rev., 128, 3413–3436. DOI:10.1175/1520-0493(2001)129<3413:OMOMMC>2.0.CO;2 |
| Parker, M. D., and R. H. Johnson, 2004: Simulated convective lines with leading precipitation. Part I: Governing dynamics. J. Atmos. Sci., 61, 1637–1655. DOI:10.1175/1520-0469(2004)061<1637:SCLWLP>2.0.CO;2 |
| Parrish, D. F., and J. C. Derber, 1992: The National Meteorologi-cal Center’s spectral statistical-interpolation analysis system. Mon. Wea. Rev., 120, 1747–1763. DOI:10.1175/1520-0493(1992)120<1747:TNMCSS>2.0.CO;2 |
| Peters, K., and C. Hohenegger, 2017: On the dependence of squall-line characteristics on surface conditions. J. Atmos. Sci., 74, 2211–2228. DOI:10.1175/JAS-D-16-0290.1 |
| Qiu, X. X., and F. Q. Zhang, 2016: Prediction and predictability of a catastrophic local extreme precipitation event through cloud-resolving ensemble analysis and forecasting with Doppler radar observations. Sci. China Earth Sci., 59, 518–532. DOI:10.1007/s11430-015-5224-1 |
| Rotunno, R., J. B. Klemp, and M. L. Weisman, 1988: A theory for strong, long-lived squall lines. J. Atmos. Sci., 45, 463–485. DOI:10.1175/1520-0469(1988)045<0463:ATFSLL>2.0.CO;2 |
| Rudari, R., D. Entekhabi, and G. Roth, 2004: Terrain and multiple-scale interactions as factors in generating extreme precipitation events. J. Hydrometeor., 5, 390–404. DOI:10.1175/1525-7541(2004)005<0390:TAMIAF>2.0.CO;2 |
| Schenkman, A. D., M. Xue, A. Shapiro, et al., 2011: The analysis and prediction of the 8–9 May 2007 Oklahoma tornadic mesoscale convective system by assimilating WSR-88D and CASA radar data using 3DVAR. Mon. Wea. Rev., 139, 224–246. DOI:10.1175/2010MWR3336.1 |
| Schlemmer, L., and C. Hohenegger, 2014: The formation of wider and deeper clouds as a result of cold-pool dynamics. J. Atmos. Sci., 71, 2842–2858. DOI:10.1175/JAS-D-13-0170.1 |
| Sever, G., and Y.-L. Lin, 2017: Dynamical and physical processes associated with orographic precipitation in a conditionally unstable uniform flow: Variation in basic wind speed. J. Atmos. Sci., 74, 449–466. DOI:10.1175/JAS-D-16-0077.1 |
| Shen, X. Y., S. J. Yue, J. Liu, et al., 2016: Effects of latent heating and surface heat fluxes on a squall line process. J. Meteor. Sci., 36, 709–720. DOI:10.3969/2016jms.0013 |
| Skamarock, W. C., J. B. Klemp, J. Dudhia, et al., 2008: A Description of the Advanced Research WRF Version 3. NCAR Technical Note NCAR/TN-475+STR. Boulder, 1–113, doi: 10.5065/D68S4MVH. |
| Sun, W. Y., and Y. Ogura, 1979: Boundary-layer forcing as a possible trigger to a squall-line formation. J. Atmos. Sci., 36, 235–254. DOI:10.1175/1520-0469(1979)036<0235:BLFAAP>2.0.CO;2 |
| Takemi, T., 2007: Environmental stability control of the intensity of squall lines under low-level shear conditions. J. Geophys. Res. Atmos., 112. DOI:10.1029/2007JD008793 |
| Tawfik, A. B., and P. A. Dirmeyer, 2014: A process-based framework for quantifying the atmospheric preconditioning of surface-triggered convection. Geophys. Res. Lett., 41, 173–178. DOI:10.1002/2013GL057984 |
| Weckwerth, T. M., 2000: The effect of small-scale moisture variability on thunderstorm initiation. Mon. Wea. Rev., 128, 4017–4030. DOI:10.1175/1520-0493(2000)129<4017:TEOSSM>2.0.CO;2 |
| Weckwerth, T. M., L. J. Bennett, L. J. Miller, et al., 2014: An observational and modeling study of the processes leading to deep, moist convection in complex terrain. Mon. Wea. Rev., 142, 2687–2708. DOI:10.1175/MWR-D-13-00216.1 |
| Weisman, M. L., 1993: The genesis of severe, long-lived bow echoes. J. Atmos. Sci., 50, 645–670. DOI:10.1175/1520-0469(1993)050<0645:TGOSLL>2.0.CO;2 |
| Weisman, M. L., J. B. Klemp, and R. Rotunno, 1988: Structure and evolution of numerically simulated squall lines. J. Atmos. Sci., 45, 1990–2013. DOI:10.1175/1520-0469(1988)045<1990:SAEONS>2.0.CO;2 |
| Wheatley, D. M., and R. J. Trapp, 2008: The effect of mesoscale heterogeneity on the genesis and structure of mesovortices within quasi-linear convective systems. Mon. Wea. Rev., 136, 4220–4241. DOI:10.1175/2008MWR2294.1 |
| Wolters, D., C. C. van Heerwaarden, J. V.-G. de Arellano, et al., 2010: Effects of soil moisture gradients on the path and the intensity of a West African squall line. Quart. J. Roy. Meteor. Soc., 136, 2162–2175. DOI:10.1002/qj.712 |
| Zhang, F. Q., Z. Y. Meng, and A. Aksoy, 2006: Tests of an ensemble Kalman filter for mesoscale and regional-scale data assimilation. Part I: Perfect model experiments. Mon. Wea. Rev., 134, 722–736. DOI:10.1175/MWR3101.1 |
| Zhang, Y., Z. Y. Meng, P. J. Zhu, et al., 2016: Mesoscale modeling study of severe convection over complex terrain. Adv. Atmos. Sci., 33, 1259–1270. DOI:10.1007/s00376-016-5221-0 |
| Zheng, L. L., J. H. Sun, X. L. Zhang, et al., 2013: Organizational modes of mesoscale convective systems over central East China. Wea. Forecasting, 28, 1081–1098. DOI:10.1175/WAF-D-12-00088.1 |
 2019, Vol. 33
2019, Vol. 33


