The Chinese Meteorological Society
Article Information
- LI, Dongdong, Yongli HE, Jianping HUANG, et al., 2018.
- Multiple Equilibria in a Land–Atmosphere Coupled System. 2018.
- J. Meteor. Res., 32(6): 950-973
- http://dx.doi.org/10.1007/s13351-018-8012-y
Article History
- Received January 22, 2018
- in final form July 26, 2018
There are two distinct patterns of large-scale atmospheric circulation over middle–high latitudes, namely, high-index flow, which has strong zonal westerlies and relatively weak wave perturbations, and low-index flow, which has relatively weak westerlies with large wave amplitudes and usually evolves into blocking (Rossby, 1939; Namias, 1950; Thompson and Wallace, 2001; Li and Wang, 2003; Faranda et al., 2016). Charney and DeVore (1979, hereafter CD) proposed the multiple flow equilibria theory to explain the two distinct flow patterns. They used a low-order (also called “highly truncated”) spectral barotropic channel model and found that multiple equilibrium states may exist in the presence of topographic and thermal forcings. Among the multiple equilibrium states, two equilibrium states of distinct characters, termed high- and low-index flow, were stable. Charney and Straus (1980, hereafter CS) extended CD’s study to a two-layer baroclinic model to investigate the instabilities that produce and feed on multiple equilibrium states. They suggested that topographic instability is merely a triggering mechanism to generate multiple equilibria, and the energy for maintenance of the wave-like equilibria comes from the conversion of mean flow potential energy.
Charney’s pioneering study prompted a great deal of research interest in the low-order spectral model and multiple flow equilibria theory. Zhu and Zhu (1982) and Zhu (1985) used a two-layer low-order spectral model and found that there were some stable equilibrium states with typical characteristics of actual blocking. They emphasized that the zonally asymmetric thermal and topographic forcings and the nonlinearity of flow were the main factors in blocking dynamics.Reinhold and Pierrehumbert (1982, 1985, hereafter RP) extended the model of CS to include synoptic-scale waves and found two distinct weather regime states. They suggested that the wave–wave interactions could transfer the model flow from one regime-equilibrium to another. Legras and Ghil (1985) used a higher-order barotropic spectral spherical model and they reported that the model may exhibit properties of an index cycle. Because Charney’s model was deterministic system, stochastic forcing was added to the model and then the model flow also showed transitions between high- and low-index states (Egger, 1981; Benzi et al., 1984; Sura, 2002). In addition, by using low-order spectral models, some studies explored the physical mechanism of abrupt change in flow patterns over midlatitudes and subtropical region (Li and Luo, 1983; Liu and Tao, 1983; Miao and Ding, 1985; Luo, 1987). Li and Chou (1996, 1997) proved that the joint action of nonlinearity, dissipation, and external forcing was the source of the atmospheric multiple equilibria. Some recent studies used Charney’s multiple flow equilibria theory to demonstrate the roles of the high- and low-index flow patterns in the interdecadal variation of the continental temperature (He et al., 2014, 2018; Huang et al., 2016, 2017a, b ). Similar models and studies have been discussed in many other papers (Tung and Rosenthal, 1985; Cai and Mak, 1987; Cehelsky and Tung, 1987; Christensen and Wiin-Nielsen, 1996; Koo and Ghil, 2002; Crommelin et al., 2004; etc.) and in some review articles (De Swart, 1988; Li and Chou, 2003).
Although many studies have followed Charney’s work, a shortcoming of the classic Charney’s model is that the “thermal forcing” (i.e., the radiative equilibrium temperature field in CS and the direct forcing of the flow wave field in CD) is always artificially specified. Therefore, the feedback from the atmospheric flow to the “thermal forcing” is absent, in other words, the atmospheric flow in Charney’s model cannot change the thermal distribution, but rather, can only be adapted to the “thermal forcing”. To some extent, the effects of “thermal forcing” on large-scale atmospheric motions in Charney’s model may be unrealistic. To overcome this shortcoming, a new model coupling the flow and temperature fields should be developed. The coupled model should include some essential physical processes, for instance, the horizontally inhomogeneous temperature fields give rise to the atmospheric motions, and in turn, the atmospheric motions change the distribution of temperature. Then to compensate for the energy dissipation due to the friction, the external energy input should be the uneven solar heating, which is zonally symmetric and decreases from low to high latitudes. This simple coupled model is established in this paper. We find that there are still multiple equilibria with distinct wave amplitude (i.e., the high- and low-index flow) when the topography is present. Interestingly, the lower layer streamfunction of some stable equilibria is either in phase or out of phase with the topography, i.e., their lower layer ridges or troughs are over the mountains, we call them ridge- or trough-type equilibria. The multiple wave phase equilibria associated with ridge- and trough-types are more prominent than the multiple wave amplitude equilibria associated with high- and low-index types in our coupled model. Besides, the multiple wave phase equilibria are more remarkable in the coupled model than in the uncoupled model. However, compared to multiple wave amplitude equilibria, there have been few studies of multiple wave phase equilibria.
In this study, the multiple wave phase equilibria associated with ridge- and trough-types and the multiple wave amplitude equilibria associated with high- and low-index types are both investigated based on a low-order coupled land–atmosphere model. The paper is organized as follows. The low-order coupled land–atmosphere model is described in Section 2. Our model is similar to the low-order coupled ocean–atmosphere model of Vannitsem et al. (2015). The greatest difference between the two models is that the underlying surface is the land with ideal sinusoidal topography in our model. In Section 3, we present the multiple equilibrium solutions and their stabilities. In Section 4, we explore the role of the land–atmosphere coupling in the existence and properties of equilibrium states. In Section 5, we investigate the ridge- and trough-type equilibria and wave phase. In Section 6, we investigate the high- and low-index equilibria and wave amplitude. The discussion and conclusions are presented in Section 7.
2 ModelSimilar to CS, the atmospheric model is a two-layer quasi-geostrophic flow confined to a periodic
| $\frac{\partial }{{\partial t}}({\nabla ^2}{\psi ^1}) + J({\psi ^1}, {\nabla ^2}{\psi ^1}) + \beta \frac{{\partial {\psi ^1}}}{{\partial x}} = - {k'_d}{\nabla ^2}({\psi ^1} - {\psi ^3}) + \frac{{{f_0}}}{{\Delta p}}\omega, $ | (1) |
| $\begin{split} & \frac{\partial }{{\partial t}}({\nabla ^2}{\psi ^3}) + J\left({\psi ^3}, {\nabla ^2}{\psi ^3} + {f_0}\frac{h}{H}\right) + \beta \frac{{\partial {\psi ^3}}}{{\partial x}} \\ &\quad \quad = {k'_d}{\nabla ^2}({\psi ^1} - {\psi ^3}) - \frac{{{f_0}}}{{\Delta p}}\omega - {k_d}{\nabla ^2}{\psi ^3}, \quad\quad\quad\quad\quad\quad \end{split}$ | (2) |
where
We define
| $\psi = ({\psi ^1} + {\psi ^3})/2,\quad \theta = ({\psi ^1} - {\psi ^3})/2, $ | (3) |
then the atmospheric motion equations become the following:
| $\begin{split} \!\!\! \frac{\partial }{{\partial t}}({\nabla ^2}\psi) & \!+\! J(\psi, {\nabla ^2}\psi) \!+\! J(\theta, {\nabla ^2}\theta) \!+\! \beta \frac{{\partial \psi }}{{\partial x}}\!=\! - 0.5\, J\left(\psi, {f_0}\frac{h}{H}\right)\\ & \!+\! 0.5\, J\left(\theta, {f_0}\frac{h}{H}\right) - 0.5\, {k_d}{\nabla ^2}(\psi - \theta),\end{split}$ | (4) |
| $\begin{split} \frac{\partial }{{\partial t}}({\nabla ^2}\theta) & + J(\psi, {\nabla ^2}\theta) + J(\theta, {\nabla ^2}\psi) + \beta \frac{{\partial \theta }}{{\partial x}}= 0.5\, J\left(\psi, {f_0}\frac{h}{H}\right)\\ & - 0.5\, J\left(\theta, {f_0}\frac{h}{H}\right) + 0.5\, {k_d}{\nabla ^2}(\psi - \theta) - 2\, {{k\,'}_{\!\!\!\!\!d}}{\nabla ^2}\theta + \frac{{{f_0}}}{{\Delta p}}\omega .\end{split} $ | (5) |
In the equation of temperature of the baroclinic atmosphere, a radiative and heat flux scheme is incorporated reflecting the exchanges in energy among the land, atmosphere, and space (Barsugli et al., 1998; Vannitsem et al., 2015; De Cruz et al., 2016):
| $\begin{split}{\gamma _{\rm{a}}} & \left(\frac{{\partial {T_{\rm{a}}}}}{{\partial t}} + J(\psi, {T_{\rm{a}}}) - \sigma \omega \frac{p}{R}\right) = - \lambda ({T_{\rm{a}}} - {T_{\rm{g}}}) \\ & + {\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}T_{\rm{g}}^4 - 2{\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}T_{\rm{a}}^4 + {R_{\rm{a}}},\end{split}$ | (6) |
where
The land temperature equation is similar to the atmospheric temperature equation as
| ${\gamma _{\rm{g}}}\frac{{\partial {T_{\rm{g}}}}}{{\partial t}} = - \lambda ({T_{\rm{g}}} - {T_{\rm{a}}}) - {\sigma _{\rm{B}}}T_{\rm{g}}^4 + {\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}T_{\rm{a}}^4 + {R_{\rm{g}}}, $ | (7) |
where
Similar to Vannitsem et al. (2015), the quartic terms in the radiative fluxes are linearized. The details of this linearization are described in Appendix A.
The system of equations is closed by the thermal wind relation:
| $\theta = \frac{R}{{2{f_0}}}\ln \left(\frac{{{p_3}}}{{{p_1}}}\right){T_{\rm{a}}} \approx \frac{R}{{2{f_0}}}{T_{\rm{a}}}.$ | (8) |
Let
Other nondimensional coefficients are
| $\left. \begin{aligned}& {{R\,'}_{\rm{\!\!\!\!g}}} = {{{R_{\rm{g}}}R}/{({\gamma _{\rm{g}}}f_0^3{L^2})}}, \quad {R_{\rm{a}}}^{\!\!\!\!\prime} = {{{R_{\rm{a}}}R}/{(2{\gamma _{\rm{a}}}f_0^3{L^2})}} \\& {{\lambda \,'}_{\rm{\!\!\!\!g}}} = {\lambda /{({\gamma _{\rm{g}}}}}{f_0}), \quad {{\lambda\, '}_{\!\!\!\!\rm{a}}} = {\lambda /{({\gamma _{\rm{a}}}}}{f_0}) \\&{\sigma _{\rm B, a}} = {{8{\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}T_{\rm a, 0}^3}/{({\gamma _{\rm{g}}}{f_0})}}, \quad {\sigma _{\rm B, g}} = {{4{\sigma _{\rm{B}}}T_{\rm g, 0}^3}/{({\gamma _{\rm{g}}}{f_0})}} \\&{S_{\rm B, a}} = 8{\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}{{T_{\rm a, 0}^3}/{({\gamma _{\rm{a}}}{f_0})}}, \quad {S_{\rm B, g}} = {{4{\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}T_{\rm g, 0}^3}/{(2{\gamma _{\rm{a}}}{f_0})}}\end{aligned} \right\}.$ | (9) |
We obtain the nondimensional equations of the model as
| $\begin{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \frac{\partial }{{\partial t'}}({\nabla ^2}\psi ') + J(\psi ', {\nabla ^2}\psi ') + J(\theta ', {\nabla ^2}\theta ') + \beta '\frac{{\partial \psi '}}{{\partial x'}} \\= - 0.5J(\psi ', h') + 0.5J(\theta ', h') - k{\nabla ^2}(\psi ' - \theta '), \end{split} \quad\quad\quad\;\;\; $ | (10) |
| $\begin{split} & \frac{\partial }{{\partial t'}}({\nabla ^2}\theta ') + J(\psi ', {\nabla ^2}\theta ') + J(\theta ', {\nabla ^2}\psi ') + \beta '\frac{{\partial \theta '}}{{\partial x'}} \\ &\quad\quad = 0.5J(\psi ', h') \!-\! 0.5J(\theta ', h')\; \!+\! k{\nabla ^2}(\psi ' \!-\! \theta ') \!-\! 2k'{\nabla ^2}\theta ' \!+\! \omega ' \end{split}, $ | (11) |
| $ \begin{split}\!\!\!\!\!\!\!\!\!\!\!\!\! & \frac{{\partial \theta '}}{{\partial t'}} + J(\psi ', \theta ') - \sigma '\omega ' = - {\lambda '_{\rm{a}}}(\theta ' - 0.5\delta {T_{\rm{g}}}^{\!\!\!\!\!\prime}\;) \\ &\quad\quad + {S_{{\rm B}, {\rm g}}}\delta {T_{\rm{g}}}^{\!\!\!\!\!\prime}\; - {S_{\rm B, a}}\theta ' + \delta {R'_{\rm{a}}}, \;\;\;\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \end{split}$ | (12) |
| $\frac{{\partial \delta {{T'}_{\!\!\!\!\rm{g}}}}}{{\partial t'}} = - {\lambda _{\rm{g}}}^{\!\!\!\!\!\prime} (\delta {T'_{\!\!\rm{g}}} - 2\theta ') - {\sigma _{\rm B, g}}\delta {T'_{\rm{g}}} + {\sigma _{\rm B, a}}\theta ' + \delta {R'_{\rm{g}}}.$ | (13) |
Note that Eqs. (12) and (13) have been linearized. The nondimensional atmospheric temperature,
We follow the work of CS, and truncate the expansions for
| $\left. \begin{aligned}& \psi = \sum\limits_{i = 1}^3 {{\psi _i}} {F_i}, \quad \theta = \sum\limits_{i = 1}^3 {{\theta _i}} {F_i}, \quad \delta {T_{\rm{g}}} = \sum\limits_{i = 1}^3 {{T_{{\rm{g}}, i}}} {F_i} \\& \omega ' = \sum\limits_{i = 1}^3 {{\omega _i}} {F_i}, \quad h' = {h_2}{F_2}\end{aligned} \right\}.$ | (14) |
We choose
| $\left. \begin{aligned}& {F_1} = \sqrt 2 \cos y \\& {F_2} = 2\cos (nx)\sin y \\& {F_3} = 2\sin (nx)\sin y\end{aligned} \right\}.$ | (15) |
Here, the zonal wavenumber
The dimensional boundary topography is given by
| $h = H{h_2}{F_2} = 2H{h_2}\cos ({{nx}/L})\sin ({y/L}).$ | (16) |
In our model, we set
The nondimensional meridional differential shortwave solar radiation absorbed by the land and the atmosphere are given by
| $\delta {R'_{\rm{g}}} = {C_{\rm{g}}}^{\!\!\!\! \prime} {F_1}, \quad \delta {R'_{\rm{a}}} = {C'_{\rm{a}}}{F_1}, $ | (17) |
where
| $\delta {R_{\rm{g}}} = \sqrt 2 {C_{\rm{g}}}\cos ({y/L}), \quad \delta {R_{\rm{a}}} = \sqrt 2 {C_{\rm{a}}}\cos ({y/L}), $ | (18) |
and we set
We can obtain 12 spectral equations and by eliminating
| ${\dot \psi _1} = - k({\psi _1} - {\theta _1}) - c\tilde h({\theta _3} - {\psi _3}), $ | (19) |
| $({n^2} + 1){\dot \psi _2} = - c{n^2}({\psi _1}{\psi _3} + {\theta _1}{\theta _3}) + \beta n{\psi _3} - {B_1}({\psi _2} - {\theta _2}), $ | (20) |
| $\begin{split} & ({n^2} + 1){\dot \psi _3} = c[{n^2}({\psi _1}{\psi _2} + {\theta _1}{\theta _2}) + \tilde h({\theta _1} - {\psi _1})] \\ &\quad\quad - \beta n{\psi _2} - {B_1}({\psi _3} - {\theta _3}), \end{split}\quad\quad\quad\;\;\;$ | (21) |
| $\begin{split} {C_1}{\dot \theta _1} =& c[{\psi _2}{\theta _3} - {\psi _3}{\theta _2} - \sigma '\tilde h({\psi _3} - {\theta _3})] - {B_3}{\theta _1}\\ & + k\sigma '{\psi _1} - {d_1}{\theta _1} + {d_2}{T_{{\rm g}, 1}} + {C_{\rm{a}}}^{\!\!\!\! \prime} \; ,\end{split}\quad\quad\quad\;\;\;$ | (22) |
| $\begin{split}({n^2} + 1){C_2}{\dot \theta _2} = & c({A_1}{\psi _3}{\theta _1} - {A_2}{\psi _1}{\theta _3}) + \beta n\sigma '{\theta _3} - {B_2}{\theta _2} \\ & + {B_1}\sigma '{\psi _2} - {d_1}{\theta _2} + {d_2}{T_{{\rm {\rm g}}, 2}},\end{split}\;\;\;$ | (23) |
| $\begin{split}({n^2} + 1){C_2}{\dot \theta _3} = & c[{A_2}{\psi _1}{\theta _2} - {A_1}{\psi _2}{\theta _1} + \sigma '\tilde h({\psi _1} - {\theta _1})] \\ & -\beta n\sigma '{\theta _2} - {B_2}{\theta _3} + {B_1}\sigma '{\psi _3} - {d_1}{\theta _3} + {d_2}{T_{{\rm g}, 3}},\end{split}$ | (24) |
| ${\dot T_{{\rm g}, 1}} = - {d_3}{T_{{\rm g}, 1}} + {d_4}{\theta _1} + {C'_{\rm{g}}}, $ | (25) |
| ${\dot T_{{\rm g}, 2}} = - {d_3}{T_{{\rm g}, 2}} + {d_4}{\theta _2}, $ | (26) |
| $ {\dot T_{{\rm g}, 3}} = - {d_3}{T_{{\rm g}, 3}} + {d_4}{\theta _3}, $ | (27) |
where the coefficients used here are
| $\left. \begin{aligned}& c = \frac{{8\sqrt 2 n}}{{3\pi }}, \quad \quad \, \tilde h = \frac{{{h_2}}}{2} \\& {d_1} = {{\lambda '}_{\!\!\!\! \rm{a}}} + {S_{\rm B, a}}, \quad \, {d_2} = {{{{\lambda '}_{\!\!\!\! \rm{a}}}}/2} + {S_{\rm B, g}} \\& {d_3} = {{\lambda '}_{\!\!\!\! \rm{g}}} + {\sigma _{\rm B, g}}, \quad {d_4} = 2{{\lambda '}_{\!\!\!\! \rm{g}}} + {\sigma _{\rm B, a}} \\& {A_1} = 1 - \sigma '{n^2}, \quad \;\, {A_2} = 1 + \sigma '{n^2} \\& {B_1} = ({n^2} + 1)k, \quad {B_3} = (2k' + k)\sigma ' \\& {B_2} = ({n^2} + 1)(2k' + k)\sigma ' \\& {C_1} = \sigma ' + 1, \quad \;\;\;\;\;{C_2} = \sigma ' + \frac{1}{{{n^2} + 1}} \\ \end{aligned} \right\}.$ | (28) |
In this section, we will show the equilibrium solutions (i.e., stationary solutions) and their stabilities of the simple coupled land–atmosphere system Eqs. (19)–(27).
We set all of the time derivatives and wave components to zero in Eqs. (19)–(27), and then obtain a specific equilibrium state:
| $\left. \begin{aligned}& {{\bar \theta }_1} = \frac{{{D_2}}}{{2k'\sigma ' - {D_1}}} \\&{{\bar \psi }_1} = {{\bar \theta }_1} \\& {{\bar T}_{{\rm{g}}, 1}} = \frac{{{d_4}{{\bar \theta }_1} + {{C'}_{\rm{\!\!\!\!g}}}}}{{{d_3}}} \end{aligned} \right\}, $ | (29) |
where
| ${D_1} = \frac{{{d_2}{d_4}}}{{{d_3}}} - {d_1}, \quad {D_2} = \frac{{{d_2}{{C'}_{\rm{\!\!\!\!g}}}}}{{{d_3}}} + {C'_{\rm{a}}}.$ | (30) |
This equilibrium state is referred to as “Hadley circulation” in CS. Note that
The method to obtain the general equilibrium solutions of Eqs. (19)–(27) and to determine the stabilities of the equilibrium solutions are shown in Appendix B.
Next, we show the results of calculations of the equilibrium solutions and their stabilities. Similar to the “demonstration case” in RP, we preferentially choose planetary zonal wavenumber
The results of the equilibrium solutions and their stabilities for
In Table 2, for a given realistic value of Cg, there may be one (Cg
For Cg = 20 W m–2, the only one equilibrium state is stable (see Table 2). All of the wave components of this equilibrium state are zero, so this is Hadley solution. For Cg = 30, 40, and
For Cg = 50 W m–2, there are three equilibrium states and only the last two are stable. Note that the first equilibrium state is the Hadley solution, and now it becomes unstable. The streamfunction and temperature fields of the second and third equilibrium states are illustrated in Fig. 1.
The second and third equilibrium states are both high-index, due to both strong zonal westerlies with weak meridional perturbations in the upper layer (Figs. 1a, e). However, there are wavy easterlies in the lower layer for the second equilibrium state (Fig. 1b) and wavy westerlies in the lower layer for the third equilibrium state (Fig. 1f). The isotherms in both atmospheric and land temperature fields of the two equilibrium states are all quite flat (Figs. 1c, d, g, h) and almost in phase with each upper layer streamfunction field. Both of the two equilibrium states have a characteristic baroclinic structure, i.e., the waves of streamfunction fields displayed westward phase shifts with height. However, they have different wave phases relative to the topography. For the second equilibrium state, its lower layer streamfunction is nearly in phase with the topography, the lower layer converse ridges (anticyclonic flow) are over the mountains (positive topographic heights), lying slightly west of the mountain crests (Fig. 1b), and the upper layer ridges are located to the west side of the mountains (Fig. 1a). We call this a “ridge-type” equilibrium. By contrast, for the third equilibrium state, the lower layer streamfunction is nearly out of phase with the topography, the lower layer low-pressure centers and troughs are over the mountains, also lying slightly west of the mountain crests (Fig. 1f), and the upper layer troughs are located to the west side of the mountains (Fig. 1e). We call this a “trough-type” equilibrium. For simplicity, we refer to the characters of the two equilibrium states as “High 2” and “High 1”, respectively. Here, “High” denotes “high-index”, “2” denotes “ridge-type”, and “1” denotes “trough-type”.
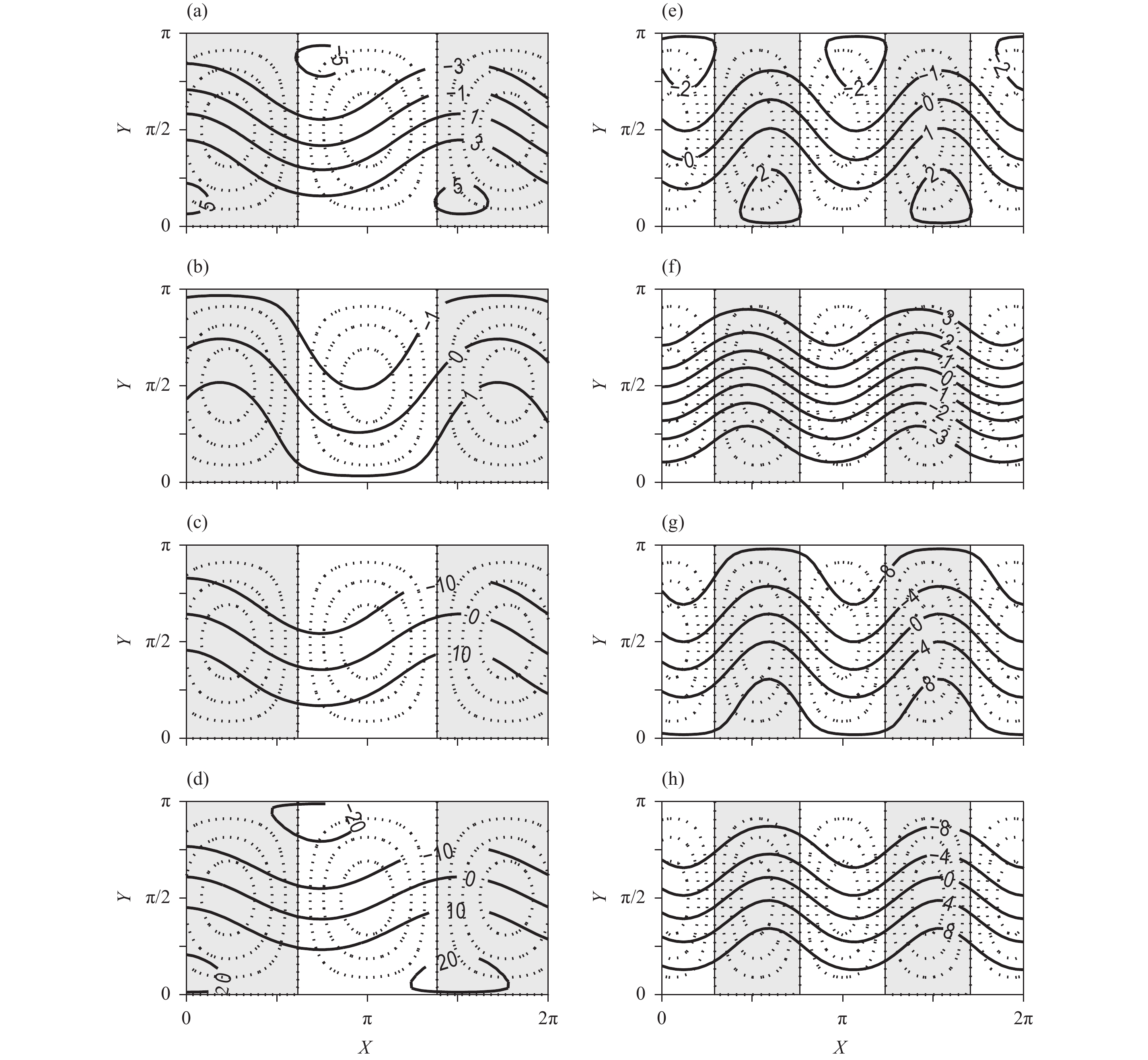
ForCg = 55 W m–2, the last two of the three equilibrium states are also stable. The first one is still “High 2” high-index equilibrium, and the second one becomes low-index equilibrium (Table 2). The streamfunction and temperature fields of this low-index equilibrium are illustrated in Fig. 2 (left panel). There are relatively weak westerlies with strong meridional flow in both the upper and lower layer streamfunction fields (Figs. 2a, b), particularly closed streamlines in the former. Note that the magnitude of the streamfunction in Fig. 2b is 106 m2 s–1 and larger than that in Fig. 1b (105 m2 s–1), indicating that the amplitude of meridional perturbations in Fig. 2b are larger than those in Fig. 1b. There are also relatively large meridional perturbations in both the atmospheric and land temperature fields (Figs. 2c, d) and even closed isotherms in the latter. In this low-index equilibrium, the lower layer streamfunction is nearly out of phase with the topography, the lower layer troughs are over the mountains and the upper layer troughs are located on the west side of the mountains, so this is a trough-type equilibrium. We refer to the character of this equilibrium state as “Low 1”, where “Low” denotes “low-index”.
|
|
Figure 2 As in Fig. 1, but for the third one of the three equilibrium states for m = 3.7 at Cg = 55 W m–2 (left panels) and for the third one of the five equilibrium states for m = 6 at Cg = 30 W m–2 (right panels). They belong to “Low 1” and “Low 2” equilibria, respectively. The “Low 2” equilibria has nondimensional solutions with
|
| Cg (W m–2) |
|
|
|
|
|
|
|
|
|
|
Character |
| 20 | 0.0258 | 0 | 0 | 0.0258 | 0 | 0 | 0.0603 | 0 | 0 | - | Hadley |
| 30 | 0.0387 | 0 | 0 | 0.0387 | 0 | 0 | 0.0905 | 0 | 0 | - | Hadley |
| 40 | 0.0516 | 0 | 0 | 0.0516 | 0 | 0 | 0.1207 | 0 | 0 | - | Hadley |
| 45 | 0.0580 | 0 | 0 | 0.0580 | 0 | 0 | 0.1358 | 0 | 0 | - | Hadley |
| 50 | 0.0644 | 0 | 0 | 0.0644 | 0 | 0 | 0.1509 | 0 | 0 | N | |
| 0.0620 | –0.0025 | –0.0071 | 0.0633 | –0.0030 | –0.0069 | 0.1487 | –0.0053 | –0.0123 | - | High 2 | |
| 0.0633 | –0.0035 | 0.0111 | 0.0618 | –0.0026 | 0.0109 | 0.1461 | –0.0047 | 0.0194 | - | High 1 | |
| 55 | 0.0709 | 0 | 0 | 0.0709 | 0 | 0 | 0.1659 | 0 | 0 | N | |
| 0.0620 | –0.0115 | –0.0092 | 0.0661 | –0.0126 | –0.0087 | 0.1575 | –0.0225 | –0.0155 | - | High 2 | |
| 0.0643 | –0.0124 | 0.0187 | 0.0612 | –0.0104 | 0.0183 | 0.1487 | –0.0186 | 0.0328 | - | Low 1 | |
| 60 | 0.0773 | 0 | 0 | 0.0773 | 0 | 0 | 0.1810 | 0 | 0 | N | |
| 0.0804 | 0.0227 | 0.0012 | 0.0711 | 0.0177 | 0 | 0.1699 | 0.0316 | 0 | N | ||
| 0.0650 | –0.0201 | 0.0219 | 0.0610 | –0.0171 | 0.0214 | 0.1517 | –0.0305 | 0.0383 | - | Low 1 | |
| 70 | 0.0902 | 0 | 0 | 0.0902 | 0 | 0 | 0.2112 | 0 | 0 | N | |
| 0.0816 | 0.0437 | 0 | 0.0685 | 0.0324 | –0.0017 | 0.1724 | 0.0579 | –0.0031 | N | ||
| 0.0664 | –0.0329 | 0.0246 | 0.0607 | –0.0279 | 0.0238 | 0.1583 | –0.0498 | 0.0426 | - | Low 1 | |
| 80 | 0.1031 | 0 | 0 | 0.1031 | 0 | 0 | 0.2414 | 0 | 0 | N | |
| 0.0816 | 0.0563 | –0.0013 | 0.0674 | 0.0412 | –0.0031 | 0.1776 | 0.0736 | –0.0055 | N | ||
| 0.0676 | –0.0433 | 0.0257 | 0.0605 | –0.0362 | 0.0248 | 0.1652 | –0.0648 | 0.0443 | - | Low 1 | |
| The column
|
|||||||||||
AtCg = 60 W m–2, only the third one of the three equilibrium states is stable, and it is “Low 1” equilibrium. The second one becomes unstable. For Cg = 70 and 80 W m–2, the results are the same as for Cg = 60 W m–2.
For comparison purposes, we have calculated the equilibrium solutions for wavenumber 6. We find there may be one, three, or five equilibrium states for a given value of Cg (figure omitted). Some of them are stable. Besides the stable “High 1”, “High 2”, and “Low 1” equilibrium, a new stable low-index equilibrium may exist. As illustrated in Fig. 2 (right panel), it has strong meridional perturbations in both the upper layer streamfunction field (Fig. 2e) and temperature fields (Figs. 2g, h). However, there are wavy easterlies in the lower layer streamfunction field (Fig. 2f). Note that the lower layer streamfunction is nearly in phase with the topography, the lower layer converse ridges are over the mountains, and the upper layer ridges are located to the west side of the mountains, so this is a ridge-type equilibrium. We refer to the character of this equilibrium state as “Low 2”.
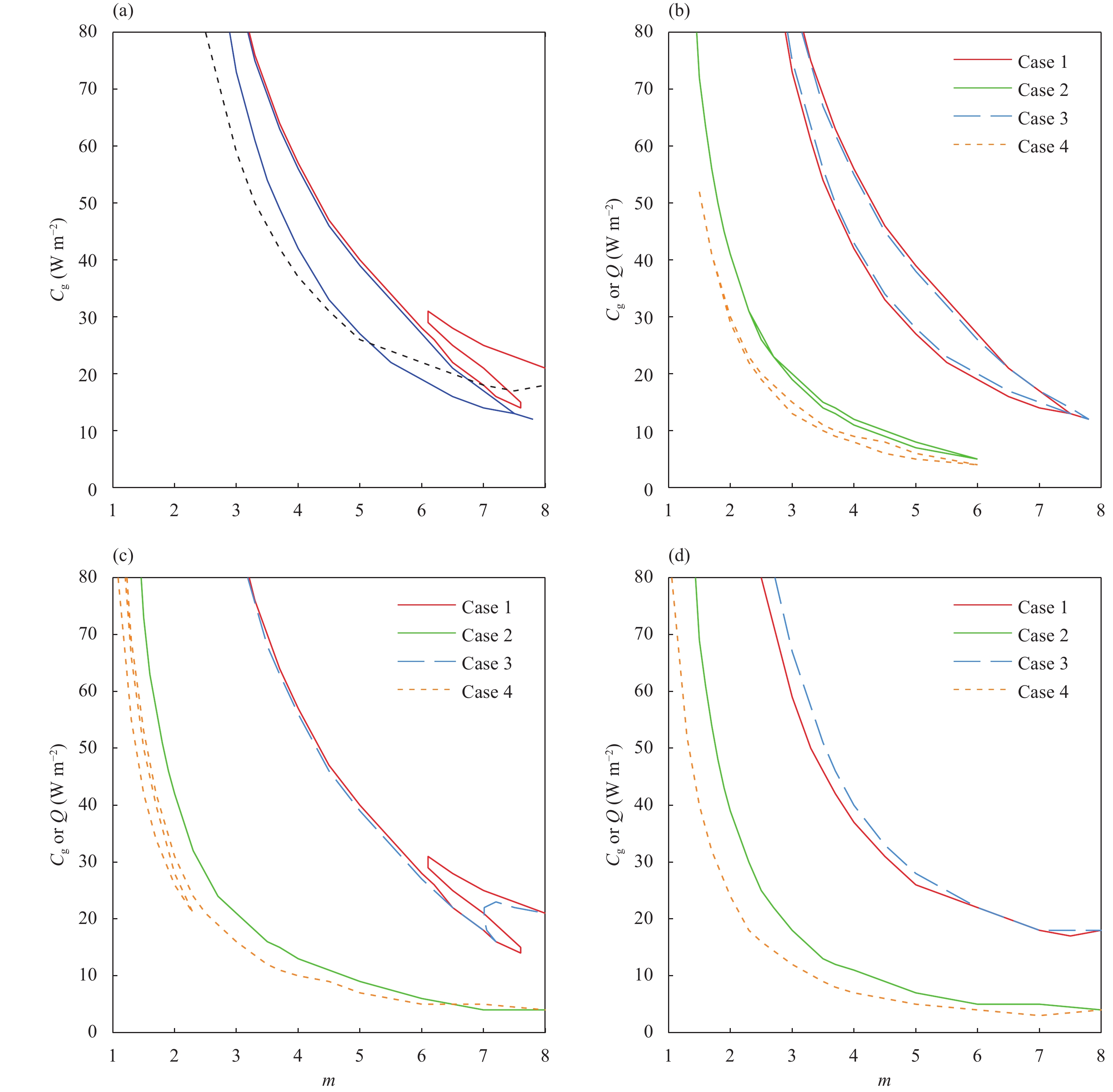
3.2 Bifurcation diagramsTo further demonstrate the multiple equilibrium states and their stabilities for wavenumbers 3.7 and 6, simple bifurcation diagrams are shown in Fig. 3. The zonal component
For wavenumber 3.7, there are four equilibrium branches (Fig. 3, left panel). For small values of Cg, the Hadley circulation (black) is the only equilibrium and it is stable. As Cg is gradually increased, around Cg = 50 W m–2, the Hadley circulation loses its stability, and two new equilibria (blue and red) appear. The blue branch represents a trough-type equilibrium, and it is always stable. It includes “High 1” (50
For wavenumber 6, there are five equilibrium branches (Fig. 3, right panel). For small values of Cg, the stable Hadley circulation (black) is still the only equilibrium. As Cg is increased to around Cg = 20 W m–2, the Hadley circulation becomes unstable, and two new equilibria (blue and red) appear. The blue branch represents a trough-type equilibrium and it is always stable. It includes “High 1” (Cg = 20 W m–2) and “Low 1” equilibrium (
The above results indicate that there are multiple equilibrium states with different wave phases and wave amplitudes in the coupled model. For a considerable range of Cg values (50
The multiple wavelike stationary equilibrium states exist in the model when the topography is present. This is proved in Appendix B.
Figure 5a shows the stability curves of the Hadley circulation in the coupled model. The blue lines enclose the orographically unstable region. In crossing the blue lines from the stable to unstable sides, the variable
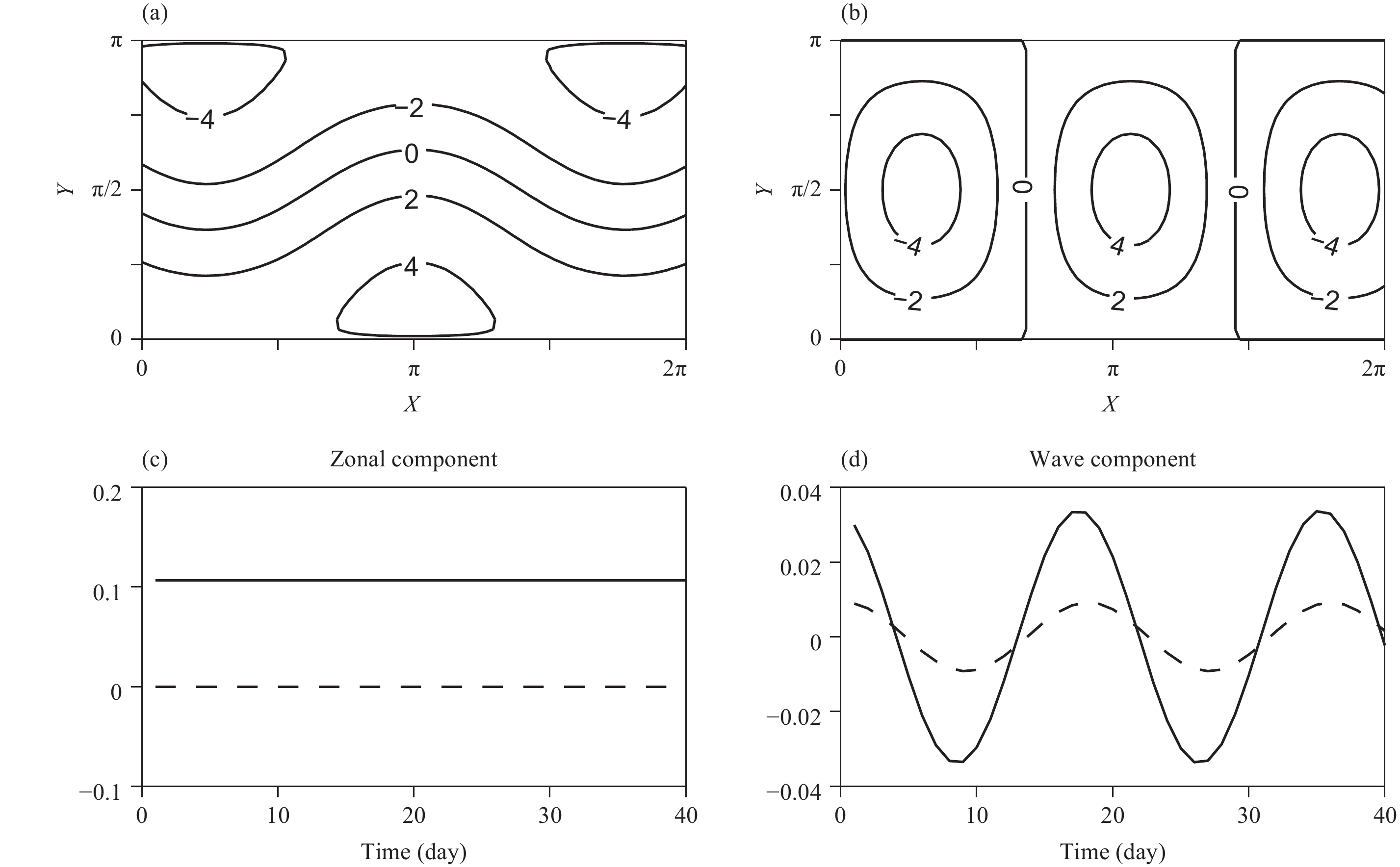
In the absence of topography, there is only the Hadley circulation (see Appendix B) or the traveling wave due to the baroclinic instability of the Hadley circulation (which is a Hopf bifurcation). For example, for
|
|
Figure 4 A traveling wave solution in the absence of topography for m = 3.7 at Cg = 50 W m–2, with
|
In the presence of topography, there may exist multiple equilibrium states. Compared Fig. 1 with Fig. 4, it seems that due to the presence of topography, the traveling wave becomes two types of stationary waves. In fact, the first bifurcation (Fig. 3, around Cg = 50 W m–2 for
Therefore, the multiple wave phase equilibria associated with the ridge- and trough-types originate from the orographic instability of the Hadley circulation, which is a pitch-fork bifurcation.
4 The role of the land–atmosphere couplingIn this section, we explore the role of the land–atmosphere coupling in the existence and properties of the equilibrium states.
Four experiments are designed with different diabatic heating terms (see Table 3). For simplicity, here we refer to the coupled land–atmosphere model as Case 1. Equations (6) and (7) indicate that the diabatic heating terms in Case 1 include three terms: heat flux, longwave radiation, and shortwave radiation. For Case 2, we replace all the terms on the right side of Eq. (6) by specified heating
| Experiment | Heat flux | Longwave radiation | Shortwave radiation | Specified heating |
| Case 1 | √ | √ | √ | |
| Case 2 | √ | |||
| Case 3 | √ | √ | ||
| Case 4 | √ | √ | ||
| The sign (√) indicates that the corresponding element has been included in the related experiment. | ||||
Figure 5b compares the orographic instability of the Hadley circulation in the four experiments. Clearly, compared with Case 1, the thresholds of orographic instability in Cases 2 and 4 are both greatly reduced for wavenumbers 1–6. Moreover, the orographically unstable regions in Cases 2 and 4 are both very narrow. Unexpectedly, the orographically unstable regions in Cases 3 and 1 almost completely overlap. Figures 5c and 5d compare the baroclinic instability of the Hadley circulation with and without topography, respectively. Similarly, compared with Case 1, the thresholds of baroclinic instability in Cases 2 and 4 are both greatly reduced for wavenumbers 1–8. However, the baroclinic stability curves in Cases 3 and 1 roughly overlap. The results indicate that compared with the uncoupled model (Case 2), the land–atmosphere coupling (Case 1) greatly stabilizes the Hadley circulation, and this stabilizing effect is primarily attributed to the presence of longwave radiation fluxes, but not the heat fluxes.
In addition, compared with Case 2, Case 4 has lower thresholds for all of the orographic instability and baroclinic instability with and without topography (Figs. 5b–d). It suggests that the presence of heat fluxes extremely destabilizes the Hadley circulation, no matter with or without topography. Nevertheless, in Case 1, which presents both the heat fluxes and the longwave radiation fluxes, the destabilizing effect of the heat fluxes on Hadley circulation is nearly entirely suppressed.
4.2 Comparing the bifurcationNext, we compare the equilibrium bifurcation in the four experiments. Figures 6a and 6b show the bifurcation diagrams in Case 3 for wavenumber
Figures 6c and 6d show the bifurcation diagrams in Cases 2 and 4 for wavenumber
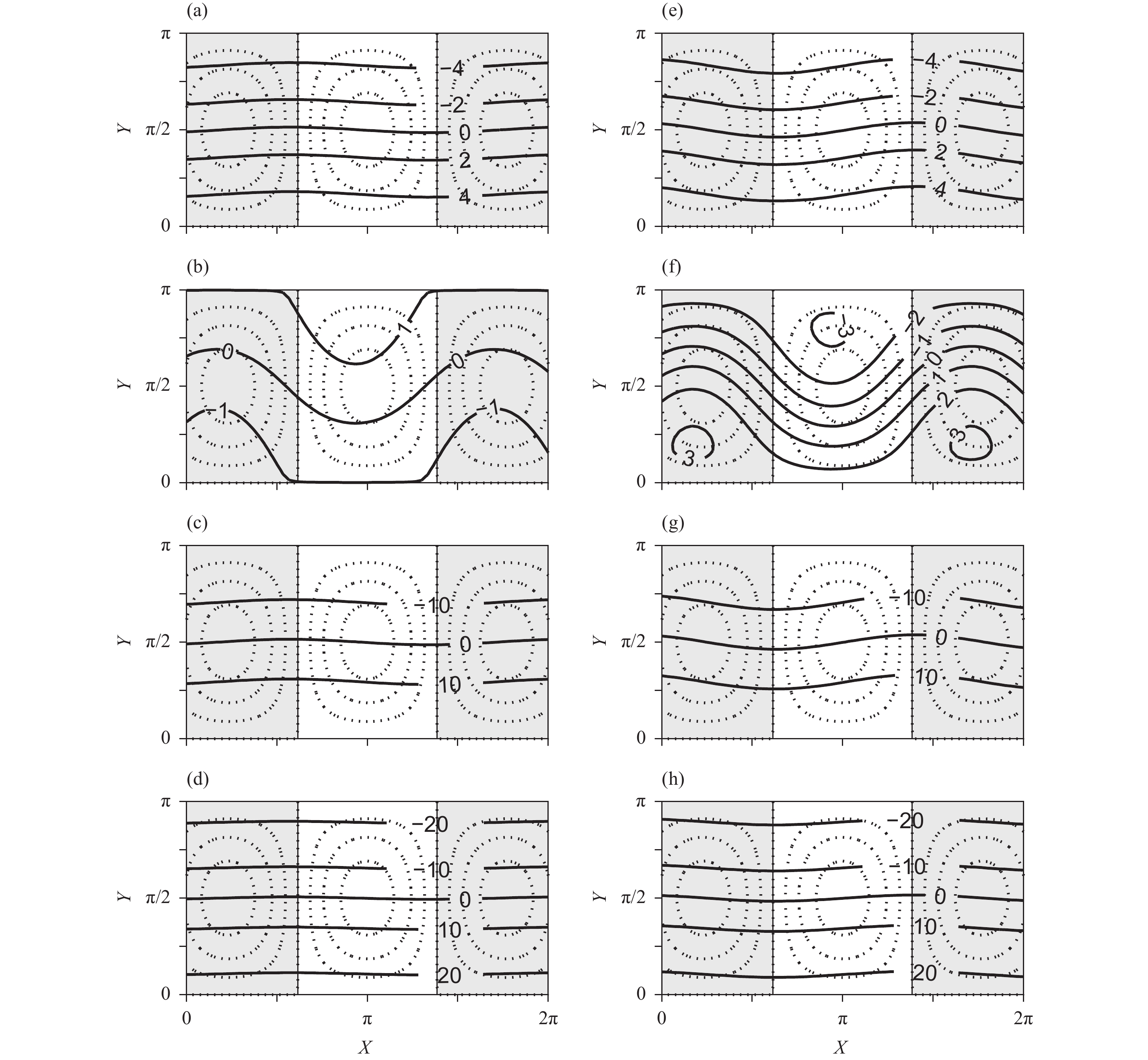
Here, we compare the streamfunction and temperature fields of equilibrium states in the four experiments for

|
|
Figure 7 As in Fig. 1, but for the only stable equilibrium state for m = 3.7 at Q = 50 W m–2 in Case 2 (left panels) and for the third one of the three equilibrium states for m = 3.7 at Cg = 50 W m–2 in Case 4 (right panels). The former has nondimensional solutions with
|
|
|
Figure 8 As in Fig. 1, but for the second one (left panels) and third one (right panels) of the three equilibrium states for m = 3.7 at Cg = 50 W m–2 in Case 3. They have nondimensional solutions with
|
These results indicate that compared with the uncoupled model (Case 2), the land–atmosphere coupling may weaken the atmospheric response to the thermal and topographic forcing, and this weakening effect is mainly contributed by the presence of longwave radiation fluxes. The presence of heat fluxes greatly strengthens the atmospheric response to the thermal and topographic forcing, but in the coupled model which combined the heat fluxes and longwave radiation fluxes, the heat fluxes just strengthen the response of the lower layer flow, and moderately reduce the meridional gradient of the land temperature.
4.4 Comparing the heating fieldsTo further understand the reason of the different results in the four experiments, we should compare the heating fields in the four experiments.
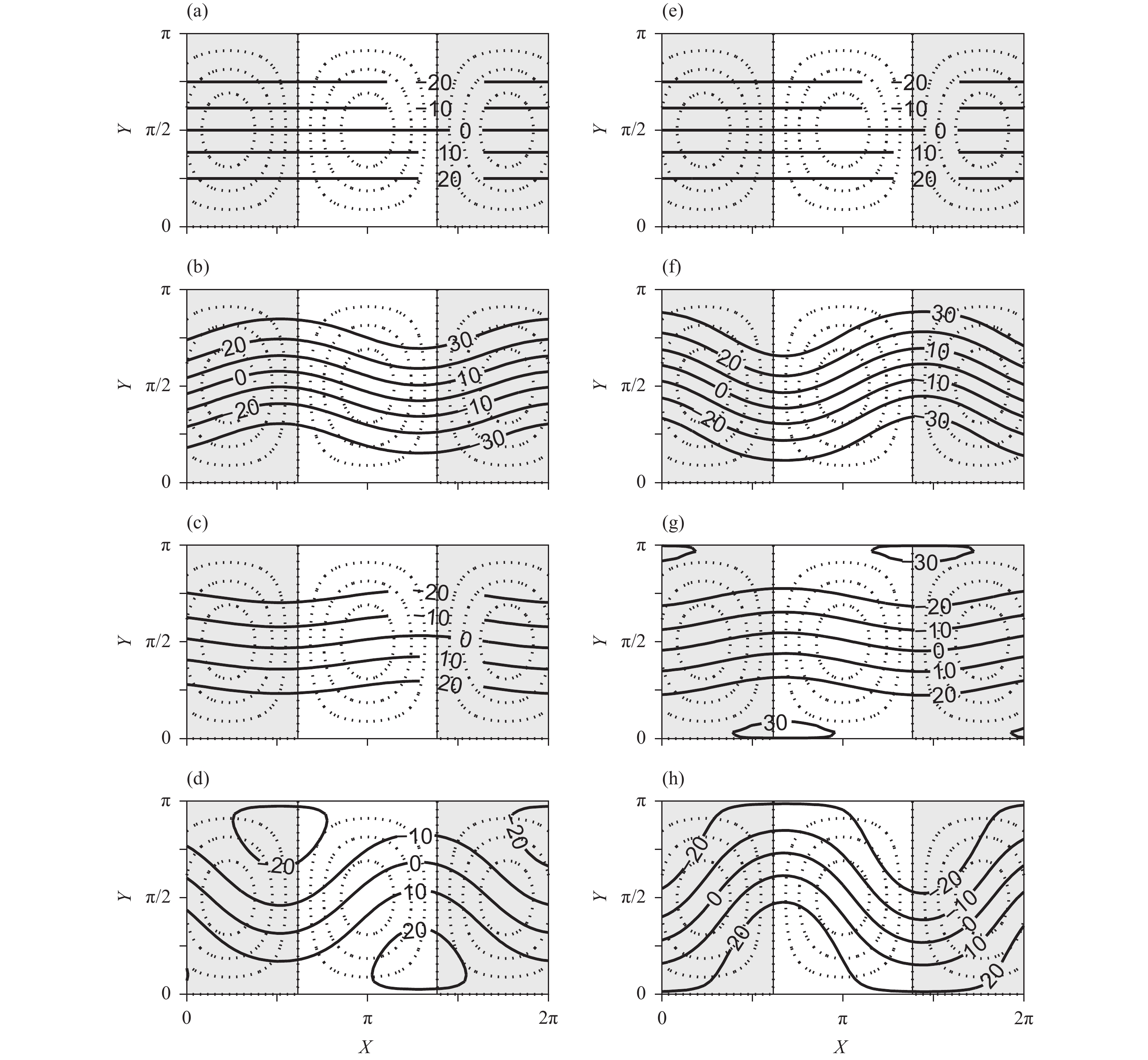
Figure 9 demonstrates the heating fields of the “High 2” and “High 1” equilibrium states shown in Fig. 1 (left and right panels), respectively. The zonally symmetric shortwave radiation fields for the two equilibrium states are identical (Figs. 9a, e). The isolines in all of the longwave radiation fields, the heat flux fields, and the net diabatic heating fields are wave-like, while the wave phases relative to the topography are different. For the “High 2” equilibrium state (Fig. 1, left panel), the “heating ridges” are located on the east side of the mountains (Fig. 9b–d); By contrary, for the “High 1” equilibrium state (Fig. 1, right panel), the “heating ridges” are located on the west side of the mountains (Figs. 9f–h). Note that for the lower layer streamfunction of the two equilibrium states, the ridges (high pressure) are always generated on west side of the “heating ridge”, and the troughs (low pressure) are always generated on east side of the “heat ridges”. Furthermore, it is noteworthy that the longwave radiation fluxes increase from low to high latitudes (Figs. 9b, f); thus, the presence of longwave radiation fluxes reduce the meridional gradient of the net diabatic heating field, resulting in a more stable atmosphere flow. On the contrary, the heat fluxes decrease from low to high latitudes (Figs. 9c, g); thus, the presence of heat fluxes increase the meridional gradient of the net diabatic heating field, resulting in a less stable atmosphere flow.
|
| Figure 9 The heating fields of the “High 2” (left panels) and “High 1” (right panels) equilibrium states shown in Fig. 1, respectively. (a, e) The shortwave radiation, (b, f) the longwave radiation, (c, g) the heat flux, and (d, h) the net diabatic heating absorbed by the atmosphere. All of the contour intervals are 10 W m–2. The background dotted lines show the topographic heights in the model, with negative regions shaded. |
The net diabatic heating field in Case 2 is zonally symmetric (Fig. 10a). Particularly, the meridional gradient of the net diabatic heating is much greater than that in Case 1 (Figs. 9d, h). The net diabatic heating fields for the “High 2” and “High 1” equilibrium states in Case 3 (Figs. 10c, d) are similar to those in Case 1 (Figs. 9d, h), while the meridional gradients of the net diabatic heating are smaller than those in Case 1. The net diabatic heating field in Case 4 (Fig. 10b) is almost the same as that in Case 2 (Fig. 10a); however, the meridional gradient of the net diabatic heating is greater than that in Case 2. It suggests that compared with the uncoupled model (Case 2), the land–atmosphere coupling reduces the meridional gradient of the net diabatic heating, and this effect is mainly attributed to the presence of longwave radiation fluxes. The presence of heat fluxes greatly increase the meridional gradient of the net diabatic heating. However, in the coupled model that combines the heat fluxes and longwave radiation fluxes, the heat fluxes just moderately increase the meridional gradient of the net diabatic heating.
To sum up, compared with the uncoupled model, the multiple wave phase equilibria associated with the ridge- and trough-types in the coupled model is more remarkable, mainly because the land–atmosphere coupling expands the region of orographic instability of the Hadley circulation. Besides, the land–atmosphere coupling greatly stabilizes the Hadley circulation and weakens the atmospheric response to the thermal and topographic forcing. Particularly, these effects of the land–atmosphere coupling are primarily attributed to the presence of longwave radiation fluxes, which increase from low to high latitudes, reducing the meridional gradient of the net diabatic heating. The presence of heat fluxes more or less modify the effects of longwave radiation fluxes.
5 Ridge- and trough-type equilibria and wave phaseNext, we investigate the wave phases of ridge- and trough-type equilibria relative to the topography. It is clear that the wave components
We have calculated the wave phase of the streamfunction relative to the mountains for wavenumbers 3.7 and 6, and the results are shown in Table 5. The ridge-type (High 2 and Low 2) equilibrium states have lower layer ridges over the mountains, their upper layer ridges are located to the west side of the mountain crests, and they have lower layer easterlies (Mean_U3 is negative, see Table 4 for definition of Mean_U3). The trough-type (High 1 and Low 1) equilibrium states have lower layer troughs over the mountains, their upper layer troughs are located to the west side of the mountain crests, and they have lower layer westerlies (Mean_U3 is positive). Figures 11b and 12b also show that the ridge-type (trough-type) equilibria has lower layer easterlies (westerlies). Therefore, the distinct characters of ridge- and trough-type equilibria are robust.
| Notation | Variable |
| U1 (m s–1) | Zonal mean upper-layeru-component (east–west) wind |
| U3 (m s–1) | Zonal mean lower-layer u-component wind |
| Mean_U1 (m s–1) | Channel-average upper-layeru-component wind, i.e., mean of U1 |
| Mean_U3 (m s–1) | Channel-average lower-layer u-component wind, i.e., mean of U3 |
| Mean_U2 (m s–1) | Middle-level u-component wind, mean of Mean_U1 and Mean_U3 |
| AH (gpm) | The amplitude of wave components of upper-layer geopotential height field |
| ΔTa (K) | Meridional gradient of atmospheric temperature, mean atmospheric temperature at the southern wall minus that at
the northern wall |
| ΔTg (K) | Meridional gradient of land temperature, mean land temperature at the southern wall minus that at the northern wall |
| ATa (K) | The amplitude of wave components of atmospheric temperature field |
| ATg (K) | The amplitude of wave components of land temperature field |
| m | Cg (W m–2) | Character | Phase | ΔPhase (°) | Mean_U3 (m s–1) | g1 (
|
g2 (
|
|
| Lower | Upper | |||||||
| 50 | High 2 | Ridge | –12 | –84 | –0.18 | 9.10 | –1.49 | |
| 50 | High 1 | Trough | –9 | –57 | 0.23 | –6.93 | 1.17 | |
| 3.7 | 55 | High 2 | Ridge | –18 | –108 | –0.61 | 2.76 | –0.44 |
| 55 | Low 1 | Trough | –9 | –45 | 0.44 | –3.57 | 0.61 | |
| 60 | Low 1 | Trough | –6 | –36 | 0.60 | –2.59 | 0.45 | |
| 80 | Low 1 | Trough | –6 | –24 | 1.03 | –1.46 | 0.26 | |
| 20 | High 2 | Ridge | 0 | –42 | –0.20 | 8.31 | –1.68 | |
| 20 | High 1 | Trough | 0 | –24 | 0.26 | –6.01 | 1.29 | |
| 26 | Low 2 | Ridge | –6 | –60 | –0.77 | 2.32 | –0.44 | |
| 6 | 26 | Low 1 | Trough | 0 | –12 | 0.49 | –3.09 | 0.69 |
| 28 | Low 2 | Ridge | –6 | –66 | –1.06 | 1.74 | –0.32 | |
| 28 | Low 1 | Trough | 0 | –12 | 0.52 | –2.90 | 0.65 | |
| 32 | Low 1 | Trough | 0 | –6 | 0.55 | –2.73 | 0.61 | |
| 40 | Low 1 | Trough | 0 | –6 | 0.56 | –2.67 | 0.60 | |
| “Ridge (trough)” in the “Phase” column indicates that the ridges (troughs) of lower layer streamfunction are over the mountains. The subsequent column “ΔPhase” gives the phase of the ridges (troughs) of the lower layer and upper layer streamfunction relative to the mountain crests, respectively, and negative values indicate that the ridges or troughs are located to the west side of the mountain crests. | ||||||||
The above phenomena can roughly be explained by the forced topographic Rossby wave theory. The forced topographic Rossby wave solution based on the barotropic potential vorticity equation (Smith, 1979; Nigam and DeWeaver, 2003; Holton and Hakim, 2012) is given by
| $\Psi (x, y) = {\mathop{\rm Re}\nolimits} \left[\frac{{{f_0}h/{H_0}}}{{{{\tilde k}^2} + {{\tilde l}^2} - \beta /\bar u - i\varepsilon ({{\tilde k}^2} + {{\tilde l}^2})/(\bar u\tilde k)}}\right], $ | (31) |
where
We might write the boundary topography as
| $h = {\mathop{\rm Re}\nolimits} \{ 2H{h_2}[\cos (nx/L) + i\sin (nx/L)]\sin (y/L)\}, $ | (32) |
and set
| $\,\,{g_1} = {\tilde k^2} + {\tilde l^2} - {\beta /{\bar u}}, \quad$ | (33) |
| ${{{g_2} = \varepsilon ({{\tilde k}^2} + {{\tilde l}^2})}/{(\bar u\tilde k)}}, $ | (34) |
then Eq. (31) becomes the following:
| $\begin{split}&\Psi (x, y) = \operatorname{Re} \{ \frac{{2{f_0}{h_2}}}{{{g_1} - i{g_2}}}[\cos ({{nx}/L}) + i\sin ({{nx}/L})]\sin ({y/L})\} \\ &= \operatorname{Re} \{ \frac{{2{f_0}{h_2}({g_1} + i{g_2})}}{{({g_1} - i{g_2})({g_1} + i{g_2})}}[\cos ({{nx}/L}) + i\sin ({{nx}/L})]\sin ({y/L})\}\\& = \frac{{2{f_0}{h_2}}}{{g_1^2 + g_2^2}}[{g_1}\cos ({{nx}/L}) - {g_2}\sin ({{nx}/L})]\sin ({y/L}).\end{split}$ | (35) |
Examples of calculated values of g1 and g2 are shown in Table 5. The absolute values of g1 are always much greater than that of g2. Thus, the wave phase of the streamfunction
In fact, the wave phase of equilibrium states depends on the direction of zonal wind and horizontal scale of the topography. Due to the conservation of potential vorticity, the absolute vorticity is decreased over the mountains. For westerly flow (
In a word, the ridge-type (trough-type) equilibrium states have lower layer ridges (trough) over the mountains and have lower layer easterlies (westerlies). The wave phases of equilibrium states relative to the topography depends on the direction of lower layer zonal wind and horizontal scale of the topography. Further discussion is presented in Section 7.
6 High- and low-index equilibria and wave amplitudeNext, we investigate the high- and low-index equilibria and wave amplitude. To further examine the differences between these two types of equilibrium, we define some dimensional physical variables, as shown in the Table 4. All of the variables are defined over the domain (
| ${\rm AH} = \frac{{{L^2}f_0^2}}{{{g_0}}}\sqrt {{{(\psi _2^1)}^2} + {{(\psi _3^1)}^2}} .$ | (36) |
The amplitude of wave components of the atmospheric and the land temperature fields are defined as
| $\!\!\!\!\!\!\!{\rm A}{{\rm T}_{\rm{a}}} = \frac{{2{L^2}f_0^2}}{R}\sqrt {{{({\theta _2})}^2} + {{({\theta _3})}^2}}, $ | (37) |
| ${\rm A}{{\rm T}_{\rm{g}}} = \frac{{{L^2}f_0^2}}{R}\sqrt {{{({T_{{\rm g}, 2}})}^2} + {{({T_{{\rm g}, 3}})}^2}}, $ | (38) |
respectively. These two variables represent the zonal asymmetry of atmospheric and land temperature fields.
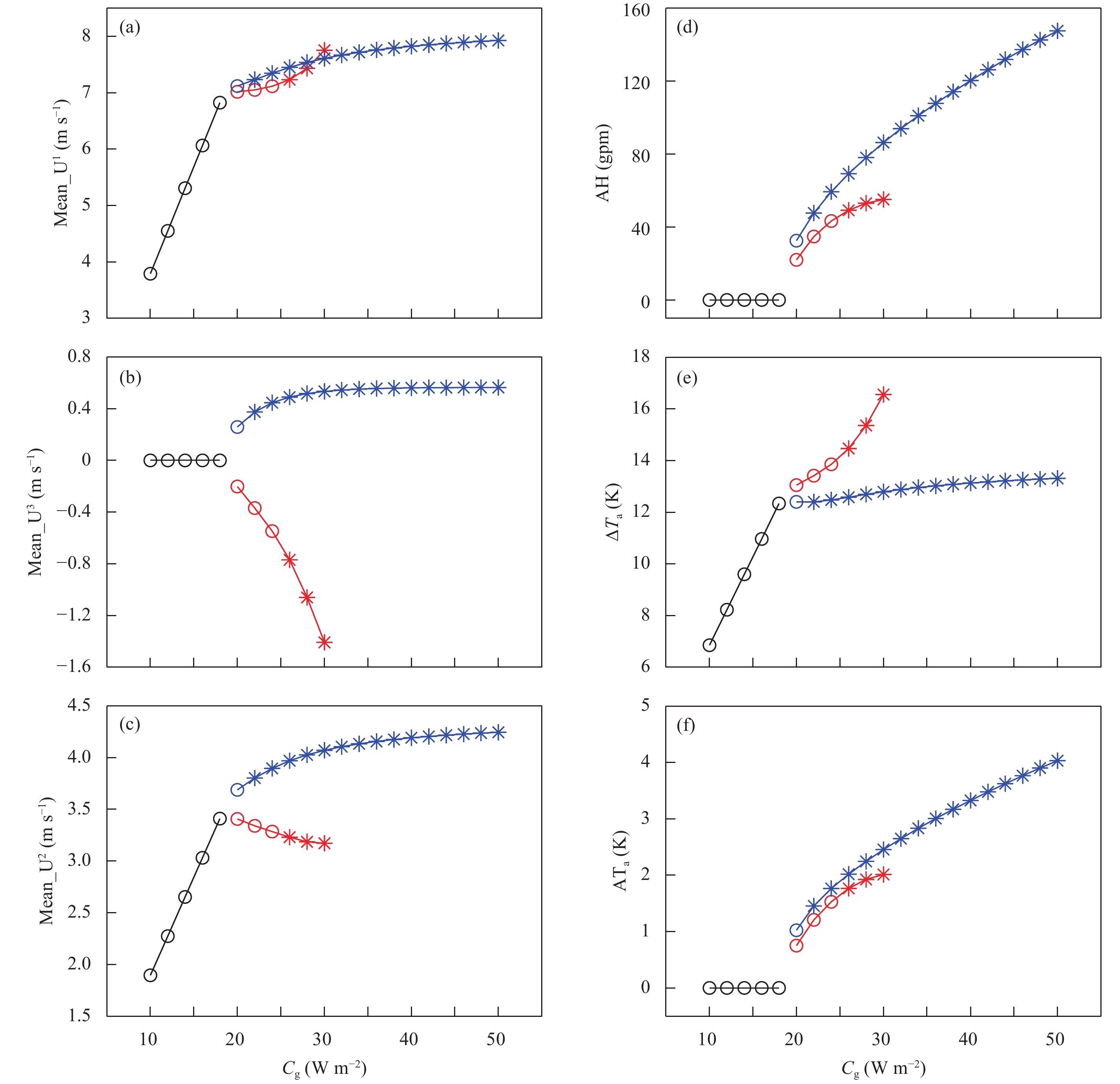
As expected, the wave amplitude AH of low-index equilibrium state is always greater than that of high-index equilibrium state at the same value of Cg (Figs. 11d, 12d). This phenomenon also occurs in wave amplitude of the atmospheric temperature field ATa (Figs. 11f, 12f). However, the meridional atmospheric temperature gradient ΔTa of low-index equilibrium state is always smaller than that of high-index equilibrium state at the same value of Cg (Figs. 11e, 12e).
These two types of equilibrium have no robust differences in the mean upper layer zonal wind speed: the Mean_U1 of the low-index equilibrium state is smaller than that of the high-index equilibrium state at Cg = 54 W m–2 for
It is notable that our results regarding the differences between the high- and low-index equilibria in zonal wind differ from previous studies based on the barotropic models, in which the zonal component
In fact, as emphasized in CS, the wavelike equilibrium is maintained not by the conversion of mean flow kinetic energy, but by the mean flow potential energy in the baroclinic atmosphere. Therefore, in our baroclinic model, as the low-index equilibria has larger wave amplitudes (Figs. 11d, 12d), there is indeed a reduction in meridional atmospheric temperature gradient of low-index equilibria (Figs. 11e, 12e) due to the consumption of mean flow potential energy. The low- and high-index equilibria certainly have no marked differences in zonal wind speed in our baroclinic model (Figs. 11a, 12a). However, in the barotropic model, the wavelike equilibria could only obtain energy from the mean flow kinetic energy. Therefore, in the barotropic model, the low-index equilibria with large wave amplitude undoubtedly has a lower zonal wind speed than the high-index equilibria with small wave amplitude.
The relationships between wave amplitude AH and meridional temperature gradient ΔTa and ΔTg are directly shown in Figs. 13a, b, e, f. As the wave amplitude of trough-type equilibria rapidly increases, the meridional atmospheric temperature gradient ΔTa remarkably decreases for
In addition, regardless of ridge- or trough-type as well as high- or low-index equilibria, the wave amplitudes of both atmospheric and land temperature fields (ATa and ATg) are highly positively correlated with wave amplitude AH (Figs. 13c, d, g, h). In fact, the atmospheric and land temperature fields of equilibrium states are always nearly in phase with each upper layer streamfunction field (Figs. 1, 2). If the atmospheric temperature field showed a lag or lead to the streamfunction field in phase, the meridional perturbations of streamfunction field would continue to grow or decay due to the temperature advection. Thus, there would be no stationary waves, i.e., equilibrium states. As we have only obtained equilibrium solutions from Eqs. (19)–(27), the atmospheric temperature field is surely in phase with the streamfunction field. The formation of the zonal asymmetric structure of the land temperature field should be attributed to the interactions between the land and atmospheric temperature fields through radiative and heat exchange. Therefore, the changes in wave amplitude of both atmospheric and land temperature fields are highly consistent with that of the upper layer streamfunction field (Figs. 11d, f; 12d, f; 13c, d g, h). This result also suggests that the wavelike equilibrium is maintained by the conversion of the mean flow potential energy.
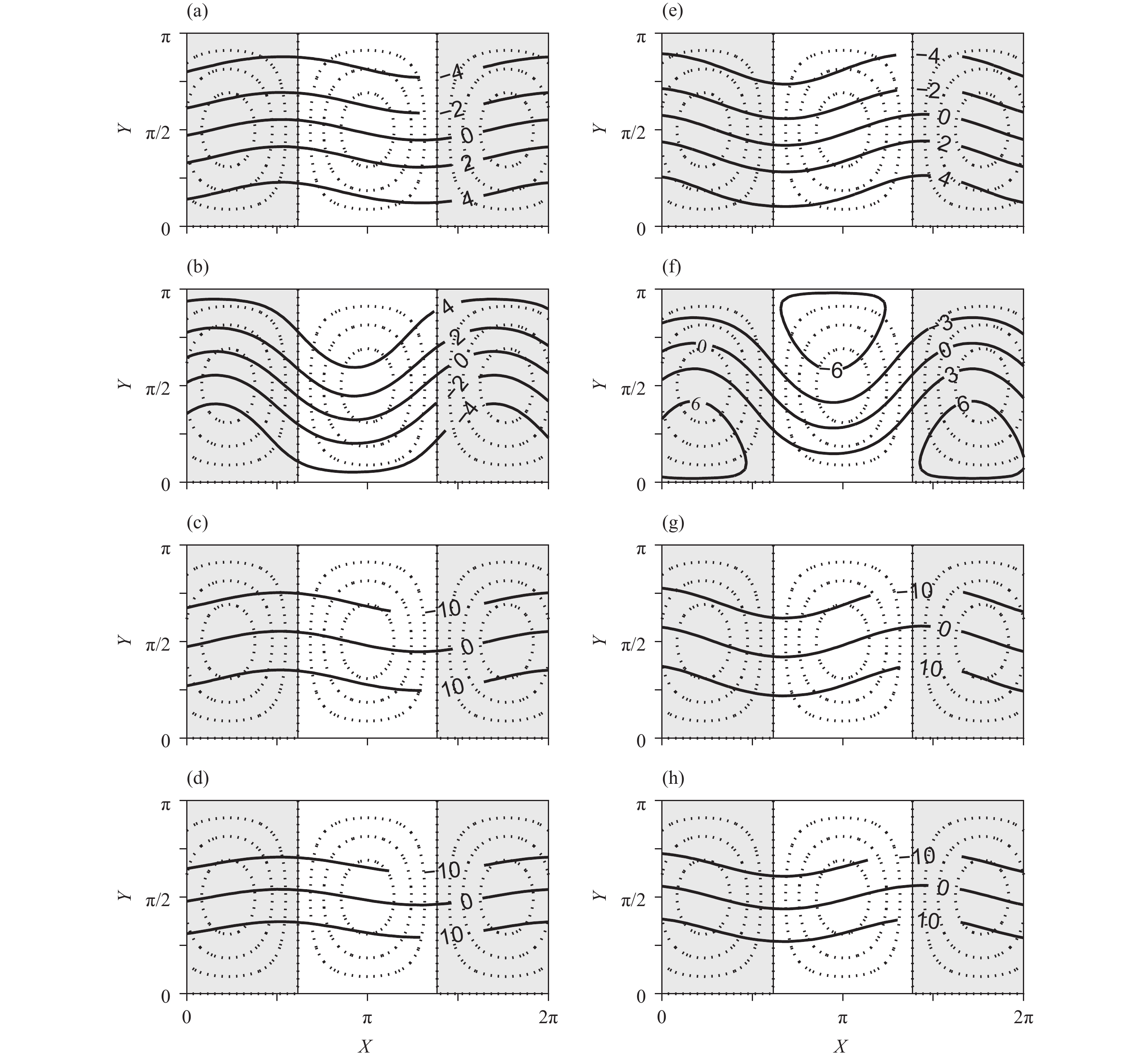
|
| Figure 1 The second one (left panels) and third one (right panels) of the three equilibrium states for m = 3.7 at Cg = 50 W m–2. They belong to “High 2” and “High 1” equilibria, respectively. The streamfunction fields of the (a, e) upper and (b, f) lower layers, respectively. The temperature fields of (c, g) the atmosphere and (d, h) the land, respectively. The contour intervals are (a, e) 2.0 × 107 m2 s–1, (b) 2.0 × 105 m2 s–1, (f) 3.0 × 105 m2 s–1, and (c, d, g, h) 10 K. The background dotted lines show the topographic heights in the model, with negative regions shaded. |

|
| Figure 13 Phase diagrams of dimensional variables for m = 3.7 (left panels) and m = 6 (right panels), respectively. Each ordinate shows the variable AH, and the abscissa gives (a, e) ΔTa, (b, f) ΔTg, (c, g) ATa, and (d, h) ATg. The meaning of colors and symbols are same as that in Fig. 3. |
The results in this section show that the low-index (high-index) equilibrium states have a larger (smaller) wave amplitude and smaller (larger) meridional atmospheric temperature gradient; however, the two types equilibrium states have no marked differences in zonal wind speed. These results are attributed to the wavelike equilibrium that is maintained by the conversion of the mean flow potential energy in the baroclinic atmosphere.
7 Conclusions and discussionTo overcome the shortcoming of the classic Charney’s model that the thermal forcing is always artificially specified, we use a coupled land–atmosphere model. We find that there are still multiple equilibrium states in the presence of topography for a given realistic uneven solar heating. Therefore, this study again verifies the multiple flow equilibria theory. However, in addition to the multiple wave amplitude equilibria associated with high- and low-index types, multiple wave phase equilibria associated with ridge- and trough-types are more prominent in our coupled baroclinic model (Fig. 3). The multiple wave phase equilibria associated with ridge- and trough-types originate from the orographic instability of the Hadley circulation in the presence of topography, which is a pitch-fork bifurcation. Thus, the ridge- and trough-type equilibria can also coexist in the uncoupled model as long as the topography is present (Fig. 6c). But the multiple wave phase equilibria in the uncoupled model is unremarkable, mainly due to the very narrow orographically unstable region (Fig. 5b, Case 2). The land–atmosphere coupling considerably expands the orographically unstable region (Fig. 5b, Case 1), and thus, the multiple wave phase equilibria in the coupled model is prominent (Fig. 3). In other words, the land–atmosphere coupling generates more ridge-type equilibria in the coupled model (Fig. 3, red branch). We have demonstrated that the effect of the land–atmosphere coupling is primarily contributed by the longwave radiation fluxes, and the heat fluxes more or less modify the effect of longwave radiation fluxes. In the longwave radiation fields, the longwave radiation fluxes increase from low to high latitudes (Figs. 9b, f), which reduces the meridional gradient of the net diabatic heating. As a result, compared with the uncoupled model, the Hadley circulation in the coupled model is much more stable; besides, the atmospheric response to the thermal and topographic forcing is much weaker in the coupled model. In a word, the land–atmosphere coupling greatly stabilizes the atmospheric flow.

|
|
Figure 3 The equilibrium bifurcation associated with the change in meridional differential solar heating parameter Cg for m = 3.7 (left panels) and m = 6 (right panels), respectively. The ordinate shows the nondimensional equilibrium values of (a, d) the zonal component
|
|
| Figure 5 (a) Stability curves of the Hadley circulation in the coupled land–atmosphere model (Case 1). The blue solid lines enclose the region of orographic instability. The red solid (black dashed) lines and the top x-axis and the right y-axis enclose the region of baroclinic instability in the presence (absence) of topography. Comparison of the regions of (b) orographic instability, (c) baroclinic instability in the presence of topography, and (d) baroclinic instability in the absence of topography for the four experiments (Cases 1–4). |

|
|
Figure 6 As in Fig. 3, but for Case 3 (without heat flux) with (a) m = 3.7 and (b) m = 6, (c) for Case 2 (without coupling) with m = 3.7, and (d) for Case 4 (without longwave radiation) with m = 3.7. Each ordinate shows the nondimensional equilibrium solution of the wave component
|
We have investigated the ridge- and trough-type equilibria and wave phase in details in this paper. The results show that the ridge-type (trough-type) equilibrium states have lower layer ridges (troughs) over the mountains and have lower layer easterlies (westerlies). We explain that the wave phase of equilibrium states relative to the topography depends on the direction of lower layer zonal wind and horizontal scale of the topography. However, why does the same solar forcing would yield two opposite directions of the lower layer zonal wind? In the absence of topography, we have demonstrated that there is no zonal flow in the lower layer for both the Hadley circulation [Eq. (29)] and the traveling wave (Figs. 4b, c). In the presence of topography, the first bifurcation of the Hadley circulation yields two branches of equilibrium states with opposite directions of the lower layer zonal wind (Figs. 11b, 12b): the trough-type equilibrium has lower layer westerlies, by contrary, the ridge-type equilibrium has lower layer easterlies. Therefore, the generation of two opposite directions of the lower layer zonal wind is still attributed to the presence of topography.

|
| Figure 11 As in Fig. 3, but for dimensional variables for m = 3.7. Only stable equilibrium states are shown here. The blue (red) branch represents trough-type (ridge-type) equilibria, and the black branch represents the Hadley equilibria. |
|
| Figure 12 As in Fig. 11, but for m = 6. |
We have also investigated the high- and low-index equilibria and wave amplitude. The results show that the low-index (high-index) equilibrium states have a larger (smaller) wave amplitude and smaller (larger) meridional atmospheric temperature gradient. However, the high- and low-index equilibrium states have no marked differences in zonal wind speed in our coupled baroclinic model, and this result is qualitatively consistent with the observations (e.g., Benzi et al., 1986; Sutera, 1986). These results can be explained that the wavelike equilibrium is maintained by the conversion of the mean flow potential energy in the baroclinic atmosphere. Therefore, the previous conclusion that the high-index (low-index) equilibria has relative stronger (weaker) zonal flow in the barotropic model (e.g., CD) should be carefully reconsidered.
However, the low-order model that we used is oversimplified and has some limitations. For example, the vertical resolution of our two-layer model is still poor; The land–sea thermal contrast is not taken into account in our model; the flow patterns of the equilibrium states are sensitive to the horizontal resolution of the model (e.g., the flow patterns of the equilibrium states in 9-, 18-, and 24-component systems are different from each other (see Supplementary Figs. S1, S2), which implies that the eddy feedback is important). Therefore, the low-order model is only heuristic and this study is just preliminary. Nevertheless, our results on multiple wave phase equilibria are enlightening to the further study of some large-scale atmospheric phenomena, such as the recurrence of quasi-stationary planetary wave trough and planetary wave ridge over some regions, e.g., the Ural (Dole and Gordon, 1983; Li and Ji, 2001; Molteni, 2003; Ren et al., 2006; Pan et al., 2009; Tan et al., 2017; or see Supplementary Fig. S3). Further studies are needed that examine the extent to which our results agree with the observations. More realistic model should also be used to study the multiple wave phase equilibria in the future.
Acknowledgments. The authors appreciate Professor Ming Cai and also two anonymous reviewers whose detailed comments and constructive suggestions helped to improve the paper. We thank Professor Ruixin Huang of the Woods Hole Oceanographic Institution for his several helpful suggestions. We also thank Stéphane Vannitsem of the Institut Royal Météorologique de Belgique for providing the code of his low-order coupled atmos-phere–ocean model, which is helpful for us to design the low-order coupled land–atmosphere model.
AppendixA. Linearization of the quartic terms in the radiative fluxes
We assume that
| ${T_{\rm{a}}}(x, y, t) = {T_{{\rm a}, 0}}(t) + \delta {T_{\rm{a}}}(x, y, t),$ | (A1) |
| ${T_{\rm{g}}}(x, y, t) = {T_{{\rm g}, 0}}(t) + \delta {T_{\rm{g}}}(x, y, t),$ | (A2) |
where
We assume that the shortwave solar radiation absorbed by the atmosphere and the land are just the function of latitude and time, i.e.,
| ${R_{\rm{a}}}(y, t) = {R_{{\rm a}, 0}}(t) + \delta {R_{\rm{a}}}(y, t),$ | (A3) |
| ${R_{\rm{g}}}(y, t) = {R_{{\rm g}, 0}}(t) + \delta {R_{\rm{g}}}(y, t),$ | (A4) |
where
Neglecting the high-order terms in
| ${\gamma _{\rm{a}}}\frac{{\partial {T_{{\rm a}, 0}}}}{{\partial t}} = - \lambda ({T_{{\rm a}, 0}} - {T_{{\rm g}, 0}}) + {\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}T_{{\rm g}, 0}^4 - 2{\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}T_{{\rm a}, 0}^4 + {R_{{\rm a}, 0}},$ | (A5) |
| $\!\!\begin{split}& {\gamma _{\rm{a}}}(\frac{{\partial \delta {T_{\rm{a}}}}}{{\partial t}} + J(\psi, \delta {T_{\rm{a}}}) - \sigma \omega \frac{p}{R}) = - \lambda (\delta {T_{\rm{a}}} - \delta {T_{\rm{g}}}) \\ &\quad\quad + 4{\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}T_{{\rm g}, 0}^3\delta {T_{\rm{g}}} - 8{\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}T_{{\rm a}, 0}^3\delta {T_{\rm{a}}} + \delta {R_{\rm{a}}},\end{split}\qquad$ | (A6) |
and the land temperature equation [Eq. (7)] becomes
| ${\gamma _{\rm{g}}}\frac{{\partial {T_{{\rm g}, 0}}}}{{\partial t}} = - \lambda ({T_{{\rm g}, 0}} - {T_{{\rm a}, 0}}) - {\sigma _{\rm{B}}}T_{{\rm g}, 0}^4 + {\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}T_{{\rm a}, 0}^4 + {R_{{\rm g}, 0}},$ | (A7) |
| ${\gamma _{\rm{g}}}\frac{{\partial \delta {T_{\rm{g}}}}}{{\partial t}} = - \lambda (\delta {T_{\rm{g}}} - \delta {T_{\rm{a}}}) - 4{\sigma _{\rm{B}}}T_{{\rm g}, 0}^3\delta {T_{\rm{g}}} + 4{\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}T_{{\rm a}, 0}^3\delta {T_{\rm{a}}} + \delta {R_{\rm{g}}}.$ | (A8) |
Note that Eqs. (A5) and (A7) for the averaged temperatures are independent of the perturbations, and thus, stationary solutions can be obtained by solving
| $ - \lambda ({T_{{\rm a}, 0}} - {T_{{\rm g}, 0}}) + {\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}T_{{\rm g}, 0}^4 - 2{\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}T_{{\rm a}, 0}^4 + {R_{{\rm a}, 0}} = 0,$ | (A9) |
| $ - \lambda ({T_{{\rm g}, 0}} - {T_{{\rm a}, 0}}) - {\sigma _{\rm{B}}}T_{{\rm g}, 0}^4 + {\varepsilon _{\rm{a}}}{\sigma _{\rm{B}}}T_{{\rm a}, 0}^4 + {R_{{\rm g}, 0}} = 0.\quad$ | (A10) |
According to the parameter values listed in Table 1, particularly,
| Parameter | Value | Parameter | Value |
|
|
6371 km |
|
5.6 × 10–8 W m–2 K–4 |
|
|
5000 km |
|
1.0 × 107 J m–2 K–1 |
|
|
7.3 km |
|
1.6 × 107 J m–2 K–1 |
|
|
45°N |
|
10 W m–2 K–1 |
|
|
9.8 m–1 s–2 |
|
2.16 × 10–6 m2 s–2 Pa–2 |
|
|
0.0001032 s–1 |
|
89 W m–2 |
|
|
1.62 × 10–11 m–1 s–1 |
|
221 W m–2 |
|
|
287 J kg–1 K–1 |
|
270.22 K |
|
|
0.76 |
|
280.40 K |
B. Equilibrium solutions and their stabilities
To obtain the general equilibrium solutions of Eqs. (19)–(27), we set all of the time derivatives to zero. We obtain
| $- k({\psi _1} - {\theta _1}) - c\tilde h({\theta _3} - {\psi _3}) = 0, \qquad\qquad\qquad\quad\quad $ | (A11) |
| $ - c{n^2}({\psi _1}{\psi _3} + {\theta _1}{\theta _3}) + \beta n{\psi _3} - {B_1}({\psi _2} - {\theta _2}) = 0,\qquad$ | (A12) |
| $c[{n^2}({\psi _1}{\psi _2} + {\theta _1}{\theta _2}) + \tilde h({\theta _1} - {\psi _1})] - \beta n{\psi _2} - {B_1}({\psi _3} - {\theta _3}) = 0, $ | (A13) |
| $c[{\psi _2}{\theta _3} - {\psi _3}{\theta _2} - \sigma '\tilde h({\psi _3} - {\theta _3})] - {B_3}{\theta _1} + k\sigma '{\psi _1} + {D_1}{\theta _1} + {D_2} = 0,$ | (A14) |
| $c({A_1}{\psi _3}{\theta _1} - {A_2}{\psi _1}{\theta _3}) + \beta n\sigma '{\theta _3} - {B_2}{\theta _2} + {B_1}\sigma '{\psi _2} + {D_1}{\theta _2} = 0,\quad$ | (A15) |
| $\begin{split} & c[{A_2}{\psi _1}{\theta _2} - {A_1}{\psi _2}{\theta _1} + \sigma '\tilde h({\psi _1} - {\theta _1})] - \beta n\sigma '{\theta _2}\\ &\quad\quad - {B_2}{\theta _3} + {B_1}\sigma '{\psi _3} + {D_1}{\theta _3} = 0,\end{split}\qquad\qquad\qquad\quad$ | (A16) |
and
| $\left. \begin{aligned}& {T_{{\rm g}, 1}} = \frac{{{d_4}}}{{{d_3}}}{\theta _1} + \frac{{{{C'}_{\rm{\!\!\!\!g}}}}}{{{d_3}}} \\& {T_{{\rm g}, 2}} = \frac{{{d_4}}}{{{d_3}}}{\theta _2} \\& {T_{{\rm g}, 3}} = \frac{{{d_4}}}{{{d_3}}}{\theta _3}\end{aligned} \right\}.$ | (A17) |
In view of Eq. (A11), Eq. (A14) may be written as
| $c[{\psi _2}{\theta _3} - {\psi _3}{\theta _2}] + ({D_1} - 2k'\sigma '){\theta _1} + {D_2} = 0,$ | (A18) |
and Eqs. (A12), (A13), (A15), and (A16) become
| $\left[ {\begin{array}{*{20}{c}} { - {B_1}}&{{B_1}}&{ - c{n^2}{\psi _1} + \beta n}&{ - c{n^2}{\theta _1}} \\ {c{n^2}{\psi _1} - \beta n}&{c{n^2}{\theta _1}}&{ - {B_1}}&{{B_1}} \\ {{B_1}\sigma '}&{{D_1} - {B_2}}&{c{A_1}{\theta _1}}&{ - c{A_2}{\psi _1} + \beta n\sigma '} \\ { - c{A_1}{\theta _1}}&{c{A_2}{\psi _1} - \beta n\sigma '}&{{B_1}\sigma '}&{{D_1} - {B_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\psi _2}} \\[7.5pt] {{\theta _2}} \\[7.5pt] {{\psi _3}} \\[7.5pt] {{\theta _3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ {c\tilde h({\psi _1} - {\theta _1})} \\ 0 \\ { - c\sigma '\tilde h({\psi _1} - {\theta _1})} \end{array}} \right].$ | (A19) |
Equation (A19) constitutes a linear system for the variables
The stability of the equilibrium solution obtained from Eqs. (19)–(27) is determined from the characteristic values of the linear perturbation equations coefficient matrix, which is a nine homogeneous linear equations governing
| Barsugli, J. J., and D. S. Battisti, 1998: The basic effects of atmosphere–ocean thermal coupling on midlatitude variability. J. Atmos. Sci., 55, 477–493. DOI:10.1175/1520-0469(1998)055<0477:TBEOAO>2.0.CO;2 |
| Benzi, R., A. R. Hansen, and A. Sutera, 1984: On stochastic perturbation of simple blocking models. Quart. J. Roy. Meteor. Soc., 110, 393–409. DOI:10.1002/qj.49711046406 |
| Benzi, R., P. Malguzzi, A. Speranza, et al., 1986: The statistical properties of general atmospheric circulation: Observational evidence and a minimal theory of bimodality. Quart. J. Roy. Meteor. Soc., 112, 661–674. DOI:10.1002/qj.49711247306 |
| Cai, M., and M. Mak, 1987: On the multiplicity of equilibria of baroclinic waves. Tellus, 39A, 116–137. DOI:10.3402/tellusa.v39i2.11746 |
| Cehelsky, P., and K. K. Tung, 1987: Theories of multiple equilibria and weather regimes—A critical reexamination. Part II: Baroclinic two-layer models. J. Atmos. Sci., 44, 3282–3303. DOI:10.1175/1520-0469(1987)044<3282:TOMEAW>2.0.CO;2 |
| Charney, J. G., and J. G. DeVore, 1979: Multiple flow equilibria in the atmosphere and blocking. J. Atmos. Sci., 36, 1205–1216. DOI:10.1175/1520-0469(1979)036<1205:MFEITA>2.0.CO;2 |
| Charney, J. G., and D. M. Straus, 1980: Form-drag instability, multiple equilibria and propagating planetary waves in baroclinic, orographically forced, planetary wave systems. J. Atmos. Sci., 37, 1157–1176. DOI:10.1175/1520-0469(1980)037<1157:FDIMEA>2.0.CO;2 |
| Christensen, C. W., and A. Wiin-Nielsen, 1996: Blocking as a wave–wave interaction. Tellus A: Dyn. Meteor. Oceanogr., 48, 254–271. DOI:10.3402/tellusa.v48i2.12059 |
| Crommelin, D. T., J. D. Opsteegh, and F. Verhulst, 2004: A mechanism for atmospheric regime behavior. J. Atmos. Sci., 61, 1406–1419. DOI:10.1175/1520-0469(2004)061<1406:AMFARB>2.0.CO;2 |
| De Cruz, L., J. Demaeyer, and S. Vannitsem, 2016: The modular arbitrary-order ocean–atmosphere model: MAOOAM v1.0. Geosci. Model Dev., 9, 2793–2808. DOI:10.5194/gmd-9-2793-2016 |
| De Swart, H. E., 1988: Low-order spectral models of the atmospheric circulation: A survey. Acta Appl. Math., 11, 49–96. DOI:10.1007/BF00047114 |
| Dole, R. M., and N. D. Gordon, 1983: Persistent anomalies of the extratropical Northern Hemisphere wintertime circulation: Geographical distribution and regional persistence characteristics. Mon. Wea. Rev., 111, 1567–1586. DOI:10.1175/1520-0493(1983)111<1567:PAOTEN>2.0.CO;2 |
| Egger, J., 1981: Stochastically driven large-scale circulations with multiple equilibria. J. Atmos. Sci., 38, 2606–2618. DOI:10.1175/1520-0469(1981)038<2606:SDLSCW>2.0.CO;2 |
| Faranda, D., G. Masato, N. Moloney, et al., 2016: The switching between zonal and blocked mid-latitude atmospheric circulation: A dynamical system perspective. Climate Dyn., 47, 1587–1599. DOI:10.1007/s00382-015-2921-6 |
| He, Y. L., J. P. Huang, and M. X. Ji, 2014: Impact of land–sea thermal contrast on interdecadal variation in circulation and blocking. Climate Dyn., 43, 3267–3279. DOI:10.1007/s00382-014-2103-y |
| He, Y. L., J. P. Huang, D. D. Li, et al., 2018: Comparison of the effect of land–sea thermal contrast on interdecadal variations in winter and summer blockings. Climate Dyn., 51, 1275–1294. DOI:10.1007/s00382-017-3954-9 |
| Holton, J. R., and G. J. Hakim, 2012: An Introduction to Dynamic Meteorology. 5th Ed., Academic Press, Amsterdam, 552 pp. |
| Huang, J. P., M. X. Ji, Y. K. Xie, et al., 2016: Global semi-arid climate change over last 60 years. Climate Dyn., 46, 1131–1150. DOI:10.1007/s00382-015-2636-8 |
| Huang, J. P., Y. K. Xie, X. D. Guan, et al., 2017a: The dynamics of the warming hiatus over the Northern Hemisphere. Climate Dyn., 48, 429–446. DOI:10.1007/s00382-016-3085-8 |
| Huang, J., Y. Li, C. Fu, et al., 2017b: Dryland climate change: Recent progress and challenges. Rev. Geophys., 55, 719–778. DOI:10.1002/2016RG000550 |
| Koo, S., and M. Ghil, 2002: Successive bifurcations in a simple model of atmospheric zonal-flow vacillation. Chaos: An Interdiscip. J. Nonlinear Sci., 12, 300–309. DOI:10.1063/1.1468249 |
| Legras, B., and M. Ghil, 1985: Persistent anomalies, blocking and variations in atmospheric predictability. J. Atmos. Sci., 42, 433–471. DOI:10.1175/1520-0469(1985)042<0433:PABAVI>2.0.CO;2 |
| Li, J. P., and J. F. Chou, 1996: Source of atmospheric multiple equilibria. Chin. Sci. Bull., 41, 2074–2077. |
| Li, J. P., and J. F. Chou, 1997: The effects of external forcing, dissipation and nonlinearity on the solutions of atmospheric equations. Acta Meteor. Sinica, 11, 57–65. |
| Li, J. P., and J. X. L. Wang, 2003: A modified zonal index and its physical sense. Geophys. Res. Lett., 30, 1632. DOI:10.1029/2003GL017441 |
| Li, J. P., and J. F. Chou, 2003: Advances in nonlinear atmospheric dynamics. Chinese J. Atmos. Sci., 27, 653–673. DOI:10.3878/j.issn.1006-9895.2003.04.15 |
| Li, M. C., and Z. X. Luo, 1983: Nonlinear mechanism of abrupt change of atmospheric circulation during June and October. Scientia Sinica (Series B), 26, 746–754. |
| Li, S. L., and L. R. Ji, 2001: Persistent anomaly in Ural area in summer and its background circulation characteristics. Acta Meteor. Sinica, 59, 280–293. DOI:10.11676/qxxb2001.030 |
| Liu, C. J., and S. Y. Tao, 1983: Northward jumping of subtropical highs and cusp catastrophe. Scientia Sinica (Series B), 26, 1065–1074. |
| Lindzen, R. S., 1986: Stationary planetary waves, blocking, and interannual variability. Adv. Geophys., 29, 251–273. DOI:10.1016/S0065-2687(08)60042-4 |
| Luo, Z. X., 1987: Abrupt change of flow pattern in baroclinic atmosphere forced by joint effects of diabatic heating and orography. Adv. Atmos. Sci., 4, 137–144. DOI:10.1007/BF02677060 |
| Miao, J. H., and M. F. Ding, 1985: Catastrophe theory of seasonal variation. Scientia Sinica (Series B), 28, 1079–1092. |
| Molteni, F., 2003: Weather regimes and multiple equilibria. Encyclopedia of Atmospheric Sciences, J. R. Holton, J. Pyle, and J. A. Curry, Eds., Academic Press, Academic, 2577–2586. |
| Monin, A. S., 1986: An Introduction to the Theory of Climate. D. Reidel Publishing Company, Dordrecht, Holland, 261 pp. |
| Namias, J., 1950: The index cycle and its role in the general circulation. J. Meteor., 7, 130–139. DOI:10.1175/1520-0469(1950)007<0130:TICAIR>2.0.CO;2 |
| Nigam, S., and E. DeWeaver, 2003: Stationary waves (orographic and thermally forced). Encyclopedia of Atmospheric Sciences, J. R. Holton, J. Pyle, and J. A. Curry, Eds., Academic Press, Academic, 2121–2137. |
| Pan, J., L. R. Ji, and C. Bueh, 2009: Intraseasonal climate characteristics of the summertime persistent anomalous circulation over Eurasian middle and high latitudes. Chinese J. Atmos. Sci., 33, 300–312. DOI:10.3878/j.issn.1006-9895.2009.02.09 |
| Reinhold, B. B., and R. T. Pierrehumbert, 1982: Dynamics of weather regimes: Quasi-stationary waves and blocking. Mon. Wea. Rev., 110, 1105–1145. DOI:10.1175/1520-0493(1982)110<1105:DOWRQS>2.0.CO;2 |
| Reinhold, B. B., and R. T. Pierrehumbert, 1985: Corrections to " Dynamics of weather regimes: Quasi-stationary waves and blocking”. Mon. Wea. Rev., 113, 2055–2056. DOI:10.1175/1520-0493(1985)113<2055:>2.0.CO;2 |
| Ren, H. L., P. Q. Zhang, J. F. Chou, et al., 2006: Large-scale low-frequency rainfall regimes and their transition modes in summertime over China. Chin. Sci. Bull., 51, 1355–1367. DOI:10.1007/s11434-006-1355-2 |
| Rossby, C. G., 1939: Relation between variations in the intensity of the zonal circulation of the atmosphere and the displacements of the semi-permanent centers of action. J. Marine Res., 2, 38–55. DOI:10.1357/002224039806649023 |
| Smith, R. B., 1979: The influence of mountains on the atmosphere. Adv. Geophys., 21, 87–230. DOI:10.1016/S0065-2687(08)60262-9 |
| Sura, P., 2002: Noise-induced transitions in a barotropic β-plane channel . J. Atmos. Sci., 59, 97–110. DOI:10.1175/1520-0469(2002)059<0097:NITIAB>2.0.CO;2 |
| Sutera, A., 1986: Probability density distribution of large-scale atmospheric flow. Adv. Geophys., 29, 227–249. DOI:10.1016/S0065-2687(08)60041-2 |
| Tan, G. R., H. L. Ren, H. S. Chen, et al., 2017: Detecting primary precursors of January surface air temperature anomalies in China. J. Meteor. Res., 31, 1096–1108. DOI:10.1007/s13351-017-7013-6 |
| Thompson, D. W. J., and J. M. Wallace, 2001: Regional climate impacts of the Northern Hemisphere annular mode. Science, 293, 85–89. DOI:10.1126/science.1058958 |
| Tung, K. K., and A. J. Rosenthal, 1985: Theories of multiple equilibria—A critical reexamination. Part I: Barotropic models. J. Atmos. Sci., 42, 2804–2819. DOI:10.1175/1520-0469(1985)042<2804:TOMEAC>2.0.CO;2 |
| Vannitsem, S., J. Demaeyer, L. De Cruz, et al., 2015: Low-frequency variability and heat transport in a low-order nonlinear coupled ocean–atmosphere model. Physica D: Nonlinear Phenomena, 309, 71–85. DOI:10.1016/j.physd.2015.07.006 |
| Yoden, S., 1983: Nonlinear interactions in a two-layer, quasi-geostrophic, low-order model with topography. Part I: Zonal flow-forced wave interactions. J. Meteor. Soc. Japan, 61, 1–38. DOI:10.2151/jmsj1965.61.1_1 |
| Zhu, Z. X., 1985: Equilibrium states of planetary waves forced by topography and perturbation heating and blocking situation. Adv. Atmos. Sci., 2, 359–367. DOI:10.1007/BF02677252 |
| Zhu, Z. X., and B. Z. Zhu, 1982: Equilibrium states of ultra-long waves driven by non-adiabatic heating and blocking situation. Scientia Sinica (Series B), 25, 1201–1212. |
 2018, Vol. 32
2018, Vol. 32



