The Chinese Meteorological Society
Article Information
- ZHANG, Chongran, and Jing ZHANG, 2018.
- Modeling Study of Foehn Wind Events in Antarctic Peninsula with WRF Forced by CCSM. 2018.
- J. Meteor. Res., 32(6): 909-922
- http://dx.doi.org/10.1007/s13351-018-8067-9
Article History
- Received June 4, 2018
- in final form September 17, 2018
2. Department of Physics, North Carolina A & T State University, Greensboro, NC 27411, USA
The Antarctic Peninsula (AP), a region where ice and snow-covered mountain ranges dominate the landscape, has undergone rapid environmental changes in the past decades. This includes temperature increase (Vaughan et al., 2003; Turner et al., 2005), retreating glacier (Cook et al., 2005), and increased melt areas (Vaughan, 2006). Dynamic thinning of glaciers, glacier surface lowering (Pritchard et al., 2009) as well as break up and disintegration of ice shelf have also been observed (Cook and Vaughan, 2010; Hogg and Gudmundsson, 2017). There remain major uncertainties regarding the current and future contribution to sea level rise due to these events within the cryosphere (Rignot et al., 2008). Major mechanisms proposed for the melt and break up of ice-shelves along AP include gravitational effect of melt water ponds (Scambos et al., 2000), warm ocean currents (Shepard et al., 2003), warm air advection, and foehn wind warming (van den Broeke, 2005). Among them, foehn wind warming and warm air advection have been linked to enhanced surface melting on the Larsen Ice Shelf. van den Broeke (2005) found that peak melt rates during the summer observed on Larsen Ice Shelf coincided with winds from the northwest, which suggested that the passage of winds over orographic barriers contributed to warming and melting. The study uses this relationship to conclude that the melting is due partly to foehn wind warming and partly to warm air advection. Marshall et al. (2006) found that higher temperatures at Esperanza station to the east of AP coincided with higher Southern Annular Mode (SAM) summers. A correlation was found in the study that linked higher SAM index during summer 1989–2004 to increased frequency of westerlies at Esperanza station. Barry (2008) and Elvidge and Renfrew (2016) have outlined that mechanisms responsible for the foehn wind warming and latent heating and isentropic drawdown are the two major ones.
Grosvenor et al. (2014) studied a foehn wind event that occurred on the east side of AP, which was observed by using aircraft instrument and simulated by using the Weather Research and Forecasting (WRF) model forced with the ECMWF operational analysis data for the initial and boundary conditions. The study concluded that while differences exist between model and observation, overall agreement gives confidence in the model representation of reality. In this study, we use the WRF model forced by both original and corrected simulations of the Community Climate System Model 4 (CCSM) to study the foehn wind events occurring in the AP area. Bruyere et al. (2014) suggested that the corrected CCSM simulations yield more accurate spatial distribution and annual frequency of simulated tropical cyclone activity. Temperature and precipitation in North America also improved in the corrected CCSM simulations, but comparison of regional simulations forced by these two CCSM simulations has not been made. We will compare WRF modeling results forced by original and corrected CCSM data. Our study will have the dual-purpose of modeling the physical features of foehn winds and comparing the impacts of forcing data on the foehn wind modeling. The latter will allow us to determine differences that arise from simulation of mesoscale foehn phenomenon when different CCSM forcing data are used. This will provide context for a future study, which will use CCSM projections to evaluate foehn wind warming and its impact on surface melting and surface mass balance under future climate change scenarios. In this study, we also explore how the properties of incoming air, such as temperature, precipitation, and wind speed on the windward side, impact foehn wind warming along the AP.
The remainder of this paper is organized into sections. Section 2 briefly describes the data, methods, and modeling area used in this study. Section 3 presents the synoptic setting of the foehn wind events in the CCSM forcing data and WRF simulations. WRF simulations of foehn wind warming along AP and the comparison forced by the original and corrected CCSM are detailed in Sections 4 and 5. Interactions between the incoming air and foehn wind warming are explored in Section 6. Finally, a summary and discussion of this study is given in Section 7.
2 Data and methodsFoehn wind events typically occur from December to February in the AP area (e.g., Cape et al., 2015; Elvidge and Renfrew, 2016). Since 2005 is the most recent year in the CCSM historical simulations, the foehn wind events occurred in January, February, or December 2005 can be more representative of current climate for the AP region. The study period covers 15–18 February 2005 during which two foehn wind events were detected along AP in the CCSM simulations. The first foehn event occurred immediately when the simulation started and lasted to 2100 UTC 15 February with peak leeward temperatures at around 1800 UTC 15 February. The second foehn event occurred from 1800 UTC 16 February to 0000 UTC 18 February with peak temperatures at around 1800 UTC 17 February. A triple nested WRF domain was used with horizontal resolutions of 50, 10, and 2 km, respectively (Fig. 1a). The model physics configurations include Morrison Double Moment for microphysics (Morrison et al., 2009), Rapid Radiative Transfer Model GCMs for shortwave and longwave schemes (Iacono et al., 2008), Noah Land Surface Model for Land Surface Physics (Chen and Dudhia, 2001), MM5 similarity scheme for surface layer (Paulson, 1970), Kain–Fritsch for cumulous parameterization (Kain, 2004), and Mellor–Yamada Nakanishi and Niino Level 2.5 for Planetary Boundary Layer (Hong et al., 2006). The simulation period is from 0000 UTC 15 February to 0000 UTC 18 February 2005.
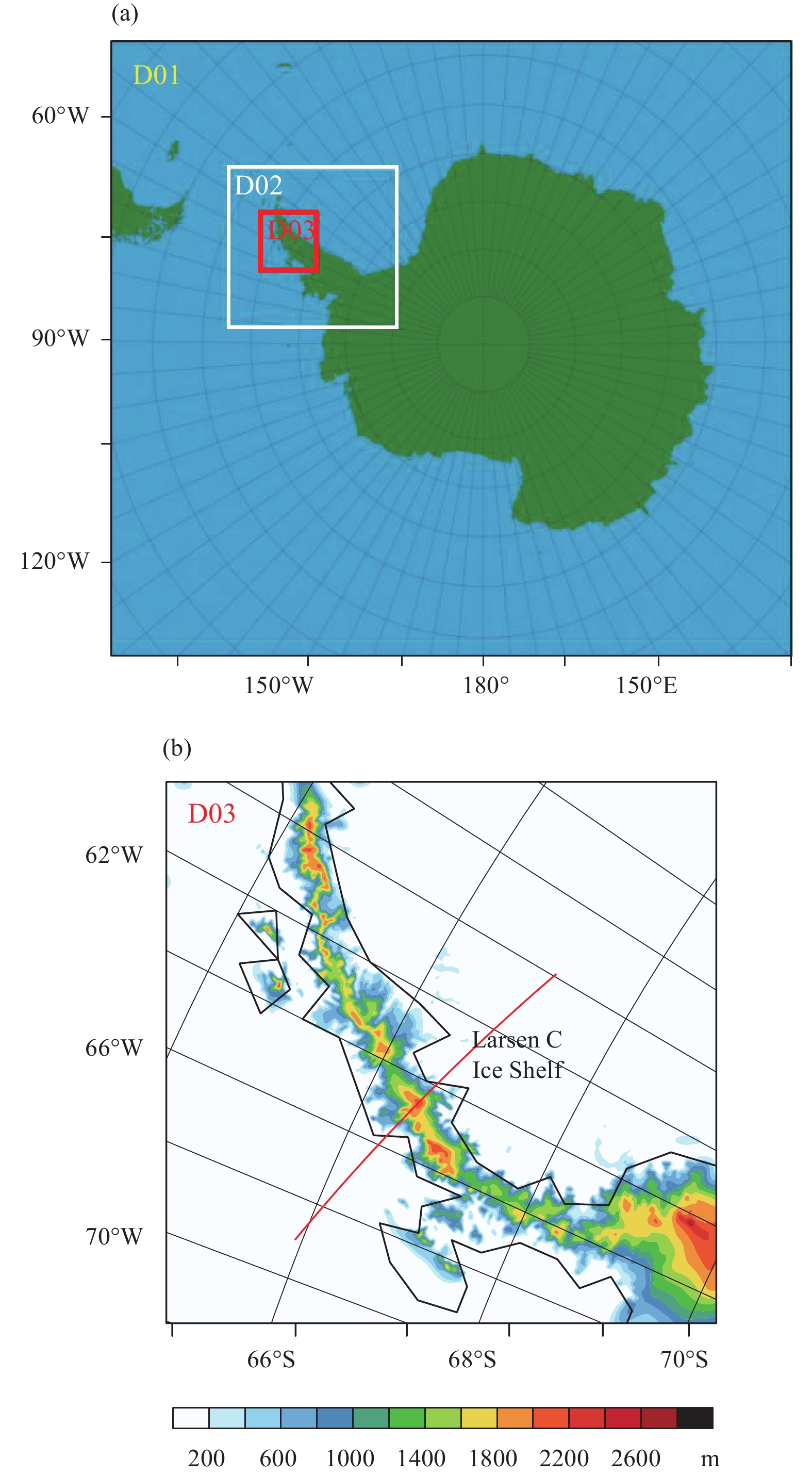
|
| Figure 1 (a) WRF domain set up for the study area with inner (D03), middle (D02), and outer (D01) domains with the grid sizes of 2, 10, and 50 km, respectively, and (b) plan view of transect (red line across AP toward the Larsen C Ice Shelf) used to study cross mountain flows and topography contours (m) in D03. |
The fifth Coupled Model Intercomparison Project (CMIP5) is an experimental project facilitating assessment of the strengths and weaknesses of climate models, which can enhance and focus the development of future models. The CCSM4 is one of the models which participate in the CMIP5. Due to the complex nature of earth’s climate, these models diverge from observations and corrections to variables are necessary for the model runs to accurately reflect observations. The use of ECMWF Reanalysis-Interim (ERA-Interim) data is involved in the CMIP5/CCSM correction process (Bruyere et al., 2014). The first step of the correction process involves breaking the variable to be corrected within the CCSM result into a seasonally varying mean climatological component plus a perturbation term. These variables include zonal and meridional wind speed, geopotential height, temperature, relative humidity, sea surface temperature, and mean sea level pressure. The second step in the correction process involves replacing the mean component in the CCSM variable with the corresponding mean value of the variable from ERA-Interim while preserving the perturbation term. In this study, WRF simulation experiments are carried out using the original and corrected CCSM simulations as initial and boundary conditions.
To depict the foehn wind events occurring in the AP area, a transect across the central part of Graham Land where Larsen C Ice Shelf is attached on the east side of AP is selected (Fig. 1b). This transect is oriented in the northwest to southeast directions and the presence of foehn winds coincides with the existence of north westerlies flowing parallel to the transect. This is consistent with previous findings linking enhanced SAM, increased westerlies and foehn winds to warmer temperatures in east AP (Orr et al., 2004, 2008; van Lipzig et al., 2008; Elvidge et al., 2016). Vertical profiles of temperature and wind vector were analyzed along this transect in order to provide a detailed view of foehn wind warming. It has been suggested that foehn wind warming be quantified by subtracting the windward temperature from the leeward temperature. The leeward temperature is taken near the base of the slopes where warming is maximized, and the windward temperature is taken at the same height as leeward temperature but further than the Rossby radius of deformation (150 km) upwind from the base of the mountain (Elvidge and Renfrew, 2016). More specifically, the Rossby radius of deformation is defined as λR = Nh/f, where f is the Coriolis parameter upwind of the mountain, N is the Brunt–Vaisala frequency upwind of the mountain, and h is the height of the mountain. It can be interpreted as the minimum distance upwind of the mountain where air does not experience the effects of blocking due to topography. In this study, we quantify foehn wind warming by following a similar method.
3 Synoptic setting of the foehn wind events in February 2005The synoptic setting of the foehn wind events in this study is illustrated with sea level pressure, surface temperature, and wind vector plots over the second nested domain (D02 in Fig. 1a). The original CCSM forcing data and WRF 10-km resolution simulation can be compared with Fig. 2. During the entire course of the two foehn wind events, prevailing winds blowing toward the AP mountain barrier are the result of cyclonic circulation crossing the AP. At 0600 UTC 15 February, a low-pressure center with cyclonic circulation was located at the bottom left corner of the study domain, which is west of the AP. This generated flow perpendicular to the AP mountains (westerly winds) over the southern and central AP as shown in both the CCSM forcing data and the WRF simulation (Figs. 2a, f). These westerly winds climbed over the AP mountain barrier and generated foehn wind warming on the leeward side as shown in the WRF simulation (Fig. 2f). At 1800 UTC, 12 h later, the low-pressure center (956 hPa in CCSM and 955 hPa in WRF) approached closer to the AP, which resulted in strong warm advection across southern AP as well as northerly wind flow parallel to the mountain barrier over the central AP (Figs. 2b, g). At 1200 UTC 16 February, the low-pressure center (959 hPa in CCSM and 962 hPa in WRF) crossed over to the eastern side of AP (Figs. 2c, h) and the associated cyclonic circulation around the low-pressure center advected cold air from the south, thereby ending the accumulated warming caused by the earlier foehn winds. The first foehn wind event ended at 2100 UTC 15 February. As the first low-pressure center continuously moved eastward out of the study domain, another cyclonic system appeared at the bottom left corner of study domain again at 0600 UTC 17 February (Figs. 2d, i). Same as before, the second foehn wind event occurred when the low-pressure center moved toward the AP barrier from 1800 UTC 16 February to 0000 UTC 18 February. It should be noted that the WRF simulation ended at 0000 UTC 18 February (Figs. 2e, j) in order to maintain the accuracy of modeling results. Both CCSM forcing and WRF simulation show that before the low-pressure center moved sufficiently close to the AP mountain barrier to cause surface level flow parallel to the mountain barrier, flow was primarily perpendicular to the barrier (Figs. 2a, d, f, i).

|
| Figure 2 Comparison of (a–e) CCSM forcing and (f–j) WRF 10-km resolution simulation of sea level pressure (SLP, black contour; hPa), surface temperature (color; °C ), and wind vector (black vector; m s-1) at (a, f) 0600, (b, g) 1800 UTC 15, (c, h) 1200, (d, i) 0600 UTC 17, and (e, j) 0000 UTC 18 February. |
A major difference between CCSM forcing and WRF simulation is the surface flow’s position relative to surface temperature gradient. This is obvious when comparing wind vector relative to temperature gradient for CCSM vs WRF to the west of AP at 0600 UTC February 15 (Figs. 2a, f). For CCSM, vectors are more perpendicular to temperature gradient and oriented more northerly implying stronger advection compared to WRF wind vectors, which are oriented more westerly. However, at the beginning of the second foehn wind event, i.e., 0600 UTC 17 February, WRF and CCSM show more resemblance relative to temperature gradient; in this case, flow within WRF and CCSM is more similar compared to 0600 UTC 15 February (Figs. 2a, d, f, i). Furthermore, temperature patterns from CCSM forcing and WRF simulation are similar to most parts of the study domain that are relatively flat but have significant differences over the mountain areas. Notable differences in temperature occur on the leeward side of the northernmost section of AP at 1800 UTC 15 and 0000 UTC 18 February when foehn wind warming is occurring and cross peninsula flows dominate. The ability of WRF simulation to resolve foehn wind warming is what accounts for these differences in leeward temperature. More details of WRF’s capability in capturing foehn wind warming are to be discussed in the following section.
4 WRF simulation of the foehn wind events in February 2005In this section, to better describe foehn wind warming captured by the WRF model, we will focus on analyzing the WRF results from the innermost, 2-km resolution domain (D03 in Fig. 1) forced by the original CCSM simulation. Surface warming along the leeward foothill was detected during the first foehn event, which occurred immediately after the start of the simulation till 2100 UTC 15 February, e.g., at 0600 UTC (Fig. 3a) and 1800 UTC 15 February (Fig. 3b). The overall much warmer temperature at 1800 UTC was attributed to strong daylight radiation. Similar warming was also seen during the second foehn event from 1800 UTC 16 to 0000 UTC 18 February, e.g., at 0600 UTC 17 (Fig. 3c) and 0000 UTC 18 February (Fig. 3d). Furthermore, when surface temperatures averaged over a 20 × 20-km2 square area (Fig. 3b) within the Larsen C Ice Shelf were calculated, it was found that the greatest leeward warming occurred in the 2-km resolution simulation, with slightly less warming in the 10-km resolution simulation and the least amount of warming in CCSM (Fig. 3e). Obviously, this is because higher resolution has better ability to resolve complex topography and has higher mountain peaks, while CCSM has the coarsest resolution, the least ability to resolve complex topography, and lower mountain peaks. In particular, peak elevation along our cross-section of study for CCSM is around 0.4 km while the peak elevation in WRF 2-km domain is around 1.8 km. A mechanism linked to the height of topography can clearly explain the differences in leeward warming. For example, since the windward side tends to be saturated, the air parcel condenses and releases latent heat as it climbs the mountain barrier. If the mountain peak is higher, it needs to climb a much longer distance before reaching the top and descending the leeward slopes. Because of this longer distance climbed, there is more opportunity to release latent heat while climbing the windward slopes for higher resolution simulation with higher topography and this will result in more warming on the leeward side.
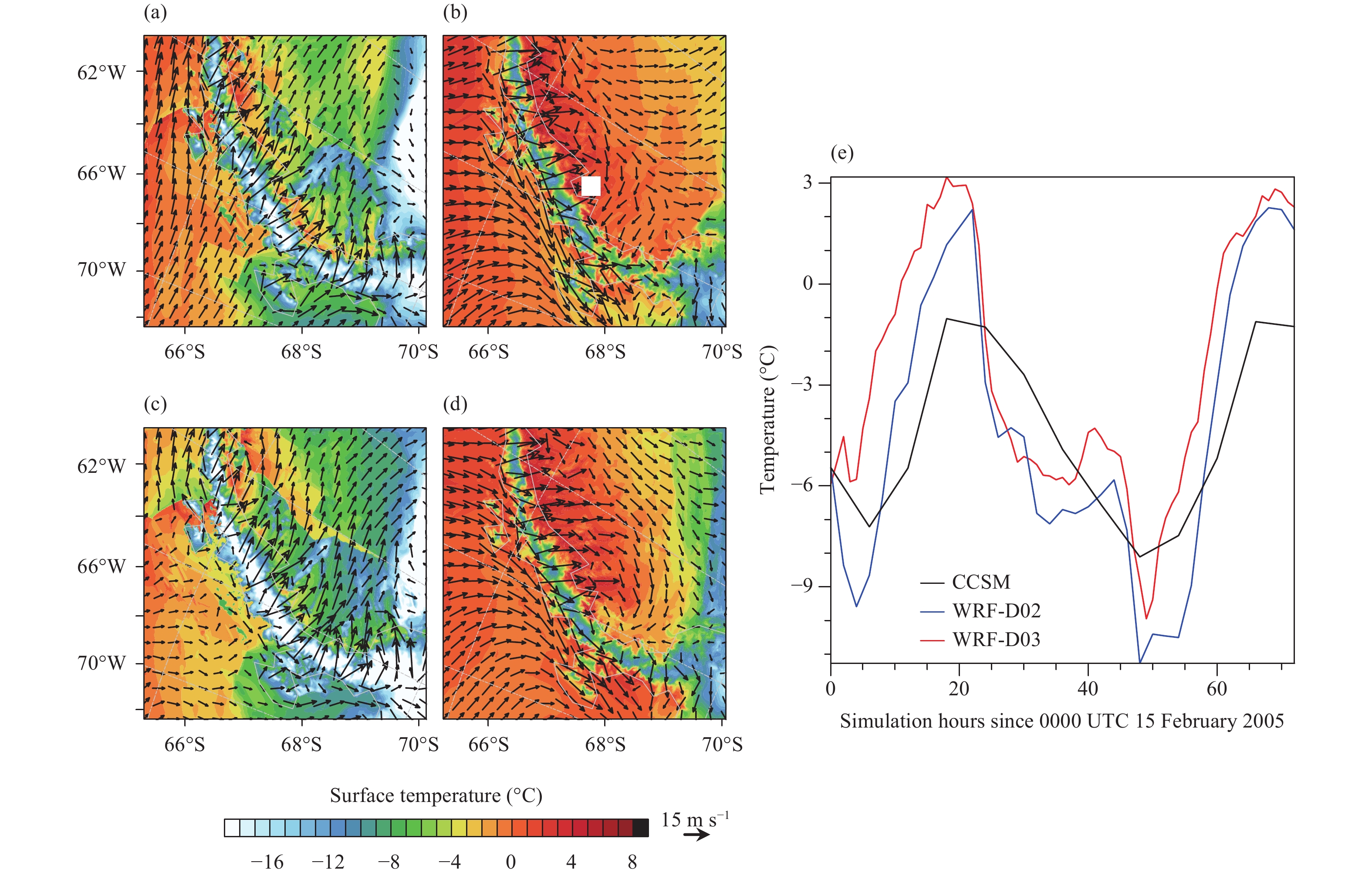
|
| Figure 3 Surface temperature (color contours) and wind vector (black vector) from WRF 2-km resolution simulation forced by CCSM at (a) 0600, (b) 1800 UTC 15, (c) 0600 UTC 17, and (d) 0000 UTC 18 February. Plot (e) represents time series of leeward surface temperatures averaged over the white square area (located at the base of the leeward slopes along the transect of study) as shown in (b) from CCSM (black), WRF 10-km resolution (D02, blue), and 2-km resolution (D03, red) simulations. |
The leeward temperature within Larsen C Ice Shelf rises much more rapidly in the WRF simulations compared to CCSM forcing because WRF is able to better resolve mesoscale foehn wind warming. As result, the leeward temperature exceeds 0°C in both foehn wind events for both 2- and 10-km resolution simulations, while in CCSM forcing, the temperature remains below 0°C (Fig. 3e). More precisely, in the 2-km resolution simulation, the 0°C melt threshold for ice is exceeded for a duration of around 13 h while it is exceeded for around 10 h in the 10-km resolution simulation. This demonstrates that melt estimates over Larsen C may vary between forcing data derived from global simulations and high-resolution WRF downscaling. Different resolutions in the downscaling simulations can also lead to differences in estimates of surface melt to some extent.
To better understand the vertical structures of foehn wind captured by WRF, we further examine the two-dimensional vertical and cross-AP wind components and temperature distribution along the cross-section shown in Fig. 1b. At 0000 UTC 15 February, the WRF simulation was initialized with CCSM forcing data and the vertical profile of temperature and wind vector showed no significant warming on the leeward side despite wind vectors, which appeared to ascend the windward and descend the leeward slopes (Fig. 4a). However, adjustments were made after 6-h spin up and by 0600 UTC 15 February, significant foehn wind warming on the leeward side was already detected (Fig. 4b). The leeward warming at this time could also be attributed to the drainage flows caused by the extreme cold mountain top (< –20°C). It is worth noting that the warming mechanism due to drainage flow involves higher elevation air on the windward side passing over the AP mountain range and descending on the leeward side. The adiabatic warming of potentially warmer air during its descending is what causes the warming here. This process is also referred to as isentropic drawdown byElvidge and Renfrew (2016). By 1500 UTC 15 February, while the leeward warming continued, there was a reversal in wind direction along the transect at lower levels (~0–0.5 km) that was absent in upper levels. It is possible that this wind reversal is partially the result of local high pressure building up due to winds incident on the base of western AP mountain barrier. As a result of this local pressure buildup, surface winds moved away from the barrier, which further impacted upstream winds and could cause greater vertical motion in upstream winds (Fig. 4c). The winds could be lifted much earlier than if no pressure built up occurred at the base of the slopes. A comparison of Figs. 4b, c, d shows noticeably stronger vertical motion along the transect at 1500 UTC. This shows that gentler slope is simulated by the wind reversal, which can help lifting and thereby generate stronger precipitation. Indeed, the strongest precipitation rate of > 2 mm h –1 over the entire simulation period along the windward side of the transect occurred between 1600 and 2000 UTC 15 February as shown in Fig. 7a. Accordingly, strong enhancement of foehn wind warming also occurred during this time. It should be noted that foehn wind warming during period with significant precipitation involves the latent heating mechanism. The time at 2100 UTC 15 February (Fig. 4d) corresponds to that when the low-pressure center of cyclonic system begins to pass through the AP region. The region where the transect is located experiences strong westerlies and wind speeds reach a peak (> 30 m s–1) during this time. By 0600 UTC 16 February, the low-pressure center had already passed over the AP mountains and had begun to advect cold southerly air thereby displacing the warmer air from earlier foehn wind warming (Fig. 4e). The warm air had been completely displaced by cyclonic circulation to the east by 1200 UTC 16 February and simultaneous cold air advection from southerly flow to the west of the AP had also cooled down the windward side (Figs. 2h and 4f). It is also worth noting that the ascending wind right after the descending wind on the leeward slope is a gravity wave (Figs. 4b, 4d, 5b, and 5d). In particular, it occurred because descending air reached the inversion layer and was unable to descend further. As a result, it bounced upward, which caused ascending motion beside the descending motion.
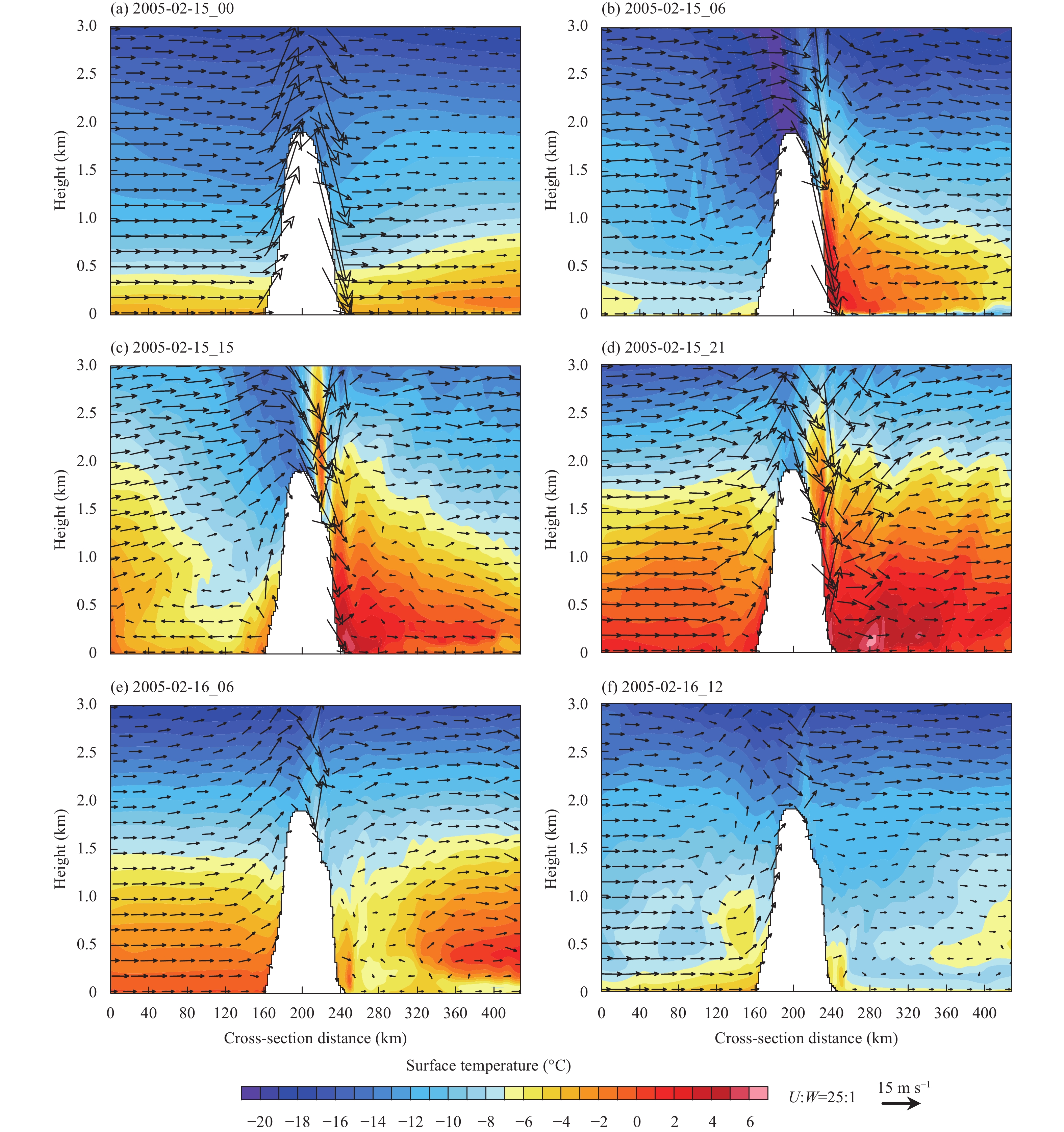
|
| Figure 4 Cross-section with AP mountain range shaded in white showing temperature contours (color) and wind vector (black arrows) from WRF 2-km resolution simulation at (a) 0000, (b) 0600, (c) 1500, and (d) 2100 UTC 15, and (e) 0600, (f) 1200 UTC 16 February along the transect as shown in Fig. 1b for the first foehn wind event of study period. |
The second foehn event began after 1800 UTC 16 February, when little warming existed on the leeward side (Fig. 5a), but by 0600 UTC 17 February, significant warming occurred on the leeward side (Fig. 5b). Similar to the first foehn event, the leeward warming at this time could be also be attributed to strong isentropic drawdown due to the drainage of cold air. It was the time at 1800 UTC 17 February when the low-pressure center moved close enough to the mountain barrier to cause surface winds to be reversed (Fig. 5c). By a similar mechanism to that described in the first foehn event, lifting happened further upstream than if no flow reversal occurred. Moreover, stronger lifting generated the second largest precipitation rate of ~1.5 mm h–1 along the windward side of the transect at this time (Fig. 7a). Significant warm advection and high precipitation also occurred when the low-pressure center moved closer to the AP (Figs. 5c, d), which favors stronger latent heat release within the ascending air. As a result, very warm temperatures (~6°C) occurred on the leeward foothill.
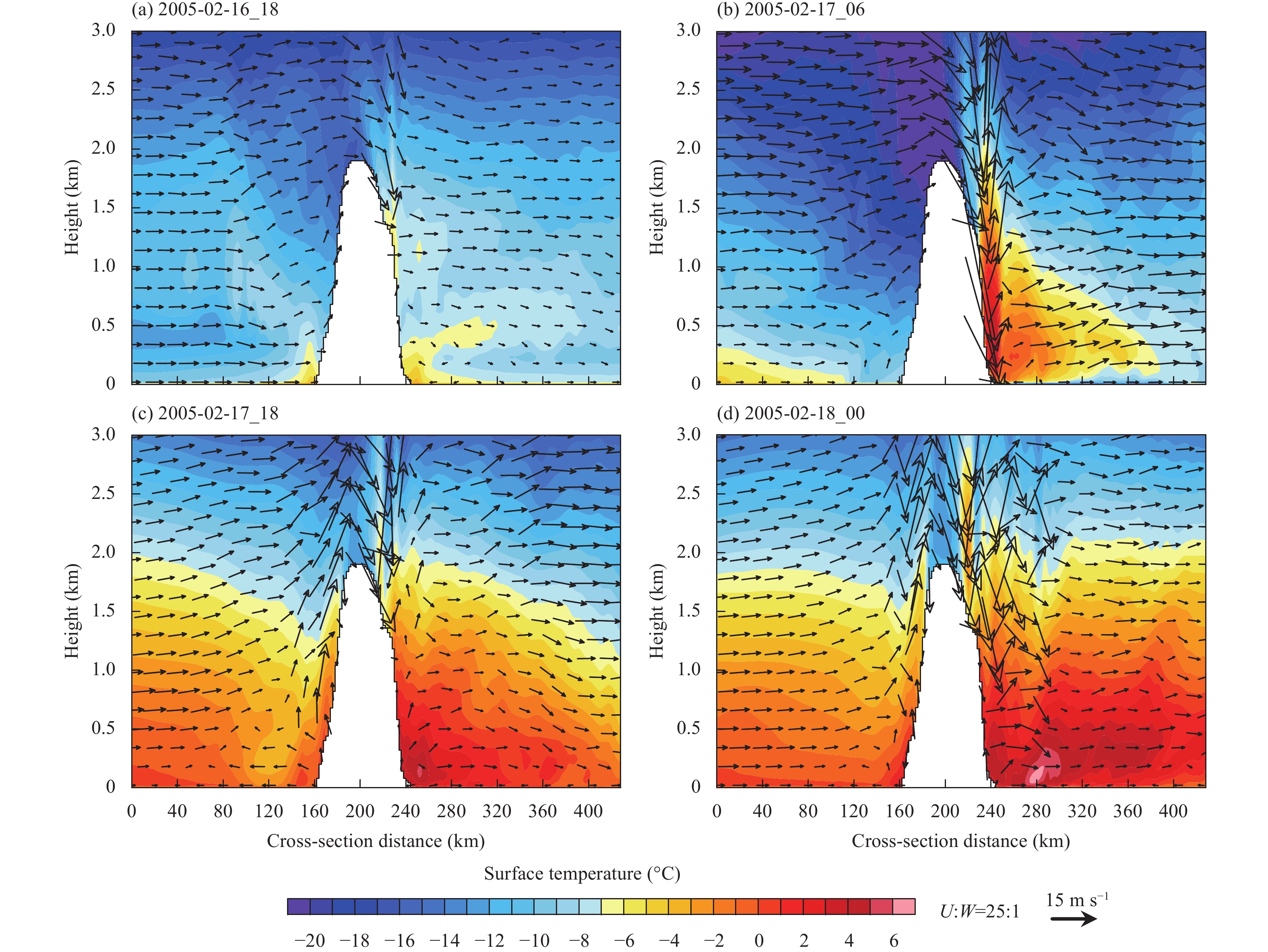
|
| Figure 5 As in Fig. 4, but for at (a) 1800 UTC 16, (b) 0600, (c) 1800 UTC 17, and (d) 0000 UTC 18 February for the 2nd foehn wind event of study period. |
Although isentropic drawdown and latent heating are the two major mechanisms, which contribute to foehn wind warming in our case study, a relation also exists between foehn wind warming and thermal advection. In particular, precipitation tends to occur when there is warm advection. Since precipitation is also correlated with latent heating, the increased prevalence of precipitation during warm advection implies that warm advection plays an important role in foehn wind warming. Without warm advection and no significant precipitation present, foehn wind warming is mainly caused by the heating mechanism of isentropic drawdown.
During the first foehn event (0600–1600 UTC 15 February), the most intense warming was adjacent to the base of the leeward slope (Figs. 4b, c), before the low-pressure center moved close to the AP region. During this time, the incoming air wind speed along the transect, calculated by averaging wind speed over 0–40 km along transect and between 1 and 1.5 km above ground, was less than ~15 m s–1. During 1800–2100 UTC 15 February, the low-pressure center was crossing the AP mountain barrier and the incoming air wind speed had increased to ~20 m s–1. In addition, vertical winds on both windward and leeward slopes of the mountain barrier increased dramatically, and the region of maximum warming moved from near the base of the leeward slopes to approximately 40 km away from the base (Figs. 4c, d). Therefore, the foehn warming extent (area experiencing warmer temperature) increases with stronger vertical winds. This warming extent can play an important role in the melting of Larsen C Ice Shelf, which is attached to the leeward slopes.
In the second foehn event (2000 UTC 17–0000 UTC 18 February), the maximum warming also extended outward, when the low-pressure center moved toward the AP mountain barrier where enhanced vertical winds occurred on both windward and leeward slopes. In fact, stronger windward lifting implied that air flow crossing the mountain barrier will ascend to higher levels. When it flowed over to the leeward side, it would crash down at a region farther away from the base of the leeward slopes compared to winds from lower levels.
5 Comparison of WRF simulations forced by original and corrected CCSMA comparison between WRF simulations forced by the original and corrected CCSM data was made in order to explore any differences in the simulated foehn warming effect when different forcing was used. To facilitate the discussion below, we name WRF simulation forced by the corrected CCSM data as C-WRF simulation, and that forced by the original CCSM data as WRF simulation. Synoptic conditions of surface temperature, wind circulation, and sea level pressure in the C-WRF 10-km resolution simulation (Fig. 6) show very similar spatial patterns as that in the WRF simulation (Fig. 2). Although both have low-pressure centers within the study domain, their magnitudes differ, with higher pressure values in the C-WRF simulation (Figs. 6a–e and 2f–j). Surface temperature in C-WRF simulation is much warmer than the WRF simulation at the start of the simulation (Figs. 6a and 2f) and marks a distinct difference in surface characteristic between the two simulations. Furthermore, the more intense low pressure within C-WRF compared to WRF might be caused by these warmer temperatures because warmer conditions create a higher tendency for air to lift and enhance lower level convergence. This will cause the low to deepen more significantly in C-WRF. However, temperature within WRF simulation rise at a faster rate and differences in temperature between WRF and C-WRF becomes smaller toward the end of the simulation (Figs. 6e and 2j). This can be attributed to stronger northwesterly wind speeds within WRF simulation compared to C-WRF, which causes stronger warm advection from the north as well as stronger foehn wind warming. These results should be considered in future applications where adjustments to temperature forcing data are made because it may cause unintended consequences for other variables within the simulation such as surface pressure.

|
| Figure 6 C-WRF 10-km resolution simulation of sea level pressure (SLP, black contour), surface temperature (color), and wind vector (black vector) at (a, f) 0600, (b, g) 1800 UTC 15, (c, h) 1200, (d, i) 0600 UTC 17, and (e, j) 0000 UTC 18 February. |
Following the method introduced in Section 2, foehn wind warming along the selected transect is defined as:
| ${\rm TD} = \left. {\left. {\bar T} \right|_{240\,\,{\rm km}}^{280\,\,{\rm km}}} \right|_0^{0.5\,\,{\rm km}} - \left. {\left. {\bar T} \right|_0^{40\,\,{\rm km}}} \right|_0^{0.5\,\,{\rm km}},$ | (1) |
where TD is the temperature difference between the leeward and windward sides along the transect. The first term on the right-hand side is the leeward temperature averaged along the transect between 240 and 280 km and from the surface to 0.5 km above the ground, and the second term is the windward temperature averaged along the transect between 0 and 40 km and from the surface to 0.5 km above the ground.
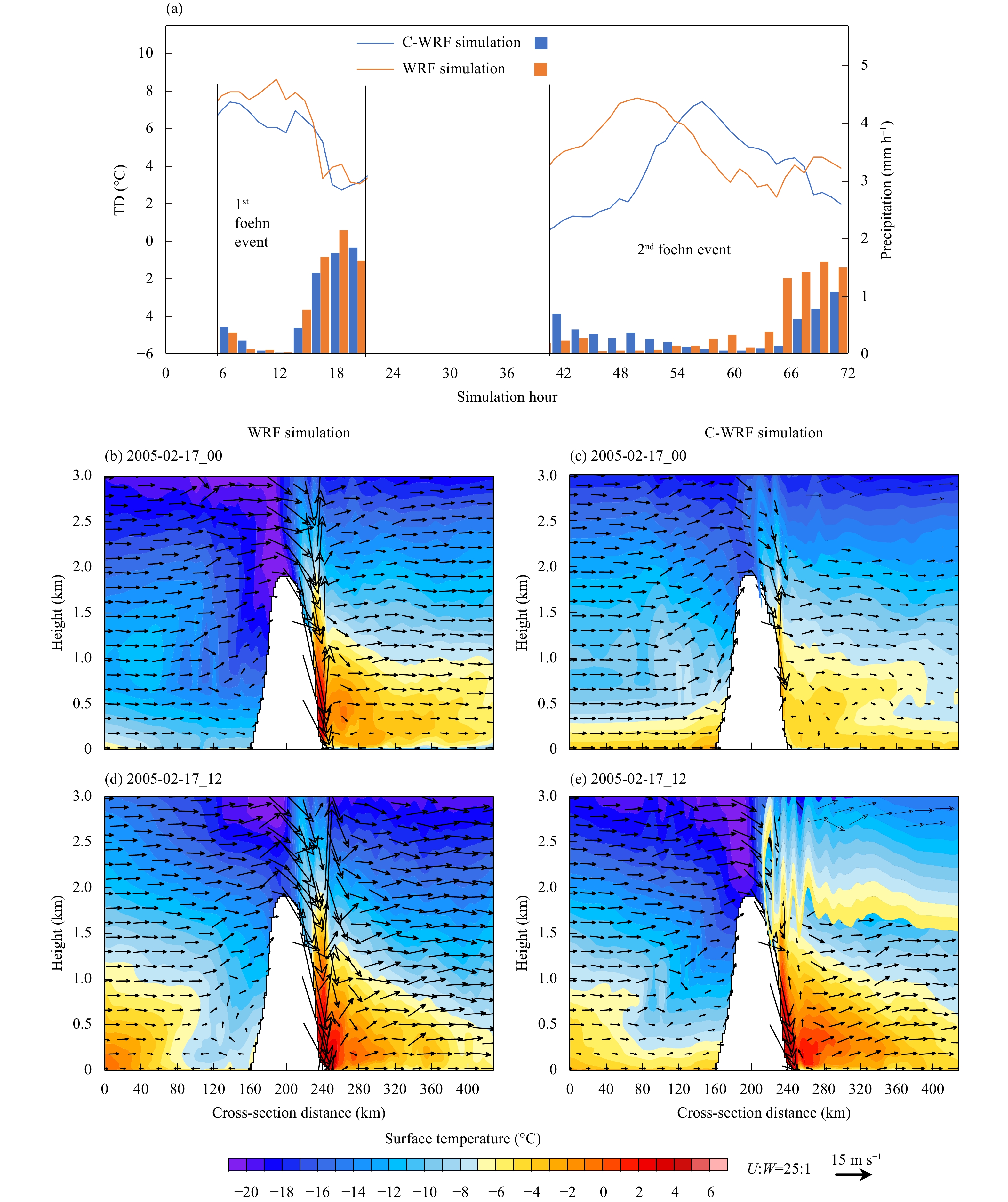
Note that TD quantifies the foehn wind warming. Comparison of foehn wind warming (TD) between WRF and C-WRF simulations demonstrates mixed result. Sometimes TD is greater in WRF results while at other times, it is greater in C-WRF results (Fig. 7a). In particular, at the beginning of the first foehn wind event at 6 h into the simulation (equivalent to 0600 UTC 15 February), there was greater TD in WRF simulation compared to C-WRF. During this time (0600 UTC 15 February), the precipitation along windward side of AP (measured with an averaged value from 0–200 km along the transect) was not significant in either simulation. From 15–21 h into the simulation (equivalent to 1500–2100 UTC 15 February), the warming became weaker in both WRF and C-WRF when significantly more precipitation was present in both compared to earlier times. At the beginning of the second event from 42–55 h into the simulation (equivalent to 1800 UTC 16–0700 UTC 17 February), TD was much greater in WRF simulation relative to C-WRF when precipitation in WRF was weaker than C-WRF. Physically speaking, less precipitation is associated with clearer skies or less cloud cover, which causes stronger longwave radiation cooling along the windward slope and on the mountain top during night time. This may promote stronger isentropic drawdown and greater TD (Figs. 6b, c). After hour 55 into the simulation (equivalent to 0700 UTC 17 February) but before hour 65 into the simulation (equivalent to 1700 UTC 17 February), TD became greater in C-WRF compared to WRF. During this time, precipitation weakened in both simulations and was generally lesser in C-WRF, which favors colder mountain top temperatures, stronger isentropic drawdown, and greater TD in C-WRF compared to WRF (Figs. 7d, e). It should also be noted that windward wind speeds in the WRF simulation were generally stronger than C-WRF. This caused stronger warm air advection along the windward side of the transect in WRF compared to C-WRF (Fig. 7d, e), which helps to reduce TD in the WRF simulation more abruptly and also at earlier times than in C-WRF. After hour 65 into the simulation (equivalent to 1700 UTC 17 February), significant precipitation occurred in both simulations and TD became smaller compared to earlier times such as hour 55 into the simulation. This comparison indicates that differences in foehn wind warming between WRF and C-WRF are not trivial. Determining that CCSM data to use in future surface mass balance studies requires further studies.
In addition, warmer temperature at lower level on the windward side generally causes greater precipitation. At 0000 UTC 17 February (49 h into the simulation), there were warmer windward temperatures at the lower level in C-WRF simulation (Figs. 7b, c), which caused greater precipitation to occur in C-WRF simulation (Fig. 7a). However, we should note that C-WRF did not always have warmer windward temperatures at lower level. At 61 h into the simulation, which corresponded to 1200 UTC 17 February, WRF simulation had warmer temperatures (Figs. 7d, e) as well as greater precipitation (Fig. 7a).
We also notice a time lag in TD between WRF and C-WRF simulations for 42–66 h. Two major mechanisms involved in foehn wind warming include latent heating and isentropic drawdown. Isentropic drawdown is mainly responsible for the warming during the dry period. This time lag occurs within the relatively dry period where isentropic drawdown dominates. From 42–54 h into the simulation, precipitation in C-WRF is greater than WRF, which might be caused by the warmer temperature in C-WRF during the time period. As a result of higher precipitation in C-WRF from 42–54 h, there is warmer mountain top temperature due to cloud radiation forcing. This process can decrease the effect of drawdown, which explains why C-WRF, with higher precipitation than WRF from 42–54 h into the simulation (Fig. 7a) has a lagging peak in temperature difference.
|
| Figure 7 (a) Time series of temperature difference TD (leeward–windward) and precipitation from WRF 2-km resolution simulations forced by original (orange) and corrected (blue) CCSM during two foehn event periods; (b, d) temperature (color) and wind vector (black vector) profiles along the transect from WRF 2-km resolution simulations forced by the original; (c, e) as in (b, d), but for corrected CCSM at (b, c) 0000 UTC and (d, e) 1200 UTC 17 February. |
Temperature difference TD in Eq. (1) is used to measure the magnitude of the foehn wind warming. Using TD rather than leeward temperature allows warming impact due to thermal advection and radiation forcing to be minimized to some extent. Incoming air is considered as being 0–40 km along transect (~150 km away from the barrier base) and 1–1.5 km above ground. The relationships between the incoming air and TD are explored in this section. From analyses presented in Sections 4 and 5, the mechanisms and magnitudes of foehn wind warming are very different during periods with or without significant windward precipitation. Therefore, we divided each foehn event into wet and dry periods with wet period beginning when precipitation experiences an abrupt increase and starts to exceed approximately 1 mm h–1. This occurred from 1600 to 2100 UTC 15 February for first event and from 1800 UTC 17 to 0000 UTC 18 February for the second event. A time lag of 3 h (1st event) and 5 h (2nd event), determined by the incoming air wind speed and travel distance, between TD and windward variables was used when analyzing their relationships because it took time for the air parcel to travel from the windward to the leeward side. It should be noted that there was lack of data for the wet period of the second event because it occurred near the end of our simulation and there was a time lag between windward variables and TD.
During dry period, it was found that temperature of incoming air has a negative correlation with TD (Fig. 8a) with correlation coefficients of 0.82 and 0.30 for the first and second foehn events, respectively, and significance level exceeding 0.05 for both. This suggests that colder incoming air can cause greater foehn wind warming, i.e., larger temperature difference TD when no significant precipitation is present along the windward slopes. This is because colder incoming air is less buoyant and the air mass at a similar elevation (1–1.5 km) to the mountain top (~ 2 km) moves toward the mountain top, which also helps to minimize the mountain top temperature. Colder and drier air descending from the mountain top generates stronger heating due to isentropic drawdown on the base of the leeward slopes. This process is also closely related to and also explains the negative relationships between the mountain top temperature and TD during dry periods (Fig. 8b) with correlation coefficient of 0.82 for the first event and 0.74 for the second event and significance level exceeding 0.05 for both. This impact of mountain top temperature on the foehn wind warming as quantified by TD can be also found in the comparison of WRF and C-WRF simulations as shown in Figs. 6b, c.

|
| Figure 8 Scatterplots for (a–c) dry and (d–g) wet periods during the first and second foehn events: (a) temperature difference (leeward–windward) (TD) vs temperature of incoming air, (b) TD vs mountain top temperature, and (c) TD vs speed of incoming air; (d) TD vs temperature of incoming air, (e) TD vs hourly precipitation on windward side, (f) TD vs LH contribution to TD, and (g) TD vs speed of incoming air. It should be noted that a time lag of 3 (1st event) and 5 h (2nd event) (determined by the incoming air wind speed and travel distance) is used in (f) considering that LH occurs along the windward slope before the foehn wind warming. In addition, there are 3- and 5-h time lags for the first and second events respectively between TD and all windward variables in all the relationships. This is because it takes time for the air parcel to travel from the windward side and to affect the leeward side. |
Contrary to the findings for dry period, during wet period, there apparently exists a positive relationship between the incoming air temperature and TD (Fig. 8d). Positive relationship also exists between the windward precipitation and TD (Fig. 8e). Due to limited sample data available during the wet periods, we neglect statistical correlation analysis here. The scatter plots of Figs. 8d and 8e suggest that latent heating (LH) is probably the main driver of foehn wind warming during wet period. Temperature change due to LH is estimated by using the method from Elvidge and Renfrew (2016), which involves calculating the presence of water vapor within an air parcel on the windward side that travels to the leeward side while undergoing the LH process. This method assumes that difference in water vapor within the air parcel once it ends up on leeward side compared to the same parcel when it was on the windward side is proportional to the amount of LH. Using this method, a positive relationship exists between LH and TD during the wet period (Fig. 8f). Thus, LH drives foehn wind warming during periods when significant precipitation occurs along the windward slopes. It should be noted that correlations between TD and 1) incoming air temperature, 2) windward precipitation, and 3) LH during wet periods (Figs. 8d–f) are very similar. These similarities are explained by a chain of physical properties such as the presence of high air temperature, which causes greater vertical motion, then higher condensation, and LH release, followed by higher precipitation. Relationships between the wind speed of incoming air and foehn wind warming measured by TD seem absent during both dry and wet periods (Figs. 8c, g).
Foehn wind warming has been attributed to the impacts of relative humidity (RH) and precipitation on the windward side in the study of Elvidge and Renfrew (2016) and the impacts vary case by case. In our simulations, it was found that greater TD or stronger foehn wind warming will occur when there is no significant precipitation along the windward slope, and relatively weaker warming occurs when there is significant windward precipitation (Figs. 6a). The windward precipitation is attributed to the warm air advection toward the mountain range. Thus, weaker foehn wind warming usually occurs when the study area is under the control of warm advection. This is because different heating mechanisms are involved during the dry and wet periods or when different thermal advections are present. When the incoming air is cold and dry, the heating mechanism of isentropic drawdown is mainly responsible for the foehn wind warming, which can be measured with the dry lapse rate on the leeward side. This can be contrasted with the wet scenario when warm advection occurs, and latent heating mechanism is the major cause for the foehn wind warming. In this case, foehn wind warming estimation involves the difference of wet lapse rate on windward side and dry lapse rate on leeward side and produces smaller warming. In addition, when there is greater precipitation, more cloud cover will be present and there will be greater longwave radiation heating due to cloud cover. On the other hand, in the absence of cloud and precipitation, there will be stronger radiation loss from the surface, which contributes to radiative cooling of mountain top and causes stronger isentropic drawdown. It has been confirmed by regional simulation forced by the ERA-Interim reanalysis that when flows from the northwest dominate over the peninsula, there is greater availability of energy at the surface for melt (Munneke et al., 2012). This is due to leeward descending winds resulting in foehn wind warming and clear skies allowing more shortwave radiation to be absorbed by the surface. The results presented here from the CCSM forced WRF simulations corroborate these findings since the leeward side was found to be dry and precipitation free during the foehn events.
7 Summary and discussionIn this study, two foehn wind events were identified in the CCSM simulation over the AP. These events occurred during 0600–2100 UTC 15 February and 1800 UTC 16–0000 UTC 18 February 2005. In addition, modellings of these foehn wind events were performed by using WRF forced by the CCSM data. WRF simulations included three nested resolutions of 50, 10, and 2 km, respectively. A comparison of CCSM forcing and WRF 10-km resolution simulation shows that the dominant weather systems generating the foehn wind events across the AP are two consecutive cyclonic systems with low-pressure centers moving to and/or crossing over the AP from west to east. Comparison of CCSM, WRF 2-, and 10-km resolution simulations also shows that significantly warmer temperatures over the leeward side of AP were present when foehn wind warming occurred in both WRF 2- and 10-km resolution simulations. It was also found that leeward warming was much milder in CCSM forcing than that in WRF. Models that use near-surface temperature to estimate surface melt may be sensitive to the differences in temperature produced by CCSM and WRF simulations. Furthermore, these differences can be the deciding factor regarding whether ice melts at all, with CCSM unable to exceed the 0°C threshold for ice melt whereas WRF 10-km resolution simulation exceeded the threshold for a period of ~10 h and WRF 2-km resolution simulation exceeded the threshold for a period of ~13 h during the first foehn wind event. The region of maximum warming during a foehn wind event is located near the base of the leeward slopes when the incoming winds are relatively weak, but tends to move outward along the transect across AP and impact the Larsen C Ice Shelf attached to the east side of AP during times of increasing windward wind speed. In fact, the region of maximum warming extends to over 40 km away from the leeward base toward the attached Larsen C Ice Shelf during both events.
Our study separates foehn wind event into dry and wet periods with wet period occurring when precipitation exceeded ~1 mm h–1. It was found that during dry periods, the foehn wind warming as measured by temperature difference [TD in Eq. (1)] between the leeward and windward sides of the AP is maximized when the mountain top temperatures are cold. This suggests that the physical processes, which cause foehn wind warming, include cold and dry drainage flows occurring when air sourced from higher elevations on windward side gather speed under the influence of gravity and warm adiabatically on leeward side during the descending process. This process was suggested as one of main mechanisms of foehn wind warming by Barry (2008) and referred to as isentropic drawdown in Elvidge and Renfrew (2016). Furthermore, when the incoming air is colder, there is greater foehn wind warming because under these conditions, warm advection is minimized, and the mountain top temperature remains cold. During wet periods, positive relationships exist between precipitation and foehn wind warming as quantified by TD. This suggests processes related to precipitation such as latent heating (LH) is primarily responsible for foehn wind warming during wet periods. When LH is quantified, a positive relationship is apparent between TD and LH during wet period. This evidence further supports the role of latent heating on foehn wind warming during periods of significant precipitation. Our analysis also shows that isentropic drawdown plays a stronger role in foehn wind warming than latent heating. Data that support this include larger TD in dry periods than wet periods. This might be because latent heating is quantified by considering dry lapse rate on leeward side and wet lapse rate on windward side and these two lapse rates offset each other but isentropic drawdown is quantified mainly by considering dry lapse rate on leeward side and no offset from windward side.
Comparison of WRF simulations forced by the original and corrected CCSM data shows surface temperature in the C-WRF simulation (forced by corrected CCSM) is much warmer than the WRF simulation (forced by original CCSM). However, the foehn wind warming is stronger in the WRF simulation when no significant windward precipitation is present. Moreover, the leeward warming becomes weaker in both simulations when there is significant windward precipitation. In both simulations, weaker precipitation caused enhanced warming on leeward side, but the amount of precipitation differed significantly. Differences in precipitation caused different amount of foehn wind warming between the simulations, which suggests that model ability to resolve warming varies with forcing data.
Our study has elucidated the impact of model resolution and forcing data on the WRF modelling of foehn wind warming. It is clear that the choice of both resolution and forcing data can impact foehn wind warming significantly. For a long term study where adding resolution can be computationally taxing, 10-km resolution would suffice to resolve warming required for surface melt estimation, although there is the chance that melt is underestimated due to inaccuracies in resolving topography. CCSM data seem to be unable to resolve these mesoscale warmings, which are present in WRF simulations. Our study also confirms that foehn wind warming may be responsible for recent melt within Larsen C Ice Shelf. Future studies can use WRF model to perform longer term studies of the impacts of foehn wind warming on the surface mass balance over AP, particularly the Larsen C Ice Shelf.
Acknowledgment. This study was sponsored by the US NSF Grants OPP-1649713 and OPP-1543445. Computing resources were provided by Visualization and Computation Advancing Research (ViCAR) Center at North Carolina A&T State University and Blue Waters Supercomputer in National Center for Supercomputing Applications, University of Illinois at Urbana-Champaign. The authors want to thank the editor and the anonymous reviewers for providing insightful suggestions and comments that have greatly improved the manuscript.
| Barry, R. G., 2008: Mountain Weather and Climate. 3rd Ed., Cambridge University Press, Cambridge, 171 pp. |
| Cape, M. R., M. Vernet, P. Skvarca, et al., 2015: Foehn winds link climate-driven warming to ice shelf evolution in Antarctica. J. Geophys. Res. Atmos., 120, 11037–11057. DOI:10.1002/2015JD023465 |
| Chen, F., and J. Dudhia, 2001: Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Wea. Rev., 129, 569–585. DOI:10.1175/1520-0493(2001)129<0569:CAALSH>2.0.CO;2 |
| Cook, A. J., and D. G. Vaughan, 2010: Overview of areal changes of the ice shelves on the Antarctic Peninsula over the past 50 years. Cryosphere, 4, 77–98. DOI:10.5194/tc-4-77-2010 |
| Cook, A. J., A. J. Fox, D. G. Vaughan, et al., 2005: Retreating glacier fronts on the Antarctic Peninsula over the past half-century. Science, 308, 541–544. DOI:10.1126/science.1104235 |
| Elvidge, A. D., and I. A. Renfrew, 2016: The causes of foehn warming in the lee of mountains. Bull. Amer. Meteor. Soc., 97, 455–466. DOI:10.1175/BAMS-D-14-00194.1 |
| Elvidge, A. D., I. A. Renfrew, J. C. King, et al., 2016: Foehn warming distributions in nonlinear and linear flow regimes: A focus on the Antarctic Peninsula. Quart. J. Roy. Meteor. Soc., 142, 618–631. DOI:10.1002/qj.2489 |
| Grosvenor, D. P., J. C. King, T. W. Choularton, et al., 2014: Downslope föhn winds over the Antarctic Peninsula and their effect on the Larsen ice shelves. Atmos. Chem. Phys., 14, 9481–9509. DOI:10.5194/acp-14-9481-2014 |
| Hogg, A. E., and G. H. Gudmundsson, 2017: Impacts of the Larsen-C ice shelf calving event. Nature Climate Change, 7, 540–542. DOI:10.1038/nclimate3359 |
| Hong, S. Y., Y. Noh, and J. Dudhia, 2006: A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Wea. Rev., 134, 2318–2341. DOI:10.1175/MWR3199.1 |
| Iacono, M. J., J. S. Delamere, E. J. Mlawer, et al., 2008: Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. Geophys. Res. Lett., 113, D13103. DOI:10.1029/2008JD009944 |
| Kain, J. S., 2004: The Kain-Fritsch convective parameterization: An update. J. Appl. Meteor., 43, 170–181. DOI:10.1175/1520-0450(2004)043<0170:TKCPAU>2.0.CO;2 |
| Marshall, G. J., A. Orr, N. P. M. van Lipzig, et al., 2006: The impact of a changing Southern Hemisphere Annular Mode on Antarctic Peninsula summer temperatures. J. Climate, 19, 5388–5404. DOI:10.1175/JCLI3844.1 |
| Morrison, H., G. Thompson, and V. Tatarskii, 2009: Impact of cloud microphysics on the development of trailing stratiform precipitation in a simulated squall line: Comparison of one- and two-moment schemes. Mon. Wea. Rev., 137, 991–1007. DOI:10.1175/2008MWR2556.1 |
| Munneke, P. K., M. R. van den Broeke, J. C. King, et al., 2012: Near-surface climate and surface energy budget of Larsen C ice shelf, Antarctic Peninsula. Cryosphere, 6, 353–363. DOI:10.5194/tc-6-353-2012 |
| Orr, A., D. Cresswell, G. J. Marshall, et al., 2004: A ‘low-level’ explanation for the recent large warming trend over the western Antarctic Peninsula involving blocked winds and changes in zonal circulation. Geophys. Res. Lett., 31, L06204. DOI:10.1029/2003GL019160 |
| Orr, A., G. J. Marshall, J. C. R. Hunt, et al., 2008: Characteristics of summer airflow over the Antarctic Peninsula in response to recent strengthening of westerly circumpolar winds. J. Atmos. Sci., 65, 1396–1413. DOI:10.1175/2007JAS2498.1 |
| Paulson, C. A., 1970: The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer. J. Appl. Meteor., 9, 857–861. DOI:10.1175/1520-0450(1970)009<0857:TMROWS>2.0.CO;2 |
| Pritchard, H. D., R. J. Arthern, D. G. Vaughan, et al., 2009: Extensive dynamic thinning on the margins of the Greenland and Antarctic ice sheets. Nature, 461, 971–975. DOI:10.1038/nature08471 |
| Rignot, E., J. L. Bamber, M. R. van den Broeke, et al., 2008: Recent Antarctic ice mass loss from radar interferometry and regional climate modelling. Nature Geoscience, 1, 106–110. DOI:10.1038/ngeo102 |
| Scambos, T. A., C. Hulbe, M. Fahnestock, et al., 2000: The link between climate warming and break-up of ice shelves in the Antarctic Peninsula. J. Glaciology, 46, 516–530. DOI:10.3189/172756500781833043 |
| Shepherd, A., D. Wingham, T. Payne, et al., 2003: Larsen ice shelf has progressively thinned. Science, 302, 856–859. DOI:10.1126/science.1089768 |
| van den Broeke, M., 2005: Strong surface melting preceded collapse of Antarctic Peninsula ice shelf. Geophys. Res. Lett., 32, L12815. DOI:10.1029/2005GL023247 |
| van Lipzig, N. P. M., G. J. Marshall, A. Orr, et al., 2008: The relationship between the Southern Hemisphere annular mode and Antarctic Peninsula summer temperatures: Analysis of a high-resolution model climatology. J. Climate, 21, 1649–1668. DOI:10.1175/2007JCLI1695.1 |
| Vaughan, D. G., 2006: Recent trends in melting conditions on the Antarctic Peninsula and their implications for ice-sheet mass balance and sea level. Arct. Antarct. Alp. Res., 38, 147–152. DOI:10.1657/1523-0430(2006)038[0147:RTIMCO]2.0.CO;2 |
| Vaughan, D. G., G. J. Marshall, W. M. Connolley, et al., 2003: Recent rapid regional climate warming on the Antarctic Peninsula. Climatic Change, 60, 243–274. DOI:10.1023/A:1026021217991 |
 2018, Vol. 32
2018, Vol. 32


