The Chinese Meteorological Society
Article Information
- RONG, Xinyao, Jian LI, Haoming CHEN, et al., 2018.
- The CAMS Climate System Model and a Basic Evaluation of Its Climatology and Climate Variability Simulation. 2018.
- J. Meteor. Res., 32(6): 839-861
- http://dx.doi.org/10.1007/s13351-018-8058-x
Article History
- Received April 8, 2018
- in final form August 7, 2018
2. State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
3. University of the Chinese Academy of Sciences, Beijing 100029
Coupled climate models can be used in a wide range of studies on topics from climate variability to future climate projection. These models numerically solve the climate system’s fundamental governing equations to simulate the interactions between the climate system components such as the atmosphere, ocean, land surface, sea ice, and so on. Coupled climate models also serve as essential tools for the climate research community and form the basis for operational dynamical prediction of climate.
Fully coupled climate model development began firstly with the coupled atmosphere–ocean general circulation model (GCM), the first of which was established in the late 1960s at the Geophysical Fluid Dynamics Laboratory (GFDL) (Manabe and Bryan, 1969). This coupled GCM was motivated by the progressive realization of the importance of air–sea interactions in shaping the global climate and climate variability. Since then, tremendous progress has been made in climate model development (Zebiak and Cane, 1987; Mechoso et al., 1995; Taylor et al., 2012). Coupled climate models were developed to ensure a more realistic simulation of the mean climate state and variability via a variety of improvements to numerical algorithm, model resolution, physical parameterization, and so on (Bellenger et al., 2014; Song and Zhou, 2014a; Koutroulis et al., 2016; Stanfield et al., 2016). Additional processes and submodels were incorporated into coupled climate models to comprehensively and accurately represent the climate system. Coupled climate models have advanced towards an “earth system model” (e.g., Dunne et al., 2012; Giorgetta et al., 2013; Hurrell et al., 2013).
Despite continuous progress over the past five decades, common and long-lasting biases remain in most present-day coupled climate models. One prevalent basin-scale bias, known as the double intertropical convergence zone (ITCZ), is still visible in the Coupled Model Intercomparison Project phase 5 (CMIP5) models, and there has been little improvement from CMIP3 to CMIP5 (Oueslati and Bellon, 2015). In addition to the large-scale biases, coupled models also exhibit distinct biases at regional scales, especially in East Asia where the climate is dominated by the monsoonal system. Given the complexity of the East Asian monsoon dynamics and thermodynamics, realistic reproduction of the East Asian climate, particularly the monsoon rainbelt, remains a great challenge in the current state-of-the-art coupled climate models (Webster et al., 1998; Kang et al., 2002; Gong et al., 2014; Song and Zhou, 2014a, b; Kusunoki and Arakawa, 2015). For example, Wang et al. (2005) argued that because of the deficiency in simulating the observed anticorrelation between sea surface temperature (SST) and rainfall in the monsoon region, the current state-of-the-art atmospheric GCM (AGCM) is generally inadequate for predicting the Asian–Pacific summer monsoon rainfall when forced by the observed SST; this necessitates the application of coupled climate models in East Asian climate simulations.Song and Zhou (2014b) reported that the climatological summer monsoon circulation and rainbelt are poorly simulated in the CMIP5 AGCM; however, this simulation can be improved in the coupled GCM (CGCM) at the cost of the local cold SST biases in coupled GCMs. In addition to the missing air–sea coupling, the inherent errors in the AGCMs, especially those associated with the physical parameterizations, is also a main source of the precipitation biases over the Asian monsoon region (Song and Zhou, 2014b; Yang et al., 2015).
The East Asian monsoon is basically driven by the seasonal land–sea thermal contrast; however, the monsoon’s maintenance and variations are connected to the comprehensive atmosphere–land, atmosphere–ocean, and atmosphere–ice interactions. Land surface processes are well known to play an important role in shaping and disturbing the East Asian climate, including heating of the Tibetan Plateau, and soil moisture and vegetation processes (Li and Yanai, 1996; Webster et al., 1998; Xue et al., 2004; Zhang and Zuo, 2011). Thus, uncertainty in land surface simulations is an important source of bias in simulations of the East Asian climate (Henderson-Sellers et al., 1995). Due to the uniqueness of terrain and complexity of the physical processes, current GCMs still contain considerable biases and uncertainties in land thermal condition simulations over the East Asian region (Su et al., 2013; Chen and Frauenfeld, 2014; Hua et al., 2014). Chen and Frauenfeld (2014) reported that most of the CMIP5 coupled GCMs show substantial cold biases over the Tibetan Plateau, particularly during the cold season. Hua et al. (2014) showed that the climatology, inter-annual variation, and trend of land surface temperature simulated over China all exhibit considerable spread among the CMIP5 models, and the spread magnitudes are comparable to those of the observations. Reducing the land surface biases requires substantial improvement of the physical parameterizations, which is a long-standing challenge in climate model development efforts.
Another well-known model bias that occurs in the East Asian region is the precipitation overestimation over the Tibetan Plateau. This bias prevails from the CMIP3 to CMIP5 models (Su et al., 2013; Xu et al., 2017) and corresponds to the cold bias over the Tibetan Plateau (Su et al., 2013). In fact, the excessive precipitation near the steep topography is a common feature in the CMIP5 models (Mehran et al., 2014) and may be related to the decoupling of the advection and condensation processes as well as the atmospheric model’s insufficient horizontal resolution (Codron and Sadourny, 2002; Li et al., 2015; Yu et al., 2015). Recent studies have shown that the Euler-type water vapor advection scheme may provide promising advantages for reducing this bias (Zhang et al., 2013; Yu et al., 2015).
In recent years, a climate system model (CSM) has been developed at the Chinese Academy of Meteorological Sciences (CAMS), which is known as CAMS-CSM. This endeavor aims to address the challenges in simulating the East Asian climate with a high performance model. First, CAMS-CSM is configured to minimize the bias in each climate system component by utilizing existing worldwide, state-of-the-art component models. Thus, as the first step, CAMS-CSM was built upon two widely used and evaluated atmospheric and oceanic models, as well as a full land model. Several modifications (such as those in the water vapor advection scheme and radiation scheme) have been made in the component models to better represent some aspects of the East Asian climate. While a higher resolution is expected to more realistically depict the monsoon rainbelt, a moderate resolution is used in the current version of CAMS-CSM.
The aim of this paper is to provide a general description and basic evaluation of the CAMS-CSM model. We will evaluate a long term pre-industrial control simulation and a “historical” simulation to provide a model performance overview, including the climatological mean state and variability. This paper is arranged as follows: component models, coupling strategy, and experimental setup are described in Section 2. The simulated climatology and seasonal cycles in the atmosphere, ocean, and cryosphere are presented in Section 3. Some major modes of climate variability are evaluated in Section 4. In Section 5, the results are briefly summarized and discussed.
2 Model description and experiment 2.1 Atmospheric modelThe atmospheric component is a modified atmosphe-ric GCM known as ECmwf-HAMburg [ECHAM5 (v5.4)], which was developed at the Max Planck Institute for Meteorology (MPI-Met; Roeckner et al., 2003). ECHAM5 is a spectral atmospheric model with a triangular truncation. The Tiedtke (1989) mass flux scheme, which includes modifications for penetrative convection according to Nordeng (1994), is applied for cumulus convection parameterization. The stratiform cloud scheme consists of a cloud microphysical scheme (Lohmann and Roeckner, 1996) and a cloud cover scheme, which diagnostically calculates the cloud fraction as a function of relative humidity (Sundqvist, 1978). For an additional detailed description of the ECHAM5 model, please refer to Roeckner et al. (2003). The resolution of the current version is T106 L31, which corresponds to a horizontal resolution of approximately 1°, with 31 vertical layers extending from the surface to 10 hPa. The major differences between the CAMS-CSM version and the standard ECHAM5 model include the following: 1) a Two-step Shape Preserving Advection Scheme (TSPAS) is used for the passive tracer transport (Yu, 1994; Zhang et al., 2013), which has shown the ability to reduce precipitation overestimation over the southern Tibetan Plateau’s steep edges (Yu et al., 2015); and 2) a correlated k-distribution scheme developed by Zhang et al. (2006a, b) is adopted for shortwave and longwave radiation transfer parameterization.
2.2 Ocean modelThe ocean component is GFDL Modular Ocean Mo-del version 4 (MOM4; Griffies et al., 2004). MOM4 uses a tripolar grid (Murray, 1996) to remove the singularity of the Arctic region, with two northern poles placed over the North American and Eurasian land areas. The zonal resolution is 1° globally, and the meridional resolution is 1/3° within the 10°S–10°N equatorial band, which ranges to 1° at 30°S (N) with a nominal 1° poleward of 60°N. There are 50 vertical layers with 23 even layers in the upper ocean above 230 m. We adopted the following major numerical and physical configurations from the MOM4 model: the multi-dimensional third order upwind biased scheme (Hundsdorfer and Trompert, 1994) with flux limiters from Sweby (1984) for horizontal and vertical tracer advection; the anisotropic Laplacian scheme for horizontal viscosity; the isoneutral/isopycnal tracer diffusion; the K-profile parameterization and Bryan–Lewis vertical diffusion/viscosity schemes; an overflow scheme for dense water crossing steep bottom topography; a full convective adjustment scheme; and shortwave penetration with spatially varying, climatological chlorophyll concentration.
2.3 Sea ice modelThe sea ice component is the GFDL Sea Ice Simula-tor (SIS), which shares the same grid set as that of the ocean model. SIS is a dynamical sea ice model with a three-layer structure similar to that of the Semtner scheme (Winton, 2000): one snow layer and two equally thick sea ice layers. The snow layer has zero heat capacity, the upper ice layer has a variable heat capacity to represent the brine pockets, and the heat capacity of the lower layer is fixed. The prognostic variables are the snow layer thickness, the ice layer thickness, and the upper and lower ice layer temperatures. The surface temperature is determined from the energy balance between the upward surface heat flux and conductive heat flux through snow or ice. Differing from the Semtner scheme, the snow temperature and brine pocket are not prognos-tic variables, as the snow heat capacity is small with regard to that of the ice, and the brine pockets can be determined by the upper ice temperature and the predefined ice salinity. The sea ice in each grid consists of five categories and could be redistributed by an enthalpy conserving approach under specific conditions. The internal stresses of ice are calculated by the elastic–viscous–plastic technique (Hunke and Dukowicz, 1997).
2.4 Land modelThe land component of CAMS-CSM is the Common Land Model (CoLM; Dai et al., 2003), which was designed to utilize the best aspects of the three existing land surface models: the Biosphere–Atmosphere Transfer Scheme (BATS;Dickinson et al., 1993), the Land Surface Model (LSM; Bonan et al., 1996), and the snow model of Dai and Zeng (1997) (IAP94). CoLM employs the “mosaic” concept of Koster and Suarez (1992), with each surface grid cell being partitioned into as many as 24 land cover types. The soil is divided exponentially into 10 uneven vertical layers to better represent the strong soil water gradient near the soil surface. Above the soil is one vegetation layer and up to five snow layers depending on the total snow depth. The soil temperature and moisture are calculated by solving tridiagonal equations formed from the Crank–Nicholson method and first order Taylor expansion, respectively. Runoff calculation is based on the concept of TOPMODEL (Stieglitz et al., 1997). CoLM uses a two-big-leaf submodel for photosynthesis, stomatal conductance, leaf temperature, and energy fluxes (Dai et al., 2004), which includes the following: 1) an improved, two-stream approximation mo-del of canopy radiation transfer, with attention to singularities in its solution and separate integrations of radiation absorption by sunlit and shaded canopy fractions; 2) separate photosynthesis–stomatal conductance models for sunlit and shaded leaves, and for the simultaneous transfers of CO2 and water vapor into and out of the leaf; and 3) a well-built quasi-Newton–Raphson method for simultaneous temperature solutions of sunlit and shaded leaves. Differing from the original version of CoLM, the CAMS-CSM version implements an unfrozen water process according to the work of Niu and Yang (2006), which allows liquid water to coexist with ice in the soil at below 0°C and has been shown to considerably impact the East Asian climate variability (Xin et al., 2012).
2.5 Coupling strategyThe CAMS-CSM uses the GFDL Flexible Modeling System (FMS) coupler for flux/state calculations and interpolations between component models. The FMS coupler employs an exchange grid concept, which is a set of tiles (polygons) formed by overlapping the cell edges of the two component grids. Fluxes and states are first placed on this set of tiles, and then the calculation and interpolation are performed. There are two advantages to this approach: 1) fluxes are calculated at the finest grid resolution and 2) conservation can be readily achieved for complex types of grids. To guarantee that the land and ocean precisely tile the global domain, the land fractions of land grid cells are modified according to the overlap area between land grid cells and active ocean grid cells. The atmosphere, ocean, and sea ice exchange fluxes every ocean time step (1 h), while the land exchange fluxes with the atmosphere every 30 minutes, and runoff routing to the ocean by the MPI-Met discharge model (Hagemann and Dümenil, 1997) occurs every hour. The detailed coupling algorithm is described in the Appendix of this paper.
2.6 Experiment and validation dataIn this study, a pre-industrial control simulation (piControl) and a “historical” simulation using the CAMS-CSM model were performed. The model was started with a resting ocean of climatological temperature and salinity, and atmospheric initial conditions of 1 January 1989; while the land states from a separate 20-yr pre-spinup run with the land model coupled to a standalone atmospheric model. A 50-yr fully coupled restoring integration was performed with the SST and sea surface salinity being restored to their climatological monthly means. Subse-quently, the restoring constraint was removed, and the coupled model was integrated for 500 yr without flux correction. The forcing used for this simulation was fixed to the prescribed pre-industrial control simulation forcing data from CMIP6 (Eyring et al., 2016) (https://esgf-node.llnl.gov/projects/input4mips), including greenhouse gases (CO2, CH4, N2O, CFC-12, and equivalent CFC-11 that summarizes the effects of all 39 other gases), ozone, total solar irradiance, and so on. The stratospheric aerosols are assumed to be zero, as their values are small during the period around the 1850s. The latest 150-yr simulation is used for the climate variability evaluation in this study. Another experiment, which is similar to that of the CMIP6 historical simulation, is also performed (hereafter referred as HIST). It uses the historical forcing data of 1900–2013, including ozone, solar forcing, greenhouse gases, and anthropogenic aerosol. The stratospheric aerosol is not considered in this simulation either. The HIST simulation began from a quasi-equilibrium state obtained from the piControl simulation. The simulation results over 1980–2013 are used to obtain the climatological mean state and annual cycle, which are comparable with the present-day climate.
The data used in this study consist of the monthly SST and sea ice concentration from the HadISST datasets (Rayner et al., 2003) and the NCEP-2 reanalysis 850-hPa wind data for 1980–2013 (Kanamitsu et al., 2002). The land surface temperature data are from the Climatic Research Unit Temperature version 4 (CRUTEM4; Osborn and Jones, 2014). Precipitation data from the Glo-bal Precipitation Climatology Project (GPCP) version 2 monthly precipitation analysis of 1980–2016 (Adler et al., 2003) and Tropical Rainfall Measuring Mission (TRMM) 3B42 (Huffman et al., 2007) of 1998–2016 are used as the observation to evaluate the simulated precipitation. The ERA-Interim monthly reanalysis data with a 0.75° horizontal resolution (Dee et al., 2011) for 1980–2013 are used to evaluate the atmospheric state variables. The National Snow and Ice Data Center (NSIDC) Sea Ice Index (Fetterer et al., 2017) is also used to evaluate the sea ice extent and area.
3 Climatological mean state and seasonal cycle 3.1 Surface air temperature and SSTOne critical quantity used to evaluate the coupled climate model is the climatological annual mean SST. Figure 1a shows the difference in the annual mean SST between the CAMS-CSM and the HadISST data. The deviation from the HadISST data is less than 1.5°C over much of the ocean areas. Over certain regions, the error is noticeable. The largest discrepancy is found in North Atlantic and North Pacific, where the biases can reach 5°C and appear to be associated with an excessive sea ice extent towards the equator (Fig. 5). Evident cold biases are also found over the subtropical Pacific and high latitude North Pacific, as well as in the midlatitudes of South Atlantic between 30° and 60°S. A common deficiency in coupled models, i.e., the equatorial Pacific cold bias, is visible in the model. In the eastern coastal regions of the tropical Pacific and Atlantic, there are warm biases, which are another prevailing feature of coupled models and might be related to the insufficient coastal upwelling and stratocumulus in the model. In the region of the Antarctic Circumpolar Current, the simulated temperature is higher with respect to the HadISST data and consistent with the underestimated Antarctic sea ice extent shown in Fig. 5.
The difference in the annual mean 2-m air temperature between the CAMS-CSM and CRUTEM4 data over land is shown in Fig. 1b. In most terrestrial regions, the biases are less than 2°C. Prominent cold biases are seen in southern Greenland, the west coasts of the major continents, and the Sahara, while warm biases are primarily located in the northeast regions of both America and Eurasia as well as northern Greenland. Preliminary diagnostics reveal that the cold biases in most of the above regions correspond to the insufficient surface shortwave radiation fluxes, which are due to the excessive cloud cover in the model. In Greenland and the central Sahara, the cold biases are likely related to the treatment of surface fluxes over the glacial ice sheets and desert in the model. A notable feature is that significant cold biases can be found over steep topography, such as the Tibetan Plateau and Andes Mountains as a result of the overestimated precipitation in those areas (Fig. 2).
3.2 PrecipitationThe global distributions of the annual mean precipitation from CAMS-CSM and GPCP data are shown in Fig. 2. Overall, the general spatial pattern of the annual mean precipitation in CAMS-CSM resembles that from the observation. The major rainfall centers, such as the ITCZ, south Pacific convergence zone (SPCZ), as well as those over the tropical Indian and tropical Atlantic Oceans, are clearly seen in the model. However, the strengths of these rainfall centers are generally greater than the observed values (Fig. 2c). The most evident discrepancy occurs with the SPCZ and the south Atlantic convergence zone (SACZ), where the differences relative to the GPCP data can exceed 6 mm day–1; and additionally, the simulated SPCZ exhibits too great of an eastward extension and zonal orientation with respect to the GPCP rainfall. Excessive large-scale precipitation also spreads over the ITCZ and the tropical Indian Ocean, with a maximum bias of more than 5 mm day–1 in the ITCZ area. In areas with steep topographies, such as the Tibetan Plateau and the Andes Mountains, the precipitation is overestimated. This bias also prevails among the CMIP5 models (Mehran et al., 2014) and corresponds to the cold bias in the surface temperature (Fig. 1b). Over some areas, the precipitation is underestimated, for example, the equa-torial Pacific and the Amazon. The dry bias in the equatorial Pacific is inherently associated with the suppressed convection as a result of the cold bias in SST.

|
| Figure 1 Annual mean differences (°C) in (a) SST and (b) 2-m air temperature between the CAMS-CSM HIST simulation and observations (1980–2013). The observational data used for SST and 2-m air temperature are HadISST and CRUTEM4 data, respectively. |
Figure 3 shows the time–latitude section of zonal mean precipitation from the model and observations, manifesting the precipitation features associated with ITCZ and SPCZ. It can be seen that the major rainbelts as well as the seasonal migration of the ITCZ and SPCZ are reasonably captured by the model. The simulated ITCZ moves to its northernmost position with a peak in precipitation from July to August, and the SPCZ is the strongest and at its southernmost position from Febuary to March, which agree well with the observations. During May to December, the ITCZ dominates the precipitation over the tropical region, while the SPCZ prevails from January to April; such a seasonal timing feature is consistent between the model and observations. How-ever, there are some discrepancies between the model and observations. The most prominent discrepancy is that the precipitation in the model is too strong, especially for the ITCZ and SPCZ. The simulated maximum precipitation of the SPCZ is approximately 60% greater than both the GPCP and TRMM data, indicating that the model has a certain double-ITCZ structure reflected in the annual mean precipitation field. On the other hand, the minimums of the ITCZ and SPCZ in the model are slightly weaker than those of the observations. For example, during January–April, the observed precipitation of the ITCZ is comparable with that of the SPCZ, which reflects a double-ITCZ structure, and the simulation exhibits a distribution more like that of a single ITCZ, with precipitation of the ITCZ being only 30%–40% that of the SPCZ. This implies that the model tends to produce a stronger seasonal cycle for both the ITCZ and SPCZ with regard to the observations.

|
| Figure 3 Climatological annual cycle of zonal mean (180°W–180°E) precipitation (mm day–1) for the (a) GPCP, (b) TRMM 3B42, and (c) CAMS-CSM HIST simulation (1980–2013). |
Figure 4a shows the vertical profiles of zonally averaged annual mean air temperature from the HIST simulation and the biases relative to ERA-Interim data. In general, the model well reproduces the thermal structure of the atmosphere. Over 50°S–50°N, the simulated annual mean temperature is colder than the ERA-Interim data within 2 K between 300 and 150 hPa, while below 300 hPa and above 150 hPa, the temperature mainly exhibits warm biases ranging from 1 to 3 K and a maximum of 3 K at 30°N and 100 hPa. In the polar atmosphere, the bias is considerably larger than those in the middle and low latitudes. Near the top of the polar atmosphere, the simulated temperature deviates from the observed values by more than –6 K in both the Northern Hemisphere (NH) and Southern Hemisphere (SH). In the high latitude regions, the bias exceeds 6 and –6 K below 300 hPa and between 300 and 150 hPa, respectively.

|
| Figure 4 Zonally averaged annual mean (a) air temperature, (b) zonal wind, (c) vertical velocity, and (d) specific humidity climatology (1980–2013) from the CAMS-CSM HIST simulation (black contours) and biases relative to the ERA-Interim climatology (color shaded; color bar is of the same units). |
The vertical profile of the zonal wind is shown in Fig. 4b. Overall, the model reasonably captures the position and strengths of the westerly jet in both hemispheres. In most regions, the bias is less than 2 m s–1. The largest deviation appears in the upper troposphere of the tropical atmosphere (400–100 hPa), where the bias can exceed 6 m s–1, indicating a weakened equatorial easterly and equatorward extent of the westerly jet in the model. To a large extent, the pattern of the zonal wind bias is physically consistent with that of the temperature bias. For example, the positive biases distributed around the equatorward edges of the westerly jet [30°S (N)–50°S (N)] above 200 hPa are associated with the increased meridional gradient in temperature biases in that region, while the easterly biases at approximately 60°S (N) from the surface to 100 hPa correspond to the decreased meridional gradient due to low-level warm biases in the polar region.
The zonally averaged vertical velocity is shown in Fig. 4c. The general features of the climatological ascending and descending motions are captured by the model. Large biases are mainly located around the tropi-cal region, where the climatological ascending flow is strongest due to the active convection. The vertical velocity biases show consistent patterns compared to the precipitation biases (Fig. 2c). For example, on the equator, the descending motion bias is associated with the underestimated precipitation along the equatorial cold tongue, while the excessive precipitation of the ITCZ and SPCZ is linked to the biased ascending flows on both sides of the equator.
Moisture is a critical factor for precipitation and cloud formation. As shown in Fig. 4d, the model is able to capture the major zonal mean vertical structure of specific humidity, such as the maximums over the ITCZ and SPCZ regions. The biases are less than 1.2 g kg–1 over most of the domain, except for the wet bias between 850 and 600 hPa in the tropics. As with the vertical velocity, the spatial distribution of the specific humidity biases also shows a consistent pattern in the precipitation field. For example, both the ITCZ and SPCZ exhibit wet biases in the middle to upper troposphere, which correspond to the overestimated precipitation over these two regions. Moreover, the bias associated with the SPCZ is much wetter than that with the ITCZ. As a result, the mean specific humidity peaks tend to be symmetrically distributed about the equator, which reflects the double-ITCZ feature in the annual mean precipitation field. At the low levels of the tropics, the simulated specific humidity tends to be drier than the ERA-Interim field, which seems to be a common bias in coupled climate models (Tian et al., 2013).
3.4 Sea iceAs a boundary between the ocean and atmosphere in the polar regions, sea ice strongly influences the heat and water fluxes into the atmosphere, and therefore, sea ice plays a critical role in the global climate system. Due to the ice-albedo/snow-albedo positive feedback, the climate sensitivity to increasing greenhouse gases is enhanced in the Arctic relative to those of other regions. Thus, sea ice usually serves as a key indicator of climate change. Realistically representing sea ice cover is crucial for reasonable climate sensitivity in climate models, but it is a challenge for coupled models. Figure 5 shows the climatological sea ice concentration in the NH and SH of the 1980–2013 HIST simulation. A reference line (black solid) is presented to indicate a mean concentration of 15% from the HadISST data. To a large extent, CAMS-CSM reproduces the distribution of sea ice in the polar regions. In general, the sea ice extension over the Arctic is overestimated during both February–March–April (FMA) and August–September–October (ASO), while in the Antarctica, sea ice is considerably underestimated during FMA. However, the Antarctic sea ice cover during ASO is well captured by the model. Excessive sea ice in the NH during FMA mainly occurs in the high latitude oceans adjacent to the North Atlantic Ocean, including Hudson Bay, the Labrador Sea, Greenland Sea, Norwegian Sea, and Barents Sea. The sea ice cover near North Pacific is also overestimated. During ASO, excessive sea ice in the NH is primarily distributed in certain areas of the Greenland Sea and Barents Sea. In the Antarctic region, sea ice is only visible over the Ross Sea and Weddell Sea during FMA. The climatological mean sea ice extent and area are shown inTable 1. The sea ice extent is defined as the area with ice concentrations greater than 15%, and this is commonly used for model validation. The simulated mean sea ice extent/area in the NH during FMA and ASO are 22.0/19.0 and 11.0/8.5 million km2, respectively, while the NSIDC extent/area is 15.2/13.0 and 7.5/5.3 million km2. In the SH, the simulated mean sea ice extent/area during FMA is 0.84/0.45 million km2, which is considerably lower than the NSIDC values. Nevertheless, the model shows better performance in simulating the sea ice extent/area in the SH during ASO, with values of 20.1/16.7 and 18.1/14.2 million km2 in the model and observations, respectively. The excessive sea ice extension in the NH may be ascribed to the underestimated Atlantic Meridional Overturning Circulation (AMOC) in the model (figure omitted), while the underestimated sea ice may be associated with the strong warm bias over the Antarctic region, which is shown in Fig. 4a.
| NH FMA | NH ASO | SH FMA | SH ASO | |
| NSIDC | 15.2/13.0 | 7.5/5.3 | 4.6/3.4 | 18.1/14.2 |
| CAMS-CSM | 22.0/19.0 | 11.0/8.5 | 0.84/0.45 | 20.1/16.7 |

|
| Figure 5 Climatological sea ice concentration in the (a, b) Arctic and (c, d) Antarctica for the period of 1980–2013 for the HIST simulation. The solid black lines indicate the 15% mean concentration values from the HadISST data in the same period. (a, c) Left and (b, d) right panels denote the averages for FMA and ASO, respectively. |
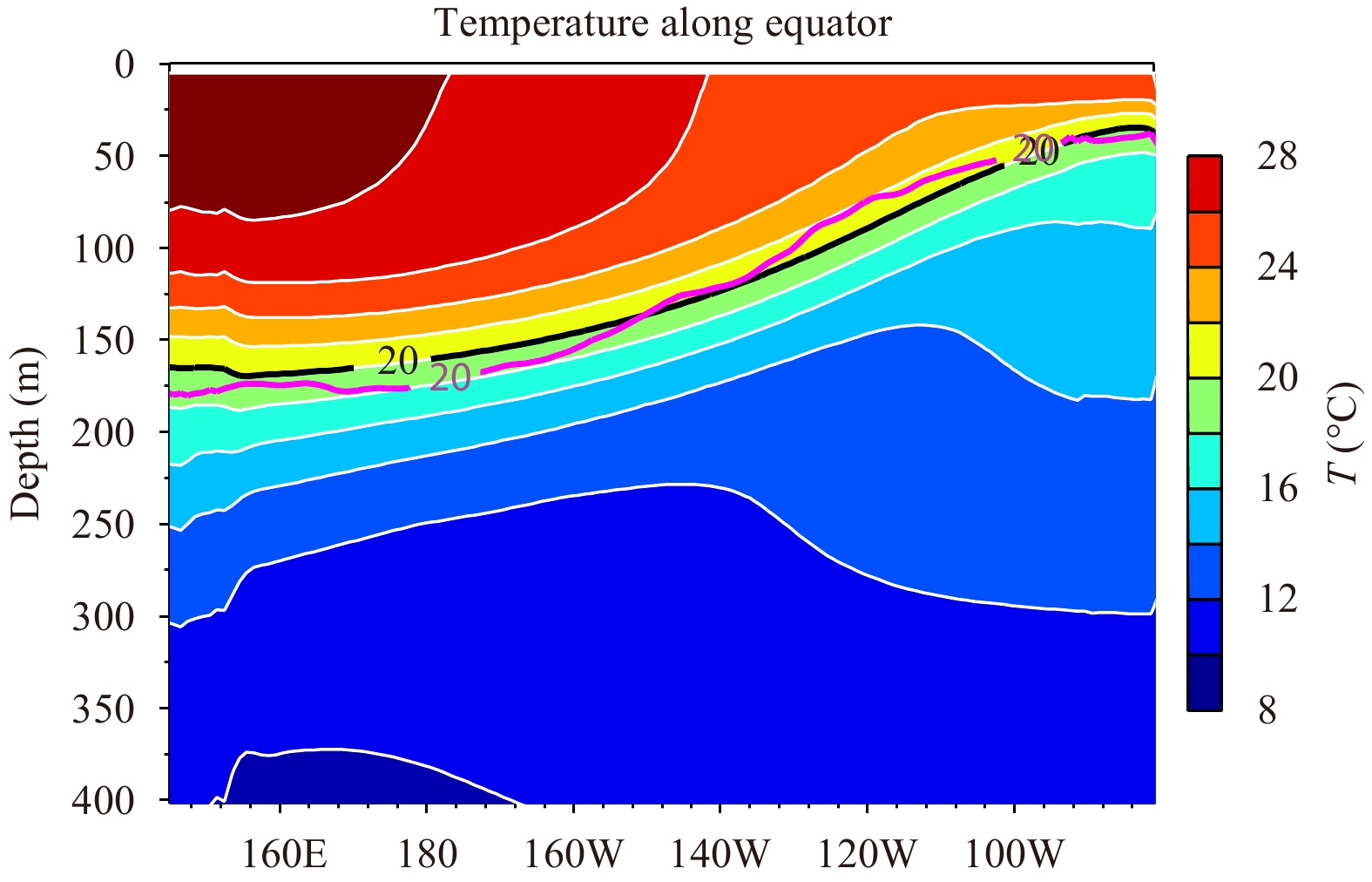
The El Niño–Southern Oscillation (ENSO) is the most prominent climate mode on the interannual timescale. Evident anomalies of the atmosphere and ocean have been observed during ENSO events, including those in SST, precipitation, zonal wind, and thermocline depth. The change in thermocline depth can lead to fluctuations in SST in the eastern equatorial Pacific by upwelling and mixing, which is referred to as thermocline feedback that plays an important role in ENSO dynamics. The thermocline feedback is most effective over the central–eastern equatorial Pacific because of the shallow thermocline depth in that region. Therefore, realistically representing the mean thermocline and its seasonal cycle are crucial for ENSO simulations.Figure 6 shows the simulated annual mean Pacific upper ocean temperatures along the equa-tor. Here, the 20°C isotherm is used to represent the thermocline depth. Compared with the observations, the thermocline depth is well reproduced by the model. The simulated thermocline is somewhat shallower in the western Pacific and deeper in the eastern Pacific, indicating a slightly weaker zonal slope of the thermocline in the model.
|
| Figure 6 Annual mean Pacific Ocean temperatures (°C) along the equator (5°S–5°N) derived from the CAMS-CSM HIST simulation (contours and shading). The black and purple lines indicate the 20°C isotherm from CAMS-CSM and Levitus climatology, respectively. |
A distinctive feature of ENSO is its phase-locking during boreal winter. Previous studies proposed that the seasonal variations in climatological states are crucial for ENSO phase-locking (Philander, 1983; Zebiak and Cane, 1987; Tziperman et al., 1997). One of the essential metrics used to measure the seasonal variation in tropical climatology is the seasonal cycle of the equatorial SST, which is shown in Fig. 7. Qualitatively, CAMS-CSM does a good job in reproducing the observed seasonal cycle of the equatorial SST. The annual cycle of SST in the eastern equatorial Pacific, as well as the semi-annual cycle in the western equatorial Pacific, is captured. There are some discrepancies, which primarily occur in the eastern Pacific. The first is that the simulated magnitude of the ENSO warm phase is weaker than the observed, whereas for the cold phase, the magnitude is stronger. Second, the cold phase in the model tends to peak earlier than that in the observations, leading by 1–2 months. Third, the westward propagation of both the warm and cold phases are too weak with respect to the observations, especially for the cold phase, which largely shows a simultaneous and zonally oriented pattern. In the Indian Ocean, the model captures the strongest seasonal cycle in the western basin. The simulated magnitude and peak time are nearly correct. However, the seasonal cycle in the eastern basin is overestimated in the model, displaying an unrealistic eastward propagation during its cold phase. While the annual cycle in the Atlantic is visible from the simulation, there is a certain limitation in the model. The most evident deficiency is the westward shift of the seasonal cycle. On average, the maximum centers are displaced to the west by approximately 10° longitudes. As a result, the observed weak semi-annual cycle in the western basin is distorted by a strong annual cycle in the model, which is likely coupled to the precipitation bias along the equatorial Atlantic Ocean, as shown in Fig. 2c.

|
| Figure 7 Annual cycle of equatorial SST (averaged over 5°S–5°N; °C) from the (a) HadISST and (b) CAMS-CSM HIST simulation. |
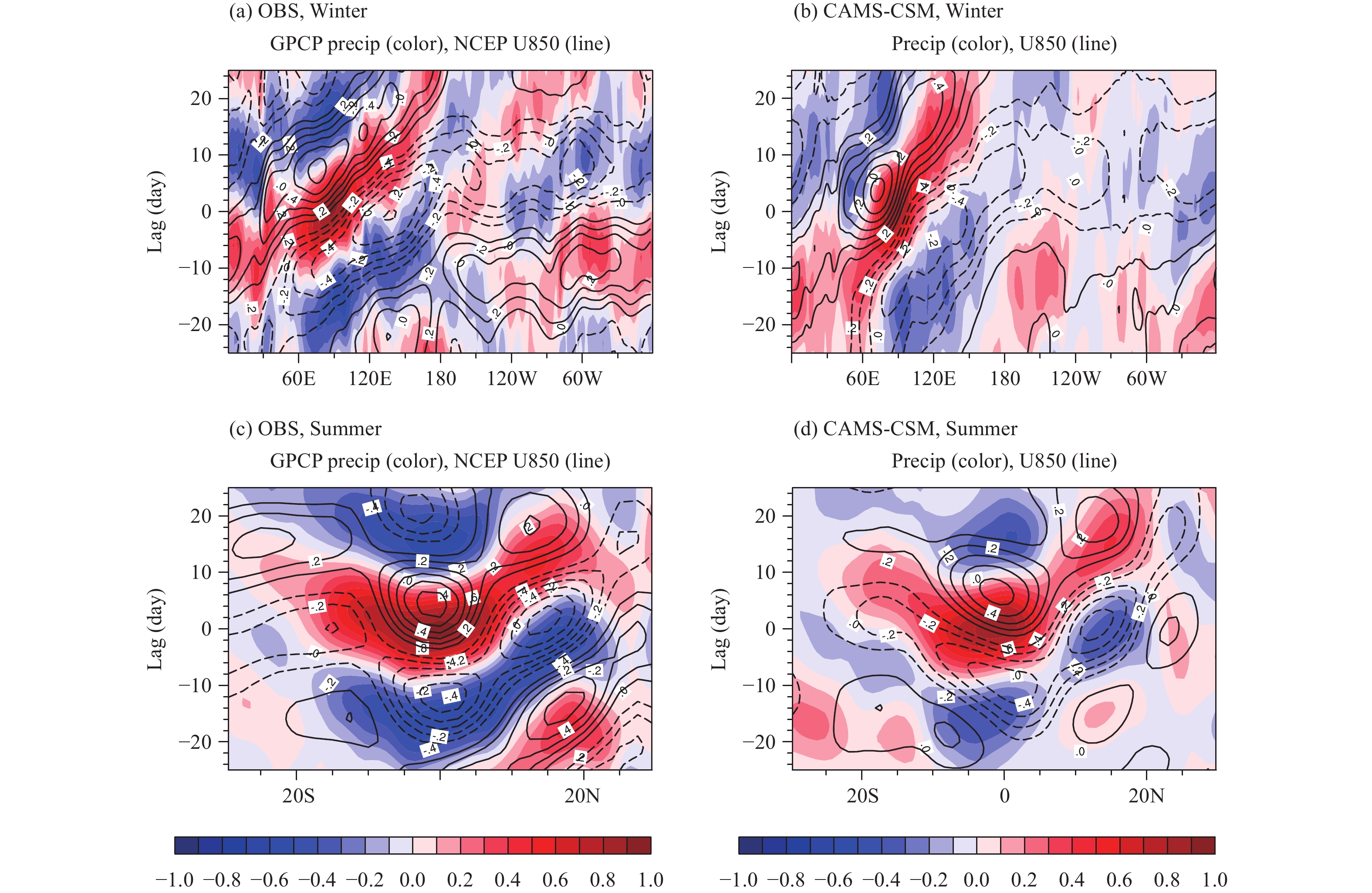
The dominant mode of intraseasonal variability in the tropics is the Madden–Julian Oscillation (MJO;Madden and Julian, 1971, 1972). While the MJO is primarily characterized by the eastward propagation of troposphe-ric circulations with a zonal wavenumber one structure and a period of 30–60 days, it exhibits pronounced seasonality in its strength, frequency, and movement (Madden, 1986; Wang and Rui, 1990; Hartmann et al., 1992). The MJO is observed to be the strongest during boreal winter, with eastward propagation along the equator; however, in boreal summer, the MJO is weaker and dominated by a northward propagation in the Indian Ocean and northwestward propagation in the western Pacific (Yasunari, 1979, 1980; Murakami, 1980; Sikka and Gadgil, 1980; Krishnamurti and Subrahmanyam, 1982; Lau and Chan, 1986; Hsu and Weng, 2001; Lawrence and Webster, 2002). In this paper, we will use the diagnostics developed by the US-CLIVAR MJO working group to evaluate the MJO features simulated by CAMS-CSM. Figures 8a and 8b show the winter lag–longitude diagram of 10°S–10°N averaged precipitation anomalies and 850-hPa zonal wind anomalies, which are correlated with precipitation anomalies averaged over a reference region in the central Indian Ocean. The eastward propagations of precipitation and zonal wind anomalies, which originate in eastern Indian Ocean and end around the dateline, are clearly seen in both the model and the observations. The observed quadrature temporal phase relationship between wind anomalies and precipitation anomalies is also reproduced by CAMS-CSM. In the observations, the phase speed of the eastward propagating anomalies is approximately 4° longitude per day (approximately 5 m s–1), while the simulated phase speed is approximately 3.5° longitude per day (4.5 m s–1), slightly slower than the observed value. One limitation is that the simulated negative correlations of precipitation and wind anomalies are lower than those in the observations, reflecting a weaker oscillating feature in the model. The limited westward propagation, as seen in the observations west of 60°E, is absent in the simulation. During boreal summer, the strong northward propagation can be clearly seen in the lag–longitude diagram from both the model and the observations (Figs. 8c, d). The simulated phase speed of the northward propagation is approximately 1.5° latitude per day, which agrees well with the observations. The correlation maximums/minimums located near 15°N as well as the limited southward propagation are well reproduced by the model. Similar to the eastward propagation, the simulated correlations, especially the negative correlations, are weaker than those of the observations.
|
| Figure 8 Winter (NDJFMA) lag–longitude diagram of 10°S–10°N averaged precipitation anomalies (color shaded) and 850-hPa zonal wind anomalies (contours), which are correlated with precipitation anomalies averaged over the reference central Indian Ocean region (10°S–5°N, 75°–100°E), for the (a) observations and (b) CAMS-CSM. The summer (MJJASO) lag–latitude diagram of 80°–100°E averaged precipitation anomalies (color shaded) and 850-hPa zonal wind anomalies (contours), which are correlated with the reference precipitation anomaly time series, for the (c) observations (d) and CAMS-CSM. The precipitation and wind fields are subjected to a Lanczos filter to retain the period of 20–100 days. The period of observation data is 1996–2006, and the 20-yr piControl simulation is used for CAMS-CSM results. |
Figure 9 shows the boreal winter equatorial wavenumber–frequency spectra of the daily precipitation and 850-hPa zonal wind anomalies. The observed precipitation shows eastward propagating power, which is concentrated in zonal wavenumbers 1–3 and periods of 40–60 days (Fig. 9a). The dominant spectrum of CAMS-CSM simulation results exhibits a spatial scale of zonal wave-number 2 and a time scale of slightly longer than 80 days (Fig. 9b). The longer period of simulated MJO also exists in the summer precipitation and outgoing longwave radiation (OLR) fields (figures omitted). For the 850-hPa zonal wind, both the observations and CAMS-CSM simulation show consistent peak power on the spatial scale of zonal wavenumber one. However, analogous to the precipitation, CAMS-CSM produces a dominant time scale of longer than 80 days. This means that the eastward propagating phase speed of the simulated MJO tends to be lower than that of the observations, as is shown in Fig. 8.

|
| Figure 9 Winter (NDJFMA) wavenumber–frequency spectra of 10°S–10°N averaged daily (a, b) precipitation and (c, d) 850-hPa zonal wind anomalies from the (a, c) observations and (b, d) piControl simulation. The observations and model simulation used for the calculation are the same as those inFig. 8 but using the unfiltered daily anomalies. The x-axis denotes the frequency (cycle day–1), with the positive (negative) value representing the eastward (westward) propagations, respectively. |
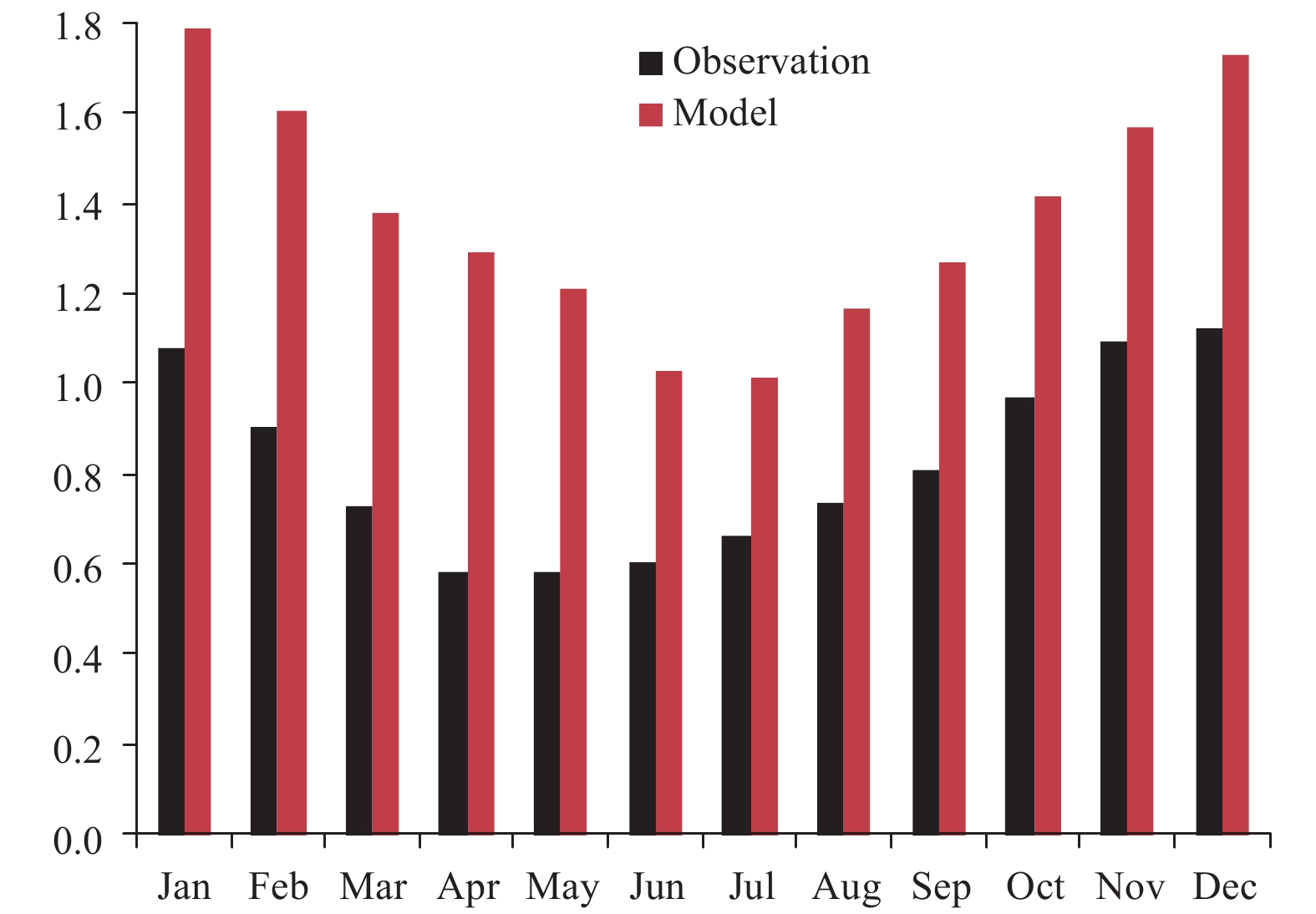
While ENSO is observed to evolve over the entire tropical Pacific Ocean, the most pronounced SST variability associated with ENSO occurs in the central–eastern equatorial Pacific.Figure 10 shows the standard deviation of the Niño3.4 index from the observations and model. Overall, the amplitude of the Niño3.4 SST variability is substantially overestimated relative to the HadISST data. The maximum standard deviation of the Niño3.4 index among all calendar months approaches 1.8°C, while in the HadISST data it is approximately 1.1°C; the minimum values are 1.05 and 0.6°C in the model and HadISST, respectively. As mentioned above, a well-known feature of ENSO is its seasonal phase-locking, which refers to the behavior wherein ENSO events tend to mature towards the end of boreal winter. CAMS-CSM shows the capability to reproduce the wintertime peak of the Niño3.4 index; however, it fails to capture the observed minimum in late spring, with the smallest value occurring in early summer. In addition, in the observations, the SST variabilities distribute asymmetrically about the minimum, which reflects a faster decay rate than growth rate. However, the simulated variabilities exhibit a rather symmetrical distribution, suggesting that the fast decay feature of El Niño events is missed in the model. The power spectra of the normalized Niño3.4 index from the model and HadISST are shown in Fig. 11. In the observations, the Niño3.4 index exhibits a powerful band with a period ranging from 2 to 6 yr. The model does reproduce the energetic power between 2 and 6 yr; however, it displays striking peaks near 3 yr, indicating that the ENSO in the model may oscillate more regularly with respect to the observations.
|
| Figure 10 Standard deviation of the Niño3.4 index (SSTA averaged over 5°S–5°N, 170°–120°E) for each calendar month as derived from the CAMS-CSM piControl simulation (red bar) and HadISST data (black bar, 1950–2013). |

|
| Figure 11 Power spectra of the Niño3.4 index from (a) HadISST and (b) CAMS-CSM piControl simulation. The power spectra method follows the work of Vautard et al. (1992). |
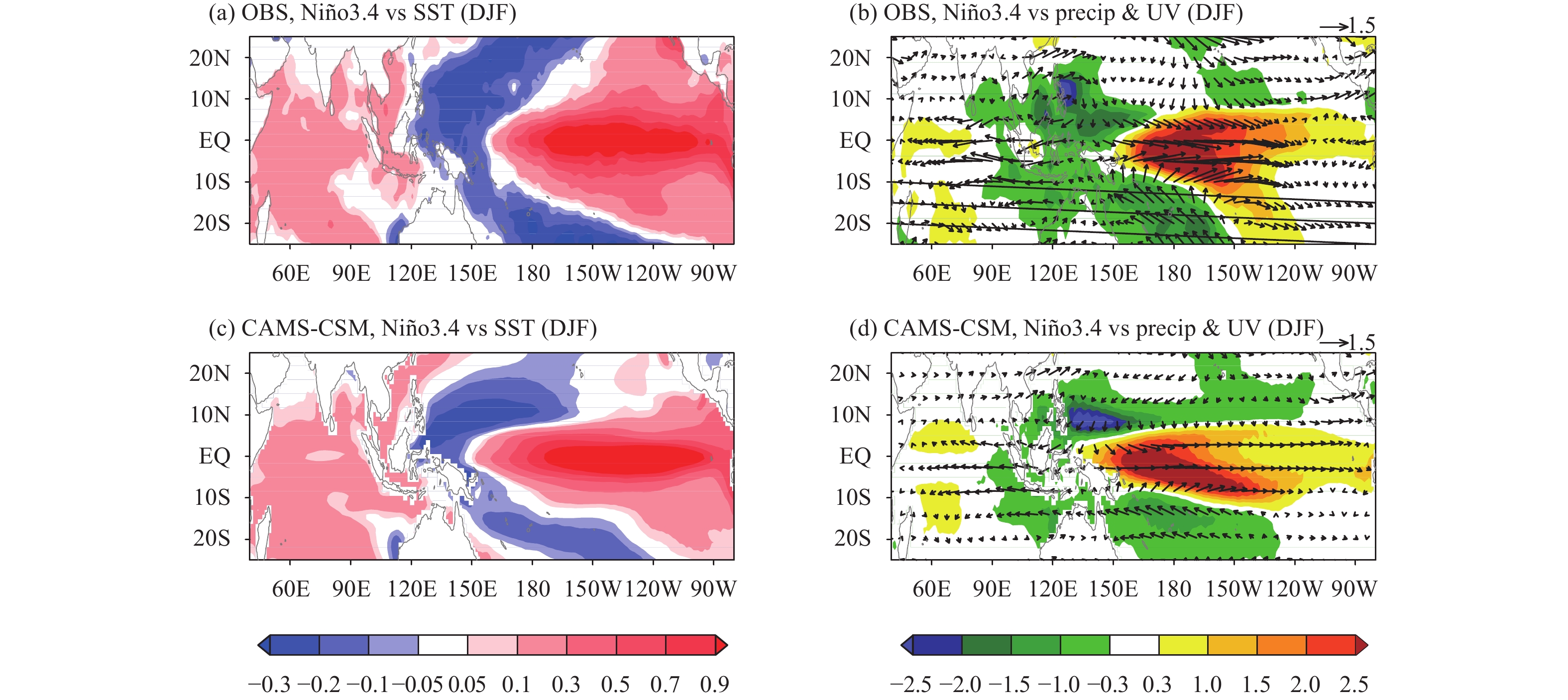
The regression pattern between the Niño3.4 index and SST anomalies of the tropical Pacific–Indian Oceans are shown inFigs. 12a, c. Overall, the anomalous SST pattern during ENSO events is reasonably captured by the model. Compared with the HadISST data, the simulated positive SST anomalies (SSTA) over the central and eastern Pacific are too narrow in the meridional direction and extend more westward as a result of the excessive westward penetration of the cold tongue in the model. The negative anomalies in the western Pacific exhibit a zonal orientation for the north lobe, while for the south lobe, the simulated strength appears to be weaker than that of the observations. The spatial pattern and magnitude of the warm signals over the South China Sea and tropical Indian Ocean are successfully simulated, as does that of the small negative area on the west coast of Australia.
|
| Figure 12 (a, c) Winter (DJF) SST (shaded; °C) and (b, d) precipitation (shaded; mm day–1) and 850-hPa wind anomalies (vector; m s–1), regressed on the Niño3.4 index from the (a, b) observations and (b, d) CAMS-CSM piControl simulation. The SST, precipitation, and 850-hPa winds are derived from the HadISST, GPCP, and NCEP2 data over 1980–2013, respectively. |
The regressions between the Niño3.4 index and precipitation and 850-hPa wind anomalies are shown in Figs. 12b, d. The anomalous pattern is characterized by increased precipitation over the central equatorial Pacific as a result of the enhanced convection responding to the warm SSTA. Meanwhile, anomalous westerlies extend from 150°E–120°W over the equatorial Pacific Ocean, which reflects the atmospheric aspect of the Bjerknes feedback. Negative precipitation anomalies spread over the eastern Indian Ocean and regions of cold SSTA due to the weakening Walker circulation and suppressed convection in that region. The model shows the ability to capture the spatial patterns of precipitation and wind anomalies associated with ENSO. The anomalous precipitation centers and low-level winds in both the Pacific and Indian Oceans are reproduced at magnitudes comparable to those of the observations. For example, the model captures the observed asymmetrical features of the precipitation and low-level wind anomalies: both precipitation and low-level wind anomalies tend to maximize south of the equator. There are two major deficiencies: 1) The precipitation anomalies exhibit a westward displacement with respect to the GPCP data, and 2) the strength of the westerly anomalies is considerably weaker than the observations, indicating an underestimated Bjerknes feedback in the model.
4.3 East Asian summer monsoon variabilityGiven the difficulty and challenge in simulating the East Asian climate, the East Asian summer monsoon (EASM) can thereby serve as a test bed for climate models (Zhou et al., 2009). As precipitation and wind are usually used to represent the EASM, in this study, the evaluation is mainly focused on the precipitation and wind variations associated with the EASM variability. While a number of indices have been proposed to measure the strength of the EASM (Wang et al., 2008), here, the monsoon index by Wang and Fan (1999) (denoted as WFI) is adopted, which is defined based on the 850-hPa zonal wind shear:
| $\begin{aligned}{\rm{WFI}} & = {\rm{U}}850_{[{5^ \circ }-{15^ \circ }{\rm{N}}, {90^ \circ }-{130^ \circ }{\rm{E}}]} \\ & \;\;\;\;\;- {\rm{U}}850_{[{22.5^ \circ }-{32.5^ \circ }{\rm{N}}, {110^ \circ }-{140^ \circ }{\rm{E}}]}.\end{aligned}$ |
Figure 13 shows the regression pattern between the negative WFI and the 850-hPa wind and precipitation anomalies from the observations and model. The observed circulation pattern is characterized by an anticyclone with anomalous southwesterly winds over southeastern China and westerly winds along the Yangtze River (YZR) basin to Southeast Japan. There is also an increased easterly stretching from the western Pacific to the South China Sea. The precipitation pattern displays an enhanced rainbelt spanning along the East Asian subtro-pical front and suppressed rainfall spreading in the southern wing of the anticyclone; and the anomalous precipitation centers are distributed close to the climatological rainfall centers (Fig. 2). Overall, the model does fairly well reproduce the observed pattern. The enhanced/deficit rainbelt over the northern/southern wing of the anticyclone is captured by the model. In particular, the model is able to capture the anomalous rainfall centers associated with the variations in the Meiyu/Baiu/Changma rainbelt, which remain poorly simulated by most present-day climate models (Song and Zhou, 2014b). However, some limitations exist in the model. For example, the intensities of the positive centers are generally weaker than the GPCP data, while the negative center over the western Pacific is too strong with respect to the observations. In addition, the negative rainfall center over the South China Sea is underestimated, and the center over the Indo-China Peninsula appears to be displaced to the south. Additionally, there is an anomalous cyclonic circulation over northern Japan in the observed pattern that is associated with the so-called East Asia–Pacific (EAP) or Pacific–Japan (PJ) pattern (Nitta, 1987; Huang and Lu, 1989). This pattern is visible in the model but with a weaker strength.
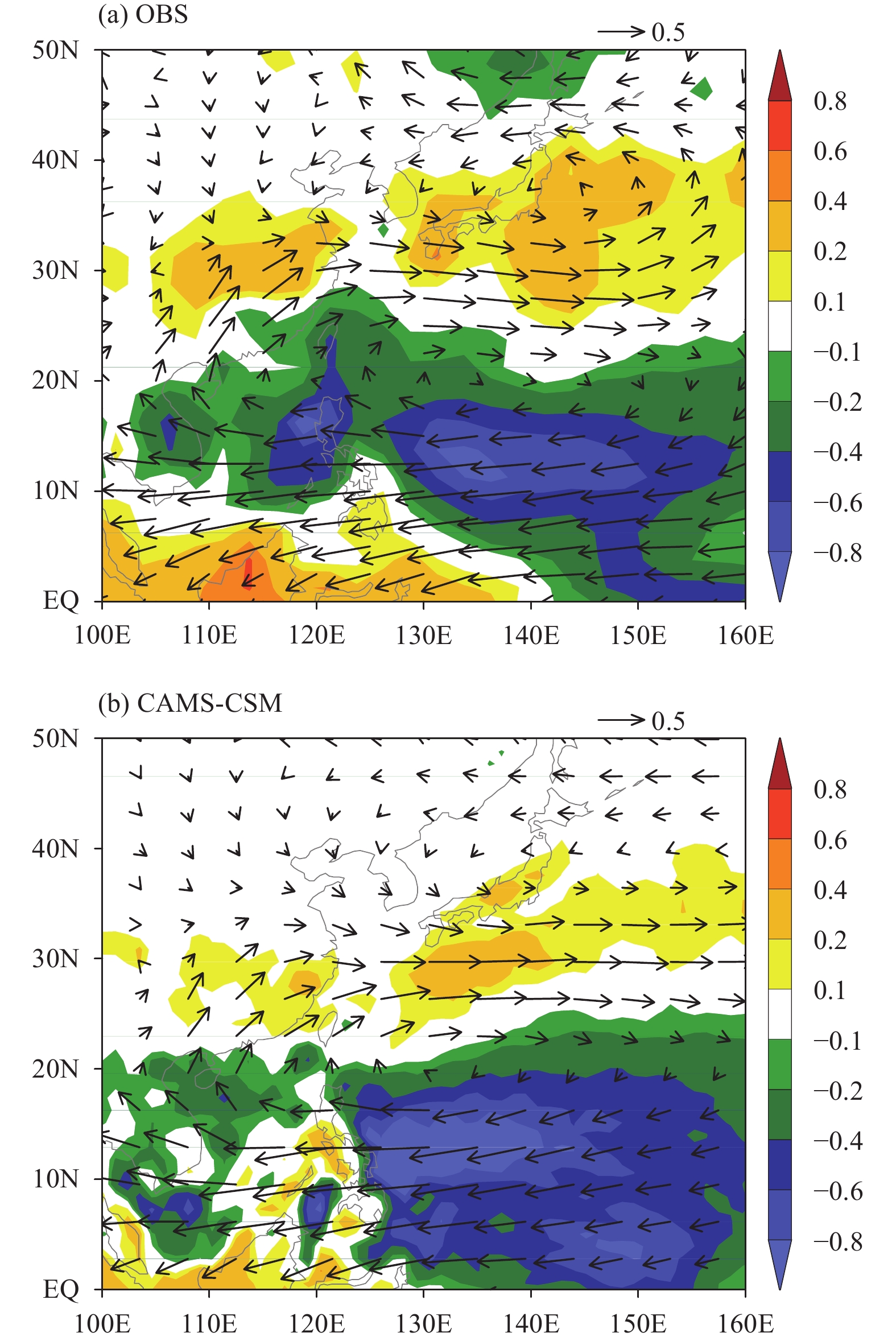
|
| Figure 13 Summer precipitation (shaded; mm day–1) and 850-hPa wind anomalies (vector; m s–1) regressed on the negative WFI index from the (a) observations and (b) CAMS-CSM piControl simulation. The observational data used for precipitation and 850-hPa winds are the same as those in Fig. 12. |

|
| Figure 2 Climatological annual mean precipitation (mm day–1) from (a) GPCP observations and (b) CAMS-CSM HIST simulation, and (c) the annual mean precipitation bias (mm day–1) of CAMS-CSM relative to the GPCP climatology. |
The distributions of the winds and precipitation in Fig. 13 reflect the anomalous pattern during the decaying summer El Niño event, which also features an anticyclone over the northwestern Pacific (Zhang et al., 1996; Wang et al., 2003) and appears to be the dominant mode of the EASM’s interannual variability (Wang et al., 2008). This anticyclone, which is referred to as the western North Pacific anticyclone (WNPAC), originates in the autumn of the El Niño developing phase and is sustained until the decaying summer El Niño event, providing a mechanism that connects the summer precipitation of China with ENSO. While the mechanism for sustaining the WNPAC into the decayed summer is controversial, it might be linked to the combined forcing from the northwestern Pacific, the Indian Ocean, and the tropical North Atlantic Ocean (Wu et al., 2009; Xie et al., 2009; Rong et al., 2010; Li et al., 2017). To examine how well the model captures this dominant pattern in the ENSO–EASM relationship, the correlations between the winter (DJF) Niño3 index, and the following summer precipitation and 850-hPa wind anomalies are calculated, as shown inFig. 14. Indeed, the correlation pattern resembles that in Fig. 13, suggesting that the dominant mode of the EASM is closely related to ENSO. The mo-del successfully reproduces the ENSO-related pattern for both precipitation and the 850-hPa winds. The anticyclonic circulation over the western North Pacific can be clearly observed from the simulated pattern. Analogous to the GPCP data, the simulated anomalous Meiyu/Baiu/Changma rainbelt stretches from eastern China to southeastern Japan, suggesting that the model has a fairly good ability to simulate the ENSO–EASM relationship. The major deficiency is that the simulated WNPAC together with the suppressed rainfall center exhibits an eastward shift with respect to the NCEP2 and GPCP data. Accordingly, the positive precipitation center over the YZR basin and the negative precipitation center over southern China are both reduced as a result of the weakened southwesterly winds. The eastward shift of the WNPAC also leads to the dismissal of the negative centers over the South China Sea and Indo-China Peninsula, and conversely, an unrealistic rainbelt appears to dominate the tropics. As the WNPAC may be locally and remotely forced, the westward shift of the WNPAC may be related to the underestimated effect from the remote oceans in the model.

|
| Figure 14 Correlations between the winter Niño3 index (DJF0) and the following summer (JJA1) precipitation (shading) and 850-hPa wind (vector) anomalies from the (a) observations and (b) CAMS-CSM piControl simulation. The observation data used for the precipitation and 850-hPa winds are the same as those in Fig. 11. Only the results at the confidence levels above 95% are shown. |
The SSTs over the global oceans are observed to exhibit significant decadal to multidecadal variability. In the Pacific Ocean, an ENSO-like decadal to bi-decadal mode has been identified from the leading principal component (PC1) of the EOF decomposition of the low-pass SST anomalies (Zhang et al., 1997), which is referred as the Pacific Decadal Oscillation (PDO; Mantua et al., 1997) or Interdecadal Pacific Oscillation (IPO; Power et al., 1998). The PDO pattern is characterized by a coherent variability over the central and western North Pacific and the opposite sign of variability over the tropical Pacific and west coast of North America. From the IPO perspective, the variability further extends into South Pacific and bears a rather symmetrical pattern about the equator. While the PDO is documented as an ENSO-like pattern, it comprises distinct characteristics with respect to ENSO. First, the PDO shows a maximum signal in North Pacific, while ENSO variability is dominant over the tropical Pacific. Second, the PDO variability in the tropical Pacific tends to maximize over the central Pacific, while ENSO shows the largest variability towards the eastern Pacific. In addition, the meridional extension of the PDO pattern over the tropical Pacific is notably broader than that of ENSO.
To evaluate the model performance in PDO simulation, the PDO patterns are calculated by regressing the PC1 of the North Pacific SSTA (20°–60°N, 110°E–100°W) onto the SSTA of the entire basin, and compared with the observations, as shown in Fig. 15. The spatial pattern of the PDO is reasonably simulated by the model (Fig. 15c), with comparable percentages of explained variance and strengths over North Pacific between the model and HadISST data. The simulated time series also shows evident decadal fluctuations, similar to those of the observations (Figs. 15b, d). While the model captures the relative strength between North Pacific and tropical Pacific, several features of the simulated PDO differ from the observed pattern. First, the largest negative SSTA signal is observed in the central and eastern North Pacific between 30° and 40°N, whereas the model exhibits its most prominent signal stretching from the central North Pacific towards the western boundary of the basin along 40°N. The westward displacement of the maximum is likely related to the overestimated width of the western boundary currents, which is due to the coarse resolution of the ocean model. Second, although the largest positive signal in the tropical Pacific is located in the central equatorial Pacific, it stretches too far to the west. In addition, the negative signal over South Pacific are generally underestimated by the model. Newman et al. (2003) showed that the decadal SST variability in North Pacific can be simulated by a first order auto-regressive (AR1) process with the remote forcing of ENSO included, and thus, the PDO may be regarded as a combined response of atmospheric noise and ENSO. The weak correlation between the North Pacific SSTA signal and those SSTA signals over the tropical Pacific and South Pacific may therefore reflect the weakened ENSO teleconnection of the model with respect to those of the observations.
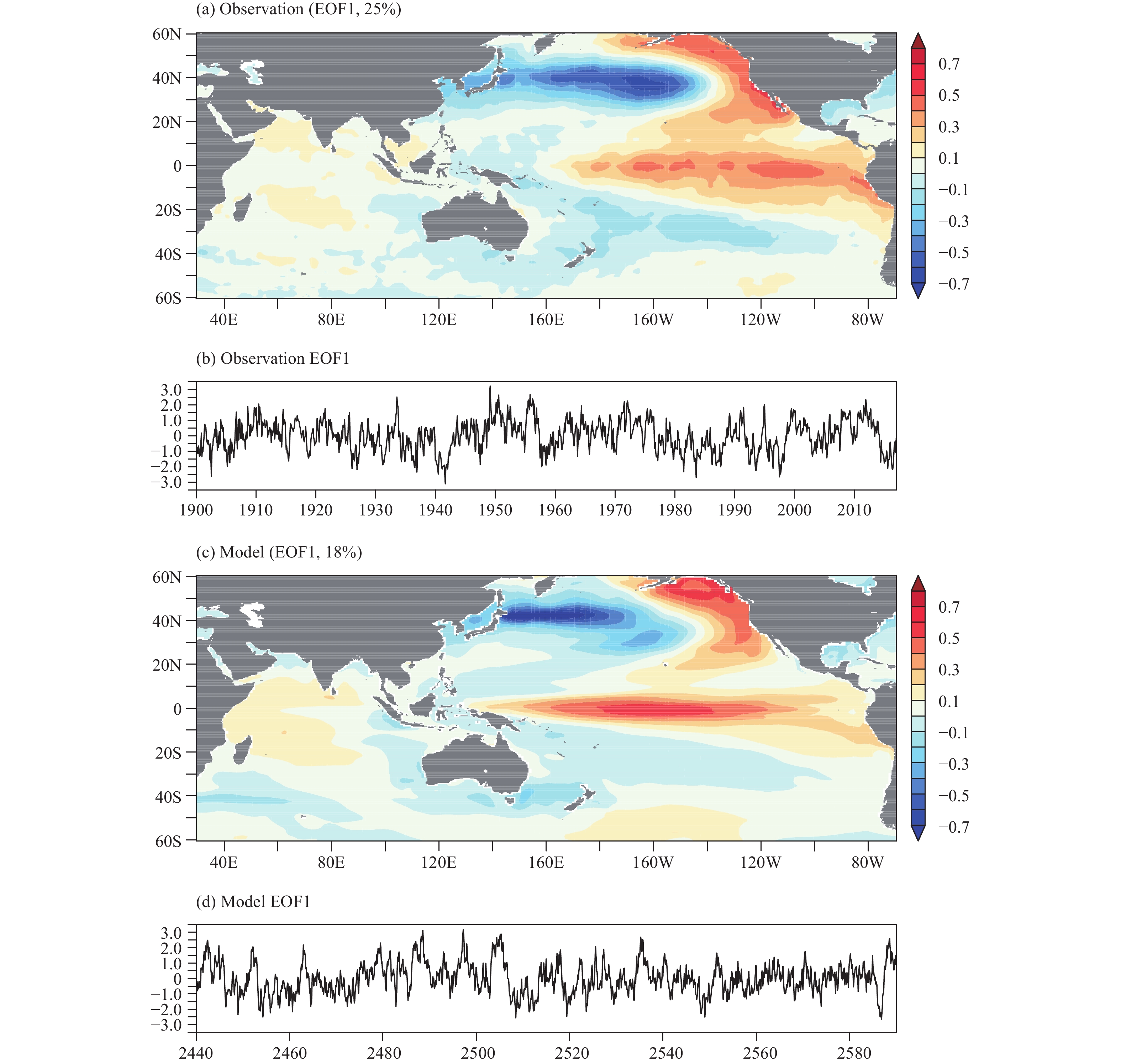
|
| Figure 15 Leading EOF patterns of the monthly SST anomalies for the North Pacific domain (20°–60°N, 110°E–100°W) derived from the (a) observations and (c) CAMS-CSM piControl simulation. The pattern is calculated by regressing the SST anomalies on the normalized PC1 of the (b) observations and (d) CAMS-CSM, respectively. The percentage of variance explained is shown in parentheses at the top of panels (a, c). |
In this study, we describe the formulation of a new coupled climate model named CAMS-CSM and evaluate the results of its pre-industrial simulation as well as a simulation similar to the CMIP6 historical simulation. The climatological mean states and seasonal cycles are evaluated with respect to a number of observational datasets, including the surface air temperature, SST, precipitation, sea ice extent, equatorial Pacific thermocline structure, as well as the vertical profiles of temperature, humidity, and winds. The model performance in simulating the major climate variability modes is also presented and discussed.
In most regions, the SST bias is less than 1.5°C, and the deviation of simulated terrestrial 2-m air temperature from CRUTEM4 data is smaller than 2°C. The model reasonably captures the climatological mean state and seasonal cycle of precipitation. The simulated seasonal timings of the ITCZ and SPCZ are consistent with those of the observations but with overestimated strengths. In general, the vertical structure of the climatological mean temperature, humidity, zonal wind, and vertical velocity is reproduced by the model. In most regions, the temperature biases are less than 2 K. The positions and magnitudes of the westerly jets in both hemispheres are well described by the model but with some error in the upper troposphere. The model captures the geographical distribution of sea ice in the polar regions. In the NH, the model tends to produce excessive sea ice extent during the cold season, whereas it experiences insufficient sea ice in the SH during the warm season. However, during the cold season, the sea ice in the SH is well simulated by the model. The model well depicts the thermocline structure of the equatorial Pacific Ocean as well as the seaso-nal cycle of the equatorial SST, including the annual cycle in the eastern Pacific and semi-annual cycle in the western Pacific.
The major characteristics of MJO are reasonably captured by CAMS-CSM, such as its spatial scale and eastward and northward propagations. The simulated phase speeds of the eastward and northward propagations are comparable with the observations. While the model tends to have a vigorous ENSO, it shows the ability to reproduce the wintertime peak features of ENSO, as well as the observed powerful band of the ENSO period between 2 and 6 yr. The spatial patterns of SST, low-level wind, and precipitation anomalies associated with ENSO are well depicted in the simulation, with the limitation of a westward shift in SST and precipitation as well as a weakened Bjerknes feedback. The model performs well in simulating the EASM variability. The major pattern of the EASM interannual variability is well described in the simulation, particularly in the distribution of the anomalous rainbelts. The model also exhibits the ability to simulate the ENSO–EASM relationship. The anomalous western North Pacific anticyclone as well as the rainfall during the ENSO decaying phase are reasonably represented. The model is able to capture the leading features of the PDO pattern, with comparable magnitude and explained variance of the North Pacific SSTA EOF PC1 with respect to the HadISST data.
In general, the model has shown a reasonable performance in simulating the climatological mean state, seaso-nal cycle and climate variabilities; however, there are some deficiencies that need to be further addressed. The first deficiency is the double-ITCZ in the annual mean precipitation field; although this has long been recognized by the climate model community, the deficiency remains not well resolved. Another bias is the overestimated ENSO strength. As the Bjerknes feedback is underestimated in the model, the enhanced ENSO amplitude is likely to be connected to the damping process underestimation of SST anomalies over central–eastern equato-rial Pacific in the model, which requires further diagnos-tics with respect to the model’s cloud and radiation processes. In addition, the model shows distinct biases in the sea ice between the Arctic and Antarctic regions, which may be associated with different physical processes. Gi-ven the important role of sea ice in the global climate, a detailed evaluation of the sea ice model and associated oceanic and atmospheric processes is required.
Appendix: Coupling algorithmFor stability considerations, the time-stepping of vertical diffusion is treated implicitly in the ECHAM5 mo-del. The use of the implicit algorithm results in a tridiagonal system for momentum, temperature, and water vapor tendencies, in which the surface fluxes rely on the states of the next time step and can only be obtained after solving the tridiagonal equations in the atmospheric mo-del. As there may be five categories of sea ice and one open water area that coexist in a single ocean grid cell, calculating the surface fluxes for each type of area in the atmospheric model will be less efficient. The reason for this is that the coupler needs to pass the sea ice states of all categories to the atmospheric model, and then, all the surface fluxes are obtained once they are solved in the atmospheric model. This procedure requires a large number of communications between the ocean, the atmos-phere, and the coupler. To avoid the communication cost, one solution is to calculate the air–ice fluxes for each sea ice category in the sea ice model, and the grid mean fluxes are provided to the atmospheric model for the tendency calculation of the vertical diffusion. However, this approach will lead to an explicit treatment of the air–ice fluxes at the cost of stability. Our strategy is a compromise, meaning that the grid mean states (e.g., surface temperature) of sea ice and open water are used for the implicit calculation of the surface fluxes and tendencies in the atmospheric model. Some intermediate quantities (mainly exchange coefficients) related to the flux calculations are passed back to the coupler and placed on the exchange grid, and the air–sea and air–ice fluxes are consequently calculated again and interpolated to the ocean grid through the exchange grid. By computing the grid mean states of sea ice and open water in a proper manner, the surface fluxes calculated in the atmospheric model and those on the exchange grid are strictly conserved. The algorithm is demonstrated as follows.
To simplify the description, we describe only the case of an atmospheric grid that contains ocean and sea ice areas, but the algorithm is also applicable to a case with a land fraction. The sensible flux is considered on an atmos-pheric grid with N exchange grids. It is assumed that each exchange grid contains M - 1 categories of sea ice and 1 open water area, and then, the grid mean sensible flux for an atmospheric cell can be computed by averaging all air–sea and air–ice fluxes over the exchange grids:
| ${\rm{sfl{x_{exch}}}} = \sum\nolimits_{n = 1}^N {\left\{ {{a_n}\sum\nolimits_{m = 1}^{M - 1} {{F_{n,m}}{{\left({\rho {C_h}\left| V \right|} \right)}_{{\rm ice},n,m}}} \left({{T_{\rm{a}}} - {T_{{\rm ice},n,m}}} \right) + {a_n}{F_{n,M}}{{\left({\rho {C_h}\left| V \right|} \right)}_{{\rm{w}},n,M}}\left({{T_{\rm{a}}} - {T_{{\rm{w}},n,M}}} \right)} \right\}} /\sum\nolimits_{n = 1}^N {{a_n}},$ | (A1) |
where an denotes the area of the exchange grid n, Fn,m is the fraction of the mth sea ice category in exchange grid n, Fn,M is the fraction of open water, and
The sensible flux calculated in the atmospheric model can be written as follows:
| $\begin{split} {\rm{sfl{x_{atm}}}} & = \left({1 - {P_{\rm ice}}} \right) \cdot {\left({\rho {C_h}\left| V \right|} \right)_{\rm{w}}} \cdot \left({{T_{\rm{a}}} - {T_{\rm{w}}}} \right) \\ & \;\;\;+ {P_{\rm ice}} \cdot {\left({\rho {C_h}\left| V \right|} \right)_{\rm ice}} \cdot \left({{T_{\rm a}} - {T_{\rm ice}}} \right), \end{split}$ | (A2) |
where Pice is the fraction of sea ice in the atmosphere grid; Tw and Tice are the SST and ice surface temperature; and
| ${\rm{sfl{x_{atm}}}} = {\rm{sfl{x_{exch}}}}. $ | (A3) |
Note that
| ${T_{\rm ice}} = \sum\nolimits_{n = 1}^N {\sum\nolimits_{m = 1}^{M - 1} {{a_n}{F_{n, m}}{T_{{\rm ice}, n, m}}/} } \sum\nolimits_{n = 1}^N {\sum\nolimits_{m = 1}^{M - 1} {{a_n}{F_{n, m}}} }, $ | (A4) |
| ${T_{\rm w}} = \sum\nolimits_{n = 1}^N {a_n}{F_{n, M}}{T_{{\rm w}, n, M}}/\sum\nolimits_{n = 1}^N {a_n}{F_{n, M}}, \quad\quad\quad\quad\;$ | (A5) |
and
| ${\left({\rho {C_h}\left| V \right|} \right)_{{\rm ice}, n, m}} = {\left({\rho {C_h}\left| V \right|} \right)_{\rm ice}}\left({n = 1 \ldots N; m = 1 \ldots M - 1} \right), \;\;\;$ | (A6) |
| ${\left({\rho {C_h}\left| V \right|} \right)_{{\rm w}, n, M}} = {\left({\rho {C_h}\left| V \right|} \right)_{\rm w}}\left({n = 1 \ldots N} \right). \quad\quad\quad\quad\;\;\;$ | (A7) |
Equations (A4)–(A7) imply that if the area-weighted grid mean sea ice surface temperature and SST are used for sensible flux calculations in the atmospheric model, and the exchange coefficients Ch on all exchange grids within an atmosphere grid are uniformly set to the value calculated in the atmospheric model, the sensible flux is completely conserved.
Follow the above derivation, the procedures for calculating sensible heat flux consist of the following steps:
(1) The grid mean ice surface temperature and SST on atmospheric grids are interpolated by an area-weighted algorithm according to Eqs. (A4) and (A5) and then are passed to the atmospheric model for fluxes and tendency calculations.
(2) Once the tridiagonal equations of the atmospheric model are solved, the air temperature at the reference height as well as the intermediate variables (i.e., the exchange coefficient multiplied by air density and wind speed) of the atmospheric grid are passed to the coupler and placed on the exchange grid. Then, the air–ice/air–sea fluxes for each category of sea ice and open water are calculated on each exchange grid. These fluxes are consequently interpolated to the ocean grid to update the ocean and sea ice model.
An analogous algorithm can be applied to the moisture flux by replacing the ice surface temperature and SST in step (1) with the saturated specific humidity of sea ice and water surface, respectively. Then, the reference height specific humidity and intermediate variables are passed back to the coupler. For surface longwave and shortwave radiation, the upward longwave radiation and surface albedo are processed via a similar area-weighted approach to guarantee their respective conservation. How-ever, the momentum fluxes are treated in a simpler way. Namely, the grid mean surface current and sea ice velocities are used for the open water and sea ice surface wind stress calculations in the atmospheric model, respectively. The resultant wind stress is then sent back to the coupler and directly interpolated to the ocean grid through using the exchange grid. This means that the surface wind stress on the exchange grids within an atmospheric cell are uniform for all sea ice categories. Such a treatment is reasonable as the differences in velocities among sea ice categories are small with respect to the reference height velocity. Calculation shows that all heat, moisture, and momentum fluxes are conserved within the machine precision by using this approach.
| Adler, R. F., G. J. Huffman, A. Chang, et al., 2003: The version-2 global precipitation climatology Project (GPCP) monthly precipitation analysis (1979–present). J. Hydrometeorol., 4, 1147–1167. DOI:10.1175/1525-7541(2003)004<1147:TVGPCP>2.0.CO;2 |
| Bellenger, H., E. Guilyardi, J. Leloup, et al., 2014: ENSO representation in climate models: From CMIP3 to CMIP5. Climate Dyn., 42, 1999–2018. DOI:10.1007/s00382-013-1783-z |
| Bonan, G. B., 1996: A Land Surface Model (LSM Version 1.0) for Ecological, Hydrological, and Atmospheric Studies: Techni-cal Description and User’s Guide. NCAR Technical Note NCAR/TN-417+STR, Boulder, Colorado, National Center for Atmospheric Research, doi: 10.5065/D6DF6P5X. |
| Chen, L., and O. W. Frauenfeld, 2014: Surface air temperature changes over the twentieth and twenty-first centuries in China simulated by 20 CMIP5 models. J. Climate, 27, 3920–3937. DOI:10.1175/JCLI-D-13-00465.1 |
| Codron, F., and R. Sadourny, 2002: Saturation limiters for water vapour advection schemes: Impact on orographic precipitation. Tellus A, 54, 338–349. DOI:10.3402/tellusa.v54i4.12148 |
| Dai, Y. J., and Q. C. Zeng, 1997: A land surface model (IAP94) for climate studies. Part I: Formulation and validation in off-line experiments. Adv. Atmos. Sci., 14, 433–460. DOI:10.1007/s00376-997-0063-4 |
| Dai, Y. J., X. B. Zeng, R. E. Dickinson, et al., 2003: The common land model. Bull. Amer. Meteor. Soc., 84, 1013–1024. DOI:10.1175/BAMS-84-8-1013 |
| Dai, Y. J., R. E. Dickinson, and Y. P. Wang, 2004: A two-big-leaf model for canopy temperature, photosynthesis, and stomatal conductance. J. Climate, 17, 2281–2299. DOI:10.1175/1520-0442(2004)017<2281:ATMFCT>2.0.CO;2 |
| Dee, D. P., S. M. Uppala, A. J. Simmons, et al., 2011: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Quart. J. Roy. Meteor. Soc., 137, 553–597. DOI:10.1002/qj.828 |
| Dickinson, R. E., A. Henderson-Sellers, and P. J. Kennedy, 1993: Biosphere–Atmosphere Transfer Scheme (BATS) version 1e as Coupled to the NCAR Community Climate Model. NCAR Technical Note NCAR/TN-387+STR, Boulder, Colorado, National Center for Atmospheric Research, 72 pp, doi: 10.5065/D67W6959 |
| Dunne, J. P., J. G. John, A. J. Adcroft, et al., 2012: GFDL’s ESM2 global coupled climate–carbon earth system models. Part I: Physical formulation and baseline simulation characteristics. J. Climate, 25, 6646–6665. DOI:10.1175/JCLI-D-11-00560.1 |
| Eyring, V., S. Bony, G. A. Meehl, et al., 2016: Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Devel., 9, 1937–1958. DOI:10.5194/gmdd-8-10539-2015 |
| Fetterer, F., K. Knowles, W. Meier, et al., 2017: Sea Ice Index, Version 3 (updated daily). Boulder, Colorado, National Snow and Ice Data Center, doi: 10.7265/N5K072F8. [Accessed on 7 August 2018] |
| Giorgetta, M. A., J. Jungclaus, C. H. Reick, et al., 2013: Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the Coupled Model Intercomparison Project phase 5. J. Adv. Model. Earth Syst., 5, 572–597. DOI:10.1002/jame.20038 |
| Gong, H. N., L. Wang, W. Chen, et al., 2014: The climatology and interannual variability of the East Asian winter monsoon in CMIP5 models. J. Climate, 27, 1659–1678. DOI:10.1175/JCLI-D-13-00039.1 |
| Griffies, S. M., M. J. Harrison, P. C. Pacanowski, et al., 2004: A Technical Guide to MOM4. GFDL Ocean Group Technical Report NO. 5, Princeton, NJ, NOAA/Geophysical Fluid Dynamics Laboratory, 339 pp. |
| Hagemann, S., and L. Dümenil, 1997: A parametrization of the lateral waterflow for the global scale. Climate Dyn., 14, 17–31. DOI:10.1007/s003820050205 |
| Hartmann, D. L., M. L. Michelsen, and S. A. Klein, 1992: Seaso-nal variations of tropical intraseasonal oscillations: A 20–25-day oscillation in the western Pacific. J. Atmos. Sci., 49, 1277–1289. DOI:10.1175/1520-0469(1992)049<1277:SVOTIO>2.0.CO;2 |
| Henderson-Sellers, A., A. J. Pitman, P. K. Love, et al., 1995: The project for intercomparison of land surface parameterization schemes (PILPS): Phases 2 and 3. Bull. Amer. Meteor. Soc., 76, 489–504. DOI:10.1175/1520-0477(1995)076<0489:TPFIOL>2.0.CO;2 |
| Hsu, H. H., and C. H. Weng, 2001: Northwestward propagation of the intraseasonal oscillation in the western North Pacific during the boreal summer: Structure and mechanism. J. Climate, 14, 3834–3850. DOI:10.1175/1520-0442(2001)014<3834:NPOTIO>2.0.CO;2 |
| Hua, W. J., H. S. Chen, and S. L. Sun, 2014: Uncertainty in land surface temperature simulation over China by CMIP3/CMIP5 models. Theor. Appl. Climatol., 117, 463–474. DOI:10.1007/s00704-013-1020-z |
| Huang, R. H., and L. Lu, 1989: Numerical simulation of the relationship between the anomaly of subtropical high over East Asia and the convective activities in the western tropical Pacific. Adv. Atmos. Sci., 6, 202–214. DOI:10.1007/BF02658016 |
| Huffman, G. J., D. T. Bolvin, E. J. Nelkin, et al., 2007: The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol., 8, 38–55. DOI:10.1175/JHM560.1 |
| Hundsdorfer, W., and R. A. Trompert, 1994: Method of lines and direct discretization: A comparison for linear advection. Appl. Numer. Math., 13, 469–490. DOI:10.1016/0168-9274(94)90009-4 |
| Hunke, E. C., and J. K. Dukowicz, 1997: An elastic–viscous– plastic model for sea ice dynamics. J. Phys. Oceanogr., 27, 1849–1867. DOI:10.1175/1520-0485(1997)027<1849:AEVPMF>2.0.CO;2 |
| Hurrell, J. W., M. M. Holland, P. R. Gent, et al., 2013: The community earth system model: A framework for collaborative research. Bull. Amer. Meteor. Soc., 94, 1339–1360. DOI:10.1175/BAMS-D-12-00121.1 |
| Kanamitsu, M., W. Ebisuzaki, J. Woollen, et al., 2002: NCEP–DOE AMIP-II reanalysis (R-2). Bull. Amer. Meteor. Soc., 83, 1631–1644. DOI:10.1175/Bams-83-11-1631 |
| Kang, I. S., K. Jin, B. Wang, et al., 2002: Intercomparison of the climatological variations of Asian summer monsoon precipitation simulated by 10 GCMs. Climate Dyn., 19, 383–395. DOI:10.1007/s00382-002-0245-9 |
| Koster, R. D., and M. J. Suarez, 1992: Modeling the land surface boundary in climate models as a composite of independent vegetation stands. J. Geophys. Res. Atmos., 97, 2697–2715. DOI:10.1029/91JD01696 |
| Koutroulis, A. G., M. G. Grillakis, I. K. Tsanis, et al., 2016: Evaluation of precipitation and temperature simulation performance of the CMIP3 and CMIP5 historical experiments. Climate Dyn., 47, 1881–1898. DOI:10.1007/s00382-015-2938-x |
| Krishnamurti, T. N., and D. Subrahmanyam, 1982: The 30–50-day mode at 850 mb during MONEX. J. Atmos. Sci., 39, 2088–2095. DOI:10.1175/1520-0469(1982)039<2088:TDMAMD>2.0.CO;2 |
| Kusunoki, S., and O. Arakawa, 2015: Are CMIP5 models better than CMIP3 models in simulating precipitation over East Asia?. J. Climate, 28, 5601–5621. DOI:10.1175/JCLI-D-14-00585.1 |
| Lau, K. M., and P. H. Chan, 1986: Aspects of the 40–50 day oscillation during the northern summer as inferred from outgoing longwave radiation. Mon. Wea. Rev., 114, 1354–1367. DOI:10.1175/1520-0493(1986)114<1354:AOTDOD>2.0.CO;2 |
| Lawrence, D. M., and P. J. Webster, 2002: The boreal summer intraseasonal oscillation: Relationship between northward and eastward movement of convection. J. Atmos. Sci., 59, 1593–1606. DOI:10.1175/1520-0469(2002)059<1593:TBSIOR>2.0.CO;2 |
| Li, C. F., and M. Yanai, 1996: The onset and interannual variability of the Asian summer monsoon in relation to land–sea thermal contrast. J. Climate, 9, 358–375. DOI:10.1175/1520-0442(1996)009<0358:TOAIVO>2.0.CO;2 |
| Li, J., R. C. Yu, W. H. Yuan, et al., 2015: Precipitation over East Asia simulated by NCAR CAM5 at different horizontal resolutions. J. Adv. Model. Earth Syst., 7, 774–790. DOI:10.1002/2014MS000414 |
| Li, T., B. Wang, B. Wu, et al., 2017: Theories on formation of an anomalous anticyclone in western North Pacific during El Niño: A review. J. Meteor. Res., 31, 987–1006. DOI:10.1007/s13351-017-7147-6 |
| Lohmann, U., and E. Roeckner, 1996: Design and performance of a new cloud microphysics scheme developed for the ECHAM general circulation model. Climate Dyn., 12, 557–572. DOI:10.1007/BF00207939 |
| Madden, R. A., and P. R. Julian, 1971: Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific. J. Atmos. Sci., 28, 702–708. DOI:10.1175/1520-0469(1971)028<0702:DOADOI>2.0.CO;2 |
| Madden, R. A., and P. R. Julian, 1972: Description of global-scale circulation cells in the tropics with a 40–50 day period. J. Atmos. Sci., 29, 1109–1123. DOI:10.1175/1520-0469(1972)029<1109:DOGSCC>2.0.CO;2 |
| Madden, R. A., 1986: Seasonal variations of the 40–50 day oscillation in the tropics. J. Atmos. Sci., 43, 3138–3158. DOI:10.1175/1520-0469(1986)043<3138:SVOTDO>2.0.CO;2 |
| Manabe, S., and K. Bryan, 1969: Climate calculations with a combined ocean–atmosphere model. J. Atmos. Sci., 26, 786–789. DOI:10.1175/1520-0469(1969)026<0786:CCWACO>2.0.CO;2 |
| Mantua, N. J., S. R. Hare, Y. Zhang, et al., 1997: A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Amer. Meteor. Soc., 78, 1069–1080. DOI:10.1175/1520-0477(1997)078<1069:APICOW>2.0.CO;2 |
| Mechoso, C. R., A. W. Robertson, N. Barth, et al., 1995: The seasonal cycle over the tropical pacific in coupled ocean–atmosphere general circulation models. Mon. Wea. Rev., 123, 2825–2838. DOI:10.1175/1520-0493(1995)123<2825:TSCOTT>2.0.CO;2 |
| Mehran, A., A. AghaKoucha, and T. J. Phillips, 2014: Evaluation of CMIP5 continental precipitation simulations relative to satellite-based gauge-adjusted observations. J. Geophys. Res. Atmos., 119, 1695–1707. DOI:10.1002/2013JD021152 |
| Murakami, T., 1980: Empirical orthogonal function analysis of satellite-observed outgoing longwave radiation during summer. Mon. Wea. Rev., 108, 205–222. DOI:10.1175/1520-0493(1980)108<0205:EOFAOS>2.0.CO;2 |
| Murray, R. J., 1996: Explicit generation of orthogonal grids for ocean models. J. Comput. Physi., 126, 251–273. DOI:10.1006/jcph.1996.0136 |
| Newman, M., G. P. Compo, and M. A. Alexander, 2003: ENSO-forced variability of the Pacific decadal oscillation. J. Climate, 16, 3853–3857. DOI:10.1175/1520-0442(2003)016<3853:EVOTPD>2.0.CO;2 |
| Nitta, T., 1987: Convective activities in the tropical western Pacific and their impact on the Northern Hemisphere summer circulation. J. Meteor. Soc. Japan, 65, 373–390. DOI:10.2151/jmsj1965.65.3_373 |
| Niu, G. Y., and Z. L. Yang, 2006: Effects of frozen soil on snowmelt runoff and soil water storage at a continental scale. J. Hydrometeorol., 7, 937–952. DOI:10.1175/JHM538.1 |
| Nordeng, T. E., 1994: Extended Versions of the Convective Parameterization Scheme at ECMWF and Their Impact on the Mean and Transient Activity of the Model in the Tropics. Technical Memorandum 206, Reading, UK, ECMWF, 41 pp. |
| Osborn, T. J., and P. D. Jones, 2014: The CRUTEM4 land-surface air temperature data set: Construction, previous versions and dissemination via Google Earth. Earth Syst. Sci. Data., 6, 61–68. DOI:10.5194/essd-6-61-2014 |
| Oueslati, B., and G. Bellon, 2015: The double ITCZ bias in CMIP5 models: Interaction between SST, large-scale circulation and precipitation. Climate Dyn., 44, 585–607. DOI:10.1007/s00382-015-2468-6 |
| Philander, S. G. H., 1983: El Niño Southern Oscillation phenomena. Nature, 302, 295–301. DOI:10.1038/302295a0 |
| Power, S., F. Tseitkin, S. Torok, et al., 1998: Australian rainfall, Australian temperature and the Southern Oscillation, 1910–1992: Coherent variability and recent changes. Aust. Meteor. Mag., 47, 85–101. |
| Rayner, N. A., D. E. Parker, E. B. Horton, et al., 2003: Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmos., 108, 4407. DOI:10.1029/2002JD002670 |
| Roeckner, E., G. Bäuml, L. Bonaventura, et al., 2003: The atmospheric general circulation model ECHAM5. Part I: Model description. Report No. 349, Hamburg, Max-Planck-Institut für Meteorologie, Germany, 127 pp. |
| Rong, X. Y., R. H. Zhang, and T. Li, 2010: Impacts of Atlantic sea surface temperature anomalies on Indo–East Asian summer monsoon–ENSO relationship. Chinese Sci. Bull., 55, 2458–2468. DOI:10.1007/s11434-010-3098-3 |
| Sikka, D. R., and S. Gadgil, 1980: On the maximum cloud zone and the ITCZ over Indian longitudes during the southwest monsoon. Mon. Wea. Rev., 108, 1840–1853. DOI:10.1175/1520-0493(1980)108<1840:OTMCZA>2.0.CO;2 |
| Song, F. F., and T. J. Zhou, 2014a: Interannual variability of East Asian summer monsoon simulated by CMIP3 and CMIP5 AGCMs: Skill dependence on Indian Ocean–western Pacific anticyclone teleconnection. J. Climate, 27, 1679–1697. DOI:10.1175/JCLI-D-13-00248.1 |
| Song, F. F., and T. J. Zhou, 2014b: The climatology and interan-nual variability of East Asian summer monsoon in CMIP5 coupled models: Does air–sea coupling improve the simulations?. J. Climate, 27, 8761–8777. DOI:10.1175/JCLI-D-14-00396.1 |
| Stanfield, R. E., J. H. Jiang, X. Q. Dong, et al., 2016: A quantitative assessment of precipitation associated with the ITCZ in the CMIP5 GCM simulations. Climate Dyn., 47, 1863–1880. DOI:10.1007/s00382-015-2937-y |
| Stieglitz, M., D. Rind, J. Famiglietti, et al., 1997: An efficient approach to modeling the topographic control of surface hydrology for regional and global climate modeling. J. Climate, 10, 118–137. DOI:10.1175/1520-0442(1997)010<0118:AEATMT>2.0.CO;2 |
| Su, F. G., X. L. Duan, D. L. Chen, et al., 2013: Evaluation of the global climate models in the CMIP5 over the Tibetan Plateau. J. Climate, 26, 3187–3208. DOI:10.1175/JCLI-D-12-00321.1 |
| Sundqvist, H., 1978: A parameterization scheme for non-convective condensation including prediction of cloud water content. Quart. J. Roy. Meteor. Soc., 104, 677–690. DOI:10.1002/qj.49710444110 |
| Sweby, P. K., 1984: High resolution schemes using flux limiters for hyperbolic conservation laws. SIAM J. Numer. Analy., 21, 995–1011. DOI:10.1137/0721062 |
| Taylor, K. E., R. J. Stouffer, and G. A. Meehl, 2012: An overview of CMIP5 and the experiment design. Bull. Amer. Meteor. Soc., 93, 485–498. DOI:10.1175/BAMS-D-11-00094.1 |
| Tian, B. J., E. J. Fetzer, B. H. Kahn, et al., 2013: Evaluating CMIP5 models using AIRS tropospheric air temperature and specific humidity climatology. J. Geophys. Res. Atmos., 118, 114–134. DOI:10.1029/2012JD018607 |
| Tiedtke, M., 1989: A comprehensive mass flux scheme for cumulus parameterization in large-scale models. Mon. Wea. Rev., 117, 1779–1800. DOI:10.1175/1520-0493(1989)117<1779:ACMFSF>2.0.CO;2 |
| Tziperman, E., S. E. Zebiak, and M. A. Cane, 1997: Mechanisms of seasonal–ENSO interaction. J. Atmos. Sci., 54, 61–71. DOI:10.1175/1520-0469(1997)054<0061:MOSEI>2.0.CO;2 |
| Vautard, R., P. Yiou, and M. Ghil, 1992: Singular-spectrum analysis: A toolkit for short, noisy chaotic signals. Physica D: Nonlinear Phenomena, 58, 95–126. DOI:10.1016/0167-2789(92)90103-T |
| Wang, B., and H. Rui, 1990: Synoptic climatology of transient tropical intraseasonal convection anomalies: 1975–1985. Meteor. Atmos. Phys., 44, 43–61. DOI:10.1007/BF01026810 |
| Wang, B., and Z. Fan, 1999: Choice of South Asian summer monsoon indices. Bull. Amer. Meteor. Soc., 80, 629–638. DOI:10.1175/1520-0477(1999)080<0629:COSASM>2.0.CO;2 |
| Wang, B., R. G. Wu, and T. Li, 2003: Atmosphere–warm ocean interaction and its impacts on Asian–Australian monsoon variation. J. Climate, 16, 1195–1211. DOI:10.1175/1520-0442(2003)16<1195:AOIAII>2.0.CO;2 |
| Wang, B., Q. H. Ding, X. H. Fu, et al., 2005: Fundamental challenge in simulation and prediction of summer monsoon rainfall. Geophys. Res. Lett., 32, L15711. DOI:10.1029/2005GL022734 |
| Wang, B., Z. W. Wu, J. P. Li, et al., 2008: How to measure the strength of the East Asian summer monsoon?. J. Climate, 21, 4449–4463. DOI:10.1175/2008JCLI2183.1 |
| Webster, P. J., V. O. Magaña, T. N. Palmer, et al., 1998: Monsoons: Processes, predictability, and the prospects for prediction. J. Geophys. Res. Oceans, 103, 14451–14510. DOI:10.1029/97JC02719 |
| Winton, M., 2000: A reformulated three-layer sea ice model. J. Atmos. Oceanic Technol., 17, 525–531. DOI:10.1175/1520-0426(2000)017<0525:ARTLSI>2.0.CO;2 |
| Wu, B., T. J. Zhou, and T. Li, 2009: Seasonally evolving dominant interannual variability modes of East Asian climate. J. Climate, 22, 2992–3005. DOI:10.1175/2008JCLI2710.1 |
| Xie, S. P., K. M. Hu, J. Hafner, et al., 2009: Indian ocean capaci-tor effect on Indo–western Pacific climate during the summer following El Niño. J. Climate, 22, 730–747. DOI:10.1175/2008JCLI2544.1 |
| Xin, Y. F., B. Y. Wu, L. G. Bian, et al., 2012: Response of the East Asian climate system to water and heat changes of global frozen soil using NCAR CAM model. Chinese Sci. Bull., 57, 4462–4471. DOI:10.1007/s11434-012-5361-2 |
| Xu, J. W., Y. H. Gao, D. L. Chen, et al., 2017: Evaluation of glo-bal climate models for downscaling applications centred over the Tibetan Plateau. Int. J. Climatol., 37, 657–671. DOI:10.1002/joc.4731 |
| Xue, Y. K., H. M. H. Juang, W. P. Li, et al., 2004: Role of land surface processes in monsoon development: East Asia and West Africa. J. Geophys. Res. Atmos., 109, D03105. DOI:10.1029/2003JD003556 |
| Yang, B., Y. C. Zhang, Y. Qian, et al., 2015: Parametric sensitivity analysis for the Asian summer monsoon precipitation simulation in the Beijing Climate Center AGCM, Version 2.1. J. Climate, 28, 5622–5644. DOI:10.1175/JCLI-D-14-00655.1 |
| Yasunari, T., 1979: Cloudiness fluctuations associated with the Northern Hemisphere summer monsoon. J. Meteor. Soc. Japan, 57, 227–242. DOI:10.2151/jmsj1965.57.3_227 |
| Yasunari, T., 1980: A quasi-stationary appearance of 30 to 40 day period in the cloudiness fluctuations during the summer monsoon over India. J. Meteor. Soc. Japan, 58, 225–229. DOI:10.2151/jmsj1965.58.3_225 |
| Yu, R. C., 1994: A two-step shape-preserving advection scheme. Adv. Atmos. Sci., 11, 479–490. DOI:10.1007/BF02658169 |
| Yu, R. C., J. Li, Y. Zhang, et al., 2015: Improvement of rainfall simulation on the steep edge of the Tibetan Plateau by using a finite-difference transport scheme in CAM5. Climate Dyn., 45, 2937–2948. DOI:10.1007/s00382-015-2515-3 |
| Zebiak, S. E., and M. A. Cane, 1987: A model El Niño–Southern Oscillation. Mon. Wea. Rev., 115, 2262–2278. DOI:10.1175/1520-0493(1987)115<2262:AMENO>2.0.CO;2 |
| Zhang, H., G. Y. Shi, T. Nakajima, et al., 2006a: The effects of the choice of the k-interval number on radiative calculations. J. Quanti. Spectros. Radiat. Trans., 98, 31–43. DOI:10.1016/j.jqsrt.2005.05.090 |
| Zhang, H., T. Suzuki, T. Nakajima, et al., 2006b: Effects of band division on radiative calculations. Optical Engineer., 45, 016002. DOI:10.1117/1.2160521 |
| Zhang, R. H., and Z. Y. Zuo, 2011: Impact of spring soil moisture on surface energy balance and summer monsoon circulation over East Asia and precipitation in East China. J. Climate, 24, 3309–3322. DOI:10.1175/2011JCLI4084.1 |
| Zhang, R. H., A. Sumi, and M. Kimoto, 1996: Impact of El Niño on the East Asian monsoon: A diagnostic study of the ’86/87 and ’91/92 events. J. Meteor. Soc. Japan, 74, 49–62. DOI:10.2151/jmsj1965.74.1_49 |
| Zhang, Y., J. M. Wallace, and D. S. Battisti, 1997: ENSO-like interdecadal variability: 1900–93. J. Climate, 10, 1004–1020. DOI:10.1175/1520-0442(1997)010<1004:ELIV>2.0.CO;2 |
| Zhang, Y., R. C. Yu, J. Li, et al., 2013: An implementation of a leaping-point two-step shape-preserving advection scheme in the high-resolution spherical latitude–longitude grid. Acta Meteor. Sinica, 71, 1089–1102. DOI:10.11676/qxxb2013.085 |
| Zhou, T. J., W. Bo, and B. Wang, 2009: How well do atmospheric general circulation models capture the leading modes of the interannual variability of the Asian–Australian monsoon?. J. Climate, 22, 1159–1173. DOI:10.1175/2008JCLI2245.1 |
 2018, Vol. 32
2018, Vol. 32


