The Chinese Meteorological Society
Article Information
- SONG, Xiaojiang, Yuejian ZHU, Jiayi PENG, et al., 2018.
- Improving Multi-Model Ensemble Forecasts of Tropical Cyclone Intensity Using Bayesian Model Averaging. 2018.
- J. Meteor. Res., 32(5): 794-803
- http://dx.doi.org/10.1007/s13351-018-7117-7
Article History
- Received August 7, 2017
- in final form July 16, 2018
2. Environmental Modeling Center, NOAA/NWS/NCEP, College Park, MD 20740, USA;
3. I. M. Systems Group, Inc., and NOAA/NWS/NCEP/EMC, College Park, MD 20740, USA;
4. System Research Group, Inc., Colorado Springs, CO 80901, and NOAA/NWS/NCEP/EMC, College Park, MD 20740, USA
Remarkable progress has been made in tropical cyclone (TC) track forecasting in recent years, owing to advanced assimilation methods with multi-source observations, improved understanding of atmospheric physical processes and the air–sea interaction, and the application of ensemble forecasting using multiple models. How-ever, due to limited knowledge on the cloud physics associated with TCs and the various uncertainties in the air–sea interaction process (Emanuel, 2000), there have been fewer improvements in TC intensity forecasts than in their associated track forecasts (Qian et al., 2012). Therefore, TC intensity forecasting remains a challenge for the international research and operational forecasting community. After several strong hurricanes (e.g., Katrina, Rita, and Wilma) impacted the United States and caused serious economic losses and numerous casualties in 2005, the Hurricane Forecast Improvement Project (HFIP) was initiated by the National Oceanic and Atmospheric Administration (NOAA) in 2008. HFIP aimed to reduce the average error in TC intensity forecasts by 20% in its first 5 yr and by 50% by the end of its 10-yr duration; it also was designed to improve the efficiency and accuracy of probabilistic forecasts of rapidly intensifying hurricanes (Gall et al., 2013).
Currently, statistics, statistical dynamics, and ensemble techniques are widely applied to TC intensity forecasting by operational forecasting centers worldwide (Chen et al., 2012; Yu et al., 2012). In 2004, based on the Statistical Hurricane Intensity Prediction System (SHIPS), the National Hurricane Center (NHC) implemented ensemble forecasting of hurricane intensity in the operational system for eastern Pacific and Atlantic (DeMaria, 1996; DeMaria and Kaplan, 1999). High skill scores were achieved for long lead-time forecasts by employing the Logistic Growth Equation Model (LGEM) and Decay-SHIPs in ensemble forecasts from the models such as the Hurricane Weather Research and Forecasting (HWRF), Geophysical Fluid Dynamics Laboratory (GFDL), Glo-bal Forecast System (GFS) of NCEP, and ECMWF (added in 2015) models (DeMaria, 1996; DeMaria and Kaplan, 1999; DeMaria et al., 2005; Wang et al., 2015). Yu et al. (2015) also demonstrated encouraging operational applications of ensemble forecasts of TC intensity. They calibrated the multiple model results with a consensus method by selecting major environmental variables with a step-wise regression.
Introducing probabilistic forecasts from traditional deterministic forecasts is a current trend in weather forecasting (Zhu, 2010; Slingo and Palmer, 2011). Simple deterministic forecasts from numerical models do not consider the objective forecast uncertainty that limits the transfer of complete information and proper guidance to forecasters and users (Krzysztofowicz, 1985). Probabilistic forecasts, in contrast, provide quantitative expressions of forecast uncertainty (Kelly and Krzysztofowicz, 1997) and more complete and comprehensive information about future weather conditions. In recent years, the ensemble-based Bayesian method has widely been used to forecast surface temperature, surface pressure, and precipitation (Herr and Krzysztofowicz, 2005; Raftery et al., 2005; Sloughter et al., 2007; Zhi et al., 2014, 2015), among others. However, no advanced studies exist that forecast TC intensity using an ensemble-based Bayesian method. In this study, we examine whether an ensemble-based Bayesian method could improve TC intensity forecasts through multi-model application. These predictions from the Bayesian model averaging (BMA) method could provide probabilistic (and/or uncertainty) forecasts rather than deterministic forecasts. Notably, the forecast uncertainty is quantitatively expressed, which allows for advanced scientific interpretation of the forecasts (Zhu, 2005).
The TC intensity forecasts and observational datasets are described in Section 2. The error analysis and bias correction are discussed in Section 3. The BMA method and its application are summarized in Section 4 and 5, respectively. Conclusions are then made in Section 6.
2 TC intensity forecasts and observational datasetsThe locations and intensities of an observed TC were determined from the tropical cyclone best-track dataset for the western North Pacific, available from the Joint Typhoon Warning Center (JTWC, http://www.usno.navy.mil/NOOC/nmfc-ph/RSS/jtwc/best_tracks/wpindex.php).
Forecast data from three models, including two global models and a regional model (Table 1), were obtained from the database created by the NCEP’s Environmental Modeling Center (NCEP/EMC). The global ECMWF Integrated Forecasting System (ECMWF-IFS) (Morcrette et al., 2009) utilizes four-dimensional variational data assimilation and had a resolution of 9 km in 2016. It is truncated at wavenumber 1279 and divided into 91 hybrid layers perpendicular to the vertical direction, with a model top pressure of 0.01 hPa. The model is initialized twice per day at 0000 UTC and 1200 UTC. NCEP-GFS is also a global model that was developed by NCEP, and it uses the Global Data Assimilation System. The model was truncated at wavenumber 574 in 2014 and at 1534 in 2015 and 2016. The GFS consists of 64 hybrid layers perpendicular to the vertical direction, with a model top pressure of 0.27 hPa. Its resolution was 22 km in 2014 and 13 km in 2015 and 2016. It is initialized at 0000, 0600, 1200, and 1800 UTC each day. The NCEP-HWRF model adopts the Gridpoint Statistical Interpolation assimilation system. It has 61 layers, a top pressure of 0.27 hPa, and an inner domain resolution of 2 km. Its forecast is initialized four times per day.
| Model name | Type | Developer | Model resolution | Is a bogus
TC used? |
Is a vortex relocation
technique used? |
Lead time and
daily frequency |
Time
period |
| ECMWF-IFS | Global model | ECMWF | 9 km/L91 | No | No | 240 h, 2 times per day | 2014–16 |
| NCEP-GFS | Global model | NCEP/EMC | 13 km/L64 | No | Yes | 240 h, 4 times per day | 2014–16 |
| NCEP-HWRF | Regional model | NCEP/EMC | 2 km/L61 | Yes | Yes | 120 h, 4 times per day | 2014–16 |
TC intensity is normally represented by the maximum wind speed near the cyclone center (Vmax) or the minimum sea-level pressure at the cyclone center (Pmin). Research has shown that Pmin has more significant linear relationships with initial error and forecast error than does Vmax (Knaff and Zehr, 2007; Yu et al., 2013). Therefore, this study used Pmin as its TC intensity indicator. This study focused on 24- to 120-h forecasts for all TCs that occurred in the western North Pacific basin during 2014–16, as produced by the three aforementioned models at 6-h intervals. TC intensity forecast error refers to the difference between the analyzed value from the JTWC best-track data and the Pmin forecast by the models.
3 Error analysis and bias correctionError analysis of the forecasts from the aforementioned models for 2014–16 was performed in an attempt to capture the forecast error characteristics. Prior to the BMA adjustment, the systematic errors for the indivi-dual forecast models were corrected to improve forecast reliability.
Forecast error is calculated as the difference between the annual average of the observed and forecast Pmin value at each lead time. The results are presented in Fig. 1. Both the GFS and HWRF include the vortex relocation technique, while the HWRF also includes a bogus TC technique. ThePmin values predicted by the HWRF mo-del for 2014 and 2015 are about 10 hPa smaller than the observed values. In 2016, the model’s forecast bias was –2.4 hPa, which was a significant decline that can likely be attributed to major model changes. In particular, the error in the 120-h forecast was weak and changed signs (Fig. 1, third bar). This suggests that the systematic forecast errors in 2014 and 2015 are different from those in 2016. The GFS forecasts for Pmin in 2014 were 10–20 hPa higher than the corresponding observed values, while the GFS forecasts for 2015 were 12–20 hPa lower than the observations. Errors in the GFS forecasts for 2016 had absolute values no greater than 3 hPa. There is no consistent sign of model error for these three years. Therefore, no correlation was found between this model’s forecast errors throughout the three years. The European Centre (EC) model was the only one that de-monstrated consistently negative forecast error (or bias) throughout the three years. As the lead time varied, the forecast errors in 2014 and 2015 showed significant correlations with the forecast error in 2016. Therefore, bias correction for the EC’s Pminforecasts in 2014–15 may substantially improve its forecasts for 2016, while the GFS and HWRF are unsuitable for bias correction, due to lack of a systematic pattern of error variation during the three years.
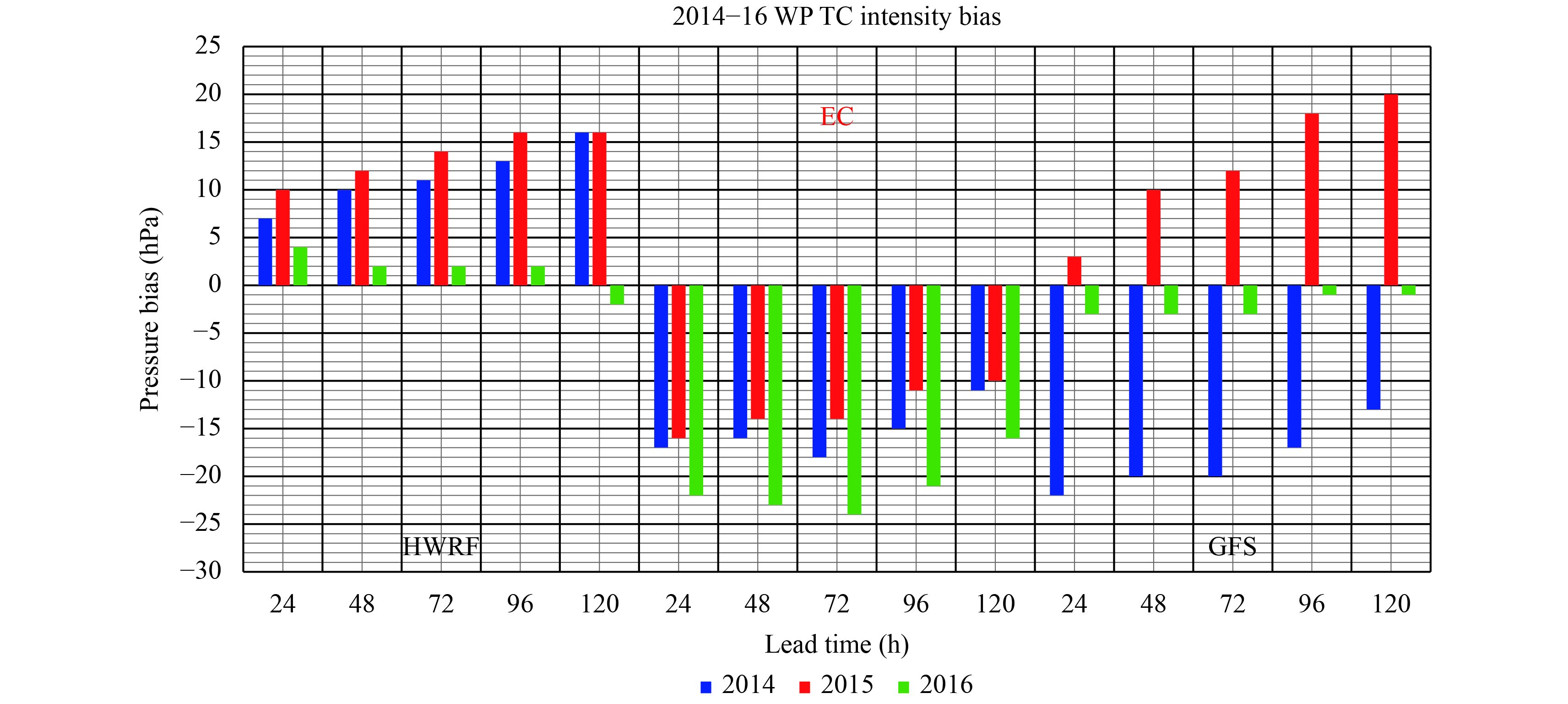
|
| Figure 1 Histogram of errors (hPa) in the model forecasts for 2014–16. The blue, red, and green bars represent the intensity forecast errors at different lead times (24, 48, 72, 96, and 120 h) for 2014, 2015, and 2016, respectively. Here, the bias = observation – forecast. |
The analysis above reveals that only the EC model’s forecast errors followed a regular pattern of distribution across the years, and its Pminforecasts were relatively high overall (indicating a weak TC). Bias correction was applied to the EC forecasts for 2016 based on the pattern of error distribution across 2014–15 from the following formula: Pmin(bc; t) = Pmin(t) – Bias(t), where t represents forecast lead time. This was achieved by subtracting 17, 15, 16, 13, and 11 hPa, respectively, from every 24- to 120-h forecast. Figure 2 compares the root-mean-square error (RMSE) of the forecasts from the three models and the bias-corrected EC, denoted as EC-BC. The Pmin forecasts from the regional model HWRF were much more accurate than those from the global models EC and GFS, as indicated by the comparatively lower errors at all lead times (Fig. 2). This is possibly due to its higher resolution and the use of a bogus TC. Compared to the RMSE of the EC forecasts, the RMSE of the EC-BC forecasts were significantly reduced: by 4.6 hPa at a lead time of 120 h and by 7–8 hPa at other lead times.

|
| Figure 2 RMSE of Pminforecasts from the four models at different lead times. The bars in each case, from left to right, denote the RMSE of the forecasts from HWRF (dark grey), GFS (light grey), EC (grey), and EC-BC (red), respectively. |
We also plotted the error distribution map for the three original models (not presented in this paper) to identify any regularity in the error distribution across latitudes and regions for further removal of systematic errors. Unfortunately, those error distributions were more random and provided little useful information.
4 Bayesian model averaging 4.1 The theoretical basis for BMABayesian model averaging (BMA) is a method of data post-processing based on Bayesian theory. It has multiple advantages over other statistical prediction models. For example, it considers subjective prior information and unavoidable unpredictability in models, allowing for the effective and accurate extraction of information from model forecasts. It has been successfully applied to temperature, pressure, wind speed, and precipitation forecasts.
There are several key steps in BMA. The first step is to calculate posterior probability. The second step is to derive the posterior probability density function (PDF) of a BMA probabilistic forecast by assuming that the likelihood function and prior PDF follow normal linear distributions (including the Poisson distribution, gamma distribution, Weibull distribution, and similar distributions). These posterior model probabilities are then adopted as the weights for the models, and the expectation of the BMA model is obtained by weighted averaging of individual model forecasts (i.e., weighted average forecasts).
BMA can be used to combine forecasts and inferences from multiple models (or ensembles of forecast models) and determine the predictive variance of the PDF of corresponding forecast variables. According to studies by Madigan and Raftery (1994) and Hoeting et al. (1999), BMA forecast models can be constructed by extending the law of total probability [see Eq. (1) below], where y represents the forecast variable, e.g., Pmin; fk is the kth forecast; wk is the weight for the kth forecast, i.e., the optimal posterior probability of forecasts from the corresponding model, which indicates each model’s contribution to forecast skill over the training period and satisfies
| $p\left( {y{\rm{|}}{f_1}, \ldots ,{f_k}} \right) = \sum\nolimits_{k = 1}^K {{w_k}} \cdot {g_k}(y|{{\tilde f}_k}).$ | (1) |
In the BMA model, the predicted value of the forecast variable y is the weighted means of the models’ expectations, which were obtained by weighting the expectations with wk [see Eq. (2)]. The BMA model’s total variance is expressed as a relationship between the observed values of ys, t and
| $E\left( {y{\rm{|}}{f_1}, \ldots ,{f_k}} \right) = \sum\nolimits_{k = 1}^K {{w_k} \cdot {{\tilde f}_k},\;\;\;\;\;\;\;} \quad\quad\quad\quad\quad\quad $ | (2) |
| $\begin{array}{l}Var\left( {{y_{s,t}}{\rm{|}}{{\tilde f}_{1,s,t}}, \ldots , {{\tilde f}_{K,s,t}}} \right) = \\\displaystyle\sum\nolimits_{k = 1}^K {{w_k}} {\left( {{{\tilde f}_{k,s,t}} - \displaystyle\sum\nolimits_{i = 1}^K {{w_i}} \cdot {{\tilde f}_{i,s,t}}} \right)^2} + \sum\nolimits_{k = 1}^K {{w_k}} \cdot \sigma _k^2.\end{array}$ | (3) |
Next, we need to solve for wk and
| $l\left( \theta \right) = \mathop \sum \nolimits_{s,t} \log \left( {\mathop \sum \nolimits_{k = 1}^K {w_k} \cdot {g_k}({y_{s,t}}|{{\tilde f}_{k,s,t}})} \right).$ | (4) |
Assume that there is a latent variable Zk,s,t whose value is 1 if
| $\hat Z_{k,s,t}^j = \frac{{w_k^{j - 1}g({y_{s,t}}|{{\tilde f}_{k,s,t}},\sigma _k^{j - 1})}}{{\mathop \sum \nolimits_{i = 1}^K w_i^{j - 1}g({y_{s,t}}|{{\tilde f}_{i,s,t}},\sigma _i^{j - 1})}},$ | (5) |
| $w_k^j = \frac{1}{n}\mathop \sum \limits_{s,t} \hat Z_{k,s,t}^j,\;\;\;\;\;\;\;\;\;\quad\quad\quad\quad\quad$ | (6) |
| ${\sigma ^2}_k^j = \frac{{\mathop \sum \nolimits_{s,t} \hat Z_{k,s,t}^j \cdot {{\left( {{y_{s,t}} - {{\tilde f}_{k,s,t}}} \right)}^2}}}{{\mathop \sum \nolimits_{s,t} \hat Z_{k,s,t}^j}},\quad\;$ | (7) |
where n is the number of cases in the training set, i.e., the number of distinct values of (s, t).
4.2 Assumption and transformation of PDFSince the BMA method relies on a normal distribution assumption (Raftery et al., 2005), we first need to ensure that the BMA input variables follow normal distributions. In Fig. 3a, we construct a histogram (with a 10-hPa bin width) with 2246 Pmin values obtained from the best-track data for the years 2014 and 2015. As shown in the figure, the best-track observed TC intensity is generally skewed toward the high Pmin values. Therefore, we must transform it into a normal distribution. Following Chou et al. (1998), we use the logistics transformation method based on the empirical formulas in Eqs. (8)–(10). The coefficients in the empirical equations are obtained through numerous comparisons and tests. The transformed distribution (see Fig. 3b) appears closer to the normal distribution. This study emphasizes the real-time application of forecasting Pmin. If we treat the data from 2014–16 as the full sample, then the real-time forecast will only have the data from 2014–15 available as the training sample. Although we acknowledge that including 2016 data in the training sample would likely improve the results, we chose to perform our analysis in the same way as the real-time operational practice.
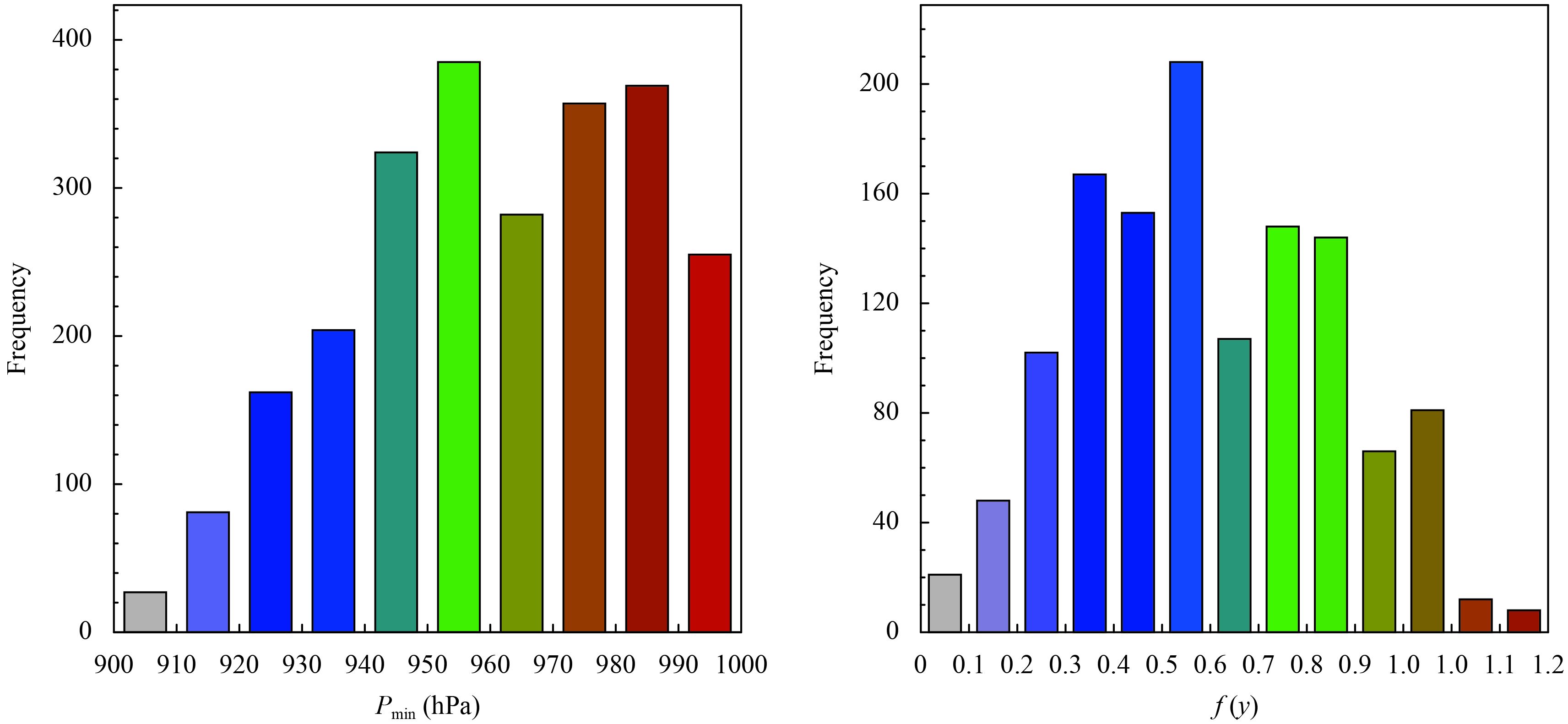
|
| Figure 3 Histograms of (a) Pmin and (b) f(y). There are 2466 samples from the best-track data for 2014–15 in panel (a), whereas there are 1265 samples for the 24-h forecasts from the three forecast models in panel (b) when best-track data are available. |
First, the observations were ranked in ascending order of Pmin as in Eq. (8), and the maximum and minimum values of Pmin in this sample were determined. We let y(i) (with a value range of 0–1) denote the original variablePmin [see Eq. (9)]. A function f(y(i)) was then constructed by changing the natural exponential [Eq. (10)]; its distribution is closer to normal than is the historical Pmin distribution. For example, when y(1) is equal to 0, f(y(1)) is equal to 0; when y(i) is equal to 0.5, f(y(i)) is equal to 0.38; and when y(n) is equal to 1, f(y(n)) is equal to 1:
| $p_{\min }^{\rm obs}\left( i \right)\left| {_{i = 1,n}} \right. \sim \left( {p_{\min }^{\rm obs}\left( 1 \right),p_{\min }^{\rm obs}\left( 2 \right),p_{\min }^{\rm obs}\left( 3 \right), \cdots , p_{\min }^{\rm obs}\left( n \right)} \right),$ | (8) |
where Pminobs(i) is sorted from low to high, and
| $y\left( i \right) = \frac{{P_{\rm min}^{\rm obs}\left( i \right) - P_{\rm min}^{\rm obs}\left( 1 \right)}}{{P_{\rm min}^{\rm obs}\left( n \right) - P_{\rm min}^{\rm obs}\left( 1 \right)}},\;\;\;\;\;\;$ | (9) |
| $f\left( {y\left( i \right)} \right) = \frac{{{e^{y\left( i \right)}} - 1}}{{e - 1}}. \quad\quad\quad\quad\;\;$ | (10) |
Figure 3b illustrates the distribution of f(y) that was obtained by matching the Pminvalues in the best-track data for 2014–16 to the 24-h forecasts from the three models after the logistics transformation (sample size: 1265). As can be seen in this figure, high frequencies are largely concentrated around the mean of the f(y) distribution.
A normality test is needed to determine whether the f(y) distribution is normal or approximately normal. The standardized skewness and kurtosis of the distribution were calculated by using Eq. (11) and (12), respectively:
| ${g_1} = \frac{{\sum\nolimits_i^N {{{\left( {{x_i} - \bar x} \right)}^3}/N} }}{{{s^3}}},\quad\;\,$ | (11) |
| ${g_2} = \frac{{\mathop \sum \nolimits_i^N {\raise0.7ex\hbox{${{{\left( {{x_i} - \bar x} \right)}^4}}$} \!/\!\lower0.7ex\hbox{$N$}}}}{{{s^4}}} - 3.$ | (12) |
In the above equations,
The dimensions of the variables were standardized to facilitate subsequent validation and comparison. After a BMA model was constructed and used to predict f(y), Eqs. (9) and (10) were rearranged to create Eqs. (13) and (14), in which f(y) has the same units as Pmin. This step will not be detailed in Section 5:
| ${\rm{y}}( i ) = \ln \left[ {\left( {e - 1} \right) \cdot f\left( {y\left( i \right)} \right) + 1} \right],\quad\quad\quad\quad\quad\quad\;$ | (13) |
| ${P_{\min}}\left( i \right) = y\left( i \right) \cdot \left( {P_{\min}^{\rm obs}\left( i \right) - P_{\min}^{\rm obs}\left( 1 \right)} \right) + P_{\min}^{\rm obs}\left( 1 \right).$ | (14) |
To construct a BMA model, we first conducted a full-sample forecast experiment. All the data for 2014–16 were used in the training period. The TC intensity forecasts for the same period were considered in the validation. Figure 4 shows the experimental forecasts for the No. 1623 TC called “MEARI” (WP26), initialized at 1200 UTC 6 November 2016. Of the three forecast models, HWRF had the highest weight, at 0.55, compared to the GFS’s 0.25. The weight of EC for the raw forecast was 0.2, which is lower than that of the other models. The weights of the three models totaled one.
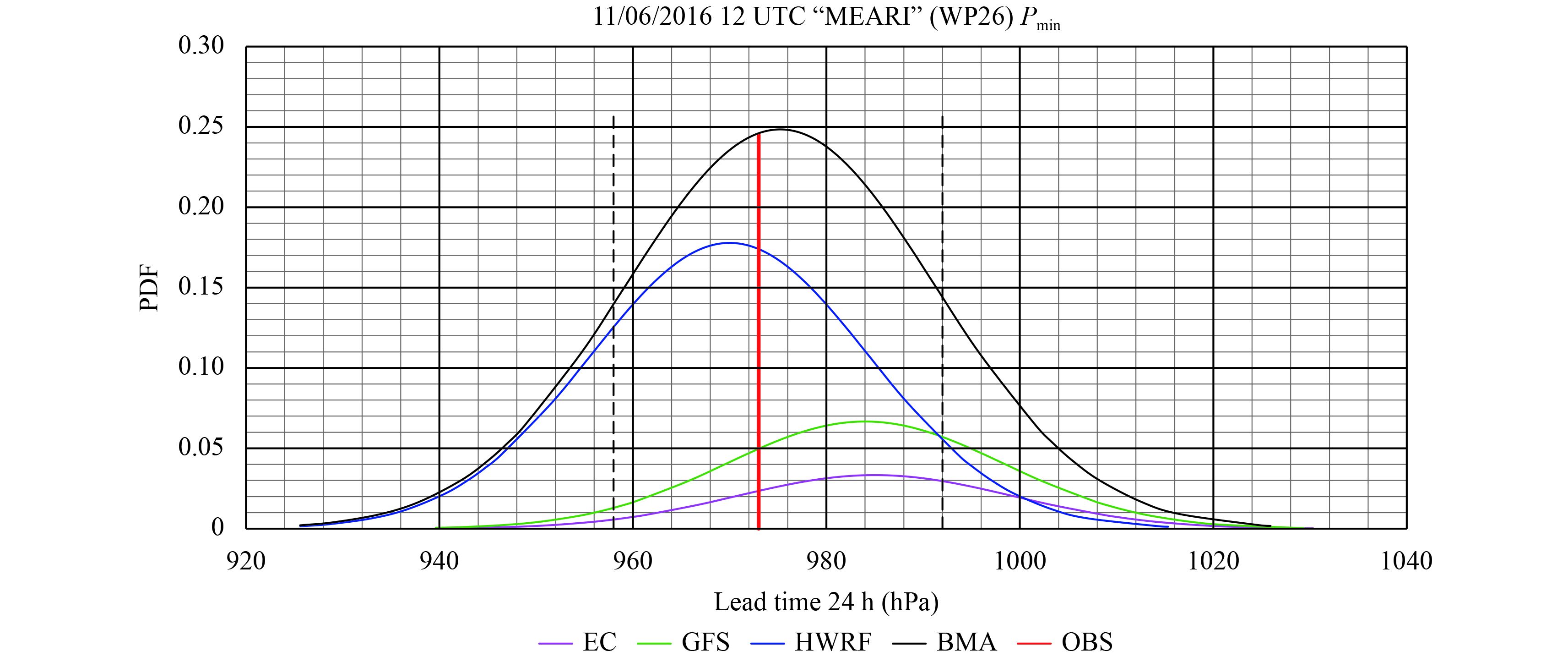
|
| Figure 4 Distributions of Pmin of the “MEARI” (WP26) TC as forecasted by the three individual models and the BMA model, initialized at 1200 UTC 6 November 2016. The purple, green, and blue thin lines represent the forecasts from the EC, GFS, and HWRF models, respectively; the thick black line represents the BMA model’s forecast. Also shown in the figure are the plus and minus one standard deviation (σ) (black dotted lines) and the observed value (OBS; the red line). |
The full-sample forecasts for this study were obtained from all 2014–16 model forecasts with the bias correction for EC, the transformation of the Pmin distribution, and dimensional standardization. Additionally, an equally weighted ensemble (EQW) of the three models was used as a benchmark for comparison. As shown in Table 2 and Fig. 5, the BMA forecasts had the lowest average RMSE during the three years, and the average RMSE of the EQW forecasts was lower than those of the three individual forecasts. The proportions of weights for the members of the BMA model show that HWRF was more skillful than the other members at each lead time. As the lead time increased, the weight for EC-BC increased significantly, while the GFS’s weight tended to decline.
| 2014–16 | BMA-weight | RMSE (hPa) | Case | ||||||
| HWRF | EC-BC | GFS | HWRF | EC-BC | GFS | EQW | BMA | ||
| 24 h | 0.55 | 0.20 | 0.25 | 17.1 | 22.5 | 21.5 | 16.6 | 15.7 | 1265 |
| 48 h | 0.48 | 0.29 | 0.23 | 21.9 | 25.4 | 26.4 | 21.3 | 20.9 | 1171 |
| 72 h | 0.45 | 0.32 | 0.23 | 24.1 | 26.6 | 29.5 | 23.4 | 22.9 | 1030 |
| 96 h | 0.48 | 0.33 | 0.19 | 25.0 | 26.5 | 30.4 | 23.8 | 23.2 | 811 |
| 120 h | 0.43 | 0.40 | 0.17 | 27.0 | 26.6 | 32.4 | 24.8 | 23.9 | 623 |
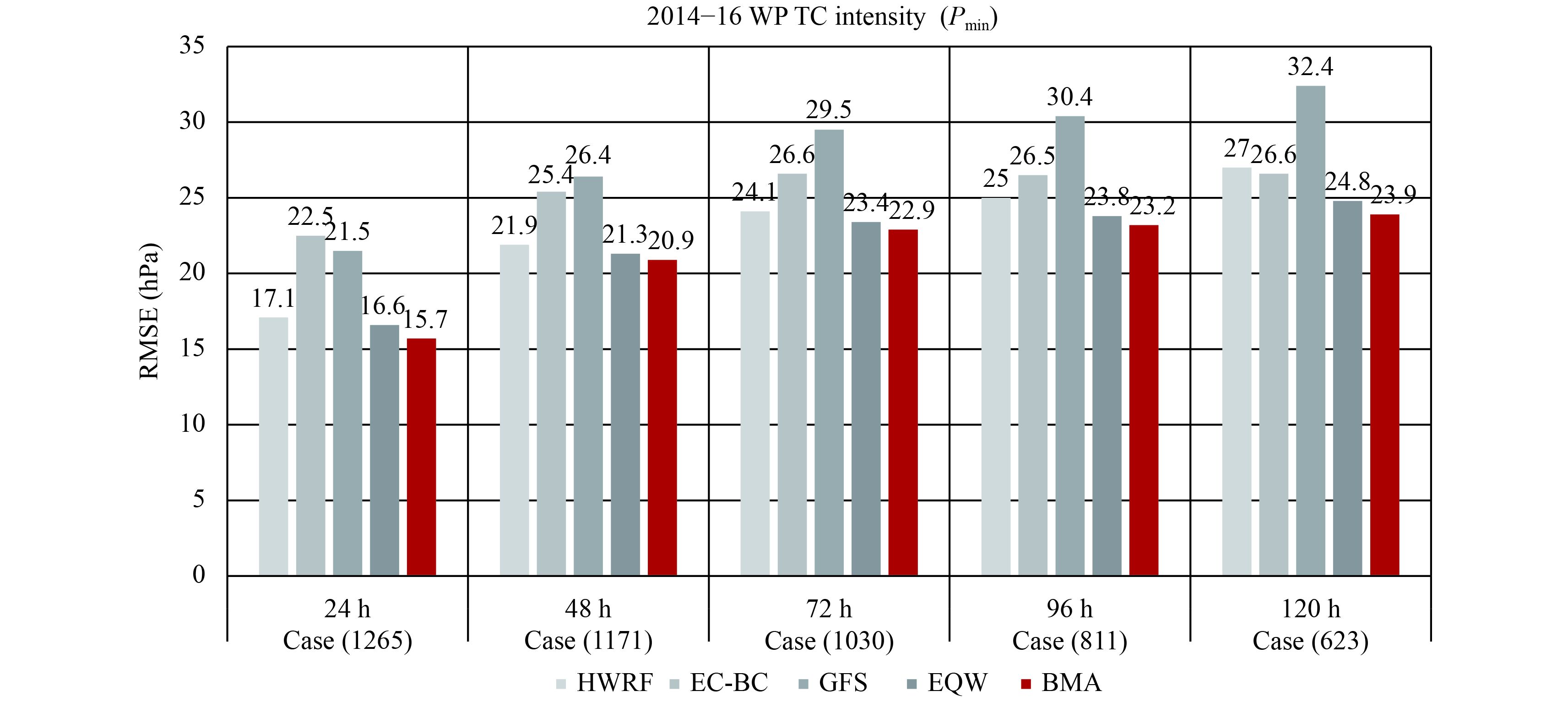
|
| Figure 5 RMSE of Pmin forecasts for 2014–16 from the models at different lead times, with the three individual forecasts shown in light grey, the EQW forecasts shown in dark grey, and the BMA forecasts shown in red. |
The experimental results demonstrate that the constructed BMA model has the best performance. However, this experimental scheme cannot solve or prevent the occurrence of possible overfitting in future applications. To make the experiment closer to the actual operational TC forecasting approach and achieve full usage of the limited sample, it is necessary to design a sample-matching scheme that does not require coincidence between the training period and the forecast period.
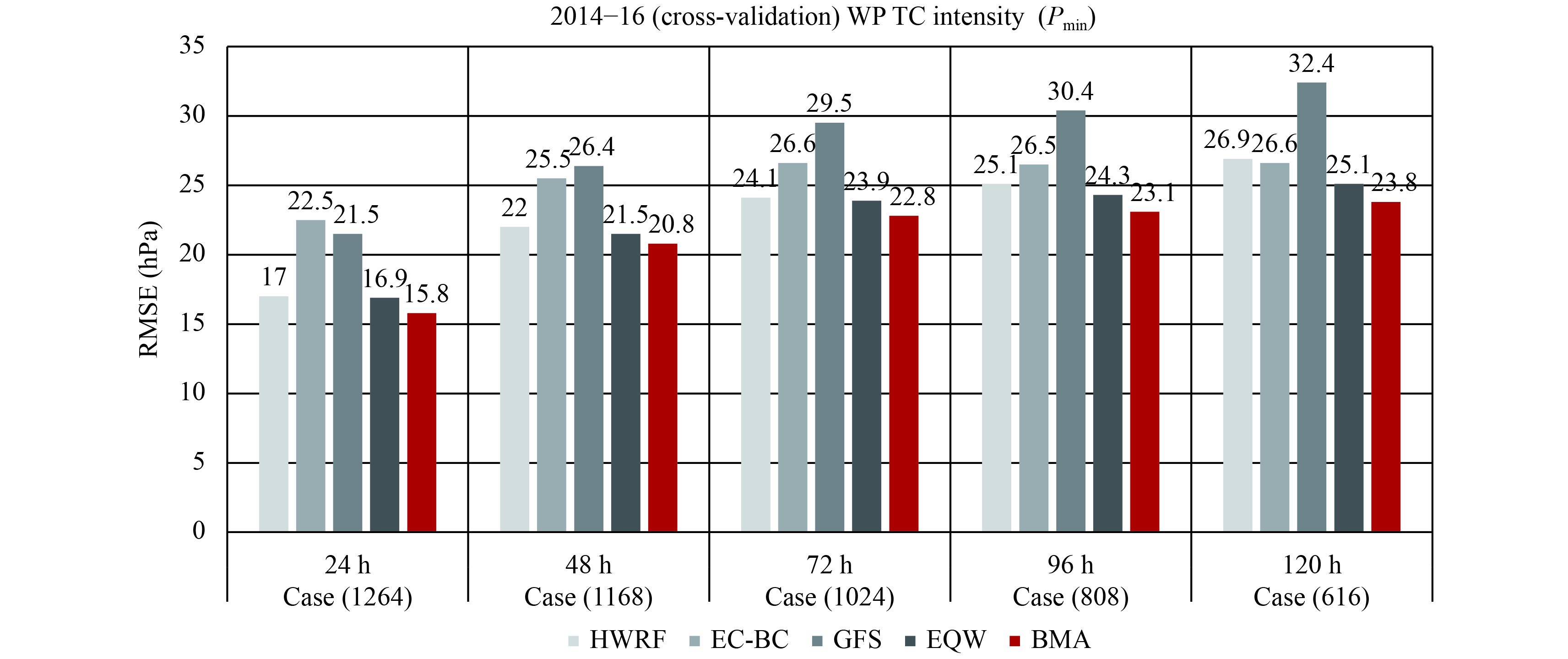
5.2 Cross validationThe main purpose of cross validation is to extract as much information as possible from the limited sample data to make up for the deficiency caused by the limited sample size and to avoid overfitting wherever possible. This study adopted an eight-fold cross validation. The dataset from 2014–16 was divided into eight folds: seven folds for training and the remaining one for validation. The results of this validation are presented in Table 3 and Fig. 6. The sample sizes are slightly different from those in Table 2 to allow for even division of the sample size by eight for the eight-fold cross validation in Table 3. As can be seen in the figure, after cross validation, the RMSEs of the BMA forecasts were the lowest at different lead times and decreased about 5%–7% from those of the forecasts from HWRF, which was the best individual model. The predictive variance (
| Cross validation | RMSE (hPa) | BMA-predictive variance | Case | ||||
| HWRF | EC-BC | GFS | EQW | BMA | |||
| 24 h | 17.0 | 22.5 | 21.5 | 16.9 | 15.8 | 15.4 | 1264 |
| 48 h | 22.0 | 25.5 | 26.4 | 21.5 | 20.8 | 19.9 | 1168 |
| 72 h | 24.1 | 26.6 | 29.5 | 23.9 | 22.8 | 21.9 | 1024 |
| 96 h | 25.1 | 26.5 | 30.4 | 24.3 | 23.1 | 22.2 | 808 |
| 120 h | 26.9 | 26.6 | 32.4 | 25.1 | 23.8 | 22.5 | 616 |
|
| Figure 6 RMSE of Pmin forecasts from the models at different lead times after cross validation, with the individual forecasts shown in grey and the BMA forecasts shown in red. |
In addition, BMA can also be used to quantify the uncertainty in TC intensity forecasts and to provide a probabilistic forecast product. In Table 3, the predictive variance from BMA can be seen to be statistically similar (or equal) to the BMA errors. This indicates that BMA may not only provide the best mean forecasts (those with the smallest errors) but also offer reliable forecast uncertainties (probability).
For example, a forecast was initialized at 0000 UTC 12 September 2016. Figure 7 displays the Pmin values predicted by the BMA model using a box plot, which visualizes the uncertainty and dispersion in the forecasts. The figure reveals that the degree of dispersion in the forecasts increased with an increasing length of lead time. In the box plot, the upper and lower bounds of each box indicate the forecast values when the cumulative probability was 75% and 25%, respectively. The black line in the middle of each box indicates the forecast value at a cumulative probability of 50%. The upper and lower ends of each dotted line represent the maximum and minimum Pmin forecasts at each lead time.

|
| Figure 7 Box plot of Pmin forecasts from the BMA model at different lead times, initialized at 0000 UTC 12 September 2016. The upper and lower bounds of each box indicate the forecast values at a cumulative probability of 75% and 25%, respectively. The black line in the middle of each box indicates the forecast value at a cumulative probability of 50%. |
Compared to deterministic forecasting, the probabili-stic forecasting method based on BMA can provide forecasts with higher accuracy and more comprehensive information. It also outperforms the forecasting method of equally weighted ensemble averaging. Moreover, the BMA model can quantify reliable forecast uncertainty, which is a distinct advantage over other models.
6 ConclusionsThis study aims to improve the accuracy of TC intensity forecasts, especially forecasts of the minimum pressure at cyclone center (Pmin). Based on Bayesian statistics, the posterior PDF of the BMA probabilistic forecasts was derived by normal approximation to the likelihood function and the prior PDF. Weighted averaging of forecasts from multiple models was implemented. The following conclusions can be drawn from the dataset processing and forecast experiments.
(1) The TC intensity (Pmin) forecasts from the HWRF, EC, and GFS models were tested and assessed. The results show that, among the three models, the regional model HWRF has the highest accuracy, due to its relatively high resolution and application of a bogus TC. The Pminvalues predicted by the EC were high overall, indicating low TC intensities. Bias corrections can be applied to the EC model forecast to improve its results, because the model demonstrates consistency in its biases.
(2) In the probabilistic forecast experiment using BMA, bias correction for the EC forecasts was performed. The Pmin PDF was approximated by an assumed distribution and then transformed. After that, cross validation was im-plemented to process the data for more efficient use of the sample. The validation results show that the BMA model outperformed the HWRF, which was the best individual model. The RMSE of the BMA forecasts was 5%–7% lower than those of other forecasts at various lead times.
(3) The forecasts from the BMA process provided probabilistic forecast guidance (i.e., mean forecasts and uncertainty forecasts) that could provide more useful information for our future research and for forecasters.
This study could be extended to enhance forecast skill by applying BMA to a pressure field and then projecting an associated wind field based on the pressure–wind relationship.
If we could remove systematic error (or bias) for the NCEP-GFS and NCEP-HWRF, the results could be even better; if the three models exhibit similar forecasting skills, the BMA method may have an even greater advantage in improving the final forecasts.
Acknowledgments. The authors thank NCEP/EMC for the instruction on understanding and applying the EMC’s advanced technology in tropical cyclone forecasting and post-processing of ensemble forecasts, in particular for setting up the BMA algorithm. With their help, the first author was able to carry out an operational forecast experiment at the National Marine Environmental Forecasting Center of China and to implement related forecasting techniques applicable to operational marine forecasting in China. The authors also thank Mr. Eric Sinsky for English grammar editing.
| Chen, L. S., Y. H. Duan, L. L. Song, et al., 2012: Typhoon Forecast and Disaster. China Meteorological Press, Beijing, China, 370 pp. (in Chinese) |
| Chou, Y. M., A. M. Polansky, and R. L. Mason, 1998: Transforming non-normal data to normality in statistical process control. J. Qual. Technol., 30, 133–141. DOI:10.1080/00224065.1998.11979832 |
| DeMaria, M., 1996: The effect of vertical shear on tropical cyclone intensity change. J. Atmos. Sci., 53, 2076–2088. DOI:10.1175/1520-0469(1996)053<2076:TEOVSO>2.0.CO;2 |
| DeMaria, M., and J. Kaplan, 1999: An updated Statistical Hurricane Intensity Prediction Scheme (SHIPS) for the Atlantic and eastern North Pacific basins. Wea. Forecasting, 14, 326–337. DOI:10.1175/1520-0434(1999)014<0326:AUSHIP>2.0.CO;2 |
| DeMaria, M., M. Mainelli, L. K. Shay, et al., 2005: Further improvements to the Statistical Hurricane Intensity Prediction Scheme (SHIPS). Wea. Forecasting, 20, 531–543. DOI:10.1175/WAF862.1 |
| Emanuel, K., 2000: A statistical analysis of tropical cyclone intensity. Mon. Wea. Rev., 128, 1139–1152. DOI:10.1175/1520-0493(2000)128<1139:ASAOTC>2.0.CO;2 |
| Gall, R., J. Franklin, F. Marks, et al., 2013: The hurricane forecast improvement project. Bull. Amer. Meteor. Soc., 94, 329–343. DOI:10.1175/BAMS-D-12-00071.1 |
| Herr, H. D., and R. Krzysztofowicz, 2005: Generic probability distribution of rainfall in space: The bivariate model. J. Hydrol., 306, 234–263. DOI:10.1016/j.jhydrol.2004.09.011 |
| Hoeting, J. A., D. Madigan, A. E. Raftery, et al., 1999: Bayesian model averaging: A tutorial (with comments by M. Clyde, D. Draper, and E. I. George, and a rejoinder by the authors). Stat. Sci., 14, 382–417. DOI:10.1214/ss/1009212519 |
| Kelly, K. S., and R. Krzysztofowicz, 1997: A bivariate meta-Gaussian density for use in hydrology. Stoch. Hydrol. Hydraul., 11, 17–31. DOI:10.1007/BF02428423 |
| Knaff, J. A., and R. M. Zehr, 2007: Reexamination of tropical cyclone wind–pressure relationships. Wea. Forecasting, 22, 71–88. DOI:10.1175/WAF965.1 |
| Krzysztofowicz, R., 1985: Bayesian models of forecasted time series. J. Amer. Water Resour. Assoc., 21, 805–814. DOI:10.1111/j.1752-1688.1985.tb00174.x |
| Madigan, D., and A. E. Raftery, 1994: Model selection and accounting for model uncertainty in graphical models using Occam’s window. J. Amer. Stat. Assoc., 89, 1535–1546. DOI:10.1080/01621459.1994.10476894 |
| Morcrette, J.-J., O. Boucher, L. Jones, et al., 2009: Aerosol analy-sis and forecast in the European Centre for Medium-range Weather Forecasts integrated forecast system: Forward modeling. J. Geophys. Res. Atmos., 114, D06206. DOI:10.1029/2008JD011235 |
| Qian, C. H., Y. H, Duan, S. H. Ma, et al., 2012: The current status and future development of China operational typhoon forecasting and its key technologies. Adv. Meteor. Sci. Technol., 2, 36–43. DOI:10.3969/j.issn.2095-1973.2012.05.005 |
| Raftery, A. E., 1993: Bayesian model selection in structural equation models. Testing Structural Equation Models, K. A. Bollen, and J. S. Long, Eds., Sage Publications, Newbury Park, 163–180. |
| Raftery, A. E., T. Gneiting, F. Balabdaoui, et al., 2005: Using Bayesian model averaging to calibrate forecast ensembles. Mon. Wea. Rev., 133, 1155–1174. DOI:10.1175/MWR2906.1 |
| Slingo, J., and T. Palmer, 2011: Uncertainty in weather and climate prediction. Phil. Trans. Roy. Soc. A, 369, 4751–4767. DOI:10.1098/rsta.2011.0161 |
| Sloughter, J. M. L., A. E. Raftery, T. Gneiting, et al., 2007: Probabilistic quantitative precipitation forecasting using Bayesian model averaging. Mon. Wea. Rev., 135, 3209–3220. DOI:10.1175/MWR3441.1 |
| Wang, Y. Q., Y. J. Rao, Z. M. Tan, et al., 2015: A statistical analysis of the effects of vertical wind shear on tropical cyclone intensity change over the western North Pacific. Mon. Wea. Rev., 143, 3434–3453. DOI:10.1175/MWR-D-15-0049.1 |
| Westfall, P. H., 2014: Kurtosis as peakedness, 1905–2014. R.I.P. Amer. Stat., 68, 191–195. DOI:10.1080/00031305.2014.917055 |
| Yu, H., S. T. Chan, B. Brown, et al., 2012: Operational tropical cyclone forecast verification practice in the western North Pacific region. Trop. Cyclone Res. Rev., 1, 361–372. DOI:10.6057/2012TCRR03.06 |
| Yu, H., P. Y. Chen, Q. Q. Li, et al., 2013: Current capability of operational numerical models in predicting tropical cyclone intensity in the western North Pacific. Wea. Forecasting, 28, 353–367. DOI:10.1175/WAF-D-11-00100.1 |
| Yu, H., G. M. Chen, and R. J. Wan, 2015: A multi-model consensus forecast technique for tropical cyclone intensity based on model output calibration. Acta Meteor. Sinica, 73, 667–678. DOI:10.11676/qxxb2015.043 |
| Zhi, X. F., G. Li, and T. Peng, 2014: On the probabilistic forecast of 2-m temperature of a single station based on Bayesian theory. Trans. Atmos. Sci., 37, 740–748. DOI:10.13878/j.cnki.dqkxxb.20130613006 |
| Zhi, X. F., J. Wang, C. Z. Lin, et al., 2015: Bayesian model average prediction on temperature by CMIP5 data. J. Meteor. Sci., 35, 405–412. DOI:10.3969/2014jms.0052 |
| Zhu, Y. J., 2005: Ensemble forecast: A new approach to uncertainty and predictability. Adv. Atmos. Sci., 22, 781–788. DOI:10.1007/BF02918678 |
| Zhu, Y. J., 2010: The prediction science. Trans. Atmos. Sci., 33, 266–270. |
 2018, Vol. 32
2018, Vol. 32


