The Chinese Meteorological Society
Article Information
- BI, Kai, Xincheng MA, Yunbo CHEN, et al., 2018.
- The Observation of Ice-Nucleating Particles Active at Temperatures above –15°C and Its Implication on Ice Formation in Clouds. 2018.
- J. Meteor. Res., 32(5): 734-743
- http://dx.doi.org/10.1007/s13351-018-7181-z
Article History
- Received December 7, 2017
- in final form June 2, 2018
2. Beijing Key Laboratory of Cloud, Precipitation, and Atmospheric Water Resources, Beijing 100089;
3. Field Experiment Base for Cloud and Precipitation Research in North China, China Meteorological Administration, Beijing 101200;
4. Department of Atmospheric and Oceanic Sciences, School of Physics, Peking University (PKU), Beijing 100871;
5. PKU–BWMO Joint Laboratory on Cloud and Precipitation Physics, Beijing 100089;
6. Institute of Urban Meteorology, China Meteorological Administration, Beijing 100089
Ice-nucleating particles (INPs) are those aerosols that are responsible for the observed heterogeneous ice nucleation (Vali et al., 2015). By nucleating ice crystals, INPs can exert remarkable influence on precipitation. In stratiform clouds, the presence of INPs results in the formation of ice crystals, which grow rapidly and can subsequently initiate precipitation. This effect was found to increase precipitation (Lohmann, 2002; Sesartic et al., 2013; Kikuro et al., 2015; Masaki et al., 2016). In convective clouds, the presence of INPs can have an opposite effect. Zeng et al. (2009) found that the presence of INPs increased the amount of cloud ice but reduced the amount of graupel. Precipitation was therefore reduced because graupel was the main hydrometeor type responsible for the formation of precipitation.
INPs can catalyze ice formation via four modes (Vali et al., 2015). In deposition nucleation mode, ice nucleation occurs when vapor deposits onto the surface of the INP. In this mode, no pre-existing liquid droplets are required. In immersion freezing, ice nucleation is catalyzed by the INP immersed within a liquid droplet. In condensation freezing, ice nucleation occurs concurrently with the initial formation of liquid droplets. In contact freezing, ice nucleation occurs when an airborne INP comes into contact with the surface of the supercooled liquid droplets. Under different conditions, ice nucleation can occur through different modes.
Different types of INP take effect at different temperatures. Mineral dust aerosols and black carbon aerosols are important INP types (Prenni et al., 2009; Hoose et al., 2010; Atkinson et al., 2013). Previous studies found that mineral dust aerosols mainly nucleated ice crystals at temperatures lower than –15°C (Hoose et al., 2010; Murray et al., 2011; Atkinson et al., 2013; Fu and Xue, 2017), and black carbon aerosols mainly took effect at temperatures several degrees lower than those required by mineral dust aerosols (DeMott, 1990; Hoose et al., 2010; Savre and Ekman, 2015). Biological aerosols are another type of INP. Although usually scarce in the atmosphere, they are potentially very important because they can nucleate ice crystals at temperatures higher than –15°C (Schnell and Vali, 1976; Hoose et al., 2010; Atkinson et al., 2013; Burrows et al., 2013; Huffman et al., 2013; Joly et al., 2014; O’Sullivan et al., 2014), and sometimes even as high as –2°C (Vali et al., 1976).
Many empirical parameterizations have been reported to predict the INP concentrations at given environmental conditions. Some of the parameterizations were based on laboratory experiments (e.g., Murray et al., 2011). In these experiments, very limited types (sometimes only one type) of INP were used. Therefore, these parameterizations could not reflect the variability of INP type in the real atmosphere. Some other parameterizations were based on measurements of the ambient INP concentration (DeMott et al., 2010; Jiang et al., 2015, 2016), and could reflect the variability of INP type. In addition, the aforementioned empirical parameterizations have been widely used in models to investigate the impact of ice crystals on clouds (e.g., Thompson and Eidhammer, 2014; Solomon et al., 2015).
Parcel model is a widely used tool to investigate cloud microphysics (e.g., Korolev and Isaac, 2003; Xue and Feingold, 2004; Korolev and Field, 2008; Sulia and Harrington, 2011; Li et al., 2013). Previous parcel model simulation showed that the vertical velocity of the parcel had great impact on the phase partitioning in mixed-phase clouds (Korolev and Isaac, 2003; Korolev and Field, 2008). Their studies showed that for a static parcel that contained a relatively high ice concentration (on the order of 10 g–1), liquid droplets were completely depleted in a very short time (< 1 h). When the parcel was ascending, liquid droplets and ice crystals first grew concurrently. After some time, the ice crystals became large enough, and could rapidly consume vapor, leading to that the saturation ratio of the parcel became lower than the equilibrium saturation ratio over water. In this situation, liquid droplets were evaporated. When the parcel was oscillating, liquid droplets could repeatedly form when the parcel was in the ascending phase so that liquid droplets and ice crystals could coexist for a long time.
In this study, we first present the measurements performed at two sites in Beijing, China. In the measurements, some INPs were found to be active at temperatures above –15°C. We then construct parameterizations by fitting the observational data, and implement the fitting results into a parcel model to investigate the effect of INPs that are active above –15°C on the phase partitioning in clouds. Section 2 describes the methods. Section 3 presents the observational results, followed by the modeling results in Section 4. A summary is given in Section 5.
2 Methods 2.1 ObservationA series of measurements were performed between November 2016 and January 2017 at two sites, as shown in Fig. 1. One site is at Beijing Meteorological Service (BMS), which is located near the center of the city. It is therefore regarded as an urban site. The other site is at Yanjiaping (YJP; Ma et al., 2017), which is 80 km to the northwest of BMS. It lies in the mountainous region with an altitude of over 1.3 km above sea level. YJP is treated as a rural site.
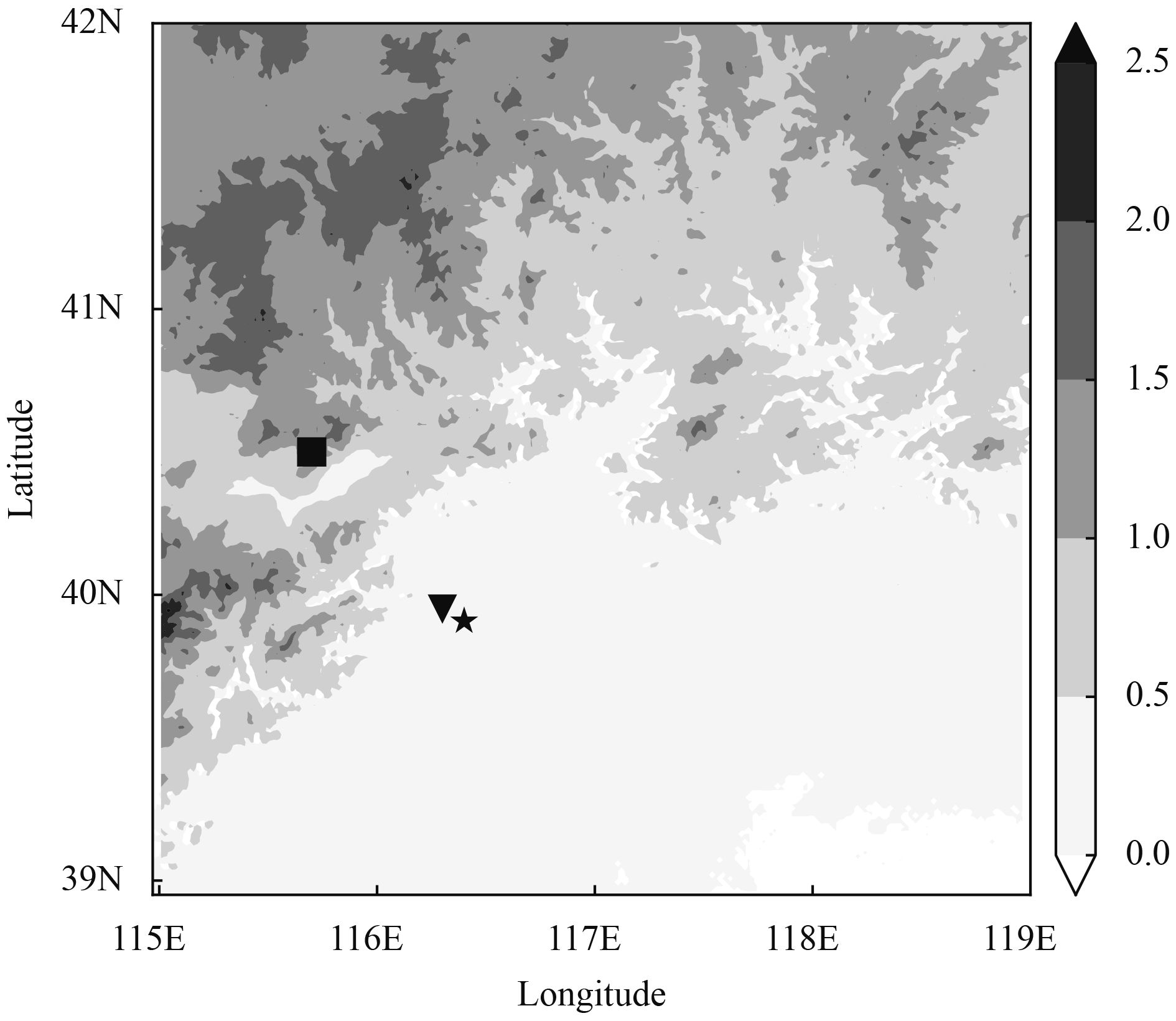
|
| Figure 1 The topography (in km) of the area around Beijing. The star indicates the center of Beijing City as a reference. The triangle and the square indicate the two sites, i.e., Beijing Meteorological Service (BMS) site and Yanjiaping (YJP) site, respectively. |
The Bigg mixing cold cloud chamber (Bigg’s chamber; Bigg, 1957; Yang et al., 2007) was used to measure the INP concentrations at the two sites in this study. The Bigg’s chamber is a 5-L cylinder (Fig. 2), which is made of bronze and can be cooled by antifreezer flowing around it. A movable sugar plate, which contains supercooled sugar solution, is mounted inside the chamber. The whole chamber is placed in a thermally insulated box.

|
| Figure 2 The structure of the Bigg’s chamber. |
In each measurement, the sugar plate was first moved from the bottom to the top of the chamber to pump out the air, and then moved back to the bottom of the chamber so the ambient air was pumped into the chamber. A lid was then used to cover the chamber to prevent air exchange between the inside and outside of the chamber. With such a sampling method, aerosols with all sizes were introduced into the chamber. After sample air was introduced into the chamber, it was cooled by the circulating antifreezer, which was kept at a predetermined temperature. In this study, the temperature of the antifreezer ranged from –30 to 0°C. When the chamber reached thermal equilibrium with the antifreezer, liquid droplets, which were generated from pure water, were sprayed into the chamber. Before being sprayed into the chamber, the liquid droplets flowed through a fog inlet that was immersed in the antifreezer (Fig. 2). The temperature of the liquid droplets were hence close to that within the chamber. Therefore, spraying the liquid droplets only caused a small (< 1°C) and short-time (< 10 s) variation of the temperature within the chamber. Besides, enough liquid droplets were sprayed into the chamber so they were never completely evaporated throughout the experiment, which typically lasted for 3.5 min.
Ice crystals formed after liquid droplets were sprayed into the chamber. They then grew and fell onto the sugar solution, where they continued to grow to sizes large enough to be easily counted (Bigg, 1957). When the INP concentration was low (i.e., < 10 g –1), the ice crystals on the sugar solution could be unambiguously identified and counted. In this situation, the uncertainty due to counting was negligible. When the INP concentration was high, ice crystals might be so close to each other and could hence be undercounted. The uncertainty due to counting was estimated to be 20%.
Several modes of ice nucleation can occur inside the Bigg’s chamber. After liquid droplets are sprayed into the chamber, the air soon becomes saturated over water. Because the saturation vapor pressure over water is higherthan that over ice, the air inside the chamber is supersaturated over ice. In this situation, ice nucleation can occur via deposition nucleation. Because the observer usually waits for about 3.5 min before counting the ice crystals, INPs have enough time to move to the proximity of the liquid droplets and contact with the droplet surface (Young, 1974). As a result, contact freezing can occur in the chamber. It is also possible that some INPs can be collected by the liquid droplets and nucleate ice crystals via immersion freezing. Condensation freezing cannot occur in Bigg’s chamber because the air inside the chamber cannot be supersaturated with respect to water. It is noteworthy that the sprayed liquid droplets cannot freeze homogeneously because the temperature within the chamber was never cooled to –38°C, the homogeneous freezing temperature of the liquid droplets.
Due to the strong inhomogeneity of temperature inside the chamber, the INP concentration must be corrected to the concentration at the reported temperature. Because the vertical temperature variation was large while the horizontal temperature variation was close to the uncertainty of the thermometer, only the vertical temperature variation was used to correct the INP concentration. We define the correction factor as
| ${f_{{\rm{cor}}}} = \displaystyle\frac{{{N_{{\rm{INP}}}}\left( {{T_{{\rm{rep}}}}} \right)}}{{\frac{1}{L}\mathop \int \nolimits_0^{L} {N_{{\rm{INP}}}}\left( T \right){\rm{d}}h}},$ | (1) |
where L is the height of the chamber, Trep the reported temperature, h the height above the bottom of the chamber, and T the temperature at height h. NINP(T) is the relation between the INP concentration and temperature, which was assumed to follow an exponential relation, i.e., NINP = Aexp(–B(T–273.2)), where A and B are constants (DeMott et al., 2010). With the aid of the exponential relation, Eq. (1) becomes
| ${f_{{\rm{cor}}}} = \frac{L}{{\mathop \int \nolimits_0^{L} \exp \left( { - B\left( {T - {T_{{\rm{rep}}}}} \right)} \right){\rm{d}}h}}.$ | (2) |
The value of B does not rely on whether the observational data are corrected or not. Thus, we first fitted the data to obtain the values of B, which were respectively 0.546 and 0.293 for BMS site and YJP site. Besides, the fitting in DeMott et al. (2010) gave B = 0.125. This value was also considered in this study because it fitted better with our data when the temperature was above –15°C. The correction factors were 1.45, 1.30, and 1.15 for B = 0.546, 0.293, and 0.125, respectively. Using different correction factor can cause an uncertainty of 26%. In this study, we used the correction factor of 1.45 to correct the data obtained from BMS site and 1.30 to correct the data obtained from YJP site.
2.2 Parcel modelA parcel model was used to investigate the effect of including the INPs active above –15°C on the phase partitioning in mixed-phase clouds. The height of the parcel z is calculated with dz/dt = w, where w is the vertical velocity describing the dynamics of the parcel. It can be set to be a small value so that the parcel represents a slowly ascending stratiform cloud or a large value so that the parcel represents a rapidly ascending convective cloud. The pressure of the parcel, which is assumed to equal the environmental pressure, is calculated by assuming hydrostatic approximation for the environment. The vapor mixing ratio qv is diagnosed based on the conservation of water substance qv = qv,0 – qliq – qice, where qv,0 is the initial vapor mixing ratio, qliq the liquid water mixing ratio, and qice the ice water mixing ratio.
The temperature of the parcel, T, is predicted with (Lamb and Verlinde, 2011, page 249)
| $\frac{{{\rm{d}}T}}{{{\rm{d}}t}} = - \frac{g}{{{c_{\rm{p}}}}}w + \frac{{{l_{\rm{v}}}}}{{{c_{\rm{p}}}}}\frac{{{\rm{d}}{q_{{\rm{liq}}}}}}{{{\rm{d}}t}} + \frac{{{l_{\rm{s}}}}}{{{c_{\rm{p}}}}}\frac{{{\rm{d}}{q_{{\rm{ice}}}}}}{{{\rm{d}}t}},$ | (3) |
where g is the gravitational acceleration, cp the specific heat capacity of air at constant pressure, lv the latent heat of evaporation, and ls the latent heat of sublimation.
The liquid water mixing ratio is predicted with
| $\frac{{{\rm{d}}{q_{{\rm{liq}}}}}}{{{\rm{d}}t}} = \mathop \sum \nolimits 4\pi {\rho _{{\rm{liq}}}}r_{{\rm{liq}},l}^2\frac{{{\rm{d}}{r_{{\rm{liq}}, l}}}}{{{\rm{d}}t}}{n_{{\rm{liq}},l}},$ | (4) |
where ρliq is the density of liquid water, and nliq,l the liquid droplet concentration in the l-th bin. The summation is performed over all liquid droplet bins. The radius of the liquid droplet rliq,l is calculated with (Lamb and Verlinde, 2011, page 329)
| $\frac{{{\rm{d}}{r_{{\rm{liq}},l}}}}{{{\rm{d}}t}} = \frac{A}{{4\pi {r_{{\rm{liq}},l}} {\rho _{{\rm{liq}}}}}}{s_{{\rm{liq}}}},$ | (5) |
where sliq is the supersaturation over water, and A is defined as
| $A = \displaystyle\frac{{4\pi }}{{\displaystyle\frac{{{R_{\rm{v}}}T}}{{{e_{{\rm{s}},{\rm{liq}}}}{D_{\rm{v}}}}} + \displaystyle\frac{{{l_{\rm{v}}}}}{{kT}}\left( {\displaystyle\frac{{{l_{\rm{v}}}}}{{{R_{\rm{v}}}T}} - 1} \right)}},$ | (6) |
in which Rv is the gas constant for vapor, es,liq the saturation vapor pressure over water, given by the polynomial fitting of experimental data (Flatau et al., 1992), Dv the diffusivity of vapor in air, and k the heat conductivity of air. Although Dv is a function of both temperature and pressure and k is a function of temperature, their variations are very small in the range considered in this study. Therefore, we set Dv to be 3 × 10–5 m2 s–1 and k to be 0.02 J m–1 s–1 °C–1.
A simple method is used to treat the activation of liquid droplets. The activation instantaneously occurs once the saturation ratio over water exceeds 1. The initial size distribution of liquid droplet follows a lognormal distribution with a mean radius of 0.2 µm and a standard deviation of 1.8, and the liquid droplet concentration is fixed at 2 × 108 kg–1. Because the size of liquid droplet increases fast when the droplet is small, the droplet size is not sensitive to its initial size (Lamb and Verlinde, 2011, page 340). It is therefore reasonable to simplify the treatment of the activation of liquid droplets. Besides, the liquid droplet concentration is much higher than the ice crystal concentration, the liquid droplet concentration is therefore not depleted when ice nucleation occurs. The initial size distribution is discretized into 25 bins. In each bin, the mass of the largest liquid droplet is 1.5 times of that of the smallest liquid droplet.
The ice water mixing ratio is predicted as in Ovchinnikov et al. (2014)
| $\frac{{{\rm{d}}{q_{{\rm{ice}}}}}}{{{\rm{d}}t}} = \mathop \sum \nolimits \frac{{{\rm{d}}{m_{{\rm{ice}},l}}}}{{{\rm{d}}t}}{n_{{\rm{ice}},l}},$ | (7) |
where mice,l is the mass of ice crystal in the l-th bin and nice,l is the ice crystal concentration in the l-th bin. The summation is performed over all ice crystal bins. The growth rate of the mass of ice crystal is
| $\frac{{{\rm{d}}{m_{{\rm{ice}}}}}}{{{\rm{d}}t}} = 4\pi {B_{\rm{l}}}{C_{\rm{l}}}{s_{{\rm{ice}}}},$ | (8) |
where sice is the supersaturation over ice. The term Bl is
| ${B_{\rm{l}}} = \displaystyle\frac{1}{{\displaystyle\frac{{{R_{\rm{v}}}T}}{{{e_{{\rm{s}},{\rm{ice}}}}{D_{\rm{v}}}}} + \displaystyle\frac{{{l_{\rm{s}}}}}{{kT}}\left( {\displaystyle\frac{{{l_{\rm{s}}}}}{{{R_{\rm{v}}}T}} - 1} \right)}},$ | (9) |
where es,ice is the saturation vapor pressure over ice, also given by the polynomial fitting of experimental data (Flatau et al., 1992). The capacitance Cl is
| ${C_{\rm{l}}} = {a_{\rm{c}}}m_{{\rm{ice}},l}^{{b_{\rm{c}}}},$ | (10) |
where ac = 0.09 m
Ice nucleation occurs over a wide range of temperature. Therefore, it cannot be calculated in a single time step. In this study, ice nucleation is calculated every time the parcel ascends by another distance of 30 m. Every time ice nucleation occurs, a new ice bin is added to represent the newly formed ice crystals. The number concentration of the newly formed ice crystals is calculated with the empirical parameterizations, which will be givenin the following Section. The radii of the newly formed ice crystals are all set to be 1 µm.
Initially, the parcel is at 1.0 km and the pressure is 900 hPa. The temperature is 5°C and the saturation ratio over water is 0.9. As mentioned in Section 1, vertical velocity exerts an important impact on the phase partitioning in mixed-phase clouds. Different vertical velocities are hence used to drive the parcel model.
3 Observational resultsFigure 3 shows the INP concentrations measured at different temperatures. Each data point represents a single measurement. It can be seen that no INPs were detected at temperatures above –15°C at the BMS site, while a remarkable portion of INPs were detected at temperatures above –15°C at the YJP site. As mentioned in Section 1, at temperatures above –15°C, ice formation is mainly catalyzed by biological INPs. Since the BMS site is located near the center of a megacity, it may not be easily affected by biological aerosols. Therefore no INPs were detected above –15°C. In contrary to the BMS site, the YJP site locates in the rural area, which may be substantially influenced by biological aerosols. Some INPs could hence be detected at temperatures above –15°C. In addition, we also note that the concentrations of the INPsactive below –15°C were similar at the two sites. This is consistent with a previous study (Chen et al., 2018), which showed that the INP concentration at Beijing was not affected by air pollution.
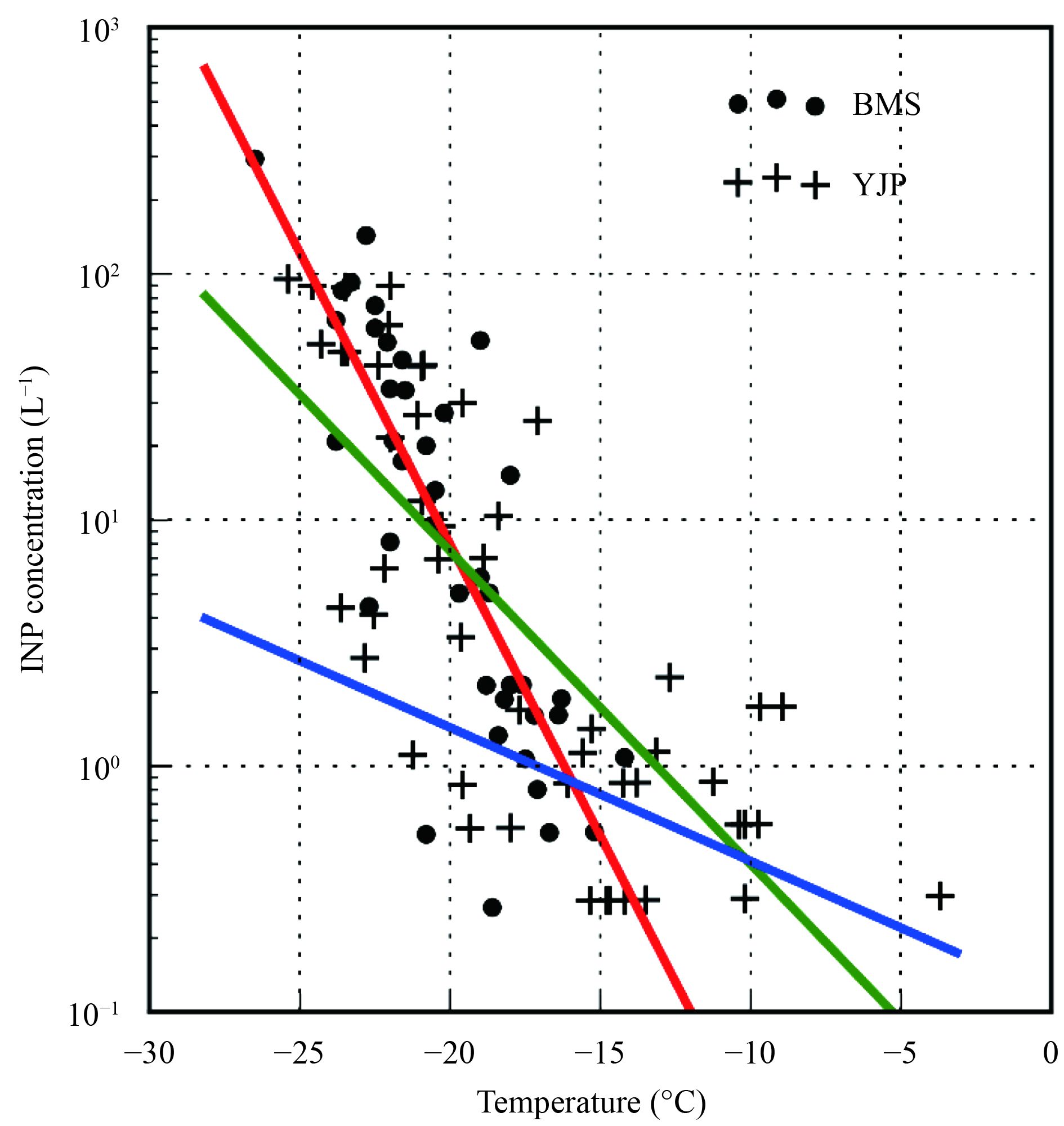
|
| Figure 3 The corrected INP concentrations at different temperatures. Data obtained at BMS and YJP are respectively shown with dots and crosses. The red line shows the fitting of data collected at BMS. The green line shows the fitting result of data collected at YJP. The blue line is obtained from DeMott et al. (2010). |
The parameterization of INP number concentration as a function of temperature is usually constructed by fitting the observational data with an exponential function (Meyers et al., 1992; DeMott et al. 2010). Here, the function form NINP = Aexp(–B(T–273.2)) was used to fit the data. The data collected at BMS and the data collected at YJP were fitted separately. The fitting results are shown in Fig. 3 and compiled in Table 1. For brevity, BMS parameterization and YJP parameterization are used to refer to the parameterizations fitted with the data collected at BMS and YJP, respectively. In addition, the parameterization of DeMott et al. (2010) is called DeMott parameterization.
| A | B | |
| BMS | 0.00014 | 0.546 |
| YJP | 0.021 | 0.293 |
| DeMott | 0.117 | 0.125 |
The predicted concentrations of INP active above –15°C are respectively 0.51, 1.73, and 0.77 g–1 based on the BMS, YJP, and DeMott parameterization. The BMS parameterization therefore predicts a low concentration of INP active above –15°C, while the YJP and the DeMott parameterization predict high concentrations of INP active above –15°C. In the parcel model study presented in the next section, these parameterizations are used to represent the situations with different concentrations of INP active above –15°C.
The parameterizations based on the data collected in this study are quite different from that of DeMott et al. (2010). Several reasons may be responsible for this difference. DeMott et al. (2010) constructed the parameterization by fitting data collected at different locations and different seasons. Their parameterization should therefore be representative of the global mean state. However, the concentration and the composition of aerosols vary remarkably with location and time. As a result, the globalmean INP concentration can be very different from that measured at a certain location and time (Wang et al., 2015). In addition, the instrument used in DeMott et al. (2010) is CFDC. It is known that CFDC mainly detects INPs that take effect via deposition nucleation, condensation freezing, and immersion freezing (DeMott et al., 2010). In contrary to the CFDC, Bigg’s chamber is appropriate for detecting INPs via deposition nucleation, immersion freezing, and contact freezing. The difference in detected nucleation modes should also contribute to the difference in the parameterizations.
4 Modeling resultsThe three parameterizations mentioned above were implemented into the parcel model to investigate the effects of different parameterizations on phase partitioning in mixed-phase clouds. Figure 4 shows the results of the simulation at a vertical velocity of 0.01 m s–1. Such a small vertical velocity can be seen in the stratiform clouds associated with midlatitude frontal system (Durran and Snellman, 1987). We first use the simulation where the ice formation is parameterized with the BMS parameterization (red lines in Fig. 4) to analyze the feedbacks occurring in the ascending parcel. Upon ascending, the expansive cooling decreases the temperature of the parcel (Fig. 4a). The parcel therefore gradually becomes supersaturated over water (Fig. 4b) and liquid droplets form at 1.2 km (Fig. 4d). After the formation, liquid water mixing ratio increases with height. In the meanwhile, the temperature of the parcel continues decreasing. Ice crystals begin to form when the temperature becomes lower than 0°C. At 2.8 km, the ice water mixing ratio becomes larger than 0.001 g kg–1 (Fig. 4e). Before the parcel rises to 4 km, the ice concentration is low (Fig. 4f) and the mean size of the ice crystals is small. In this situation, the total growth rate of the ice crystals is small (Korolev and Field, 2008), leading to that the growth of ice crystals cannot substantially affect the growth of liquid droplets. Consequently, liquid water mixing ratio keeps increasing until the parcel reaches 4 km.

|
| Figure 4 (a) Temperature, (b) saturation ratio over water, (c) saturation ratio over ice, (d) liquid water mixing ratio, (e) ice water mixing ratio, and (f) ice number concentration from the parcel model simulation. The vertical velocity is 0.01 m s–1. The red, green, and blue lines respectively indicate the simulations with the BMS, YJP, and DeMott parameterization. Note that (e) ice water mixing ratio and (f) ice number concentration are in logarithmic scale. |
When the parcel rises above 4 km, the ice concentration becomes high. More importantly, the mean size of the ice crystals becomes large. The total growth rate of ice crystals therefore becomes sufficiently large so that the growth of ice crystals reduces the saturation ratio to be lower than the equilibrium saturation ratio over water (Fig. 4b), but still higher than the equilibrium saturation ratio over ice (Fig. 4c). In this situation, ice crystals grow while liquid droplets evaporate, resulting in the continuous increase of ice water mixing ratio (Fig. 4e) and the continuous decrease of the liquid water mixing ratio (Fig. 4d).
At a vertical velocity of 0.01 m s–1, the amount of INPs that are active above –15°C can remarkably modify the phase partitioning in the mixed-phase clouds. Note that the layer of –15°C is approximately at 4 km (Fig. 4a). As has been discussed, the BMS parameterization, the DeMott parameterization, and the YJP parameterization respectively predict the lowest, moderate, and highest concentrations of INPs that are active above –15°C. Compared with the simulation with the BMS parameterization, the simulation with either the YJP or the DeMott parameterization has more ice crystals at the lower levels (Fig. 4f), leading to that the ice water mixing ratio reaches 0.001 g kg–1 at a lower altitude (Fig. 4e). The higher ice concentration also makes the ice crystals consume more vapor. In this situation, liquid water mixing ratio starts to decrease at an earlier time. Particularly, the high concentration of INPs active above –15°C in the YJP parameterization reduces the maximum liquid water mixing ratio by 1 g kg–1 (Fig. 4d).
Using different parameterizations can also affect the size distribution of ice crystals. Figure 5 shows the size distributions of ice crystal at 3 km, where the temperature is –9°C. The ice crystals produced in the three simulations have the same radius, provided they are in the same bin. This is because the ice crystals in the same bin are nucleated at the same height and undergo very similar growth processes. The ice crystals that are nucleated at a higher temperature have a longer time to grow, and therefore have a larger size. However, at a higher temperature, the amount of ice crystals nucleated during a same period of time is smaller. As a result, the ice concentration increases with decreasing radius of the ice crystals.

|
| Figure 5 Size distributions of ice crystals at 3 km. The vertical velocity is 0.01 m s–1. The color scheme is the same as that in Fig. 4. |
The presence of INPs that are active above –15°C has important implications on the initiation of precipitation in large-scale stratiform clouds. On the one hand, INPs active above –15°C can nucleate ice crystals at lower altitudes. These ice crystals grow rapidly by competing vapor with the surrounding liquid droplets and quickly begin to fall. The falling ice crystals collect liquid droplets and they can soon fall out of the cloud and form precipitation. On the other hand, INPs active above –15°C nucleate ice crystals in the temperature range where secondary ice formation is active. Previous studies pointed out that the riming-splintering process and the shattering process, both of which are important secondary ice formation process, are only effective at the temperature of –3 to –15°C (Hobbs and Alkezweeny, 1968; Hallett and Mossop, 1974; Mossop and Hallett, 1974; Heymsfield and Mossop, 1984). Therefore, the existence of INPs active above –15°C can results in a much higher ice concentration and further accelerate the formation of precipitation.
When the vertical velocity is increased to 0.1 m s–1, the temperature profiles are hardly altered (Fig. 6a). Because of the larger vertical velocity, the nucleated ice crystals have shorter time to grow. They hence consume less vapor, leading to that the liquid water mixing ratio starts to decrease at higher altitudes and the maximum liquid water mixing ratios are also higher (Fig. 6d). In addition, although the simulation with the BMS parameterization only has a small amount of ice crystals at low levels, it has much more ice crystals when the parcel rises above 4 km (Fig. 6f). As a result, vapor is rapidly consumed by the growth of ice crystals (Fig. 6b), and liquid droplets begin to evaporate in a short time. Compared with the simulation with the BMS parameterization, the simulation with the DeMott parameterization has more ice crystals at low levels (Fig. 6f). However, these ice crystals do not have enough time to grow. The growth of these ice crystals therefore only consumes a small amount of vapor. In this situation, liquid droplets keep growing until the parcel reaches 6 km. The longevity of liquid droplets maintains a high saturation ratio over ice (Fig. 6c), resulting in the continuous increase of ice water mixing ratio (Fig. 6e). As for the simulation with the YJP parameterization, its ice concentration also increases rapidly when the parcel rises above 4 km (Fig. 6f), so the evolution of liquid water mixing ratio is similarto that in the simulation with the BMS parameterization (Fig. 6d).

|
| Figure 6 As in Fig. 4 except that the vertical velocity is 0.1 m s–1. |
Figure 7 shows the results of the simulation at a verticalvelocity of 0.1 m s–1. At a vertical velocity of 0.1 m s–1, the size distributions are also different when different parameterizations are used (Fig. 7). More importantly, due to the shorter growth time, the ice crystals at 3 km are much smaller than those at a vertical velocity of 0.01 m s–1. The smaller ice crystals have smaller falling velocity. This will reduce the ability of INPs active above –15°C in initiating precipitation. Note that when the vertical velocity is further increased, the phase partitioning is also controlled by the INPs active below –15°C, as in the simulations at a vertical velocity of 0.1 m s–1.

|
| Figure 7 As in Fig. 5 except that the vertical velocity is 0.1 m s–1. |
A series of measurements of INP were performed with the Bigg’s chamber at two sites in Beijing. At the Beijing Meteorological Service (BMS) site, which was located near the center of the city, no INPs were found to be active at temperatures above –15°C. On the contrary, at the Yanjiaping (YJP) site, which was located in the rural area, the concentration of INP active at temperatures above –15°C was found to be 1.73 g–1. By fitting the data collected at the two sites, two parameterizations, which were respectively called BMS parameterization and YJP parameterization, were constructed.
The two parameterizations constructed with data collected in Beijing, as well as a parameterization obtained from DeMott et al. (2010), were implemented into a parcel model to investigate the effect of the INPs active above –15°C on the phase partitioning in mixed-phase clouds. At a vertical velocity of 0.01 m s–1, which is typical for the stratiform clouds associated with frontal systems, the ice crystals nucleated by the INPs active above –15°C have a long time to grow. These ice crystals can therefore consume a lot of vapor. Compared with the liquid water mixing ratio in the simulations without INPs active above –15°C, the liquid water mixing ratio in the simulations with INPs active above –15°C starts to decrease at lower altitude, leading to a smaller maximum liquid water mixing ratio. When the vertical velocity of the parcel is increased to 0.1 m s–1 or an even higher value, the evolution of liquid water mixing ratio is no longer controlled by the INPs active at temperature above –15°C but by the INPs active at temperatures below –15°C.
Acknowledgments. We are grateful to Deping Ding for initiating the collaboration between Beijing Weather Modification Office and Peking University.
| Atkinson, J. D., B. J. Murray, M. T. Woodhouse, et al., 2013: The importance of feldspar for ice nucleation by mineral dust in mixed-phase clouds. Nature, 498, 355–358. DOI:10.1038/nature12278 |
| Bigg, E. K., 1957: A new technique for counting ice-forming nuclei in aerosols. Tellus, 9, 394–400. DOI:10.1111/j.2153-3490.1957.tb01895.x |
| Burrows, S. M., C. Hoose, U. Pöschl, et al., 2013: Ice nuclei in marine air: Biogenic particles or dust?. Atmos. Chem. Phys., 13, 245–267. DOI:10.5194/acp-13-245-2013 |
| Chen, J., Z. J. Wu, S. Augustin-Bauditz, et al., 2018: Ice-nucleating particle concentrations unaffected by urban air pollution in Beijing, China. Atmos. Chem. Phys., 18, 3523–3539. DOI:10.5194/acp-18-3523-2018 |
| DeMott, P. J., 1990: An exploratory study of ice nucleation by soot aerosols. J. Appl. Meteor., 29, 1072–1079. DOI:10.1175/1520-0450(1990)029<1072:AESOIN>2.0.CO;2 |
| DeMott, P. J., A. J. Prenni, X. Liu, et al., 2010: Predicting global atmospheric ice nuclei distributions and their impacts on climate. Proc. Natl. Acad. Sci. USA, 107, 11217–11222. DOI:10.1073/pnas.0910818107 |
| Durran, D. R., and L. W. Snellman, 1987: The diagnosis of synoptic-scale vertical motion in an operational environment. Wea. Forecasting, 2, 17–31. DOI:10.1175/1520-0434(1987)002<0017:TDOSSV>2.0.CO;2 |
| Flatau, P. J., R. L. Walko, and W. R. Cotton, 1992: Polynomial fits to saturation vapor pressure. J. Appl. Meteor., 31, 1507–1513. DOI:10.1175/1520-0450(1992)031<1507:PFTSVP>2.0.CO;2 |
| Fu, S. Z., and H. W. Xue, 2017: The effect of ice nuclei efficiency on arctic mixed-phase clouds from large-eddy simulations. J. Atmos. Sci., 74, 3901–3913. DOI:10.1175/JAS-D-17-0112.1 |
| Hallett, J., and S. C. Mossop, 1974: Production of secondary ice particles during the riming process. Nature, 249, 26–28. DOI:10.1038/249026a0 |
| Heymsfield, A. J., and S. C. Mossop, 1984: Temperature dependence of secondary ice crystal production during soft hail growth by riming. Quart. J. Roy. Meteor. Soc., 110, 765–770. DOI:10.1002/qj.49711046512 |
| Hobbs, P. V., and A. J. Alkezweeny, 1968: The fragmentation of freezing water droplets in free fall. J. Atmos. Sci., 25, 881–888. DOI:10.1175/1520-0469(1968)025<0881:TFOFWD>2.0.CO;2 |
| Hoose, C., J. E. Kristjánsson, J.-P. Chen, et al., 2010: A classical-theory-based parameterization of heterogeneous ice nucleation by mineral dust, soot, and biological particles in a globalclimate model. J. Atmos. Sci., 67, 2483–2503. DOI:10.1175/2010JAS3425.1 |
| Huffman, J. A., A. J. Prenni, P. J. DeMott, et al., 2013: High concentrations of biological aerosol particles and ice nuclei during and after rain. Atmos. Chem. Phys., 13, 6151–6164. DOI:10.5194/acp-13-6151-2013 |
| Jiang, H., Y. Yin, H. Su, et al., 2015: The characteristics of atmospheric ice nuclei measured at the top of Huangshan (the Yellow Mountains) in Southeast China using a newly built static vacuum water vapor diffusion chamber. Atmos. Res., 153, 200–208. DOI:10.1016/j.atmosres.2014.08.015 |
| Jiang, H., Y. Yin, X. Wang, et al., 2016: The measurement and parameterization of ice nucleating particles in different backgrounds of China. Atmos. Res., 181, 72–80. DOI:10.1016/j.atmosres.2016.06.013 |
| Joly, M., P. Amato, L. Deguillaume, et al., 2014: Quantification of ice nuclei active at near 0°C temperatures in low-altitude clouds at the Puy de Dôme atmospheric station. Atmos. Chem. Phys., 14, 8185–8195. DOI:10.5194/acp-14-8185-2014 |
| Kikuro, T., S. Masaki, W. Kenji, et al., 2015: An example of canal formation in a thick cloud induced by massive seeding using liquid carbon dioxide. J. Meteor. Res., 29, 682–690. DOI:10.1007/s13351-015-5005-y |
| Korolev, A., and G. Isaac, 2003: Phase transformation of mixed-phase clouds. Quart. J. Roy. Meteor. Soc., 129, 19–38. DOI:10.1256/qj.01.203 |
| Korolev, A., and P. R. Field, 2008: The effect of dynamics on mixed-phase clouds: Theoretical considerations. J. Atmos. Sci., 65, 66–86. DOI:10.1175/2007JAS2355.1 |
| Lamb, D., and J. Verlinde, 2011: Physics and Chemistry of Clouds. Cambridge University Press, Cambridge, United Kingdom, 584 pp. |
| Li, Z., H. W. Xue, and F. Yang, 2013: A modeling study of ice formation affected by aerosols. J. Geophys. Res. Atmos., 118, 11213–11227. DOI:10.1002/jgrd.50861 |
| Lohmann, U., 2002: A glaciation indirect aerosol effect caused by soot aerosols. Geophys. Res. Lett., 29, 11-1–11-4. DOI:10.1029/2001GL014357 |
| Ma, X. C., K. Bi, Y. B. Chen, et al., 2017: Characteristics of winter clouds and precipitation over the mountains of northern Beijing. Adv. Meteor., 2017, 3536107. DOI:10.1155/2017/3536107 |
| Masaki, S., T. Kikuro, and N. Koji, 2016: Model analysis of radar echo split observed in an artificial cloud seeding experiment. J. Meteor. Res., 30, 386–400. DOI:10.1007/s13351-016-5053-y |
| Meyers, M. P., P. J. DeMott, and W. R. Cotton, 1992: New primary ice-nucleation parameterizations in an explicit cloud model. J. Appl. Meteor., 31, 708–721. DOI:10.1175/1520-0450(1992)031<0708:NPINPI>2.0.CO;2 |
| Mossop, S. C., and J. Hallett, 1974: Ice crystal concentration in cumulus clouds: Influence of the drop spectrum. Science, 186, 632–634. DOI:10.1126/science.186.4164.632 |
| Murray, B. J., S. L. Broadley, T. W. Wilson, et al., 2011: Heterogeneous freezing of water droplets containing kaolinite particles. Atmos. Chem. Phys., 11, 4191–4207. DOI:10.5194/acp-11-4191-2011 |
| O’Sullivan, D., B. J. Murray, T. L. Malkin, et al., 2014: Ice nucleation by fertile soil dusts: Relative importance of mineral and biogenic components. Atmos. Chem. Phys., 14, 1853–1867. DOI:10.5194/acp-14-1853-2014 |
| Ovchinnikov, M., A. S. Ackerman, A. Avramov, et al., 2014: Intercomparison of large-eddy simulations of Arctic mixed-phase clouds: Importance of ice size distribution assumptions. J. Adv. Model. Earth Syst., 6, 223–248. DOI:10.1002/2013MS000282 |
| Prenni, A. J., P. J. DeMott, D. C. Rogers, et al., 2009: Ice nuclei characteristics from M-PACE and their relation to ice formation in clouds. Tellus, 61, 436–448. DOI:10.1111/j.1600-0889.2009.00415.x |
| Savre, J., and A. M. L. Ekman, 2015: Large-eddy simulation of three mixed-phase cloud events during ISDAC: Conditions for persistent heterogeneous ice formation. J. Geophys. Res. Atmos., 120, 7699–7725. DOI:10.1002/2014JD023006 |
| Schnell, R. C., and G. Vali, 1976: Biogenic ice nuclei: Part I. Terrestrial and marine sources. J. Atmos. Sci., 33, 1554–1564. DOI:10.1175/1520-0469(1976)033<1554:BINPIT>2.0.CO;2 |
| Sesartic, A., U. Lohmann, and T. Storelvmo, 2013: Modelling the impact of fungal spore ice nuclei on clouds and precipitation. Environ. Res. Lett., 8, 014029. DOI:10.1088/1748-9326/8/1/014029 |
| Solomon, A., G. Feingold, and M. D. Shupe, 2015: The role of ice nuclei recycling in the maintenance of cloud ice in Arctic mixed-phase stratocumulus. Atmos. Chem. Phys., 15, 10,631–10,643. DOI:10.5194/acp-15-10631-2015 |
| Sulia, K. J., and J. Y. Harrington, 2011: Ice aspect ratio influences on mixed-phase clouds: Impacts on phase partitioning in parcel models. J. Geophys. Res. Atmos., 116, D21309. DOI:10.1029/2011JD016298 |
| Thompson, G., and T. Eidhammer, 2014: A study of aerosol impacts on clouds and precipitation development in a large winter cyclone. J. Atmos. Sci., 71, 3636–3658. DOI:10.1175/JAS-D-13-0305.1 |
| Vali, G., M. Christensen, R. W. Fresh, et al., 1976: Biogenic ice nuclei. Part II: Bacterial sources. J. Atmos. Sci., 33, 1565–1570. DOI:10.1175/1520-0469(1976)033<1565:BINPIB>2.0.CO;2 |
| Vali, G., P. J. DeMott, O. Möhler, et al., 2015: Technical Note: A proposal for ice nucleation terminology. Atmos. Chem. Phys., 15, 10263–10270. DOI:10.5194/acp-15-10263-2015 |
| Wang, D. H., J. F. Yin, and G. Q. Zhai, 2015: In-situ measurements of cloud–precipitation microphysics in the East Asian monsoon region since 1960. J. Meteor. Res., 29, 155–179. DOI:10.1007/s13351-015-3235-7 |
| Xue, H. W., and G. Feingold, 2004: A modeling study of the effect of nitric acid on cloud properties. J. Geophys. Res. Atmos., 109, D18204. DOI:10.1029/2004JD004750 |
| Yang, S. Z., X. F. Lou, G. Huang, et al., 2007: A 15 L mixing cloud chamber for testing ice nuclei. J. Appl. Meteor. Sci., 18, 716–721. |
| Young, K. C., 1974: The role of contact nucleation in ice phase initiation in clouds. J. Atmos. Sci., 31, 768–776. DOI:10.1175/1520-0469(1974)031<0768:TROCNI>2.0.CO;2 |
| Zeng, X. P., W.-K. Tao, M. H. Zhang, et al., 2009: An indirect effect of ice nuclei on atmospheric radiation. J. Atmos. Sci., 66, 41–61. DOI:10.1175/2008JAS2778.1 |
 2018, Vol. 32
2018, Vol. 32


