The Chinese Meteorological Society
Article Information
- QIAN, Daili, Zhaoyong GUAN, and Weiya TANG, 2018.
- Joint Impacts of SSTA in Tropical Pacific and Indian Oceans on Variations of the WPSH. 2018.
- J. Meteor. Res., 32(4): 548-559
- http://dx.doi.org/10.1007/s13351-018-7172-0
Article History
- Received November 20, 2017
- in final form May 25, 2018
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
The western Pacific subtropical high (WPSH) is an important component of the East Asian monsoon system. Its area, intensity, north–south position (the northern edge or ridge line), and east–west extension (the western ridge point) play the dominant role in the East Asian monsoon activities, and henceforth dominating the Meiyu/Baiu processes, especially droughts/floods as well as temperature changes in Yangtze River basin, North and South China (Dao and Hsu, 1962; Guan et al., 2010; Zhao et al., 2012; Liu et al., 2013). In the first half of 2016, the WPSH was stronger and extending more westward than normal, which leaded to frequent occurrences of rainstorms and floods in the south of China (Yuan et al., 2016; Zhai et al., 2016). Thereby, researchers in China have been trying all the time to understand the variations of the WPSH intensity and position better.
Previous studies have suggested that many factors can affect the WPSH changes. SST anomalies (SSTAs) over various ocean areas have different impacts on the WPSH (He et al., 2015; Li et al., 2017). Over the Pacific, the subtropical high activity is affected not only by local SSTA in the western Pacific (Kurihara and Kawahara, 1986; Wong et al., 1996; Zhang et al., 1996; Chung et al., 2011; Lu et al., 2014), but also by SSTA in the equatorial central-eastern Pacific. In most of the years when an El Niño event happens, the WPSH is weaker than normal and shifts eastward. In the winter when El Niño reaches its mature stage, an abnormal anticyclonic circulation appears over the western Pacific and maintained there until the subsequent summer (Li and Hu, 1987; Wang et al., 2000; Xiang et al., 2013; Zhang et al., 2017; Qian and Guan, 2018). This anticyclonic circulation promotes abnormal development of the WPSH. During the decaying stage of El Niño, reduced convection over the central Pacific enhances WPSH via Rossby wave response (Wang et al., 2013). This is further reconfirmed in Chen et al. (2016) that the WPSH intensification is induced by the central-eastern Pacific cooling during the rapid transition from El Niño to La Niña. Simultaneously, increased convection over Maritime Continent (MC) motivates easterlies over the western Pacific, leading to WPSH strengthening (Chung et al., 2011; Wang et al., 2017).
SSTA in the Indian Ocean (IO) can also strongly affect the WPSH activities. The Indian Ocean basin mode (IOBM) is the first important factor (Behera et al., 1999), which mainly reflects the lagged response of the Indian Ocean to ENSO (El Niño and Southern Oscillation) signals (Alexander et al., 2002; Ashok et al., 2003). The IOBM reaches its peak in the spring and can maintain until the summer via the ocean–atmosphere interaction (Klein et al., 1999). During positive IOBM phase, the WPSH intensifies due to the two-stage thermodynamic adaptation mechanism (Wu and Liu, 1992; Wu et al., 2000). Terao and Kubota (2005), Xie et al. (2009), and Wu et al. (2009, 2010) argued that SSTA in the tropical Indian Ocean could trigger eastward propagation of warm Kelvin waves; meanwhile, abnormal anticyclonic circulation could occur over the northwestern Pacific (NWP) due to the Ekman pumping, which subsequently affects the WPSH. It is similar to the role of “capacitor”, which transmits the impact of El Niño on WPSH in subsequent summer. And the “capacitor”-effect strengthens in response to global warming (Xie et al., 2010; Tao et al., 2015). As the second mode of SSTA in the Indian Ocean, the Indian Ocean dipole (IOD) is an important SST mode independent of ENSO, though correlated with ENSO signals to a certain extent (Saji et al., 1999; Webster et al., 1999; Ashok et al., 2003). The IOD can affect the summertime East Asian circulation through a triangular correlation mechanism (Guan and Yamagata, 2003). In addition, several previous studies focused on the impact of SSTA in northern Indian Ocean and the Bay of Bengal on the WPSH (Jiang et al., 1992; Huang and Hu, 2008).
According to the different impacts of SSTA in various ocean areas on the WPSH, some recent studies emphasized the combined effect of SSTA in Indo-Pacific. The warming in tropical Indian Ocean–western Pacific is found to be very important in leading to the westward extension of the WPSH since 1970 (Zhou et al., 2009). It is also found that an anomalous strong WPSH can be induced by the anomalous zonal SST gradient between warmer IO and colder Pacific (Ohba and Ueda, 2006; Cao et al., 2013).
The above shows that the relationships between the WPSH and SSTA in oceanic regions such as northwestern Pacific, MC, central equatorial Pacific (CEP), and IO have been extensively investigated in the past. However, there are still some important questions of interest to be answered. What are the temporal variations of the joint impacts of the SSTA in the Indian Ocean and Pacific on summertime WPSH as the IO SSTA signals obviously lag to those in the Pacific? What are physical processes that dominate these joint impacts of SSTA? Is it possible to set up a model for predicting the WPSH area in summer? In the present study, we examine these issues with emphasis on area changes of the WPSH.
The present paper is organized as follows. After the brief introduction, we present in Section 2 with descriptions of data and methodology. In Section 3, we examine the relationship between abnormal changes in WPSH area and SSTA over tropical Indian Ocean and Pacific. In Section 4, the mechanism behind the impact of SSTA on the WPSH is investigated. The prediction model for WPSH area variations is presented in Section 5. In the final section, we summarize the present study.
2 Data and methodologyThe data used in the present study include: (1) monthly mean SST from the Met Office Hadley Centre observation datasets (Rayner et al., 2003) with a resolution of 1° × 1°; and (2) NCEP/NCAR reanalysis product (Kalnay et al., 1996) of the geopotential height and winds with a resolution of 2.5° × 2.5° at 17 pressure levels. The data cover the period from September 1980 to October 2016.
The variation of area of the WPSH is highly correlated with its intensity with a correlation coefficient up to 0.89 in the summer (Qian et al., 2009). Thereby, in the present study, we focus on changes in the WPSH area to study the characteristics of WPSH activity. The WPSH moves mainly in region (10°–40°N, 90°E–180°), which is denoted by BOX-W. The WPSH area (WPSHA) is defined by surface areas of those 2.5° × 2.5° grids with monthly mean geopotential height not less than 588 dagpm at 500 hPa. For convenience, the WPSH area index is denoted by IWH, which is expressed as:
| ${I_{{\rm{WH}}}} = {\frac{1}{\sum}}\iint\limits_{_{{\rm BOX} {\text{-}} {\rm W}}} {\varepsilon \left( {\lambda ,\;\varphi } \right) M\left( {\lambda ,\;\varphi } \right){\rm d}\varphi {\rm d}\lambda } ,$ | (1) |
where M(λ, φ) is the area weight factor. When H
| $I{'_{{\rm{WH}}}} = {I_{{\rm{WH}}}} - {\bar I_{{\rm{WH}}}}.$ | (2) |
Besides, the atmospheric apparent heat source <Q1> is computed ( Luo and Yanai, 1984; Li et al., 2016) for analyzing the anomalous thermal forcing in tropical regions.
In the following text, the preceding autumn and winter refers to September–December (SOND); late winter and early spring is February–April (FMA); the spring is March–May (MAM); and the summer is June–August (JJA).
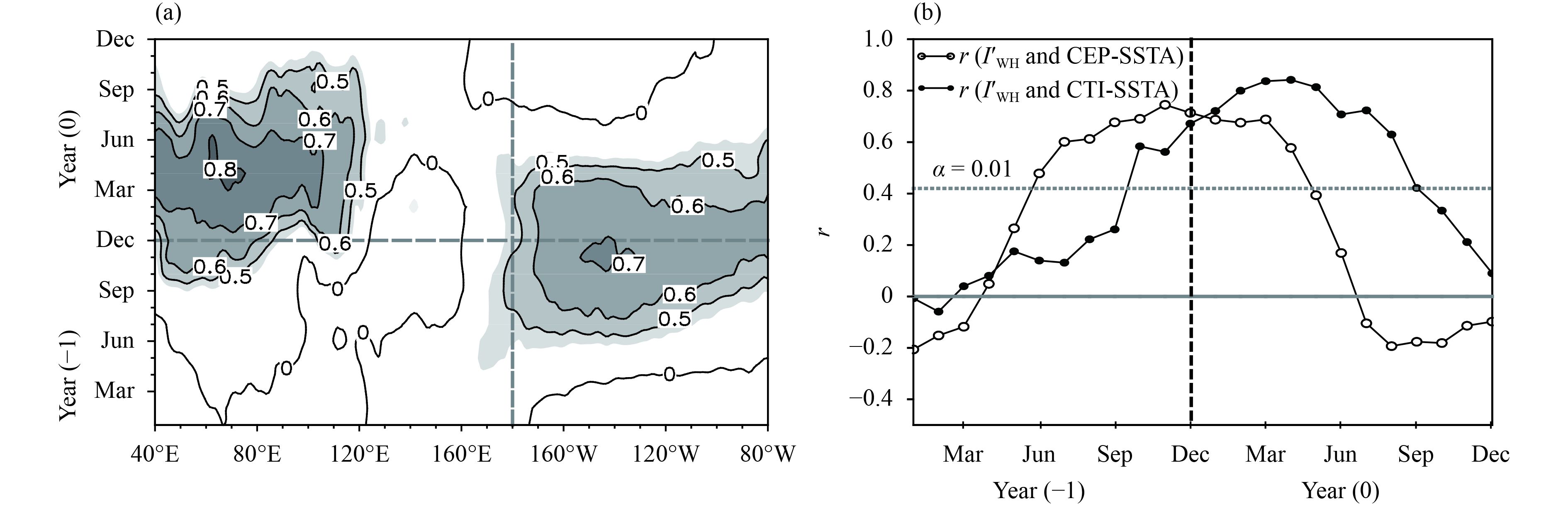
3 The relationship between WPSH area and SSTA over tropical IO and Pacific 3.1 The key region affecting the WPSH areaIn order to determine the key regions in the tropical Indian Ocean and Pacific where SSTA most possibly affect variations in the WPSH area, the correlation coefficient between
|
|
Figure 1 (a) Longitude–time cross-section of changes in the lead–lag correlation coefficients between
|
The regions of high correlation coefficient between SSTA from January of the last year to the June of the present year and the summertime WPSH area, i.e., (5°S–5°N, 160°–140°W) in CEP and (10°S–5°N, 60°–80°E) in the central tropical Indian Ocean (CTI), are identified to be the key regions where SSTA can significantly affect the interannual variability of WPSH. Lead–lag correlations between SSTA in the two key regions and the WPSH area are calculated (Fig. 1b). It shows that the WPSHA in summer is affected by the preceding SOND ENSO signals in the tropical central Pacific, while it is more significantly affected by CTI-SSTA in the early spring (FMA) of the same year. This result indicates that positive SSTA often occurs in the CEP since the preceding autumn and winter. In response, warm SSTA appears in the Indian Ocean in the subsequent spring. The correlation coefficient between the CEP-SSTA averaged over preceding SOND and the CTI-SSTA averaged over subsequent FMA is up to 0.84 (above 99% confidence level). As a result, the WPSH area in the summer is larger than normal. The above results suggest that SST over CEP and CTI and the WPSH area are closely related to each other.
Time series of CEP-SSTA averaged over the preceding SOND and CTI-SSTA averaged over the subsequent FMA during the 36-yr period are calculated and defined as the SSTA indices
In order to further reveal the impacts of CTI-SSTA and CEP-SSTA on the WPSH and the possible mechanisms behind them, the linear trends during 1981–2016 are first removed from
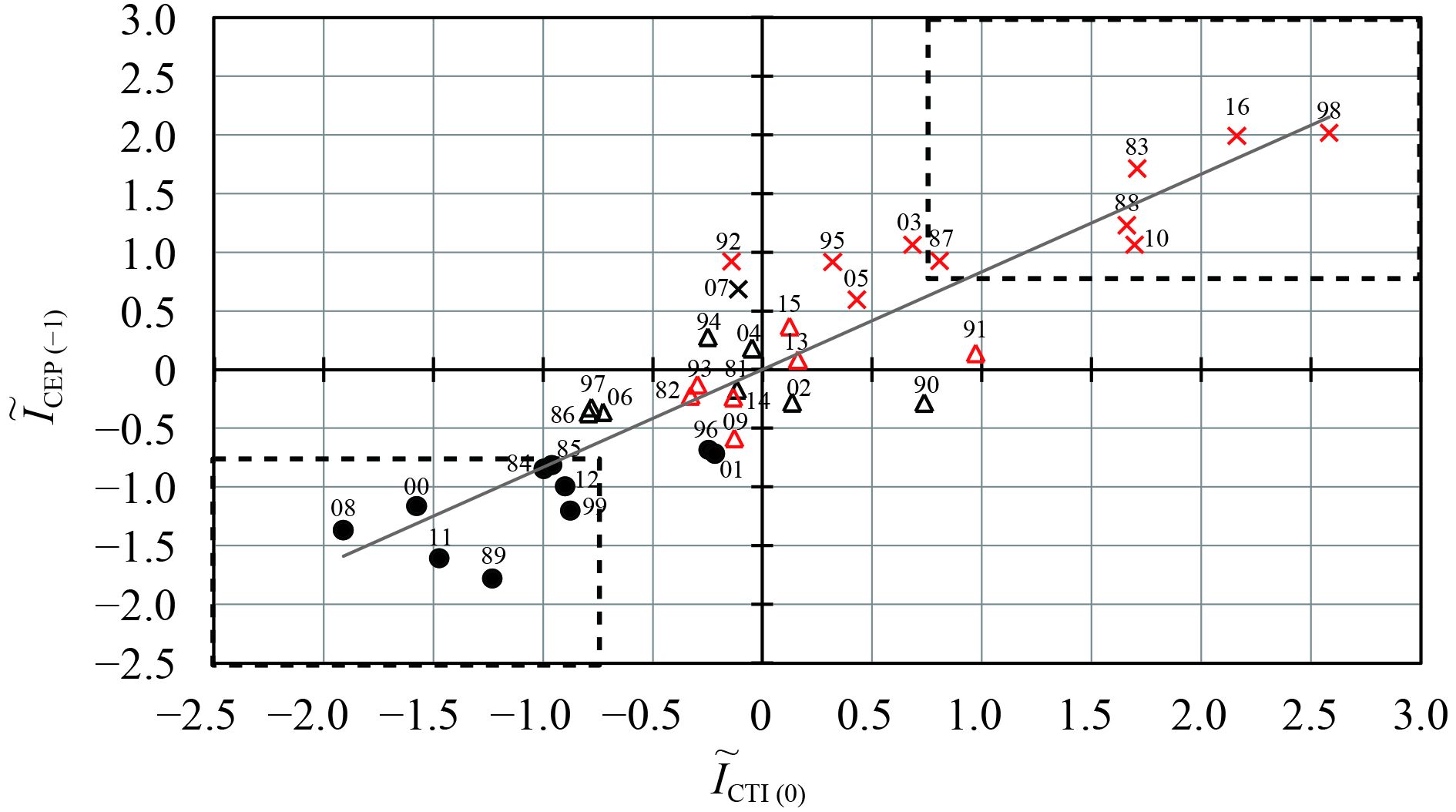
The variations of WPSH area are examined for cases with the above six types of SSTA events. It is seen from Fig. 2 that positive WPSH area anomalies (denoted by red marks) most possibly occur in the years when both
As described previously, the variations of SSTA in CTI are influenced by the SSTA in CEP; the lagged correlation coefficient of
Note that there are no cases of P-N and N-P types of SSTA appearing during the study period, reconfirming that the CTI-SSTA in current year is almost a result of IO response to the CEP-SSTA in the preceding autumn–winter. Interestingly, there are some particular cases when significant SSTA occurs in one region while SSTA in the other region is not large enough. These situations are indeed observed in Fig.2, denoted as cases of P-0, 0-P, and N-0 types of SSTA. When these cases occur, the relations of WPSH area variations are not highly correlated with
|
|
Figure 2 Scatter plot of SSTA indices
|
The SSTA patterns related to WPSH area variations can be displayed by the composites of SSTA differences between P-P and N-N cases, which are presented in Fig 3. It is seen that when warm SSTA occurs over CEP in the preceding autumn and winter (SOND) (Fig. 3a), abnormally cold SSTA occurs in the western Pacific and the MC region. At this time, SST warming at CTI is weak. According to the Delayed Oscillator theory (Suarez and Schopf, 1988), accompanied with the eastward propagation of Kelvin waves and westward propagation of Rossby waves in the ocean, El Niño enters decaying stage in the subsequent spring (Fig. 3b), with CEP-SSTA gradually weakening. During the entire period of the ENSO cycle, continuous ocean–air interaction leads to the lagged response of CTI to ENSO signals through the “Atmospheric Bridge” (Klein et al., 1999; Alexander et al., 2002; Lau and Nath, 2003) and results in significant warm CTI-SSTA in spring (FMA) (Fig. 3b) (Ashok et al., 2003; Zhou et al., 2004).

|
| Figure 3 Composite anomalies of SST between P-P and N-N types of years for (a) the preceding autumn and winter (SOND), (b) the following early spring (FMA), and (c) the current summer (JJA). Shaded areas are for SSTA (°C) whereas the dotted areas are for values exceeding the 99% confidence level; the green boxes show the key ocean areas of SSTA. |
In the following summer (JJA) (Fig. 3c), El Niño disappears; CEP-SSTA is very weak and the tropical western Pacific starts to become warming. Meanwhile the abnormal warm center in the CTI shifts northward to the Arabian Sea and Bay of Bengal, which is due to both the more absorption of solar radiation and the anomalous oceanic convergence of warm water by the anomalous anticyclonic circulations near the ocean surface. However, SSTA still remains high in the west and low in the east from the equatorial Indian Ocean to western Pacific. Such an SSTA pattern is favorable for the intensification and maintenance of the WPSH (Ohba and Ueda, 2006; Wu et al., 2014).
4.2 Mechanisms for the WPSH area changeDue to the joint influence of SSTA in the Pacific and Indian Ocean, significant convergence and divergence anomalies appear over the entire Indo-Pacific sector (Fig. 4). In the autumn and winter, surface air pressure over the CEP decreases following the abnormal increase in SST. As a result, the pressure difference between eastern and western sides of the CEP decreases, leading to weakened equatorial easterlies. Anomalous convergence occurs over the eastern Pacific (EP) around 140°W, while abnormal divergence occurs above the MC (120°–130°E). The Walker circulation is weakened (Fig. 4a). The intensities of the convergence and divergence anomalies are associated with the amplitude of SSTA. Anomalous cyclonic circulations symmetric about the equator occur to the west of the convergence center in EP, while anomalous anti-cyclonic circulations symmetric about the equator appear to the west of the divergence anomaly over the MC. This phenomenon is consistent to the results of Gill (1980) and Sardeshmukh and Hoskins (1988). The situation at 200 hPa in the upper troposphere is almost opposite to that at 850 hPa (Fig. 4d).

|
| Figure 4 Composites of circulation anomalies between P-P and N-N types of SSTA years for the preceding autumn and winter (SOND), the early spring (FMA), and summer (JJA) at (a–c) 850 hPa and (d–f) 200 hPa. Streamlines and arrows are respectively for the rotational and divergent component of winds (m s–1) whereas shaded areas are for velocity potential (10–6 m2 s–1). Capital “C” and “A” denote anomalous cyclonic and anticyclonic circulations respectively, while green boxes show the key regions of ocean . The stippled areas are for the anomalous velocity potential at/above the 95% confidence level whereas streamlines are for the zonal or meridional component of the rotational winds at/above the 90% confidence level. |
In the early spring, following the decrease in CEP-SSTA and the lagged response of warm CTI-SSTA to CEP thermal forcing, the convergence and divergence anomalies at 850 hPa over the Pacific weakens and the centers of them displace northeastward because of both the eastward shifting of the thermal forcing centers (Fig. 5) and the poleward moving of the sun during seasonal cycle. The northern branch of the anomalous anticyclonic circulations resulted from the Gill response extends to the northeast with the center locating above the South China Sea (SCS) (e.g., Wang and Zhang, 2002) (Fig. 4b). Then it moves further northeastward to Northwest Pacific (NWP) in following summer. These partly explain the increase of the WPSH area.

|
| Figure 5 Zonal–time cross-section of composited apparent heat source <Q1> anomalies between P-P and N-N types SSTA years. Contours are for <Q1> anomalies (W m –2) averaged over 10°S–10°N with shades for values at/above 90% confidence level, particularly the orange and red for values respectively at/above 95% and 99% confidence level for positive anomalies. |
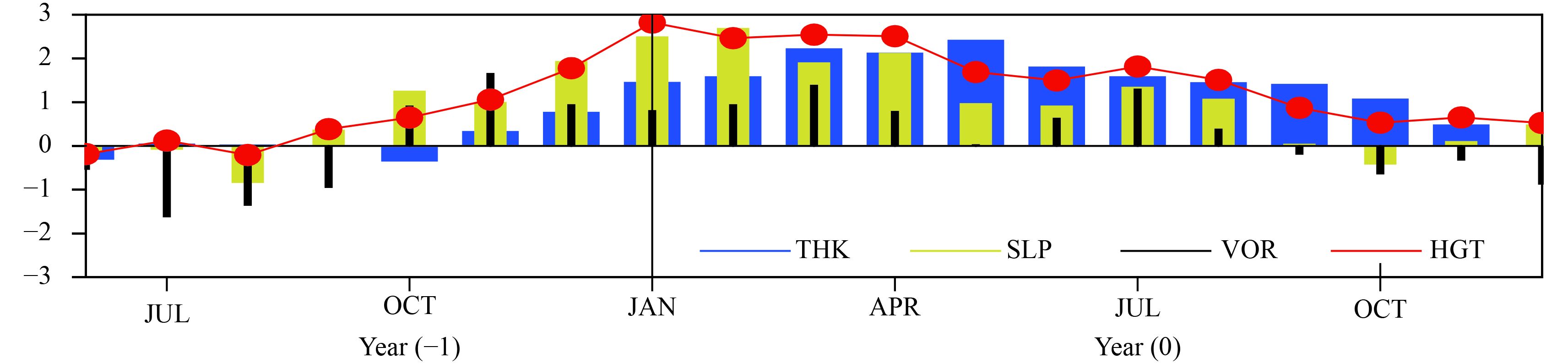
However, in JJA, El Niño disappearing or La Niña developing (Fig. 3c), although the anomalous divergence near MC region is weakened (Fig. 4c), the anomalous anticyclonic circulation over NWP is still strong; the anomalous vorticity (multiplied by –1) averaged over the region (10°–30°N, 90°–160°E) at 850 hPa in July of (0) year reaches its second peak phase (Fig. 6). The areal averaged geopotential height anomaly at 500 hPa over 10°–30°N, 90°–160°E also increases as compared to those in May and June of (0) year (Fig. 6). This kind of intensification over NWP is induced by the remote forcing of CTI-SSTA, which is the second mechanism for the summertime strengthening of the WPSH.
In both spring and summer during El Niño decaying phase, IOBM develops as a lagged response to CEP warming. The atmosphere above tropical IO responds to the warmed SSTA over there, leading to sea level pressure decreasing and tropospheric warming by enhanced convection (Figs. 6, 7).
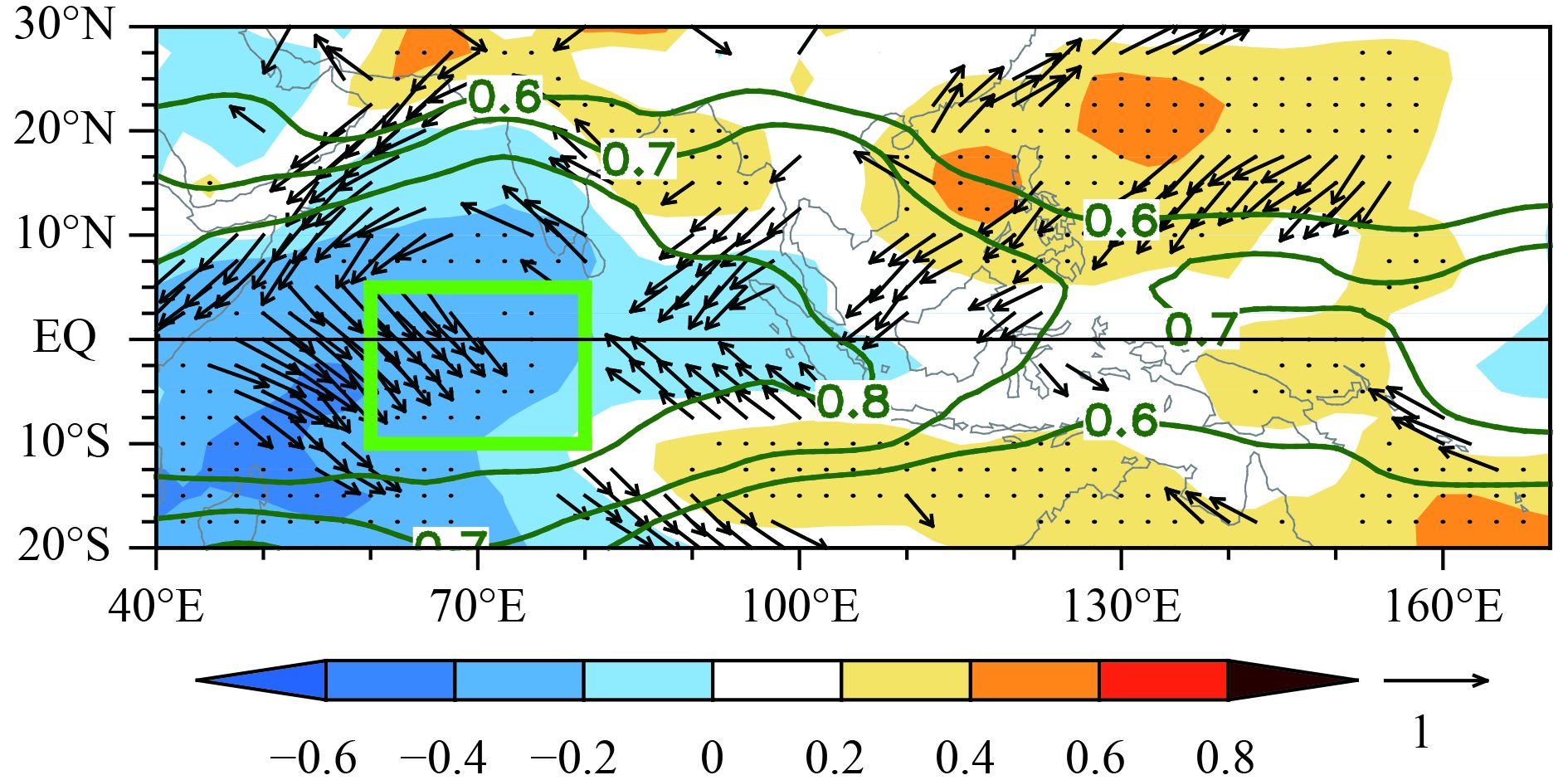
The warm equatorial Kelvin wave is excited and maintained via moist-adiabatic adjustment (Emanuel et al., 1997; Neelin and Su, 2005), inducing the anomalous easterlies in equatorial region due to eastward propagation of the wave in the lower troposphere. In the northeast of tropical IO and even NWP, the easterlies associated with the Kelvin wave are trapped in equatorial region and weaken from the equator to the polar (Fig. 7). The anomalous gradient of easterly winds in meridional is hence to intensify the anticyclonic shear over the SCS. Therefore, via the Ekman pumping in atmospheric boundary layer, significant descending motions develop in the lower troposphere over NWP (Fig. 4c). These downward motions as a feedback will induce the negative vorticity there, being favorable for further intensification and enlargement of WPSH (Wu et al., 2009; Xie et al., 2009).
|
| Figure 6 Composited disturbances of sea level pressure (SLP; yellow bars), the vorticity (multiplied by –1) at 850hPa (VOR; black bars), geopotential height at 500 hPa (HGT; red curve), and 850–200 hPa thickness (THK; blue bars) between P-P and N-N types of SSTA years. The former three quantities are averaged over 10°–30°N, 90°–160°E whereas the thickness is averaged over 20°S–20°N, 50°–150°E. All these four quantities are respectively divided by their own standard deviations. The x-coordinate is for time from July of the preceding year to December of the current year while the y-coordinate is for values of physical quantities. |
|
|
Figure 7 Simultaneous correlations between
|
Thus, the anomalous anticyclonic circulation over the western Pacific is induced by the anomalous divergence over MC in (–1) year SOND, and intensified in (0) year spring to summer, due to the anomalous anticyclonic vorticity above the SCS and western Pacific as a result of anomalous easterly wind motivated by the eastward propagating Kelvin waves. The joint effect of the two mechanisms results in an intensified WPSH that expanded over a larger area. The intensified anticyclonic anomaly will reinforce the horizontal divergence in the planetary boundary layer via Ekman pumping and lead to stronger meridional monsoon circulation (e.g., Xie et al., 2009; Zhang et al., 2017).
Figure 8 displays zonal–vertical cross-section of circulation anomalies averaged over 15°–25°N and meridional–vertical cross-section of circulation anomalies averaged over 100°–140°E. Significant descending motions appear over 15°–25°N, 100°–160°E, which promote increases in negative vorticity in the lower troposphere and help maintain the WPSH over a large area.

|
| Figure 8 Composites of summer JJA anomalous vorticity and vertical circulation between P-P type and N-N type SSTA years. (a) The zonal–vertical cross-section of circulation anomalies averaged over 15°–25°N while (b) the meridional–vertical cross-section of circulation anomalies averaged over 100°–140°E. Contours are for vorticity anomalies (10–5 s–1) with shades for values at/above 90% confidence level whereas streamlines are for vertical circulations with thick streamlines for vertical velocity anomalies at/above 90% confidence level. |
Furthermore, these descending motions can not only intensify the positive vorticity at 200 hPa in the upper troposphere over the South China Sea–western Pacific (Fig. 8), but also transport climatological negative vorticity from the upper troposphere to the middle and lower troposphere. It is found that
The joint effect of preceding CEP and CTI SSTA is extremely important for changes in the WPSH area in the subsequent summer. The WPSH area changes will directly affect summertime precipitation and temperature in China. Thereby, it is necessary to construct a statistical prediction model for the WPSH area. In the present study, a multiple regression model is constructed to predict the summertime WPSH area index. For this purpose, 25-yr observations over the period of 1981–2005 are used for model training. Since linearly independent predictors are required for multiple regression model,
| Model | Variance of
the model for 1981–2005 |
Complex correlation coefficient between
from observations and simulations |
|
|
78.6% | 0.77 |
| Note: Indices
|
||
Based on the constructed prediction model, it is clear that among those factors affecting the summertime WPSH area index, CEP-SSTA has a greater ratio, i.e., with every one σ increase in

|
|
Figure 9 The normalized time series of summertime
|
Significant positive correlations exist between preceding CEP and CTI SSTA, and between these SSTA and area of subsequent summertime WPSH. The CEP-SSTA averaged over the preceding SOND along with the CTI-SSTA averaged over FMA of the same year is important.
There exist two mechanisms for the joint effect of CTI and CEP SSTA on the summertime WPSH (Fig.10). First, during preceding SOND, the cold SSTA in the western Pacific and MC can lead to divergence anomalies in this region. The warm SSTA in CEP induces anomalous convergence there, facilitating the anomalous divergence in the western Pacific. This anomalous divergence subsequently forces the development of anomalous anticyclonic circulation over Bay of Bengal to northwestern Pacific via the Gill-type response. Since the divergence center near equator over the western Pacific displaces eastward following the thermal forcing center, the anomalous anticyclonic circulation is located eastward over the subtropical northwestern Pacific, intensifying the negative vorticity there. Second, the lagged response of CTI-SSTA to CEP-SSTA triggers the eastward propagating Kelvin wave, which leads to tropical easterly wind anomalies and subsequently intensifies the anticyclonic shear over the SCS and NWP. As a result, the anticyclonic anomaly above the northwestern Pacific further intensifies and expands. The joint effect of the above two mechanisms strengthens the anomalous anticyclone over the northwestern Pacific, which subsequently results in stronger monsoonal meridional-vertical circulation via the Ekman pumping. Significant anomalous descending motions are generated in the middle and upper troposphere, inducing negative vorticity anomalies in the lower troposphere, and henceforth leading to the intensification and enlargement of WPSH.
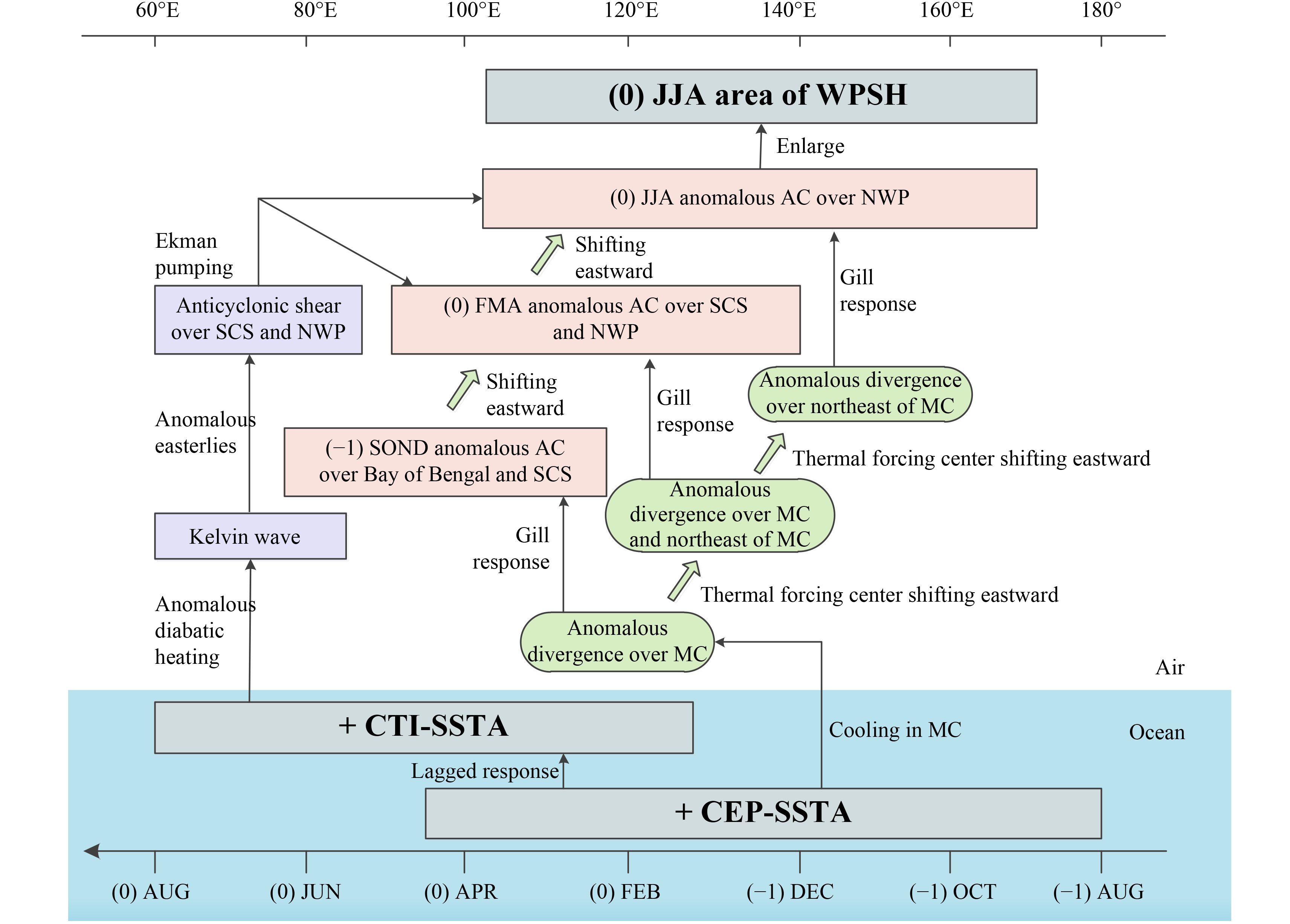
|
| Figure 10 The illustration of joint impacts of tropical Indian Ocean and Pacific SSTA on area changes of the WPSH. Thin arrows are for causalities while the colored arrows are for shifts of anomalous circulations. The bottom abscissa is for time evolution whereas the top abscissa is for longitudes. |
Using the preceding autumn and winter (SOND)
However, it is worth noting that, the correlation coefficient between
In addition, in the present study, we study the SSTA–WPSH relations statistically in a dynamical context. But, the deep insight into the SSTA–WPSH relations should be further examined by using the numerical models. This also deserves further investigations.
Acknowledgment. Authors are very thankful to the two anonymous reviewers for their helpful comments and the staff at the NUIST Data Service Center under the Geoscience Division of NSFC for their data services. The SST data are from the Met Office Hadley Centre observations datasets (https://www.metoffice.gov.uk/hadobs/hadisst/data/download.html) and the NCEP-NCAR reanalysis data are from https://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis.html. All the figures in this paper were plotted by using Grads software package.
AppendixIndex
| ${I'_{{\rm{CTI}}(0)}} = \beta {I'_{{\rm{CEP}}(- 1)}} + {I'_{{\rm{CTI}}(0)\_{\rm{R}}}},$ | (A1) |
where
| ${I'_{{\rm{WH}}}} = \gamma {I'_{{\rm{CEP}}(- 1)}} + {I'_{{\rm WH}\_{\rm{R}}}},$ | (A2) |
where
Relative contributions of SSTA in the two key regions (Table A1) are different.
| Index |
|
|
|
|
|
|
0.66* (43.59) | 0.75* (56.41) | 0.87* (75.69) | 0.44* (19.36) |
|
|
1 (100.00) | 0.00 (0.00) | 0.36* (12.96) | 0.67* (44.89) |
| Note: The values with asterisks * are for those at/above 99% confidence level. | ||||
| Alexander, M. A., I. Bladé, M. Newman, et al., 2002: The atmospheric bridge: The influence of ENSO teleconnections on air–sea interaction over the global oceans. J. Climate, 15, 2205–2231. DOI:10.1175/1520-0442(2002)015<2205:TABTIO>2.0.CO;2 |
| Ashok, K., Z. Y. Guan, and T. Yamagata, 2003: A look at the relationship between the ENSO and the Indian Ocean dipole. J. Meteor. Soc. Japan, 81, 41–56. DOI:10.2151/jmsj.81.41 |
| Behera, S. K., R. Krishnan, and T. Yamagata, 1999: Unusual ocean–atmosphere conditions in the tropical Indian Ocean during 1994. Geophys. Res. Lett., 26, 3001–3004. DOI:10.1029/1999GL010434 |
| Cao, J., R. Y. Lu, J. M. Hu, et al., 2013: Spring Indian Ocean-western Pacific SST contrast and the East Asian summer rainfall anomaly. Adv. Atmos. Sci., 30, 1560–1568. DOI:10.1007/s00376-013-2298-6 |
| Chen, Z. S., Z. P. Wen, R. G. Wu, et al., 2016: Relative importance of tropical SST anomalies in maintaining the western north Pacific anomalous anticyclone during El Niño to La Niña transition years. Climate Dyn., 46, 1027–1041. DOI:10.1007/s00382-015-2630-1 |
| Chung, P. H., C. H. Sui, and T. Li, 2011: Interannual relationships between the tropical sea surface temperature and summertime subtropical anticyclone over the western North Pacific. J. Geophys. Res., 16, D13111. DOI:10.1029/2010JD015554 |
| Dao, S. Y., and S. Y. Hsu, 1962: Some aspects of the circulation during the periods of the persistfnt drought and flood in Yantze and Hwai-ho valleys in summer. Acta Meteor. Sinica, 32, 1–10. |
| Emanuel, K. A., J. D. Neelin, and C. S. Bretherton, 1997: Reply to comments by Bjorn Stevens, David A. Randall, Xin Lin and Michael T. Montgomery on ‘On large-scale circulations in convecting atmospheres’ (July B, 1994, 120, 1111–1143). Quart. J. Roy. Meteor. Soc., 123, 1779–1782. DOI:10.1002/qj.49712354217 |
| Gill, A. E., 1980: Some simple solutions for heat-induced tropical circulation. Quart. J. Roy. Meteor. Soc., 106, 447–462. DOI:10.1002/qj.49710644905 |
| Guan, Z. Y., and T. Yamagata, 2003: The unusual summer of 1994 in East Asia: IOD teleconnections. Geophys. Res. Lett., 30, 1554. DOI:10.1029/2002GL016831 |
| Guan, Z. Y., J. X. Cai, W. Y. Tang, et al., 2010: Variations of west Pacific subtropical high associated with principal patterns of summertime temperature anomalies in the middle and lower reaches of the Yangtze River. Scientia Meteor. Sinica, 30, 666–675. DOI:10.3969/j.issn.1009-0827.2010.05.014 |
| He, C., T. J. Zhou, and B. Wu, 2015: The key oceanic regions responsible for the interannual variability of the western North Pacific subtropical high and associated mechanisms. J. Meteor. Res., 29, 562–575. DOI:10.1007/s13351-015-5037-3 |
| Huang, G., and K. M. Hu, 2008: Impact of North Indian Ocean SSTA on northwest Pacific lower layer anomalous anticyclone in summer. J. Nanjing Inst. Meteor., 31, 749–757. DOI:10.3969/j.issn.1674-7097.2008.06.001 |
| Jiang, G. R., W. Y. Sha, and J. P. Cai, 1992: The space–time feature of sea surface temperature in the Indian Ocean and the subtropical high over the western Pacific and interaction between them. J. Trop. Meteor., 8, 77–81. |
| Kalnay, E., M. Kanamitsu, R. Kistler, et al., 1996: The NCEP/NCAR 40-year reanalysis project. Bull. Amer. Meteor. Soc., 77, 437–470. DOI:10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2 |
| Klein, S. A., B. J. Soden, and N. C. Lau, 1999: Remote sea surface temperature variations during ENSO: Evidence for a tropical atmospheric bridge. J. Climate, 12, 917–932. DOI:10.1175/1520-0442(1999)012<0917:RSSTVD>2.0.CO;2 |
| Kurihara, K., and M. Kawahara, 1986: Extremes of East Asian weather during the post ENSO years of 1983/84: Severe cold winter and hot dry summer. J. Meteor. Soc. Japan, 64, 494–503. DOI:10.2151/jmsj1965.64.4_493 |
| Lau, N. C., and M. J. Nath, 2003: Atmosphere–Ocean variations in the Indo-Pacific sector during ENSO episodes. J. Climate, 16, 3–20. DOI:10.1175/1520-0442(2003)016<0003:AOVITI>2.0.CO;2 |
| Li, C. Y., and J. Hu, 1987: A study on interaction between the East-Asia atmospheric circulation and El Niño. Chinese J. Atmos. Sci., 11, 359–364. DOI:10.3878/j.issn.1006-9895.1987.04.03 |
| Li, M. G., Z. Y. Guan, D. C. Jin, et al., 2016: Anomalous circulation patterns in association with two types of daily precipitation extremes over southeastern China during boreal summer. J. Meteor. Res., 30, 183–202. DOI:10.1007/s13351-016-5070-x |
| Li, T., B. Wang, B. Wu, et al., 2017: Theories on formation of an anomalous anticyclone in western North Pacific during El Niño: A review. J. Meteor. Res., 31, 987–1006. DOI:10.1007/s13351-017-7147-6 |
| Liu, Y. M., J. L. Hong, C. Liu, et al., 2013: Meiyu flooding of Huaihe River valley and anomaly of seasonal variation of subtropical anticyclone over the western Pacific. Chinese J. Atmos. Sci., 37, 439–450. DOI:10.3878/j.issn.1006-9895.2012.12313 |
| Lu, C. H., L. Huang, J. H. He, et al., 2014: Interannual variability of heat content in western Pacific warm pool and its impact on the eastern Asian climatic anomaly. J. Trop. Meteor., 30, 64–72. DOI:10.3969/j.issn.1004-4965.2014.01.007 |
| Luo, H. B., and M. Yanai, 1984: The large-scale circulation and heat sources over the Tibetan Plateau and surrounding areas during the early summer of 1979. Part II: Heat and moisture budgets. Mon. Wea. Rev., 112, 966–989. DOI:10.1175/1520-0493(1984)112<0966:TLSCAH>2.0.CO;2 |
| Neelin, J. D., and H. Su, 2005: Moist teleconnection mechanisms for the tropical South American and Atlantic sector. J. Climate, 18, 3928–3950. DOI:10.1175/JCLI3517.1 |
| Ohba, M, and H. Ueda, 2006: A role of zonal gradient of SST between the Indian Ocean and the western pacific in localized convection around the Philippines. SOLA, 2, 176–179. DOI:10.2151/sola.2006-045 |
| Qian, D. L., and Z. Y. Guan, 2018: Different features of super and regular El Niño events and their impacts on the variation of the west Pacific subtropical high. Acta Meteor. Sinica, 76(3), 394–407. DOI:10.11676/qxxb2018.011 |
| Qian, D. L., Z. Y. Guan, and L. J. Wang, 2009: Interdecadal variations of West Pacific subtropical high area and changes in summer precipitation over China in boreal summer during the last 57 years. Trans. Atmos. Sci., 32, 677–685. DOI:10.3969/j.issn.1674-7097.2009.05.012 |
| Rayner, N. A., D. E. Parker, E. B. Horton, et al., 2003: Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res., 108, 4407. DOI:10.1029/2002JD002670 |
| Saji, N. H., B. N. Goswami, P. N. Vinayachandran, et al., 1999: A dipole mode in the tropical Indian Ocean. Nature, 401, 360–363. DOI:10.1038/43854 |
| Sardeshmukh, P. D., and B. J. Hoskins, 1988: The generation of global rotational flow by steady Idealized tropical divergence. J. Atmos. Sci., 45, 1228–1251. DOI:10.1175/1520-0469(1988)045<1228:TGOGRF>2.0.CO;2 |
| Suarez, M. J., and P. S. Schopf, 1988: A delayed action oscillator for ENSO. J. Atmos. Sci., 45, 3283–3287. DOI:10.1175/1520-0469(1988)045<3283:ADAOFE>2.0.CO;2 |
| Tao, W. C., G. Huang, K. M. Hu, et al., 2015: Interdecadal modulation of ENSO teleconnections to the Indian Ocean basin mode and their relationship under global warming in CMIP5 models. Int. J. Climatol., 35, 391–407. DOI:10.1002/joc.3987 |
| Terao, T., and T. Kubota, 2005: East-west SST contrast over the tropical oceans and the post El Niño western north Pacific summer monsoon. Geophys. Res. Lett., 32, L15706. DOI:10.1029/2005GL023010 |
| Wang, B., and Q. Zhang, 2002: Pacific–East Asian teleconnection. Part II: How the Philippine sea anomalous anticyclone is established during El Niño development. J. Climate, 15, 3252–3265. DOI:10.1175/1520-0442(2002)015<3252:PEATPI>2.0.CO;2 |
| Wang, B., B. Q. Xiang, and J. Y. Lee, 2013: Subtropical high predictability establishes a promising way for monsoon and tropical storm predictions. Proc. Natl. Acad. Sci. U.S.A., 110, 2718–2722. DOI:10.1073/pnas.1214626110 |
| Wang, B., J. Li, and Q. He, 2017: Variable and robust East Asian monsoon rainfall response to El Niño over the past 60 years (1957–2016). Adv. Atmos. Sci., 34, 1235–1248. DOI:10.1007/s00376-017-7016-3 |
| Wang, B., R. G. Wu, and X. H. Fu, 2000: Pacific–East Asian teleconnection: How does ENSO affect East Asian climate? J. Climate, 13, 1517–1536. DOI:10.1175/1520-0442(2000)013<1517:PEATHD>2.0.CO;2 |
| Webster, P. J., A. M. Moore, J. P. Loschnigg, et al., 1999: Coupled ocean–atmosphere dynamics in the Indian Ocean during 1997–98. Nature, 401, 356–360. DOI:10.1038/43848 |
| Wong, X. C., Q. L. Zhang, and T. Z. Yan, 1996: Variation of the subsurface water heat content in the tropical western Pacific warm pool area and its relation to precipitation in eastern China and to the western Pacific subtropical high. Studia Marina Sinica, 37, 1–9. |
| Wu, B., T. Li, and T. J. Zhou, 2010: Relative contributions of the Indian Ocean and local SST anomalies to the maintenance of the western North Pacific anomalous anticyclone during El Niño decaying summer. J. Climate, 23, 2974–2986. DOI:10.1175/2010JCLI3300.1 |
| Wu, B., T. J. Zhou, and T. Li, 2009: Seasonally evolving dominant interannual variability modes of East Asian climate. J. Climate, 22, 2992–3005. DOI:10.1175/2008JCLI2710.1 |
| Wu, G. X., and H. Z. Liu, 1992: Atmospheric precipitation in response to equatorial and tropical sea surface temperature anomalies. J. Atmos. Sci., 49, 2236–2255. DOI:10.1175/1520-0469(1992)049<2236:APIRTE>2.0.CO;2 |
| Wu, G. X., P. Liu, Y. M. Liu, et al., 2000: Impacts of the sea surface temperature anomaly in the Indian Ocean on the subtropical anticyclone over the western Pacific—Two-stage thermal adaptation in the atmosphere. Acta Meteor. Sinica, 58, 513–522. DOI:10.3321/j.issn:0577-6619.2000.05.001 |
| Wu, R. G., G. Huang, and Z. C. Du, 2014: Cross-season relation of the South China Sea precipitation variability between winter and summer. Climate Dyn., 43, 193–207. DOI:10.1007/s00382-013-1820-y |
| Xiang, B. Q., B. Wang, W. D. Yu, et al., 2013: How can anomalous western North Pacific subtropical high intensify in late summer?. Geophys. Res. Lett., 40, 2349–2354. DOI:10.1002/grl.50431 |
| Xie, S. P., Y. Du, G. Huang, et al., 2010: Decadal shift in El Niño influences on Indo–western Pacific and East Asian climate in the 1970s. J. Climate, 23, 3352–3368. DOI:10.1175/2010JCLI3429.1 |
| Xie, S. P., K. M. Hu, J. Hafner, et al., 2009: Indian ocean capacitor effect on Indo–western Pacific climate during the summer following El Niño. J. Climate, 22, 730–747. DOI:10.1175/2008JCLI2544.1 |
| Yuan, Y., H. Gao, X. L. Jia., et al., 2016: Influences of the 2014–2016 super El Niño event on climate. Meteor. Mon., 42, 532–539. DOI:10.7519/j.issn.1000-0526.2016.05.002 |
| Zhai, P. M., R. Yu, Y. J. Guo et al., 2016: The strong El Niño of 2015/16 and its dominant impacts on global and China’s climate. J. Meteor. Res., 30, 283–297. DOI:10.1007/s13351-016-6101-3 |
| Zhang, R. H., A. Sumi, and M. Kimoto, 1996: Impact of El Niño on the East Asian monsoon: A diagnostic study of the ’86/87 and ’91/92 events. J. Meteor. Soc. Japan, 74, 49–62. DOI:10.2151/jmsj1965.74.1_49 |
| Zhang, R. H., Q. Y. Min, and J. Z. Su, 2017: Impact of El Niño on atmospheric circulations over East Asia and rainfall in China: Role of the anomalous western North Pacific anticyclone. Sci. China Earth Sci., 60, 1124–1132. DOI:10.1007/s11430-016-9026-x |
| Zhao, J. H., G. L. Feng, J. Yang, et al., 2012: Analysis of the distribution of the large-scale drought/flood of summer in China under different types of the western Pacific subtropical high. Acta Meteor. Sinica, 70, 1021–1031. DOI:10.11676/qxxb2012.085 |
| Zhou, T. J., Y. Q. Yu, R. C. Yu, et al., 2004: Indian Ocean response to ENSO: Observation and air–sea coupled model simulation. Chinese J. Atmos. Sci., 28, 357–373. |
| Zhou, T. J., R. C. Yu, J. Zhang, et al., 2009: Why the western Pacific subtropical high has extended westward since the late 1970s. J. Climate, 22, 2199–2215. DOI:10.1175/2008JCLI2527.1 |
 2018, Vol. 32
2018, Vol. 32


