The Chinese Meteorological Society
Article Information
- LI, Xiaohan, and Xindong PENG, 2018.
- Long-Term Integration of a Global Non-Hydrostatic Atmospheric Model on an Aqua Planet. 2018.
- J. Meteor. Res., 32(4): 517-533
- http://dx.doi.org/10.1007/s13351-018-8016-7
Article History
- Received January 15, 2018
- in final form April 30, 2018
2. University of Chinese Academy of Sciences, Beijing 100049
Multi-scale atmospheric simulations have become popular in numerical weather prediction with the development of complex global non-hydrostatic models. Weather service centers worldwide are promoting the advances in highly efficient atmospheric general circulation models (AGCMs) and detailed physical parameterizations that include “gray zone” processes, which cannot be entirely resolved by the model. The horizontal grid structure of an AGCM is a key factor affecting the scalability, computational efficiency, and accuracy of the model (Williamson, 2007). Most operational numerical weather prediction models use the latitude–longitude (Lat–Lon) grid for spatial discretization, including the Global/Regional Assimilation and Prediction System (GRAPES; Chen et al., 2008; Niu et al., 2017; Shen et al., 2017) developed by the China Meteorological Administration. However, the shrinking of meridional lines in the polar regions increases the cost of the Helmholtz solver and the communication required as a result of the large Courant number. Hence, some quasi-uniform grid systems, including structured and unstructured grids, have been implemented in the dynamical cores of models to overcome these issues (Sadourny et al., 1968; Sadourny, 1972; Kageyama and Sato, 2004). The applicability of numerical models using a uniform mesh is increased to an extended timescale and the representativeness of physical parameterization schemes is improved with a uniform grid space from the equator to the polar regions. Typical examples of models using different grid systems are the High Order Method Modeling Environment (HOMME) dynamical core of the Community Atmosphere Model (CAM), which is based on a cubed-sphere grid (Dennis et al., 2005; Taylor et al., 2007), the Non-hydrostatic ICosahedral Atmospheric Model (NICAM; Tomita and Satoh, 2004; Tomita et al., 2005), and the hydrostatic dynamical core on the Yin–Yang grid of the Canadian Global Environmental Multi-Scale model (Qaddouri et al., 2008; Qaddouri and Lee, 2011).
The quasi-uniform overset Yin–Yang grid system (Kageyama and Sato, 2004) is composed of a pair of perpendicular zones with an identical mesh structure (Fig. 1). A number of studies have been published on the solution of partial differential equations for hydrostatic and non-hydrostatic dynamical cores on the Yin–Yang grid (Li et al., 2008; Baba et al., 2010; Allen and Zerroukat, 2016). Li et al. (2015) reconstructed the GRAPES dynamical core on the Yin–Yang grid (GRAPES_YY) to address the polar problem and to enhance computational performance. The Yin–Yang grid is well suited to the GRAPES for two reasons. First, it is composed of two low-latitude parts of the Lat–Lon grid and is compatible with methods based on the Lat–Lon grid. Second, the practice of mesh refinement and grid nesting are convenient due to the structured distribution of the grid, which provide high scalability for high-resolution compu-tations. The dynamical core of GRAPES_YY has shown reasonable numerical results through a series of idealized standard tests proposed by Jablonowski et al. (2008).
The GRAPES_YY dynamical core has been coupled with a physical parameterization package consisting of convective parameterization, cloud physics processes, short- and longwave radiation, and surface and planetary boundary layer (PBL) turbulent mixing processes. Although this physical package has been used in the operational version of GRAPES, numerical testing is required to assess its performance when coupled with the GRAPES_YY dynamical core. However, it is hard to examine the feasibility of the model dynamics and physics in the real atmosphere due to the complexity of the spatial and temporal variability of the boundary conditions, such as the land–sea contrast, the detailed orography, and the complex distribution of sea surface temperatures (SSTs; Blackburn and Hoskins, 2013).
Idealized tests and simplified model configurations have been proposed to assess the model dynamical core and physical parameterization package in a straightforward way. Neale and Hoskins (2000a, b) proposed an Aqua Planet Experiment (APE) to examine AGCMs that couple dynamical core and physical processes on an idealized water-covered earth. A set of idealized SST profiles were designed to investigate how AGCMs respond to changes in the surface boundary conditions. Although simpler than more realistic configurations, the aqua planet simulations captured the main characteristics of the earth and most of the models produced realistic responses of the large-scale circulation and hydrological cycle to changes in SSTs (Medeiros et al., 2015). Wang et al. (2008) proposed that the performance of models and the impact of individual physical parameterizations can be understood by comparison with other model simulations under specified SST conditions. The results from other models, such as those in the atlas of model simulation statistics (Williamson, 2012; Blackburn et al., 2013; Williamson et al., 2013, hereafter referred to simply as ATLAS) and the 16-yr aqua planet climate in NCAR-CAM5 (Medeiros et al., 2016), provide a wealth of reference data. However, most models in the ATLAS are hydrostatic and there is no standard solution to which the APE can be referred. The non-hydrostatic models NICAM (which integrated for only 90 days) and pre-HadGAM1 showed a single versus a twin InterTropical Convergence Zone (ITCZ) in the CONTROL simulation. In this study, the non-hydrostatic GRAPES_YY is examined in a 3.5-yr integration of CONTROL and FLAT simulations to evaluate the coupled moist dynamical core and physical parameterizations and to provide insights into the sensitivity of the model to changes in the meridional SST pattern. The accuracy of the long-term integration of GRAPES_YY can be assessed in comparison with other models in APEs. The precipitation, general circulation, eddy statistics, and other specific aspects of the GRAPES_YY simulation are analyzed and compared with other model simulations to show the similarities and differences of GRAPES_YY with respect to other models.

|
| Figure 1 The Yin–Yang grid. |
GRAPES_YY is a global non-hydrostatic model developed on the Yin–Yang grid and is solved by using a semi-implicit semi-Lagrangian (SISL) method. It focuses on short-term, medium-range weather predictions and also provides seasonal climate projections. It aims at multi-scale atmospheric simulations with improved model dynamics and physics. The governing equations in spherical coordinates are:
| $\frac{{{\rm d}u}}{{{\rm d}t}} = - \frac{{{c_p}\theta }}{{a\cos \varphi }}\frac{{\partial \prod }}{{\partial \lambda }} + {f_r}v - {f_\varphi }w + \left(\frac{{uv\tan \varphi }}{a} - \frac{{uw}}{a}\right) + {F_u}, $ | (1) |
| $\frac{{{\rm d}v}}{{{\rm d}t}} = - \frac{{{c_p}\theta }}{a}\frac{{\partial \prod }}{{\partial \varphi }} - {f_r}u + {f_\lambda }w - \left(\frac{{{u^2}\tan \varphi }}{a} + \frac{{vw}}{a}\right) + {F_v}, \quad\,\,\,\,\, $ | (2) |
| $\frac{{{\rm d}w}}{{{\rm d}t}} = - {c_p}\theta \frac{{\partial \prod }}{{\partial r}} - g + {f_\varphi }u - {f_\lambda }v + \left(\frac{{{u^2} + {v^2}}}{a}\right) + {F_w},\qquad\quad $ | (3) |
| $\left(\frac{{{c_p}}}{{{R_{\rm d}}}} - 1\right)\frac{{{\rm d}\prod }}{{{\rm d}t}} = - {\textstyle\prod }{D_3} + \frac{{{Q_\theta } + {F_\theta }}}{{{c_p}\theta }}, \qquad\qquad\qquad\qquad\,\,\,$ | (4) |
| $\frac{{{\rm d}\theta }}{{{\rm d}t}} = \frac{{{Q_\theta } + {F_\theta }}}{{{c_p}\prod }},\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad $ | (5) |
| $\begin{split} \frac{{\partial q}}{{\partial t}} & + \frac{{\partial \left( {q\displaystyle\frac{u}{{a\cos \varphi }}} \right)}}{{\partial \lambda }} + \frac{{\partial \left( {q\displaystyle\frac{{v\cos \varphi }}{a}} \right)}}{{\partial \sin \varphi }} + \frac{{\partial \left( {qw} \right)}}{{\partial r}}\qquad\qquad\quad \\ & = q\left( {\frac{{\partial \displaystyle\frac{u}{{a\cos \varphi }}}}{{\partial \lambda }} + \frac{{\partial \displaystyle\frac{{v\cos \varphi }}{a}}}{{\partial \sin \varphi }} + \frac{{\partial w}}{{\partial r}}} \right) + {Q_q} + {F_q}, \end{split} $ | (6) |
where Π represents the Exner function, θ is the virtual potential temperature, q is the specific humidity of six different forms of moisture (water vapor, rain droplets, cloud droplets, cloud ice, snow, and graupel), and u, v, and w are the horizontal and vertical velocities. The variable cp = 1004.64 J kg–1 K–1 is the specific heat at constant pressure and f is the Coriolis parameter; Rd is the ideal gas constant for dry air, and g = 9.80616 m s–2 is the acceleration due to gravity; λ and φ are the longitude and latitude, r denotes the vertical coordinate, t means time, and a = 6371.22 km is the radius of earth; D3 is the three-dimensional divergence. The source/sink term Qθ is non-adiabatic heating, Qq is the water source (sink) term, and Fu (v, w, θ, q) are the physical effects and horizontal diffusion terms. Both Q and F are represented by physical parameterizations. The Yin and Yang subdomains share the same governing equations and computational techniques, in addition to unified computer code and straightforward parallel computation among each tile.
The spatial discretization is based on the Arakawa-C grid (Arakawa and Lamb, 1997) in horizontal space and Charney–Phillips staggering (Charney and Phillips, 1953) in the vertical direction. The prognostic variables in the dry core are updated by using the non-centered second-order temporal discretization scheme (Semazzi et al., 1995; Qian et al., 1998). The boundaries of the Yin–Yang grid are updated by bi-cubic Lagrangian interpolation at each time step (Li et al., 2006). The Helmholtz problem is iteratively solved by the generalized conjugate residual method and the first type boundary condition in the classical Schwarz method (Qaddouri et al., 2008). Details of the computing procedures for the dry core have been reported by Li et al. (2015). An explicit diffusion in a form of fourth-order horizontal divergence damping (Whitehead et al., 2011) is added to the momentum equations to dissipate spurious high-frequency waves. In order to conserve mass in the long-term integration, a fixer is added when solving the equation of Π, that is
| $\begin{split} \!\! & {\Pi _{{\text{new}}}}(\lambda ,\varphi ,k) = \\& \quad \Pi (\lambda ,\varphi ,k)\frac{{\displaystyle\sum\limits_{\varphi = - \textstyle\frac{\pi }{2}}^{\varphi = \textstyle\frac{\pi }{2}} {\sum\limits_{\lambda = 0}^{\lambda = 2\pi } {\Delta \lambda \Delta \varphi \cos \varphi {\pi _{{\text{init}}}}(\lambda ,\varphi ,1)} } }}{{\displaystyle\sum\limits_{\varphi = - \textstyle\frac{\pi }{2}}^{\varphi = \textstyle\frac{\pi }{2}} {\sum\limits_{\lambda = 0}^{\lambda = 2\pi } {\Delta \lambda \Delta \varphi \cos \varphi \pi (\lambda ,\varphi ,1)} } }}, \qquad\end{split} $ |
where the subscript “init” means the initial time step, and “new” the Π revised by the fixer.
The variable q in Eq. (6) represents the specific humidity of the six categories of moisture (water vapor, rain droplets, cloud droplets, cloud ice, snow, and graupel). To avoid the problem of negative water vapor in the numerical integration, the positive-definite piecewise rational method (PRM; Xiao and Peng, 2004) was used to calculate the advection of water substances based on its excellent monotonicity and shape-preserving properties. The dimensional splitting method allowed us to solve the three-dimensional problem with the one-dimensional PRM algorithm. The transport of the cloud fraction, specific humidity, and the number concentration of the six categories of moisture are all predicted with the PRM.
2.2 Physical parameterization schemesThe physical parameterization package implemented in GRAPES_YY is the same as the operational application version of GRAPES. The sub-grid physical processes are considered as forcing terms in the governing equations [Eqs. (1)–(6)], including the long- and shortwave radiative transfer, the PBL turbulent diffusion and surface fluxes, the shallow and deep convection, and the cloud microphysical processes. The short- and longwave radiative fluxes are calculated with the rapid radiation transfer model for general circulation models (RRTMG) (Mlawer et al., 1997; Iacono et al., 2008). The radiative processes include absorption due to water vapor, ozone, carbon dioxide, methane, nitrous oxide, oxygen, halocarbons, and cloud water. The shortwave radiation additionally involves absorption by aerosols and scattering by cloud water droplets and aerosols. Clouds are assumed to have maximum/random overlap in the radiative flux calculations.
The surface turbulent eddy fluxes are solved by an iterative numerical method (Zeng et al., 1998) derived from Monin–Obukhov similarity theory (Beljaars, 1995). The non-local boundary layer vertical diffusion approach of the medium-range forecast (MRF) model (Hong and Pan, 1996) calculates the vertical exchange of heat, momentum, and moisture due to sub-grid scale turbulence. This PBL parameterization uses a counter-gradient flux for θ and q under unstable conditions. It handles vertical diffusion in the mixed layer with a non-local diffusion approach (Troen and Mahrt, 1986) and uses the local-K approach in the free atmosphere (Louis, 1979). The NCEP simplified Arakawa–Schubert (NSAS) convection scheme (Pan and Wu, 1995) based on the widely employed mass flux method (Arakawa and Schubert, 1974;Zhang and McFarlane, 1995; Liu and Ding, 2002) is used for the convective parameterization. The NSAS deep convection scheme has been revised by Han and Pan (2011) to suppress unrealistic grid point storms. The entrainment coefficient is 0.1. The liquid water in the updraft layers is assumed to be detrained from the layers above the level of the minimum moist static energy into cloud water and convective rain with the same conversion parameter of 0.002 m–1. The shallow convection scheme uses a mass flux parameterization, which produces heating (or cooling) throughout the convection layers (Han and Pan, 2011; Liu et al., 2015). The cloud top is limited to p/p
A two-moment mixed-phase cloud microphysics scheme (Hu et al., 1998; Liu et al., 2003; Tan et al., 2013; Ma et al., 2018) explicitly describes the six resolved categories of moisture and the transforming processes. Prognostic variables include the specific humidity of water vapor, cloud droplets, cloud ice, rain, snow, and graupel, and the number concentrations of cloud ice, rain, snow, and graupel. The main microphysical processes include condensation and evaporation, the freezing and melting of ice-phase hydrometeors, and collision growth and automatic conversion among the hydrometeors. The threshold for condensation is set at the level when the relative humidity reaches 80%–85%. The microphysical processes of ice phase and liquid phase is determined by temperature T, for T > 273.15 K only liquid, T < 248.15 K only ice, and both phases exist between 248.15 and 273.15 K. The particle size is determined by Gamma functions, where the associated intercept and slope parameters are derived from the predicted specific humidity and number concentration.
2.3 Configuration of the Aqua Planet ExperimentThe APE is an idealized atmospheric configuration with specified external forcing on a water-covered earth devoid of sea ice, topography, and land. As a surface boundary condition, the SST is simplified to be latitudinally symmetrical about the equator and fixed in time. Hess et al. (1993) designed a group of varying SST profiles and confirmed that the model simulated tropical circulation and ITCZ depend on the distribution of SSTs. Theoretic model of Held and Hou (1980) predicted that the ascending limb of Hadley circulation will exist on the equator when the meridional profile of temperature is steeper than quartic in the tropics, because the circulation must maintain a thermal wind balance that is consistent with the angular momentum conservation. Williamson et al. (2013) reported that tropical circulation and the location of ITCZ under the APE configurations depend on the distribution/gradient of SSTs and the model formulation and, possibly, resolution. In the ATLAS, only three (CCSM-CAM3, pre-HadGAM1, and NSIPP-1) of the 16 models have double structures for the ITCZ in the CONTROL simulation (Fig. 4 in Blackburn et al., 2013), and 15 models (except SAMIL) show clear twin ITCZs in the FLAT (Fig. 5.28 in Williamson, 2012).
To assess the performance of GRAPES_YY on the aqua planet and the sensitivity of this non-hydrostatic model to changes in the SST profile, the CONTROL and FLAT simulations of the APE were considered. As in Neale and Hoskins (2000a), the SST profiles are formulated as:
| ${\rm{SST}} = \left\{ {\begin{array}{*{20}{c}} {27[1 - {{\sin }^2}(\displaystyle\frac{{3\varphi }}{2})], \begin{array}{*{20}{c}} {}&{\displaystyle - \frac{\pi }{3} < \varphi < \displaystyle\frac{\pi }{3}}; \end{array}} \\ {0,\qquad\qquad \!\!\!\!\!\! \begin{array}{*{20}{c}} {}&{}&{}&{} \end{array} \begin{array}{*{20}{c}} {}&{{\rm{otherwise}}}, \end{array}} \end{array}} \right. $ | (7) |
| ${\rm{SST}} = \left\{ {\begin{array}{*{20}{c}} {27[1 - {{\sin }^4}(\displaystyle\frac{{3\varphi }}{2})], \begin{array}{*{20}{c}} {}&{ - \displaystyle\frac{\pi }{3} < \varphi < \displaystyle\frac{\pi }{3}}; \end{array}} \\ {0,\qquad\qquad \!\!\!\!\!\! \begin{array}{*{20}{c}} {}&{}&{}&{} \end{array} \begin{array}{*{20}{c}} {}&{{\rm{otherwise}}}, \end{array}} \end{array}} \right. $ | (8) |
in the CONTROL and FLAT, respectively. Figure 2 shows the zonally averaged SST profiles in these two simulations, which vary with cosine of latitude, in comparison with annual averaged SST (the earth) from the HadISST dataset (Rayner et al., 2003) during 1981–2010. The CONTROL SST is more peaked about the equator than the annual average for the earth. This is expected to force a stronger meridional circulation in the tropics (Blackburn et al., 2013). The FLAT SST has its maximum gradient at about 20° latitude, giving a broad equatorial SST maximum in the tropics and flat profile approaching the equator. At latitudes higher than 20°, the FLAT profile is similar to the annual mean SST for the earth. The equatorial symmetrical insolation is perpetually equinoctial and includes only a diurnal cycle. For simplicity, a 360-day year with fixed-length months is considered. Ozone is specified to have a zonally and meridionally symmetrical latitude–height distribution determined from the annual mean climatology used in the Atmospheric Model Intercomparison Project (AMIP) II (Wang et al., 1995; Liang and Wang, 1996). Other aspects of the experiment configuration, such as the solar constant and radiatively active gases, are the same as those proposed in Blackburn and Hoskins (2013).

|
| Figure 2 Zonal average SST for CONTROL and FLAT experiments, and the annual mean for the earth. |
In the APE simulations, the model is initiated with the real atmospheric climate state for easy dynamic adjustment. The 3-yr mean of the ERA-Interim dataset (Dee et al., 2011) is used for the initial conditions in both simulations. The simulations are performed for 3.5 yr and the last 3 years are used for analysis, omitting the first 6 months as the spin-up period. A time of 3.5 yr is long enough for an AGCM to obtain robust climatology, as evidenced in Medeiros et al. (2016). Both simulations are run for 1° in the horizontal direction and 37 levels in the vertical direction. The model top is set at 32.5 km, and a solid top boundary condition is used in the dynamical core. The time interval of the dynamical core is set as 10 min. Physical parameterization terms are updated at each time step, except for long- and shortwave radiation, which use an interval of 30 min.
3 Numerical results 3.1 PrecipitationFigure 3 shows the simulated daily convective precipitation (CPP), the large-scale precipitation (LSP), and the total precipitation (TPP) of the CONTROL and FLAT simulations. From several randomly chosen daily snapshots, it can be found that the features of precipitation are similar to those on the earth, which are consisted of steady ITCZ rain bands and fast-moving baroclinic rain belts in the midlatitude. One arbitrarily selected representative instant of each simulation is shown in Fig. 3. A significant difference in the precipitation structure between the tropical and midlatitude regions can be observed in both simulations. A zonally oriented structure composed of individual vortices is predominant in the tropics, whereas a baroclinic wave-like meridionally oriented structure is predominant in midlatitudes. Although the same maximum SST is set at 27°C, tropical precipitation in the CONTROL simulation is much stronger than that in FLAT as a result of the different gradient of SST near the equator.
The most salient difference between the two simulations is the single versus twin ITCZ. In the CONTROL simulation, the ITCZ remains as a single peak over the equator. The successive distribution of well-organized tropical rainfall implies a narrow ascent limb of the Hadley cell over the equator. The tropical precipitation and midlatitude baroclinic precipitation are clearly separated by dry zones. Compared with Fig. 1 of Mishra et al. (2011), the ITCZ in the CONTROL simulation in GRAPES_YY is similar to that in the HOMME and the CAM Eulerian Spectral model (CAM-CES), and it is sharper and more confined to the equator than in the finite volume (CAM-FV) model. In the FLAT simulation, the decrease in the tropical SST gradient weakens the convective organization and scatters the tropical precipitation over a wide area that flanks the equator. The ITCZ moves off the equator with a twin structure that is symmetrical about the equator and the dry zone is located on the equator. Baroclinic wave-like systems are found in the region immediately adjacent to the ITCZ. Separation of the TPP into CPP and LSP shows that, in the FLAT simulation, the CPP flanks the ITCZ rather than does the LSP. Neale and Hoskins (2000b) explained that more intense troughs resulting from stronger baroclinicity trigger convection over warmer waters that extend further poleward. The propagation of CPP in the ITCZ is different from that in the baroclinic region, which can be easily distinguished in an animation of daily precipitation (figure omitted). In the FLAT simulation, the distribution of CPP in the tropics and subtropics shows meridional perturbations, indicating the complexity of precipitation in the transitional region where barotropic systems interact with baroclinic systems.

|
| Figure 3 Daily precipitation (mm day–1) for the (a, c, e) CONTROL and (b, d, f) FLAT simulations. (a, b) Total precipitation (TPP), (c, d) convective precipitation (CPP), and (e, f) large-scale precipitation (LSP). |
Precipitation is one of the results of complex interactions among atmospheric circulation, water vapor transport, and the unresolved sub-grid processes in the model, such as moist convection and cloud formation. The time-zonal mean precipitation provides a good overview of the response of the Hadley circulation to changes in the SST profile in the tropics. Figure 4 shows the time-zonally averaged TPP, CPP, and LSP of the two simulations to analyze the meridional distribution of precipitation. The abscissa is set to be a sine function of latitude to highlight the visibility of structures in the tropical and subtropical regions. The tropical TPP in the CONTROL simulation mainly occurs from 5° S to 5° N and reaches a maximum of 35 mm day–1. The rate of tropical precipitation in GRAPES_YY is close to that in NICAM and higher than that in WRF, pre-HadGAM1, and other hydrostatic models (Fig. 4 in Blackburn et al., 2013; Fig. 1 in Yang et al., 2017). The TPP band is broader and weaker in the FLAT simulation than in the CONTROL. In the FLAT, the TPP peak is located at around 10° N with a maximum of about 6 mm day–1. The zonal mean curve is not so smooth as that in the CONTROL due to the scattered distribution of precipitation (Fig. 3d). The transition of the ITCZ structure in response to the variation in SST is different from that in the pre-HadGAM1 (3.75° × 2.5°), which shows a twin ITCZ in both simulations, but it is consistent with most hydrostatic models in the ATLAS. The strength and curve of the tropical FLAT-TPP in GRAPES_YY generally falls within the bounds of other model results in ATLAS (Fig. 5.28 in Williamson, 2012). There is a secondary peak of TPP in midlatitudes in both the CONTROL and FLAT simulations associated with baroclinic waves. This peak reaches 4 mm day–1 at around 40° N in the CONTROL simulation, and it is 12° latitude more poleward in the FLAT with the magnitude slightly dropped. This result is the same as the multi-model mean in the ATLAS. The poleward shift of midlatitude precipitation is consistent with the position of the westerly jets and the baroclinic region (see Fig. 8).
The CPP is the main contributor to the tropical TPP in both simulations, especially in the FLAT that almost all the tropical precipitation is due to convective activities. There are two peaks of LSP in the CONTROL simulation, one over the equator and the other at 40° N. As in Fig. 5.30 in the ATLAS (Williamson, 2012), the midlatitude peak of LSP in the FLAT simulation is at 52° N—that is, 12° latitude more poleward than in the CONTROL simulation. The global average TPP is 2.3 mm day–1 in the CONTROL simulation, where the CPP contributes 0.93 mm day–1 and LSP contributes 1.37 mm day–1 (figure omitted). The global average precipitation is 0.6 mm day–1 less than the CAM-FV at the same resolution (Fig. 1 in Williamson, 2008) and this discrepancy is mainly attributed to the convective component. In the FLAT simulation, the global average TPP is 2.35 mm day–1, whereas the CPP accounts for 0.84 mm day–1 and the LSP accounts for 1.51 mm day–1. The global TPP in the FLAT simulation is slightly larger than that in the CONTROL, which may be a consequence of the higher global average SST. The larger share of CPP in the CONTROL simulation than in the FLAT is most likely to be due to stronger tropical convective activities.

|
| Figure 4 Zonal time averaged (a) total precipitation (TPP), (b) convective precipitation (CPP) and (c) large-scale precipitation (LSP) in the CONTROL (black) and FLAT (red) simulations (mm day–1). |
Because the most significant difference in precipitation between the CONTROL and FLAT simulations occurs in the tropics, the region between 20° S and 20° N is chosen to study the intensity and frequency distribution of tropical precipitation. Figures 5a and 5b separately show the fractions of occurrence of daily precipitation by 1-mm day–1 intervals within 0–120 mm day–1 and by 10-mm day–1 intervals within 0–600 mm day–1. The extreme rainfall in the simulation can also be seen in this figure. The dry zone that flanks the ITCZ in both CONTROL and FLAT runs (see Fig. 3) is included in the statistics. The fraction 0 mm day–1 is the highest in both simulations and accounts for 60% of the total occurrences in the CONTROL and 55% in the FLAT. This implies that little condensation and precipitation occur in the dry zone, and this result is similar to that in models such as CCAM (Conformal-Cubic AtmosphericModel), SAMIL (spectral atmosphere model), and pre-HadGAM1 while different from that in AFES (AGCM For the Earth Simulator), AM2.1 (atmospheric model of the GFDL coupledmodel 2.1), and CAM3. A common feature among GRAPES_YY and the most models is the trend that the fraction of occurrence decreases with the increasing intensity of precipitation. For the smallest non-zero bin (0 < precipitation ≤ 1 mm day –1), the fraction of occurrence reaches about 0.3 in the CONTROL run and 0.2 in the FLAT. The fraction of occurrence from 1 to 66 mm day–1 decreases much faster in the CONTROL than in FLAT simulation. For precipitation > 66 mm day –1, the slope of occurrence in the FLAT becomes steeper than that in the CONTROL. It can be found in Fig. 5b that the maximum precipitation rate is 280 mm day–1 with a frequency of occurrence at 7 × 10–8 in the FLAT simulation and reaches 350 mm day–1 in the CONTROL with a frequency at 2 × 10–7.
The water vapor budget during the 3.5-yr integration is mirrored by the evaporation minus precipitation (EMP) calculated from the time series of the daily global average and shown as bar plots in Fig. 5c. The whiskers denote the temporal standard deviation of the EMP. The balance between precipitation and evaporation is generally maintained in the 3.5-yr integration, with an EMP of –0.022 mm day–1 in the CONTROL and –0.012 mm day–1 in the FLAT simulation. It shows a net decrease in water vapor in the model atmosphere. This negative residual is mainly a result of surface evaporation in the ocean surface model and partially the result of interpolation from the Yin–Yang grid to the Lat–Lon grid in the post-processing procedure. No conservative constraint is implemented to ensure global water vapor conservation. The standard deviation of the EMP time series (0.016 and 0.015 in the CONTROL and FLAT simulations, respectively) shows large variations in evaporation and condensation on a global scale.

|
| Figure 5 (a, b) Fractional occurrence of the daily precipitation from 20° S to 20° N at 1-mm day–1 intervals within 0–120 mm day–1 and at 10-mm day–1 intervals within 0–600 mm day–1, and (c) global temporal average of evaporation minus precipitation (EMP). |
Figure 6 shows the longitude–time diagrams of the propagation of tropical rainfall in both simulations. The precipitation is averaged between 5°S and 5°N in the CONTROL simulation. Considering that the ITCZ location shifts poleward in the FLAT simulation, we chose the average region over 5°–15°N. The model shows a clear difference in the propagation characteristics of tropical rainfall cells between the CONTROL and FLAT simulations. In the CONTROL simulation (Fig. 6a), the precipitation shows an eastward movement of rain bands, with some westward-propagating smaller scale cells. This characteristic of wave propagation agrees well with models such as pre-HadGAM1, CAM3, and NICAM in Blackburn et al. (2013). Rain bands and intensive rainfall indicate well-organized convection in the tropical zone. In the FLAT simulation (Fig. 6b), the precipitation shows westward propagation of both the rain bands and the convective-scale cells in the off-equator region. Weak organization of convection can be observed in the FLAT. The phase speed is much slower than in the CONTROL.
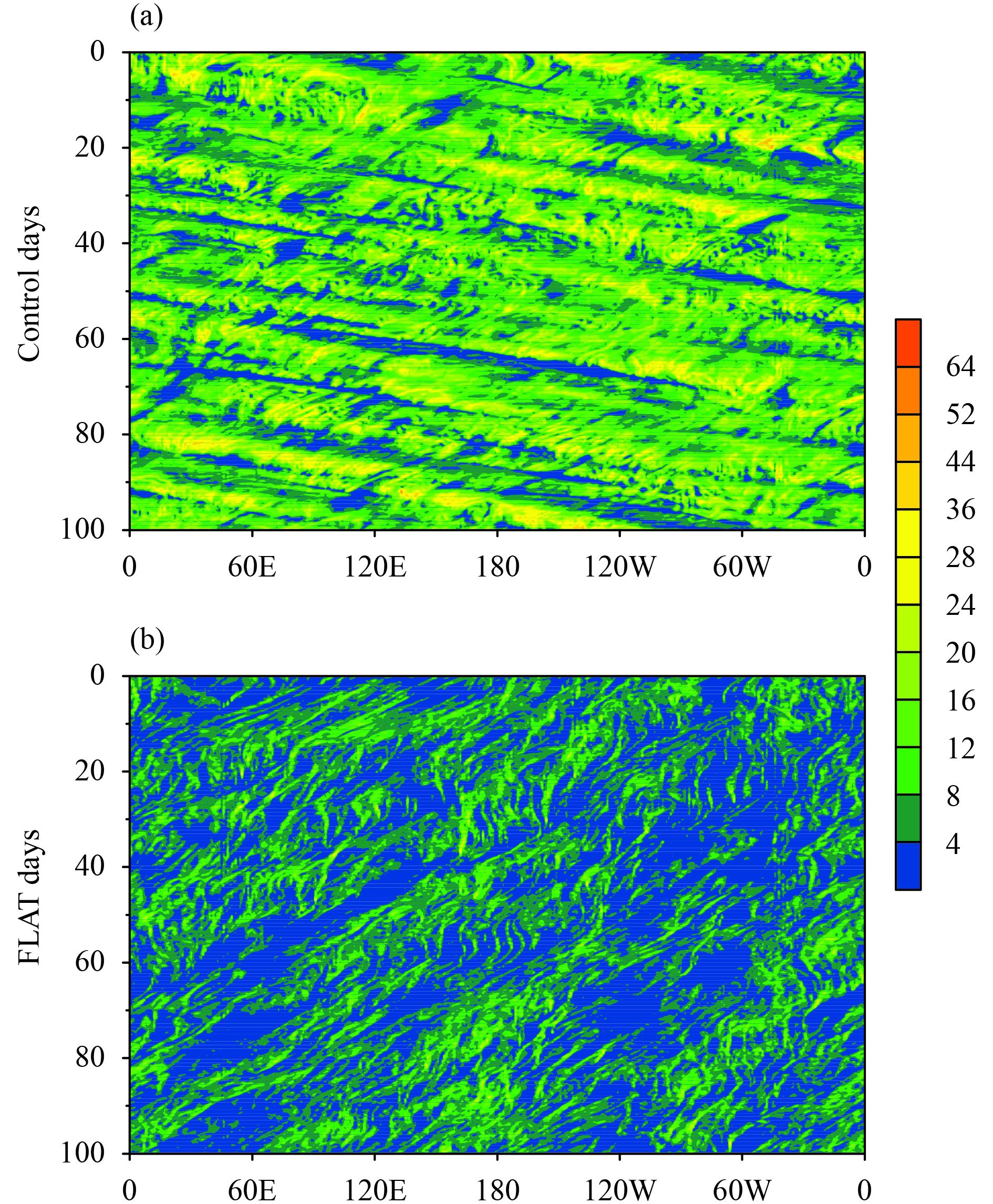
|
| Figure 6 Longitude–time diagrams of tropical precipitation (mm day–1). (a) Average tropical precipitation from 5°S to 5°N in the CONTROL simulation and (b) average tropical precipitation from 5° to 15°N in the FLAT simulation. |
To quantify the zonal waves of tropical precipitation, wavenumber–frequency analysis is carried out with the methodology of Wheeler and Kiladis (1999) using the 6-h precipitation between 20°S and 20°N (Fig. 7). The temporal window is set as 96 days and successively overlaps by 60 days. The logarithm of the full power of the symmetrical component in the CONTROL and FLAT simulations is shown in Figs. 7a, c; and Figs. 7b, d show the normalized spectra with the background spectrum removed. In general, the equatorial wave modes are embedded in a background spectrum in which the power increases with period. In both the CONTROL and FLAT simulations, most of the total power projects onto the westward-propagating equatorial Rossby (ER) mode. In the CONTROL simulation, the westward-propagating ER mode peaks at frequencies of about 0.04 cycles day–1 and wavenumbers 1–4, and it extends to higher frequencies of around 0.1 cycles day–1. Eastward-propagating Kelvin modes are also predominant in the CONTROL simulation and can be seen in the normalized power spectra in Fig. 7b. Eastward-propagating Kelvin waves have most of their variance centered on an equivalent depth of about 50 m. Almost no indication of eastward-propagating Kelvin modes can be found in the FLAT. The precipitation in the off-equator ITCZs does not couple with the equatorial Kelvin waves, but it shows obvious westward-propagating ER wave pattern.

|
| Figure 7 Symmetrical components of the wavenumber–frequency distribution of precipitation between 20°S and 20°N for (a) the CONTROL and (c) FLAT simulations. (b, d) Normalized spectra with the background spectrum removed. |
The precipitation patterns are closely connected with the large-scale circulation status (Stevens and Bony, 2013). To obtain a comprehensive insight into the general circulation in GRAPES_YY simulations, the last 1-yr time-zonal mean quantities—including the temperature, zonal wind, stream function, and specific humidity—and their standard deviations derived from the average of the last 12 months are plotted in Fig. 8. The Northern and Southern Hemispheres are averaged together because of the latitudinal symmetrical distribution of the time-zonal mean quantities, which is expected the hemispheric symmetry of external forcings. The modest standard deviation of each quantity in the third year indicates the robustness of the model.
The distribution of temperature (Fig. 8a) is similar to that in both the hydrostatic and non-hydrostatic models in the ATLAS (Figs. 4.19 and 5.70 in Williamson, 2012). In the CONTROL simulation, the maximum gradient of temperature occurs at about 30° latitude. The temperature difference between the equator and midlatitudes is about 25 K at the surface and reduces to about 5 K from midlatitudes to the poles. The maximum temperature between 800 and 600 hPa is located off the equator in the CONTROL simulation. This may be attributed to the strong tropical upward motion of the Hadley cell in the lower troposphere and a weak divergent flow at about 700 hPa. The strong tropical ascending motion between 900 and 700 hPa facilitates the upward transport of water vapor. Abundant condensation and the release of latent heat (see Fig. 10) are observed in the lower troposphere on the equator. The 800–600-hPa divergent flow (Fig. 8c) over the equator transports heated air poleward to 10° latitude. A peak appears when the vertical mixing of heat by the boundary layer turbulence is weak. In Blackburn et al. (2013), all models except MIT-GCM also show compensated divergent flow to some degree above the low level convergent flow, and a convergent flow below the 200-hPa divergent flow. In the lower stratosphere, the temperature increases by about 20 K from the equator to 40° latitude and then decreases further poleward. Compared with the CONTROL simulation, the FLAT shows maximum surface temperature from the equator to 25° latitude. The location of maximum temperature gradient in horizontal shifts poleward to about 55° latitude. The standard deviation increases with height in the CONTROL simulation, with a maximum near the model top at 55° latitude. In the troposphere, the local maximum at each level is generally co-located with the largest temperature gradient. The standard deviation in the FLAT simulation is less than that in the CONTROL and mainly appears over the polar region.
Figure 8b shows the time-zonal mean of the zonal winds. In both the CONTROL and FLAT simulations, the strongest vertical gradient of the zonal wind is located at the same position as the largest latitudinal gradient in temperature. It is clearly associated with the establishment of a thermal wind balance in these regions. The westerly jet core of the CONTROL is located at 200 hPa at 30° latitude and reaches a maximum of 62 m s–1. The location of the westerly jet core is the same in GRAPES_YY and the other models, and the strength of the jet core falls between that of hydrostatic models such as CAM4 (Fig. 16 in Mishra et al., 2011) and the non-hydrostatic NICAM model (Fig. 4.17 in Williamson, 2012). The maximum low-level westerly wind speed is about 15 m s–1 at 35° and 6° latitudes poleward of the upper level jet core.
In the FLAT simulation, the westerly jet core at about 30° latitude is 30 m s–1 and another core of 30 m s–1 appears at 50° latitude. One direct reason for the weaker jet core at 30° latitude is due to the poleward shift of the maximum horizontal SST gradient from 30° latitude (CONTROL) to 40° latitude (FLAT), where the thermal wind peak appears. The increased Coriolis parameter weakens the thermal wind in the midlatitudes of the FLAT (Williamson et al., 2013). Consequently, a poleward shift and weakening of precipitation occur in midlatitudes (Fig. 3). The westerly jet core in the CONTROL simulation tilts to the equator with increasing height, whereas it is upright in the FLAT. It can be inferred that the effect of the tropical overturning circulation weakens from the CONTROL to FLAT simulations, where the midlatitude eddy force dominates (Fig. 9). In both the CONTROL and FLAT simulations, the standard deviation of the zonal wind in the troposphere appears both poleward and equatorward of the jet core, where there is a strong wind gradient. Animation of the monthly mean zonal wind shows that the deviation is mainly associated with the slight meridional shift of the jet, rather than the width of the jet. In the CONTROL simulation, another standard deviation peak is seen at the model top, which may be related to the solid top boundary condition in GRAPES_YY.
The width and strength of the meridional circulation are characterized by the meridional stream function in Fig. 8c. The ascending limb of the Hadley cell moves off the equator to 10° latitude when the SST changes from the CONTROL to FLAT simulations. In the CONTROL, the maximum meridional stream function is 24 × 1010 kg s–1 at 4° latitude, which is 7 × 1010 kg s–1 stronger than the QOBS simulation in CAM5 (a moderate SST pattern between the CONTROL and FLAT) (Medeiros et al., 2015). In the FLAT simulation, the maximum meridional stream function is 7 × 1010 kg s–1 at 15° latitude. The width of the Hadley circulation is determined by the location at which the stream function equals 0. It vanishes at 26° latitude in the CONTROL simulation and at 35° latitude in the FLAT. The QOBS simulations in Medeiros et al. (2015) also show that the Hadley circulation weakens and widens with warmer SSTs and the magnitudes of weakening and widening vary across models. The standard deviations of the stream function are distributed in a similar manner to their temporal means.
The Hadley cell in the CONTROL is stronger than other hydrostatic models, and the tropical convective precipitation and convective heating are more intense. Possible contributions to the differences may stem from the cumulus parameterization schemes and nonhydrostatic effects. As pointed out by Han and Pan (2011), the NSAS convection scheme tends to make cumulus convection stronger and deeper, the tropical precipitation and convective heating also become stronger. The monthly mean tropical precipitation by GRAPES global model at 0.5° × 0.5° resolution are stronger than the observation from Tropical Rainfall Measuring Mission (TRMM) satellite (Liu et al., 2015). In addition, the statistical results indicated that the NCEP-GFS models using the NSAS scheme, both T62 and T126, have positive bias in precipitation as compared to the observation (Lien et al., 2016). In addition, the tropical non-hydrostatic dynamics should not be ignored, since the strong convection and vertical velocity can be found in the aqua planet CONTROL run, which may be connected with super-cloud clusters that cover thousands of kilometers. The 3.5-km CONTROL simulation by NICAM displays super-cloud clusters that are tightly coupled to convective systems, and the vertical velocity in cloud exists 1 m s–1 (Tomita et al., 2005; Nasuno et al., 2008; Nasuno and Satoh, 2011). The tropical precipitation of CONTROL simulated by the non-hydrostatic WRF at 36-km horizontal resolution is also stronger than by the hydrostatic version (Yang et al., 2017). Similar precipitation difference appears among the CONTROL simulations by the non-hydrostatic CAM-CEU (Eulerian/semi-Lagrangian fluid solver) at 2.5° × 2.5° resolution and the hydrostatic CAM-FV (2.5° × 2.5°) and CAM-CES (T42) (Abiodun et al., 2008).
The climatology of water vapor is shown as the time zonal mean specific humidity in Fig. 8d. The specific humidity of water vapor maximizes in the surface layer in both simulations and decreases with latitude and altitude because surface evaporation occurs at the lowest model level. The maximum specific humidity in the CONTROL simulation exceeds 18 g kg–1 at the equator and the quantity only reaches to 16 g km–1 at 10° latitude in the FLAT simulation. The water vapor in the troposphere is redistributed by the meridional circulation and the troposphere becomes moister in the convergence zone and drier in the divergence zone.

|
| Figure 8 Zonal time averaged (a) temperature (K), (b) zonal wind (m s–1), (c) stream function (1010 kg s–1), and (d) specific humidity (g kg–1) for the CONTROL and FLAT simulations (contours), and the standard deviation (color shading) of the average of the last 12 months. |
Figure 9 shows the zonal mean eddy statistics that reflect the midlatitude baroclinic activities in the GRAPES_YY simulation. The eddy kinetic energy (EKE), meridional eddy momentum flux (EMF), and eddy heat flux (EHF) at different vertical levels are shown in Figs. 9a–c, respectively. The EKE and EMF are vertically coherent and are mainly concentrated in the upper troposphere (consistent with the results of Ait-Chaalal and Schneider, 2015). The EKE has a maximum at 30° latitude in the CONTROL simulation and at 50° latitude in the FLAT. The peak EKE increases with height. In the CONTROL simulation, another poleward maximum (at 47° latitude) flanking the westerly jet decreases with height in the lower troposphere. This pattern shows the EKE source at the polar side of the westerly jet in the lower troposphere and at the equatorial side in the upper troposphere, which is different from the results obtained by QOBS in CAM5 (Fig. 5 in Medeiros et al., 2015). The EMF shows a peak on the equatorward flank of the EKE throughout the troposphere, at about 28° latitude in the CONTROL and 40° latitude in the FLAT simulations. A larger EMF is observed in the FLAT simulation than in the CONTROL simulation, the same as in Fig. 5.132 in the ATLAS (Williamson, 2012). It can be inferred that a greater conversion of momentum is needed to maintain a more poleward westerly belt. The vertical structure of the EHF (Fig. 9c) is more baroclinic than that of the EMF, similar to the results of Thompson and Woodworth (2014). The magnitude of the EHF is higher in the lower troposphere than in the upper troposphere.

|
| Figure 9 Zonal mean of (a) the eddy kinetic energy (m2 s–2), (b) the meridional eddy momentum flux (m2 s–2), and (c) the meridional eddy heat flux (K m s–1) at 850, 700, 500, and 250 hPa. Solid curves show the CONTROL simulation and the dashed curves show the FLAT simulation. |
The parameterized thermodynamic forcing required to maintain the large-scale circulation is mainly illustrated by the temperature tendency and the specific humidity tendency (Fig. 10). The largest difference in heating between the CONTROL and FLAT simulations is seen in the tropics (Fig. 10a) and is associated with convective activities and cloud parameterization. The strong tropical convection in the CONTROL simulation is consistent with the ITCZ and brings up to 16 K day–1 of convective heating and 7 g kg–1 day–1 of negative humidity tendency in this region. The convective temperature tendency is about 6 K day–1 higher than that obtained in the pre-HadGAM1 and other hydrostatic models in the ATLAS. In the FLAT simulation, the maximum convective heating is only 4 K day–1 at 10° latitude. The non-adiabatic cooling between 800 and 900 hPa is dominated by longwave radiative cooling of the low-level clouds in the subtropics. These low-level clouds in the CONTROL simulation are shallow cumulus clouds and occur on the earth in similar dynamical environments (Medeiros and Stevens, 2011).
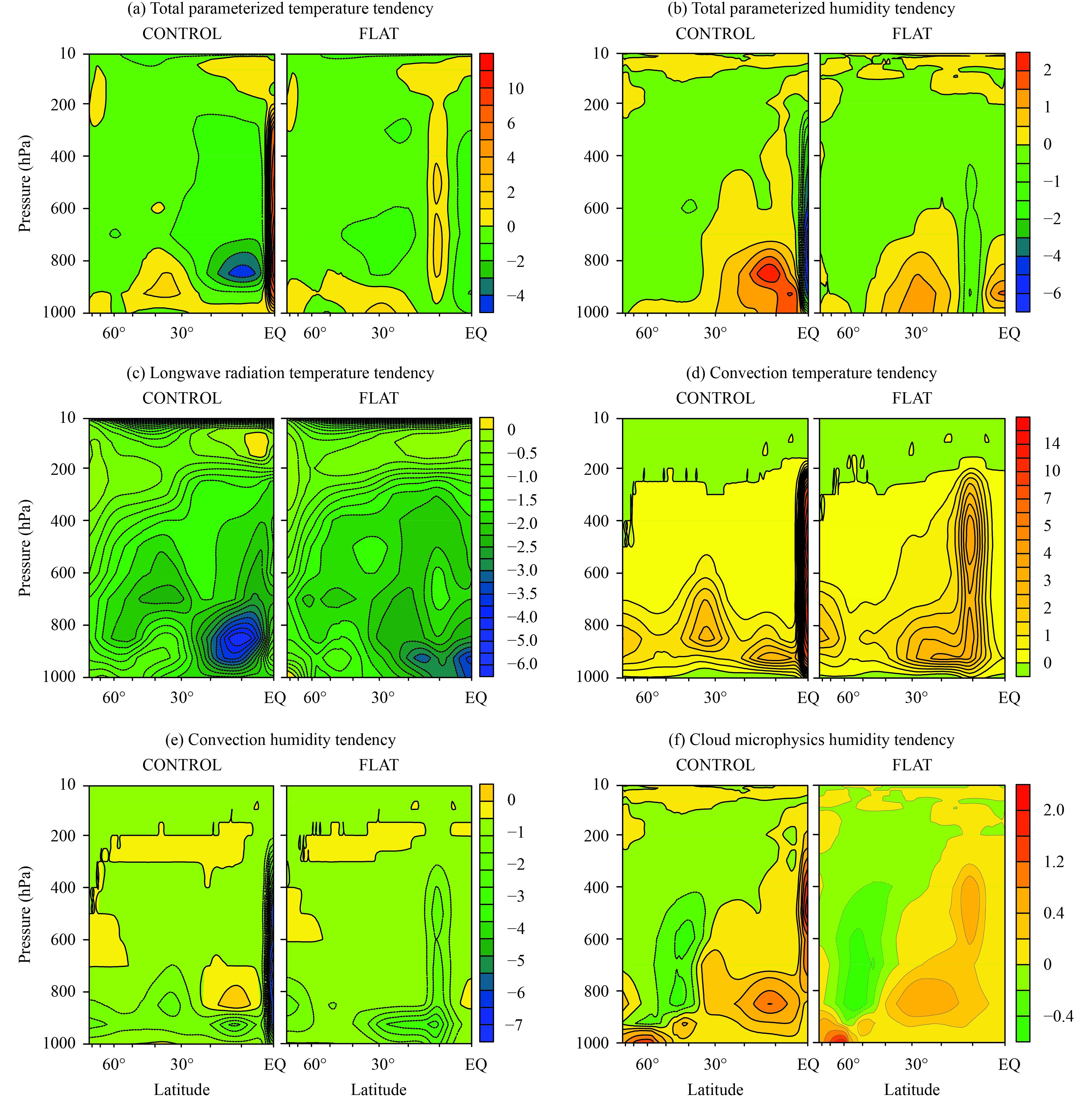
|
| Figure 10 (a) Time zonal mean of parameterized temperature tendency (K day–1), and that due to (c) longwave radiation and (d) convection. (b) Total parameterized humidity tendency of water vapor (g kg–1 day–1), and that due to (e) convection and (f) cloud microphysics. |
This study investigates the feasibility of the long-term integration of GRAPES_YY on the aqua planet. The global non-hydrostatic GRAPES_YY model has been developed with the implementation of a physical parameterization package into a dynamical core based on the Yin–Yang grid. The physical package includes the rapid longwave and shortwave radiation transfer model for GCMs, the medium-range forecast boundary layer turbulent scheme, the Arakawa–Schubert cumulus convection scheme, and the two-moment mixed-phase cloud microphysics scheme. Long-term integrations are completed on the aqua planet using CONTROL and FLAT SST profiles, separately. Precipitation and general circulation of both simulations are analyzed and compared with other models to assess the reasonability and fidelity of the simulation. The GRAPES_YY simulations also provide supplementary information about the performance of non-hydrostatic models on the aqua planet.
The daily distribution and the time-zonal mean of precipitation show a strong single ITCZ located over the equator in the CONTROL simulation, which is much stronger and more confined to the equator than in the pre-HadGAM1 and other hydrostatic models. The most intense precipitation occurs over the equator in the CONTROL simulation and reaches 350 mm day–1. Very little rainfall occurs in the dry zone. The ITCZ precipitation belt is weaker and moves off the equator with a twin structure symmetrical about the equator when the tropical gradient of the SST decreases in the FLAT simulation.
Very different propagation features of the tropical precipitation are observed in the CONTROL and FLAT simulations. The CONTROL shows tropical precipitation bands moving eastward, with some envelopes of westward convective-scale disturbance. Less organized westward-propagating rainfall cells and bands are seen in the FLAT simulation. The wavenumber–frequency analysis of the tropical precipitation shows that the equatorial wave activities tend to decrease from the CONTROL to FLAT simulations. Westward-propagating equatorial Rossby waves are predominant in both simulations. In the CONTROL simulation, the eastward propagation projects onto the Kelvin modes, but it is very weak in the FLAT.
The sensitivity of GRAPES_YY in response to the variation in the SST profile is also reflected in the general circulation. The equatorial ascent limb in the CONTROL simulation is more poleward than in the FLAT simulation and the corresponding adjustments occur in the westerly jet and temperature. The location of the westerly jet core is the same in GRAPES_YY and the other models and the strength of the jet core falls between that of hydrostatic models such as CAM4 and the non-hydrostatic NICAM. The EKE and EMF play an important part in maintaining the westerly jet and are vertically coherent and mainly concentrated in the upper troposphere. In the CONTROL simulation, the EKE source comes from the polar side in the lower troposphere and from the equatorial side in the upper troposphere.
In general, aspects of the precipitation and large-scale circulation in GRAPES_YY fall within the bounds of other model simulations. The stronger ITCZ, convective heating, and Hadley circulation in the CONTROL simulation may be due to the combination of intensely parameterized convection and non-hydrostatic effects. The NSAS convection scheme tends to make cumulus convection stronger and deeper, and the tropical precipitation and convective heating also become stronger. Moreover, the tropical non-hydrostatic dynamics should not be ignored, since strong convection and vertical motion can be found in the CONTROL run, which may be connected with super-cloud clusters that cover thousands of kilometers.
Acknowledgments. We appreciate the editors and the anonymous reviewers’ constructive comments and valuable suggestions. We would like to thank Qijun Liu, Xingliang Li, and Zhanshan Ma for their help in developing the model code and providing insightful comments on the manuscript.
| Abiodun, B. J., J. M. Prusa, and W. J. Gutowski Jr, 2008: Implementation of a non-hydrostatic, adaptive-grid dynamics core in CAM3. Part I: Comparison of dynamics cores in aqua-planet simulations. Climate Dyn., 31, 795–810. DOI:10.1007/s00382-008-0381-y |
| Ait-Chaalal, F., and T. Schneider, 2015: Why eddy momentum fluxes are concentrated in the upper troposphere. J. Atmos. Sci., 72, 1585–1604. DOI:10.1175/JAS-D-14-0243.1 |
| Allen, T., and M. Zerroukat, 2016: A deep non-hydrostatic compressible atmospheric model on a Yin–Yang grid. J. Comput. Phys., 319, 44–60. DOI:10.1016/j.jcp.2016.05.022 |
| Arakawa, A., and W. H. Schubert, 1974: Interaction of a cumulus cloud ensemble with the large-scale environment, Part I. J. Atmos. Sci., 31, 674–701. DOI:10.1175/1520-0469(1974)031<0674:IOACCE>2.0.CO;2 |
| Arakawa, A., and V. R. Lamb, 1997: Computational design of the basic dynamical processes of the UCLA General Circulation Model. Methods Comput. Phys. Adv. Res. Appl., 17, 173–265. DOI:10.1016/B978-0-12-460817-7.50009-4 |
| Baba, Y., K. Takahashi, and T. Sugimura, 2010: Dynamical core of an atmospheric general circulation model on a Yin–Yang grid. Mon. Wea. Rev., 138, 3988–4005. DOI:10.1175/2010MWR3375.1 |
| Beljaars, A. C. M., 1995: The parametrization of surface fluxes in large-scale models under free convection. Quart. J. Roy. Meteor. Soc., 121, 255–270. DOI:10.1002/qj.49712152203 |
| Blackburn, M., and B. J. Hoskins, 2013: Context and aims of the Aqua-Planet Experiment. J. Meteor. Soc. Japan, 91, 1–15. DOI:10.2151/jmsj.2013-A01 |
| Blackburn, M., D. L. Williamson, K. Nakajima, et al., 2013: The Aqua-Planet Experiment (APE): CONTROL SST simulation. J. Meteor. Soc. Japan, 91, 17–56. DOI:10.2151/jmsj.2013-A02 |
| Charney, J. G., and N. A. Phillips, 1953: Numerical integration of the quasi-geostrophic equations for barotropic and simple baroclinic flows. J. Meteor., 10, 71–99. DOI:10.1175/1520-0469(1953)010<0071:NIOTQG>2.0.CO;2 |
| Chen, D. H., J. S. Xue, X. S. Yang, et al., 2008: New generation of multi-scale NWP system (GRAPES): General scientific design. Chinese Sci. Bull., 53, 3433–3445. DOI:10.1007/s11434-008-0494-z |
| Dee, D. P., S. M. Uppala, A. J. Simmons, et al., 2011: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Quart. J. Roy. Meteor. Soc., 137, 553–597. DOI:10.1002/qj.828 |
| Dennis, J., A. Fournier, W. F. Spotz, et al., 2005: High-resolution mesh convergence properties and parallel efficiency of a spectral element atmospheric dynamical core. Int. J. High Perform. Comput. Appl., 19, 225–235. DOI:10.1177/1094342005056108 |
| Han, J., and H. L. Pan, 2011: Revision of convection and vertical diffusion schemes in the NCEP Global Forecast System. Wea. Forecasting, 26, 520–533. DOI:10.1175/WAF-D-10-05038.1 |
| Held, I. M., and A. Y. Hou, 1980: Nonlinear axially symmetric circulations in a nearly inviscid atmosphere. J. Atmos. Sci., 37, 515–533. DOI:10.1175/1520-0469(1980)037<0515:NASCIA>2.0.CO;2 |
| Hess, P. G., D. S. Battisti, and P. J. Rasch, 1993: Maintenance of the intertropical convergence zones and the large-scale tropical circulation on a water-covered earth. J. Atmos. Sci., 50, 691–713. DOI:10.1175/1520-0469(1993)050<0691:MOTICZ>2.0.CO;2 |
| Hong, S. Y., and H. L. Pan, 1996: Nonlocal boundary layer vertical diffusion in a medium-range forecast model. Mon. Wea. Rev., 124, 2322–2339. DOI:10.1175/1520-0493(1996)124<2322:NBLVDI>2.0.CO;2 |
| Hu, Z. J., X. F. Lou, S. W. Bao, et al., 1998: A simplified explicit scheme of phase-mixed cloud and precipitation. Quart. J. Appl. Meteor., 9, 257–264. |
| Iacono, M. J., J. S. Delamere, E. J. Mlawer, et al., 2008: Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos., 113, D13103. DOI:10.1029/2008JD009944 |
| Jablonowski, C., P. H. Lauritzen., R. D. Nair, et al., 2008: Idealized test cases for the dynamical cores of atmospheric general circulation models: A proposal for the NCAR ASP 2008 summer colloquium. [Available online at http://esse.engin. umich.edu/admg/publications.php] |
| Kageyama, A., and T. Sato, 2004: " Yin–Yang grid”: An overset grid in spherical geometry. Geochem. Geophys. Geosyst., 5, Q09005. DOI:10.1029/2004GC000734 |
| Li, X. H., X. D. Peng, and X. L. Li, 2015: An improved dynamic core for a non-hydrostatic model system on the Yin–Yang grid. Adv. Atmos. Sci., 32, 648–658. DOI:10.1007/s00376-014-4120-5 |
| Li, X. L., D. H. Chen, X. D. Peng, et al., 2006: Implementation of the semi-lagrangian advection scheme on a quasi-uniform overset grid on a sphere. Adv. Atmos. Sci., 23, 792–801. DOI:10.1007/s00376-006-0792-9 |
| Li, X. L., D. H. Chen, X. D. Peng, et al., 2008: A multimoment finite-volume shallow-water model on the Yin–Yang overset spherical grid. Mon. Wea. Rev., 136, 3066–3086. DOI:10.1175/2007MWR2206.1 |
| Liang, X. Z., and W. C. Wang, 1996: Atmospheric ozone climatology for use in General Circulation Models. PCMDI Report No. 43: UCRL-MI-125650; 25 pp. [Accessible online at https://pcmdi.llnl.gov/mips/amip/AMIP2EXPDSN/OZONE/OZONE2/o3wangdoc.html] |
| Lien, G. Y., E. Kalnay, T. Miyoshi, et al., 2016: Statistical properties of global precipitation in the NCEP GFS model and TMPA observations for data assimilation. Mon. Wea. Rev., 144, 663–679. DOI:10.1175/MWR-D-15-0150.1 |
| Liu, K., Q. Y. Chen, and J. Sun, 2015: Modification of cumulus convection and planetary boundary layer schemes in the GRAPES global model. J. Meteor. Res., 29, 806–882. DOI:10.1007/s13351-015-5043-5 |
| Liu, Y. M., and Y. H. Ding, 2002: Modified mass flux cumulus convective parameterization scheme and its simulation experiment. Part I: Mass flux scheme and its simulation of the 1991 flood event. Acta Meteor. Sinica, 16, 37–49. |
| Liu, Q. J., Z. J. Hu, and X. J. Zhou, 2003: Explicit cloud schemes of HLAFS and simulation of heavy rainfall and clouds. Part I: Explicit cloud schemes. J. Appl. Meteor. Sci., 14, 60–67. DOI:10.3969/j.issn.1001-7313.2003.z1.008 |
| Lock, A. P., A. R. Brown, M. R. Bush, et al., 2000: A new boundary layer mixing scheme. Part I: Scheme description and single-column model tests. Mon. Wea. Rev., 128, 3187–3199. DOI:10.1175/1520-0493(2000)128<3187:ANBLMS>2.0.CO;2 |
| Louis, J. F., 1979: A parametric model of vertical eddy fluxes in the atmosphere. Bound.-Layer Meteor., 17, 187–202. DOI:10.1007/BF00117978 |
| Ma, Z. S., Q. J. Liu., C. F. Zhao, et al., 2018: Application and evaluation of an explicit prognostic cloud-cover scheme in GRAPES global forecast system. J. Adv. Model. Earth Syst., 10, 652–667. DOI:10.1002/2017MS001234 |
| Medeiros, B., and B. Stevens, 2011: Revealing differences in GCM representations of low clouds. Climate Dyn., 36, 385–399. DOI:10.1007/s00382-009-0694-5 |
| Medeiros, B., B. Stevens, and S. Bony, 2015: Using aquaplanets to understand the robust responses of comprehensive climate models to forcing. Climate Dyn., 44, 1957–1977. DOI:10.1007/s00382-014-2138-0 |
| Medeiros, B., D. L. Williamson, and J. G. Olson, 2016: Reference aquaplanet climate in the Community Atmosphere Model, Version 5. J. Adv. Model. Earth Syst., 8, 406–424. DOI:10.1002/2015MS000593 |
| Mishra, S. K., M. A. Taylor, R. D. Nair, et al., 2011: Evaluation of the HOMME dynamical core in the aquaplanet configuration of NCAR CAM4: Rainfall. J. Climate, 24, 4037–4055. DOI:10.1175/2011JCLI3860.1 |
| Mlawer, E. J., S. J. Taubman, P. D. Brown, et al., 1997: Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos., 102, 16663–16682. DOI:10.1029/97JD00237 |
| Nasuno, T., and M. Satoh, 2011: Properties of precipitation and in-cloud vertical motion in a global nonhydrostatic aquaplanet experiment. J. Meteor. Soc. Japan, 89, 413–439. DOI:10.2151/jmsj.2011-502 |
| Nasuno, T., H. Tomita, S. Iga, et al., 2008: Convectively coupled equatorial waves simulated on an aquaplanet in a global nonhydrostatic experiment. J. Atmos. Sci., 65, 1246–1265. DOI:10.1175/2007JAS2395.1 |
| Neale, R. B., and B. J. Hoskins, 2000a: A standard test for AGCMs including their physical parametrizations. I: The proposal. Atmos. Sci. Lett., 1, 101–107. DOI:10.1006/asle.2000.0022 |
| Niu, Y. J., X. D. Peng, and G. Z. Fan, 2017: Impact of the three-dimensional Coriolis force in GRAPES model. Acta. Meteor. Sinica, 76, 473–484. DOI:10.11676/qxxb2018.003 |
| Neale, R. B., and B. J. Hoskins, 2000b: A standard test for AGCMs including their physical parametrizations. II: Results for the Met Office model. Atmos. Sci. Lett., 1, 108–114. DOI:10.1006/asle.2000.0024 |
| Pan, H. L., and W. S. Wu, 1995: Implementing a mass flux convection parameterization package for the NMC Medium-Range Forecast model. NMC Office Note 409, 40 pp |
| Qaddouri, A., and V. Lee, 2011: The Canadian global environmental multiscale model on the Yin–Yang grid system. Quart. J. Roy. Meteor. Soc., 137, 1913–1926. DOI:10.1002/qj.873 |
| Qaddouri, A., L. Laayouni, L. Loisel, et al., 2008: Optimized Schwarz methods with an overset grid for the shallow-water equations: Preliminary results. Appl. Numer. Math., 58, 459–471. DOI:10.1016/j.apnum.2007.01.015 |
| Qian, J., F. H. M. Semazzi, and J. S. Scroggs, 1998: A global nonhydrostatic semi-lagrangian atmospheric model with orography. Mon. Wea. Rev., 126, 747–771. DOI:10.1175/1520-0493(1998)126<0747:AGNSLA>2.0.CO;2 |
| Rayner, N. A., D. E. Parker, E. B. Horton, et al., 2003: Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmos., 108, 4407. DOI:10.1029/2002JD002670 |
| Sadourny, R., 1972: Conservative finite-difference approximations of the primitive equations on quasi-uniform spherical grids. Mon. Wea. Rev., 100, 136–144. DOI:10.1175/1520-0493(1972)100<0136:CFAOTP>2.3.CO;2 |
| Sadourny, R., A. Arakawa, and Y. Mintz, 1968: Integration of the nondivergent barotropic vorticity equation with an icosahedral-hexagonal grid for the sphere. Mon. Wea. Rev., 96, 351–356. DOI:10.1175/1520-0493(1968)096<0351:IOTNBV>2.0.CO;2 |
| Semazzi, F. H. M., J. H. Qian, and J. S. Scroggs, 1995: A global nonhydrostatic semi-lagrangian atmospheric model without orography. Mon. Wea. Rev., 123, 2534–2550. DOI:10.1175/1520-0493(1995)123<2534:AGNSLA>2.0.CO;2 |
| Shen, X. S., Y. Su, J. L. Hu, et al., 2017: Development and operation transformation of GRAPES global middle-range forecast system. J. Appl. Meteor. Sci., 28, 1–10. DOI:10.11898/1001-7313.20170101 |
| Stevens, B., and S. Bony, 2013: What are climate models missing?. Science, 340, 1053–1054. DOI:10.1126/science.1237554 |
| Tan, C., Q. J. Liu, and Z. S. Ma, 2013: Influences of sub-grid convective processes on cloud forecast in the GRAPES global model. Acta Meteor. Sinica, 71, 867–878. DOI:10.11676/qxxb2013.067 |
| Taylor, M. A., J. Edwards, S. Thomas, et al., 2007: A mass and energy conserving spectral element atmospheric dynamical core on the cubed-sphere grid. J. Phys. Conf. Ser., 78, 012074. DOI:10.1088/1742-6596/78/1/012074 |
| Thompson, D. W. J., and J. D. Woodworth, 2014: Barotropic and baroclinic annular variability in the Southern Hemisphere. J. Atmos. Sci., 71, 1480–1493. DOI:10.1175/JAS-D-13-0185.1 |
| Tomita, H., and M. Satoh, 2004: A new dynamical framework of nonhydrostatic global model using the icosahedral grid. Fluid Dyn. Res., 34, 357–400. DOI:10.1016/j.fluiddyn.2004.03.003 |
| Tomita, H., H. Miura, S. Iga, et al., 2005: A global cloud-resolving simulation: Preliminary results from an aqua planet experiment. Geophys. Res. Lett., 32, L08805. DOI:10.1029/2005GL022459 |
| Troen, I. B., and L. Mahrt, 1986: A simple model of the atmospheric boundary layer; sensitivity to surface evaporation. Bound.-Layer Meteor., 37, 129–148. DOI:10.1007/BF00122760 |
| Wang, W. C., X. Z. Liang, M. P. Dudek, et al., 1995: Atmospheric ozone as a climate gas. Atmos. Res., 37, 247–256. DOI:10.1016/0169-8095(94)00080-W |
| Wang, Z. Z., J. Y. Mao, and G. X. Wu, 2008: The wavenumber-frequency characteristics of the tropical waves in an aqua-planet GCM. Adv. Atmos. Sci., 25, 541–554. DOI:10.1007/s00376-008-0541-3 |
| Wheeler, M., and G. N. Kiladis, 1999: Convectively coupled equatorial waves: Analysis of clouds and temperature in the wavenumber-frequency domain. J. Atmos. Sci., 56, 374–399. DOI:10.1175/1520-0469(1999)056<0374:CCEWAO>2.0.CO;2 |
| Whitehead, J. P., C. Jablonowski, R. B. Rood, et al., 2011: A stability analysis of divergence damping on a latitude–longitude grid. Mon. Wea. Rev., 139, 2976–2993. DOI:10.1175/2011MWR3607.1 |
| Williamson, D. L., 2007: The evolution of dynamical cores for global atmospheric models. J. Meteor. Soc. Japan, 85, 241–269. DOI:10.2151/jmsj.85B.241 |
| Williamson, D. L., 2008: Equivalent finite volume and Eulerian spectral transform horizontal resolutions established from aqua-planet simulations. Tellus A: Dyn. Meteor. Oceanogr., 60, 839–847. DOI:10.1111/j.1600-0870.2008.00340.x |
| Williamson, D. L., M. Blackburn, B. J. Hoskins, et al., 2012: The APE ATLAS. NCAR/TN-484+STR, Boulder, Colorado, National Center for Atmospheric Research, 508 pp, doi: 10.5065/D6FF3QBR |
| Williamson, D. L., M. Blackburn, K. Nakajima, et al., 2013: The Aqua-Planet Experiment (APE): Response to changed meridional SST profile. J. Meteor. Soc. Japan, 91, 57–89. DOI:10.2151/jmsj.2013-A03 |
| Xiao, F., and X. D. Peng, 2004: A convexity preserving scheme for conservative advection transport. J. Comput. Phys., 198, 389–402. DOI:10.1016/j.jcp.2004.01.013 |
| Zhang, G. J., and N. A. McFarlane, 1995: Sensitivity of climate simulations to the parameterization of cumulus convection in the Canadian Climate Centre general circulation model. Atmos.-Ocean, 33, 407–446. DOI:10.1080/07055900.1995.9649539 |
| Yang, Q., L. R. Leung, J. Lu, et al., 2017: Exploring the effects of a nonhydrostatic dynamical core in high-resolution aquaplanet simulations. J. Geophys. Res. Atmos., 122, 3245–3265. DOI:10.1002/2016JD025287 |
| Zeng, X. B., M. Zhao, and R. E. Dickinson, 1998: Intercomparison of bulk aerodynamic algorithms for the computation of sea surface fluxes using TOGA COARE and TAO data. J. Climate, 11, 2628–2644. DOI:10.1175/1520-0442(1998)011<2628:IOBAAF>2.0.CO;2 |
 2018, Vol. 32
2018, Vol. 32


