The Chinese Meteorological Society
Article Information
- Zhou, C. H., X. J. Shen, Z. R. Liu, et al., 2018.
- Simulating Aerosol Size Distribution and Mass Concentration with Simultaneous Nucleation, Condensation/Coagulation, and Deposition with the GRAPES–CUACE. 2018.
- J. Meteor. Res., 32(2): 265-278
- http://dx.doi.org/10.1007/s13351-018-7116-8
Article History
- Received July 31, 2017
- in final form December 14, 2017
2. Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
3. Jiangsu Collaborative Innovation Center of Climate Change, Nanjing 210093
Aerosol particles are different in size, generally expressed in size distribution (Willeke and Whitby, 1975; Andreae and Rosenfeld, 2008). The size distribution of aerosols can be sorted into number, surface area, and volume size distributions, in which volume size distribution is compatible to mass size distribution (Zhang et al., 1999). Since the aerosol activation is mainly determined by the atmospheric super-saturation and the number of particles with diameter larger than the critical activation radius, the particle number size distribution is of great importance to aerosol and cloud interaction (Zhang et al., 2002; Dusek et al., 2006). Surface area size distribution plays an important role in aerosol heterogeneous reactions and optical properties (Ku and Evans, 2012), and volume size distribution is mainly used for mass integration and the transport of aerosols. Currently, most micro- and macrophysics of aerosols have been resolved in mass size distribution. It is indicated that the numerical diffusion of aerosols is minimal when the aerosol mass is taken as a conserved variable (Wu and Biswas, 1998). Generally speaking, a model can use only one kind of such size distributions, guaranteeing its conservation at the same time, and then the other two size distributions have to be diagnosed. Such diagnosed size distributions could be erroneous and their conservations cannot be guaranteed.
There are three approaches to depicting the aerosol size distribution: continuous, sectional, and modal. The continuous approach is comparatively accurate but computationally expensive. The modal approach is cheaper but it is not so accurate, especially for the condensation process (Zhang et al., 2002). The accuracy and computation cost of the sectional approach lies in between, so it is more favorable in application. However, there are still inherent shortcomings in the sectional approach, which include truncation errors and numerical diffusion in solving rigid functions (Shampine and Gear, 1979). This is because the distribution of particles for the sectional approach in each bin is constant, and the particle growth caused by condensation or coagulation will be redistributed evenly within each bin, resulting in spectra broadening. This kind of errors will be enlarged especially in heavy pollution episodes. A more effective way to solve the simulation diffusion is to increase the number of sections or to use different computational schemes such as implicit integrals (Jacobson et al., 1994; Jacobson and Turco, 1995; Wu and Biswas, 1998). There are also three ways to depicting the growth of the inner core and its coating of an aerosol in the size segregated model: fixed, full moving, and hybrid (Jacobson and Turco, 1995; Zhang et al., 1999). The aerosol mass size distribution in the China Meteorological Administration (CMA) Unified Atmospheric Chemistry Environment (CUACE) model is based on the hybrid sectional approach for both accuracy and computation efficiency (Zhou et al., 2012).
Previous studies on the variation of aerosol size distributions at first involved only one microphysical process like coagulation, later gradually included both condensation and coagulation (Gelbard and Seinfeld, 1980; Warren and Seinfeld, 1985; Seigneur et al., 1986; Tsang and Rao, 1988; Jacobson and Turco, 1995; Meng et al., 1998). The size distribution of aerosols in large-scale air quality models is influenced by several processes such as emission, nucleation, condensation, coagulation, deposition, and gas–particle conversion, as well as large-scale advection and turbulent transport processes. However, limited by the imperfect models and observations, there are rare studies combining simultaneously all the processes above for aerosol particle size distribution research.
The CUACE has been coupled with the CMA numerical weather model GRAPES (the Global/Regional Assimilation and PrEdiction System). The coupled system is named GRAPES–CUACE. It is a comprehensive online chemical and weather forecasting system (Wang et al., 2010; Zhou et al., 2016). It includes emission, nucleation, condensation, coagulation, deposition, and gas–particle conversion, as well as large-scale transport and diffusion of aerosols and their precursors. The aerosol mass is size resolved with the number size distribution diagnosed. An aerosol–cloud interaction scheme has also been developed and effectively improved the accuracy of precipitation simulation with this model system (Zhou et al., 2016). The GRAPES–CUACE has accommodated all the processes related to aerosol microphysics into a three-dimensional mesoscale model, making it possible to simulate the aerosol size distribution and its variation. This is important to carry out real time haze–fog forecast and aerosol and cloud interaction research in a more realistic atmosphere since most aerosol–cloud interaction studies use idealized two-dimensional models.
The initial aerosol size distribution plays a determinative role for the aerosol–cloud interaction in the atmosphere, and it is usually prescribed through hypothesis. In this paper, the initial emission aerosol size distribution has been re-schemed by taking into account the relations of number and mass size distributions, and the aging effects influenced by the length of the model mesh. Three important aerosol microphysics processes have also been improved. The competing scheme for nucleation and condensation has been carefully evaluated and improved to make it more reasonable, and the depositing distance has been improved to vary with deposition velocity and model vertical levels. These all help to obtain more accurate aerosol size distribution. The results before and after the improvements have been evaluated by using the PM2.5 observations from the China Atmosphere Watch Network (CAWNET) in January 2013 when sustained heavy haze–fog events occurred. Both mass concentration and number size distribution will be compared with observations at two sites of Beijing and Lin’an.
This paper is organized as follows. Section 2 introduces the key microphysics in the CUACE and related improvements in initial aerosol mass size distribution, coagulation, condensation, nucleation, and deposition. In Section 3, numerical experiment design and observation data are presented. Section 4 compares the simulation results before and after the proposed improvements and analyzes the underlying reasons. Section 5 concludes the paper with a summary.
2 Key microphysics in CUACE and associated improvements 2.1 Initial aerosol mass size distributionThe initial emission particles size distribution can affect the subsequent size distribution of aerosols in the atmosphere (Adams, 2002; Zhou et al., 2012). In CUACE, the initial mass size distribution of black carbon (BC), organic carbon (OC), and sulfate aerosols (SF) are in log-normal functions with the first two peaking at the particle size of 0.1 μm and the SF peaking at the size of 0.25 μm. Among the three aerosol components, only the initial mass size distribution of BC is from the laboratory observations (Berner et al., 1996). The mass size distribution of dust aerosols is a bi-logarithmic normal distribution of 12 soil types sorted from the observation in deserts of China (Gong et al., 2003). Size distribution of sea-salt (SS) is calculated directly in the emission scheme peaking at the coarse particles mode (Gong and Barrie, 1997). The size distribution of nitrate aerosols is from observations in Beijing, which is also peaking mainly at the coarse mode (Xu et al., 2007).
The initial mass size distributions of BC, OC, and SF emissions in CUACE have been reconstructed by using the observations at Beijing and Mount Tai, effectively reducing overestimation of fine particles and aerosol opti-cal depth (Zhou et al., 2012). However, that work only improved the mass size distribution, but failed to fully take into account the number size distribution, especially for small particles in the nucleation mode in which the mass is very small. As in the nucleation mode, a very small difference in mass will lead to a relatively large difference in the number concentrations. It is observed that peak values of aerosol number size distribution in China are mainly concentrated in the size of 60–100 nm (Gao et al., 2007; Peng et al., 2014), and aerosols can be activated at appropriate saturations only when they are bigger than 80 nm in diameter (Dusek et al., 2006). Those modified mass size distributions produce an overwhelmingly high amount of particles in nucleation mode which will cause problems for these small particles to grow into condensation mode and to be activated into cloud droplets. Thus, the mass size distribution of each component of aerosols in CUACE was again modified by considering its observed number concentration distributions over China (Peng et al., 2014).
The time required for aerosols to diffuse from the emission sectors to one entire model grid is related to the size of the grids and the stability of atmosphere. For example, in a Gaussian diffusion model with the horizontal wind speed of 4 m s–1 and the grid length of 25 km, it would take about 3 h or even longer for the aerosol to diffuse evenly to the whole gird under a moderate stable atmospheric condition in the boundary layer. This time is identical to the aging time, about 3–5 h, of the newly nucleated particles (Kulmala et al., 2004); while in severe pollution conditions, it will take longer time for such diffusion. The original version of CUACE homogeneously diffuses the aerosols in the initial mass size distribution from the emission sectors directly to the entire grid within one time step, ignoring the impact of the aging during the diffusion. This is reasonable for models of high resolutions but would be irrational for models on coarse resolutions. Therefore, the prescribed initial emission particle size distribution cannot represent the final emission par-ticle size distribution of the coarse grid. Thus, the aging effect has to be considered. According to the grid length, the time step, and the typical time needed for the aerosol aging in clean conditions, a parameterization scheme using the median radius formula of the logarithmic normal number distribution of the aerosol has been set up with the dispersion sigma value of 2.0, as follows
| $\begin{align} & ({\text{log}} r - \log {{r_{\text{a}}}} )/(\log {{r_{\text{n}}}} - \log {{r_{\text{a}}}} ) \hfill \\ & = \min (L/U/3600,T)/T, \hfill \\ \end{align} $ | (1) |
where the aged peak radius rn is 40 nm and the initial peak radius ra of the new particle is 20 nm. T is the aging characteristic time with the value of 4 h, L is the model grid length, and U is mean surface wind speed. In this paper, the model grid length of CUACE is 0.25° and it is about 25 km in midlatitude regions; the average wind speed is 2 m s–1; and the peak diameter of logarithmic normal distribution of the number concentration is set as 60 nm.
2.2 CoagulationCoagulation can simultaneously change the aerosol size distribution of both number and mass. Coagulation consists of three processes, in which Brownian motion acts on submicron aerosols while the terminal velocity difference and the turbulence are mainly applied to aerosols with diameter bigger than 1 μm. The coagulation is calculated on the basis of the number concentrations, so it also depends on the accuracy of number size distribution diagnosed through the mass size distribution. At present, the coagulation scheme in CUACE has also been applied in most aerosol modules, for it is suitable not only for Brownian motion but also for the situation of both continuum of small Nusen number and Nusen numbers greater than 10 (Fuchs and Davies, 1964). Although multiple coagulations can occur among particles, in this scheme, it is assumed that there is only one collision between two particles before bonding. A semi-implicit integration method for mass exchange among different bins for coagulation in CUACE is also adopted to reduce the amount of computation while ensuring the mass conservation simultaneously (Jacobson et al., 1994).
2.3 Condensation and nucleationCondensation is the process by which gaseous matters condense on aerosols. It changes both the number and the mass size distributions, but cannot change the total number concentration. In the case of heavy pollution, the effect of condensation is very noticeable and might be much larger than that of the coagulation. Then, concentration peaks can appear in both the nucleation mode and the accumulation mode, narrowing the mass size distribution (Zhang et al., 1999). The condensing rate is decided by the physical and chemical characteristics of the aerosols, the concentrations of condensable gases, and the atmospheric temperature and humidity. It is found that when the humidity is very low, it would take more than 10 days to reach the gas–particle balance, but when the humidity is very high, at the value of 90% for example, it would take only 1–2 h to achieve the balance (Jacobson, 1997). Several aerosol models, including CUACE, use the Fuchs parameterization scheme to calculate the condensing rate (Fuchs and Sutugin, 1971). The condensation process in the sectional model can also produce great diffusion errors, especially in the situation of heavy pollution (Seigneur et al., 1986; Tsang and Rao, 1988; Jacobson and Turco, 1995; Wu and Biswas, 1998). To reduce the impacts of the diffusion, the semi-implicit integration method has been adopted in CUACE too.
Nucleation is another process for gaseous substances to become aerosols. The nucleation rate is calculated by using the Fuchs scheme (Fuchs and Sutugin, 1971). It is important to calculate the critical concentration of gas-eous sulfuric acid which determines the initiating of the nucleation process. In CUACE, nucleation rate and the critical concentration of gaseous sulfuric acid are calculated based on the Kulmala’s scheme, which is more parameterized and more reasonable (Kulmala et al., 1998). Since the nucleated aerosol particles are placed in the smallest section of the model, the number concentration of the nucleated aerosols is also affected by the size of the tiniest particles that can be resolved.
Condensation and nucleation occur simultaneously and compete for the condensable gas species. CUACE adopts the competition mechanism by Gong’s scheme, which used an ordinary differential equation (ODE) solver to solve the two processes together with sulfur oxidation chemistry, in which both the nucleation rate and the condensation rate are largely dependent on the initial sulfu-ric acid gas concentration and the sulfuric acid production rate (Gong et al., 2003). In Gong’s scheme, sulfur dioxcide and sulfuric acid can feed back to sulfur chemistry simutaniously; while in CUACE, the sulfate chemistry only supplies the oxidation rate of SO2 for secondary sulfate production and is not directly connected with condensation and nucleation processes. That is why it is shown that there is no tight competition between the two processes in CUACE (Fig. 1). The concentration of nucleated sulfuric acid aerosols is mostly decided by the atmospheric state and it is much lower than the condensation rate. Therefore, in this paper, the competing process has been changed. The nucleation of the sulfate is calculated with the Kulmala method firstly (Kulmala et al., 1998), and the condensation rate of the gaseous sulfuric acid is calculated with the Fuchs scheme thereafter (Fuchs and Sutugin, 1971). This is consistent with what many other models do (Zhang et al., 1999).

|
| Figure 1 Variations of nucleation rate and condensation rate according to sulfate production rate. The curve with hollow circles is for nucleation rate, the curve with triangles is for condensation rate, and the curve with solid circles is for gas sulfate concentration. |
Deposition, including dry deposition and wet deposition, is an important way of aerosol removal, which can change both the number and the mass size distributions of aerosols. The aerosol dry deposition rate is affected not only by land surface features, but also by atmosphe-ric state as well as the size and amount of aerosols. Observations show that tiny particles (with diameter less than 100 nm) and bigger particles (with diameter larger than 2.5 μm) deposit faster, while the particles with the diameter near one micron deposit slowly, so these particles can stay longer. In CUACE, based on the theory of Slinn (1982), the aerosol dry deposition scheme is extended to multi-component sectional aerosols (Gong and Barrie, 1997; Zhang et al., 2001). This scheme combines the effects of gravitational setting, aerodynamic resistance, and the collection efficiency of the surface. The deposited aerosols of each layer in previous CUACE can directly reach the ground as removal at each time step. This fits climate models with larger time steps; while in mesoscale models with a much shorter time step, it can cause aerosols to deposit faster than reality. Therefore, in this paper, the deposition is recalculated according to the sectional deposition velocity, time step, and the model layer depth. The aerosols that actually reach the ground are used as dry deposition and those that cannot reach the ground are used as the exchanges between different layers.
The wet deposition of aerosols includes removal processes in and below clouds. The removal below clouds means that the aerosols are removed in the layer from cloud base to ground as a consequence of inertia coagulation and Brown diffusion of falling raindrops or snowflakes. Thus, this process is determined by atmospheric conditions, aerosols, and water content distributions. Cur-rently, the below-cloud wet-removal in CUACE is parameterized by the precipitation rate and aerosol mass concentration, of which the terminal velocity and number concentration of raindrops or snowflakes are obtained according to the precipitation rate (Slinn, 1984).
3 Experiments and data 3.1 Experimental designWe conducted two numerical experiments: control test (OLD) and comparative test (NEW). In both experiments, the aerosol components are prescribed as SF, nitrate (NT), ammonium (AM), BC, OC, dust (SD), and SS. Each component is divided into 12 sections ranging 10 nm–40 μm (Zhou et al., 2012). The simulation area covers 15°–60°N, 35°–150°E and the model is set with 32 layers in the vertical. The experiment ran from 1 to 31 January 2013, and the initial meteorological conditions were taken from the outputs of the CMA Operational Medium-Range Numerical Prediction Model T213. The anthropogenic emissions of aerosols and their precursors of BC, OC, PM2.5, SO2, and NOx are based on the 2010 HTAP_v2 source database (Wang et al., 2015). The mo-del horizontal resolution is 0.25°.
The difference between the two experiments lies in that the model in the NEW experiment was run with the improved aerosol and cloud microphysical processes including the initial emission particle size distribution, the changed condensation and nucleation competition mechanism, and the improved deposition scheme, which have been mentioned in Section 2; while the OLD experiment did not include these improvements.
3.2 Observational dataThe PM2.5 concentrations were monitored at 24 stations of the CAWNET from 2006 to 2014 by using the GRIMM EDM 180 environmental dust monitoring instruments with 31 different size channels at a flow rate of 1.2 L min–1 (Wang et al., 2015). The PM2.5 observations from the 24 stations are used to compare with the model results over the whole country (Table 1). According to the geographical locations, 18 sites are selected for the comparison in eastern China, including Hohhot, Taiyuan, Shijiazhuang, Gucheng, Jinan, Chongqing, Changsha, Guilin, Hefei, Dongtan, Ningbo, Nanchang, Fuzhou, Xiamen, Nanning, Panyu, Haikou, and Taiyangshan; and the rest 6 sites, which are Guiyang, Yinchuan, Kunming, Zhuzhang, Lhasa, and Sanya, are mostly in West China, representing the remote areas of China.
| STID | Station | Longitude (°) | Latitude (°) |
| 53466 | Hohhot | 111.70 | 40.80 |
| 53614 | Yinchuan | 106.22 | 38.48 |
| 53677 | Taiyuan | 112.48 | 37.93 |
| 53698 | Shijiazhuang | 114.42 | 38.03 |
| 54500 | Gucheng | 115.80 | 39.13 |
| 54823 | Jinan | 116.98 | 36.68 |
| 55591 | Lhasa | 91.13 | 29.67 |
| 56449 | Zhuzhang | 99.73 | 28.02 |
| 56778 | Kunming | 102.68 | 25.02 |
| 57516 | Chongqing | 106.48 | 29.52 |
| 57687 | Changsha | 112.87 | 28.23 |
| 57816 | Guiyang | 106.72 | 26.58 |
| 57957 | Guilin | 110.30 | 25.32 |
| 58321 | Hefei | 117.23 | 31.87 |
| 58363 | Dongtan | 121.80 | 31.51 |
| 58562 | Ningbo | 121.56 | 29.86 |
| 58606 | Nanchang | 115.92 | 28.60 |
| 58940 | Fuzhou | 119.33 | 26.08 |
| 59134 | Xiamen | 118.08 | 24.48 |
| 59431 | Nanning | 108.35 | 22.82 |
| 59481 | Panyu | 113.35 | 23.00 |
| 59758 | Haikou | 110.35 | 20.03 |
| 59948 | Sanya | 109.95 | 18.23 |
| Z9736 | Taiyangshan | 111.71 | 29.17 |
During the experiment period, mass concentration of the soluble aerosols including OC, SF, NT, and AM, and the aerosol number size distribution were intensively observed in Beijing and at Lin’an of Zhejiang Province. The observing site in urban Beijing is located in the Institute of Atmospheric Physics (IAP; 39°58′N, 116°22′E) (Liu et al., 2014; Wang Y. S. et al., 2014; Liu et al., 2016). The observing site in Lin’an is at 30°18′N, 119°45′E (Zhang et al., 2014; Shen et al., 2015; Wang et al., 2015). The data of the Aerosol Mass Spectrometer total mass concentration of soluble aerosols and the data of number size distribution observed at the two sites coincide with the model outputs through the matching of time and bins. The temporal resolution is 3 h, the number size distribution is in 12 bins, and the particle size range (with diameter less than 1 μm) covered by the total concentration of each kind of soluble aerosols also corresponds to the output of the model.
4 Results and discussion 4.1 Comparison of number size distributions of aerosols 4.1.1 Number size distributionA high detection resolution helps to obtain a more complete particle size distribution and to better understand the process of new particle formation and the particle growth mechanism. At early time, it was difficult to obtain a more complete aerosol size distribution because of the coarsely resolvable particle size by the observation instruments. With the advancement of obser-ving techniques, the smallest aerosol particle size observed has decreased from 10 to 3 nm, and now in some laboratory particles of 0.1 nm in size can be detected (Deshler, 2003; Kulmala et al., 2004; Venzac et al., 2009). The particle size resolution observed in China can reach the diameter of 10 nm (Xu et al., 2011; Wang H. L. et al., 2014; Li et al., 2015), partially even approaching 3 nm (Wu et al., 2008; Shen et al., 2011; Peng et al., 2014). The minimum particle size observed at the sites of Beijing and Lin’an for this experiment is 10 nm, consistent with the minimum aerosol particle size in CUACE.
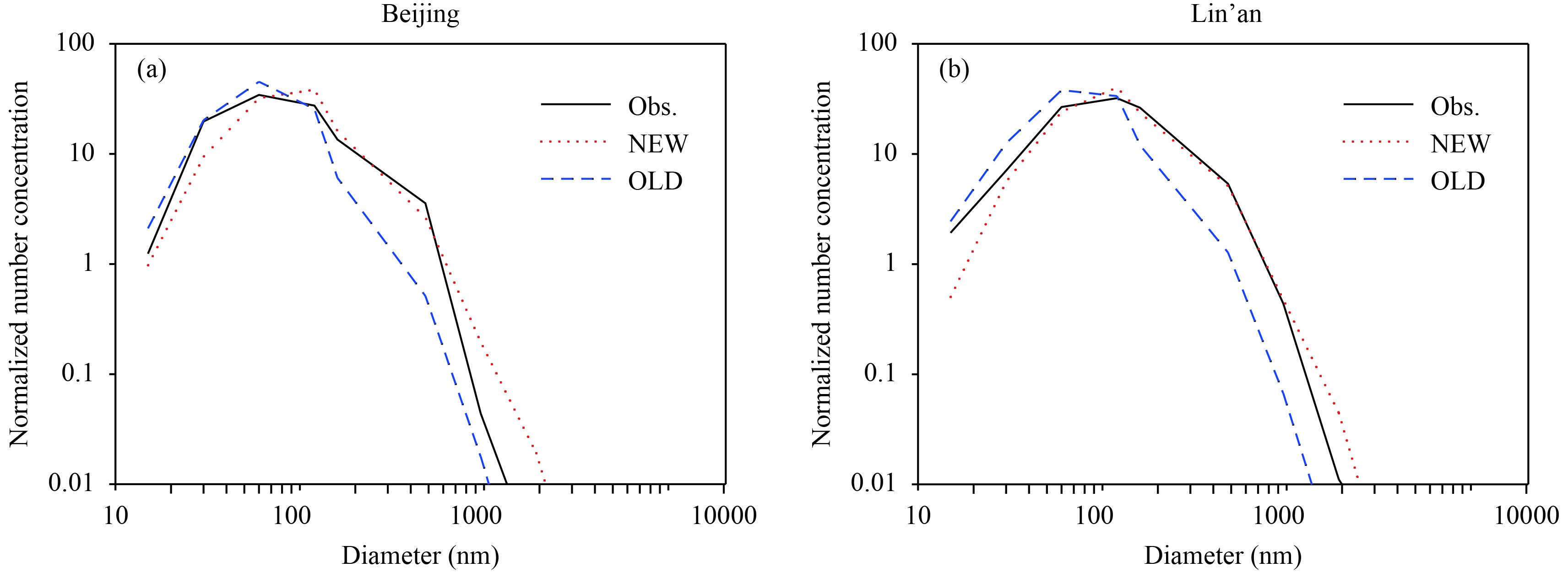
The simulated monthly average normalized number size distributions in OLD and NEW experiments are compared with the observations at Beijing and Lin’an (Figs. 2a, b). It is shown that the peak values of the observed number size distribution and those in OLD and NEW are concentrated in the range of 60–120 nm, falling mainly in the nucleation mode. This is consistent with the number size distributions observed at other time in North China (Gao et al., 2007; Wu et al., 2008; Shen et al., 2011; Lang et al., 2013),and also close to the observations from other places like Nanjing, Guangzhou, and Jinan (Kang et al., 2009; Yue et al., 2013). It is also seen that the normalized number size distribution in the NEW experiment is in decent agreement with the observation in the range from 60 to 600 nm, while it is slightly lower than the observed for ultrafine particles (less than 60 nm) in the nucleation mode. However, the number size distribution in the OLD experiment is higher than the observation for ultrafine particles (less than 90 nm), and is generally lower than the observation in the accumulation mode. Thus, after the model was improved, the condition that the original number size distribution was mainly concentrated in the fine particles and could not grow sufficiently to the accumulation mode has been corrected.
The improvement of the size distribution at the Beijing site is slightly different from that at the Lin’an site. For the Beijing site, the model-simulated number size distribution coincides well with the observation in the accumulation mode. The improved number size distribution at the Lin’an site shows much better agreement with the observation in both nucleation and accumulation modes. For the Lin’an site, the observation data covered the periods of 1–5, 13–16, and 27–31 January 2013, of which the two major pollution processes dated from 13 to 16 and from 27 to 31 were included. This is to say that the observations at the Lin’an site only correspond to two heavy pollution periods because of missing data on most of the remaining days in January 2013. Thus, the result indicates that the improved size distribution is more consistent with the observation during the heavy pollution episodes at Lin’an, implying that the number size distribution of aged aerosols is much closer to the observation.
|
| Figure 2 Number size distributions of aerosols at (a) Beijing and (b) Lin’an. The black solid line denotes observation, the blue dashed one denotes experiment OLD, and the red dotted one denotes experiment NEW. |
To analyze the error of the aerosol number size distribution diagnosed from sectional mass size distribution, we use the aerosol number concentration data, with diameter of 10–680 nm and time frequency per 3 h, obtained at the top of Mount Tai during 22–26 September 2010 in an intensive observation experiment (Zhang et al., 2014). These data also include the mass size distributions of soluble SF, NT, AM, and OC with diameters less than 1 μm on a 5-min temporal resolution, as well as the corresponding meteorological elements such as hourly wind direction, wind speed, temperature, air pressure, relative humidity, dew point temperature, etc. After these data are matched rigorously with the model’s output temporal interval, 20 sets of complete samples are obtained, including meteorological data and mass and number size distribution data. Both the number and mass size distribution data are then paired into the 12 bins by using the CUACE binning parameters such as densities of different aerosol components, bin size, and mixture state. Since SS, SD, and BC are absent in the aerosol mass spectrometer observations, their mass size distributions need to be reconstructed. SS can be ignored because its concentration at the top of Mount Tai is very low. For SD and BC, they can be reconstructed by using the observed mass concentration size distribution and the ratio of different aerosol components in China (Zhang et al., 2012; Zhang et al., 2014). Observations show that there exists a certain ratio of BC to OC mass concentration. In China, the mean ratio of OC and BC is about 3:1 in urban area but about 6:1 in rural area (Zhang et al., 2008). Since the altitude of Mount Tai is over 1500 m, the BC mass concentration is taken as 1/6 of the OC’s. Observations also show that the mass concentration of SD accounts for 35% of PM10, and in dusty season in some arid regions of northern China it can even reach up to 60% or higher. For the reasons that the observation period is in autumn, a season with few sand and dust storms, Mount Tai is located at a high altitude, and the sand–dust mass is mainly concentrated in coarse particles, the dust aerosol is taken as accounting for 20% of the PM10 mass concentration in this experiment.
Based on the mass size distribution information of the multi-component aerosols mentioned above, the sectio-nal number concentrations are calculated by using the CUACE model binning scheme and compared to the observed number concentration size distributions that are also sorted into the same 12 bins. Only the number concentrations in the range of 20–640 nm are selected to compare with the observations. Others are ignored because of high observation errors existing in aerosols with diameters less than 20 nm or larger than 1 μm. The selected aerosols cover 5 bins, which are Bin 1 (20–40 nm), Bin 2 (40–80 nm), Bin 3 (80–160 nm), Bin 4 (160–320 nm), and Bin 5 (320–640 nm), respectively, of which the first two are in the nucleation mode and the last three fall in the accumulation mode.

|
| Figure 3 Number concentration ratio between that diagnosed from mass size distribution and the observed. The dots are the ratios of each sample in each bin, the blue solid line is for the average ratio, and the red line is the baseline. |
All the results are shown in Fig. 3. In Bins 1 and 2, the number concentrations of most samples obtained by sectional diagnostic calculation are higher than the actual observations. The number concentrations of only 4 sam-ples among 20 in Bin 1 and 3 samples in Bin 2 are less than the observed, while all the rest are higher than the observations with the crest value getting up to 56 times and more. On average, the diagnostic number concentration of Bin 1 is 8.2 times of the observation, and that of Bin 2 is 2.2 times of the observation. However, in the accumulation mode, the diagnostic number concentrations are generally lower than the observed, and averagely, the number concentration values of Bins 3–5 are 0.58, 0.41, and 0.64 times of the observation, respectively. Thus, compared with the observed sectional number concentrations, those diagnosed from the observed sectional aerosol mass concentration on the basis of densities of different aerosol components, bin size, and mixture state in CUACE are overestimated in the nucleation mode, but underestimated in the accumulation mode. The errors of number size distribution, caused by reproduction from actual sectional mass size distribution, are mainly due to the following three points. First, aerosols are in different shapes in the actual atmosphere while the aerosols in every section of the model are assumed to be ideal balls and the change in particle size inside the sections is not taken into account (Shampine and Gear, 1979). Second, every aerosol particle in the actual atmosphere is loosely compacted and not as tightly solid as that in the model. Third, the density of each aerosol component, affected by its structure, is not fixed in real atmosphere. If too many fine particles concentrate in the nucleation mode, they not only slow down the aerosol aging, but also affect their interactions with clouds and fog in the activation process.
It is shown that the improved number size distribution from the NEW experiment is lower than that of the original scheme in the nucleation mode (Fig. 2). Since the number concentration diagnosed from observed sectio-nal mass concentration would be overestimated as indicated in the above analysis of the case of Mount Tai, it can be concluded that the newly improved scheme not only coincides well with the observation in the accumulation mode, but also can, to a certain extent, inhibit the situation that the bin-scheme causes too many particles in the nucleation mode.
4.2 Assessment of simulations of SF, OC, AM, and NTHourly concentrations of SF, OC, AM, and NT with diameter less than 1 μm are output by the model every 3 h and compared with the corresponding component concentrations observed at the Lin’an site and Beijing site. After the time matching, there are 240 sets of data available at the Beijing site but only 104 sets available at Lin’an because of data missing. The mean values, correlation coefficients, and normalized standard deviations of the observed and simulated mass concentration of the four aerosol components at the two sites are shown in Tables 2 and 3. The normalized standard deviation is the standard deviation divided by the average concentration (Zhou et al., 2012).
| Mean value | r | Mean bias | Normalized mean bias (%) | ||||||||||
| Obs | NEW | OLD | NEW | OLD | NEW | OLD | NEW | OLD | |||||
| SF | 21.2 | 23.1 | 32.7 | 0.32 | 0.38 | 1.7 | 11.3 | 8.0 | 52.0 | ||||
| OC | 41.6 | 48.9 | 21.3 | 0.26 | 0.39 | 7.6 | –20.0 | 18.0 | –48.0 | ||||
| NT | 15.3 | 58.0 | 5.2 | 0.20 | 0.18 | 42.9 | –9.9 | 281.0 | –65.0 | ||||
| AM | 10.1 | 17.6 | 11.0 | 0.29 | 0.33 | 7.5 | 1.0 | 74.0 | 9.0 | ||||
| Mean value | r | Mean bias | Normalized mean bias (%) | ||||||||||
| Obs | NEW | OLD | NEW | OLD | NEW | OLD | NEW | OLD | |||||
| SF | 10.6 | 17.7 | 24.7 | 0.37 | 0.36 | 7.1 | 14.1 | 67.0 | 131.0 | ||||
| OC | 21.8 | 35.6 | 7.1 | 0.42 | 0.16 | –14.6 | 13.8 | 63.0 | –67.0 | ||||
| NT | 15.7 | 11.7 | 5.4 | 0.56 | 0.36 | –4.0 | –11.4 | –66.0 | –26.0 | ||||
| AM | 9.2 | 7.5 | 9.1 | 0.54 | 0.40 | –1.6 | –0.1 | –18.0 | –1.0 | ||||
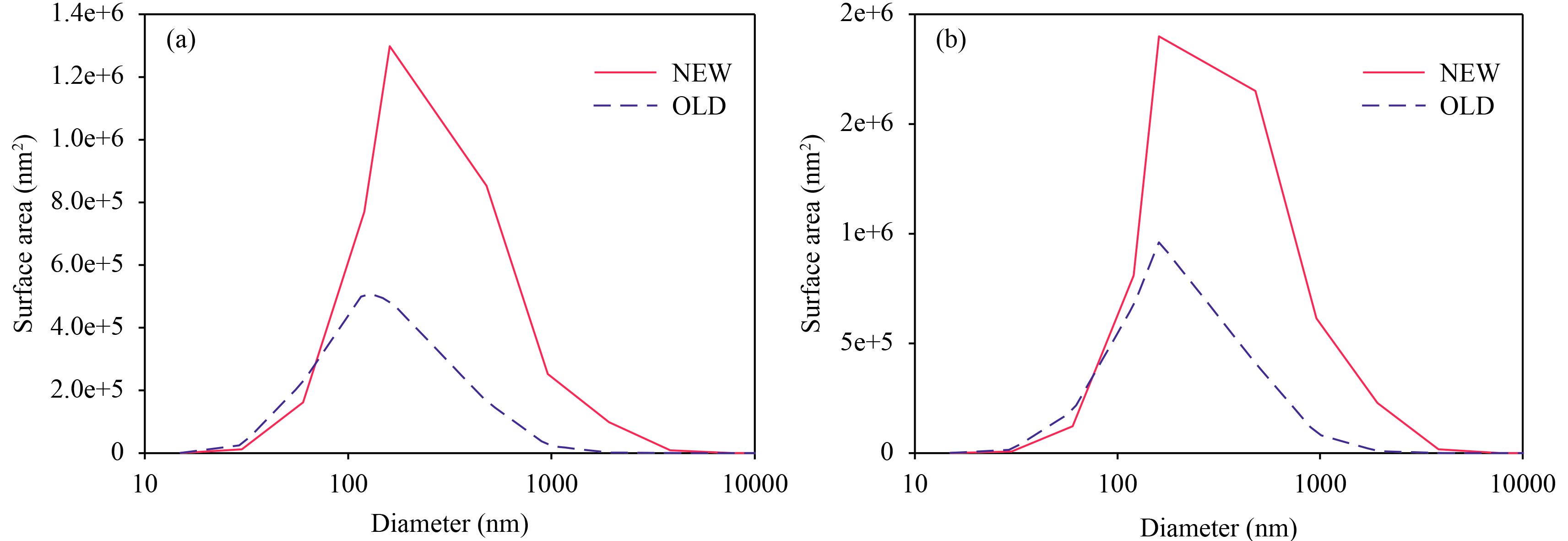
In the OLD experiment, the average concentrations of OC simulated at the Beijing and Lin’an sites are only 51% and 33% of the observation, which are seriously underestimated (Tables 2, 3). In the NEW experiment, the simulated values are 120% and 163% of the observation, respectively, approaching much closer to the observation. The normalized standard biases at the two stations are reduced sharply from –48% and –67% to 18% and 63%, respectively. Comparison between the simulated and observed hourly OC concentration also shows that the peak of the pollution episode at Beijing during the experiment period and at Lin’an in 13–36 and 27–31 January are also well represented, which are underestimated in the OLD experiment (Fig. 4). OC is mainly from the primary emission and the secondary conversion. Taking the aerosols with mass concentration of 100 μg m–3 as an example, the surface areas of the aerosol in the NEW experiment are significantly increased at both sites, especially in the accumulation mode, more than twice of those in OLD. This can significantly increase the chance of secondary organic aerosol formation through condensation (Fig. 5). This should be the main reason for the OC increasing since the primary emission of OC remains unchanged. Previous studies showed that the contribution of the secondary organic aerosol to the haze–fog in China has been increasing in recent years (Huang et al., 2014), and the explosive growth of secondary organic aerosol plays an important role in the increase of PM10 during heavy pollution events (Wang Y. S. et al., 2014; Zhong et al., 2017). In light of the lower OC simulation results in East Asia by other models (Han et al., 2014; Park and Kim, 2014), the advantages of CUACE in simulating OC would help capture the extreme peak OC concentrations during heavy pollutions.

|
| Figure 4 Time series of hourly OC concentration at (a) Beijing and (b) Lin’an. The blue, red, and green solid lines are for observation (Obs.), the NEW experiment, and the OLD experiment, respectively. The data are plotted at 3-h intervals. |
|
| Figure 5 Aerosol area size distributions at (a) Beijing and (b) Lin’an with the aerosol mass concentration of 100 μg m–3. The red solid line is for the NEW experiment and the blue dashed one is for the OLD experiment. |
The average SF concentrations at the two sites of Beijing and Lin’an decrease from 153% and 232% in OLD to 108% and 168% in NEW of the observations, with the overestimation being significantly reduced (Tables 2, 3). The normalized biases for the two sites have also decreased obviously from 52% and 131% to 8% and 67%. Besides the initial size distribution improvement, the two processes, nucleation and condensation, revised after ignoring the ODE solver, should be the main reason for the reduction in the overestimation of SF concentrations.
NT and AM are very complex and difficult to simulate due to their unstable properties. In the atmosphere, AM is mainly combined with sulfates and nitrates, forming ammonium sulfate and ammonium nitrate. Studies have shown that, as the ability of the ammonium salt to bind to the sulfate is one order of magnitude higher than that to the nitrate, the ammonium in the atmosphere tends to bind to sulfate first to form ammonium sulfate (Stockwell et al., 1990). Thus, in addition to the atmospheric state, the concentrations of ammonium and sulfate also influence the concentration of nitrate. CUACE calculates the unstable NT and AM concentrations by using a thermodynamic equilibrium model ISORROPIA (Nenes et al., 1998). The results show that the NT concentrations at the Beijing and Lin’an sites are significantly higher than the values in the OLD experiment (Tables 2, 3). A careful analysis reveals that the concentration of SF at the Beijing site is significantly reduced while the concentration of AM is increased by about 74%. This change leads to a significant increase of 280% in NT generation. Comparatively, the decline rate of SF at the Lin’an site is not as big as that at the Beijing site, and accordingly, the growth rate of NT is not so big, either. Unlike the cases of SF and OC, the normalized biases of AM and NT at both sites are increased dramatically after the model improvements. In the thermal equilibrium, other anions such as chloride ions in the atmosphere would also compete for ammonium salt cations, but the chlorine salts in CUACE are mainly from natural sources of sea-salt without considering the anthropogenic sources; thus, the concentrations of chlorine salts in the mainland region of China are low and unable to compete for cations with NOx to inhibit NT formation. This may be one reason for the overestimation of NT.
The correlation analysis between the simulation and observation for different aerosol components also shows that the correlation coefficients of the four components of aerosols at the Lin’an site have increased obviously in the NEW experiment (Table 3), in which the OC correlation coefficient increases from 0.16 to 0.42 (160%), the nitrate correlation coefficient increases from 0.36 to 0.62 (100%), and the ammonium salt correlation coefficient increases from 0.4 to 0.54 (36%). In comparison, at the Beijing site, though the correlation coefficient of NT increases, the correlation coefficients of SF and AM do not change much, and the correlation coefficient of OC is significantly decreased. The reason for the decreased correlations in Beijing is probably because observation in the urban site is influenced by the very local land surface, complex emission, and chemical transformation neighboring the site, but all of these local characteristics cannot be quite clearly represented in the same model grid. On the contrary, the regional representation of the rural site is better than the urban site, so the correlation is better at the Lin’an site.
4.3 Assessment of PM2.5 concentrationThe mass concentrations of all components with particle size less than 2.5 μm are summed and averaged as the simulated daily mean PM2.5 mass concentration, and then interpolated to the corresponding 24 sites as designated in Table 1. Compared with the observed daily mean value, the scatter diagrams of the sites all over China, in eastern China, and in the remote areas of western China are shown in Fig. 6; and the related statistics are analyzed in Table 4. The scatter plots of the whole China show that the improvement of PM2.5 concentration manifests mainly in that the underestimation and overestimation are both effectively relieved in the NEW experiment (Figs. 6a, b). The result makes the scatter plots of simulation and observation more concentrated. The correlation coefficient increases by more than 70%, from 0.304 to 0.532, and the standard deviation decreases by about 11%, from 87 to 77 μg m–3. The effect in eastern China, where pollution is heavier, is similar to that in the whole country in the NEW experiment (Figs. 6c, d). The lower and higher values are both effectively controlled, with the correlation coefficient increasing from 0.195 to 0.445. More than that, the average concentrations of the whole China and of eastern China have all increased by about 10 μg m–3, closer to the mean of observations (Table 4). Since the experiments are conducted during a series of heavy pollution events, this result reveals the improved ability of the model in better simulating aerosol concentrations during periods of heavy pollution. For the western remote areas, due to the particular low concentration and isolated emission sources, the simulations are more complicated and also affected by the atmospheric state and complex terrain. In the NEW experiment, the scatter points of observation and simulation get closer to the 1:1 axis, while in the OLD experiment, the simulation is much lower than the observation (Figs. 6e, f). The statistical results also suggest that in the NEW experiment, the correlation coefficient in this region increases from 0.348 to 0.607, and the mean simulated value increases from 27.3 to 55.5 μg m–3, i.e., from 43% to 87.5% of the observed (Table 4). All of these results show that the improved model can significantly enhance not only the simulation of aerosols with particle size less than 2.5 μm in the polluted areas, but also in the remote areas in China. In a word, the simulation capability of the model for aerosols has been improved comprehensively.

|
| Figure 6 Scatter plots for the simulated and observed PM2.5 concentration (μg m–3) for (a, b) whole China, (c, d) eastern China, and (e, f) western (remote areas of) China. Obs. is for observation and model is for simulation. Left (right) panels are for the OLD (NEW) experiment. |
| Correlation coefficient | Standard error | Mean concentration | |||||||
| NEW | OLD | NEW | OLD | NEW | OLD | Obs | |||
| Whole China | 0.532 | 0.304 | 77.0 | 87.0 | 101.9 | 91.3 | 129.0 | ||
| Eastern China | 0.445 | 0.195 | 78.0 | 84.1 | 113.8 | 98.9 | 142.6 | ||
| Remote areas | 0.607 | 0.348 | 35.1 | 23.1 | 55.5 | 27.3 | 63.4 | ||
The coupled aerosol–cloud model is a useful and advanced tool for studying the formation of haze and fog and the impact of aerosols on clouds and precipitation. Due to the limitation in physical understanding and the scarcity of observations, assessment and improvement of mass and number size distributions of aerosols are still limited. The related investigations using large-scale three-dimensional online models are even less. In this paper, more precise number size distribution and particulate mass concentrations were obtained through sectional diagnosis and improved representations of several microphysical processes of aerosols. Moreover, the results have been evaluated comprehensively by use of observational data.
A parameterization scheme for adapting the aerosol initial emission mass size distribution to the number size distribution and the model grid length has been established. Meanwhile, problems such as that the condensation and nucleation processes were overly dependent on gaseous sulfuric acid concentration and that the competition between the two processes was not obvious, have been corrected to calculate nucleation first and condensation second just as most aerosol models do. The two processes are critical for secondary aerosol generation, especially for SF and OC. After the improvements, the aerosol number concentration of the nucleation mode decreases. Since the sectional number concentration diagnosed from the observed mass size distribution was previously overestimated in nucleation mode, this decrease in nucleation mode by the sectional diagnosis approach has effectively rectified the serious overestimation error, and made the number concentration in the nucleation mode much closer to the reality. The results also show a more reasonable increase in simulated aerosol number concentration in the accumulation mode, which is much closer to the observation. These improvements are expected to improve simulation of the aerosol–cloud interaction and then the precipitation, since larger particles are more easily to be activated.
Meanwhile, this study has also effectively improved the simulation effects of different aerosol components and the total aerosol concentration. Among them, the simulated values of OC and SF are much closer to the observations, and the normalized error is decreased significantly. At the same time, the simulated PM2.5 concentration is improved obviously, and the correlation coefficient increases by more than 70%, from 0.304 to 0.532. For the remote regions with complex terrains and isolated emission sources, the mean value of the model simulated PM2.5 concentration increases from 43% to 87.5% of the observed value, and the correlation coefficient increases from 0.348 to 0.607.
In general, the results of this study demonstrate that the performance of the GRAPES–CUACE model in simulating aerosol number size distribution and the total and sectional mass concentration of aerosols has been improved considerably. This paves the way for further studying the formation of haze and fog and the mechanism of aerosol participation in the process of cloud formation. However, affected by many factors, the performance of the model in simulating the thermodynamically instable nitrate and ammonium salt is not satisfying. The related issues need to be further investigated. In addition, due to lack of observational data, the simulations of aerosol number and mass size distributions in the vertical and in the upper troposphere cannot be verified; thus, it is also needed to extend the work in this respect in the near future.
Acknowledgments. The authors wish to thank Ms. Hua Liu of the China Meteorological Administration Training Centre and Dr. Qiudan Dai of the Institute of Atmospheric Physics, Chinese Academy of Sciences for providing language help.
| Adams, P. J., and J. H. Seinfeld, 2002: Predicting global aerosol size distributions in general circulation models. J. Geophys. Res., 107, 4370. DOI:10.1029/2001JD001010 |
| Andreae, M. O., and D. Rosenfeld, 2008: Aerosol–cloud–precipitation interactions. Part 1. The nature and sources of cloud-active aerosols. Earth-Sci. Rev., 89, 13–41. DOI:10.1016/j.earscirev.2008.03.001 |
| Berner, A., S. Sidla, Z. Galambos, et al., 1996: Modal character of atmospheric black carbon size distributions. J. Geophys. Res., 101, 19,559–19,565. DOI:10.1029/95JD03425 |
| Deshler, T., M. E. Hervig, D. J. Hofmann, et al., 2003: Thirty years of in situ stratospheric aerosol size distribution measurements from Laramie, Wyoming (41°N), using balloon-borne instruments. J. Geophys. Res., 108, 4167. DOI:10.1029/2002jd002514 |
| Dusek, U., G. P. Frank, L. Hildebrandt, et al., 2006: Size matters more than chemistry for cloud-nucleating ability of aerosol particles. Science, 312, 1375–1378. DOI:10.1126/science.1125261 |
| Fuchs, N. A., and C. N. Davies, 1964: Aerosol mechanics. (Book Reviews: The Mechanics of Aerosols). Science, 146, 1033–1034. DOI:10.1126/science.146.3647.1033 |
| Fuchs, N. A., and A. G. Sutugin, 1971: High-dispersed aerosols. Topics in Current Aerosol Research, G. M. Hidy, and J. R. Brock, Eds., New York, Elsevier, 38–47. |
| Gao, J., J. Wang, S.-H. Cheng, et al., 2007: Number concentration and size distributions of submicron particles in Jinan urban area: Characteristics in summer and winter. J. Environ. Sci., 19, 1466–1473. DOI:10.1016/s1001-0742(07)60239-3 |
| Gelbard, F., and J. H. Seinfeld, 1980: Simulation of multicomponent aerosol dynamics. J. Colloid Interface Sci., 78, 485–501. DOI:10.1016/0021-9797(80)90587-1 |
| Gong, S. L., L. A. Barrie, and J.-P. Blanchet, 1997: Modeling sea-salt aerosols in the atmosphere: 1. Model development. J. Geophys. Res., 102, 3805–3818. DOI:10.1029/96JD02953 |
| Gong, S. L., L. A. Barrie, J.-P. Blanchet, et al., 2003: Canadian aerosol module: A size-segregated simulation of atmospheric aerosol processes for climate and air quality models. 1. Module development. J. Geophys. Res., 108, 4007. DOI:10.1029/2001JD002002 |
| Han, X., M. Zhang, J. Gao, et al., 2014: Modeling analysis of the seasonal characteristics of haze formation in Beijing. Atmos. Chem. Phys., 14, 10231–10248. DOI:10.5194/acp-14-10231-2014 |
| Huang, R. J., Y. Zhang, C. Bozzetti, et al., 2014: High secondary aerosol contribution to particulate pollution during haze events in China. Nature, 514, 218–222. DOI:10.1038/nature13774 |
| Jacobson, M. Z., 1997: Numerical techniques to solve condensational and dissolutional growth equations when growth is coupled to reversible reactions. Aerosol Sci. Technol., 27, 491–498. DOI:10.1080/02786829708965489 |
| Jacobson, M. Z., and R. P. Turco, 1995: Simulating condensatio-nal growth, evaporation, and coagulation of aerosols using a combined moving and stationary size grid. Aerosol Sci. Technol., 22, 73–92. DOI:10.1080/02786829408959729 |
| Jacobson, M. Z., R. P. Turco, E. J. Jensen, et al., 1994: Modeling coagulation among particles of different composition and size. Atmos. Environ., 28, 1327–1338. DOI:10.1016/1352-2310(94)90280-1 |
| Kang, H. Q., B. Zhu, and S. G. Fan, 2009: Size distributions and wet scavening properties of winter aerosol particles in north suburb of Nanjing. Climatic Environ. Res., 14, 523–530. DOI:10.3878/j.issn.1006-9585.2009.05.07 |
| Ku, B. K., and D. E. Evans, 2012: Investigation of aerosol surface area estimation from number and mass concentration measurements: Particle density effect. Aerosol Sci. Technol., 46, 473–484. DOI:10.1080/02786826.2011.639316 |
| Kulmala, M., A. Laaksonen, L. Pirjola, 1998: Parameterizations for sulfuric acid/water nucleation rates. J. Geophys. Res., 103, 8301–8307. DOI:10.1029/97JD03718 |
| Kulmala, M., H. Vehkamäki, T. Petäjä, et al., 2004: Formation and growth rates of ultrafine atmospheric particles: A review of observations. J. Aerosol Sci., 35, 143–176. DOI:10.1016/j.jaerosci.2003.10.003 |
| Lang, F. L., W. Q. Yan, Q. Zhang, et al., 2013: Size distribution of atmospheric particle number in Beijing and association with meteorological conditions. China Environ. Sci., 33, 1153–1159. |
| Li, J. X., Y. Yin, P. R. Li, et al., 2015: Aircraft measurements of the vertical distribution and activation property of aerosol particles over the Loess Plateau in China. Atmos. Res., 155, 73–86. DOI:10.1016/j.atmosres.2014.12.004 |
| Liu, Z. R., B. Hu, Q. Liu, et al., 2014: Source apportionment of urban fine particle number concentration during summertime in Beijing. Atmos. Environ., 96, 359–369. DOI:10.1016/j.atmosenv.2014.06.055 |
| Liu, Z. R., Y. S. Wang, B. Hu, et al., 2016: Source appointment of fine particle number and volume concentration during severe haze pollution in Beijing in January 2013. Environ. Sci. Pollut. Res., 23, 6845–6860. DOI:10.1007/s11356-015-5868-6 |
| Meng, Z. Y., D. Dabdub, and J. H. Seinfeld, 1998: Size-resolved and chemically resolved model of atmospheric aerosol dynamics. J. Geophys. Res., 103, 3419–3435. DOI:10.1029/97jd02796 |
| Nenes, A., S. N. Pandis, and C. Pilinis, 1998: ISORROPIA: A new thermodynamic equilibrium model for multiphase multicomponent inorganic aerosols. Aquat. Geochem., 4, 123–152. DOI:10.1023/A:1009604003981 |
| Park, R. J., and S.-W. Kim, 2014: Air quality modeling in East Asia: Present issues and future directions. Asia-Pac. J. Atmos. Sci., 50, 105–120. DOI:10.1007/s13143-014-0030-9 |
| Peng, J. F., M. Hu, Z. B. Wang, et al., 2014: Submicron aerosols at thirteen diversified sites in China: Size distribution, new particle formation and corresponding contribution to cloud condensation nuclei production. Atmos. Chem. Phys., 14, 10249–10265. DOI:10.5194/acp-14-10249-2014 |
| Seigneur, C., A. B. Hudischewskyj, J. H. Seinfeld, et al., 1986: Simulation of aerosol dynamics: A comparative review of mathematical models. Aerosol Sci. Technol., 5, 205–222. DOI:10.1080/02786828608959088 |
| Shampine, L. F., and C. W. Gear, 1979: A user’s view of solving stiff ordinary differential equations. SIAM Rev., 21, 1–17. DOI:10.1137/1021001 |
| Shen, X. J., J. Y. Sun, Y. M. Zhang, et al., 2011: First long-term study of particle number size distributions and new particle formation events of regional aerosol in the North China Plain. Atmos. Chem. Phys., 11, 1565–1580. DOI:10.5194/acp-11-1565-2011 |
| Shen, X. J., J. Y. Sun, X. Y. Zhang, et al., 2015: Characterization of submicron aerosols and effect on visibility during a severe haze–fog episode in Yangtze River delta, China. Atmos. Environ., 120, 307–316. DOI:10.1016/j.atmosenv.2015.09.011 |
| Slinn, W. G. N., 1982: Predictions for particle deposition to vegetative canopies. Atmos. Environ., 16, 1785–1794. DOI:10.1016/0004-6981(82)90271-2 |
| Slinn, W. G. N., 1984: Precipitation scavenging. Atmospheric Science and Power Production. D. Randerson, Ed., Office of Scientific and Technical Information, Ork Ridge, USA, 466–532. |
| Stockwell, W. R., P. Middleton, J. S. Chang, et al., 1990: The second generation regional acid deposition model chemical mechanism for regional air quality modeling. J. Geophys. Res., 95, 16343–16376. DOI:10.1029/JD095iD10p16343 |
| Tsang, T. H., and A. Rao, 1988: Comparison of different numeri-cal schemes for condensational growth of aerosols. Aerosol Sci. Technol., 9, 271–277. DOI:10.1080/02786828808959214 |
| Venzac, H., K. Sellegri, P. Villani, et al., 2009: Seasonal variation of aerosol size distributions in the free troposphere and residual layer at the puy de Dôme station, France. Atmos. Chem. Phys., 9, 1465–1478. DOI:10.5194/acp-9-1465-2009 |
| Wang, H., X. Y. Zhang, S. L. Gong, et al., 2010: Radiative feedback of dust aerosols on the East Asian dust storms. J. Geophys. Res., 115, D23214. DOI:10.1029/2009JD013430 |
| Wang, H. L., B. Zhu, L. J. Shen, et al., 2014: Number size distribution of aerosols at Mt. Huang and Nanjing in the Yangtze River Delta, China: Effects of air masses and characteristics of new particle formation. Atmos. Res., 150, 42–56. DOI:10.1016/j.atmosres.2014.07.020 |
| Wang, Y. S., L. Yao, L. L. Wang, et al., 2014: Mechanism for the formation of the January 2013 heavy haze pollution episode over central and eastern China. Sci. China Earth Sci., 57, 14–25. DOI:10.1007/s11430-013-4773-4 |
| Wang, Y. Q., X. Y. Zhang, J. Y. Sun, et al., 2015: Spatial and temporal variations of the concentrations of PM10, PM2.5 and PM1 in China . Atmos. Chem. Phys., 15, 13585–13598. DOI:10.5194/acp-15-13585-2015 |
| Warren, D. R., and J. H. Seinfeld, 1985: Simulation of aerosol size distribution evolution in systems with simultaneous nucleation, condensation, and coagulation. Aerosol Sci. Technol., 4, 31–43. DOI:10.1080/02786828508959037 |
| Willeke, K., and K. T. Whitby, 1975: Atmospheric aerosols: Size distribution interpretation. J. Air Pollut. Contr. Assoc., 25, 529–534. DOI:10.1080/00022470.1975.10470110 |
| Wu, C. Y., and P. Biswas, 1998: Study of numerical diffusion in a discrete-sectional model and its application to aerosol dynamics simulation. Aerosol Sci. Technol., 29, 359–378. DOI:10.1080/02786829808965576 |
| Wu, Z. J., M. Hu, P. Lin, et al., 2008: Particle number size distribution in the urban atmosphere of Beijing, China. Atmos. En-viron., 42, 7967–7980. DOI:10.1016/j.atmosenv.2008.06.022 |
| Xu, H. H., Y. S. Wang, T. X. Wen, et al., 2007: Size distributions and vertical distributions of metal elements of atmospheric aerosol in Beijing. Environ. Sci., 26, 675–679. DOI:10.3321/j.issn:0254-6108.2007.05.027 |
| Xu, P. J., W. X. Wang, L. X. Yang, et al., 2011: Aerosol size distributions in urban Jinan: Seasonal characteristics and variations between weekdays and weekends in a heavily polluted atmosphere. Environ. Monit. Assess., 179, 443–456. DOI:10.1007/s10661-010-1747-2 |
| Yue, D. L., M. Hu, Z. B. Wang, et al., 2013: Comparison of particle number size distributions and new particle formation between the urban and rural sites in the PRD Region, China. Atmos. Environ., 76, 181–188. DOI:10.1016/j.atmosenv.2012.11.018 |
| Zhang, L. M., S. L. Gong, J. Padro, et al., 2001: A size-segregated particle dry deposition scheme for an atmospheric aerosol module. Atmos. Environ., 35, 549–560. DOI:10.1016/S1352-2310(00)00326-5 |
| Zhang, X. Y., Y. Q. Wang, X. C. Zhang, et al., 2008: Carbonaceous aerosol composition over various regions of China during 2006. J. Geophys. Res., 113, D14111. DOI:10.1029/2007JD009525 |
| Zhang, X. Y., Y. Q. Wang, T. Niu, et al., 2012: Atmospheric aerosol compositions in China: Spatial/temporal variability, chemical signature, regional haze distribution and comparisons with global aerosols. Atmos. Chem. Phys, 12, 779–799. DOI:10.5194/acp-12-779-2012 |
| Zhang, Y., C. Seigneur, J. H. Seinfeld, et al., 1999: Simulation of aerosol dynamics: A comparative review of algorithms used in air quality models. Aerosol Sci. Technol., 31, 487–514. DOI:10.1080/027868299304039 |
| Zhang, Y., R. C. Easter, S. J. Ghan, et al., 2002: Impact of aerosol size representation on modeling aerosol–cloud interactions. J. Geophys. Res., 107, 4558. DOI:10.1029/2001jd001549 |
| Zhang, Y. M., X. Y. Zhang, J. Y. Sun, et al., 2014: Chemical composition and mass size distribution of PM1 at an elevated site in central East China . Atmos. Chem. Phys., 14, 12237–12249. DOI:10.5194/acp-14-12237-2014 |
| Zhou, C. H., S. L. Gong, X. Y. Zhang, et al., 2012: Towards the improvements of simulating the chemical and optical properties of Chinese aerosols using an online coupled model—CUACE/Aero. Tellus B, 64, 18965. DOI:10.3402/tellusb.v64i0.18965 |
| Zhou, C. H., X. Zhang, S. Gong, et al., 2016: Improving aerosol interaction with clouds and precipitation in a regional chemi-cal weather modeling system. Atmos. Chem. Phys., 16, 145–160. DOI:10.5194/acp-16-145-2016 |
| Zhong, J. T., X. Y. Zhang, Y. Q. Wang, et al., 2017: Relative contributions of boundary-layer meteorological factors to the explosive growth of PM2.5 during the red-alert heavy pollution episodes in Beijing in December 2016 . J. Meteor. Res., 31, 809–819. DOI:10.1007/s13351-017-7088-0 |
 2018, Vol. 32
2018, Vol. 32


