The Chinese Meteorological Society
Article Information
- Zhang, M., H. Wang, X. Y. Zhang, et al., 2018.
- Applying the WRF Double-Moment Six-Class Microphysics Scheme in the GRAPES_Meso Model: A Case Study. 2018.
- J. Meteor. Res., 32(2): 246-264
- http://dx.doi.org/10.1007/s13351-018-7066-1
Article History
- Received May 9, 2017
- in final form November 3, 2017
2. State Key Laboratory of Severe Weather/Institute of Atmospheric Composition, Chinese Academy of Meteorological Sciences, Beijing 100081;
3. Center for Excellence in Regional Atmospheric Environment, Institute of Urban Environment, Chinese Academy of Sciences, Xiamen 361021;
4. Key Laboratory for Aerosol–Cloud–Precipitation of China Meteorological Administration, Nanjing University of Information Science & Technology, Nanjing 210044;
5. Beijing Meteorological Service Center, Beijing 100089
Clouds are a key link between the water cycle and the radiative balance in the earth–atmosphere system (Hartmann et al., 1992; Baker, 1997; Ramanathan et al., 2001; Stephens, 2005). The formation and evolution of clouds play a vital role in physics of clouds and precipitation. Direct calculation of precipitation and the formation, evolution, and interaction of hydrometeors on a grid-scale is known as the explicit cloud microphysics scheme in atmospheric numerical models, which can be broadly classified into bin schemes and bulk schemes.
Bin schemes involve developing a hydrometeor size distribution that is discretized into bins based on microphysical properties, such as size or quality, without limiting the size distribution and can describe the accretion of particles on a particular scale in the particle size distribution. However, its forecast variables are numerous with the huge computation. Earlier models developed by Clark (1973), Soong (1974), and Takahashi (1975) were relatively simple, as they employed bin schemes in their studies without ice-phase microphysical schemes. Later, bin schemes were incorporated into cloud models to study the liquid and ice-phase cloud microphysical process (Hall, 1980; Khain and Sednev, 1996; Reisin et al., 1996; Ovtchinnikov and Kogan, 2000), autoconversion between cloud condensation nuclei (CCN) and cloud droplets (Khain et al., 2004, 2005), and other aspects of cloud microphysics (Kogan, 1991; Stevens et al., 1996; Guo et al., 1999; Yin et al., 2000; Pinsky and Khain, 2002; Rong and Yin, 2010). Bulk schemes, known as bulk microphysics parameterization (BMP) schemes, assume the size distribution of each type of hydrometeor, and can describe the overall properties of particles. However, BMP schemes also have limitations in reflecting particle changes on a particular scale in the particle size distribution. Because of its small number of forecast variables, computation time is reduced. Hence, most current numerical weather prediction (NWP) models employ the BMP schemes.
Based on the difference in forecast variables, BMP schemes can be further classified into single- and double-moment schemes. Single-moment schemes (Lin et al., 1983; Hong and Lim, 2006) can only forecast the mixing ratio of hydrometeors, whereas double-moment schemes, in addition to the mixing ratio of hydrometeors, can also forecast the number concentration of hydrometeors. Although double-moment schemes require longer computation time, they incorporate the number concentration of hydrometeors, thereby increasing the degrees of freedom of the particle size distribution, so that the number and quality of hydrometeor particles in the physical mechanism are more coordinated. Hence, an increasing number of studies have started incorporating the use of double-moment schemes. Cotton et al. (1986) employed a cloud model to simulate the orographic snowfall process using a double-moment scheme, such that the model could simulate surface precipitation, liquid water content, and ice crystal number concentration. Hu and He (1988) presented a relatively complete double-moment microphysical model in cumulonimbus, which could forecast the number concentrations of five hydrometeors. Murakami (1990) utilized a bulk microphysics scheme in a case study, which predicted the mixing ratios of six hydrometeors, with the number concentrations of snow and cloud ice that were also taken into account. Wang and Chang (1993) proposed a cloud model that described the dynamics, microphysical, and chemical processes of clouds, where the model could simulate the mixing ratio and the number concentration of liquid- and solid-phase hydrometeors. Ferrier (1994) adopted the double-moment ice-phase BMP scheme to simulate convective precipitation under different large-scale environmental conditions and the concentration of hydrometeors in stratiform precipitation. This scheme included 90 different microphysical processes. In addition to forecasting the mixing ratio of liquid water in snow, graupel, and frozen drops, this scheme could also forecast the mixing ratio and concentration of small ice crystals, snow, graupel, and hail/frozen drops. Meyers et al. (1997) added a double-moment BMP scheme into the Regional Atmospheric Modeling System (RAMS). In an idealized convection simulation experiment, this scheme increased the degrees of freedom of the particle size distribution compared with the single-moment scheme and was very sensitive to input parameters, including the concentration and morphology of cloud droplets. An explicit double-moment microphysics scheme was used in the Mesoscale Model version 5 (MM5) model (Reisner et al., 1998), which added three options for forecasting complex accretion of supercooled water in order to forecast supercooled water that significantly affected aircraft during regional snowstorms in the Rocky Mountains, Colorado, USA. They found that the double-moment scheme produced forecasts of mixing ratio and number concentration of ice-phase hydrometeors were closer to the actual observation. Cohard and Pinty (2000a) proposed a double-moment warm-rain microphysics scheme that was characterized by the use of the gamma distribution in the droplet size distribution, and carried out analytical integration of microphysical conversion rate of most hydrometeors. Through the change of simulated radar reflectivity with time, this scheme could analyze the formation of large raindrops so as to achieve a more accurate simulation of the warm-rain processes (Cohard and Pinty, 2000b). Seifert and Beheng (2001) obtained the warm-rain double-moment microphysics scheme by solving stochastic collection equations and obtained the formulae of explicit autoconversion, accretion, and self-collection rates. Afterwards, Seifert and Beheng (2006) improved this scheme that could distinguish between continental and oceanic conditions and was used to research the effect of aerosols in mixed clouds on the formation of precipitation. Morrison and Pinto (2005) incorporated a new double-moment bulk microphysics scheme into the MM5 model to simulate stratiform clouds in the Arctic boundary layer. This scheme could forecast the number concentration and mixing ratio of four types of hydrometeors (cloud droplets, small ice crystals, raindrops, and snow) based on the specific aerosol size distribution obtained from observations. Thompson et al. (2004, 2008) only forecasted the number concentration of cloud ice and raindrop using the microphysics scheme for winter precipitation, and employed a new snow parameter with the assumption that snow particles were non-spherical and bulk density was inversely proportional to diameter.
Many studies compared the microphysical schemes with different numbers of moments, especially the single-moment with the double-moment schemes. Morrison et al. (2009) forecasted the mixing ratio and the number concentration of five types of hydrometeors (cloud, ice, snow, rain, and graupel) contained in stratiform precipitation behind a simulated squall line using the Weather Research and Forecasting (WRF) model and compared the results with the single-moment scheme. They revealed that the double-moment scheme increased the area of the trailing stratiform precipitation region but greatly weakened convective activities in the convection core. This scenario was caused by different rain evaporation rates due to variable raindrop size distribution compared with the single-moment scheme. Lim and Hong (2010) applied the WRF double-moment 6-class (WDM6) microphysics scheme, which is an improved version of the WRF single-moment 6-class (WSM6) scheme (Hong and Lim, 2006), in a mesoscale model for the first time, and conducted idealized 2D thunderstorm tests. They found that this scheme could forecast hydrometeors including water vapor, cloud water, rain, cloud ice, snow, and graupel. The WDM6 employed a double-moment scheme in warm-rain processes and could forecast the number concentration of CCN, cloud droplets, and raindrops, while other processes were basically the same as in the WSM6. Molthan and Colle (2012) simulated an event of widespread snowfall that occurred in American–Canadian border with single- and double-moment schemes in the WRF model, and compared the results with the observation. It is suggested that the double-moment scheme performed well in representing ice crystal aggregation and obtained overall better forecasts than the single-moment scheme.Van Weverberg et al. (2014) simulated a case of intense precipitation and compared single- and double-moment schemes in a climate model. They showed that the double-moment scheme predicted well when adopted a large breakup equilibrium diameter and a diagnostic shape parameter for all hydrometeors that followed gamma distributions. Kovačević and Ćurić (2015) used a cloud-resolving mesoscale model with single- and double-moment schemes in precipitation sensitivity research by changing the mean radius of droplet spectra. In this study, we also make sensitivity tests by changing the CCN concentrations to examine the ensuing influence on hydrometeors in clouds and precipitation.
In recent years, many studies have been conducted on cloud microphysics in China. Aerosols were activated into CCN to influence the formation of clouds and precipitation (Xiao and Yin, 2011; Deng et al., 2013; Guo et al., 2014), and can also affect radiation through indirect effects (Zhao et al., 2006; Wang et al., 2015). Thus, it is vital to obtain aerosol properties and particle size distributions (Liu et al., 2011; Ma et al., 2012; Yuan et al., 2016). Because of different macroscopic properties and precipitation mechanisms, the distribution of hydrometeors in stratiform clouds (Zhao and Lei, 2008; Hong and Li, 2011; Xiao et al., 2015) and convective clouds (Yin et al., 2012; Tao et al., 2013; Yang et al., 2014; Zhao et al., 2015) may differ. Studying the microphysical processes of different types of cloud and precipitation can help improve the precipitation forecasts. The spatiotemporal distribution of liquid water and aerosols in clouds could be directly obtained by using aircraft observation and other means (Yin et al., 2010; Li et al., 2014; Zhao and Lei, 2014). In addition to observations, most of the current numerical simulations of cloud microphysics are based on the WRF model (Xu et al., 2007; Gao et al., 2012; Hou et al., 2013, 2016; Shen et al., 2015; He et al., 2016). This paper employed the mesoscale version of the Global/Regional Assimilation and PrEdiction System (GRAPES_Meso), which has been used to investigate cloud microphysics in many studies with decent results (Wu et al., 2007; Sun et al., 2008, 2011; Shi et al., 2015).
This paper is organized as follows. The model and microphysics scheme are described in Section 2. Experimental design and simulation results are presented in Sections 3 and 4, respectively. Finally, Section 5 shows conclusions and discussion.
2 Model and microphysics scheme 2.1 GRAPES_MesoThe GRAPES_Meso model (Chen and Shen, 2006; Chen et al., 2008) is a new generation of regional numerical forecast system developed by the Chinese Academy of Meteorological Sciences (CAMS), the China Meteorological Administration (CMA). The framework of this model (Wu et al., 2005) can be divided into three sections: the driver layer, the middle layer, and the model layer. The driver layer is used for handling problems including integration parameter settings, partitioning for parallel computing, allocation and release of memory space, and reading of initial data. The middle layer links both the driver layer and the model layer, and includes model integration processing. The model layer, as the core layer, involves linear and non-linear computations, calculation of upstream points, and solving the Helmholtz equation. Yang et al. (2008) adopted fully compressible equations in the dynamic framework, a semi-implicit semi-Lagrangian time difference scheme and advection scheme, a grid design using latitude–longitude lattice, height-based terrain-following coordinates, and horizontal Arakawa-C staggered grid format. For physical processes, Xu et al. (2008, 2010) studied the effect of time accuracy on precipitation forecasts and optimized the physical processes.
2.2 WDM6This study coupled the WDM6 double-moment cloud microphysics scheme, which has been widely used in the WRF model, into the GRAPES_Meso model. Compared with the WSM6 scheme, the WDM6 scheme added CCN activation and evaporation of rainwater into cloud water in the simulation of mixing ratio. This scheme also increased microphysical processes related to the number concentrations of cloud droplets, raindrops, and CCN, including CCN activation into cloud droplets, evaporation of cloud droplets into CCN, autoconversion of cloud droplets into raindrops, evaporation of raindrops into cloud droplets, self-collection of cloud droplets and raindrops, melting of cloud ice and snow, and homogeneous or heterogeneous nucleation of cloud droplets into cloud ice, which would help improve the ability of the model in describing cloud microphysical processes and laid the foundation for studying the effect of CCN on clouds and precipitation in the model.
In the cloud microphysical processes of the WDM6 scheme, the size distribution function of cloud droplets and raindrops used for calculation is:
| $\begin{split} {n_x}({D_x}) = & {N_x}\frac{{{\alpha _x}}}{{\Gamma ({\nu _x})}}{\lambda ^{{\alpha _x}{\nu _x}}}{D_x}^{{\alpha _x}{\nu _x} - 1} \\& \cdot \exp [ - {({\lambda _x}{D_x})^{{\alpha _x}}}],x \in \left[ {C,R} \right],\end{split} $ | (1) |
where the slope parameter is:
| ${\lambda _x} = {[\frac{\pi }{6}{\rho _{\rm w}}\frac{{\Gamma ({\nu _x} + 3/{\alpha _x})}}{{\Gamma ({\nu _x})}}\frac{{{N_x}}}{{{\rho _{\rm a}}{q_x}}}]^{\frac{1}{3}}}, $ | (2) |
where Γ is the Gamma function; ν and α are diffusion parameters, with 2, 1 representing raindrops and 1, 3 representing cloud droplets; x is the category of hydrometeors (cloud droplets or raindrops), qx is mixing ratio of the category x, ρw is density of water, ρa is air density, and Nx and Dx are the number concentration and the diameter of the category x, respectively. The boundary between cloud droplet and raindrop diameter is 82 μm, where all raindrops are converted into cloud droplets by evaporation. The maximum raindrop diameter is 2000 μm, and the minimum cloud droplet diameter is 10–4 μm.
The governing equation for the number concentration of each particle is:
| $\frac{\partial {N_x}}{{\partial t}} = - { V} \cdot \nabla {N_x} - \frac{1}{{{\rho _{\rm a}}}}\frac{\partial }{{\partial z}}({\rho _{\rm a}}{N_x}{V_x}) + {S_{\!\! x}}, $ | (3) |
where the first term on the right-hand side of the equation represents the advection term, the second term is the sedimentation term, and the third term is the source/sink term.
The number of activated CCN (na):
| ${n_{\rm a}} = CS_{\!\! {\rm w}}^k = \left({n + {N_{\rm C}}} \right){\left({\frac{{{S_{\!\! {\rm w}}}}}{{{S_{\!\!{\max }}}}}} \right)^k}, $ | (4) |
where
The growth rate of the cloud water mixing ratio obtained through CCN activation (Pcact) is:
| ${P_{\rm {cact}}} = \frac{{4\pi {\rho_{\rm w}}}}{{3{\rho _{\rm a}}}}r_{\rm {act}}^3{N_{\rm {cact}}}.$ | (5) |
CCN activation ratio is:
| $\begin{split} &{N_{{\text{cact}}}} =\\ & \frac{{\max \left\{ {0,\left( {n + {N_{\rm C}}} \right)\min \left[ {1,{{\left( {{S_{\rm w}}/{S_{\max }}} \right)}^k}} \right] - {N_{\rm C}}} \right\}}}{{\Delta t}}. \end{split}$ | (6) |
When cloud water is evaporated into CCN, the growth rate of CCN is:
| ${N_{{\text{cevp}}}} = \frac{{{N_{\rm C}}}}{{{q_{\rm C}}}}{P_{\rm {cond}}}, $ | (7) |
where Pcond is the growth rate of the mixing ratio of cloud water converted from water vapor, which is represented by:
| ${P_{\rm {cond}}} = \left({q - {q_{\rm {sw}}}} \right){\left[ {\Delta t\left({1 + \frac{{L_{\rm v}^2{q_{\rm {sw}}}}}{{{C_{\rm {pm}}}{R_{\rm v}}{T^2}}}} \right)} \right]^{ - 1}}, $ | (8) |
whereLv is the latent heat of condensation; Cpm is the specific heat of air under constant atmospheric pressure; Rv is a constant related to water vapor; and qsw is the value of the mixing ratio during saturation of cloud water.
Hence, the source/sink term for CCN is:
| ${S_{\rm {CCN}}} = - {N_{\rm {cact}}} + {N_{\rm {cevp}}}.$ | (9) |
During the autoconversion of cloud water into raindrops (Cohard and Pinty, 2000a), the growth rate of the rain mixing ratio (Praut) is:
| ${P_{\rm {raut}}} = \frac{L}{\tau }, $ | (10) |
where
| $\begin{split} \tau& = 3.7\frac{1}{{{\rho _{\rm a}}{q_{\rm C}}}}{\left( {0.5 \times {{10}^6}{\sigma _{\rm C}} - 7.5} \right)^{ - 1}}\qquad\qquad \\ & = 3.7\frac{1}{{{\rho _{\rm a}}{q_{\rm C}}}}{\left( {\frac{{0.5 \times {{10}^6}}}{{{\lambda _{\rm C}}}} - 7.5} \right)^{ - 1}},\qquad\qquad\,\,\,\,\end{split} $ | (11) |
| $\begin{split} L & = 2.7 \times {10^{ - 2}}{\rho _{\rm a}}{q_{\rm C}}\left( {\frac{1}{{16}} \times {{10}^{20}}\sigma _{\rm C}^3{D_{\rm C}} - 0.4} \right)\quad\\& = 2.7 \times {10^{ - 2}}{\rho _{\rm a}}{q_{\rm C}}\left( {\frac{{{{10}^{20}}}}{{16\lambda _{\rm C}^4}} - 0.4} \right). \end{split}$ | (12) |
In both equations, σC is the standard deviation of the raindrop size distribution. The growth rate of rain mixing ratio is calculated only if σC > 15 μm.
When cloud water turns into raindrops, the growth rate of the rain mixing ratio (Pracw) is divided into two stages based on the volume-average raindrop diameter (DR):
When DR ≥ 100 μm,
| ${P_{\rm {racw}}} = \frac{\pi }{6}\frac{{{\rho_{\rm w}}}}{{{\rho _{\rm a}}}}{K_1}\frac{{{N_{\rm C}}{N_{\rm R}}}}{{\lambda _{\rm C}^3}}\left({\frac{2}{{\lambda _{\rm C}^3}} + \frac{{24}}{{\lambda _{\rm R}^3}}} \right).$ | (13) |
When DR < 100 μm,
| ${P_{\rm {racw}}} = \frac{\pi }{6}\frac{{{\rho_{\rm w}}}}{{{\rho _{\rm a}}}}{K_2}\frac{{{N_{\rm C}}{N_{\rm R}}}}{{\lambda _{\rm C}^3}}\left({\frac{6}{{\lambda _{\rm C}^6}} + \frac{{5040}}{{\lambda _{\rm R}^6}}} \right).$ | (14) |
When the WDM6 scheme was first proposed, Hong et al. (2010) assessed the scheme using a case study of a convective system in the Great Plains of North America. They found that the WDM6 scheme has improved properties of convective development, such as bow echoes in front of the squall line. Moreover, the WDM6 scheme has also eliminated false precipitation in some WSM6 schemes. Later, more studies chose to use the WDM6 scheme in the WRF model and made comparisons with other cloud microphysics schemes in order to understand the performance of different schemes (Dong et al., 2012; Duda et al., 2014; Wang et al., 2014;Zhu et al., 2014; Chen et al., 2016). Zhou et al. (2016) and Bae et al. (2016) also adopted the methods similar to this study and coupled WDM6 into other models to evaluate its performance in simulating radiation and precipitation.
3 Experimental designThis study employed the GRAPES_Meso (v3.3) model to simulate and analyze a precipitation process including light and moderate rain, as well as local heavy rain, during 3–5 June 2015 in North China, caused by the eastward movement of an upper-level trough.
3.1 Model parametersChina and its surrounding area (20.00°–49.85°N, 100.00°–144.85°E) were chosen as the model simulation domain. The starting time was 1800 UTC 3 June 2015, and the integration time was 30 h. The integration step was 100 s, and the time interval for model result output was 1 h. The horizontal resolution was 0.15° × 0.15°, and the number of vertical layers was 32 from surface to 30-km height. This study focused on Region A (Beijing and its surrounding area, 38°–43°N, 113°–120°E) to study the effects of cloud microphysics on the cloud and precipitation. In addition to using the WDM6 scheme, the WSM6 scheme, and the NCEP 5-class scheme as cloud microphysics scheme, other schemes employed included the RRTM (Rapid Radiative Transfer Model) longwave radiation scheme, the Goddard shortwave radiation scheme, the Monin–Obukhov surface layer scheme, the Noah land surface scheme, the MRF (Medium-Range Forecast) boundary layer scheme, and the BMJ (Betts–Miller–Janjic) cumulus convection scheme. Before running the model coupled with WDM6 scheme, it was necessary to preset an initial CCN number concentration (CCN0) as the assumed background atmospheric condition. In this study, CCN0 was chosen as 1 × 108 m–3.
3.2 Data usedThis study used the NCEP global final analysis at a horizontal resolution of 1° × 1° and a time interval of 6 h, as the initial and boundary conditions to the GRAPES_Meso. The 24-h cumulative precipitation data were taken from the CMA observations of hourly rainfall collected at 2700 automatic weather stations in North China including Beijing, Tianjin, Hebei, Shanxi, and Inner Mongolia on 4 June 2015. The station data were interpolated into a 0.15° × 0.15° grid, matching the grids of the GRAPES_Meso. Since direct observation of clouds was difficult, remote sensing was generally chosen to understand the vertical distribution of hydrometeors. This study employed level-3 products of the Terra and Aqua satellites equipped with Moderate Resolution Imaging Spectrometer (MODIS); times of passing territory were 0230 and 0530 UTC, respectively, and both satellites were capable of obtaining cloud liquid water path (CLWP) at a 1° × 1° resolution.
4 Results 4.1 PrecipitationThe model required some time to adjust itself at the initial stage of precipitation. Moreover, precipitation in Region A occurred mainly after 0000 UTC 4 June. Therefore, the 24-h cumulative precipitation recorded between 0000 UTC 4 and 0000 UTC 5 June was chosen as the sample for this study. The 24-h cumulative precipitation distribution in Region A based on observation (Fig. 1a) showed that precipitation occurred mainly in northern and eastern Beijing and turned a distribution of northwest to southeast. As this study employed the method of interpolation from station data to grid data, the amount of precipitation shown in Fig. 1a was found to be slightly lower than that based on observations at station points, where the highest amount of precipitation based on observation at individual stations could reach up to 40 mm. From Fig. 1b, it was found that apart from the appearance of a false heavy precipitation core in northeastern Beijing and southern boundary of Region A based on the WDM6 scheme, the position of other precipitation cores shown in this scheme was consistent with observation; the range of heavy precipitation cores was slightly larger than observation, especially the area that was greater than 28 mm; the maximum precipitation amount was 45 mm, which was closer to the observation. In the WSM6 scheme (Fig. 1c), a false heavy precipitation core also appeared in northeastern Beijing. The range of precipitation shown in this scheme was generally consistent with the WDM6 scheme. However, the magnitude of precipitation and the range of heavy precipitation areas shown in this scheme were greater than the WDM6 scheme, with the false heavy precipitation core in the north showing the most obvious difference. Figure 1d shows the simulation results from the NCEP 5-class scheme, where the distribution and magnitude of precipitation were clearly lower than the observation, with a maximum precipitation amount of 33 mm.
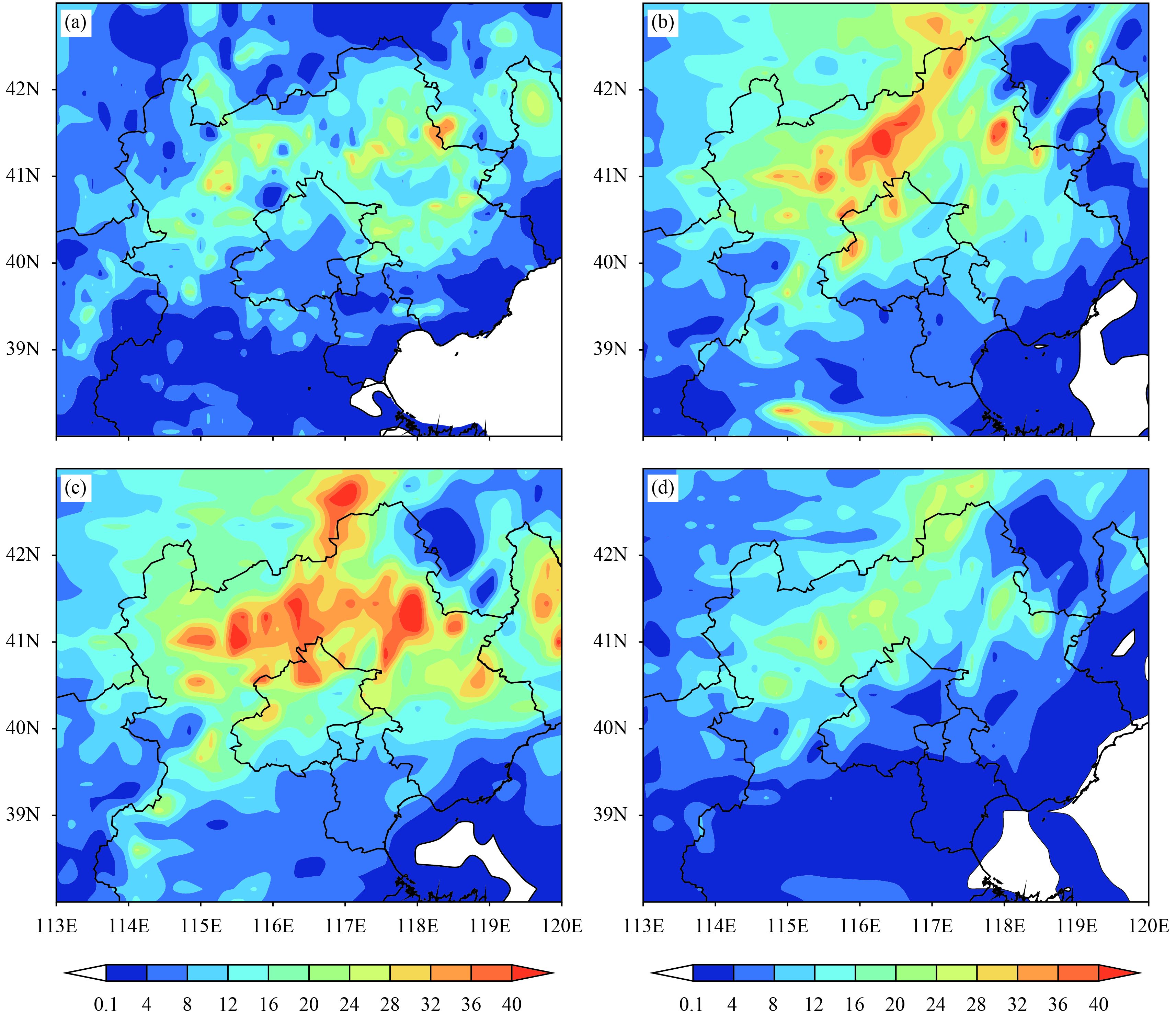
|
| Figure 1 Observed and simulated 24-h cumulative precipitation (mm): (a) observation, (b) WDM6, (c) WSM6, and (d) NCEP 5-class. |
Though the simulated precipitation was the summation produced by cumulus convection scheme and microphysics scheme, the different results of precipitation could be considered as causing by microphysics schemes, as the same cumulus convection scheme was adopted in research. In summary, the WDM6 scheme indicated the best simulation effect, as the magnitude and distribution of precipitation shown in this scheme were found to be closest to observation. The WSM6 scheme was the second-best simulation effect, as the distribution of precipitation was basically same with the WDM6 scheme and the magnitude of precipitation was slightly greater than it. The NCEP 5-class scheme was the worst simulation effect, as the area of precipitation shown in this scheme was found to be much smaller than the observation, especially in eastern Beijing. Moreover, from a series tests, we draw a conclusion that the NCEP 5-class scheme always had a systematic omission in simulating the heavy precipitation and an underestimate in precipitation. Besides, it could not forecast the number concentration. Thus, the following section primarily focuses on the analyses of the results obtained by the WDM6 and WSM6 schemes. As the false heavy precipitation cores appeared in all three microphysics schemes and results were all more north than the observation, their formation might not due to microphysics schemes but rather the dynamic transport processes.
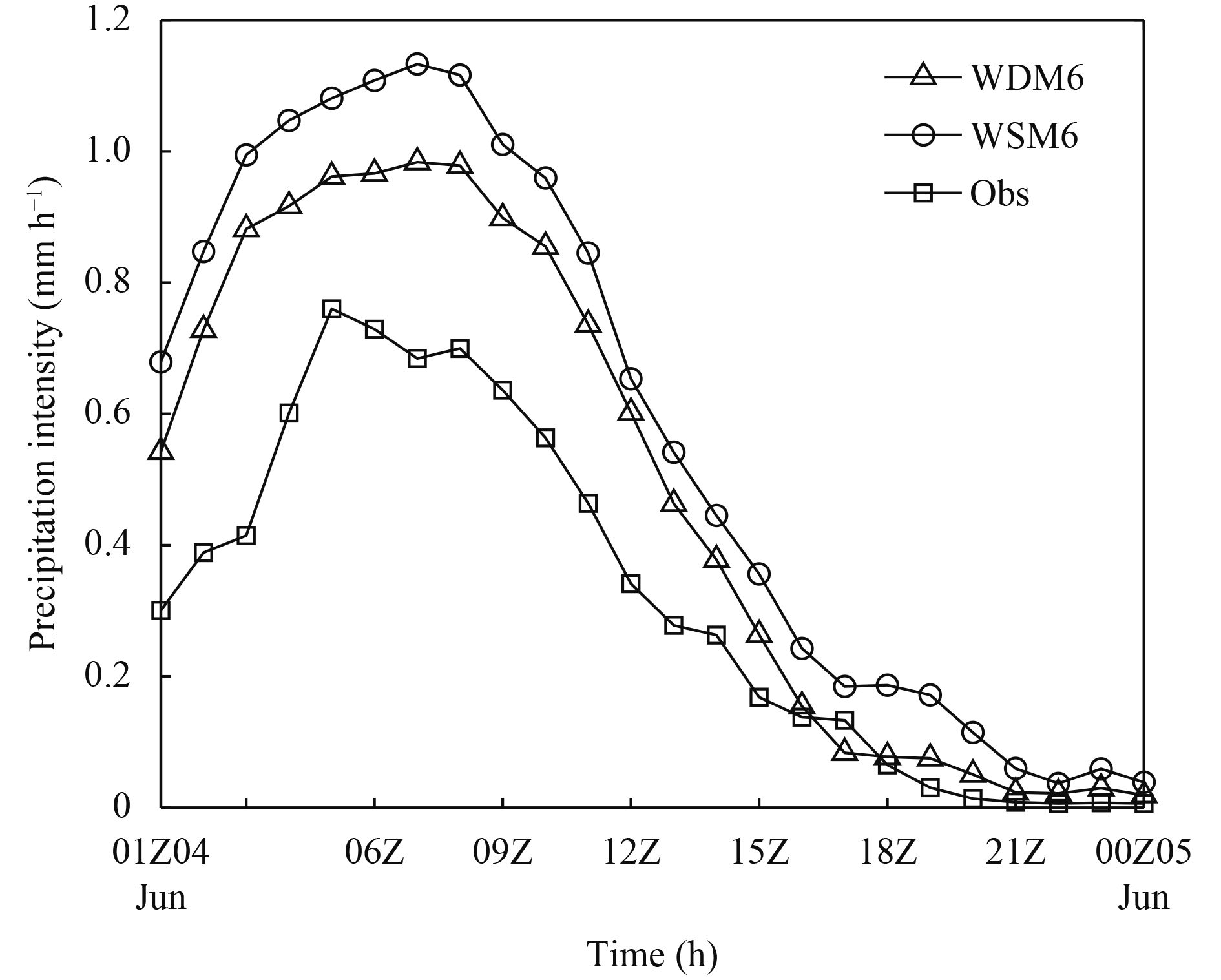
|
| Figure 2 Time series of the observed and simulated domain-averaged precipitation intensity (mm h–1) in Region A. The letter Z in the x axis is equal to UTC. |
To analyze the precipitation intensity in Region A, both WDM6 and WSM6 simulated domain-averaged hourly precipitation values were compared against the observation data from the automatic weather stations. As shown in Fig. 2, the observed domain-averaged hourly precipitation showed a peak value of 0.76 mm h–1 at 0500 UTC, followed by a slight decrease later. This may have happened because of a loss of observation data for hourly precipitation collected by automatic stations located in northern Beijing, to which the precipitation system traveled eastward. After 0800 UTC, precipitation gradually weakened and left Region A. From the comparison of domain-averaged precipitation intensity produced by use of WDM6 and WSM6, it was found that the simulation results using both schemes indicated an increasing trend initially and reached a maximum value at 0700 UTC, with respective peak values of 0.98 and 1.13 mm h–1 for the WDM6 and WSM6 schemes. In contrast, the simulation results of both schemes were greater than observation values. However, the results of the WDM6 scheme were closer to the observation. After 0800 UTC, precipitation simulated by both schemes indicated a decreasing trend, similar to the observation.
In general, although the domain-averaged precipitation intensity simulated by both schemes was slightly higher than the observation, their variations with time were consistent with the observation. Based on the results above, the WDM6 scheme indicated a slightly better simulation effect than the WSM6 scheme. This is likely due to introduction of the double-moment warm-rain processes in the WDM6 scheme. The next section focuses on examining the cloud microphysical properties in simulations using both schemes.
4.2 Analyzing cloud and rain parametersThe WDM6 scheme can simulate the mixing ratios of six water substances, including water vapor (qv), cloud water (qc), rain (qr), cloud ice (qi), snow (qs), and graupel (qg), similar to the WSM6 scheme. Through simulation results of domain-averaged mixing ratios at different time periods (Fig. 3), the spatiotemporal distribution of hydrometeors in Region A can be analyzed.
|
| Figure 3 (Continued). |
Comparing the simulation results of domain-averaged mixing ratios of cloud droplets between the WDM6 scheme (Fig. 3a) and the WSM6 scheme (Fig. 3b), both sets of results included a certain amount of supercooled cloud water. A large amount of cloud water was distributed below 0°C, with most of the cloud water reaching approximately 700 hPa. The cloud water content and spatiotemporal distribution adopted the WDM6 scheme were lower than the WSM6 scheme, with maximum cloud water mixing ratios of 0.022 and 0.05 g kg–1, respectively. However, it is evident in Figs. 3c, d that the simulation results of domain-averaged rain mixing ratio were completely opposite to the cloud water. The mixing ratio of supercooled raindrops simulated by the WDM6 scheme were higher; the maximum central values of rainwater content using the WDM6 and WSM6 schemes at 0300 UTC 4 June were 0.09 and 0.07 g kg–1, respectively. These results were caused by differences in autoconversion process of cloud droplets to raindrops. First, the initial condition of starting the autoconversion process was different. In the WSM6 scheme, the condition was that the cloud water mixing ratio must be greater than the critical value (qc0), which was represented by the following equation:
| ${{{q}}_{{\text{c}}0}} = \frac{{4\pi {\rho _{\text{w}}}}}{{3{\rho _{\text{a}}}}}{{{r}}_0}^3{{x}_{{\text{ncr}}}}, $ | (15) |
where ρw is water vapor density, ρa is air density, r0 is a constant (8 × 10–6 m), and xncr is cloud droplet concentration (3 × 108 m–3) for the WSM6 scheme. In the WDM6 scheme, the condition is that the volume averaged cloud droplet diameter must be greater than 15 μm [Eqs. (10)–(12)]. Second, the accretion processes of cloud droplets into raindrops were different. For the WDM6 scheme, small raindrops, which are formed by the autoconversion of cloud droplets with volume averaged diameters less than 100 μm, would also accretion into large raindrops [Eq. (14)].
In conclusion, the WDM6 scheme was more effective than the WSM6 scheme with respect to autoconversion process of cloud droplets to raindrops, and its simulated rain mixing ratio was also higher. Despite of higher rain mixing ratio at high levels adopted the WDM6 scheme, it was found from the 0.02 g kg–1 contour range that rain mixing ratio near the ground was lower than the WSM6 scheme, resulting in lower surface precipitation. There are two possible reasons for lower surface precipitation simulated by the WDM6 scheme. First, the WDM6 scheme added the evaporation process from rain into cloud water in the simulation of mixing ratio, thus reducing rain content during raindrops falling process. Second, the WDM6 scheme only added the double-moment microphysics scheme into the warm-rain processes. With respect to the cold-rain processes, both schemes were different but were generally consistent.
From Figs. 3e to 3j, it was found that the content and distribution of snow and cloud ice among the ice-phase hydrometeors in both schemes were generally consistent. However, both schemes showed slightly different simulation results for graupel. The simulated graupel content in the WSM6 scheme was slightly higher than the WDM6 scheme. This may have been due to higher cloud water content simulated by the WSM6 scheme, such that the collection of ice-phase hydrometeors resulted in higher graupel content. This scenario would be more obvious if heavier precipitation occurred. It explains the great contribution of graupel to precipitation, as graupel melting helps increase of the ground precipitation.
CLWP shows the overall content of cloud water from the ground to the top of the atmosphere, and can objectively reflect the distribution of cloud water. From the average value of the observed CLWP between two satellites on 4 June, as shown in Fig. 4a, it was found that cloud water was mainly distributed in central China and South China, with a maximum value of 0.5 kg m–2. Due to the eastward movement of the upper-level trough, a cloud water conveyor belt traveling from south to north emerged in front of the trough, primarily covering Henan, Hebei, and their surrounding areas. Figure 4b shows the average values of CLWP simulated by the WDM6 scheme between 0300 and 0500 UTC 4 June. From this figure, it is evident that cloud water was mainly distributed in the areas mentioned above. However, the core of CLWP was found to be more scattered and indicated a slightly smaller range compared with the satellite observation. The cloud water conveyor belt turned a distribution of southwest to northeast and was slightly different from the satellite observation, but its location was generally consistent with the satellite observations.
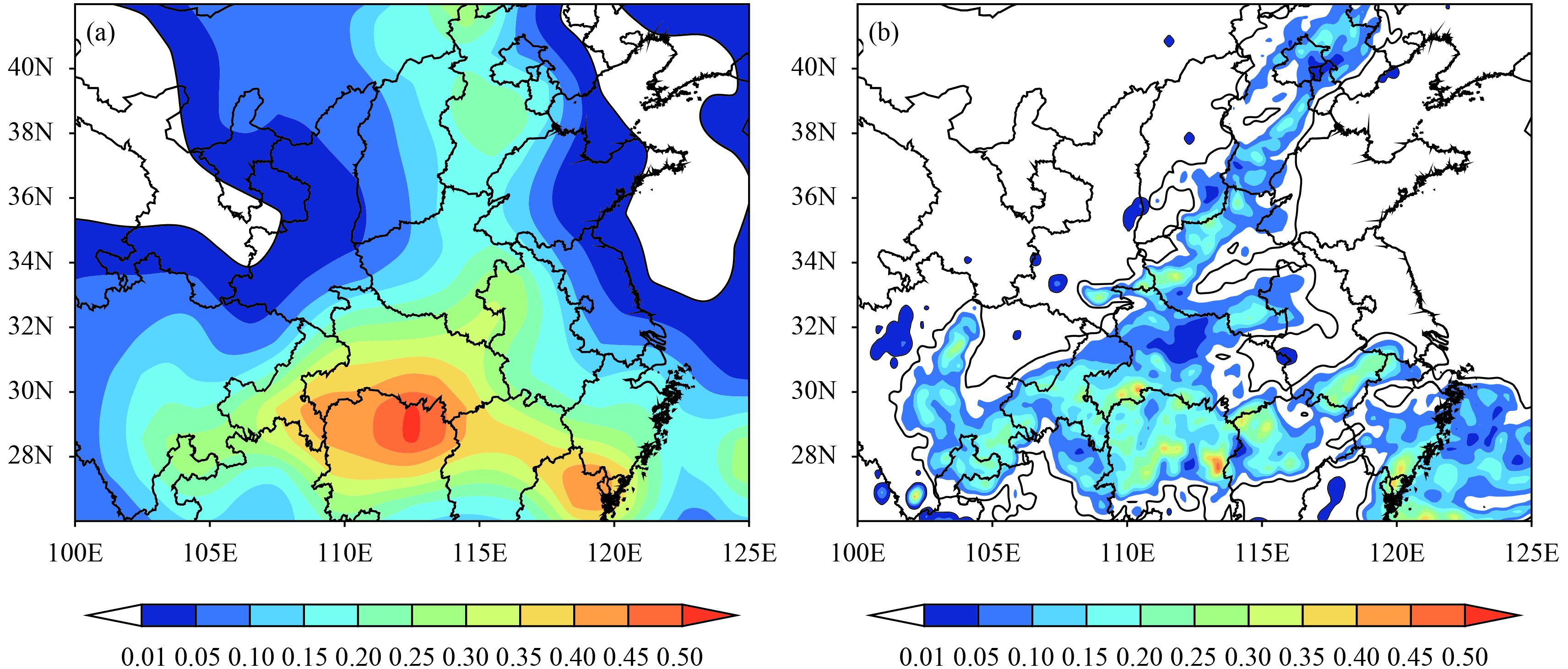
|
| Figure 4 Observed and simulated CLWP (kg m–2): (a) average values between the Terra and Aqua MODIS satellite observation, respectively, at 0230 and 0530 UTC 4 June; (b) average values of simulation results adopted WDM6 between 0300 and 0500 UTC 4 June. |
In summary, the results of CLWP simulated by the WDM6 scheme generally reflected the distribution of cloud water. Integrating the simulation of the cloud water conveyor belt with Fig. 3a could contribute to further studies of the variation of cloud water over time in Region A.
The WDM6 scheme, as a double-moment microphysics scheme, not only can predict mixing ratios of hydrometeors, but also can forecast number concentration. Figures 5a and 5b show the spatiotemporal distribution of domain-averaged cloud droplet number concentration (Nc; cm–3) and raindrop number concentration (Nr; L–1) simulated by the WDM6 scheme. From these figures, the distributions of both Nc and Nr were more consistent with each mixing ratio distribution; the number concentration distribution cores simulated by both schemes were located close to 700 hPa. The maximum value of Nc was 5 cm–3, which appeared at 0200 UTC June 4. With the increase in precipitation, Nc gradually decreased during the heavy precipitation period, whereas the corresponding Nr gradually increased, with a maximum value of 25 L–1. As precipitation gradually weakened and moved out of Region A, both Nc and Nr also decreased, but there was still a small quantity of raindrops near the ground, which then evaporated into cloud droplets, resulting in an obvious increase in Nc near the ground during 1900–2100 UTC.

|
| Figure 5 Spatiotemporal distributions of domain-averaged number concentration for hydrometeors in Region A simulated by WDM6: (a) cloud droplets (cm–3) and (b) raindrops (L–1). The solid line in figures represents the 0°C isotherm. |
In the cloud microphysical process, CCN number concentration has an important influence on Nc and Nr, as well as on the precipitation process. Based on the observation results for the North China region (Shi and Duan, 2007; Feng et al., 2012; Lu and Guo, 2012; Li et al., 2015), the findings showed that CCN number concentration differed according to location, pollution conditions, supersaturation, and height. CCN number concentration near ground reached a maximum value of 40,000 cm–3. With the increase in height, CCN number concentration generally showed a decreasing trend. CCN number concentrations at heights close to 3000 m could reach a maximum value of 1000 cm–3. Hence, in addition to using 100 cm–3 as the fixed value of CCN0, this study also designed a set of sensitivity tests, where 10, 100, 500, 1000, 3000, 5000, 7000, 9000, and 10,000 cm–3 were chosen as values of CCN0 to study the effect of CCN number concentration on precipitation trend, precipitation amount, and the microphysical process.
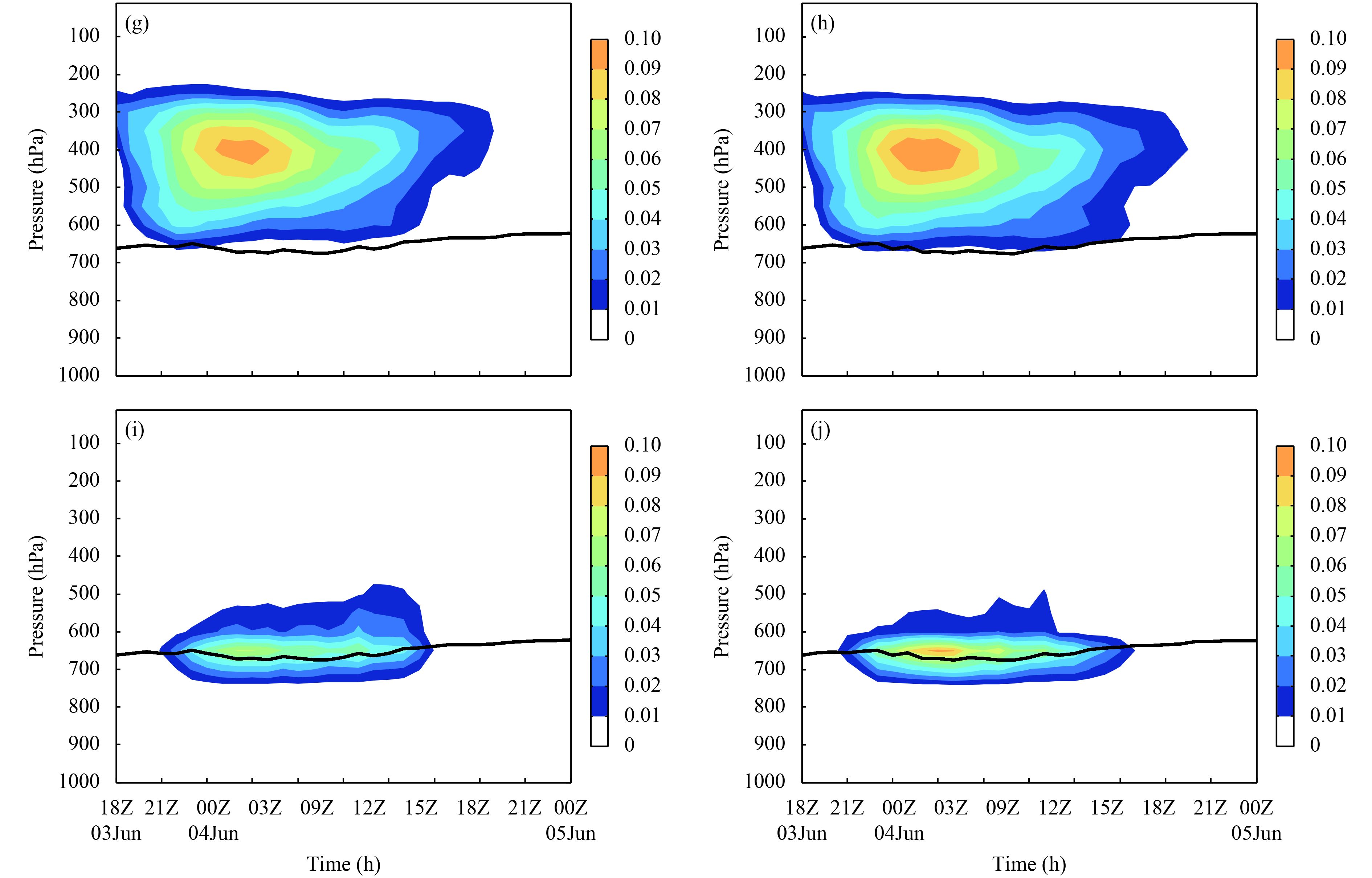
Figures 6a and 6b show the results for 24-h cumulative precipitation in Region A between 0000 UTC 4 and 0000 UTC 5 June simulated by the WDM6 scheme with CCN0 values of 10 and 3000 cm–3. By combining both figures above and Fig. 1b with a CCN0 value of 100 cm–3, it was evident that with the increase in CCN number concentration, the false precipitation core in the southern boundary of Region A weakened and disappeared after becoming stronger. This indicated that CCN number concentration could more or less affect precipitation. From composite reflectivity data at 0542 UTC (Fig. 7a), it was shown that the detection areas of Beijing south suburb radar were mainly suffering the stratiform precipitation process and composite reflectivity data were less than 35 dBZ in most regions. Even in the strong echo zones, hydrometeors almost distributed below than 4 km (Fig. 7c), where were dominated by the warm-rain processes. However, as the precipitation system moved from west to east, the stratiform precipitation process in the north of detection areas bashed on radar gradually weakened and a convective precipitation process took charge of the southeastern detection areas (Fig. 7b). The reflectivity of strong echo zones could reach 55 dBZ and distributed even 10 km (Fig. 7d), where the cold-rain processes played a crucial role. Hence, Region B (40.5°–42.0°N, 115.0°–117.0°E) and Region C (38.5°–40.0°N, 117.0°–119.0°E) were chosen to study the effect of CCN number concentration on cloud microphysical quantities during the main precipitation period at their respective locations.

|
| Figure 6 The 24-h cumulative precipitation (mm) simulated by WDM6 in Region A: (a) CCN0 = 10 cm–3 and (b) CCN0 = 3000 cm–3. |

|
| Figure 7 Composite reflectivity (dBZ) measured by the Beijing south suburb radar at (a) 0542 and (b) 1112 UTC June 4. (c) and (d) are RHI (range–height-indicator) data (dBZ) based on different vertical profiles (black thin thread) in (a) and (b), respectively. |
Figure 8a shows the vertical profile of the average mixing ratio of hydrometeors simulated by the WDM6 scheme in Region B during the main precipitation period from 0200 to 0800 UTC June 4 with CCN0 value of 100 cm–3. Based on Fig. 8a, cloud water content was mainly concentrated between 650 and 900 hPa but was found to be lower than the content of other hydrometeors. Rain content was mainly concentrated between 650 and 1000 hPa, with a maximum value of 0.18 g kg–1 near 750 hPa. In Figs. 8a, b, cloud water content increased with the increasing CCN number concentration, reaching a maximum value of 0.03 g kg–1 near 750 hPa. Despite a slight increase in rain content near the ground, the rain content at the upper level reduced significantly, thus indicating that rain content decreased as CCN number concentration increased. Among the ice-phase hydrometeors, cloud ice content slightly increased unobviously, whereas snow content reduced significantly. Despite an increase in graupel content, the overall content of ice-phase hydrometeors in Region B remained basically unchanged.
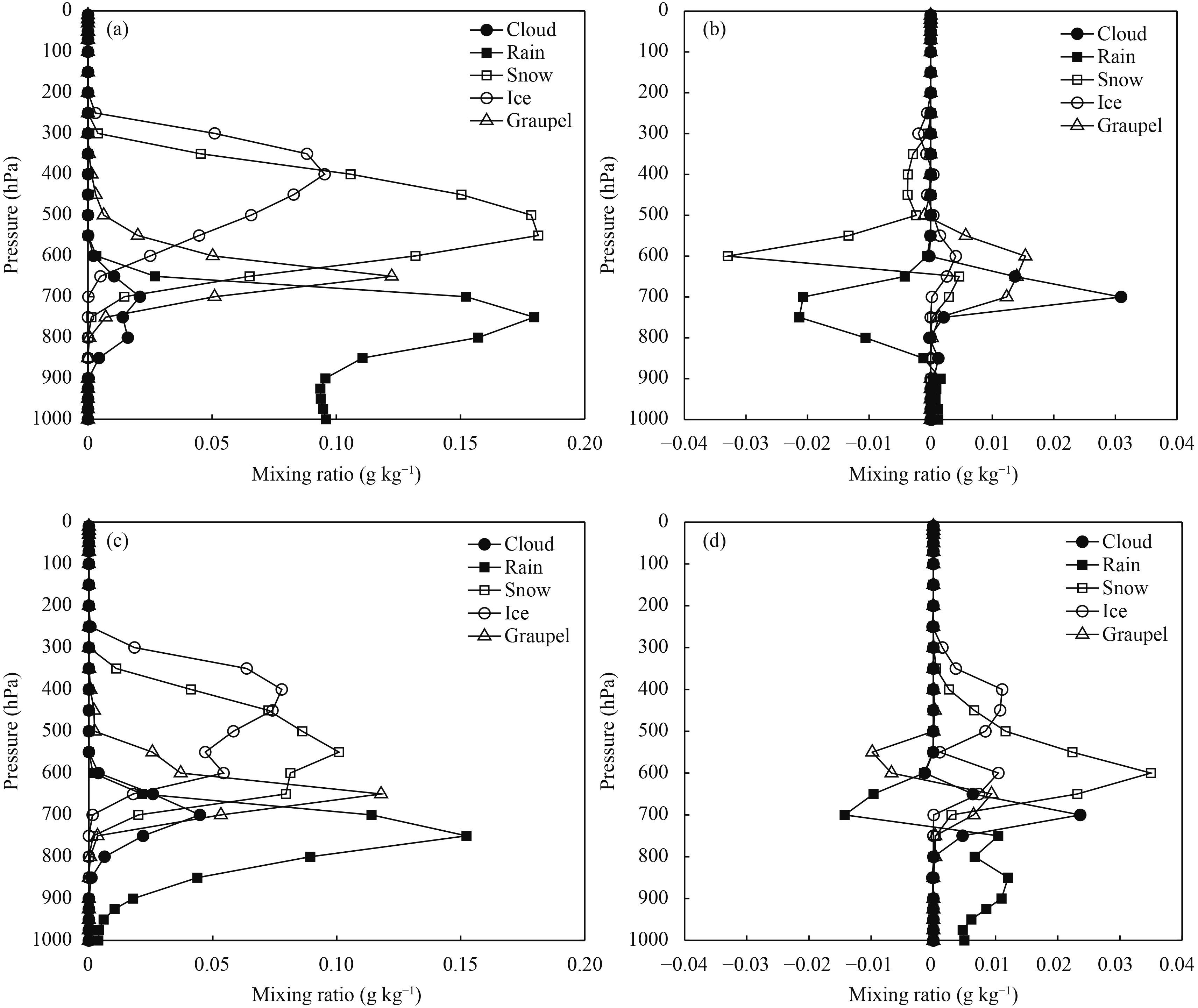
|
| Figure 8 Vertical profiles of average mixing ratio for hydrometeors simulated by WDM6 during the main precipitation period: (a, c) CCN0 = 100 cm–3, (b, d) difference in values between CCN0 = 3000 cm–3 and CCN0 = 100 cm–3; (a, b) Region B and (c, d) Region C. |
Figure 8c was the same as Fig. 8a but in Region C during the main precipitation period from 0800 to 1100 UTC. Compared to Region B, the cloud water content in Region C was higher, but the rain content was lower, with the difference near ground being particularly evident. Among the ice-phase hydrometeors, excluding graupel that indicated a higher content, cloud ice content and snow content in Region C were lower than that in Region B. Based on Figs. 8b, d, cloud water content increased, with the increasing CCN number concentration. The change of rain water content showed fluctuation with decrease first and then increase. But the rain water content decreased in general. Among the ice-phase hydrometeors, graupel content marginally decreased, whereas cloud ice content and snow content increased significantly. All in all, the total content of ice-phase hydrometeors in Region C showed a substantial increase.
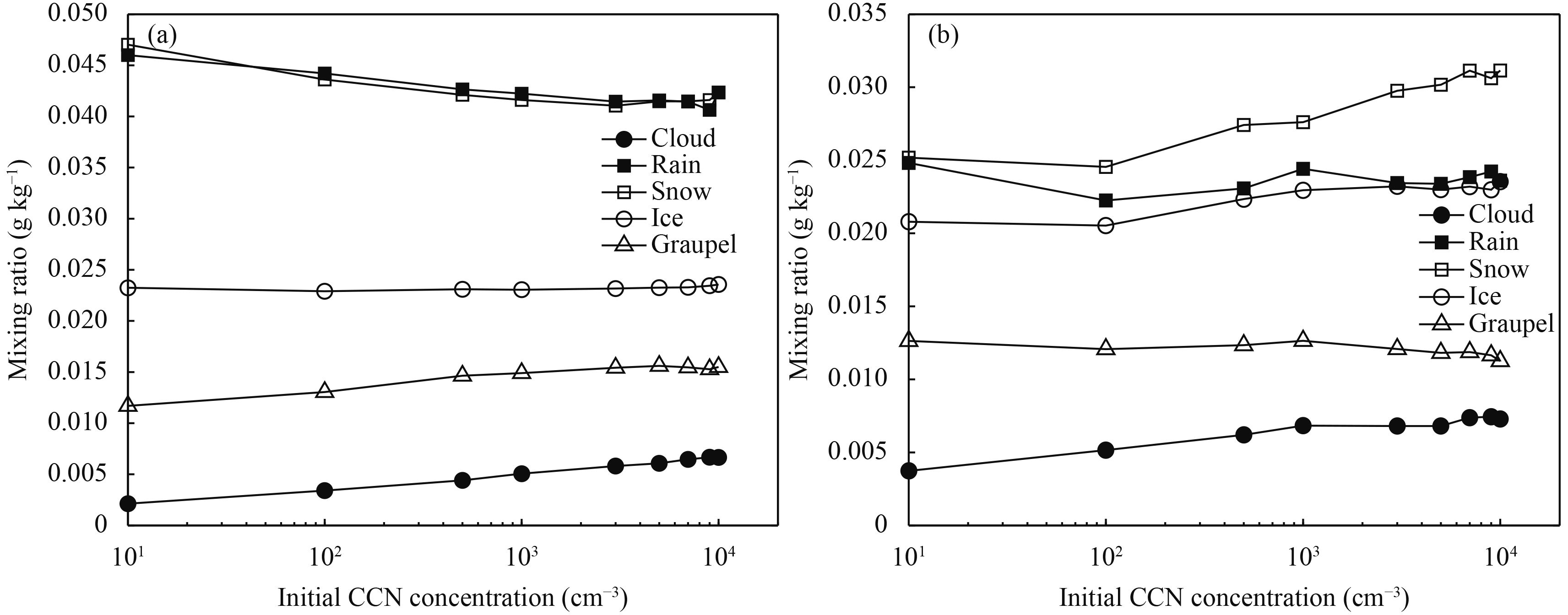
|
| Figure 9 Changes of domain-averaged mixing ratio for hydrometeors with CCN0 simulated by WDM6 during the main precipitation period: (a) Region B and (b) Region C. |
From Fig. 10, it can be seen that during the main precipitation period in Region B, volume-averaged cloud droplet diameter decreased with the increasing CCN number concentration (Fig. 10a). This resulted in a significant decrease of Praut (Fig. 10d), a corresponding decrease of Nr (Fig. 10f), and an increase of cloud water content in cloud areas, thus leading to a corresponding increase in the cloud water mixing ratio and a decrease in the rain mixing ratio. CCN activation rate (Pcact) indicated a gradually increasing trend (Fig. 10c), followed by an increase in Nc (Fig. 10e). On the other hand, a decrease of Praut (Fig. 10d) resulted in an increase in cloud water mixing ratio, providing the conditions for the growth of raindrops, with volume-averaged raindrop diameter correspondingly showing a gradually increasing trend (Fig. 10b). Despite slowing down the decreasing trend of the rain mixing ratio, the warm-rain processes were inhibited in general.

|
| Figure 10 Changes of the domain-averaged various cloud microphysical quantities in cloud areas with CCN0 values during each main precipitation period in Region B (solid-circle line) and Region C (hollow-circle line): (a) cloud droplet mean volume diameter, (b) raindrop mean volume diameter, (c) Pcact, (d) Praut, (e) Nc, and (f) Nr. A cloud area is defined if qc + qi > 0.01 g kg –1 or qr + qs > 0.01 g kg –1. |
In the warm-rain processes, Praut and Pracw were major considerations in increasing the rain mixing ratio, as the melting rate of snow (Psmlt) and graupel (Pgmlt) in cold-rain processes, and the evaporation rate of rain (Prevp) was taken into account in reducing the rain mixing ratio. From the vertically integrated domain-averaged production rates for major cloud microphysical processes influencing the rain mixing ratio in Region B (Fig. 11a), following the increasing CCN number concentration, the vertically integrated value of Praut significantly reduced, Pracw increased on the whole but with a reduced trend at the end, Prevp slightly reduced, and the sum of Psmlt and Pgmlt slightly barely changed. It suggested that the cold-rain processes were generally not influenced by the increasing CCN number concentration. Though the vertically integrated value of Pracw increased, the rain mixing ratio (Fig. 9a) and Nr (Fig. 10f) both decreased in Region B, so the warm-rain processes were inhibited. With an increase in CCN number concentration, the domain-averaged 24-h cumulative precipitation in Region B indicated a decreasing trend, as shown in Fig. 12a.
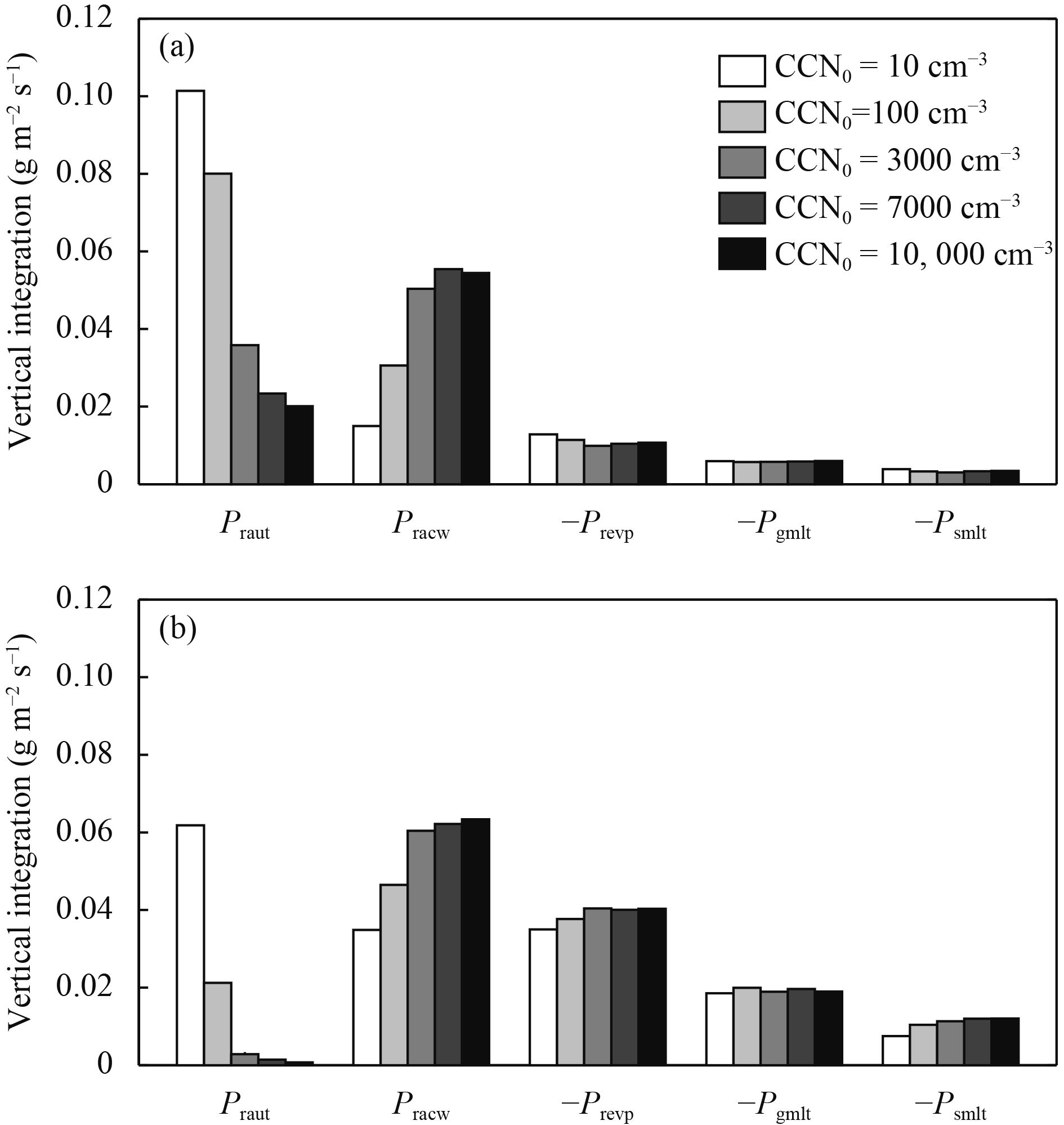
|
| Figure 11 Changes of the vertically integrated domain-averaged production rates for major cloud microphysical processes influencing the rain mixing ratio with CCN0 values during each main precipitation period: (a) Region B and (b) Region C. |
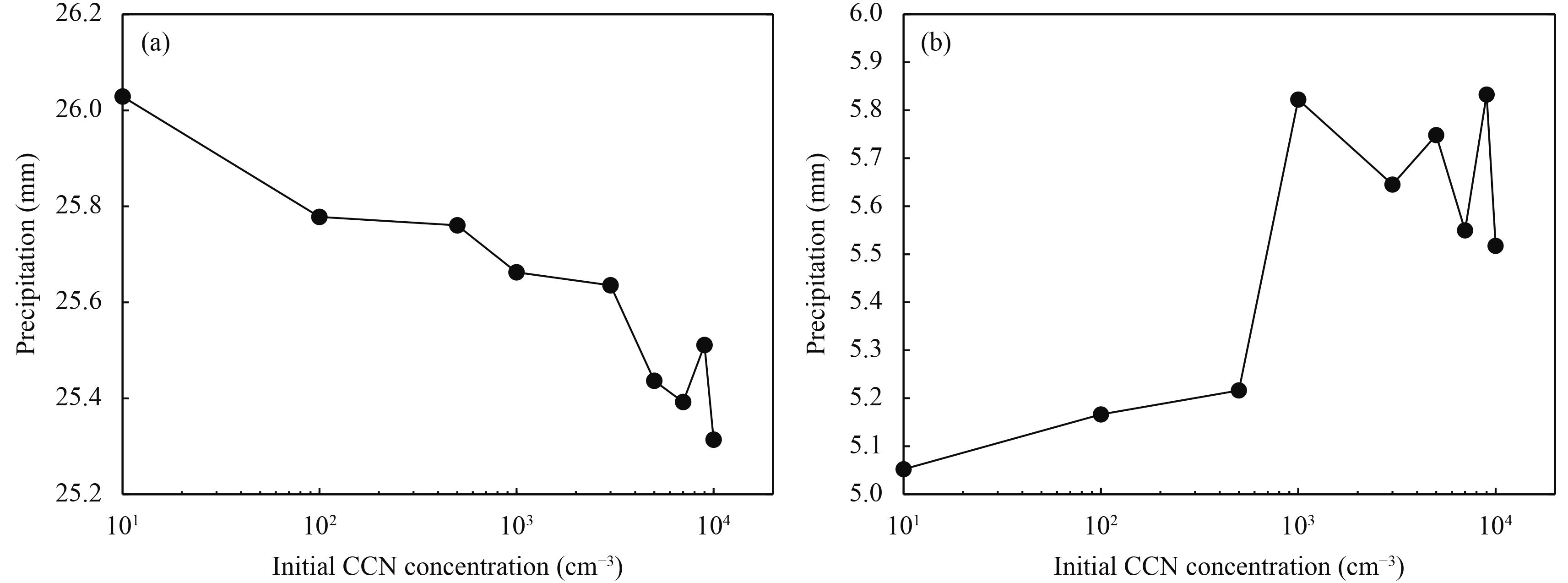
|
| Figure 12 Changes of domain-averaged 24-h (between 0000 UTC 4 and 0000 UTC 5 June) cumulative precipitation with CCN0: (a) Region B and (b) Region C. |
During the main precipitation period in Region C, the increase in Pcact was significantly greater than that in Region B, following the increase in CCN number concentration. This resulted in the formation of more small-scale cloud droplets in Region C. However, the condensation growth of cloud droplet was inversely proportional to its diameter, such that small-scale cloud droplets grew faster than large-scale cloud droplets. This not only depleted a large amount of cloud water content required for the growth of cloud droplets, but also inhibited the growth of large-scale cloud droplets into raindrops. In Fig. 10b, a decreasing trend is limited only at the end of the line, for the high values of CCN number concentration. Changes in the domain average of other cloud microphysical quantities in cloud areas with respect to CCN number concentration in Region C were consistent with those in Region B.
In Fig. 11b, the sum of Psmlt and Pgmlt in Region C was larger than Region B, and appeared an increasing trend. As the rain mixing ratio near the ground also showed an increase trend (Fig. 8d), so the cold-rain processes were certainly enhanced, and had a great contribution on ground precipitation in Region C. The vertically integrated values of Praut and Pracw were same with Region B in the changing trend. Praut reduced significantly, when CCN number concentrations were in low values. Thus, in Fig. 8b, the rain mixing ratio decreased at the beginning. As the cold-rain processes enhanced, the rain mixing ratio increased afterward. The growth of rain mixing ratio was based on the accretion of raindrop by collecting cloud water. However, Nr decreased in Region C (Fig. 10f), and the rain mixing ratio showed a decreased trend in general. With an increase of CCN number concentration, the warm-rain processes in Region C were inhibited, which was similar to Region B. Therefore, the domain-averaged 24-h cumulative precipitation in Region C, as the cold-rain processes enhanced, showed an increasing trend in Fig. 12b. However, the warm-rain processes were significantly inhibited, Prevp increased at high values of CCN number concentrations, and the amount of precipitation exhibited a decreasing trend.
In summary, spatial inconsistencies were found in the effect of CCN number concentration on precipitation. Although the increase in CCN number concentration resulted in the inhibition of warm-rain processes, the amount of precipitation increased in regions dominated by the cold-rain processes. However, when CCN number concentration exceeded 1000 cm–3, the amount of precipitation indicated a decreasing trend.
5 Conclusions and discussionThis study coupled the WDM6 double-moment microphysics scheme into the GRAPES_Meso model, and simulated a precipitation process from 3 to 5 June 2015 in North China, especially in Beijing and its surrounding area. The simulations results were compared with those from the WSM6 and NCEP 5-class schemes. In addition, a set of sensitivity tests were performed, with values of CCN0 varing among 10, 100, 500, 1000, 3000, 5000, 7000, 9000, and 10,000 cm–3, to study the effect of CCN number concentration on precipitation and cloud microphysics in the WDM6 scheme. The findings in this paper are summarized as follows.
(1) Although the 24-h cumulative precipitation simulated by the WDM6 scheme was somewhat different from the observation, the intensity and range of the precipitation core were basically consistent with observation. The hourly amount of precipitation was found to be slightly greater than that of the automatic station observation, but the trends over time were in accord with observation. In this precipitation process, the simulation by WDM6 demonstrated the best effect, with its simulated precipitation closest to the observation. The simulation results of the WSM6 scheme were second best, with the size range of the precipitation core and the hourly amount of precipitation much greater than the observation. The NCEP 5-class scheme exhibited the worst simulation, with the intensity of the precipitation core slightly less than the observation and the range of precipitation particularly smaller.
(2) Different treatment of warm rain between WDM6 and WSM6 led to lower cloud water content and higher rain content in the simulations using WDM6. The cold-rain processes as well as the treatment of cloud ice and snow content in both schemes were approximately the same. However, the cloud water content simulated by WSM6 found to be higher, leading to higher graupel content, which contributed to increased precipitation during cold-rain processes. This was one of the main reasons for the higher amount of precipitation from the simulations using the WSM6 scheme. The WDM6 scheme could forecast the number concentration of CCN, cloud droplets, and raindrops, and the mixing ratios of cloud droplet and raindrop were found to be consistent with their number concentrations in the spatial distribution. Both the amount and distribution of CLWP simulated by the WDM6 scheme were generally consistent with satellite observations.
(3) The effect of CCN number concentration on precipitation showed spatial inconsistencies. These occurred because of the issues related to whether precipitation was dominated by the warm- or cold-rain processes, whether precipitation was heavy or weak, or issues related to the WDM6 double-moment scheme itself. The findings from the sensitivity tests in this study showed that with an increase in CCN number concentration, the warm-rain processes were inhibited, resulting in a decrease in the precipitation. The effect on the cold-rain processes was mainly determined by the melting of ice-phase hydrometeors. If the melting rate increased, the cold-rain processes significantly enhanced, leading to higher ground precipitation. Thus, in areas where the cold-rain processes were dominant, the precipitation increased in general. But when CCN number concentration exceeded 1000 cm–3, the precipitation gradually decreased. In cloud microphysical processes, with the increasing CCN number concentration, cloud droplet effective diameter decreased, whereas raindrop effective diameter increased at first but gradually decreased later, both Praut and Pcact increased, and an increase of Nc was coupled with the decrease of Nr.
In summary, the results of this case study show that the WDM6 scheme produces a more reasonable description of precipitation and cloud microphysical processes in the study area. Its simulation of precipitation is closer to the observation compared with the WSM6 and NCEP 5-class schemes. Hence, the WDM6 scheme can be used as one of the alternative cloud microphysics schemes for the GRAPES_Meso model.
This study was based on the NWP simulation results of a precipitation case. In view of the complexity of the effect of CCN on clouds and precipitation, more cloud and precipitation cases in different seasons and areas at different intensities will be simulated and examined in the future. Besides, as the stratiform precipitation was dominant in this case with long precipitation duration and small precipitation intensity, the grid resolution of 0.15° was chosen. But when simulating convective precipitation, higher resolution and smaller model domain should be adopted. If compared with the Morrison scheme, which includes the double-moment microphysics scheme in both the warm- and cold-rain processes, different simulation results would be produced for ice-phase hydrometeors, thus affecting the precipitation simulation. Comparative studies of the WDM6 scheme with other schemes will be carried out next. Furthermore, the effect of double-moment schemes on the effective diameter of cloud droplet and raindrop will result in significant changes in cloud radiative properties and have an important influence on the cloud radiative processes and the energy balance, which will be discussed in the future studies.
| Bae, S. Y., S.-Y. Hong, and K.-S. S. Lim, 2016: Coupling WRF double-moment 6-class microphysics schemes to RRTMG radiation scheme in weather research forecasting model. Adv. Meteor., 2016, 1–11. DOI:10.1155/2016/5070154 |
| Baker, M. B., 1997: Cloud microphysics and climate. Science, 276, 1072–1078. DOI:10.1126/science.276.5315.1072 |
| Chen, D. H., and X. S. Shen, 2006: Recent progress on GRAPES research and application. J. Appl. Meteor. Sci., 17, 773–777. DOI:10.3969/j.issn.1001-7313.2006.06.014 |
| Chen, D. H., J. S. Xue, X. S. Yang, et al., 2008: New generation of multi-scale NWP system (GRAPES): General scientific design. Chinese Sci. Bull., 53, 3433–3445. DOI:10.1007/s11434-008-0494-z |
| Chen, Y. D., R. Z. Zhang, D. M. Meng, et al., 2016: Variational assimilation of satellite cloud water/ice path and microphysics scheme sensitivity to the assimilation of a rainfall case. Adv. Atmos. Sci., 33, 1158–1170. DOI:10.1007/s00376-016-6004-3 |
| Clark, T. L., 1973: Numerical modeling of the dynamics and microphysics of warm cumulus convection. J. Atmos. Sci., 30, 857–878. DOI:10.1175/1520-0469(1973)030<0857:NMOTDA>2.0.CO;2 |
| Cohard, J.-M., and J.-P. Pinty, 2000a: A comprehensive two-moment warm microphysical bulk scheme. I: Description and tests. Quart. J. Roy. Meteor. Soc., 126, 1815–1842. DOI:10.1002/qj.49712656613 |
| Cohard, J.-M., and J.-P. Pinty, 2000b: A comprehensive two-moment warm microphysical bulk scheme. II: 2D experiments with a non-hydrostatic model. Quart. J. Roy. Meteor. Soc., 126, 1843–1859. DOI:10.1002/qj.49712656614 |
| Cotton, W. R., G. J. Tripoli, R. M. Rauber, et al., 1986: Numerical simulation of the effects of varying ice crystal nucleation rates and aggregation processes on orographic snowfall. J. Climate Appl. Meteor., 25, 1658–1680. DOI:10.1175/1520-0450(1986)025<1658:NSOTEO>2.0.CO;2 |
| Deng, Z. Z., C. S. Zhao, N. Ma, et al., 2013: An examination of parameterizations for the CCN number concentration based on in situ measurements of aerosol activation properties in the North China Plain. Atmos. Chem. Phys., 13, 145–176. DOI:10.5194/acp-13-6227-2013 |
| Dong, H., H. M. Xu, and Y. L. Luo, 2012: Effects of cloud condensation nuclei concentration on precipitation in convection permitting simulations of a squall line using WRF model: Sensitivity to cloud microphysical schemes. Chinese J. Atmos. Sci., 36, 145–169. DOI:10.3878/j.issn.1006-9895.2012.01.12 |
| Duda, J. D., X. G. Wang, F. Y. Kong, et al., 2014: Using varied microphysics to account for uncertainty in warm-season QPF in a convection-allowing ensemble. Mon. Wea. Rev., 142, 2198–2219. DOI:10.1175/MWR-D-13-00297.1 |
| Feng, Q. J., P. R. Li, M. Y. Fan, et al., 2012: Observational analysis of cloud condensation nuclei in some regions of North China. Trans. Atmos. Sci., 35, 533–540. DOI:10.3969/j.issn.1674-7097.2012.05.003 |
| Ferrier, B. S., 1994: A double-moment multiple-phase four-class bulk ice scheme. Part I: Description. J. Atmos. Sci., 51, 249–280. DOI:10.1175/1520-0469(1994)051<0249:ADMMPF>2.0.CO;2 |
| Guo, X. L., M. Y. Huang, H. Y. Xu, et al., 1999: Rain category numerical simulations of microphysical processes of precipitation formation in stratiform clouds. Chinese J. Atmos. Sci., 23, 745–752. DOI:10.3878/j.issn.1006-9895.1999.06.11 |
| Gao, W. H., F. S. Zhao, Z. J. Hu, et al., 2012: Improved CAMS cloud microphysics scheme and numerical experiment coupled with WRF model. Chinese J. Geophys., 55, 396–405. DOI:10.6038/j.issn.0001-5733.2012.02.004 |
| Guo, X. L., D. H. Fu, X. Guo, et al., 2014: A case study of aerosol impacts on summer convective clouds and precipitation over northern China. Atmos. Res., 142, 142–157. DOI:10.1016/j.atmosres.2013.10.006 |
| Hall, W. D., 1980: A detailed microphysical model within a two-dimensional dynamic framework: Model description and preliminary results. J. Atmos. Sci., 37, 2486–2507. DOI:10.1175/1520-0469(1980)037<2486:ADMMWA>2.0.CO;2 |
| Hartmann, D. L., M. E. Ockert-Bell, and M. L. Michelsen, 1992: The effect of cloud type on earth’s energy balance: Global analysis. J. Climate, 5, 1281–1304. DOI:10.1175/1520-0442(1992)005<1281:TEOCTO>2.0.CO;2 |
| He, H., X. L. Guo, X. E. Liu, et al., 2016: Mesoscale numerical simulation study of warm fog dissipation by salt particles seeding. Adv. Atmos. Sci., 33, 579–592. DOI:10.1007/s00376-015-5151-2 |
| Hong, S.-Y., and J.-O. J. Lim, 2006: The WRF single-moment 6-class microphysics scheme (WSM6). J. Korean Meteor. Soc., 42, 129–151. |
| Hong, S.-Y, K.-S. S. Lim, Y.-H. Lee, et al., 2010: Evaluation of the WRF double-moment 6-class microphysics scheme for precipitating convection. Adv. Meteor., 707253. DOI:10.1155/2010/707253 |
| Hong, Y. C., and H. Y. Li, 2011: Cloud structure, precipitation mechanism and artificial enhancement precipitation condition for a frontal stratiform cloud system. Plateau Meteor., 30, 1308–1323. |
| Hou, T.-J., H.-C. Lei, Z.-X. Hu, et al., 2013: Observations and modeling of ice water content in a mixed-phase cloud system. Atmos. Oceanic Sci. Lett., 6, 210–215. DOI:10.3878/j.issn.1674-2834.13.0020 |
| Hou, T. J., H. C. Lei, J. F. Yang, et al., 2016: Investigation of riming within mixed-phase stratiform clouds using weather research and forecasting (WRF) model. Atmos. Res., 178–179, 291–303. DOI:10.1016/j.atmosres.2016.04.007 |
| Hu, Z. J., and G. F. He, 1988: Numerical simulation of microphysical processes in cumulonimbus. Part I: Microphysical model. Acta Meteor. Sinica, 2, 471–489. |
| Khain, A. P., and I. Sednev, 1996: Simulation of precipitation formation in the eastern Mediterranean coastal zone using a spectral microphysics cloud ensemble model. Atmos. Res., 43, 77–110. DOI:10.1016/S0169-8095(96)00005-1 |
| Khain, A., A. Pokrovsky, M. Pinsky, et al., 2004: Simulation of effects of atmospheric aerosols on deep turbulent convective clouds using a spectral microphysics mixed-phase cumulus cloud model. Part I: Model description and possible applications. J. Atmos. Sci., 61, 2963–2982. DOI:10.1175/JAS-3350.1 |
| Khain, A., D. Rosenfeld, and A. Pokrovsky, 2005: Aerosol impact on the dynamics and microphysics of deep convective clouds. Quart. J. Roy. Meteor. Soc., 131, 2639–2663. DOI:10.1256/qj.04.62 |
| Kovačević, N., and M. Ćurić, 2015: Precipitation sensitivity to the mean radius of drop spectra: Comparison of single- and double-moment bulk microphysical schemes. Atmosphere, 6, 451–473. DOI:10.3390/atmos6040451 |
| Kogan, Y. L., 1991: The simulation of a convective cloud in a 3-D model with explicit microphysics. Part I: Model description and sensitivity experiments. J. Atmos. Sci., 48, 1160–1189. DOI:10.1175/1520-0469(1991)048<1160:TSOACC>2.0.CO;2 |
| Li, L., Y. Yin, X. S. Gu, et al., 2014: Observational study of cloud condensation nuclei properties at various altitudes of Huangshan mountains. Chinese J. Atmos. Sci., 38, 410–420. DOI:10.3878/j.issn.1006-9895.2013.13149 |
| Li, J. X., Y. Yin, G. Ren, et al., 2015: Observational study of the spatial–temporal distribution of cloud condensation nuclei in Shanxi Province, China. China Environ. Sci., 35, 2261–2271. DOI:10.3969/j.issn.1000-6923.2015.08.003 |
| Lim, K.-S. S., and S.-Y. Hong, 2010: Development of an effective double-moment cloud microphysics scheme with prognostic cloud condensation nuclei (CCN) for weather and climate models. Mon. Wea. Rev., 138, 1587–1612. DOI:10.1175/2009MWR2968.1 |
| Lin, Y.-L., R. D. Farley, and H. D. Orville, 1983: Bulk parameterization of the snow field in a cloud model. J. Climate Appl. Meteor., 22, 1065–1092. DOI:10.1175/1520-0450(1983)022<1065:BPOTSF>2.0.CO;2 |
| Liu, P. F., C. S. Zhao, T. Göbel, et al., 2011: Hygroscopic properties of aerosol particles at high relative humidity and their diurnal variations in the North China Plain. Atmos. Chem. Phys., 11, 3479–3494. DOI:10.5194/acp-11-3479-2011 |
| Lu, G. X., and X. L. Guo, 2012: Distribution and origin of aerosol and its transform relationship with CCN derived from the spring multi-aircraft measurements of Beijing cloud experiment (BCE). Chinese Sci. Bull., 57, 2460–2469. DOI:10.1007/s11434-012-5136-9 |
| Ma, N., C. S. Zhao, T. Müller, et al., 2012: A new method to determine the mixing state of light absorbing carbonaceous using the measured aerosol optical properties and number size distributions. Atmos. Chem. Phys., 12, 2381–2397. DOI:10.5194/acp-12-2381-2012 |
| Meyers, M. P., R. L. Walko, J. Y. Harrington, et al., 1997: New RAMS cloud microphysics parameterization. Part II: The two-moment scheme. Atmos. Res., 45, 3–39. DOI:10.1016/<1065:BPOTSF>S0169-8095(97)00018-5 |
| Molthan, A. L., and B. A. Colle, 2012: Comparisons of single-and double-moment microphysics schemes in the simulation of a synoptic-scale snowfall event. Mon. Wea. Rev., 140, 2982–3002. DOI:10.1175/MWR-D-11-00292.1 |
| Morrison, H., and J. O. Pinto, 2005: Mesoscale modeling of springtime arctic mixed-phase stratiform clouds using a new two-moment bulk microphysics scheme. J. Atmos. Sci., 62, 3683–3704. DOI:10.1175/JAS3564.1 |
| Morrison, H., G. Thompson, and V. Tatarskii, 2009: Impact of cloud microphysics on the development of trailing stratiform precipitation in a simulated squall line: Comparison of one-and two-moment schemes. Mon. Wea. Rev., 137, 991–1007. DOI:10.1175/2008MWR2556.1 |
| Murakami, M., 1990: Numerical Modeling of dynamical and microphysical evolution of an isolated convective cloud: The 19 July 1981 CCOPE cloud. J. Metor. Soc. Japan, 68, 107–128. DOI:10.2151/jmsj1965.68.2_107 |
| Ovtchinnikov, M., and Y. L. Kogan, 2000: An investigation of ice production mechanisms in small cumuliform clouds using a 3D model with explicit microphysics. Part I: Model description. J. Atmos. Sci., 57, 2989–3003. DOI:10.1175/1520-0469(2000)057<2989:AIOIPM>2.0.CO;2 |
| Pinsky, M. B., and A. P. Khain, 2002: Effects of in-cloud nucleation and turbulence on droplet spectrum formation in cumulus clouds. Quart. J. Roy. Meteor. Soc., 128, 501–533. DOI:10.1256/003590002321042072 |
| Ramanathan, V., P. J. Crutzen, J. T, Kiehl, et al., 2001: Aerosols, climate, and the hydrological cycle. Science, 294, 2119–2124. DOI:10.1126/science.1064034 |
| Reisin, T., Z. Levin, and S. Tzivion, 1996: Rain production in convective clouds as simulated in an axisymmetric model with detailed microphysics. Part I: Description of the model. J. Atmos. Sci., 53, 497–519. DOI:10.1175/1520-0469(1996)053<0497:RPICCA>2.0.CO;2 |
| Reisner, J., R. M. Rasmussen, and R. T. Bruintjes, 1998: Explicit forecasting of supercooled liquid water in winter storms using the MM5 mesoscale model. Quart. J. Roy. Meteor. Soc., 124, 1071–1107. DOI:10.1002/qj.49712454804 |
| Rong, Y. M., and Y. Yin, 2010: The response of convective clouds to aerosol and relative humidity: A numerical study. Chinese J. Atmos. Sci., 34, 815–826. DOI:10.3878/j.issn.1006-9895.2010.04.13 |
| Seifert, A., and K. D. Beheng, 2001: A double-moment parameterization for simulating autoconversion, accretion and selfcollection. Atmos. Res., 59–60, 265–281. DOI:10.1016/S0169-8095(01)00126-0 |
| Seifert, A., and K. D. Beheng, 2006: A two-moment cloud microphysics parameterization for mixed-phase clouds. Part 1: Model description. Atmos. Phys., 92, 45–66. DOI:10.1007/s00703-005-0112-4 |
| Shen, X. Y., H. X. Mei, W. G. Wang, et al., 2015: Numerical simulation of ice-phase processes using a double-moment microphysical scheme and a sensitivity test of ice nuclei concentration. Chinese J. Atmos. Sci., 39, 83–99. DOI:10.3878/j.issn.1006-9895.1405.13310 |
| Shi, L. X., and Y. Duan, 2007: Observations of cloud condensation nuclei in North China. Acta Meteor. Sinica, 75, 644–652. DOI:10.3321/j.issn:0577-6619.2007.04.016 |
| Shi, R. G., Q. J. Liu, and Z. S. Ma, 2015: Numerical simulation of aerosol effects on cloud and precipitation using GRAPES model. Meteor. Mon., 41, 272–285. DOI:10.7519/j.issn.1000-0526.2015.03.002 |
| Soong, S.-T, 1974: Numerical simulation of warm rain development in an axisymmetric cloud model. J. Atmos. Sci., 31, 1262–1285. DOI:10.1175/1520-0469(1974)031<1262:NSOWRD>2.0.CO;2 |
| Stephens, G. L., 2005: Cloud feedbacks in the climate system: A critical review. J. Climate, 18, 237–273. DOI:10.1175/JCLI-3243.1 |
| Stevens, B., G. Feingold, W. R. Cotton, et al., 1996: Elements of the microphysical structure of numerically simulated nonprecipitating stratocumulus. J. Atmos. Sci., 53, 980–1006. DOI:10.1175/1520-0469(1996)053<0980:EOTMSO>2.0.CO;2 |
| Sun, J., X. F. Lou, Z. J. Hu, et al., 2008: Numerical experiment of the coupling of CAMS complex microphysical scheme and GRAPES model. J. Appl. Meteor. Sci., 19, 315–325. DOI:10.3969/j.issn.1001-7313.2008.03.007 |
| Sun, J., X. F. Lou, and Y. Q. Shi, 2011: The effects of different microphysical schemes on the simulation of a meiyu front heavy rainfall. Acta Meteor. Sinica, 69, 799–809. |
| Takahashi, T., 1975: Tropical showers in an axisymmetric cloud model. J. Atmos. Sci., 32, 1318–1330. DOI:10.1175/1520-0469(1975)032<1318:TSIAAC>2.0.CO;2 |
| Tao, Y., H. Y. Li, and Y. C. Hong, 2013: Numerical studies on cloud physics characteristic and influence of the graupel/hail category on cloud and precipitation during a heavy rainstorm over North China. Plateau Meteor., 32, 166–178. DOI:10.7522/j.issn.1000-0534.2012.00017 |
| Thompson, G., R. M. Rasmussen, and K. Manning, 2004: Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part I: Description and sensitivity analysis. Mon. Wea. Rev., 132, 519–542. DOI:10.1175/1520-0493(2004)132<0519:EFOWPU>2.0.CO;2 |
| Thompson, G., P. R. Field, R. M. Rasmussen, et al., 2008: Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part II: Implementation of a new snow parameterization. Mon. Wea. Rev., 136, 5095–5115. DOI:10.1175/2008MWR2387.1 |
| Van Weverberg, K., E. Goudenhoofdt, U. Blahak, et al., 2014: Comparison of one-moment and two-moment bulk microphysics for high-resolution climate simulations of intense precipitation. Atmos. Res., 147–148, 145–161. DOI:10.1016/j.atmosres.2014.05.012 |
| Wang, C., and J. S. Chang, 1993: A three-dimensional numerical model of cloud dynamics, microphysics, and chemistry. 1: Concepts and formulation. J. Geophys. Res., 98, 14827–14844. DOI:10.1029/92JD01393 |
| Wang, H., J. F. Yin, and D. H. Wang, 2014: Comparative analysis of single-moment and double-moment microphysics schemes on a local heavy rainfall in South China. Plateau Meteor., 33, 1341–1351. DOI:10.7522/j.issn.1000-0534.2013.00119 |
| Wang, H., G. Y. Shi, X. Y. Zhang, et al., 2015: Mesoscale modelling study of the interactions between aerosols and PBL meteorology during a haze episode in China Jing–Jin–Ji and its near surrounding region—Part 2: Aerosols’ radiative feedback effects. Atmos. Chem. Phys., 15, 3277–3287. DOI:10.5194/acp-15-3277-2015 |
| Wu, X. J., Z. Y. Jin, L. P. Huang, et al., 2005: The software framework and application of GRAPES model. J. Appl. Meteor. Sci., 16, 539–546. DOI:10.3969/j.issn.1001-7313.2005.04.015 |
| Wu, H. Y., D. H. Chen, and G. Q. Xu, 2007: Sensitive experiments of various parameterization schemes in different physical processes on Guizhou precipitation. Meteor. Mon., 33, 23–28. DOI:10.3969/j.issn.1000-0526.2007.04.004 |
| Xiao, H., and Y. Yin, 2011: A numerical study of polluted aerosol effects on precipitation in Shanxi Province. Chinese J. Atmos. Sci., 35, 235–246. DOI:10.3878/j.issn.1006-9895.2011.02.04 |
| Xiao, H., Y. Yin, L. J. Jin, et al., 2015: Simulation of the effects of aerosol on mixed-phase orographic clouds using the WRF model with a detailed bin microphysics scheme. J. Geophys. Res., 120, 8345–8358. DOI:10.1002/2014JD022988 |
| Xu, G. Q., X. D. Liang, H. Yu, et al., 2007: Precipitation simulation using different cloud–precipitation schemes for a landfall typhoon. Plateau Meteor., 26, 891–900. |
| Xu, G. Q., D. H. Chen, J. S. Xue, et al., 2008: The program structure designing and optimizing tests of GRAPES physics. Chinese Sci. Bull., 53, 3470–3476. DOI:10.1007/s11434-008-0418-y |
| Xu, G. Q., D. H. Chen, H. L. Zhang, et al., 2010: The impacts of time-level computation precision of physics in the GRAPES model on precipitation prediction. Chinese J. Atmos. Sci., 34, 875–881. DOI:10.3878/j.issn.1006-9895.2010.05.03 |
| Yang, X. S., J. L. Hu, D. H. Chen, et al., 2008: Verification of GRAPES unified global and regional numerical weather prediction model dynamic core. Chinese Sci. Bull., 53, 3458–3464. DOI:10.1007/s11434-008-0417-z |
| Yang, J. F., H. C. Lei, Z. X. Hu, et al., 2014: Particle size spectra and possible mechanisms of high ice concentration in nimbostratus over Hebei Province, China. Atmos. Res., 142, 79–90. DOI:10.1016/j.atmosres.2013.12.018 |
| Yin, Y., Z. Levin, T. Reisin, et al., 2000: Seeding convective clouds with hygroscopic flares: Numerical simulations using a cloud model with detailed microphysics. J. Appl. Meteor., 39, 1460–1472. DOI:10.1175/1520-0450(2000)039<1460:SCCWHF>2.0.CO;2 |
| Yin, Y., C. Chen, K. Chen, et al., 2010: An observational study of the microphysical properties of atmospheric aerosol at Mt Huang. Trans. Atmos. Sci., 33, 129–136. DOI:10.3969/j.issn.1674-7097.2010.02.001 |
| Yin, Y., Q. Chen, L. J. Jin, et al., 2012: The effects of deep convection on the concentration and size distribution of aerosol particles within the upper troposphere: A case study. J. Geophys. Res. Atmos., 117, D22202. DOI:10.1029/2012JD017827 |
| Yuan, L., Y. Yin, H. Xiao, et al., 2016: A closure study of aerosol optical properties at a regional background mountainous site in eastern China. Sci. Total Environ., 550, 950–960. DOI:10.1016/j.scitotenv.2016.01.205 |
| Zhao, C. S., X. X. Tie, G. Brasseur, et al., 2006: Aircraft measurements of cloud droplet spectral dispersion and implications for indirect aerosol radiative forcing. Geophys. Res. Lett., 33, L16809. DOI:10.1029/2006GL026653 |
| Zhao, Z., and H. C. Lei, 2008: A numerical simulation of cloud physical structure and microphysical processes associated with stratiform precipitation in Northwest China. Chinese J. Atmos. Sci., 32, 323–334. DOI:10.3878/j.issn.1006-9895.2008.02.11 |
| Zhao, Z., and H. C. Lei, 2014: Aircraft observations of liquid and ice in midlatitude mixed-phase clouds. Adv. Atmos. Sci., 31, 604–610. DOI:10.1007/s00376-013-3083-2 |
| Zhao, P. G., Y. Yin, and H. Xiao, 2015: The effects of aerosol on development of thunderstorm electrification: A numerical study. Atmos. Res., 153, 376–391. DOI:10.1016/j.atmosres.2014.09.011 |
| Zhou, C., X. Zhang, S. Gong, et al., 2016: Improving aerosol interaction with clouds and precipitation in a regional chemical weather modeling system. Atmos. Chem. Phys., 16, 145–160. DOI:10.5194/acp-16-145-2016 |
| Zhu, G. L., W. T. Lin, and Y. H. Cao, 2014: Numerical simulation of a rainstorm event over South China by using various cloud microphysics parameterization schemes in WRF model and its performance analysis. Chinese J. Atmos. Sci., 38, 513–523. DOI:10.3878/j.issn.1006-9895.2013.13202 |
 2018, Vol. 32
2018, Vol. 32


