The Chinese Meteorological Society
Article Information
- GUAN, Liang, and Xuyang GE, 2018.
- How Does Tropical Cyclone Size Affect the Onset Timing of Secondary Eyewall Formation?. 2018.
- J. Meteor. Res., 32(1): 124-134
- http://dx.doi.org/10.1007/s13351-018-7023-z
Article History
- Received March 9, 2017
- in final form October 18, 2017
2. Shanghai Meteorological Science and Technology Service Center, Shanghai 200030
Tropical cyclone (TC) intensity forecast is one of the most challenging tasks for operational forecasting. TC intensity change is closely related to its structure change. For instance, a strong TC (e.g., the maximum wind speed greater than 60 m s–1) often has a secondary eyewall (SE) and then experiences eyewall replacement cycle (ERC). The SE, also called concentric eyewall (CE), is generally accompanied by ring-like convective clouds with a local maximum wind speed. The weak-echo area between the outer and primary inner eyewalls is called the moat region. As the SE is formed, the primary one starts to weaken and will be replaced by the outer one (i.e., the SE) eventually. During this ERC, the TC may experience dramatic intensity fluctuation and structure change (Willoughby et al., 1982; Black and Willoughby, 1992; Houze et al., 2006, 2007; Kuo et al., 2009; Sitkowski et al., 2011; Zhou and Wang, 2011, 2013; Zhou et al., 2011; Kossin and Sitkowski, 2012; Yang et al., 2013, 2014; Ge, 2015). Meanwhile, the convective SE formation results in damaging winds broadening and thus affects the extent of heavy rainfall and storm surge.
Recently, Ge et al. (2016) found that the onset timing of the SE has large variability. In their study, 45 typhoons over the western North Pacific were identified as CE events based on the Morphed Integrated Microwave Imagery (MIMIC) of 15-min intervals from the Cooperative Institute for Meteorological Satellite Studies (CIMSS)/University of Wisconsin–Madison. The SE formation (SEF) timing is defined as the period from the official warning time to the onset of SEF when the deep convection of the outer region covers at least two-thirds of a circle. Based on these TC samples, the mean timing of SEF is about 84 h, with standard deviation of 33 h. It is speculated that both internal dynamics and external forcing play vital roles in SEF (Willoughby et al., 1984; Nong and Emanuel, 2003; Kuo et al., 2004, 2008; Zhou and Wang, 2011; Huang et al., 2012; Rozoff et al., 2012; Abarca and Montgomery, 2013; Kepert, 2013; Qiu and Tan, 2013; Wang et al., 2013; Menelaou et al., 2014; Zhu and Zhu, 2014; Wang et al., 2016). Montgomery and Kallenbach (1997) addressed the roles of the vortex Rossby waves (VRWs) in the SEF. Nong and Emanuel (2003) suggested that SEF requires an external forcing. Terwey and Montgomery (2008) pointed out that the so-called “β-skirt” is necessary for SEF. Huang et al. (2012) suggested that the planetary boundary layer (PBL) imbalance serves as an important mechanism for triggering and supporting a ring of deep convection in a narrow supergradient wind zone around the ensuing outer eyewall. Qiu and Tan (2013) emphasized the role of asymmetric active outer spiral rainbands. Some studies focused on the impacts of environmental conditions on SEF (Kossin and Sitkowski, 2009; Zhou and Wang, 2013; Ge, 2015). For instance, moist environment favors a quicker SEF (Ge, 2015).
Ge et al. (2016) examined the sensitivity of SEF to TC initial size represented by the initial radius of maximum wind (RMW) and the outer radius of the gale-force wind (R34), and found that a TC with a larger initial size is apt to form SE (see their Fig. 1). They showed a relationship between the SEF timing and the initial radius of maxi-mum wind (RMW). The initial RMW is obtained from the best-track data of the Joint Typhoon Warning Center (JTWC). Specifically, there exists a significant negative correlation between the SEF timing and the initial RMW of TC; namely, the larger initial RMW the TC has, the quicker the SEF is. Nevertheless, no underlying mechanism was provided. Hence, the main purpose of this study is to reveal the possible physical processes involved.
The organization of this paper is as follows. In Section 2, the model and experimental design are introduced. An overview of the SEF simulation results is given in Section 3. Detailed analyses are conducted to give physical interpretations in Section 4. Conclusions and discussion are given in Section 5.
2 Model and experimental designIn this study, we use the ARW-WRF model (version 3.3.1) that has four nested domains with horizontal grids of 54, 18, 6, and 2 km, respectively. The Kain–Frisch convective parameterization scheme (Kain and Fritsch, 1993) is applied to the two outermost domains, and the microphysics scheme from Lin et al. (1983) is use for all the domains. All the simulations are conducted on an f-plane centered at 10°N in a quiescent environment with a constant sea surface temperature of 29°C. The longwave radiation scheme is the RRTM (A Rapid Radiative Transfer Model, Mlawer et al. 1997), and the shortwave radiation scheme is from Dudhia (1989). The YSU (Yonsei University) scheme (Hong et al., 2006) is used to calculate the PBL process.
The initial vortex is specified as a modified Rankine vortex. Specifically,
| (1) |
where r is the radius, b = 0.75 is the shape factor, and the initial maximum wind speed (Vmax) is set to 25 m s–1. By changing the RMW, five idealized vortices are tested with the RMW of 50, 70, 90, 110, and 130 km, respectively. The initial radial profiles of near-surface winds are presented in Fig. 1. For simplicity, these experiments are named as RMW50, RMW70, RMW90, RMW110, and RMW130, respectively. These vortices are simulated with a spin-up period of 10 days.

|
| Figure 1 Initial radial profiles of near-surface tangential wind (m s–1) in the five experiments. |
To obtain an overall comparison of the evolution features, Fig. 2 displays the time–radius cross-section of the azimuthal-mean tangential wind at the height ofz = 1 km for all the experiments. We can see that the tangential wind gradually enhances, and the outer size broadens with time. A second maximum wind appears in certain outer region in each experiment. Once the outer entity forms, the inner one demises progressively, and is eventually replaced by the outer one. Of particular interest is that the SEF occurs earlier in the cases with larger initial RMWs. For example, the onset of SEF occurs the earliest at t = 107 h in RMW130. In contrast, the onset of SEF is much later (about t = 202 h) in RMW50, since its initial size is the smallest; that is, the development rate of SE is highly sensitive to TC initial size.
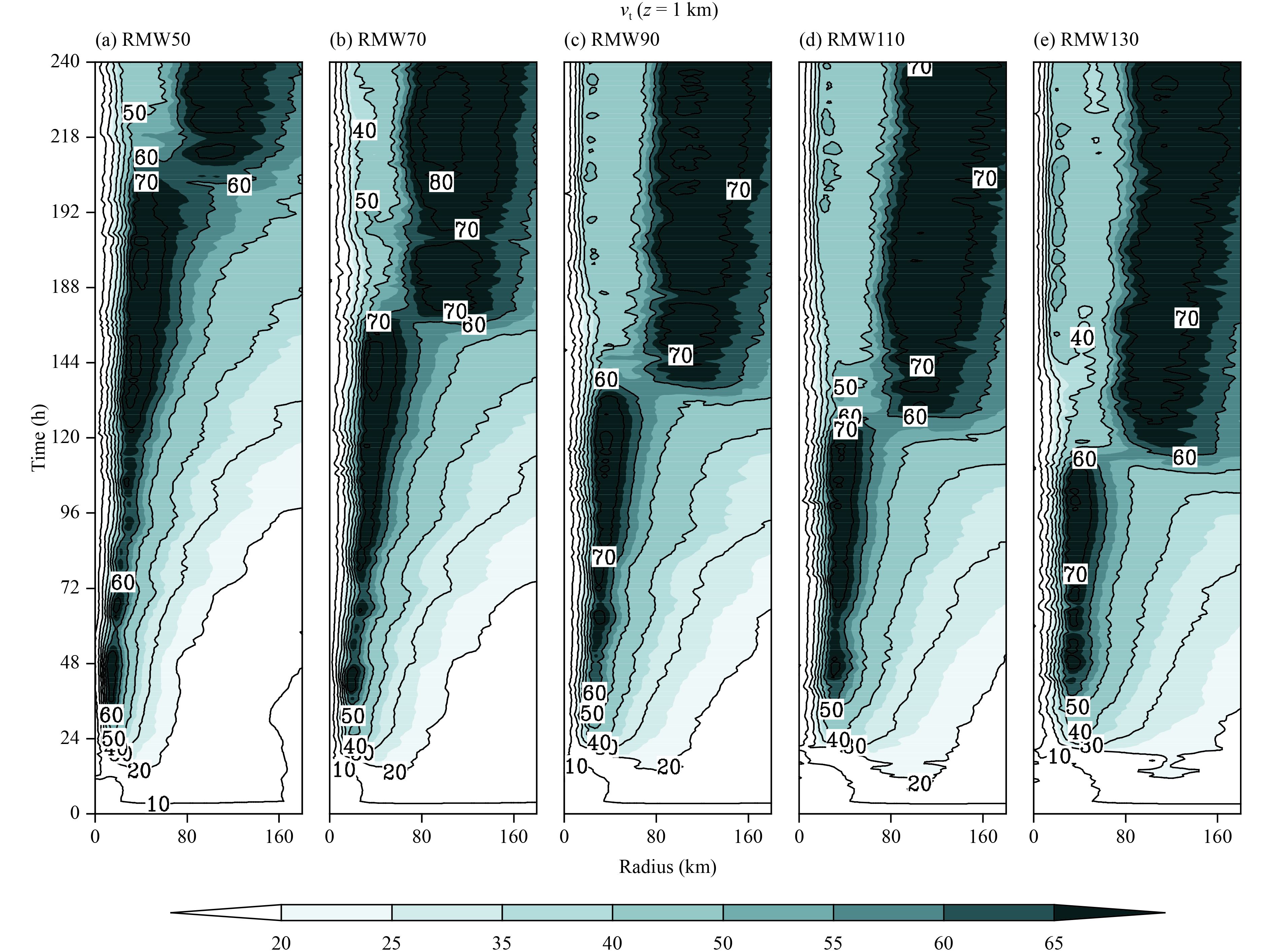
|
| Figure 2 The radius–time cross-section of azimuthally-averaged tangential velocities (m s–1) at the height of z = 1 km in the five experiments. |
To further illustrate the salient differences in SEF, Fig. 3 presents the time–radius cross-section of azimuthally-averaged vertical velocity atz = 1 km. Initially, there is a maximum vertical velocity associated with the primary eyewall in the inner-core area. With time, an outer active convective ring emanates, which is collocated with the SE. Once the outer convective ring is established, the inner one weakens quickly and the outer one becomes dominated. In this regard, the simulations capture the major evolution characteristics of convection during an ERC. The timing of the establishment of the active outer convection reflects the development rate of SE. Hence, an earlier prolific convective updraft indicates a quicker SEF in the cases with a larger initial size.
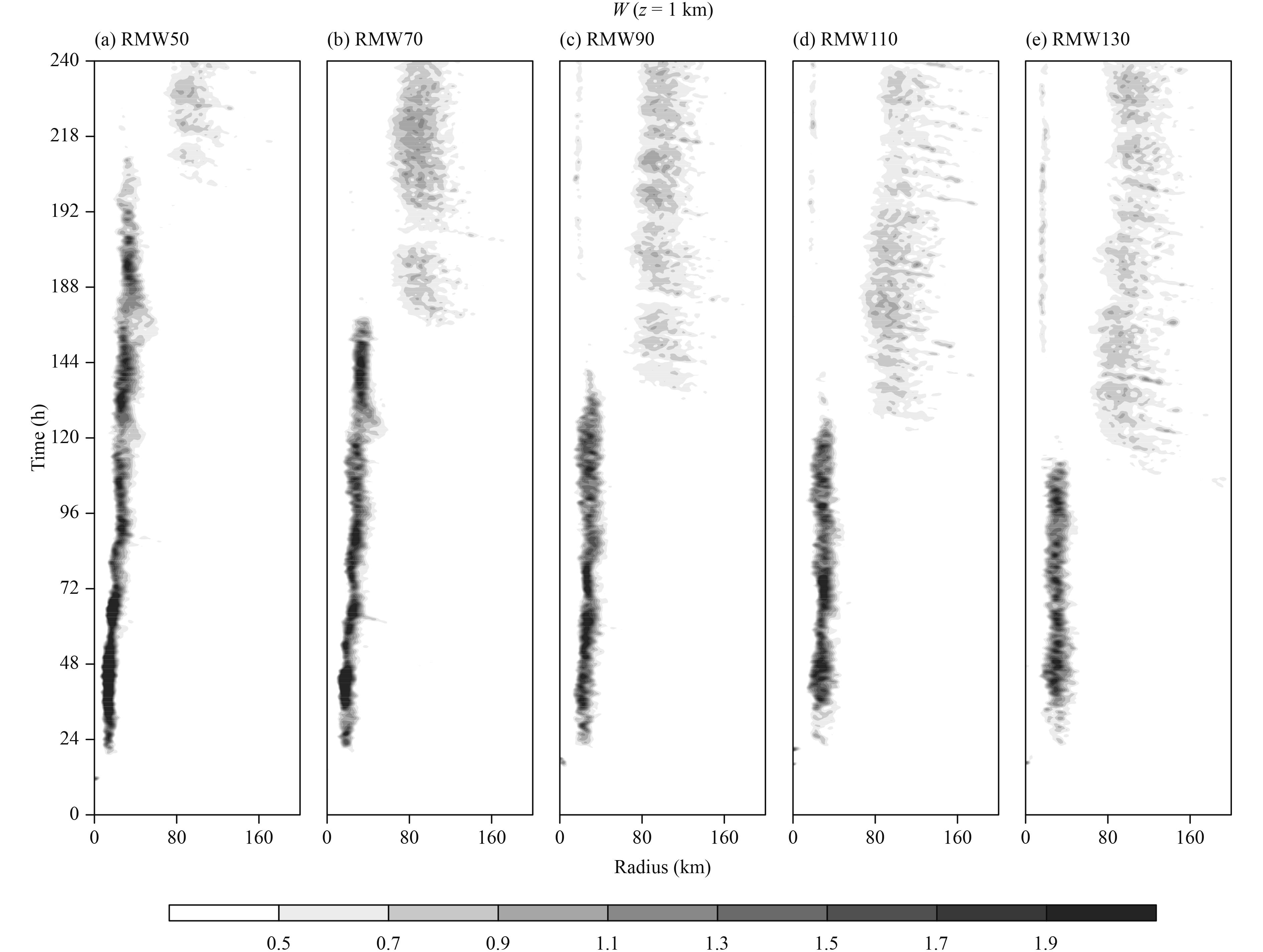
|
| Figure 3 As in Fig. 2, except for vertical velocity (m s–1) at the height of z = 1 km in the five experiments. |
Figure 4 presents the sequences of simulated radar reflectivity at the height of z = 1 km during the SEF, using RMW50 and RMW130 as examples. In this study, the inner and outer eyewall radii are referred to as the mean radius of convective ring, and the moat width is represented by the distance between the two eyewalls. For RMW130, the inner eyewall is located at the radius of about 40 km around t = 102 h, surrounded by outer ring-like convection. Thereafter, the outer convection contracts gradually and evolves into the SE at the radius of 120 km. A clear moat region can be identified during this period of interest. Once SE starts to emerge, TC intensity begins to decrease (figure omitted). The SEF in RMW50 bears many similarities as that in RMW130, except that the SEF occurs much later (i.e., t = 202 h). In addition, there are some remarkable differences in the structure of SE. For example, the moat size shows a positive correlation with the initial TC size. More specifically, the moat is much wider (about 80 km) in RMW130 than in RMW50 (about 40 km). Furthermore, the intensity fluctuation is greater in RMW130 during the ERC, which is consistent with Zhou and Wang (2013). They found that a TC with a larger SE may experience more significant intensity fluctuation. Since our focus is to examine the development speed of SE, the structure and intensity changes during the ERC are not covered in the current work.

|
| Figure 4 Evolution of simulated radar reflectivity in (a, b, c) RMW50 and (d, e, f) RMW130 during the SEF at a time interval of 4 h. |
To summarize, the onset timing of SEF exhibits remarkable sensitivity to initial TC size, indicating that the development rate of the SE is highly sensitive to TC structure. A TC with a larger initial size is apt to create a SE more quickly. This supports the observational results of Ge et al. (2016). In addition, the SE is apt to emanate farther away from the center. Naturally, a question arises—How does the initial TC size influence the sequential SEF? We will address this question in the next section.
4 Possible mechanismsPhysically, TC size reflects the radial distribution of surface wind speed, which directly determines surface heat fluxes. Surface heat fluxes can modulate atmosphe-ric moisture supplies, and thus convective activities. In this regard, the differences in surface heat fluxes between RMW50 and RMW130 should be compared. Figure 5 presents the time–radius cross-sections of azimuthally-averaged surface heat fluxes. As anticipated, after 96 h of integration, pronounced surface heat fluxes are evident in the region outside of the primary eyewall (i.e., around the radius of 120 km) in RMW130. On the contrary, the surface heat fluxes in the outer region in RMW50 increase much more slowly untilt = 192 h. One remaining issue here is the role of the heat fluxes from the lateral boundary. As shown in Fig. 5, beyond the radius of 180 km, the differences in heat fluxes in both cases are smaller than those in the inner-core area. It is likely that the local surface heat fluxes play a dominant role. However, Gao et al. (2017) pointed out that total precipitable water in the outer environment, where moisture is mainly provided by surface evaporation, is also vital to storm’s rapid intensification (RI) because RI is favored when there is less dry air intruded into the storm circulation. Ge (2015) also found that a TC is apt to create SEF more quickly under a moist environment. Both studies suggested the important impacts of lateral boundary or environmental condition, which awaits further studies.
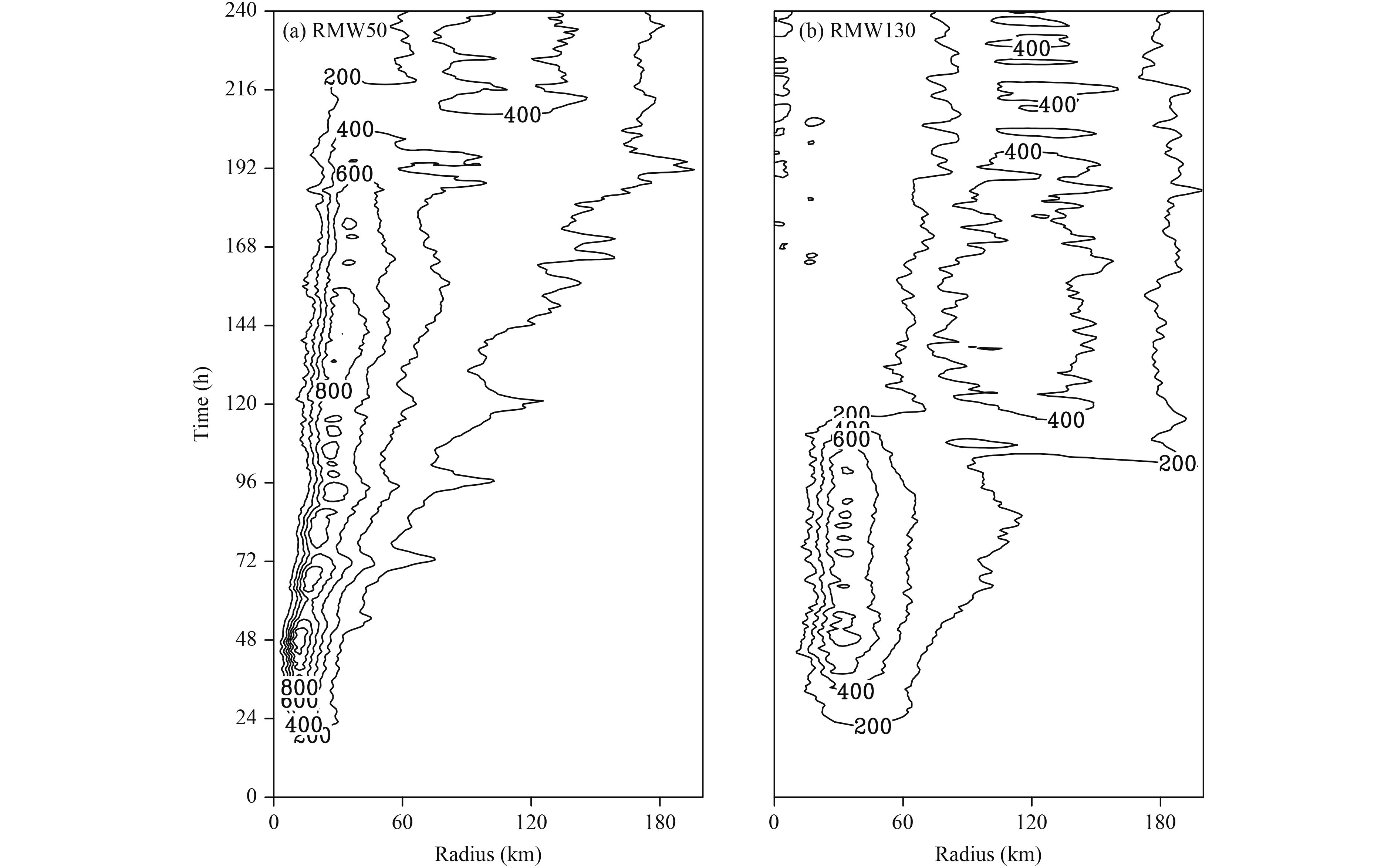
|
| Figure 5 The radius–time cross-section of azimuthally-averaged surface heat fluxes (W m–2) in (a) RMW50 and (b) RMW130. |
Accordingly, stronger surface entropy fluxes in the outer region favor greater convective available potential energy (CAPE) and thus active convection. Toward this end, Fig. 6 displays the evolution of simulated diabatic heating averaged between 4 and 8 km in RMW50 and RMW130. Obviously, the onset timing of strong diaba-tic heating is consistent with that of surface heat flux. Hence, different initial wind profiles can likely account for distinct radial distributions of surface heat fluxes and convection.
|
| Figure 6 The radius–time cross-section of azimuthally-averaged diabatic heating (× 10–3 K s–1) averaged between the heights of 4 and 8 km in (a) RMW50 and (b) RMW130. |
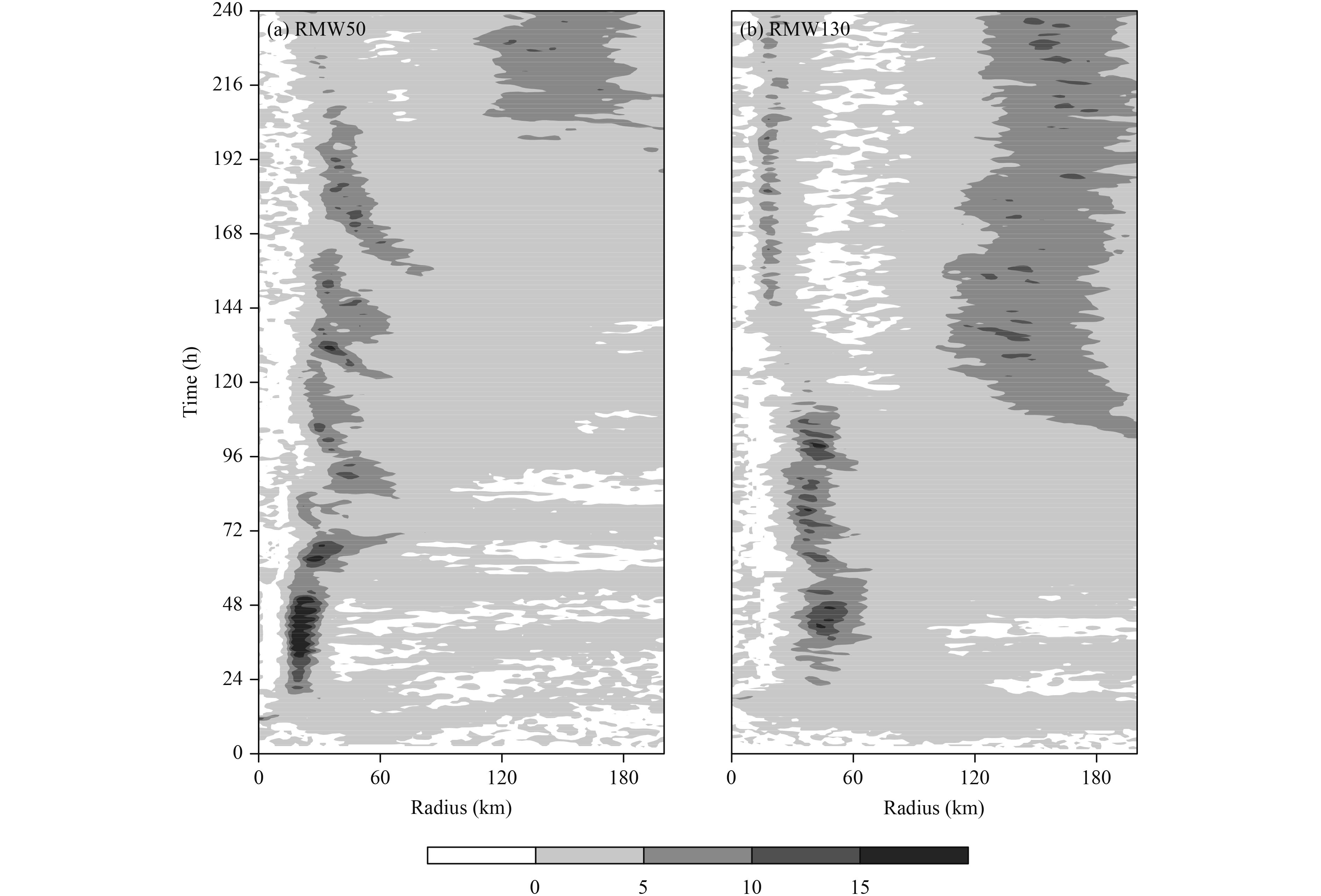
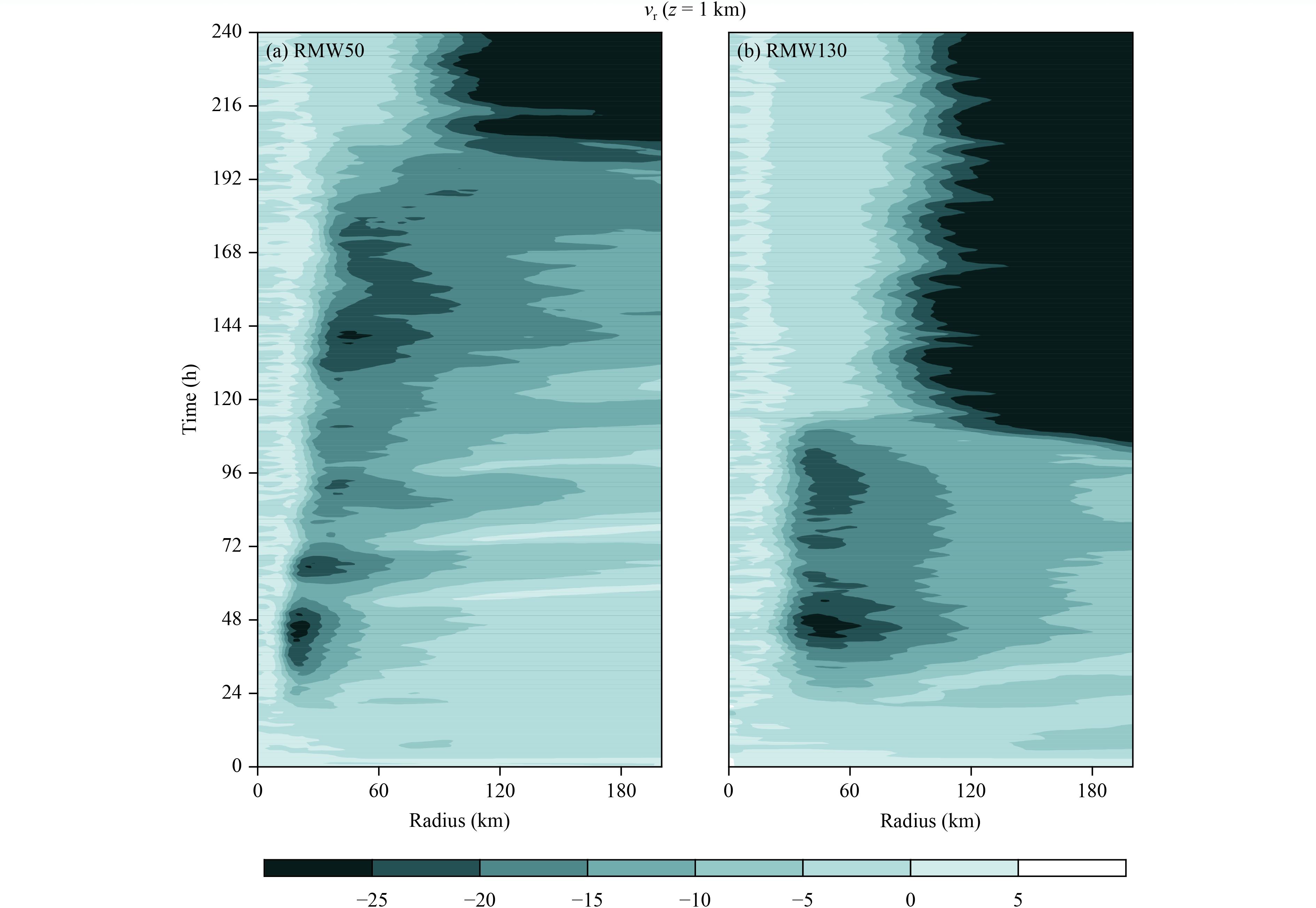
In general, the latent heating released in the outer region helps enhance the low-level radial inflows and accelerate tangential winds outside the eyewall, leading to a broadening of tangential wind field. To demonstrate this, the radius–time cross-section of azimuthally-averaged radial wind field at the low level is given inFig. 7. We can see that marked enhancement of radial inflows occurs in the outer region. In turn, the radial inflow helps accelerate the tangential wind.
|
| Figure 7 The radius–time cross-section of azimuthally-averaged radial winds (m s–1) at the height of z = 1 km in (a) RMW50 and (b) RMW130. |
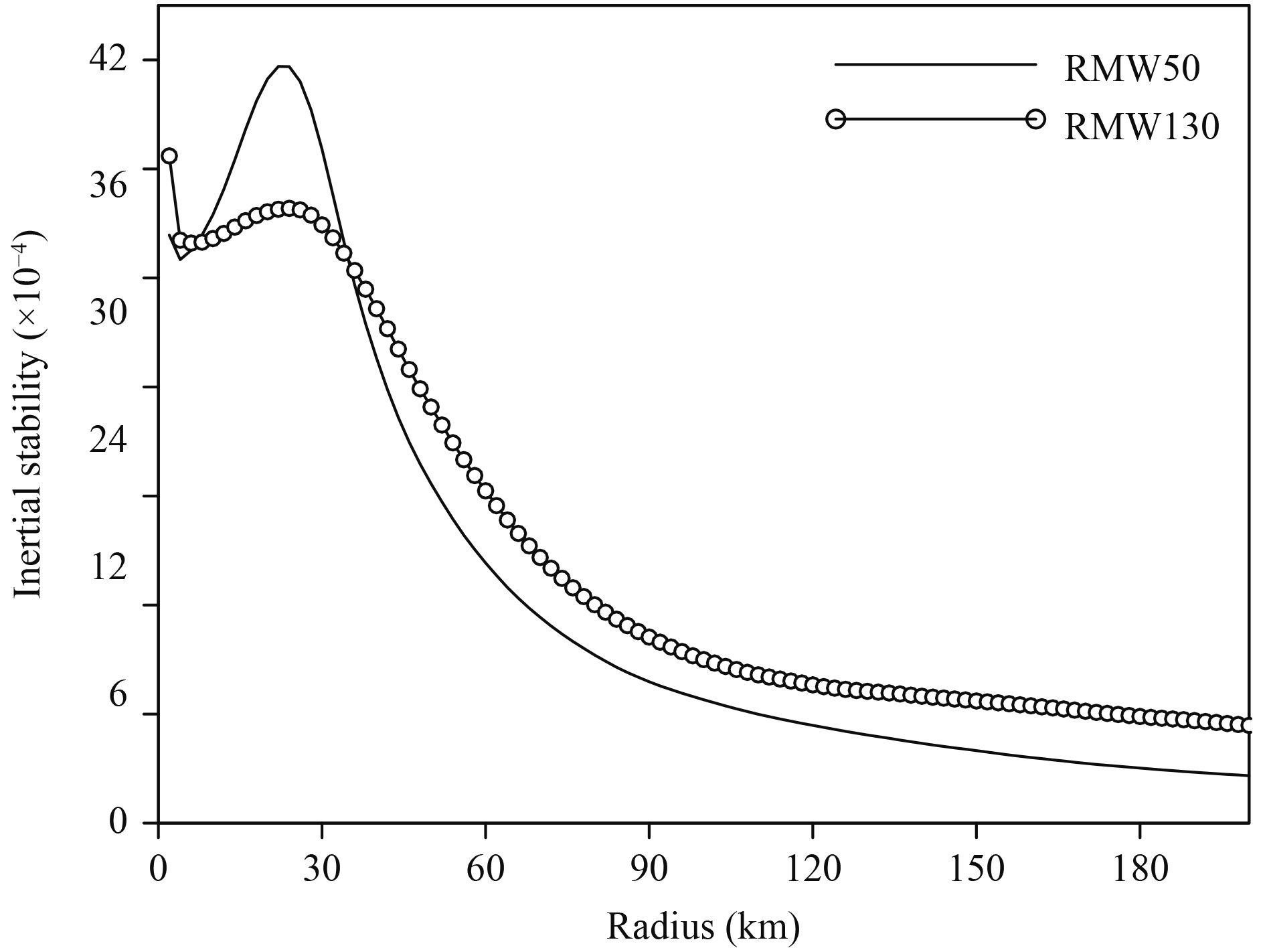
A greater tangential wind reflects a larger inertial parameter. From the balanced dynamics viewpoint, a greater inertial stability helps the conversion from diaba-tic heating to kinetic energy, and favors local secondary maximum wind (Shapiro and Willoughby, 1982; Rozoff et al., 2012; Sun et al., 2013). In this regard, the evolution of inertial stability should be compared. Figure 8 presents the radial distribution of inertial stability averaged during 104–116 h at the height of z = 4 km. Essentially, the inertial stability is larger in the inner-core area. As the radius increases, the stability decreases rapidly. This tendency is more pronounced in RMW50 than in RMW130. As such, the inertial stability becomes larger beyond the radius of 40 km in RMW130.
|
| Figure 8 Time-averaged azimuthal-mean inertial stability (× 10–4 s–1) at the height of z = 4 km in RMW50 (solid line) and RMW130 (line with circles) during 104–116 h. |
A budget analysis of the azimuthal-mean tangential wind tendency (Wang et al., 2016) is conducted. The budget equation can be approximated by:
| (2) |
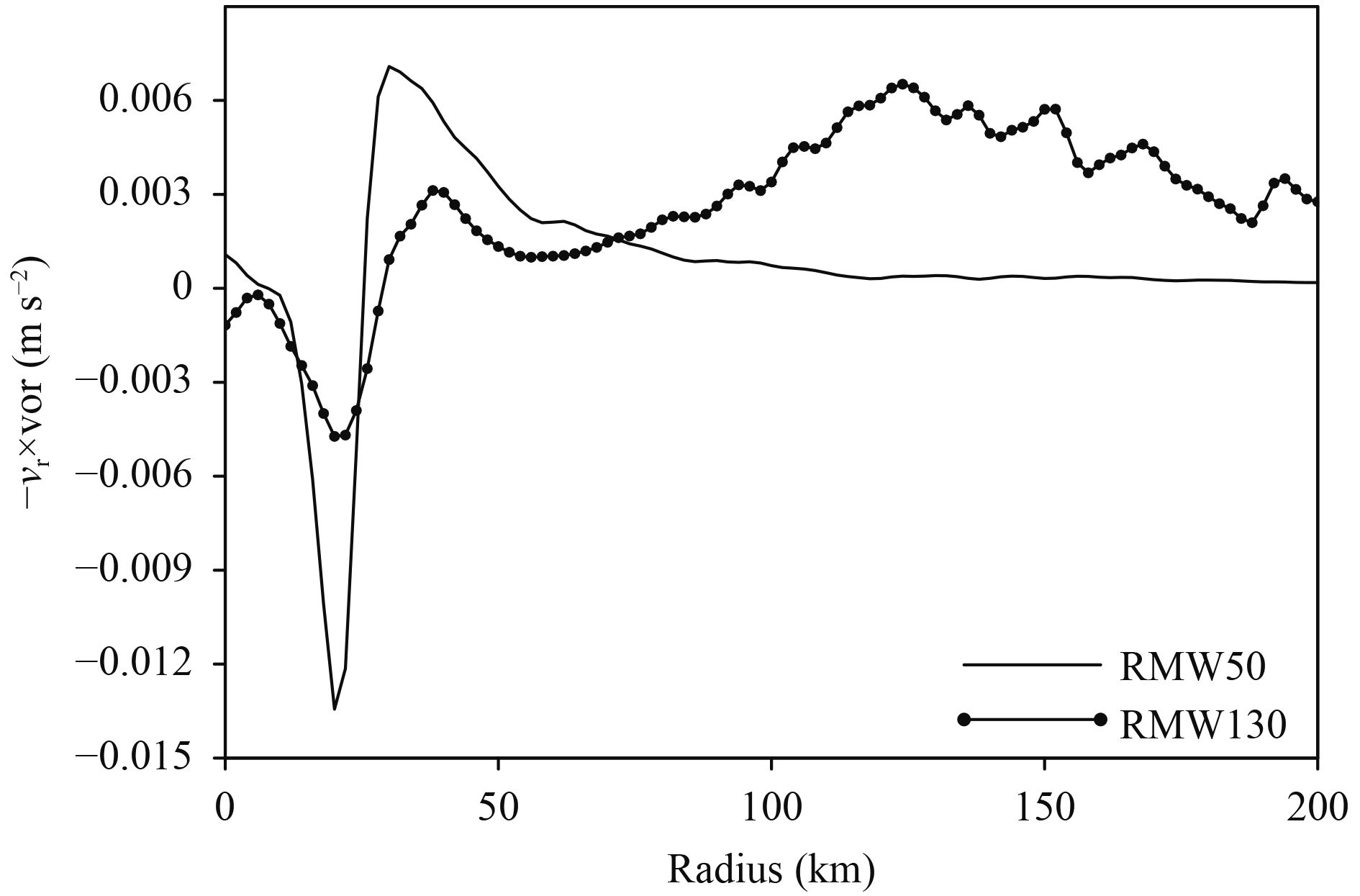
where vt, vr, and w are the tangential, radial, and vertical velocities, respectively; and ζa is the absolute vorticity. The overbar denotes the azimuthal mean and the prime is the deviation from the azimuthal mean. The terms on the right-hand side are the mean radial advection, mean vertical advection, eddy radial advection, eddy vertical advection, and friction, respectively. The analysis shows that the mean radial advection term (
|
| Figure 9 Radial distribution of the mean radial advection term (m s–2) averaged during 104–116 h at the height of z = 1 km. |
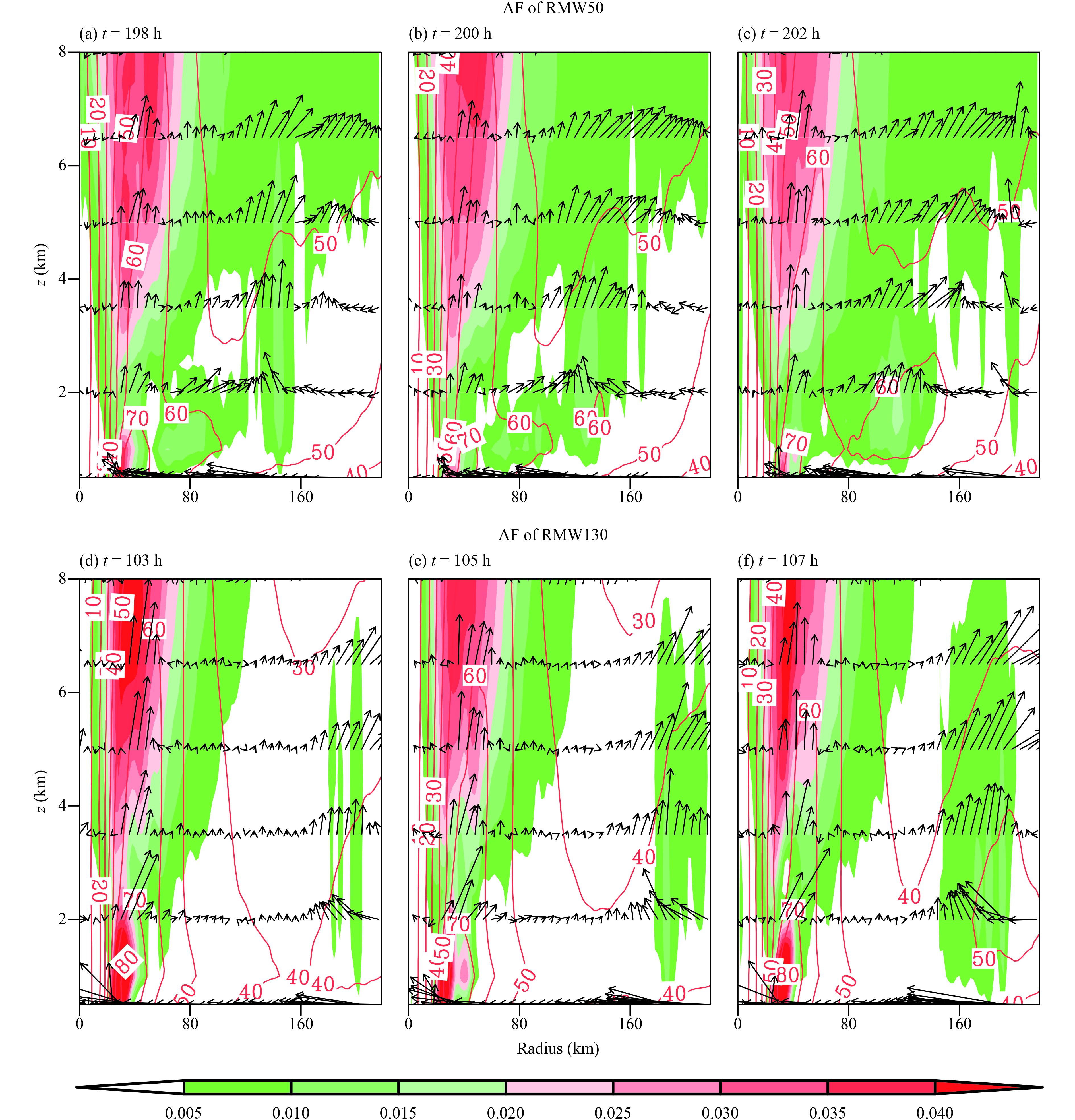
Huang et al. (2012) proposed that the unbalanced PBL process plays an important role in the initiating and maintenance of a convective ring in a supergradient wind zone outside the primary eyewall. As the tangential wind field broadens progressively, it will induce significant PBL imbalance. The supergradient wind converges with the mean PBL inflows, which will force strong updrafts in a narrow zone where the ensuing SE is situated. Figure 10 illustrates the evolution of the radial imbalance and secondary circulation prior to the SEF. The unbalanced boundary layer component represented by agradient force (AF) is considered as the residual term of the gradient wind balance, representing the difference between local radial pressure gradient and the sum of the Coriolis and centrifugal forces in the radial momentum equation. If the radial pressure gradient force is greater (smaller) than the latter, the flow is supergradient (subgradient). As a result, there is a tendency to decelerate (accelerate) radial inflows towards the vortex center.
In both cases, the increasing tangential wind in the boundary layer of the outer zone is evident prior to the SEF. Furthermore, the radial outflow starts to occupy certain radius in the boundary layer. This radial outflow is ascribed to the supergradient force. On the one hand, enhanced tangential wind enlarges both the Coriolis and centrifugal forces. On the other hand, the diabatic heating associated with outer convection warms the air column aloft and thus lowers the surface pressure therein, reducing the local radial pressure gradient. Consequently, it results in a supergradient force. In the SEF area, this radial outflow strengthens with time. In conjunction with the boundary layer radial inflow, it leads to convergence, and thus the airflow out of the boundary layer erupts to support deep convection in a favorable thermodynamic environment. In this regard, both the timing and location of the supergradient zone are important in controlling the SEF. Note that remarked differences exist in terms of the onset timing and location of the supergradient zone in the outer region between RMW50 and RMW130. Specifically, the timing of supergradient force emanates at a much earlier time (i.e., t = 102 h) in RMW130 compared with RMW50 (t = 200 h), reflecting a quicker establishment of the SEF in RMW130. Meanwhile, the location of significant PBL imbalance extends farther away from the center in RMW130. This is consistent with the fact that RMW130 has a larger SE and thus a wider moat as shown in Fig. 4. To summarize, both unbalanced boundary layer process and balanced dynamics account for the different behaviors of the SEF.
|
| Figure 10 Evolutions of structural change and boundary layer imbalance in (a, b, c) RMW50 and (d, e, f) RMW130. The contours are the axisymmetric component of tangential wind velocity (m s–1). Positive agradient force (AF, m s–2) values are shaded and vectors indicate the radial circulation. |
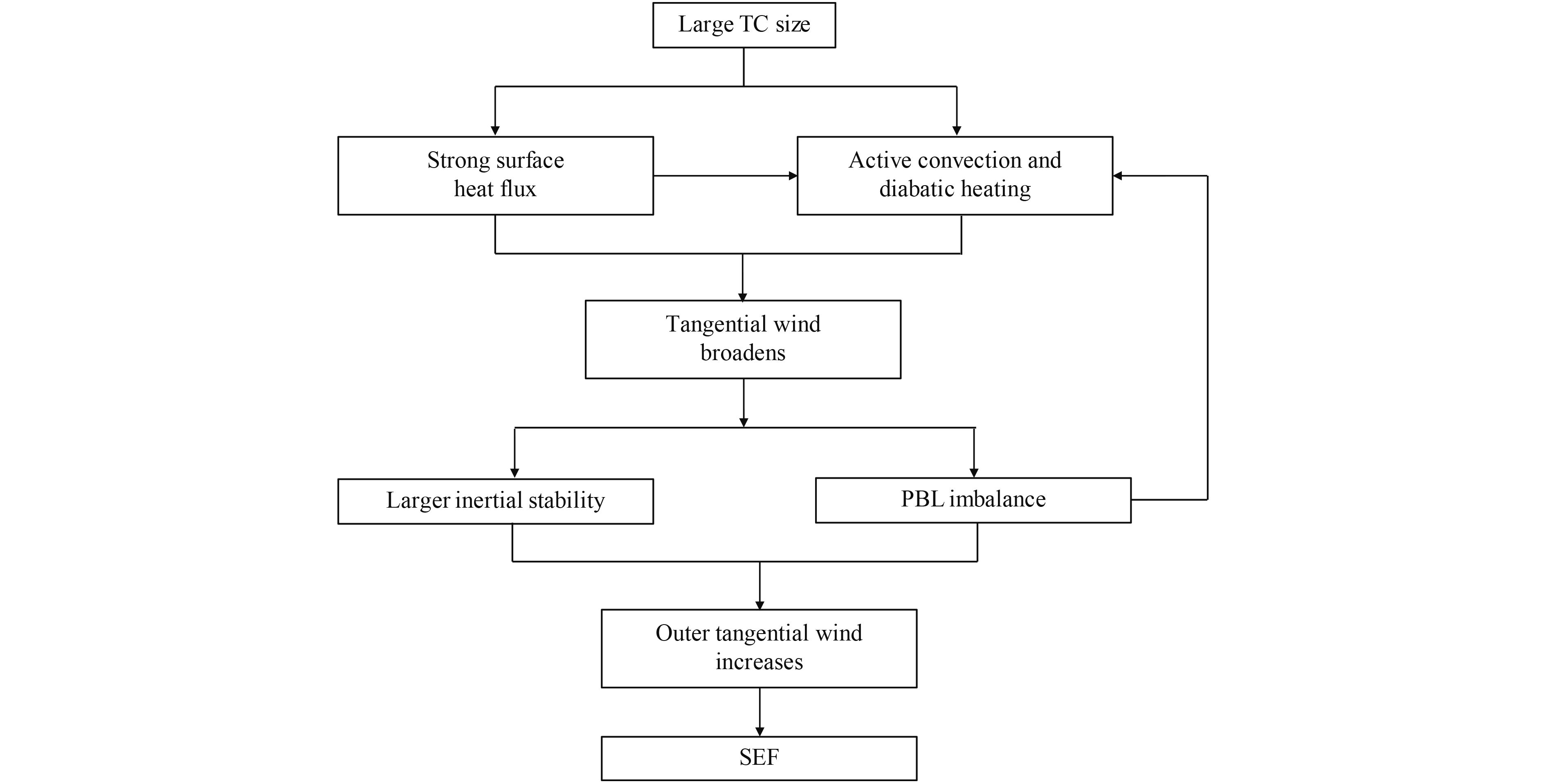
In this study, the sensitivity of SEF to initial TC structure is examined by using idealized numerical simulations. The sensitivity experiments support the observation that the SEF is highly sensitive to initial TC structure. Figure 11 summarizes the possible impacts of TC size on the SEF. It is shown that when a TC has a larger initial size (i.e., RMW and outer size, such as R34), it is apt to establish an SE more quickly. The diagnoses show that TC size influences surface entropy flux, which likely modulates outer convective activities. A larger TC leads to greater surface entropy flux and larger CAPE in the outer region, which are favorable for prolific convection. Meanwhile, different tangential wind profiles are responsible for dissimilar inertial stabilities. From the balanced dynamics viewpoint, a greater inertial stability favors the conversion of diabatic heating to kinetic energy, and thus a quicker enhancement of the tangential wind in the outer region. The broadening of the tangential wind field and enhanced diabatic heating in the outer region influence the unbalanced PBL processes. This result is consistent with Huang et al. (2012), in which the authors pointed out that the PBL imbalance plays a vital role in the initiation and maintenance of the deep convection in a supergradient wind zone around the outer eyewall. By these reasonings, the different behaviors of the PBL imbalance likely account for the different development rates of the SE.
|
| Figure 11 A schematic diagram showing the possible processes when TC size affects the SEF. |
Admittedly, our numerical experiments are highly idealized with an unchanging environment. In reality, TC size during the intensification period is largely controlled by both the internal dynamics and large-scale environmental conditions such as moisture and temperature fields. For instance, the ambient humidity may modulate the outer convective cells and affect the swirling wind field. In a moist environment, a TC tends to generate active outer convection and thus a larger outer size (Hill and Lackmann, 2009). Therefore, more complicated environmental conditions should be examined to gain more insights on how the storm structure influences its dynamics and thermodynamics.
| Abarca, S. F., and M. T. Montgomery, 2013: Essential dynamics of secondary eyewall formation. J. Atmos. Sci., 70, 3216–3230. DOI:10.1175/JAS-D-12-0318.1 |
| Black, M. L., and H. E. Willoughby, 1992: The concentric eyewall cycle of Hurricane Gilbert. Mon. Wea. Rev., 120, 947–957. DOI:10.1175/1520-0493(1992)120<0947:TCECOH>2.0.CO;2 |
| Dudhia, J., 1989: Numerical study of convection observed during the Winter Monsoon Experiment using a mesoscale two-dimensional model. J. Atmos. Sci., 46, 3077–3107. DOI:10.1175/1520-0469(1989)046<3077:NSOCOD>2.0.CO;2 |
| Gao, S., S. N. Zhai, B. Q. Chen, et al., 2017: Water budget and intensity change of tropical cyclones over the western North Pacific. Mon. Wea. Rev., 145, 3009–3023. DOI:10.1175/MWR-D-17-0033.1 |
| Ge, X. Y., 2015: Impacts of environmental humidity on concentric eyewall structure. Atmos. Sci. Let., 16, 273–278. DOI:10.1002/asl2.553 |
| Ge, X. Y., L. Guan, and S. W. Zhou., 2016: Impacts of initial structure of tropical cyclone on secondary eyewall formation. Atmos. Sci. Let., 17, 569–574. DOI:10.1002/asl.707 |
| Hill, K, and G. M. A., 2009: Influence of environmen-tal humidity on tropical cyclone size. Mon. Wea. Rev., 137, 3294–3315. DOI:10.1175/2009MWR2679.1 |
| Hong, S.-Y., Y. Noh, and J. Dudhia, 2006: A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Wea. Rev., 134, 2318–2341. DOI:10.1175/MWR3199.1 |
| Houze, A. Jr., Cetrone R., R. Brodzik J., et al., 2006: The hurricane rainband and intensity change experiment (RAINEX): Observations and modeling of hurricanes Katrina, Ophelia, and Rita (2005). Bull. Amer. Meteor. Soc., 87, 48–55. DOI:10.1175/BAMS-87-11-1503 |
| Houze, A. Jr., S. Chen R., F. Smull S., et al., 2007: Hurricane intensity and eyewall replacement. Science, 315, 1235–1239. DOI:10.1126/science.1135650 |
| Huang, Y.-H., M. T. Montgomery, and C.-C. Wu, 2012: Concentric eyewall formation in Typhoon Sinlaku (2008). Part II: Axisymmetric dynamical processes. J. Atmos. Sci., 69, 662–674. DOI:10.1175/JAS-D-11-0114.1 |
| Kain, S., and J. M. J., 1993: The role of the convective " trigger function” in numerical forecasts of mesoscale convective systems. Meteor. Atmos. Phys., 49, 93–106. DOI:10.1007/BF01025402 |
| Kepert, J. D., 2013: How does the boundary layer contribute to eyewall replacement cycles in axisymmetric tropical cyclones?. J. Atmos. Sci., 70, 2808–2830. DOI:10.1175/JAS-D-13-046.1 |
| Kossin, J. P., and M. Sitkowski, 2009: An objective model for identifying secondary eyewall formation in hurricanes. Mon. Wea. Rev., 137, 876–892. DOI:10.1175/2008MWR2701.1 |
| Kossin, J. P., and M. Sitkowski, 2012: Predicting hurricane intensity and structure changes associated with eyewall replacement cycles. Wea. Forecasting, 27, 484–488. DOI:10.1175/WAF-D-11-00106.1 |
| Kuo, H.-C., L.-Y. Lin, C.-P. Chang, et al., 2004: The formation of concentric vorticity structures in typhoons. J. Atmos. Sci., 61, 2722–2734. DOI:10.1175/JAS3286.1 |
| Kuo, H.-C., W. H. Schubert, C.-L. Tsai, et al., 2008: Vortex interactions and barotropic aspects of concentric eyewall formation. Mon. Wea. Rev., 136, 5183–5198. DOI:10.1175/2008MWR2378.1 |
| Kuo, H.-C., C.-P. Chang, Y.-T. Yang, et al., 2009: Western North Pacific typhoons with concentric eyewalls. Mon. Wea. Rev., 137, 3758–3770. DOI:10.1175/2009MWR2850.1 |
| Lin, Y.-L., R. D. Farley, and H. D. Orville, 1983: Bulk parameterization of the snow field in a cloud model. J. Appl. Meteor., 22, 1065–1092. DOI:10.1175/1520-0450(1983)022<1065:BPOTSF>2.0.CO;2 |
| Menelaou, K., M. K. Yau, and Y. Martinez, 2014: Some aspects of the problem of secondary eyewall formation in idealized three-dimensional nonlinear simulations. J. Adv. Mod. Earth Syst., 63, 491–512. DOI:10.1002/2014MS000316 |
| Mlawer, E. J., S. J. Taubman, P. D. Brown, et al., 1997: Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res., 102, 16663–16682. DOI:10.1029/97JD00237 |
| Montgomery, M. T., and R. J. Kallenbach, 1997: A theory for vortex rossby-waves and its application to spiral bands and intensity changes in hurricanes. Quart. J. Roy. Meteor. Soc., 123, 435–465. DOI:10.1002/qj.49712353810 |
| Nong, S. Y., and K. Emanuel, 2003: A numerical study of the genesis of concentric eyewalls in hurricanes. Quart. J. Roy. Meteor. Soc., 129, 3323–3338. DOI:10.1256/qj.01.132 |
| Qiu, X., and Z. M. Tan, 2013: The roles of asymmetric inflow forcing induced by outer rainbands in tropical cyclone secondary eyewall formation. J. Atmos. Sci., 70, 953–974. DOI:10.1175/JAS-D-12-084.1 |
| Rozoff, C. M., D. S. Nolan, J. P. Kossin, et al., 2012: The roles of an expanding wind field and inertial stability in tropical cyclone secondary eyewall formation. J. Atmos. Sci., 69, 2621–2643. DOI:10.1175/JAS-D-11-0326.1 |
| Shapiro, J., and H. E. L., 1982: The response of balanced hurricanes to local sources of heat and momentum. J. Atmos. Sci., 39, 378–394. DOI:10.1175/1520-0469(1982)039<0378:TROBHT>2.0.CO;2 |
| Sitkowski, M., J. P. Kossin, and C. M. Rozoff, 2011: Intensity and structure changes during hurricane eyewall replacement cycles. Mon. Wea. Rev., 139, 3829–3847. DOI:10.1175/MWR-D-11-00034.1 |
| Sun, Y. Q., Y. X. Jiang, B. K. Tan, et al., 2013: The governing dynamics of the secondary eyewall formation of Typhoon Sinlaku (2008). J. Atmos. Sci., 70, 3818–3837. DOI:10.1175/JAS-D-13-044.1 |
| Terwey, W. D., and M. T. Montgomery, 2008: Secondary eyewall formation in two idealized, full-physics modeled hurricanes. J. Geophys. Res., 113, D12112. DOI:10.1029/2007JD008897 |
| Wang, H., C.-C. Wu, and Y. Q. Wang, 2016: Secondary eyewall formation in an idealized tropical cyclone simulation: Balanced and unbalanced dynamics. J. Atmos. Sci., 73, 3911–3930. DOI:10.1175/JAS-D-15-0146.1 |
| Wang, X. B., Y. M. Ma, and N. E. Davidson, 2013: Secondary eyewall formation and eyewall replacement cycles in a simulated hurricane: Effect of the net radial force in the hurricane boundary layer. J. Atmos. Sci., 70, 1317–1341. DOI:10.1175/JAS-D-12-017.1 |
| Willoughby, H. E., J. A. Clos, and M. G. Shoreibah, 1982: Concentric eye walls, secondary wind maxima, and the evolution of the hurricane vortex. J. Atmos. Sci., 39, 395–411. DOI:10.1175/1520-0469(1982)039<0395:CEWSWM>2.0.CO;2 |
| Willoughby, H. E., H. L. Jin, S. J. Lord, et al., 1984: Hurricane structure and evolution as simulated by an axisymmetric, nonhydrostatic numerical model. J. Atmos. Sci., 41, 1169–1186. DOI:10.1175/1520-0469(1984)041<1169:HSAEAS>2.0.CO;2 |
| Yang, Y. T., H. C. Kuo, E. A. Hendricks, et al., 2013: Structural and intensity changes of concentric eyewall typhoons in the western North Pacific basin. Mon. Wea. Rev., 141, 2632–2648. DOI:10.1175/MWR-D-12-00251.1 |
| Yang, Y. T., E. A. Hendricks, H.-C. Kuo, et al., 2014: Long-lived concentric eyewalls in Typhoon Soulik (2013). Mon. Wea. Rev., 142, 3365–3371. DOI:10.1175/MWR-D-14-00085.1 |
| Zhou, X. Q., and B. Wang, 2011: Mechanism of concentric eyewall replacement cycles and associated intensity change. J. Atmos. Sci., 68, 972–988. DOI:10.1175/2011JAS3575.1 |
| Zhou, X. Q., and B. Wang, 2013: Large-scale influences on secondary eyewall size. J. Geophys. Res., 118, 11088–11097. DOI:10.1002/jgrd.50605 |
| Zhou, X. Q., B. Wang, X. Y. Ge, et al., 2011: Impact of secondary eyewall heating on tropical cyclone intensity change. J. Atmos. Sci., 68, 450–456. DOI:10.1175/2010JAS3624.1 |
| Zhu, Z. D., and P. Zhu, 2014: The role of outer rainband convection in governing the eyewall replacement cycle in numerical simulations of tropical cyclones. J. Geophys. Res., 119, 8049–8072. DOI:10.1002/2014JD021899 |
 2018, Vol. 32
2018, Vol. 32


