The Chinese Meteorological Society
Article Information
- BI, Mingyu, Xuyang GE, and Tim LI, 2018.
- Dependence of Tropical Cyclone Intensification on the Latitude under Vertical Shear. 2018.
- J. Meteor. Res., 32(1): 113-123
- http://dx.doi.org/10.1007/s13351-018-7055-4
Article History
- Received April 21, 2017
- in final form September 13, 2017
2. International Pacific Research Center/Department of Atmospheric Sciences, University of Hawaii at Manoa, Honolulu, HI 96822, USA
Numerous studies have examined the impacts of the latitude on tropical cyclone (TC) intensification (e.g., DeMaria and Pickle, 1988; Bister, 2001; Li et al., 2012; Smith et al., 2015). In a quiescent idealized environment, Li et al. (2012) found that the simulated TCs are systematically apt to intensify more rapidly at lower latitudes. Since the inertial stability is smaller at lower latitudes, it favors a rapid establishment of boundary inflow layer. As a result, this leads to a faster vortex spin-up than that at higher latitudes. Smith et al. (2015) confirmed such distinctive evolution characteristics. By using a steady slab boundary layer model, they found that there is stronger boundary layer inflow together with larger diabatic heating rates at lower latitudes. However, these studies focused on TC development in a quiescent environment where the effects of environmental flows were not considered.
The environmental flows influence both TC intensity and structure. For instance, the impacts of vertical shear on TC intensification have been extensively studied (DeMaria, 1996; Frank and Ritchie, 2001; Zhang and Kieu, 2006; Riemer et al., 2010; Tang and Emanuel, 2010; Rappin and Nolan, 2012; Ge et al., 2013; Zhang and Tao, 2013). The vertical shear generally inhibits TC development through venting moisture out of the TC inner-core region (Gray, 1968; Frank and Ritchie, 2001) or transporting low-entropy air into the boundary layer (Powell, 1990; Riemer et al., 2010). Recently, Zhou (2015) examined the influence of the vertical shear on TC development under different environmental rotations and thermodynamic conditions. It was found that under the vertical shear, a TC’s intensification rate is greater with a larger Coriolis parameter (f) regardless of the ambient thermodynamic condition. It was argued that the planetary rotation influences the TC re-alignment process. In the presence of vertical shear, the TC will develop into a vertically tilted system. However, a higher f favors the restoration of a vertical upright structure in a TC compared with a lower f. Given the critical role of vertical shear in regulating the TC development, it is worthwhile to further investigate its impact on tropical cyclone development with different planetary vorticities. Hence, the primary purpose of this study is to explore the possible processes through which the TC intensification depends on the latitude under vertical shear.
The paper is organized as the follows. In Section 2, the model and experiment designs are introduced. In Section 3, we examine the possible mechanisms accounting for the dependency of TC development on the latitude under vertical shear. Finally, a short summary and discussion are given in the last section.
2 Model and experimental designIn this study, a hurricane research model, TCM3 (Wang, 2001), is used. The system has been used to investigate the dependence of tropical cyclone intensification on the latitude without a mean flow (Li et al., 2012) and many other aspects of TCs (Ge et al., 2007, 2008). The model is configured with three nested domains with the grid spacing of 22.5, 7.5, and 2.5 km, respectively. The model is on an aqua planet with a constant sea surface temperature (SST) of 29°C. The environmental condition is based on the mean tropical sounding (Holland, 1997). More details on the model configurations can be referred to Li et al. (2012).
The initial vortex is an axisymmetric entity with a maximum tangential wind speed of 20 m s–1 at a radius of 125 km. The tangential wind decreases with height and vanishes at 100 hPa. By specifying the tangential wind field, the mass and thermodynamic fields are obtained by solving a nonlinear balance equation (Wang, 1995). Hence, the initial vortex satisfies both the hydrostatic and gradient wind balance. In this study, two sets of experiments are designed. In the first group, all the vortices are spin up in a resting environment at different latitudes, similar to Li et al. (2012). In order to understand the impacts of vertical shear on the sensitivity of TC intensification to the latitude, an idealized easterly vertical shear is embedded in the second group. Specifically, the zonal mean wind decreases linearly from 0 to –5 m s–1 between 850 and 200 hPa (Fig. 1). Six experiments are designed by running the model on an f-plane centered at different latitudes including 7.5, 10, 15, 20, 25, and 30°N, respectively. In brevity, the experiments are named as F7.5, F10, F15, F20, F25, and F30, respectively. By doing so, the comparisons between two groups may reflect the possible impacts of the vertical shear.

|
| Figure 1 The vertical profile of an idealized easterly vertical shear (m s–1). |
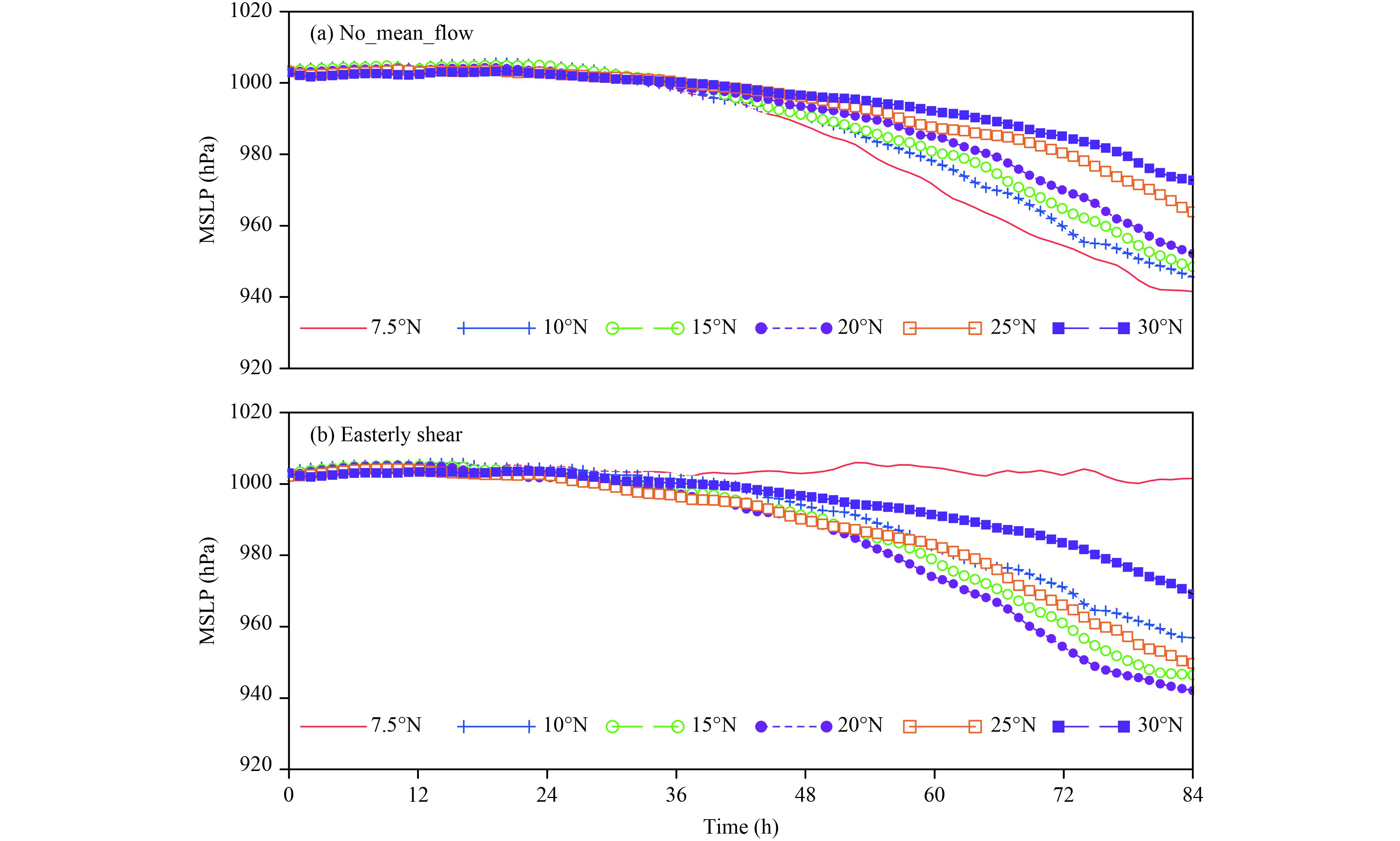
Figure 2 compares the time evolution of the simulated intensities represented by the minimum sea-level pressure (MSLP). In the top panel (Fig. 2a), the results are from the experiments in a quiescent environment. In the absence of vertical shear, all the initially weak vortices develop into strong TCs within 84 h. Notice that TCs develop faster at lower latitudes than at higher latitudes systematically, and it agrees well with previous studies (Li et al., 2012; Smith et al., 2015). However, when vertical shear is present, the vortices show marked different developments. That is, the vortex in F7.5 fails to develop into a TC at the end of the integration period, which is in contrast to the counterpart in group one with the shear. Furthermore, an interesting feature is that the intensification rate does not depend linearly on the increase of the Coriolis parameter. From F10 to F20, the intensification rate becomes greater. As the latitude is further increased, the tendency of intensification rate is reversed. That is, the TC intensification rate decreases beyond 20°N. As a consequence, the largest intensification rate occurs at an intermediate latitude of 20N among our experiments.
|
| Figure 2 Time evolutions of the tropical cyclone intensity represented by minimum sea-level pressure (MSLP; hPa) from the six experiments conducted (a) without mean flow and (b) with an easterly vertical shear. |
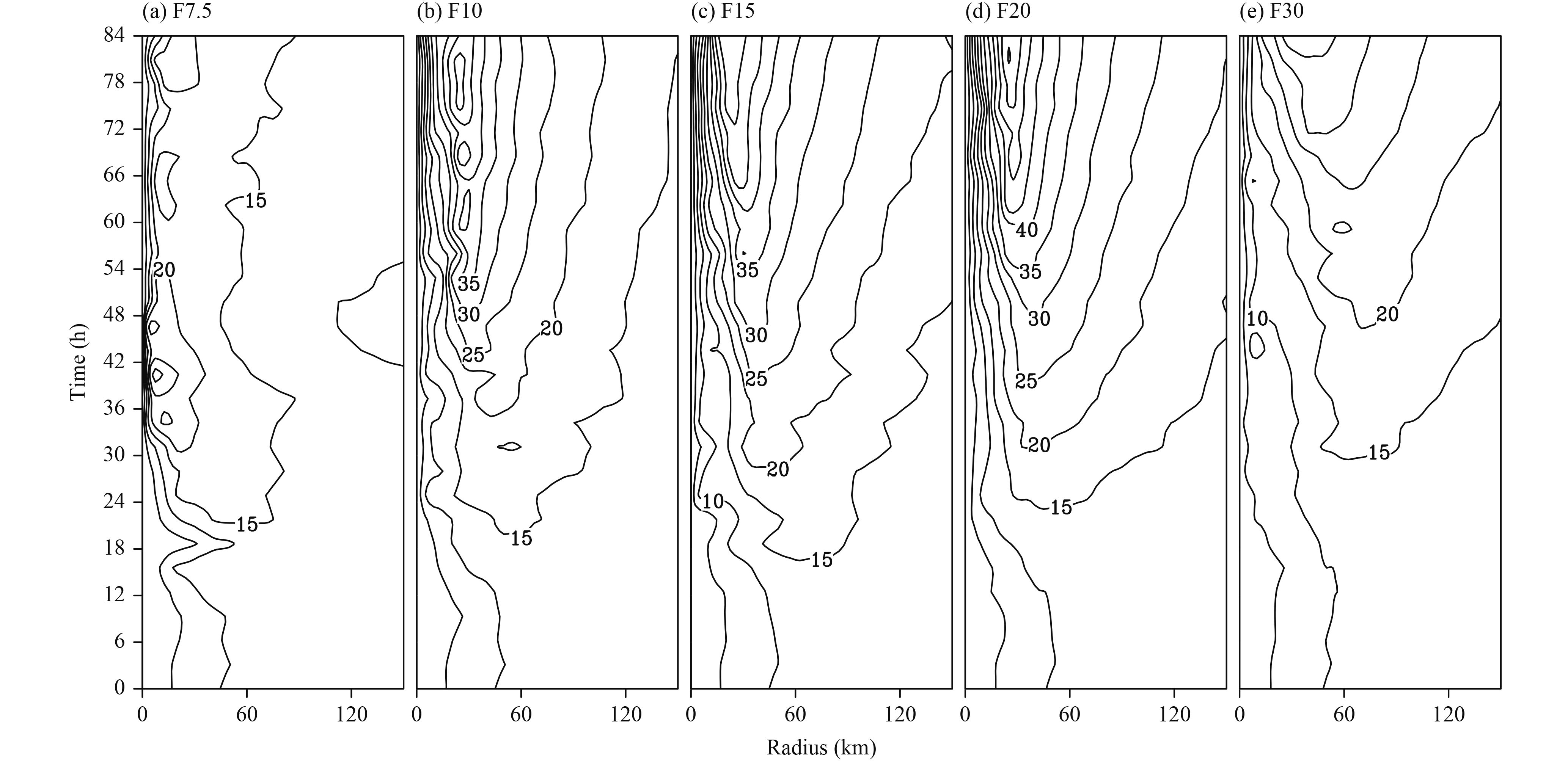
To further demonstrate this evolution characteristic, Figure 3 displays the time–radial cross-section of the azimuthal mean tangential wind near the surface layer. From F10 to F20 (Figs. 3b–d), the symmetric tangential velocities become stronger as the latitude is increased. Nevertheless, as the latitude further increases, the primary circulations become weaker (Fig. 3e). The development for F7.5 is sporadic and fails to organize and vortex contraction in F30 is very slow. F10, F15, and F20 all show organized contraction of the core. Figure 4 displays the radial profile of the tangential winds at t = 84 h. It is evident that the tangential velocity is the strongest (weakest) in F20 (F7.5), respectively. The results indicate that, in the presence of vertical shear, an intermediate background rotation favors more intensification. This suggests an optimal background rotation rate for the TC development under vertical shear, which is different from the previous studies (Li et al., 2012; Smith et al., 2015). The three profiles for F10, F15, and 20 are similar, corresponding to similar developments in time shown in Fig. 3. Some specific scientific questions arise here are:
1) Why is the TC development with respect to different planetary rotations different in the presence of vertical shear?
2) Is there is an optimal latitude for TC development under vertical shear? If yes, what physical processes account for it?
We will address these questions in the following sections.
|
| Figure 3 Time–radial cross-sections of azimuthal-mean tangential velocity (m s–1) near the surface layer for different latitudes (see labels on top of each panel) with an easterly shear. |

|
| Figure 4 The radial profiles of low-level azimuthal-mean tangential wind (Vt; m s–1) at t = 84 h in the five experiments (F7.5, F10, F15, F20, and F30) with an easterly shear. |
As mentioned before, the environmental vertical shear is generally detrimental to TC development (Gray, 1979; McBride and Zehr, 1981; DeMaria et al., 2001; Frank and Ritchie, 2001; Rappin and Nolan, 2012; Tang and Emanuel, 2012; Ge et al., 2013). In the presence of a vertical shear, a vortex tends to tilt vertically with height. Namely, the mid- or upper-level vortex center will shift to the downshear flank, leading to a separation between the mid- and the low-level circulation center. This tilting will induce a so-called shear-forced secondary circulation (FSC; Zhang and Kieu, 2006) with anomalous rising motion (sinking motion) in the downshear (upshear) side. Accordingly, a significant asymmetric pattern is evident in the vertical motion field. Although the identical verti-cal shear is imposed, the shear FSCs and latent heating FSCs acting to reduce the destructive effect of vertical shear differ greatly due to the different Coriolis parameters and TCs inner core status. Under a favorable environment, the ascending branch will be greatly reinforced itself through the release of diabatic heating. The reinforced FSC may resist the shear-induced tilting and help restore the vertical alignment. A rapid intensification is generally ascribed to a quick vertical realignment process. In this regard, the vertical realignment process is first examined.
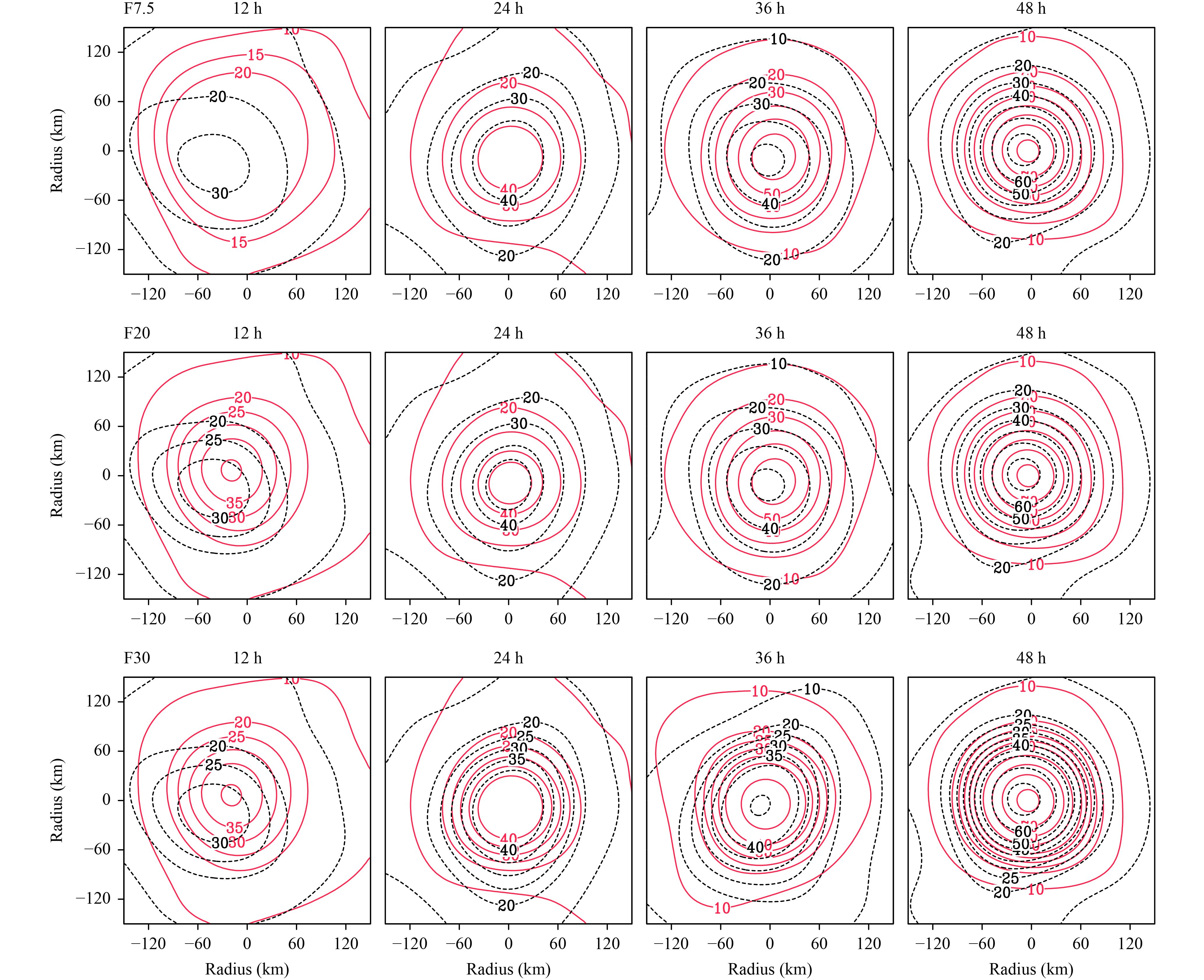
Figure 5 shows the time evolution of the relative locations of low- and mid-level vortices for F7.5, F20, and F30. To clearly represent the circulation, a spatial filtering (Ge et al., 2013) is applied to the vorticity field. In this study, the signals with wavelength greater than 100 km are retained, by which we remove the signals of small-scale convective cells. As expected, due to the different advection effects, vertical shear leads to a zonal displacement between the mid- and low-level vortices. Under the easterly shear, the mid-level circulations in all experiments are initially advected westward compared to the low-level vortices. Interestingly, it shows a negative correlation between the magnitude of tilting and the Coriolis parameter. Visibly, the displacements of vortices in higher latitude are smaller. To demonstrate this, the time evolution of displacements between mid- and low-level circulation centers are compared in Fig. 6, with the circulation center defined as the location with the maximum relative vorticity at each level. In F30, the vertical separation distance is initially about 20 km, and then is reduced rapidly in time. The storm becomes nearly upright around t = 48 h. In contrast, the split distance is significantly larger in F7.5. That is, the displacement reaches up to 60 km at t = 36 h, and remains consistently large although there are some oscillations thereafter. The comparisons indicate that with a higher f, the TC generally experiences a smaller vertical tilting and then a quicker realignment. Nevertheless, with a lower f, the storm may fail to restore its vertical alignment and thus has a slow development or fails to develop at all. This emphasizes the role of the earth rotation in regulating the intensification process under the vertical shear. The result agrees with Zhou (2015) regarding the impact of the earth rotation on the precession process of the tilted vortex. It is hypothesized that a faster vertical realignment of a vortex with a higher f is likely attributed to the enhanced dynamical coupling between the low and mid-level vortices. Previous studies (Jones, 1995; Zhou, 2015) attempted to give an explanation in terms of the Rossby penetration depth (Hoskins et al., 1985), which is defined as
|
| Figure 5 Plan-view of relative vorticity (1×10–4 s–1) fields at 5 km (black dashed line) and 1.5 km (red solid lines) at 12, 24, 36, and 48 h in experiments F7.5 (first row), F20 (second row), and F30 (third row), under easterly shear. |

|
| Figure 6 Time evolution of the magnitude of tilting represented by the separation distance (km) between mid- and low-level vortex center. |
The frictional boundary layer plays a critical role in the thermodynamics and dynamics of TCs. The behavior of the radial flow is largely regulated by the boundary layer imbalance. Previous studies (Li et al., 2012; Smith et al., 2015) showed that the timing of TC intensification at different latitudes is primarily ascribed to the boundary layer imbalance. Initially, the vortices satisfy the gradient wind balance. Due to the friction, the surface tangential wind will be decreased. This results in gradient wind imbalance and thus radial inflow. With a smaller f, a strong subgradient inflow layer develops more quickly, which leads to a larger boundary layer inflow. The larger boundary layer inflow and enhanced moisture convergence lead to greater diabatic heating. In this regard, we will investigate the simulated boundary layer process under vertical shear.
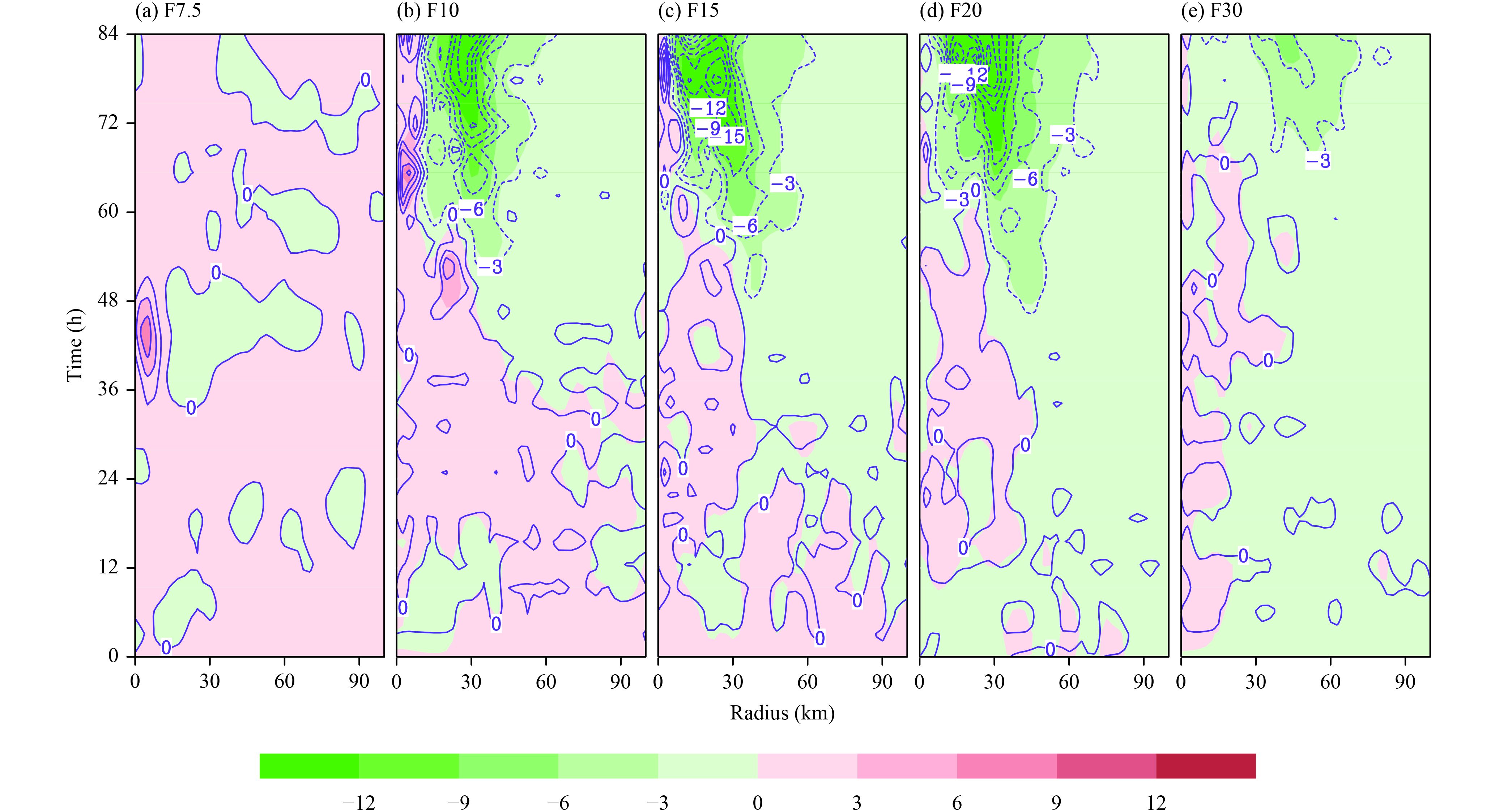
To illustrate the boundary layer gradient wind imbalance, we calculate the agradient wind force (AF). The AF is defined as the differences among the local radial pressure gradient, the centrifugal and Coriolis forces in the radial momentum equation. The magnitude of AF quantifies the deviation from the gradient wind balance. A negative (positive) AF denotes that the flow accelerates inward (outward) where it is subgradient (supergradient). Figure 7 presents the time–radial cross-sections of AF field at the height of 500 m. Notice that there are substantial differences in the experiments. In our simulations, the timing of the intensification depends largely on when the boundary layer imbalance is enhanced. The AF in F7.5 is trivial during the whole integration. As the latitude increases, AF becomes stronger from F10 to F20 experiments. Particularly, starting fromt = 36 h, a pronounced negative AF emanates and continues to strengthen in F20. The negative AF indicates that there is a tendency to enhance the inflow toward the vortex center. Interestingly, as the latitude is further increased, this negative inflow tendency becomes much smaller (i.e., F30), which is consistent with the reversed tendency of intensification rate beyond 20°N (Fig. 2b). It seems that the AF has a saturation effect when latitude further increases. Two possible factors is speculated to account for the scenario. One is the Coriolis forcing, as the Coriolis parameter increases with the latitude, this forcing will increase as storm intensifies. Another is due to the storm size; the storm generally has a large size (i.e., large ra-dius of maximum wind). For a similar maximum wind, the pressure gradient force will be weaker compared with the small one. By combining these two effects, the AF likely reaches a saturation effect.
|
| Figure 7 Time–radial cross-sections of agradient force (AF; 1×10–3 m s–2). |
Figure 8 displays the evolution of the boundary layer radial flow. Consistent with the AF field, there are noticeable differences in the boundary layer inflow. In particular, the boundary layer radial inflow is the weakest (strongest) in F7.5 (F20). To gain insights into the possible processes accounting for the strength of the tangential wind, a budget for the azimuthal mean tangential wind tendency is conducted. The budget equation can be approximated by:
| (1) |
where vt, vr and w are the tangential, radial and vertical velocity, and

|
| Figure 8 As in Fig. 7, but for the boundary layer radial flow (m s–1) at z = 500 m. |

|
| Figure 9 Radial distributions of the mean radial vorticity flux (m s–1 h–1) in Eq. (1) averaged during 48–72 h in the five experiments. |
Previous studies (Powell, 1990; Frank and Ritchie, 2001; Riemer et al., 2010; Tang and Emanuel, 2010, 2012) pointed out that vertical shear acts to decrease the efficiency of the hurricane heat engine by ventilating the TC with low-entropy air at mid levels. Riemer et al. (2010) suggested that convective downdrafts due to evaporative cooling flush the low-entropy air into the boundary layer, where it is then advected inward by the radial inflow. Therefore, the ventilation is realized to be an important mechanism in modulating TC intensification process. Tang and Emanuel (2012) introduced a ventilation index to quantitatively evaluate the probability of TC intensity change. The ventilation index, which is defined as:
| (2) |
where χm is the non-dimensional entropy deficit, Ushear is the vertical wind shear, and UPI is the maximum potential intensity. The UPI is a theoretical upper bound estimated following Bister and Emanuel (2002). Basically, the ventilation index is the combination of the entropy deficit, the vertical wind shear, and the maximum potential intensity. The smaller the index, the greater the potential of rapid intensification rate is. It is interesting to compare the evolution of the ventilation effect in the experiments (Fig. 10). During the period of interest, the values decrease significantly except in F7.5. In F7.5, the value remains the largest during the whole period, implying that it is unfavorable for the vortex to intensify. On the contrary, the value is the smallest in F20 especially in the first 24 hours, indicating the greatest possibility of rapid intensification. In short, the ventilation effect reasonably explains the different intensification rates in our simulations. Further examination shows that χm is the dominant factor during the evolution of the ventilation index.

|
| Figure 10 Time evolution of the ventilation index in the experiments under vertical shear. |
TC development is in general accompanied by the diabatic heating associated with precipitation, especially deep convection. Both the location and magnitude of diabatic heating will influence the TC intensification rate. In the study, the time-evolution of the magnitude of rainfall rates are compared in Fig. 11. With the rainfall amount reflects the diabatic heating, it is clear the rainfall rate is the strongest (weakest) in F20 (F7.5), consistent with the different intensification rates. Given that the secondary circulation is primarily forced by diabatic heating, it is helpful to compare the differences in the secondary circulations in association with the heating. To this end, the Sawyer–Eliassen (SE) equation is applied, which has been widely used in TC research (Shapiro and Willoughby, 1982; Hendricks et al., 2004; Fang and Zhang, 2012; Ge et al., 2015). By using this tool, we can examine the secondary circulation forced by the specified momentum or heat forcing. In here, only the heat forcing is taken into consideration for comparison. The azimuthal mean diabatic heating (

|
| Figure 11 As in Fig. 7, but for the rainfall rate (mm h–1). |
Figure 12 displays the radius-height cross section of the azimuthal mean heating and its forced secondary circulation in three experiments. The magnitude of heating source is the strongest in F20, the weakest in F7.5, and the one in F30 is in between. In F20, the strong diabatic heating appears in the primary eyewall region, and extends vertically with the maximum located at the height of 4–8 km. The heating source in F7.5 is insignificant since no primary eyewall is identified. Notice that remarkable differences in the forced secondary circulations. Compared with F7.5 and F30, F20 has a stronger secondary circulation with a strong lower (upper) inflow (outflow). That is, along with stronger diabatic heating, the secondary circulation is more pronounced. These diagnostics conform to different intensification rates in our simulations. To summarize, a greater heating source can strengthen a secondary circulation. In turn, the stronger boundary layer inflow leads to a larger moisture convergence and thus further enhances the diabatic heating. Moreover, as the storm is enhanced, the enhanced primary circulation reflects a larger inertial stability, which favors the conversion of diabatic heating to the kinetic energy (Schubert and Hack, 1982; Hack and Schubert, 1986). These positive feedbacks likely lead to distinctive evolution characteristics of TCs at different latitudes.

|
| Figure 12 Height–radius cross-sections of the diabatic heating (shaded; K h–1) averaged during 48–72 h and its forced radial flow (contours; m s–1) based on the Sawyer–Eliassen equation in (a) F7.5, (b) F20, and (c) F30, respectively. |
In this study, the dependence of tropical cyclone intensification on the latitude under a vertical shear is examined. It is found that, in the presence of easterly vertical shear, there is likely an optimal background rotation rate for the TC development, which is different from the previous studies without the environmental flow. In a quiescent environment, it is shown systematically that TCs will intensify more rapidly as the latitude is decreased. In this study, we observe that the TC develops more rapidly with an intermediate earth rotation. Our diagnosis shows that the ambient rotation has two effects. On the one hand, it modulates the vertical realignment process. When a vertical shear is presented, a TC tends to develop a vertically tilted structure. At lower latitudes, the mid-level vortices are vulnerable to being advected away from the low-level center, unfavorable for TC development. On the other hand, the boundary layer imbalance is largely controlled by the Coriolis parameter with lower latitude in favor of the boundary layer inflow and thus in favor of TC development. The different development is likely ascribed to the boundary layer imbalance. It is likely that the weaker agradient forcing for low latitude (i.e., 7.5°N) TC is due to the storm never really developing. Based on our previous idealized stimulations with no environmental flows, the TC at low-latitude intensifies rapidly and thus has a pronounced PBL imbalance, since the storm intensifies rapidly with no VWS. By this reasoning, the significant AF is largely ascribed to the enhanced storm intensity. For a TC at lower latitude, due to a smaller inertial stability, a stronger boundary layer inflow is quickly established, which brings about a greater moisture convergence into the core region and leads to stronger diabatic heating. The greater heating source will force a stronger secondary circulation. Through this positive feedback, the vortex spins up at a faster rate at low latitude. To summarize, a larger Coriolis parameter favors a vertical realignment of the tilted vortex while a smaller Coriolis parameter favors TC development through boundary layer process. In this regard, the combination of these two effects results in an optimal latitude for TC intensification under vertical shear.
In this study, we only focus on an idealized vertical shear. To make a comprehensive conclusion, more sensitivity tests should be conducted by using different vertical shear profiles (i.e., deep vs. shallow layer shear). In the current model configuration, the optimal latitude is about 20°N. Admittedly, the value may change with different shear or other environmental factors. It is speculated that the value is sensitive to other factors such as the environmental thermodynamic condition. For instance, a moist environment may help TC resist the vertical shear than a dry condition. Of course, the initial vortices with varied intensities and sizes should be examined as well. These topics require further investigation.
| Bister, M., 2001: Effect of peripheral convection on tropical cyclone formation. J. Atmos. Sci., 58, 3463–3476. DOI:10.1175/1520-0469(2001)058<3463:EOPCOT>2.0.CO;2 |
| Bister, M., and K. A. Emanuel, 2002: Low frequency variability of tropical cyclone potential intensity. 1. Interannual to interdecadal variability. J. Geophys. Res., 107, 4801. DOI:10.1029/2001JD000776 |
| DeMaria, M., 1996: The effect of vertical shear on tropical cyclone intensity change. J. Atmos. Sci., 53, 2076–2088. DOI:10.1175/1520-0469(1996)053<2076:TEOVSO>2.0.CO;2 |
| DeMaria, M., and J. D. Pickle, 1988: A simplified system of equations for simulation of tropical cyclones. J. Atmos. Sci., 45, 1542–1554. DOI:10.1175/1520-0469(1988)045<1542:ASSOEF>2.0.CO;2 |
| DeMaria, M., J. A. Knaff, and B. H. Connell, 2001: A tropical cyclone genesis parameter for the tropical Atlantic. Wea. Forecasting, 16, 219–233. DOI:10.1175/1520-0434(2001)016<0219:ATCGPF>2.0.CO;2 |
| Fang, J., and F. Zhang, 2012: Effect of beta shear on simulated tropical cyclones. Mon. Wea. Rev., 140, 3327–3346. DOI:10.1175/MWR-D-10-05021.1 |
| Frank, W. M., and E. A. Ritchie, 2001: Effects of vertical wind shear on the intensity and structure of numerically simulated hurricanes. Mon. Wea. Rev., 129, 2249–2269. DOI:10.1175/1520-0493(2001)129<2249:EOVWSO>2.0.CO;2 |
| Ge, X. Y., T. Li, and X. Q. Zhou, 2007: Tropical cyclone energy dispersion under vertical shears. Geophys. Res. Lett., 34, L23807. DOI:10.1029/2007GL031867 |
| Ge, X. Y., T. Li, Y. Q. Wang, et al., 2008: Tropical cyclone energy dispersion in a three-dimensional primitive equation model: Upper-tropospheric influence. J. Atmos. Sci., 65, 2272–2289. DOI:10.1175/2007jas2431.1 |
| Ge, X. Y., T. Li, and M. Peng, 2013: Effects of vertical shears and midlevel dry air on tropical cyclone developments. J. Atmos. Sci., 70, 3859–3875. DOI:10.1175/jas-d-13-066.1 |
| Ge, X. Y., W. Xu, and S. W. Zhou, 2015: Sensitivity of tropical cyclone intensification to inner-core structure. Adv. Atmos. Sci., 32, 1407–1418. DOI:10.1007/s00376-015-4286-5 |
| Gray, W. M., 1968: Global view of the origin of tropical disturbances and storms. Mon. Wea. Rev., 96, 669–700. DOI:10.1175/1520-0493(1968)096<0669:GVOTOO>2.0.CO;2 |
| Gray, W. M., 1979: Tropical cyclone intensity determination through upper-tropospheric aircraft reconnaissance. Bull. Amer. Meteor. Soc., 60, 1069–1074. DOI:10.1175/1520-0477(1979)060<1069:TCIDTU>2.0.CO;2 |
| Hack, J. J., and W. H. Schubert, 1986: Nonlinear response of atmospheric vortices to heating by organized cumulus convection. J. Atmos. Sci., 43, 1559–1573. DOI:10.1175/1520-0469(1986)043<1559:NROAVT>2.0.CO;2 |
| Hendricks, E. A., M. T. Montgomery, and C. A. Davis, 2004: The role of " vortical” hot towers in the formation of tropical cyclone Diana (1984). J. Atmos. Sci., 61, 1209–1232. DOI:10.1175/1520-0469(2004)061<1209:TROVHT>2.0.CO;2 |
| Holland, G. J., 1997: The maximum potential intensity of tropical cyclones. J. Atmos. Sci., 54, 2519–2541. DOI:10.1175/1520-0469(1997)054<2519:TMPIOT>2.0.CO;2 |
| Hoskins, B. J., M. E. McIntyre, and A. W. Robertson, 1985: On the use and significance of isentropic potential vorticity maps. Quart. J. Roy. Meteor. Soc., 111, 877–946. DOI:10.1002/qj.49711147002 |
| Jones, S. C., 1995: The evolution of vortices in vertical shear. I: Initially barotropic vortices. Quart. J. Roy. Meteor. Soc., 121, 821–851. DOI:10.1002/qj.49712152406 |
| Li, T., X. Y. Ge, M. Peng, et al., 2012: Dependence of tropical cyclone intensification on the Coriolis parameter. Trop. Cyclone Res. Rev., 1, 242–253. DOI:10.6057/2012TCRR02.04 |
| McBride, J. L., and R. Zehr, 1981: Observational analysis of tropical cyclone formation. Part II: Comparison of non-developing versus developing systems. J. Atmos. Sci., 38, 1132–1151. DOI:10.1175/1520-0469(1981)038<1132:OAOTCF>2.0.CO;2 |
| Powell, M. D., 1990: Boundary layer structure and dynamics in outer hurricane rainbands. Part II: Downdraft modification and mixed layer recovery. Mon. Wea. Rev., 118, 918–938. DOI:10.1175/1520-0493(1990)118<0918:BLSADI>2.0.CO;2 |
| Rappin, E. D., and D. S. Nolan, 2012: The effect of vertical shear orientation on tropical cyclogenesis. Quart. J. Roy. Meteor. Soc., 138, 1035–1054. DOI:10.1002/qj.977 |
| Riemer, M., M. T. Montgomery, and M. E. Nicholls, 2010: A new paradigm for intensity modification of tropical cyclones: Thermodynamic impact of vertical wind shear on the inflow layer. Atmos. Chem. Phys., 10, 3163–3188. DOI:10.5194/acp-10-3163-2010 |
| Schubert, W. H., and J. J. Hack, 1982: Inertial stability and tropi-cal cyclone development. J. Atmos. Sci., 39, 1687–1697. DOI:10.1175/1520-0469(1982)039<1687:ISATCD>2.0.CO;2 |
| Shapiro, L. J., and H. E. Willoughby, 1982: The response of balanced hurricanes to local sources of heat and momentum. J. Atmos. Sci., 39, 378–394. DOI:10.1175/1520-0469(1982)039<0378:TROBHT>2.0.CO;2 |
| Smith, R. K., G. Kilroy, and M. T. Montgomery, 2015: Why do model tropical cyclones intensify more rapidly at low latitudes?. J. Atmos. Sci., 72, 1783–1804. DOI:10.1175/jas-d-14-0044.1 |
| Tang, B., and K. Emanuel, 2010: Midlevel ventilation’s constraint on tropical cyclone intensity. J. Atmos. Sci., 67, 1817–1830. DOI:10.1175/2010JAS3318.1 |
| Tang, B., and K. Emanuel, 2012: A ventilation index for tropical cyclones. Bull. Amer. Meteor. Soc., 93, 1901–1912. DOI:10.1175/BAMS-D-11-00165.1 |
| Wang, Y. Q., 1995: An inverse balance equation in sigma coordinates for model initialization. Mon. Wea. Rev., 123, 482–488. DOI:10.1175/1520-0493(1995)123<0482:AIBEIS>2.0.CO;2 |
| Wang, Y. Q., 2001: An explicit simulation of tropical cyclones with a triply nested movable mesh primitive equation model: TCM3. Part I: Model description and control experiment. Mon. Wea. Rev., 129, 1370–1394. DOI:10.1175/1520-0493(2001)129<1370:AESOTC>2.0.CO;2 |
| Zhang, D.-L., and C. Q. Kieu, 2006: Potential vorticity diagnosis of a simulated hurricane. Part II: Quasi-balanced contributions to forced secondary circulations. J. Atmos. Sci., 63, 2898–2914. DOI:10.1175/JAS3790.1 |
| Zhang, F. Q., and D. D. Tao, 2013: Effects of vertical wind shear on the predictability of tropical cyclones. J. Atmos. Sci., 70, 975–983. DOI:10.1175/JAS-D-12-0133.1 |
| Zhou, W. Y., 2015: The impact of vertical shear on the sensitivity of tropical cyclogenesis to environmental rotation and thermodynamic state. J. Adv. Model. Earth Syst., 7, 1872–1884. DOI:10.1002/2015ms000543 |
 2018, Vol. 32
2018, Vol. 32


