The Chinese Meteorological Society
Article Information
- WANG, Chao, Xingqin AN, Shixian ZHAI, et al., 2018.
- Tracking a Severe Pollution Event in Beijing in December 2016 with the GRAPES–CUACE Adjoint Model. 2018.
- J. Meteor. Res., 32(1): 49-59
- http://dx.doi.org/10.1007/s13351-018-7062-5
Article History
- Received April 29, 2017
- in final form September 18, 2017
2. State Key Laboratory of Severe Weather/Key Laboratory of Atmospheric Chemistry of China Meteorological Administration, Chinese Academy of Meteorological Sciences, Beijing 100081;
3. Key Laboratory for Aerosol–Cloud–Precipitation of China Meteorological Administration, Nanjing University of Information Science & Technology, Nanjing 210044;
4. Institute of Urban Meteorology, China Meteorological Administration, Beijing 100089;
5. Environmental Meteorology Forecast Center of Beijing–Tianjin–Hebei, China Meteorological Administration, Beijing 100089
Air pollution characterized by fine particulate matter (PM2.5) has become increasingly prevalent with the rapid development of industrialization and urbanization in China. Severe air pollution in the Beijing–Tianjin–Hebei region, in particular, has caused widespread concern (Wang et al., 2014; Jiang et al., 2015; Zheng et al., 2015). In September 2013, the State Council promulgated the comprehensive Air Pollution Prevention and Control Action Plan. The Chinese government has attached great importance to this problem and has put forward new requirements for the prevention and control of air pollution.
The Chinese government, environmental protection departments, and scientific researchers have carried out much work on preventing and controlling air pollution, such as implementing environmental laws and regulations, adjusting industrial layouts, developing clean energy, and improving vehicle emission standards. The effectiveness and economic efficiency of air pollution control measures must be considered, which requires that a quantitative scientific basis be provided before the implementation of control measures so as to minimize capital investment and economic losses. This may also reduce unnecessary social contradictions (Zhu and Zeng, 2003). Severe air pollution currently occurs over central and eastern regions of China and in the Beijing–Tianjin– Hebei region. The challenge is to meet environmental air quality standards while reducing the economic cost to the lowest level. The development of scientifically based and effective emission reduction control measures is therefore urgently required.
Atmospheric chemical models have the ability to quantitatively simulate spatial and temporal changes in the concentration of air pollutants. Researchers have analyzed the sources of PM2.5 in Beijing, estimated the contribution of emissions from the surrounding regions to the PM2.5 in Beijing, designed sensitivity tests to evaluate the effect of source reduction schemes in reducing PM2.5 concentrations, and determined the crucial source areas using the Lagrangian particle diffusion model FLEXPART (An et al., 2007; Zhai et al., 2014, 2015, 2016; Jiang et al., 2015). These studies have helped to determine the sources of PM2.5 in Beijing and the contributions of local and neighboring sources and have laid a good foundation for developing scientifically based and effective control measures to reduce pollutant emissions.
As a result of the complex structure of atmospheric chemical models and the large number of input parameters, the emission source on which the traditional forward sensitivity analysis method is based must be adjusted and the model needs to run many times. The calculation efficiency of the method is therefore low, costs are high, and the method is prone to truncation errors (Dunker, 1981). The atmospheric chemical adjoint model is an efficient approach and a useful sensitivity analysis tool based on the adjoint operator theory and an atmospheric chemical model. An objective function is configured to provide sensitive information (Hakami et al., 2006). The adjoint method relies on reverse simulation, which means that by establishing an adjoint of the tangential mode, the adjoint model only needs to be run once to obtain the sensitivity of the objective function for all emission sources (or other input parameters). The efficiency is therefore much higher than in a model that analyzes the sensitivity of every factor (Liu, 2005; Sandu et al., 2005; Yumimoto and Uno, 2006). The adjoint method has a unique advantage in complex multi-parameter systems in that it only needs a few simulations to calculate the sensitivity or gradient of the objective function for all input parameters (Zhu et al., 1999) and it can use gradient information to quickly solve the problems related to opti-mum control (Cheng et al., 1998; Liu and Hu, 2003). Marchuk and Skiba (1976) and Marchuk (1986) applied the adjoint method to the atmospheric environment for the optimum reduction and rational locating of pollution sources. They used the conjugate properties of the adjoint operators to avoid repeatedly solving the pollutant transmission problem, thus greatly reducing the computational requirements.
Skiba and Parra-Guevara (2000) and Skiba and Davydova-Belitskaya (2002, 2003) developed the Marchuk method and further applied it to issues of atmospheric environmental control. At present, corresponding adjoint models have been developed for some of the most widely used atmospheric chemical models and assimilation and sensitivity analyses have been conducted based on these adjoint models. These atmospheric chemical models include the European air pollution diffusion model of the University of Cologne, Germany (Elbern et al., 2000), the US air quality model STEM-III (Sandu et al., 2005), the US atmospheric chemical transfer model CAMx (Liu, 2005), and the US atmospheric chemical model GEOS_Chem (Henze et al., 2007). The US CMAQ model was developed with its own adjoint code (Hakami et al., 2007). Sfetsos et al. (2013) used the CMAQ adjoint mo-del for the sensitivity analysis of ground surface ozone in Athens. Chinese researchers have developed the adjoint model of the atmospheric chemical model—Global/Regional Assimilation and Prediction System (GRAPES) coupled with the China Meteorological Administration Unified Atmospheric Chemistry Environmental (CUACE) forecasting system (Gong et al., 2003) and used it to trace the source areas of atmospheric pollution (Zhai, 2015; An et al., 2016; Wang et al., 2017).
This study focused on one severe pollution event that occurred in Beijing in December 2016. The GRAPES–CUACE adjoint model is used to track the sensitive source area affecting the Beijing PM2.5 concentration and to evaluate the contribution of local and neighboring sources. The results will serve as a scientific basis for the development of control measures for emission reduction.
The meteorological data used in this study are conventional surface and upper-air observations. The pollutant concentration data are hourly mean PM2.5 observations from the Beijing Meteorological Observatory Nanjiao (NJ) and Shangdianzi (SDZ) stations. The NJ station (39°48'N, 116°28'E) is located at the atmospheric observation test base in the southern suburbs of Beijing and can be used to represent the PM2.5 concentrations in the Beijing urban area. The SDZ station (40°39'N, 117°07'E) is the regional atmospheric background station located in Miyun county northeast of Beijing. It represents the background of the monitored parameters in North China.
2.2 GRAPES–CUACE adjoint modelThe GRAPES–CUACE adjoint model (Zhai, 2015; An et al., 2016) was constructed based on the atmospheric chemistry model of GRAPES–CUACE (Wang et al., 2010a, b, 2015), which is an online coupled system of the atmospheric model GRAPES (Chen et al., 2008) and the aerosol model CUACE (Gong et al., 2003). A flowchart of the structures and parameters of the GRAPES–CUACE adjoint model are shown inFig. 1.
The detailed steps to run the adjoint model are given in Zhai (2015) and An et al. (2016). The forward integration to the GRAPES–CUACE atmospheric chemical model is performed first and the related data information is stored via the savedat module. Taking the gradient ( ∂J/∂c) of the state variables (such as the pollutant concentration, c) and the stored information of the objective function J as the input data, the adjoint model is integrated in reverse chronological order and the gradient ( ∂J/∂c) of the control variables (such as the emission source, s) of the objective function J can be obtained.

|
| Figure 1 Schematic diagram showing the coupling of GRAPES–CUACE atmospheric chemical model with its adjoint model. |
The CUACE model is composed of three modules: the aerosol module (module_ae_cam), the gas module (module_gas_radm), and the thermodynamic equilibrium module (module_isopia). To date, we have only developed the adjoint model of the aerosol module. The adjoint model of the gas module is currently being constructed and therefore this study first simulates the changing trend of the total PM2.5 concentration by the GRAPES–CUACE model and then traces backward the key emission sources and sensitive emission period of the primary PM2.5 in one severe pollution event in Beijing in winter 2016 using the GRAPES–CUACE aerosol adjoint model.
The simulation region is eastern China (32.25°–43.25°N, 105°–125°E), covering 41 × 23 horizontal grids with a resolution of 0.5° × 0.5° and vertically divided into 31 layers. The length of the integration step is 300 s. The INTEX-B2006 data on a 0.5° × 0.5° resolution (Zhang et al., 2009), including SO2, NOx, CO, black carbon, organic carbon, non-methane volatile organic compounds, PM2.5, and PM10, are used as the emissions inventory. The anthropogenic emission sources in North China are updated by using the emission base data and emission factors for 2010 through the EMission Inventory Processing System, which is applied in the atmospheric chemistry model CUACE (Lyu, 2015). The INTEX-B2006 data have been widely used in the atmospheric environment field for simulating variations in the PM2.5 concentration (Liu et al., 2014; Yang et al., 2016), studying the effects of sulfate and nitrate aerosols on the chemical and transport process of O3 (Yang et al., 2014; Zhu et al., 2015), and evaluating the impacts of the emission inventory on SO2, NO2, CO, and O3 simulations in conjunction with the observed data (An et al., 2013). The simulation period is from 2000 Beijing Time (BJT) 27 November to 1900 BJT 5 December 2016. The first three days are set as the model spin-up time to eliminate the difference between the idealized initial concentration and the observed concentration.
3 Results 3.1 Synoptic situation during the pollution processDuring 2–5 December 2016, Beijing and the surrounding areas experienced a continuous severe pollution event. The synoptic situation during the pollution process is analyzed based on the MICAPS meteorological information processing system of the China Meteorological Administration and other related observational data. Figure 2 shows that Beijing was influenced by a weak pressure field on 2 December 2016 and was affected by an eastward-moving low pressure convergence zone during the next two days, so that the conditions for diffusion progressively worsened. During 2–4 December 2016, the winds at 500 hPa were controlled by the zonal airflow, and a high-level trough with a small spatial scale passed over Beijing. On 2 December, northwesterly winds blew at 700 and 850 hPa, leading slowly to weak cold advection. The cold air was not strong enough to intrude into the bottom of the boundary layer and the environmental capacity of the near-surface atmosphere was compressed. Affected by the warming effect of upper air subsidence, a subsidence temperature inversion emerged between 700 and 850 hPa, but the atmospheric humidity was not high. On 3 December, southerly winds blew at both 700 and 850 hPa and the induced warm advection effect favored further stabilization of the atmospheric stratification. The top of the inversion layer dropped to near 850 hPa and the inversion intensity below 850 hPa increased. During the night of 3 December, the top of the inversion layer dropped further to 850–925 hPa and the near-surface humidity showed an increasing trend. On 4 December, cold air gradually infiltrated downward from the upper air, and later arrived at the ground. The downward penetration of cold air with a frontal transit contributed to the increase in the near-surface dynamic convergence and a decrease in the capacity of the atmosphere to hold pollutants. In the morning of 4 December, the near-surface atmosphere had a high humidity, approaching saturation, and the temperature inversion layer was located between 925 and 1000 hPa. Therefore, 4 December was the most unfavorable period for pollutants to diffuse during the severe pollution event. By 5 December, the heavy pollution event ended as a result of the cold air moving southeastward.

|
| Figure 2 Sea-level pressure fields at 0800 Beijing Time (BJT) on (a) 2, (b) 3, (c) 4, and (d) 5 December 2016. |
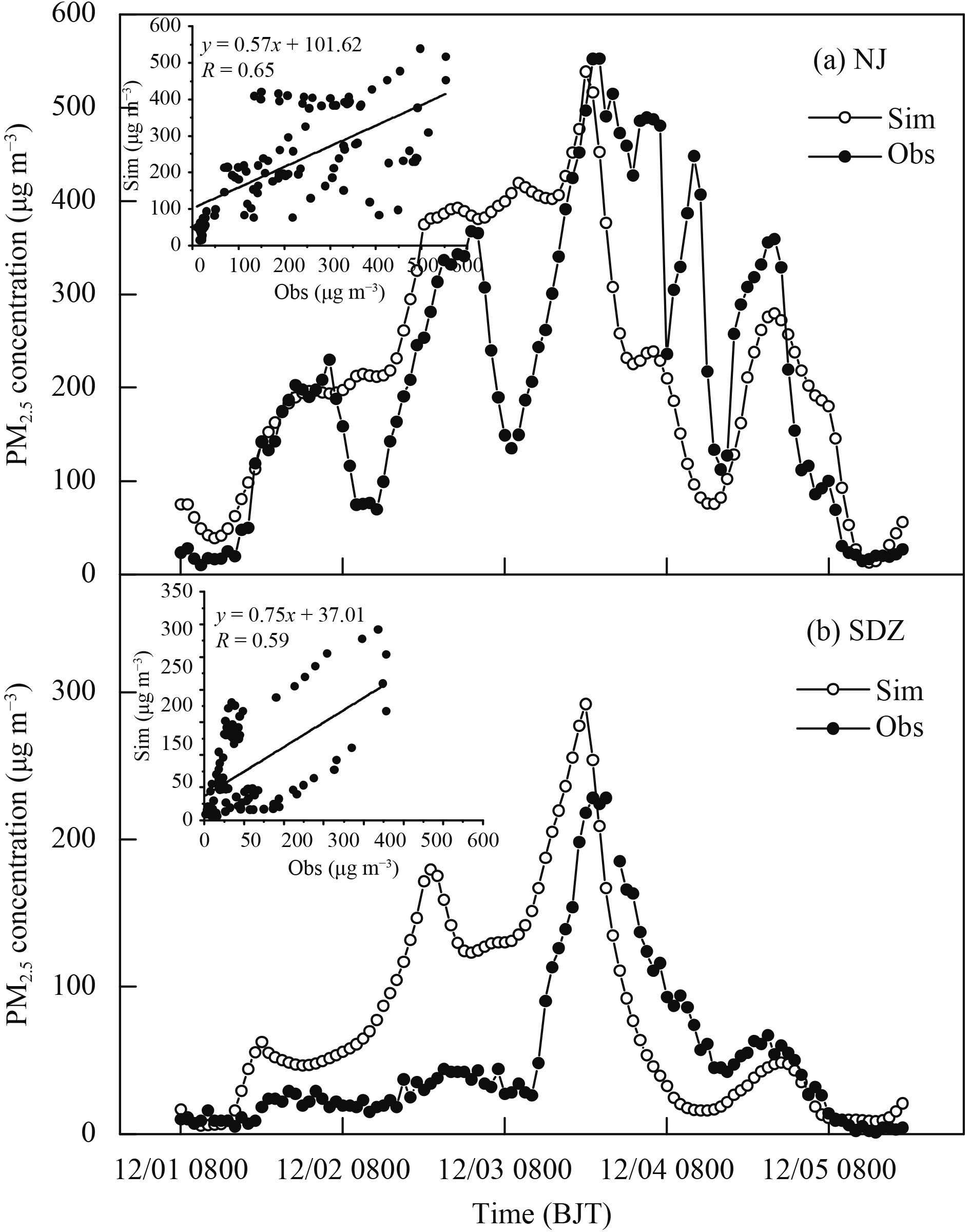
The PM2.5 mass concentrations observed during 1–5 December 2016 at the NJ and SDZ stations are used to verify the simulation performance of the model. Figure 3 and Table 1 show that the GRAPES–CUACE simulation results are in good agreement with the observational data. The correlation coefficients of the observed PM2.5 concentration and the simulated values are 0.65 and 0.59 at NJ and SDZ, respectively. By using the mean bias (MB) (
|
| Figure 3 Variation curves and scatter graphs of the observed and simulated hourly PM2.5 concentration at (a) Nanjiao (NJ) station and (b) Shangdianzi (SDZ) station from 0800 BJT 1 December to 1900 BJT 5 December 2016. |
| Station | No. of observations | Simulated
maximum (μg m–3) |
Observed
maximum (μg m–3) |
Simulated
mean (μg m–3) |
Observed
mean (μg m–3) |
Mean bias
(μg m–3) |
Normalized
mean bias (%) |
RMSE
(μg m–3) |
R | Index of agreement |
| NJ | 108 | 538.73 | 552.50 | 224.43 | 216.91 | 7.52 | 3.47 | 121.60 | 0.65 | 0.80 |
| SDZ | 107 | 291.71 | 228.00 | 75.43 | 51.10 | 24.33 | 47.61 | 62.53 | 0.59 | 0.73 |
| Notes: Mi is simulated concentration; Oi is observed concentration; mean bias
|
||||||||||
For the adjoint sensitivity analysis, we first need to define an objective function and then obtain the sensitivity of the input variable (pollution sources, μg m–2 s–1) to the objective function by the backward integration of the GRAPES–CUACE adjoint model. The peak value of the simulated average PM2.5 concentration in Beijing appears at 2000 BJT 3 December 2016 and the peak concentration is as high as 343.50 μg m–3. To track the key pollution sources and periods of the PM2.5 peak concentration, 2000 BJT 3 December 2016 is defined as the objective time and the city of Beijing as the objective area. The objective function is the average PM2.5 concentration in Beijing at 2000 BJT 3 December 2016.
Running the adjoint model once, we obtain the gradient (sensitivity)
Figure 4 shows the time-accumulated distribution of the sensitivity coefficient for the objective function of the primary PM2.5 emission source, which describes the accumulated effect of the intensity of the emission source on the target concentration for a certain period of time before the objective time. The sensitivity coefficient accumulates to 1 h before the objective time (Fig. 4a) along with the inverse time series, with only Beijing having a 1–3 μg m–3 sensitivity coefficient. The inverse time series continues to accumulate, the sensitivity coefficient grad-ually increases, and the range also expands in a constant manner. By 31 h before the objective time (Fig. 4f), the sensitivity coefficient has extended to northwestern Tian-jin, southern Hebei, and eastern Shanxi, indicating that the peak value of the PM2.5 concentration in Beijing at the objective time is jointly influenced by the emission of pollution sources in Beijing, Tianjin, Hebei, and Shanxi, and at this time, the maximum value of the sensitivity coefficient is 24 μg m–3. This means that if we reduce N% of the emission of the pollution source in the largest grid of the sensitivity coefficient from 1300 BJT 2 December 2016 to the objective time (31 h in total), then the average PM2.5 concentration in Beijing will decrease N% × 24 μg m–3 by 2000 BJT 3 December 2016 (objective time).
By comparing the situation 37 and 72 h before the objective time (Figs. 4g, h), we can see a slight difference between the distribution and values of the accumulated sensitivity coefficients. However, the rate of increase 37–72 h before the objective time is much smaller than the rate of increase 1–37 h ahead of the objective time, which indicates that early source emissions, such as the source emission prior to 37 h before the objective time, do not have much influence on the high concentration of PM2.5 at the objective time.

|
| Figure 4 Time-accumulated sensitivity coefficient distributions at (a) 1, (b) 7, (c) 13, (d) 19, (e) 25, (f) 37, (g) 47, and (h) 72 h ahead of the objective time (2000 BT 3 December 2016). |
The time series of the hourly (Fig. 5a) and accumulated (Fig. 5b) sensitivity coefficients of the local and neighboring sources reflect the changes in their hourly contribution and accumulated contribution, respectively, within a certain period to the PM2.5 peak concentration at the objective time. With the inverse time integral, the hourly sensitivity coefficients of the local and neighboring sources reach their maximum values before decreasing, although the two trends are significantly different (Fig. 5a). The peak concentration of PM2.5 responds quickly to the local source of emission. At 1 h before the objective time, the hourly sensitivity coefficient of the local source reaches its maximum value of 9.31 μg m–3. The contribution of the local source to the PM2.5 peak concentration remains at a higher level in the period 1–4 h before the objective time, but the local source hourly sensitivity coefficient starts to decrease sharply 4 h prior to the objective time and falls down to around 0 at about 1400 BJT 2 December 2016 (30 h before the objective time). Thus, the local emission source 1–30 h before the objective time has a greater influence on the PM2.5 peak concentration at the objective time, but weakens rapidly prior to 30 h before the target time.
The hourly sensitivity coefficients show an obvious cyclical fluctuation (Fig. 5a). They decrease overall with the inverse time integral with a fluctuation period of about 24 h, which may be related to the large-scale background atmospheric circulation, the local circulation, and the diurnal variation of the boundary layer. The peak values of the three sensitivity coefficients of the neighboring sources successively emerge at 1600 BJT 3 December 2016 (4 h before the objective time), 0300 BJT 3 December 2016 (17 h before the objective time), and 0400 BJT 2 December 2016 (40 h before the objective time) with values of 4.05, 5.11, and 1.17 μg m–3, respectively. Before 1400 BJT 1 December 2016 (54 h before the objective time), the neighboring source sensitivity coefficient is reduced to nearly 0. This indicates that the surrounding sources continuously convey pollutants into Beijing 1–54 h before the objective time and have the most significant effect on the PM2.5 peak concentration about 4 and 17 h before the objective time.
Figure 5b shows that, under the inverse time integral, the temporal accumulated sensitivity coefficient of the neighboring source increases and intersects with the lo-cal source about 20 h before the objective time (0000 BJT 3 December 2016). At any time before this, the value is greater than the sensitivity coefficient of the lo-cal source. This indicates that the local source is the dominant contributor to the PM2.5 concentration in the 20 h prior to the objective time, but before 20 h the neighboring source is dominant.

|
| Figure 5 Variations of the (a) hourly and (b) time-accumulated sensitivity coefficient (SC) of the local and surrounding emissions. |
Adding the hourly and temporal accumulated coefficients of the local and neighboring sources together, we obtain the percentage contributions of the hourly and temporally accumulated local and neighboring sources to the PM2.5 peak concentration at this time (Fig. 6). With the inverse time integral, the percentages of the local hourly and temporal accumulated contribution show a decreasing trend and the contribution ratios are 3% and 34%, respectively, before 72 h prior to the objective time. By contrast, the percentages of the hourly and temporal accumulated contribution of the surroundings show an upward trend, exceeding the local source at 8 and 21 h before the objective time, respectively. The proportions of the contribution of local and neighboring sources are 97% and 66% 72 h before the objective time.

|
| Figure 6 Percentage variations of the hourly and time-accumulated contribution of local and surrounding emissions to the PM2.5 peak concentration at the objective time (2000 BJT 3 December 2016). |
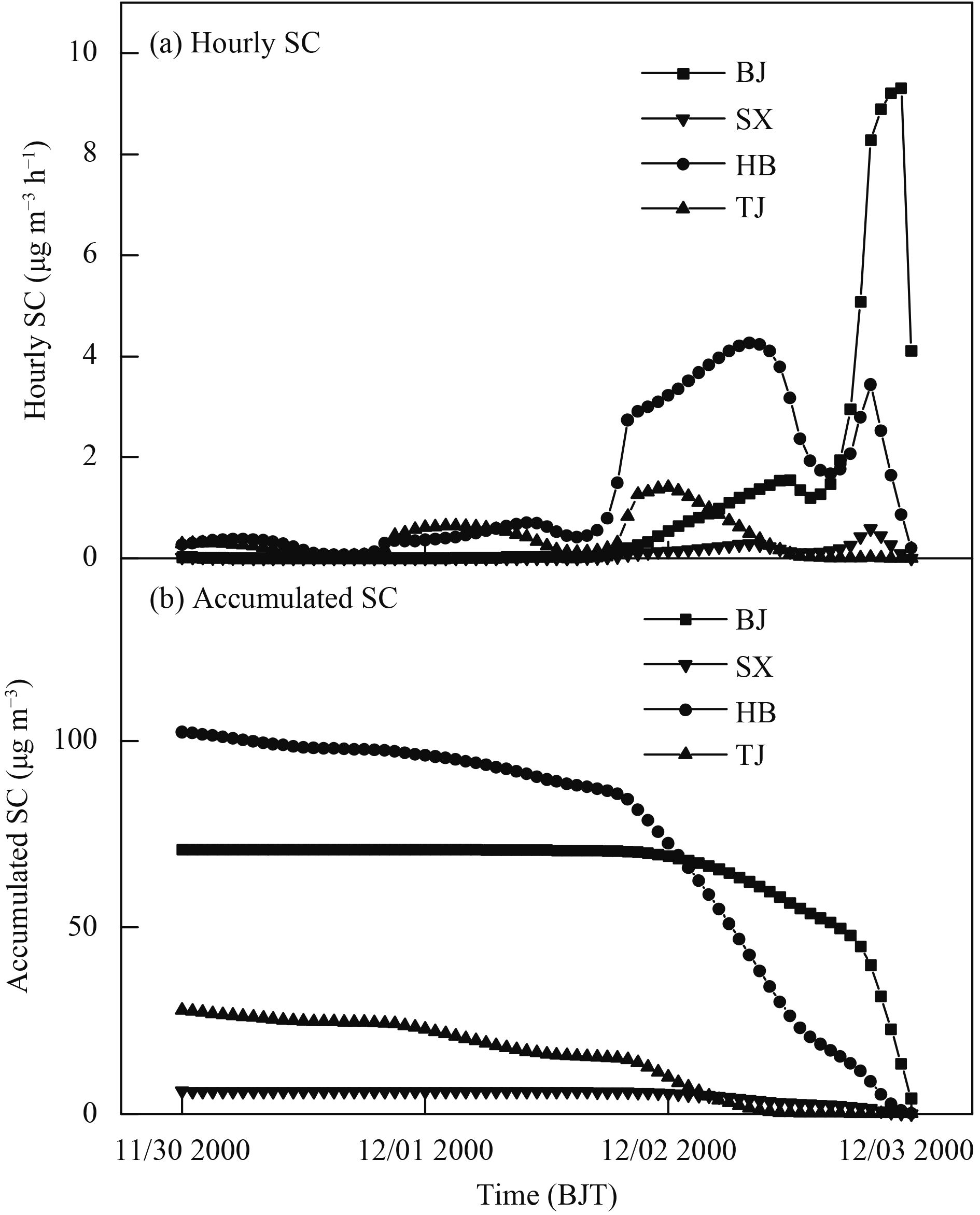
The neighboring sources in this pollution event are the emission sources in the northwest of Tianjin, central and southern Hebei, and eastern Shanxi provinces. Figure 7 shows the time series of hourly (Fig. 7a) and time-accumulated (Fig. 7b) sensitive coefficients for the local Beijing and neighboring emissions. The effects of the Hebei, Tianjin, and Shanxi sources on the PM2.5 peak concentration in Beijing are very different in both time and degree. The hourly sensitivity coefficient of the Hebei source fluctuates periodically and three peaks of the sensitivity coefficient (3.45, 4.27, and 0.71 μg m–3) appear at 1600 BJT 3 December 2016 (4 h before the objective time), 0400 BJT 3 December 2016 (16 h before the objective time), and 0600 BJT 2 December 2016 (38 h before the objective time). From 0800 BJT 3 December 2016 (12 h before the objective time) to 1800 BJT 2 December 2016 (26 h before the objective time), the hourly sensitivity coefficients are all > 3.00 μg m –3. The sensitivity coefficient decreases to about 0 before 1400 BJT 1 December 2016 (54 h before the objective time). The hourly sensitivity coefficient for the Tianjin source shows a slight peak from 1900 BJT 3 December 2016 (1 h before the objective time) to 1800 BJT 2 December 2016 (26 h before the objective time) and the peak value is 0.59 μg m–3 at 1600 BJT (4 h before the objective time). The sensitivity coefficients for the other periods are all < 0.10 μg m –3. Similar to the Hebei source, the hourly sensitivity coefficient of Shanxi shows cyclical fluctuations, except that only two peaks are obvious, one at 0200 BJT 2 December 2016 (24 h before the objective time) and another of 0.64 μg m–3 at 2300 BJT 1 December 2016 (45 h before the objective time). At 1500 BJT 1 December 2016 (53 h before the objective time), the sensitivity coefficient is reduced and approaches zero.
|
| Figure 7 Variations in the (a) hourly and (b) time-accumulated sensitivity coefficients for the Beijing (BJ), Tianjin (TJ), Hebei (HB), and Shanxi (SX) emissions. |
Figure 7b shows that, with the inverse time integral, the time-accumulated sensitivity coefficients of the local and Tianjin sources remain mostly unchanged, whereas the time-accumulated sensitivity coefficient of Hebei increases, exceeding that of the local source at 2100 BJT 2 December 2016 (23 h before the objective time). The time-accumulated sensitivity coefficient for the Shanxi source remains near 0 during the 14-h period before the objective time. At 2300 BJT 2 December 2016 (21 h before the objective time), it becomes higher than that of the Tianjin source. Corresponding to this, with the inverse time integral, the hourly contribution of the local and Tianjin sources tend to decrease to nearly 0 at 0200 BJT (42 h before the objective time) and 1200 BJT (32 h before the objective time), respectively, on 2 December 2016. The hourly contribution ratio of Hebei increases to 50% at 1200 BJT 3 December 2016 (8 h before the objective time), but fluctuates up and down by 50% before this time. The Shanxi hourly contribution ratio fluctuates upward before 0900 BJT 3 December 2016 (11 h before the objective time) and its trend before 0200 BJT 2 December 2016 (42 h before the objective time) is opposite to that of the Hebei source (Fig. 8a). The time-accumulated contribution rate of the Hebei source is greater than that of other three sources before 2100 BJT 2 December 2016 (23 h before the objective time). The time-accumulated sensitivity coefficient of the Shanxi source increases with the inverse time integral, exceeding that of Tianjin at 2300 BJT 2 December 2016 (21 h before the objective time) (Fig. 8b).
These results show that the response time of the PM2.5 peak concentration to the Hebei and Tianjin sources is faster than its response to the Shanxi source. This is because Shanxi is farther away from Beijing and the pollutants need to be transported for about 14 h before they affect the PM2.5 concentration in Beijing. The Hebei source makes a continuous contribution 1–54 h before the objective time and is dominant 24–54 h before the objective time. The Tianjin source contributes only a small amount 1–26 h before the objective time. The contribution period of the Shanxi source is 14–53 h before the objective time.
Figure 8b shows that the accumulated proportions of the Beijing, Tianjin, Hebei, and Shanxi emission sources to the objective time PM2.5 peak concentration are 34.2%, 3.0%, 49.4%, and 13.4%, respectively, in the 72-h period before the objective time. Compared with the pollution process observed from 27 November to 2 December 2015 (Wang et al., 2017), the contribution rates of the Tianjin and Hebei sources decrease slightly, whereas the contributions of the local Beijing and Shanxi emissions increase; the proportion of Shanxi’s contribution increases by nearly 10% (Table 2). This is because the Beijing area was located at the rear of a surface high during the 2015 pollution event and the Tianjin and Hebei sources contributed more to the Beijing PM2.5 peak concentration as a result of the southeasterly winds. The Beijing region was controlled by the eastward low pressure convergence zone during this pollution event and southwesterly winds continued to transport the Shanxi pollutants to Beijing, leading to a significant increase in the Shanxi contribution. There are significant differences in the contribution time of different regions as a result of different weather conditions. During the 2016 pollution event, the contribution times of the local and Shanxi emissions were extended by 17 and 23 h, respectively, compared with their contributions in 2015. By contrast, the contribution time of the Tianjin and Hebei emissions was shortened by 7 and 3 h, respectively.

|
| Figure 8 Percentage variations of (a) hourly and (b) time-accumulated contribution of the Beijing (BJ), Tianjin (TJ), Hebei (HB), and Shanxi (SX) emissions to the PM2.5 peak concentration at the objective time (2000 BJT 3 December 2016). |
| Pollution event | Surface weather conditions | Main contribution period
(hours before objective time) |
Contribution rate in the 72-h period
before objective time (%) |
||||||
| BJ | TJ | HB | SX | BJ | TJ | HB | SX | ||
| 27 November to 2 December 2015 (Wang et al., 2017) | At the rear of a surface high | 1–13 | 1–33 | 1–57 | 17–33 | 31.0 | 9.0 | 56.0 | 4.0 |
| 2–5 December 2016 | Under a surface low | 1–30 | 1–26 | 1–54 | 14–53 | 34.2 | 3.0 | 49.4 | 13.4 |
Based on these results, it is possible to consider joint control measures in Beijing, Hebei, Tianjin, and Shanxi within 1–54 h before the arrival of PM2.5 peak concentrations, which could effectively control the accumulation of PM2.5 due to the transport of pollutants, thereby reducing the PM2.5 peak concentration at 2000 BJT 3 December 2016. Therefore, a predictable peak pollutant concentration in the region could be set as an objective function based on the results of the air quality model prediction. The changes in the contribution of different emission regions can be calculated by the adjoint model and then used to provide effective guidance in developing dyna-mic control measures for air pollution.
4 Conclusions and discussionThe GRAPES–CUACE adjoint model was used to track the PM2.5 heavy pollution event in Beijing during 2–5 December 2016. The following conclusions have been drawn.
(1) The GRAPES–CUACE model may reflect the varying trend of the PM2.5 concentration more reasonably and capture more accurately the PM2.5 peak that occurred in Beijing at 2000 BJT 3 December 2016. The PM2.5 hourly concentration correlation coefficients between the simulation and the observed values at NJ and SDZ stations are 0.65 and 0.59, respectively.
(2) The sensitivity analysis shows that the PM2.5 peak concentration of the pollution event responds rapidly to local emissions and the local hourly sensitivity coefficient reaches a peak value of 9.31 μg m–3 1 h before the objective time. From the perspective of the accumulated sensitivity coefficient, the local source dominates within 20 h of the objective time. The hourly sensitivity coefficient of the neighboring emission fluctuates cyclically and the peak values are 4.05, 5.11, and 1.17 μg m–3 at 4, 17, and 40 h before the objective time, respectively. Accompanied by southerly winds, the neighboring sources continuously send pollutants to Beijing in the period 1–54 h before the objective time.
(3) The contribution time and ratio of each regional emission source to the objective time PM2.5 peak concentration are related to the synoptic situation during the pollution event. The accumulated contribution rates of emissions from Beijing, Tianjin, Hebei, and Shanxi are 34.2%, 3.0%, 49.4%, and 13.4%, respectively, 72 h ahead of the objective time. In terms of the hourly sensitivity coefficient, the main contribution period of the Tianjin source is 1–26 h before the objective time and the hourly contribution peak value of 0.59 μg m–3 occurs 4 h before the objective time. The main contribution periods of the Hebei and Shanxi emission sources are 1–54 and 14–53 h before the objective time, respectively. The hourly sensitivity coefficients of the two sources show periodic fluctuations. The sensitivity coefficients of the Hebei emission have three peaks at 3.45, 4.27, and 0.71 μg m–3, respectively, appearing prior to 4, 16, and 38 h before the objective time. The peak values of the sensitivity coefficient of the Shanxi emission are 1.41 and 0.64 μg m–3 at 24 and 45 h before the objective time, respectively.
The adjoint sensitivity analysis can capture the influence of emission sources on the objective pollutant concentration in different regions and different time periods. The adjoint model is an effective method of tracking the crucial sources and key periods of emissions and could therefore provide a good reference for developing measures for the effective reduction of emissions and regional prevention and control of air pollution. However, as a result of the limitations of the resolution of the current model and other problems, the derived contribution of each emission source is only approximate and is specific to the pollution event investigated. Further research is required on many other pollution events in different seasons and on different types. We will continue to develop gas adjoint modules similar to the aerosol adjoint module to explore secondary sources of PM2.5 and to provide more effective schemes for the control and prevention of air pollution.
| An, X., T. Zhu, Z. Wang, et al., 2007: A modeling analysis of a heavy air pollution episode occurred in Beijing. Atmos. Chem. Phys., 7, 3103–3114. DOI:10.5194/acp-7-3103-2007 |
| An, X. Q., Z. B. Sun, W. L. Lin, et al., 2013: Emission inventory evaluation using observations of regional atmospheric background stations of China. J. Environ. Sci., 25, 537–546. DOI:10.1016/S1001-0742(12)60082-5 |
| An, X. Q., S. X. Zhai, M. Jin, et al., 2016: Development of an adjoint model of GRAPES–CUACE and its application in tracking influential haze source areas in north China. Geosci. Mo-del Dev., 9, 2153–2165. DOI:10.5194/gmd-9-2153-2016 |
| Chen, D. H., J. S. Xue, X. S. Yang, et al., 2008: New generation of multi-scale NWP system (GRAPES): General scientific design. Chinese Sci. Bull., 53, 3433–3445. DOI:10.1007/s11434-008-0494-z |
| Cheng, H. Y., F. Hu, Q. C. Zeng, et al., 1998: Some practical problems of optimizing emissions from pollution sources in air. Climatic Environ. Res., 3, 163–172. |
| Dunker, A. M., 1981: Efficient calculation of sensitivity coefficients for complex atmospheric models. Atmos. Environ., 15, 1155–1161. DOI:10.1016/0004-6981(81)90305-X |
| Elbern, H., H. Schmidt, O. Talagr, et al., 2000: 4D-variational data assimilation with an adjoint air quality model for emission analysis. Environ. Model. Softw., 15, 539–548. DOI:10.1016/S1364-8152(00)00049-9 |
| Gong, S. L., L. A. Barrie, J. -P. Blanchet, et al., 2003: Canadian Aerosol Module: A size-segregated simulation of atmosphe-ric aerosol processes for climate and air quality models 1. Module development. J. Geophys. Res. Atmos., 108. DOI:10.1029/2001JD002002 |
| Hakami, A., J. H. Seinfeld, A. Sandu, et al., 2006: Development of adjoint sensitivity analysis capabilities for CMAQ. The 5th Annual CMAS Conference, Chapel Hill, NC, California Institute of Technology, 1–4. |
| Hakami, A., D. K. Henze, J. H. Seinfeld, et al., 2007: The adjoint of CMAQ. Environ. Sci. Technol., 41, 7807–7817. DOI:10.1021/es070944p |
| Henze, D. K., A. Hakami, and J. H. Seinfeld, 2007: Development of the adjoint of GEOS-Chem. Atmos. Chem. Phys., 7, 2413–2433. DOI:10.5194/acp-7-2413-2007 |
| Jiang, C., H. Wang, T. Zhao, et al., 2015: Modeling study of PM2.5 pollutant transport across cities in China’s Jing–Jin–Ji region during a severe haze episode in December 2013 . Atmos. Chem. Phys., 15, 5803–5814. DOI:10.5194/acp-15-5803-2015 |
| Liu, F., 2005: Adjoint model of comprehensive air quality model CAMx—Construction and application. Post-doctoral Research Report, Peking University, Beijing, 101 pp. (in Chinese) |
| Liu, F., and F. Hu, 2003: Inversion of diffusion coefficients and effect of related difference schemes. J. Appl. Meteor. Sci., 14, 331–338. |
| Liu, J., X. Q. An, T. Zhu, et al., 2014: Evaluation of PM2.5 decrease in Beijing after emission restrictions in the Beijing–Tianjin–Hebei and surrounding regions . China Environ. Sci., 34, 2726–2733. |
| Lyu, Y., 2015: The development and application of air pollutant emission source processing system. Master dissertation, Xi’an University of Architecture and Technology, Xi’an, 59 pp. (in Chinese) |
| Marchuk, G. I., 1986: Mathematical Models in Environmental Problems. Elsevier, New York, 217 pp. |
| Marchuk, G. I., and Y. N. Skiba, 1976: Numerical calculation of the conjugate problem for a model of the thermal interaction of the atmosphere with the oceans and continents. Izv. Atmos. Ocean. Phy., 12, 279–284. |
| Su, A., D. N. Daescu, G. R. Carmichael, et al., 2005: Adjoint sensitivity analysis of regional air quality models. J. Comput. Phy., 204, 222–252. DOI:10.1016/j.jcp.2004.10.011 |
| Sfetsos, A., D. Vlachogiannis, and N. Gounaris, 2013: An investigation of the factors affecting the ozone concentrations in an urban environment. Atmos. Climate Sci., 3, 11–17. DOI:10.4236/acs.2013.31003 |
| Skiba, Y. N., and D. Parra-Guevara, 2000: Industrial pollution transport. Part 1. Formulation of the problem and air pollution estimates. Environ. Model. Assess., 5, 169–175. DOI:10.1023/A:1019065728972 |
| Skiba, Y. N., and V. Davydova-Belitskaya, 2002: Air pollution estimates in Guadalajara City. Environ. Model. Assess., 7, 153–162. DOI:10.1023/A:1016349021425 |
| Skiba, Y. N., and V. Davydova-Belitskaya, 2003: On the estimation of impact of vehicular emissions. Ecol. Model., 166, 169–184. DOI:10.1016/S0304-3800(03)00133-9 |
| Wang, C., X. Q. An, S. X. Zhai, et al., 2017: The application of an adjoint model in tracking influential haze source areas of pollution episodes. China Environ. Sci., 37, 1283–1290. |
| Wang, H., S. L. Gong, H. L. Zhang, et al., 2010a: A new-generation sand and dust storm forecasting system GRAPES_CUACE/Dust: Model development, verification and numeri-cal simulation. Chinese Sci. Bull., 55, 635–649. DOI:10.1007/s11434-009-0481-z |
| Wang, H., X. Y. Zhang, S. L. Gong, et al., 2010b: Radiative feedback of dust aerosols on the East Asian dust storms. J. Geophys. Res. Atmos., 115. DOI:10.1029/2009JD013430 |
| Wang, H., M. Xue, X. Y. Zhang, et al., 2015: Mesoscale modeling study of the interactions between aerosols and PBL meteorology during a haze episode in Jing–Jin–Ji (China) and its nearby surrounding region. Part 1: Aerosol distributions and meteorological features. Atmos. Chem. Phys., 15, 3257–3275. DOI:10.5194/acp-15-3257-2015 |
| Wang, Z. F., J. Li, Z. Wang, et al., 2014: Modeling study of regional severe hazes over mid–eastern China in January 2013 and its implications on pollution prevention and control. Sci. China Earth Sci., 57, 3–13. DOI:10.1007/s11430-013-4793-0 |
| Wu, Q. Z., Z. F. Wang, A. Gbaguidi, et al., 2011: A numerical study of contributions to air pollution in Beijing during CAREBeijing-2006. Atmos. Chem. Phys., 11, 5997–6011. DOI:10.5194/acp-11-5997-2011 |
| Yang, P., B. Zhu, J. H. Gao, et al., 2016: A numerical simulation study of the case of a PM2.5 pollutant island in summer of Nanjing . China Environ. Sci., 36, 321–330. |
| Yang, Y., H. Liao, and S. J. Lou, 2014: Simulated impacts of sulfate and nitrate aerosol formation on surface-layer ozone concentrations in China. Atmos. Oceanic Sci. Lett., 7, 441–446. DOI:10.3878/j.issn.1674-2834.14.0033 |
| Yumimoto, K., and I. Uno, 2006: Adjoint inverse modeling of CO emissions over Eastern Asia using four-dimensional variational data assimilation. Atmos. Environ., 40, 6836–6845. DOI:10.1016/j.atmosenv.2006.05.042 |
| Zhai, S. X., 2015: Development of the adjoint of GRAPES–CUACE aerosol module and model application to air pollution optimal control problems. Master dissertation, Chinese Academy of Meteorological Sciences, Beijing, 81 pp. (in Chinese) |
| Zhai, S. X., X. Q. An, J. Liu, et al., 2014: Effects of emission-sources reduction at different time points on PM2.5 concentration over Beijing Municipality . China Environ. Sci., 34, 1369–1379. |
| Zhai, S. X., X. Q. An, Z. B. Sun, et al., 2015: Effects of emission-sources reduction time and ratios on PM2.5 concentration over Beijing Municipality . China Environ. Sci., 35, 1921–1930. |
| Zhai, S. X., X. Q. An, Z. Liu, et al., 2016: Model assessment of atmospheric pollution control schemes for critical emission regions. Atmos. Environ., 124, 367–377. DOI:10.1016/j.atmosenv.2015.08.093 |
| Zhang, Q., D. G. Streets, G. R. Carmichael, et al., 2009: Asian emissions in 2006 for the NASA INTEX-B mission. Atmos. Chem. Phys., 9, 5131–5153. DOI:10.5194/acp-9-5131-2009 |
| Zheng, G. J., F. K. Duan, H. Su, et al., 2015: Exploring the severe winter haze in Beijing: The impact of synoptic weather, regional transport and heterogeneous reactions. Atmos. Chem. Phys., 15, 2969–2983. DOI:10.5194/acp-15-2969-2015 |
| Zhu, B., H. Q. Kang, T. Zhu, et al., 2015: Impact of Shanghai ur-ban land surface forcing on downstream city ozone chemistry. J. Geophys. Res. Atmos., 120, 4340–4351. DOI:10.1002/2014JD022859 |
| Zhu, J., and Q. C. Zeng, 2003: A mathematical formulation for optimal control of air pollution. Sci. China Earth Sci., 46, 994–1002. DOI:10.1007/BF02959394 |
| Zhu, J., Q. C. Zeng, D. J. Guo, et al., 1999: Optimal control of sedimentation in navigation channels. J. Hydraul. Eng., 125, 750–759. DOI:10.1061/(ASCE)0733-9429(1999)125:7(750) |
 2018, Vol. 32
2018, Vol. 32


