The Chinese Meteorological Society
Article Information
- FANG, Yihe, Haishan CHEN, Zhiqiang GONG, et al., 2017.
- Multi-Scheme Corrected Dynamic–Analogue Prediction of Summer Precipitation in Northeastern China Based on BCC_CSM. 2017.
- J. Meteor. Res., 31(6): 1085-1095
- http://dx.doi.org/10.1007/s13351-017-7069-3
Article History
- Received May 13, 2017
- in final form July 12, 2017
2. Regional Climate Center of Shenyang, Shenyang 110016;
3. Laboratory for Climate Studies and Climate Monitoring and Diagnose, National Climate Center, China Meteorological Administration, Beijing 100081;
4. Liaoning Meteorological Service Center, Shenyang 110016
Northeastern China (NEC) is the major commodity grain base of China, and changes in its weather and climate have important restrictive impacts on crops. Summer is the main crop-growing and rainfall-concentration season in NEC. Anomalous summer precipitation can result in flood/drought disasters over a large area and may have serious impacts on the yields of crops. Meteorologists have conducted much research on the characteristics of the climate variability and factors influencing summer precipitation in NEC (He et al., 2006; Wu et al., 2008; Shen et al., 2011). In addition, the prediction of summer precipitation is important for disaster prevention and mitigation at the government management level. Therefore, research on short-term climate prediction—especially, improving the prediction accuracy of summer precipitation—is a major and longstanding scientific issue and a focus of domestic and international meteorologists.
There are two main methods for short-term climate prediction: the statistical method, which analyzes the evolution of climate on the basis of historical data; and the dynamic method, which involves establishing numerical models based on physical mechanisms. Each method has its own advantages and shortcomings. Chou (1986) proposed the idea that combining the statistical method with the dynamic method might be a reasonable way to correct the dynamic method’s prediction errors by using historical analogue information. Overseas scholars have conducted corresponding research on how to combine the two methods more effectively (Mo and Straus, 2002; Tippett et al., 2005), while Chinese scholars have used the dynamic–analogue method based on historical data (Qiu and Chou, 1989; Huang et al., 1993; van den Dool, 1994; Ren and Chou, 2005, 2007) and atmospheric self-memory theory (Cao, 1993; Feng et al., 2001) to improve the dynamical–statistical prediction method. There-after, meteorologists applied the dynamical–statistical combined prediction approach to summer precipitation in East Asia (Gong et al., 2015, 2016), and conducted investigations on appropriate dynamical and statistical schemes for seasonal precipitation prediction in the Yangtze River basin (Wang et al., 2011), NEC (Xiong et al., 2011), and North China (Yang et al., 2012). The dynamical–statistical prediction based on the year-to-year increment approach (Fan et al., 2008; Fan and Wang, 2009, 2010) and the tropical analogue theory that considers the fact that the predictability of the models is higher in the tropics than in the extratropics (Wang and Fan, 2009), has been carried out, leading to improved accuracy in climate prediction in East Asia. Meanwhile, meaningful results from a number of associated studies (Smith et al., 2007; Kim et al., 2012; MacLeod et al., 2012; Van Oldenborgh et al., 2012; Fang et al., 2016) have also been reported.
The second-generation ocean–atmosphere coupled model titled the Beijing Climate Center Climate System Model (BCC_CSM) has been applied in operational climate prediction in China. Compared with the first-generation model, BCC_CSM has shown many improvements in the prediction of sea surface temperature (SST) and atmospheric circulation, especially in low-latitude regions (Wu et al., 2013). However, evaluations have also revealed that this model has relatively constrained ability in predicting summer (June–August) precipitation in NEC, and corrections are needed for the successful application of this model in NEC.
Based on correlation analysis between the error sets of summer precipitation in NEC and the SST fields in previous winters, the present study attempts to establish an internal connection between them, acquire historical analogue information by using the time series of the SST fields averaged over key regions, and then develop a dynamic–analogue correction method for summer precipitation prediction in NEC with physical rationales (Qiang and Yang, 2013; Gao and Gao, 2014). Seven correction schemes are also designed and compared with one another to clarify their advantages and disadvantages in the prediction of summer precipitation in NEC. Moreover, as probabilistic prediction can provide a broad range of information for climate prediction (Zhi et al., 2014), we intend to use the multiple correction schemes to configure probabilistic prediction for the NEC summer precipitation. Probabilistic prediction has become increasingly popular since its introduction (Zhi et al., 2014). See Section 2.6 for details about probabilistic prediction.
Following this introduction, the BCC_CMS model, data, and methods applied in this study are introduced in Section 2. An evaluation of the simulation ability of BCC_CSM for summer precipitation in NEC is presented in Section 3. Correction of BCC_CSM’s prediction of summer precipitation in NEC, along with cross-validation and probabilistic prediction, is performed in Section 4. Finally, the conclusions and a brief discussion are presented in Section 5.
2 Data and methods 2.1 Introduction to BCC_CSMBCC_CSM is a global land–atmosphere–sea-ice coupled climate system model with a resolution of nearly 110 km. In BCC_CSM, the atmospheric component model is BCC_AGCM2.2, with a horizontal resolution of T106 and 26 layers in the vertical; the land surface component model is BCC_AVIM1.0, with a horizontal resolution of T106; the oceanic component model is MOM_L40, which uses a three-level grid with a horizontal resolution of 1/3°–1° and 40 layers in the vertical; and the sea-ice component model is the U.S. Geophysical Hydrodynamics Laboratory’s Sea Ice Simulator. These component models are directly coupled by the coupler CPL5 (Wu et al., 2013).
2.2 DataThe model data used in this paper are the hindcast precipitation data for June–August 1991–2013 generated by BCC_CSM, and the model results with Gaussian resolution are interpolated to a 1°×1° spatial lattice. The actual cumulative precipitation observations for June–August are based on the daily precipitation data at 226 meteorological stations in NEC during 1991–2013. The error field for the summer precipitation prediction in NEC is the difference between the model hindcast and the observation. The SST data used are the monthly average SSTs from December 1990 through January 2013 reconfigured by NOAA at a resolution of 2° × 2°, which are downloaded from ftp://ftp.cdc.noaa.gov/Datasets/noaa.ersst/sst.mnmean.v4.nc.
2.3 Dynamic–analogue correction for SSTs in previous periodsThe dynamic–analogue correction method consists of the following steps:
(1) Obtain the error field of the summer precipitation hindcasts in NEC by calculating the difference values between the hindcast fields of BCC_CSM for summer precipitation in NEC and the observational precipitation fields during 1991–2008. Then, obtain the error time series by calculating the regional averages of the error field.
(2) Calculate the correlation coefficients between the time series of summer precipitation error in NEC for 1991–2008 and the global SST field in the previous winters (1990–2007). The region with correlation coefficients that pass the significance test will be regarded as the key ocean region in the previous winters. The time series of SST over the key region are computed as the average values of SSTs at each grid in the key region for 1991–2013.
(3) On the basis of the time series of SST over the key region, select historical years that are the best analogues with the year to be corrected (2009–13). “Best analogue” refers to there being the same sign of the SST value between the year to be corrected and the analogue year, as well as a minimum absolute difference value. The appropriate number of analogue years can be determined through comparative testing.
(4) The error of the year to be corrected is obtained by calculating the average values of the errors in historical analogue years. Then, subtract the error from the hindcast results of the year to be corrected, so as to obtain the prediction result after dynamic–analogue correction.
2.4 Design of various correction schemesScheme 1: Systematic bias correction; hereafter called “system correction.” Using the 18-yr average value of summer precipitation error (June–August) in NEC for 1991–2008 as the error in the year to be corrected to correct the summer precipitation results of the model in the year to be corrected.
Scheme 2: Pure statistical correction of SST analogues in the previous winters; hereafter called “pure statistical correction.” Based on the correlation between time series of the regional average summer precipitation error in NEC and SSTs in previous winters, establish the time series of SST over the key region and calculate the analogue years to the year to be corrected. Then, use the average value of summer precipitation in the analogue years as the prediction result for summer precipitation in the year to be corrected. The correction results are not based on the model prediction results.
Scheme 3: Dynamic–analogue correction of analogue SSTs in previous winters as the regional average error; hereafter called “analogue correction.” Based on the correlation between the time series of regional average summer precipitation error in NEC and SSTs in previous winters, establish the time series of SST over the key sea region and calculate the analogue years to the year to be corrected. Then, use the average hindcast errors of summer precipitation in the analogue years as the summer precipitation error in the year to be corrected and subtract it from the model hindcast result (hereafter called the “model prediction”) to correct the summer precipitation results from the model in the year to be corrected. This scheme realizes the combination of the statistical method with the dynamic method.
Scheme 4: Dynamic–analogue correction of analogue SSTs in the previous winters as single-point errors; hereafter called “analogue correction (single point).” This method is the same as Scheme 3 except that each gird point in NEC is corrected, instead of the regional average. This scheme takes the regional differences into account.
Scheme 5: Equally weighted averages of the analogue correction and analogue correction (single point) results; hereafter called “weighted-correction-I”.
Scheme 6: Equally weighted average of the system correction, analogue correction, and analogue correction (single point) results; hereafter called “weighted-correction-II”. Schemes 5 and 6 take the advantages of the other schemes.
Scheme 7: Directly use the uncorrected model prediction results. This scheme is temporarily called “Scheme 7” to facilitate the description.
2.5 Evaluation of the correction resultsThe evaluation method for the correction results in this paper follows the standard recommended by the World Meteorological Organization. The anomaly correlation coefficient (ACC) and root-mean-square error (RMSE) are used for the purposes of testing and error analysis.
The ACC is calculated as follows:
| $X(j) \!\!=\!\! \frac{{\sum\limits_{i = 1}^{{N_j}} {\left[ {F(i,j) - C(i,j)} \right]\left[ {A(i,j) - C'(i,j)} \right]} }}{{\sqrt {\sum\limits_{i = 1}^{{N_j}} {{{\left[ {F(i,j) \!\!-\!\! C(i,j)} \right]}^2}\sum\limits_{i = 1}^{{N_j}} \!{{{\left[ {A(i,j) \!\!-\!\! C'(i,j)} \right]}^2}} } } }},$ | (1) |
where X(j) is the ACC value, F(i, j) is the prediction value, A(i, j) is the actual situation, and C(i, j) and C'(i, j) are the climate mean states of the model climatology and observed climatology, respectively. The ACC values range between –1 and 1, and a larger value implies that the prediction is better.
The RMSE is calculated as follows:
| $Y(j){\rm{ = }}\sqrt {\frac{1}{{{N_j}}}{{\sum\limits_{i = 1}^{{N_j}} {\left[ {F(i,j) - A(i,j)} \right]^2} }}} .$ | (2) |
The smaller the RMSE value, the better the prediction. The RMSE is 0 when the prediction is fully consistent with the actual observation.
2.6 Probabilistic prediction and testingThe probabilistic prediction is performed as follows. On the basis of the first six schemes in Section 1.4, we correct the model hindcast results of each grid point in NEC, and then the precipitation anomaly percentage of the correction results is calculated, so each grid point has six precipitation anomaly percentage correction results. The number of correction schemes with the precipitation anomaly percentage greater than zero at each grid point is divided by six (total number of schemes) to obtain the probability of precipitation anomaly percentage greater than zero at each grid point. For a grid point where the probability of precipitation anomaly percentage greater than zero is more than (or below) 50%, the precipitation is recognized as anomalously high (or low). If the probability is 50%, the probabilistic prediction result will not be considered.
In order to test the effect of the probabilistic prediction, we make a comparison between the accuracy rate of probabilistic prediction and that of the model prediction. If the accuracy rate of probabilistic prediction is higher than that of the model prediction, the probabilistic prediction is regarded as successful. The method for calculating the accuracy rate of probabilistic prediction is as follows: for each grid point, if the probability of precipitation anomaly percentage greater than zero is higher (lower) than 50% and the actual precipitation is anomalously high (low), the probabilistic prediction result of this grid point is correct and the correct number of grid points will be divided by the total number of grid points for the region of NEC to calculate the proportion of correct grid points in the probabilistic prediction result. Similarly, if the model prediction precipitation anomaly percentage at each grid point has the same sign as the actual precipitation percentage, the model prediction result at this grid point is accepted as correct and the correct number of grid points will be divided by the total number of grid points to calculate the proportion of correct grid points in the model prediction result.
3 Evaluation of BCC_CSM simulation of summer precipitation in NECFirst, we evaluate the ability of BCC_CSM to simulate summer precipitation in NEC. Figure 1 shows the average summer precipitation in NEC during 1990–2010 as predicted by the model, the actual average summer precipitation distribution diagram, and the distribution diagram for the difference between predicted precipitation and observed precipitation. By comparing Fig. 1a with Fig. 1b, it is found that the model captures the observed characteristics that precipitation in the northwestern part of NEC is less than that in the southeast, and that the rough location of the small precipitation center (northwestern part) and the large precipitation center (southern part) can be predicted; however, there is a large difference in the specific distributions and in the precipitation values. Figure 1c shows the differences between the model prediction and the observed precipitation, in which it can be seen that the difference in most areas of NEC is negative, meaning that the model prediction results are lower than the actual precipitation. In accordance with the difference values, the prediction results are lower overall than the actual precipitation by approximately 50–100 mm. In the southern regions outside of the three provinces, the prediction result is lower overall than the actual precipitation by approximately 100–250 mm.

|
| Figure 1 (a) Average summer precipitation in northeastern China predicted by BCC_CSM for 1990–2010, (b) observed average summer precipitation, and (c) difference between predicted precipitation and actual precipitation. Units: mm. |
Next, we will further evaluate the model’s ability to predict summer precipitation with respect to the ACC between the summer precipitation predicted by the model for 1990–2010 and the actual precipitation. Figure 2 shows that the ACCs in most regions do not pass the significance test, except for a small part in the northwest of NEC, and that most of the southern regions in NEC have negative ACC values. According to the average hindcast results over 20 yr, it appears that BCC_CSM is not able to accurately predict summer precipitation in NEC and corrections should be made before the model is applied in this region.
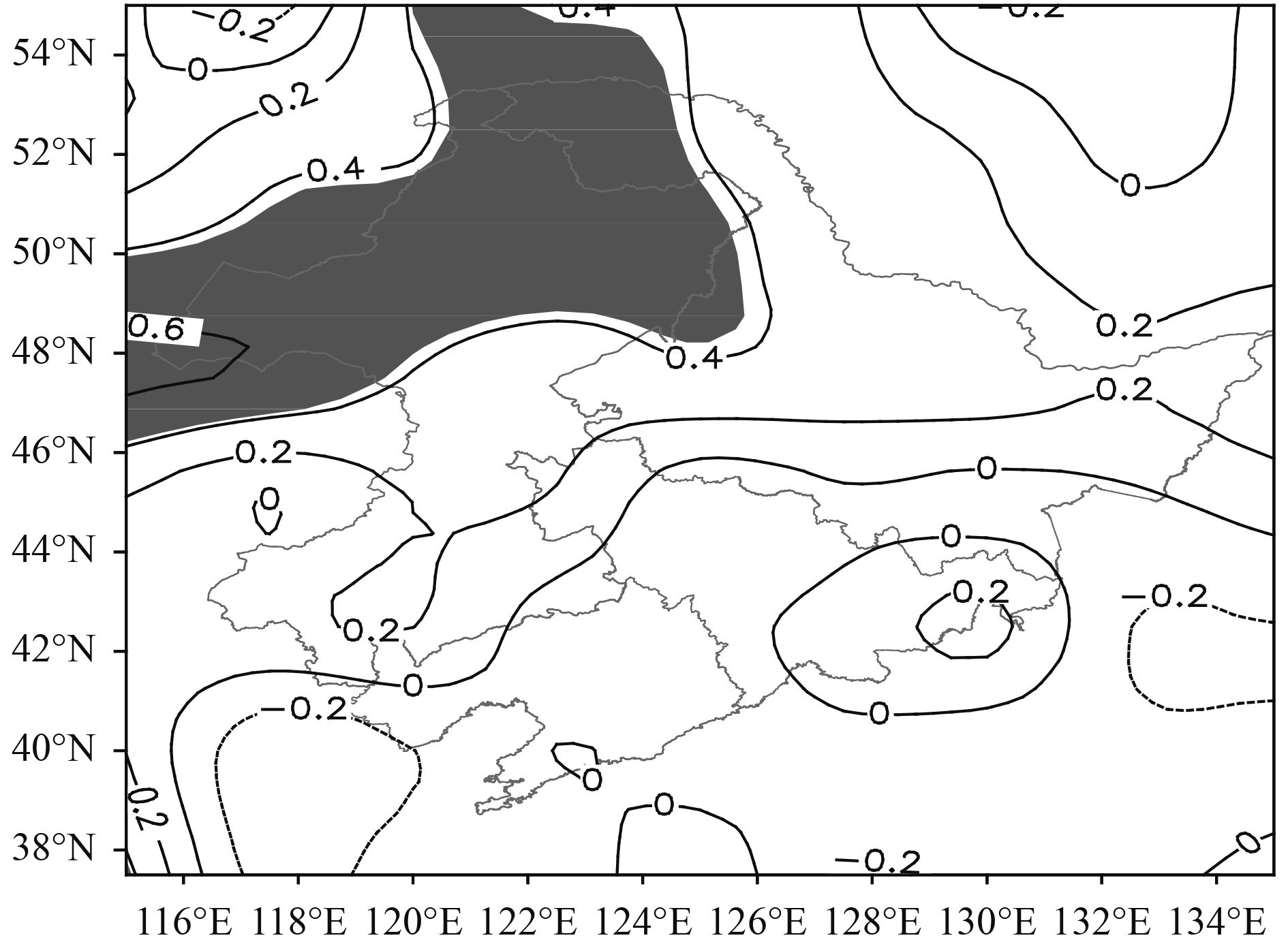
|
| Figure 2 Anomaly correlation coefficients between the 20-yr average summer precipitation in northeastern China predicted by the model for 1990–2010 and the actual precipitation. The shaded area represents correlation coefficients passing the significance test at the 0.05 level. |
Shen et al. (2011) noted that midsummer (July and August) precipitation in NEC is mainly influenced by the East Asian summer monsoon and the western Pacific subtropical high. Studies also show that the SST in the previous winters has a significant influence on the shape, location, and strength of the summer subtropical high in later periods, which then influences the summer precipitation in NEC and other places (Qiang and Yang, 2013; Gao and Gao, 2014). That is to say, the SST in the previous winters is a precursor prediction signal and can provide a reference for the analogue prediction method. Therefore, we considered by using the errors in analogue years to correct the summer precipitation model results by searching for analogue years on the basis of the relationship between the summer precipitation error and the SST field in the previous winters. On the basis of this analysis, we conduct correction and test the effect on five independent samples of the summer precipitation from model prediction results in NEC during 2009–13 by analyzing the correlation between the summer precipitation errors and the SST fields in the previous winters (1990–2007) in NEC during 1991–2008.
According to the distribution diagram (Fig. 3) of the correlation coefficients between the regional average time series of the summer precipitation error fields and the SST fields in the previous winters, the main significant correlation region is located in North Pacific and the correlation coefficient distribution is significantly negatively correlated in the equatorial East Pacific and significantly positively correlated in the middle of North Pacific. The absolute value of the central correlation coefficient is up to and above 0.6, a distribution situation similar to that of the El Niño–Southern Oscillation (ENSO). This conclusion is similar to the conclusion of Zong and Chen (2013) that “the ENSO circulation in the equatorial East Pacific in previous winter has a certain impact on the Chinese rainband in July and August.” Therefore, we conclude that the model’s prediction error for summer precipitation is related to the SST in the equatorial East Pacific in the previous winters and the SST in the middle of North Pacific. This is because of the insufficient response of BCC_CSM to the SST anomaly (ENSO).

|
| Figure 3 Distribution of the correlation coefficient between the regional average time series of the summer precipitation error in northeastern China for 1991–2008 and the sea surface temperature in previous winters. The dotted area represents the correlation coefficient passing the significance test at the 0.05 level. |
Based on the preceding analysis, we determined that the equatorial East Pacific and the middle of the North Pacific Ocean are the key SST areas for the errors in the previous winters. The difference values between the average SST in the equatorial East Pacific region and the average SST in the middle of the North Pacific Ocean for 1991–2013 are regarded as the SST time series of the key region. On the basis of the SST time series of this key region, we determined the analogue years calculated by SST in the previous winters (2008–12) in 2009–13. Table 1 lists five analogue years of summer precipitation errors for the years to be corrected (2009–13) according to the analogue degree. When the number of analogue years is one to five, the average value of errors in the analogue years is used as the error in the years to be corrected, in accordance with the steps in Section 2.3 (when the number of analogue years is one, the error of the analogue years is the error of the years to be corrected). Finally, the average error in analogue years is subtracted from the model prediction results for the years to be corrected to obtain the correction results of the years to be corrected.
| Year to be corrected | Analogue year |
| 2009 | 2007, 1995, 2004, 2013, 2003 |
| 2010 | 1992, 2003, 2005, 1997, 1991 |
| 2011 | 2012, 2001, 2000, 2002, 1999 |
| 2012 | 2011, 2001, 2000, 2002, 1999 |
| 2013 | 2002, 2001, 2007, 2011, 2009 |
It is necessary to determine the number of analogue years before correcting the model results, and in this study, we use comparative testing to determine the number of analogue years. Figure 4a shows the average ACC of the corrected results for the seven schemes after averaging the ACCs for the five correction scheme results in the years to be corrected and the actual situation when the number of analogue years is one to five. Note that the average ACC gradually becomes smaller with the increase in the number of analogue years; the average ACC is 0.083 when the number of analogue years is one, and the average ACC is negative when the number of analogue years is two to five.
Figure 4b shows the average ACCs between the correction results in 5 yr to be corrected in the various schemes and the actual situation when the number of analogue years is one to five. The 5-yr average ACC in most schemes is negative when the number of analogue years is two to five; although the average ACC is positive in certain schemes, the value is generally lower than 0.05. When the number of analogue years is one, the 5-yr average ACC is positive in the other 6 schemes except for Scheme 7, where the value is negative, which means that the ACC of the corrected results is superior to the ACC of the uncorrected results for whichever scheme is selected. The analogue correction has the largest 5-yr average ACC value (0.24), whereas the 5-yr average ACC of the weighted-correction-I and -II schemes are 0.16 and 0.14, respectively. The 5-yr average ACCs in these three schemes pass the significance test with a confidence degree of 0.01; the 5-yr average ACC of the pure statistical scheme is 0.11 and passes the significance test with a confidence degree of 0.05. The 5-yr average ACCs in the system correction and analogue correction (single point) schemes are 0.02 and 0.04, respectively, but these values fail to pass the significance test. Therefore, when the number of analogue years is one, the analogue correction scheme and the two weighted correction schemes can obtain obviously improved results for ACCs compared with the system error or pure statistical correction results, and these three dynamic–analogue correction schemes are most suitable for operational use. From the preceding results, the ACC has an obviously greater advantage when the number of analogue years is one rather than two to five. Therefore, the number of analogue years will be one for making corrections, and the following analyses are conducted when the number of analogue years is one.

|
| Figure 4 (a) Comparison of the influence of the number of analogue years on the average anomaly correlation coefficient (ACC) of five independent sample years and seven correction schemes. (b) Average ACCs of 5 yr to be corrected in various correction schemes when the number of analogue years is one to five. |
Figure 5a shows the RMSEs of the correction results for five independent samples for the various correction schemes when the number of analogue years is one. The RMSE of Scheme 7 (uncorrected model result) is the largest value in the various schemes for 5 yr; therefore, the RMSE of the corrected result is superior to the RMSE of the uncorrected result regardless of which scheme is selected. In addition, the analogue correction, pure statistical correction, and analogue correction (single point) schemes have the largest RMSE values for 5 yr except for the RMSE of Scheme 7. The system correction and the two weighted correction schemes have lower RMSE values, which have small year-to-year fluctuations and are relatively stable.
Figure 5b gives the average RMSE of five independent samples in the correction results of each scheme. The RMSE values from low to high for each scheme are as follows: systematic correction (90), weighted-correction-II (92), weighted-correction-I (97), analogue correction (single point) (103), pure statistical correction (116), analogue correction (116), and model result (157). For the RMSE, the system correction and two weighted correction schemes have the lowest values when the number of analogue years is one.

|
| Figure 5 (a) RMSEs of the correction results in various schemes for the five independent samples. (b) Annual average RMSEs of five independent samples in the correction results of various schemes. |
From the analyses in the preceding two sections, we can see that the two weighted correction schemes achieve significant improvements as seen in the ACC and RMSE results and have the greatest advantages among the various correction schemes. To intuitively display the correction effect of the weighted correction scheme, we analyzed the spatial distribution of the precipitation anomaly percentage after correction by using the weighted-correction-I scheme as an example.
The summer precipitation in NEC was abnormally high in 2013 (Zhao et al., 2015), and here we conduct a comparative analysis of the results of the weighted-correction-I scheme, the model prediction results, and the system correction results. Based on the actual summer precipitation anomaly percentage in NEC in 2013 and a comparative analysis of the model prediction results and weighted-correction-I results (Fig. 6), the actual precipitation in most areas of NEC in the summer of 2013 was anomalously high, but the model prediction results show that the precipitation in most areas was anomalously low, which resulted in an inaccurate trend prediction. The results of the weighted-correction-I scheme show that most areas in NEC were anomalously high; therefore, the result of weighted-correction-I was closer to the actual situation than the trend prediction made by BCC_CSM. The model result of weighted-correction-I was improved to a certain degree, and the correction results for other years (figures omitted) resulted in similar conclusions. Additionally, the weighted-correction-I scheme was closer to the actual situation than the weighted-correction-II scheme (figure omitted) according to the distribution results of the precipitation anomaly percentage.

|
| Figure 6 (a) Actual summer precipitation anomaly percentage, (b) model prediction result, and (c) weighted-correction-I result in northeastern China in 2013. Units: %. |
The weighted correction method provided accurate results compared with other correction methods for the five independent samples in 2009–13. To further verify the effect of the weighted-correction-I scheme, the model results for 1991–95 were corrected to investigate the correction effect. Figure 7 shows the ACC of the weighted-correction-I scheme, the system correction scheme,and the model results. The 5-yr average ACC of the weighted-correction-I scheme was 0.24 and passed the significance test with a confidence degree of 0.01; the ACC was higher than the system correction scheme and the model results. Moreover, the system correction method produced a negative value in 2 out of 5 yr; therefore, the value is not stable. For the ACC, the weighted-correction-I scheme had a better correction effect for the period 1991–95.

|
| Figure 7 ACC of the weighted-correction-I scheme, system correction scheme, and model results in 1991–95. |
The 5-yr average RMSEs of the weighted-correction-I scheme, the systematic correction scheme, and the model results were 82.6, 79.2, and 135.2, respectively. The RMSE was obviously decreased by the weighted-correction-I and system correction schemes. However, the effect of the weighted-correction-I scheme was slightly worse than that of the system correction scheme; the reason for this result has yet to be investigated.
Figure 8 shows the results of the comparative analysis on the actual summer precipitation anomaly percentage, model prediction results, and the results of the weighted-correction-I scheme in NEC in 1991. In accordance with the trend of the actual situation, summer precipitation in most areas of NEC was anomalously high in 1991; however, the model prediction results show that the precipitation in most areas was anomalously low. The result of weighted-correction-I shows that the precipitation in most areas was anomalously high. In accordance with the trend, the result of the weighted-correction-I scheme was closer to the actual situation and the distribution of the precipitation anomaly percentage was also closer to the actual situation. The model results of the weighted-correction-I scheme were greatly improved, and the correction results of other years (figures omitted) produced similar conclusions.

|
| Figure 8 As Fig. 6, but for 1991. |
Six correction schemes were presented in Section 2.4 (except for the model result itself), and the probabilistic prediction results for summer precipitation in NEC are presented here. Moreover, we take the summer precipitation in 2013 as an example to discuss the probabilistic prediction results. Based on the spatial distribution diagram (Fig. 9) of the probabilistic prediction of anomalously high precipitation in NEC in 2013, the probability of anomalously high precipitation was above 50% in most areas of NEC, which is consistent with the actual higher summer precipitation situation in most areas of NEC in 2013, but the model prediction results show that the summer precipitation in most areas of NEC in 2013 was anomalously low, which is contrary to the actual situation. Thus, the probabilistic prediction better predicted the summer precipitation trend in NEC in 2013 and was greatly improved compared with the model prediction results. The probabilistic prediction results for other years (figures omitted) are similar.

|
| Figure 9 Probability prediction results of anomalously high summer precipitation in northeastern China in 2013 based on six correction schemes. |
| Testing year | Model prediction
accuracy rate |
Probability prediction
accuracy rate |
| 2009 | 34.8% | 54.8% |
| 2010 | 49.7% | 47.1% |
| 2011 | 48.9% | 53.5% |
| 2012 | 22.2% | 69.3% |
| 2013 | 24.1% | 73.5% |
To further verify the effects of probabilistic prediction, we compared (Table 2) the model prediction accuracy rates and probabilistic prediction accuracy rates in 2009–13. In 5 yr, only the probability accuracy rate in 2010 was slightly lower than the model prediction accuracy rate, whereas the probabilistic prediction accuracy rate in the other four years was higher. The probability accuracy rate was approximately 20%, 47.1%, and 49.4% higher than the model prediction accuracy rate for 2009, 2012, and 2013, respectively. The 5-yr accuracy rate is improved by 23.7%. Therefore, probabilistic prediction that is based on multiple schemes should be considered to realize a breakthrough from single deterministic prediction to probabilistic prediction.
5 Conclusions and discussionThis study began by evaluating BCC_CSM’s ability in predicting the summer precipitation in NEC, which showed that the model has limited skill in this respect. BCC_CSM’s limited ability in prediction of summer precipitation in NEC may be due to it containing insufficient atmospheric remote responses to SST anomalies, that is, ENSO. Moreover, the model performance evaluation also indicated that the predicted value of summer precipitation was systematically lower than the observation. Therefore, supplementary corrections should be performed before BCC_CSM can be effectively applied for operational summer precipitation prediction in NEC.
This paper describes how to improve the summer precipitation prediction skill of BCC_CSM through integrating historical prediction errors of analogue years, extracted from model hindcasts, with the real-time prediction. This kind of integration between analogue prediction errors and current model output is referred to as the “dynamic–analogue correction method”, as proposed by Chou (1986). Based on this main idea, several schemes were designed for improving the model’s summer precipitation prediction skill in NEC. Corresponding independent sample validations show the feasibility and physical meaning of estimating analogue prediction errors by using the SST series of previous winters, which is significantly correlated with summer precipitation in NEC. Meanwhile, independent sample validations further show that the 5-yr averaged ACC of BCC_CSM’s summer precipitation prediction in NEC is respectively improved from –0.13/0.15 to 0.16/0.24 for 2009–13/1991–95 by using the weighted-correction-I scheme. Compared to the pure statistical scheme and other dynamic–analogue schemes, the weighted-correction-I scheme exhibits the best performance in terms of high ACC and low RMSE, which verified that the weighted-correction-I scheme is an appropriate correction method for reducing BCC_CSM’s summer precipitation prediction errors in NEC.
This paper also proposes the idea of using probabilistic prediction to present the precipitation tendency based on results of multiple correction schemes described in Section 2.4. After verification, the 5-yr averaged probability prediction accuracy can be improved by 23.7%. Therefore, the probabilistic prediction based on multiple correction schemes can be considered as another approach that can be successfully applied in summer precipitation predictions in NEC.
Based on the above statement, it is inferred that the prediction skill of BCC_CSM can be improved by integrating historical analogue information extracted through the statistical method (Chou, 1986) with the model’s current prediction. The dynamic–analogue schemes introduced in this paper make obvious contributions to improvements in BCC_CSM’s prediction accuracy and could be applied operationally in terms of predicting summer precipitation in NEC.
| Cao, H. X., 1993: Self-memorization equation in atmospheric motion. Sci. China (Series B), 36, 845. |
| Chou, J. F., 1986: Why should we combine the dynamics with statistics and how to combine. Plateau Meteor., 5, 367–372. |
| Fan, K., H. J. Wang, and Y. J. Choi, 2008: A physically-based statistical forecast model for the middle–lower reaches of the Yangtze River valley summer rainfall. Chinese Sci. Bull., 53, 602–609. DOI:10.1007/s11434-008-0083-1 |
| Fan, K., and H. J. Wang, 2009: A new approach to forecasting typhoon frequency over the western North Pacific. Wea. Forecasting, 24, 974–978. DOI:10.1175/2009WAF2222194.1 |
| Fan, K., and H. J. Wang, 2010: Seasonal prediction of summer temperature over Northeast China using a year-to-year incremental approach. Acta Meteor. Sinica, 24, 269–275. |
| Fang, Y. H., Z. Q. Gong, and H. S. Chen, 2016: Objective identification research on China Northeast Cold Vortex precipitation period. Meteor. Mon., 42, 80–88. DOI:10.7519/j.issn.1000-0526.2016.01.010 |
| Feng, G. L., H. X. Cao, F. Y. Wei, et al., 2001: On area rainfall ensemble prediction and its application. J. Meteor. Res., 59, 206–212. DOI:10.3321/j.issn:0577-6619.2001.02.007 |
| Gao, H., and J. Gao, 2014: Increased influences of the SST along the Kuroshio in previous winter on the summer precipitation in northeastern China. Acta Oceanol. Sinica, 36, 27–33. DOI:10.3969/j.issn.0253-4193.2014.07.004 |
| Gong, Z. Q., J. H. Zhao, G. L. Feng, et al., 2015: Dynamic–statistics combined forecast scheme based on the abrupt decadal change component of summer precipitation in East Asia. Sci. China: Earth Sci., 58, 404–419. DOI:10.1007/s11430-014-4967-4 |
| Gong, Z. Q., C. Hutin, and G. L. Feng, 2016: Methods for improving the prediction skill of summer precipitation over East Asia–West Pacific. Wea. Forecasting, 31, 1381–1392. DOI:10.1175/WAF-D-16-0007.1 |
| He, J. H., Z. W. Wu, L. Qi, and A. J. Jiang, 2006: Relationships among the Northern Hemisphere Annual Mode, the Northeast Cold Vortex and the summer rainfall in Northeast China. J. Meteor. & Environ., 22, 1–5. DOI:10.3969/j.issn.1673-503X.2006.01.001 |
| Huang, J. P., Y. H. Yi, S. W. Wang, et al., 1993: An analogue-dynamical long-range numerical weather prediction system incorporating historical evolution. Quart. J. Roy. Meteor. Soc., 119, 547–565. DOI:10.1002/qj.49711951111 |
| Kim, H. M., P. J. Webster, and J. A. Curry, 2012: Evaluation of short-term climate change prediction in multi-model CMIP5 decadal hindcasts. Geophys. Res. Lett., 39, L10701. DOI:10.1029/2012GL051644 |
| MacLeod, D. A., C. Caminade, and A. P. Morse, 2012: Useful decadal climate prediction at regional scales? A look at the ENSEMBLES stream 2 decadal hindcasts.. Environ. Res. Lett., 7, 044012. DOI:10.1088/1748-9326/7/4/044012 |
| Mo, R. P., and D. M. Straus, 2002: Statistical dynamical seasonal prediction based on principal component regression of GCM ensemble integrations. Mon. Wea. Rev., 130, 2167–2187. DOI:10.1175/1520-0493(2002)130<2167:SDSPBO>2.0.CO;2 |
| Qiang, X. M., and X. Q. Yang, 2013: Relationship between the first rainy season precipitation anomaly in South China and the sea surface temperature anomaly in the Pacific. Chinese J. Geophys., 56, 2583–2593. DOI:10.6038/cjg20130808 |
| Qiu, C. J., and J. F. Chou, 1989: The analogic–dynamical method of forecasting weather. Sci. Atmos. Sinica, 13, 22–28. DOI:10.3878/j.issn.1006-9895.1989.01.03 |
| Ren, H. L., and J. F. Chou, 2005: Analogue correction method of errors by combining both statistical and dynamical methods together. Acta Meteor. Sinica, 63, 988–993. DOI:10.11676/qxxb2005.094 |
| Ren, H. L., and J. F. Chou, 2007: Strategy and methodology of dynamical analogue prediction. Sci. China Earth Sci., 50, 1589–1599. DOI:10.1007/s11430-007-0109-6 |
| Shen, B. Z., Z. D. Lin, R. Y. Lu, et al., 2011: Circulation anomalies associated with interannual variation of early- and late-summer precipitation in Northeast China. Sci. China Earth Sci., 54, 1095–1104. DOI:10.1007/s11430-011-4173-6 |
| Smith, D. M., S. Cusack, A. W. Colman, et al., 2007: Improved surface temperature prediction for the coming decade from a global climate model. Science, 317, 796–799. DOI:10.1126/science.1139540 |
| Tippett, M. K., L. Goddard, and A. G. Barnston, 2005: Statistical–dynamical seasonal forecasts of Central-Southwest Asian winter precipitation. J. Climate, 18, 1831–1843. DOI:10.1175/JCLI3371.1 |
| Van, den Dool, and M. H., 1994: Searching for analogues, how long must we wait?. Tellus, 46A, 314–324. DOI:10.3402/tellusa.v46i3.15481 |
| van, Oldenborgh, J. G., J. Doblas-Reyes F., Wouters B., et al., 2012: Decadal prediction skill in a multi-model ensemble. Climate Dyn., 38, 1263–1280. DOI:10.1007/s00382-012-1313-4 |
| Wang, Q. G., G. L. Feng, Z. H. Zheng, et al., 2001: A study of the objective and quantifiable forecasting based on optimal factors combinations in precipitation in the middle and lower reaches of the Yangtze River in summer. Chinese J. Atmos. Sci., 35, 287–297. DOI:10.3878/j.issn.1006-9895.2011.02.08 |
| Wang, H. J., and K. Fan, 2009: A new scheme for improving the seasonal prediction of summer precipitation anomalies. Wea. Forecasting, 24, 548–554. DOI:10.1175/2008WAF2222171.1 |
| Wu, Y., H. Zhang B., and D’Arrigo R., 2008: Arctic dipole anomaly and summer rainfall in Northeast China. Chinese. Sci. Bull., 53, 2222–2229. DOI:10.1007/s11434-008-0229-1 |
| Wu, T. W., L. C. Song, X. W. Liu, et al., 2013: Progress in developing the short-range operational climate prediction system of China National Climate Center. J. Appl. Meteor. Sci., 24, 533–543. DOI:10.3969/j.issn.1001-7313.2013.05.003 |
| Xiong, K. G., G. L. Feng, J. P. Huang, et al., 2011: Analogue-dynamical prediction of monsoon precipitation in Northeast China based on dynamic and optimal configuration of multiple predictors. J. Meteor. Res., 25, 316–326. DOI:10.1007/s13351-011-0307-1 |
| Yang, J., J. H. Zhao, Z. H. Zheng, et al., 2012: Estimating the prediction errors of dynamical climate model on the basis of prophase key factors in North China. Chinese J. Atmos. Sci., 36, 11–22. DOI:10.3878/j.issn.1006-9895.2012.01.02 |
| Zhao, J. H., J. Yang, Z. Q. Gong, et al., 2015: Analysis of and discussion about dynamic–statistical climate prediction for summer rainfall of 2013 in China. Adv. Met. S.&T., 5, 24–28. DOI:10.3969/j.issn.2095-1973.2015.02.004 |
| Zhi, X. F., T. Peng, G. Li, et al., 2014: Advances in multimodel ensemble probabilistic prediction. Trans. Atmos. Sci., 37, 248–256. DOI:10.3969/j.issn.1674-7097.2014.02.016 |
| Zong, H. F., and L. T. Chen, 2013: Characteristics of the atmospheric circulation and sea surface temperature for different modes of intraseasonal variation of summer monsoon rain belt in eastern China. Chinese J. Atmos. Sci., 37, 1072–1082. DOI:10.3878/j.issn.1006-9895.2013.12069 |
 2017, Vol. 31
2017, Vol. 31


