The Chinese Meteorological Society
Article Information
- WANG, Fei, Yijun ZHANG, Dong ZHENG, et al., 2017.
- Semi-Idealized Modeling of Lightning Initiation Related to Vertical Air Motion and Cloud Microphysics. 2017.
- J. Meteor. Res., 31(5): 976-986
- http://dx.doi.org/10.1007/s13351-017-6201-8
Article History
- Received January 4, 2017
- in final form May 17, 2017
2. Laboratory of Lightning Physics and Protection Engineering, Chinese Academy of Meteorological Sciences, Beijing 100081
Most lightning results from dynamical and microphysical processes associated with thunderstorms. Understanding the conditions at the site of initiation is an important topic in lightning research and forms the basis of forecasting the occurrence and evolution of lightning activity in thunderstorms.
Ice particles in general, and graupel and ice crystals in particular, are the main carriers of charge in thunderstorms (e.g., Takahashi, 1978; Gardiner et al., 1985), which require close contact between lightning initiation and ice particles. Cloud monitoring by radar and satellite primarily monitors the size and distribution of hydrometeors, and is the most common tool in existing research on the environmental conditions for lightning initiation, particularly for studies that focus on microphysical conditions.
Proctor (1991) analyzed radar and lightning data, and found that 66% of lightning initiated near the 20-dBZ contour, while 27% of lightning initiated at the edge of the strong echo. After analyzing data from convective lines, Lund et al. (2009) showed that most lightning flashes originated within the 35-dBZ contour. In addition, multiple studies have found that significant signals can be detected with radar before the first lightning flash of a thunderstorm (e.g., Martinez, 2002; Vincent et al., 2003). Detected signals include a strong echo (e.g., 40 dBZ) at a given level and a strong echo volume that, above a given level, rises to a threshold (e.g., Hondle and Eilts, 1994; Gremillion and Orville, 1999; Martinez, 2002; Vincent et al., 2003; Wang et al., 2008). Based on these signals, radar data can be used to forecast the onset of lightning activity. Martinez (2002) treated the top of the 40-dBZ echo rising to 7 km as an indicator, while other researchers have used a predetermined isotherm level (e.g., –10°C) in place of an absolute height threshold (e.g.,Gremillion and Orville, 1999; Vincent et al., 2003; Wang et al., 2008). The height of a thunderstorm has been found to correlate with lightning frequency (Shackford, 1960; Jacobson and Krider, 1976; Williams, 1985). Based on this observation, Price and Rind (1992) constructed a parameterization scheme that linked cloud top height to lightning frequency in a global model.
Observational data show the size and distribution of hydrometeors in clouds, while dynamic conditions in some cloud regions can be qualitatively described based on sounding data and echo evolution. Recently, in some regions covered by double radars, the vertical velocity profiles of clouds have been quantitatively estimated by inversion, which facilitates further research into the dynamic conditions associated with lightning initiation. Many studies have found that strong updrafts in the mixed-phase zone (–40° to 0°C) are a key condition for lightning generation (e.g.,Workman and Reynolds, 1949; Williams and Lhermitte, 1983; Dye et al., 1988; Rutledge et al., 1992; Carey and Rutledge, 1996; Petersen et al., 1996, 1999; Pickering et al., 1998; Baker et al., 1999; Black and Hallett, 1999). Barthe and Barth (2008) proposed that updraft speed could be used to estimate whether a storm can produce lightning. Payne et al. (2010) and Wang (2014) suggested that lightning flashes always originated from regions with relatively weak vertical velocities. Some researchers found that updraft volume correlated well with lightning frequency. Tessendorf et al. (2005) and Wiens et al. (2005) reported that updraft volumes of > 10 m s –1 were strongly correlated with total lightning frequency. Deierling and Petersen (2008) demonstrated that a strong correlation existed between updraft volumes greater than 5 and 10 m s–1 within the charging zone (< –5°C) and the total lightning frequency. These results were then used to estimate lightning frequency in numerical models without explicitly simulating the charge and discharge processes (e.g.,Pickering et al., 1998; Barthe and Barth, 2008; Barthe et al., 2010).
Dual-polarization radar has become a fundamental part of detailed research on the microphysical conditions under which lightning initiates. Carey et al. (2014) and Mecikalski et al. (2015) used dual-polarization radar to demonstrate that graupel echo volume, graupel mass, and 30-dBZ echo volume within the charging zone, all showed empirical relationships with lightning frequency. Preston and Fuelberg (2015) and Wang et al. (2016) used dual-polarization radar data to improve existing lightning warning methods using Doppler radar data, by adding new parameters for particle identification and improving warning efficiency. Zheng and MacGorman (2016) used dual-polarization radar and the lightning mapping array to observe a supercell, and analyzed the characteristics of particle distribution near lightning initiation sites, finding that graupel and dry snow were dominant in most positions. Such results provide valuable insights into the characteristics of lightning activity in regions with a range of dynamic conditions, and show the relationship between lightning activity and particle distribution.
The limitations of observational data mean that it remains difficult to obtain high-resolution three-dimensional direct observations of the dynamical and microphysical processes in clouds, which is a barrier to further observational research. However, high-resolution numerical modeling can complement the existing body of research. For example, Zhou and Guo (2009) employed numerical models to suggest that lightning always originated from regions with weak updrafts and low liquid water content. Wang et al. (2015a) used a high-resolution three-dimensional spatiotemporal model to simulate a thunderstorm, and found that charging processes primarily happened within or near updrafts, but net charge layers always tended to form in regions with low vertical velocities. This explains the observed phenomenon that most lightning originates from regions with relatively weak vertical velocities.
To further investigate the dynamical and microphysical conditions at the lightning initiation sites, this paper attempts to analyze the characteristics of vertical air motion and graupel mixing ratio at lightning initiation sites (Wini and qg-ini) based on successful simulation of a thunderstorm by using a three-dimensional charge–discharge numerical model. The results explore the main area of lightning initiation in detail, parameterize the relationship between vertical air motion/cloud microphysics and the lightning initiation, and provide a basis for further improvements to lightning warning techniques.
2 SimulationsThe three-dimensional modeling technique used here is based on Hu and He (1987) and Tan et al. (2017). The dynamic framework adopts the nonhydrostatic balance equation, and the microphysical process simulates five kinds of hydrometeors including cloud droplets, ice crystals, rain droplets, graupel, and hail. The model couples the non-inductive charging mechanism (Gardiner et al., 1985; Pereyra et al., 2000; Tan et al., 2006a), inductive charging mechanism (Ziegler et al., 1991), and ice multiplication charging mechanism (Hallett and Saunders, 1979). Discharge adopts the scheme proposed by Mansell et al. (2002), which is constructed from a bi-directional leader development mechanism (Kasemir, 1960, 1984) and the discharging electric threshold introduced by Marshall et al. (1995). Only the simulated discharge developing more than five steps will be treated as a lightning flash. If the channel of lightning can develop to the ground (< 0.5 km), the lightning is classified as cloud-to-ground (CG) lightning. This model has been used successfully in many previous studies (e.g.,Tan et al., 2006b, 2007, 2014, 2017; Shi et al., 2015, 2016; Wang et al., 2009, 2015a, b).
The sounding data recorded in Beijing on 6 September 2008 are used in the present case study. Comparison of real and simulated data has been carried out by Wang et al. (2015b). The results suggest that: (1) the magnitudes and evolution of real and synthetic lightning frequencies are in agreement; and (2) the height range of the main positive charge layer, as determined by inversion of lightning observation data, is coincident with the height of the simulated main positive charge layer (Wang et al., 2015b). Therefore, the simulation of the thunderstorm is accurate. In the following, the thunderstorm simulation will be used to analyze the distribution of graupel near sites of lightning initiation.
The time step, horizontal resolution, and vertical resolution are set to 1 s, 1 km, and 0.5 km, respectively, which are the same as those mentioned in Wang et al. (2015b). But, for assessing in detail the dynamical and microphysical characteristics at lightning initiation sites, the output time of the simulation is set to be variable: when lightning initiation occurs, the simulation results are output more frequently. The first output time is 956 s and the last is 1891 s. The time interval between adjacent output times changes from 1 to 102 s.
In the simulated thunderstorm cell, the non-inductive charging process between graupel and icy crystals is dominant among the three simulated charging processes (Wang et al., 2015b). The mean charging rate of the non-inductive charging process during the lightning activity is three times of the mean inductive charging rate. Especially for the first stage of the lightning activity, the non-inductive charging rate is one order of magnitude greater than the inductive charging rate. Therefore, in the following analysis, the graupel charging region is illustrated based on the charges obtained by graupel per unit volume of air through the non-inductive charging process.
3 Data analysisThe first lightning flash in the simulated thunderstorm occurs at 956 s after the simulation begins; the lightning frequency peaks at 19 min; and the last lightning flash ends at 1891 s. The range of the lightning initiation heights is 7–11 km. The peak interval is 9–10 km, from which greater than 45% of flashes originate. This is broadly consistent with existing findings about lightning initiation height (zini) (e.g., Proctor, 1991; Lund et al., 2009; Payne et al., 2010; Calhoun et al., 2013; Zheng and MacGorman, 2016). Five CG lightning flashes are simulated from the peak frequency time to 22 min. The zini of these lightning flashes is distributed from 8 to 9.5 km, which is almost the same as the zini of intra-cloud lightning flashes at the same time.
In the following, the characteristics of Wini and qg-ini are analyzed. Then, the region with a high probability to initiate lightning is deduced theoretically and related microphysical characteristics are also analyzed.
3.1 Characteristics of WiniThe maximum updraft of the storm cell (Wcell-max) peaks at about 31 m s–1 at 13 min. Before that, the Wcell-max keeps increasing; and afterwards, the Wcell-max decreases quickly. At 17 min, it drops to 20 m s–1, and after 20 min, the Wcell-max begins to drop below 10 m s–1.
The lightning flashes occur when the updraft center (where Wcell-max is located) is weakening (Fig. 1). In the vertical direction, the lightning flashes initiate slightly higher than the updraft center in the first stage of the lightning activity; then, the vertical distance from the lightning initiation site to the updraft center begins to increase gradually until its peak of 3 km at about 20.5 min; thereafter, the distance continues to decrease, and from about 25.5 min the distance falls fully into negative territory. For the horizontal distance from the lightning initiation site to the updraft center, its evolution looks linear in growth before 25.5 min, but thereafter falls back to about 2.1 km before experiencing growth again. At 25.5 min, the Wcell-max falls to only 1.38 m s–1, and the speed evolves steadily within the range of 1–1.5 m s–1 from that time on. But, the height of the updraft center jumps from 6.5 to 14.5 km, because the obvious updraft has disappeared and the main positive vertical speed only exists at the upper level. Therefore, during most of the time, when the updraft in the cell is still evident, lightning flashes initiate above the updraft center and the distance between them increases roughly according to a quasi-linear correlation.

|
| Figure 1 Evolution of Wcell-max and the vertical and horizontal distances from the lightning initiation site to the updraft center. |
The relationship between Wcell-max and Wini illustrates a good cubic polynomial correlation (Fig. 2). The adjusted R2 of the cubic polynomial fitting, which indicates the percentage of total variance explained by the regression line, is about 0.97. The cubic polynomial regression equation is
| $y \!=\! - 0.00313{x^3} \!+\! {\rm{ }}0.16346{x^2}\!-\!1.39973x \!+\! {\rm{ }}1.7136.$ | (1) |
The evolution of the time series indicates that, before the time when the Wcell-max falls to 10 m s–1, all lightning flashes initiate from the region with positive updraft speed. Thereafter, most lightning initiation sites are located in the regions with negative updraft speed, and the maximum downdraft speed at the lightning initiation sites is near –3 m s–1. However, when the Wcell-max falls to below 5 m s–1, the range of Wini begins to turn back to positive. During the last several minutes of lightning activity, lightning initiation sites mainly assemble within the range of 0–1 m s–1. This result indicates that lightning flashes tend to initiate within the special region where vertical air motion relates well to the Wcell-max.

|
| Figure 2 Relationship between Wcell-max and Wini. |
When the first lightning flash occurs, both the maximum graupel mixing ratio of the storm cell (qg-cell-max) and the total mass of graupel are increasing. The height of the graupel center reaches a peak of about 9.5 km when the first lightning occurs. About 2 min later, the qg-cell-max also reaches its peak value (approximately 9 g kg–1). The change in graupel mixing ratio at the lightning initiation sites (qg-ini) is similar to that at the graupel center; qg-ini of the first lightning flash initiation is about 8.3 g kg–1, and the qg-ini continues to increase to a peak of about 8.7 g kg–1, 43 s after the first lightning flash.
Lightning initiation sites always contain graupel and ice crystals, and at these sites the graupel mixing rate has a mean of 5.5 ± 1.6 g kg –1, while the ice crystal mixing rate has a mean of 0.2 ± 0.1 g kg –1. Graupel always has a lower ratio of standard deviation to mean than ice crystals, which indicates that graupel mixing rates are more stable than ice crystal mixing rates at lightning initiation. In addition, these observations suggest that most lightning flashes originate from regions dominated by larger particles (e.g., Bruning et al., 2007; Lund et al., 2009; Zheng and MacGorman, 2016). Thus, it is appropriate to use graupel to analyze the microphysical characteristics of lightning initiation sites.
All lightning initiation sites have significant graupel mixing ratio. The ratio of the qg-ini to the qg-cell-max lies in the range 0.2–1.0. The mean value of these ratios is about 0.7, while the peak interval is 0.7–0.8. Figure 3 shows the relationship between qg-cell-max and qg-ini. On the whole, they have a good linear correlation with each other. The correlation coefficient reaches 0.86. But, obviously, the widest spectrum is in the first stage of lightning activity; as lightning activity decays, the linear relationship becomes better. Some observations indicate that most lightning flashes initiate from, or near the edge of, areas of high reflectivity (e.g., Proctor, 1991; Makowski et al., 2013). From the relationship given above, it can be found that, for most lightning flashes in the first stage, the qg-ini varies at a wider range than that of the graupel center, although the latter is still larger than the former later. This means that most lightning during the first stage should have been generated near the graupel center, which is consistent with the observations, and is responsible for the wide spectrum around this time. However, when the lightning frequency descends to a lower value, the ratios of qg-ini to qg-cell-max are more centralized to a lower value or to the linear fitting line. Overall, the good correlation can provide a clue towards determining in more detail the region in which most lightning flashes tend to initiate.

|
| Figure 3 Relationship between qg-cell-max and qg-ini. |
Also, the relationship between qg-ini and zini shows a good linear correlation (Fig. 4). The coefficient reaches up to about 0.85. This indicates that qg-ini declines steadily with a reduction in its zini. In view of the relationship mentioned above, the qg-ini decreases with a decline in both zini and qg-cell-max. A question rises as to how the connection between them forms?

|
| Figure 4 Relationship between qg-ini and zini. |
In the vertical direction at lightning initiation sites, most lightning flashes generate from or slightly above the height of the local graupel mixing ratio center (zqg-local-max). The height differences between the lightning initiation sites to zqg-local-max fall in the range from –0.5 to 1 km. More than 87% of lightning flashes initiate from 0–1 km above zqg-local-max, and more than 8% of initiation sites are located within 1–2 km above the zqg-local-max. Less than 5% of lightning flashes are from the region –1 to 0 km lower than the zqg-local-max.
Figure 5 illustrates the vertical profiles of the lightning initiation sites at 956, 1139, 1386, and 1679 s, respectively. These times correspond to the first stage, peak stage, weakening stage, and last stage of lightning activity.
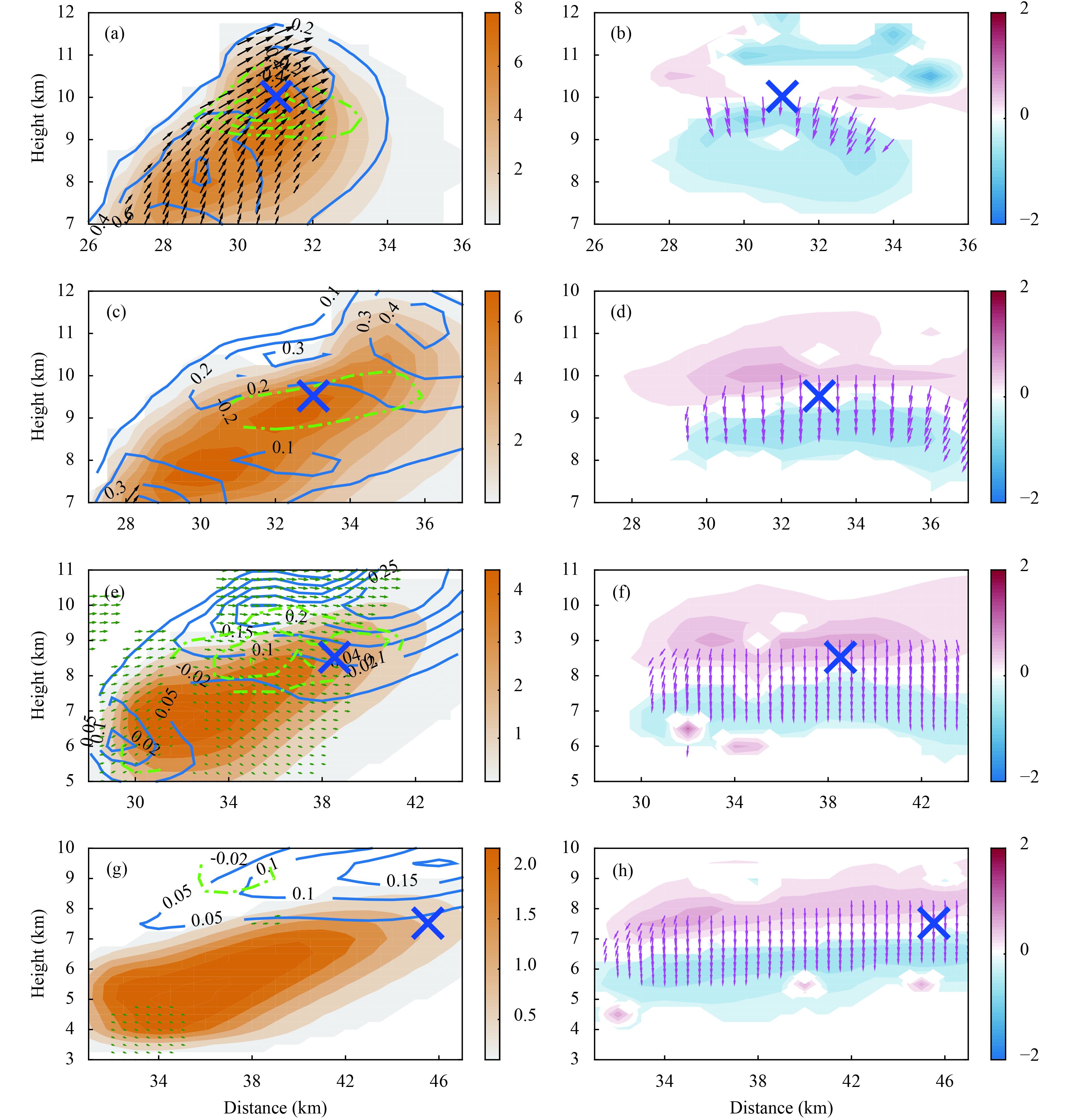
|
| Figure 5 (a, c, e, g) Distributions of qg (color fill) and qice (blue solid contours), the graupel charging region (dot-dashed green contours), and the wind field (black arrows: |vertical speed| ≥ 10 m s–1; green arrows: |vertical speed| > 1 m s –1). (b, d, f, h) Distributions of net charge density (color fill) and electric field intensity (pink arrows: |electric field intensity| > 30 kV m –1). (a, b) 956, (c, d) 1139, (e, f) 1386, and (g, h) 1679 s, respectively. The blue cross marks the lightning initiation site. |
In the first stage (Figs. 5a, b), the graupel distribution region mostly overlaps with the ice crystal distribution region while the updraft is strong, and these distribution regions are all located within or near the updraft area. Also, graupel and ice crystals are charged strongly in the upper part of this region. Almost in the same region, some graupel areas, mainly including the graupel center (which is slightly higher than the charging center), separate from the ice crystal center, but the ice crystal center is still mainly mixed with graupel in the upper part of the graupel areas (Fig. 5a). This situation causes a relatively strong and large ranging negative charge layer near the graupel center and the fragmentation of the positive charge layer around the upper part of the graupel distribution region (Fig. 5b). The electric field intensity reaches a maximum at the upper edge of the negative charge layer, which is close to the graupel center, and initiates a lightning flash. Because almost all the graupel region is being lifted by the updraft, it is inevitable that the Wini is positive and reaches more than 18 m s–1.
In the peak stage (Figs. 5c, d), an evidently strong updraft has disappeared and the separation between graupel and ice crystals is more obvious. The ice crystal center has been lifted from about 9.7–11.3 km in the first stage to about 11.6–1.7 km, which is at the edge of the graupel region. The main charging on graupel occurs near the graupel center in the middle part of the graupel distribution region, and the charging intensity is evidently weakening but keeps relatively strong (Fig. 5c). The more obvious separation between graupel and ice crystals produces a wide range of negative and positive charge layers (Fig. 5d). The lightning flash initiates from the region between the main positive charge layer and the main negative charge layer, the location of which is slightly higher than the graupel center. Although the updraft declines significantly both in its maximum updraft speed and height of the updraft center, most of the graupel region is still in an upward movement with relatively weak positive vertical speed. The Wini marked in Figs. 5c, d is still about 3 m s–1.
In the weakening stage (Figs. 5e, f), the strong updraft (> 10 m s–1) has disappeared; only a very low updraft remains on the left-hand side of the graupel distribution region, and a weak downdraft is in the domain of the main mixing area of graupel and ice crystals (Fig. 5e). The Wini at this time turns to a negative value of about –0.1 m s–1. The ice crystal distribution region is separated significantly from the graupel distribution region. The charging intensity on graupel continues to fall. Lightning flashes initiate near the boundary between the positive charge layer and the negative charge layer (Fig. 5f). The zini is also descending. However, because the graupel center has a more evident decline, the height difference from the lightning initiation site to the graupel center increases. Simultaneously, the qg-ini reduces markedly, mainly due to the sinking movement of the graupel region, which leads to the boundary of positive and negative charge layers rising closer to the upper edge of the graupel region.
In the last stage (Figs. 5g, h), the evident updraft disappears and the graupel region and the ice crystal region are almost totally separated. The charging region is small and the charging intensity is also very weak (Fig. 5g). The boundary between positive and negative charge layers spreads along the upper boundary of the graupel distribution region (Fig. 5h). It makes lightning initiate near the upper boundary of the graupel region, which has a low graupel mixing ratio, while qg-cell-max also falls greatly. The Wini remains stable in a narrow range of very low values. The Wini in Figs. 5g, h is still about –0.1 m s–1.
The above analysis indicates that the location of the boundary of opposite-polarity charge layers and its evolution impacts directly on the lightning initiation site. This boundary normally starts near the graupel center, and is then lifted to the upper boundary of the graupel region with the sinking of this region. During this process, the graupel center is also weakening and descending. Therefore, qg-ini is weakening due to its location becoming increasingly closer to the upper boundary of the graupel region. In addition, zini keeps descending, but qg-ini maintains a certain proportional relation to qg-cell-max.
3.3 Characteristics of the zero-charge zoneAccording to Bruning et al. (2007) and Lund et al. (2009), lightning discharge typically initiates near the boundary between graupel and ice crystals, often within or near the graupel region. The above analysis in this paper also found that all lightning flashes initiate within the graupel region, and most of them generate within the upper part of the graupel region above the graupel center. Only a few lighting flashes in the first stage of lightning activity initiated near the graupel center. Our simulation has good consistency with the observations, but what causes this phenomenon?
According to Gauss’ Law, the relationship between electric field intensity and net charge density is
| $\nabla \cdot {E} = \frac{\rho }{\varepsilon },$ | (2) |
where E is the electric field intensity, ρ is the net charge density, and ε is the air dielectric constant. If the calculation is carried out in a special coordinate system, in which one of the coordinate directions is parallel to the electric field direction and the other two directions are perpendicular to the electric field direction, the formula can be changed to
| $\frac{{\partial {E_a}}}{{\partial l}} = \frac{\rho }{\varepsilon },$ | (3) |
where a indicates the direction of the electric field and Ea is the amplitude of E, l represents the vector of the electric force line. Then, if Δl is short enough, the directions of electric field intensity at the beginning (l0) and the end (l1) of l can be regarded as parallel. Based on the derived integral formula,
| ${E_{{l_1}}} - {E_{{l_0}}} = \int_{{l_0}}^{{l_1}} {\frac{\rho }{\varepsilon }} {\rm{d}}l,$ | (4) |
and in Eq. (3), the amplitude of the electric field intensity will be enhanced along the direction of electric force with the integration of net charge density. From the center of the positive net charge layer to the center of the negative net charge layer, the electric field intensity will keep increasing until it meets the boundary between the positive charge layer and negative charge layer. Then, when it invades the negative charge layer, the electric field intensity will decrease gradually. In theory, the electric field intensity will reach its maximum at the boundary between positive and negative charge layers, and lightning flashes also have the largest probability to initiate at the boundary. Therefore, the area with a net charge density of nearly zero between positive and negative charge layers should be a very important zone for lightning initiation. In the following analysis, this area is referred to as the “zero-charge zone.”
Our simulation also confirms this derived result. All lightning initiation sites are almost located within the zero-charge zone (e.g., Figs. 5b, d, f, h). Obviously, the zero-charge zone is primarily distributed in the upper part of the graupel region, above the graupel center, because graupel is always heavier than ice crystals and normally charged with charges of opposite polarity. The zero-charge zone is slightly above the graupel center when the first lightning flash initiates (Fig. 5b). Then, the zero-charge zone moves from the graupel center to the upper boundary of the graupel region due to the falling of graupel (e.g., Figs. 5d, f, h).
All the grids within the zero-charge zone and with |E| > 50 kV m –1 are selected. The ratios of ice crystal mixing ratio (qice) to graupel mixing ratio (qg) (RIGs) at these grids are calculated. The RIGs illustrate an exponential relationship with the qg, except for some flying-points (Fig. 6). These flying points all appear when the grid has a relatively large qg. The qg at most of the grids is less than 2.5 g kg–1. For these grids with relatively low qg, the exponential relationship between the RIG and qg is better. This indicates that most of these grids appear when the separation between graupel and ice crystals has been more evident, which makes these grids have low qg and strong electric field intensity.

|
| Figure 6 Relationship between the RIG and the qg at the grids within the zero-charge zone with |E| > 50 kV m –1. |
Simultaneously, the evolution of the zero-charge zone can also explain the characteristics of Wini shown in Section 3.1. When the updraft is strong enough, primary graupel is distributed within the updraft. This leads to the zero-charge zone, which is in the upper part of the graupel region, mainly in the region with positive vertical speed, and all lightning flashes also inevitably initiate in the positive vertical speed region. With the updraft weakening, the updraft can no longer lift graupel, thus the main graupel region begins to fall, making the vertical speed of the zero-charge zone turn to negative. That causes the vertical speed direction of lightning initiation sites to be flipped. In the last stage, the main body of the graupel region has dropped to a lower level; only near the upper edge of the graupel region can weak positive vertical speed maintain the mixture of spare graupel and ice crystals, which causes few lightning flashes in this stage to primarily initiate in the region with weak positive vertical speed.
4 DiscussionFrom the negative charge center (or positive charge center), along the largest charge density gradient, E will increase most sharply until it reaches a peak in the zero-charge zone. Therefore, the intersection point between this pathway and the zero-charge zone should have the highest chance to initiate lightning if the net charge density is strong enough. If the net charge density is too weak to initiate lightning from this point, E must travel a longer way, meaning that it needs to pass more single-polarity net charge areas and be cumulatively pushed up to the breakdown threshold when it touches the zero-charge zone at a new intersection point. Obviously, this new intersection point will move away from the original intersection point, with the descent of the net charge density. On the whole, the area around the original intersection point on the zero-charge zone should be the area of focus for lightning initiation sites.
Based on the above analysis, when the graupel region and the ice crystal region are sufficiently separated, the zero-charge zone should spread near the upper edge of the graupel region and within the region with low vertical speed. Lightning initiation sites mostly located within this zone will also have the same environmental situation. Simultaneously, the sufficient separation of graupel and ice crystals will produce large areas of net positive and negative charge layers, which provides a larger space for positive and negative leaders to propagate. This means that lightning is more likely to develop to a larger scale. Therefore, the qg-ini is speculated to have a close relationship with the scale of lightning. Figure 7 illustrates the relationships between the qg-ini and the steps of lightning, positive leaders, and negative leaders. Although the steps of lightning or leaders cannot reflect the scale of lightning very accurately, they should correlate positively. The results of linear fitting show that the qg-ini does have a negative correlation with the steps of lightning, positive leaders, and negative leaders, with linear coefficients of about –0.66, –0.56, and –0.64, respectively. This proves our speculation that lightning of large scale tends to occur in the region with relatively low graupel concentration. However, at this time, the lightning initiation frequency should be low because of the lack of charging processes within or near the strong updraft. Some lightning initiated near the graupel center and propagating along the net charge layer with a wide area may contaminate the correlation.

|
| Figure 7 Relationship between qg-ini and the steps of lightning, positive leaders, and negative leaders. |
In fact, the dynamical and microphysical conditions in the declining stage of lightning activity mentioned above should be similar to the conditions far away from the convective core, such as the stratiform region in a thunderstorm. Some observations have found that lightning of larger scale and lower frequency is more readily observed farther from the updraft core (Bruning and MacGorman, 2013; Calhoun et al., 2013; Mecikalski et al., 2015). This is consistent with the results mentioned above that the lightning initiated from the lower graupel concentration region may be larger in scale. Nevertheless, it cannot be totally excluded that some lightning initiated close to the convective core, with high graupel concentration at its initiation site, could propagate into the stratiform region and also be large in scale. But overall, lightning initiated from the stratiform region, where the graupel concentration at the initiation site is relatively lower, should be more likely to grow to a larger size.
5 ConclusionsTo better understand the dynamical and microphysical characteristics of the initiation sites of lightning flashes, a three-dimensional charge–discharge numerical model is used to analyze the characteristics of Wini and qg-ini. The results show that:
(1) The Wini correlates well with the Wcell-max. The adjusted R2 of the cubic polynomial fitting between them is about 0.97. After the Wcell-max falls to about 10 m s–1, most lightning initiation sites begin to appear in positions with negative weak vertical speed, the maximum of which never exceeds –3 m s–1. When the Wcell-max is less than 5 m s–1, the Wini begins to rise towards zero. Only during the last few minutes of the lightning activity is Wini primarily located within the positive range of 0–1 m s–1.
(2) Most lightning flashes initiate from the upper part of the graupel distribution region, which is consistent with observations (Bruning et al., 2007; Lund et al., 2009). Further analysis indicates that qg-ini has a good linear correlation with qg-cell-max and zini. The coefficients reach 0.86 and 0.85, respectively. This linear correlation is especially strong during the middle and later stage of lightning activity.
(3) The zero-charge zone between positive and negative charge layers is an important area for lightning initiation. It normally lies between the area above the graupel center and the upper edge of the graupel distribution region. Within the zero-charge zone, the RIG has an exponential relationship with the qg at most grids with large electric field intensity. This provides clues for identifying regions with large electric field intensity in the zero-charge zone.
These results reveal the dynamical and microphysical characteristics at lightning initiation sites and provide some quantitative relationships regarding the Wini and qg-ini with the Wcell-max and qg-cell-max. The findings are beneficial towards further our understanding of the environmental conditions of lightning initiation. Also, these relationships can be used in numerical models without charging and discharging schemes to effectively estimate the high-risk area of lightning initiation.
| Baker, M. B., A. M. Blyth, H. J. Christian, et al., 1999: Relationships between lightning activity and various thundercloud parameters: Satellite and modelling studies. Atmos. Res., 51, 221–236. DOI:10.1016/S0169-8095(99)00009-5 |
| Barthe, C., and M. C. Barth, 2008: Evaluation of a new lightning-produced NOx parameterization for cloud resolving models and its associated uncertainties . Atmos. Chem. Phys., 8, 4691–4710. DOI:10.5194/acp-8-4691-2008 |
| Barthe, C., W. Deierling, and M. C. Barth, 2010: Estimation of total lightning from various storm parameters: A cloud-resolving model study. J. Geophys. Res., 115, D24202. DOI:10.1029/2010JD014405 |
| Black, R. A., and J. Hallett, 1999: Electrification of the hurricane. J. Atmos. Sci., 56, 2004–2028. DOI:10.1175/1520-0469(1999)056<2004:EOTH>2.0.CO;2 |
| Bruning, E. C., and D. R. MacGorman, 2013: Theory and observations of controls on lightning flash size spectra. J. Atmos. Sci., 70, 4012–4029. DOI:10.1175/JAS-D-12-0289.1 |
| Bruning, E. C., W. D. Rust, T. J. Schuur, et al., 2007: Electrical and polarimetric radar observations of a multicell storm in TELEX. Mon. Wea. Rev., 135, 2525–2544. DOI:10.1175/MWR3421.1 |
| Calhoun, K. M., D. R. MacGorman, C. L. Ziegler, et al., 2013: Evolution of lightning activity and storm charge relative to dual-Doppler analysis of a high-precipitation supercell storm. Mon. Wea. Rev., 141, 2199–2223. DOI:10.1175/MWR-D-12-00258.1 |
| Carey, L. D., and S. A. Rutledge, 1996: A multiparameter radar case study of the microphysical and kinematic evolution of a lightning producing storm. Meteor. Atmos. Phys., 59, 33–64. DOI:10.1007/BF01032000 |
| Carey, L. D., A. L. Bain, and R. Matthee, 2014: Kinematic and microphysical control of lightning in multicell convection over Alabama during DC3. 5th International Lightning Meteorology Conference, 20–21 March, Tucson, Arizona, USA. |
| Deierling, W., and W. A. Petersen, 2008: Total lightning activity as an indicator of updraft characteristics. J. Geophys. Res., 113, D16210. DOI:10.1029/2007JD009598 |
| Dye, J. E., J. J. Jones, A. J. Weinheimer, et al., 1988: Observations within two regions of charge during initial thunderstorm electrification. Quart. J. Roy. Meteor. Soc., 114, 1271–1290. DOI:10.1002/(ISSN)1477-870X |
| Gardiner, B., D. Lamb, R. L. Pitter, et al., 1985: Measurements of initial potential gradient and particle charges in a Montana summer thunderstorm. J. Geophys. Res., 90(D4), 6079–6086. DOI:10.1029/JD090iD04p06079 |
| Gremillion, M. S., and R. E. Orville, 1999: Thunderstorm characteristics of cloud-to-ground lightning at the Kennedy Space Center, Florida: A study of lightning initiation signatures as indicated by the WSR-88D. Wea. Forecasting, 14, 640–649. DOI:10.1175/1520-0434(1999)014<0640:TCOCTG>2.0.CO;2 |
| Hallett, J., and C. P. R. Saunders, 1979: Charge separation associated with secondary ice crystal production. J. Atmos. Sci., 36, 2230–2235. DOI:10.1175/1520-0469(1979)036<2230:CSAWSI>2.0.CO;2 |
| Hondle, K. D., and M. D. Eilts, 1994: Doppler radar signatures of developing thunderstorms and their potential to indicate the onset of cloud-to-ground lightning. Mon. Wea. Rev., 122, 1818–1836. DOI:10.1175/1520-0493(1994)122<1818:DRSODT>2.0.CO;2 |
| Hu, Z. J., and G. F. He, 1987: Numerical simulation of microprocesses in cumulonimbus clouds. I: Microphysical model. Acta Meteor. Sinica, 45, 467–484. |
| Jacobson, E. A., and E. P. Krider, 1976: Electrostatic field changes produced by Florida lightning. J. Atmos. Sci., 33, 103–117. DOI:10.1175/1520-0469(1976)033<0103:EFCPBF>2.0.CO;2 |
| Kasemir, H. W., 1960: A contribution to the electrostatic theory of a lightning discharge. J. Geophys. Res., 65, 1873–1878. DOI:10.1029/JZ065i007p01873 |
| Kasemir, H. W., 1984: Theoretical and experimental determination of field, charge and current on an aircraft hit by natural and triggered lightning. International Aerospace and Ground Conference on Lightning and Static Electricity, Orlando, National Interafency Coordinating Group. |
| Lund, N. R., D. R. MacGorman, T. J. Schuur, et al., 2009: Relationships between lightning location and polarimetric radar signatures in a small mesoscale convective system. Mon. Wea. Rev., 137, 4151–4170. DOI:10.1175/2009MWR2860.1 |
| Makowski, J. A., D. R. MacGorman, M. I. Biggerstaff, et al., 2013: Total lightning characteristics relative to radar and satellite observations of Oklahoma mesoscale convective systems. Mon. Wea. Rev., 141, 1593–1611. DOI:10.1175/MWR-D-11-00268.1 |
| Mansell, E. R., D. R. MacGorman, C. L. Ziegler, et al., 2002: Simulated three-dimensional branched lightning in a numerical thunderstorm model. J. Geophy. Res., 107(D9), ACL 2-1–ACL 2-12. DOI:10.1029/2000JD000244 |
| Marshall, T. C., M. P. McCarthy, and W. D. Rust, 1995: Electric field magnitudes and lightning initiation in thunderstorms. J. Geophys. Res., 100(D4), 7097–7103. DOI:10.1029/95JD00020 |
| Martinez, M., 2002: The relationship between radar reflectivity and lightning activity at initial stages of convective storms. 82nd Annual Meeting, First Annual Student Conference, Orlando, Florida, 14 January, American Meteorological Society. |
| Mecikalski, R. M., A. L. Bain, and L. D. Carey, 2015: Radar and lightning observations of deep moist convection across Northern Alabama during DC3: 21 May 2012. Mon. Wea. Rev., 143, 2774–2794. DOI:10.1175/MWR-D-14-00250.1 |
| Payne, C. D., T. J. Schuur, D. R. MacGorman, et al., 2010: Polarimetric and electrical characteristics of a lightning ring in a supercell storm. Mon. Wea. Rev., 138, 2405–2425. DOI:10.1175/2009MWR3210.1 |
| Pereyra, R. G., E. E. Avila, N. E. Castellano, et al., 2000: A laboratory study of graupel charging. J. Geophys. Res., 105(D16), 20803–20812. DOI:10.1029/2000JD900244 |
| Petersen, W. A., S. A. Rutledge, and R. E. Orville, 1996: Cloud-to-ground lightning observations from TOGA COARE: Selected results and lightning location algorithms. Mon. Wea. Rev., 124, 602–620. DOI:10.1175/1520-0493(1996)124<0602:CTGLOF>2.0.CO;2 |
| Petersen, W. A., S. A. Rutledge, R. C. Cifelli, et al., 1999: Shipborne Dual-Doppler operations during TOGA COARE: Integrated observations of storm kinematics and electrification. Bull. Amer. Meteor. Soc., 80, 81–97. DOI:10.1175/1520-0477(1999)080<0081:SDDODT>2.0.CO;2 |
| Pickering, K. E., Y. S. Wang, W. K. Tao, et al., 1998: Vertical distributions of lightning NOx for use in regional and global chemical transport models . J. Geophys. Res., 103(D23), 31203–31216. DOI:10.1029/98JD02651 |
| Preston, A. D., and H. E. Fuelberg, 2015: Improving lightning cessation guidance using polarimetric radar data. Wea. Forecasting, 30, 308–328. DOI:10.1175/WAF-D-14-00031.1 |
| Price, C., and D. Rind, 1992: A simple lightning parameterization for calculating global lightning distributions. J. Geophys. Res., 97, 9919–9933. DOI:10.1029/92JD00719 |
| Proctor, D. E., 1991: Regions where lightning flashes began. J. Geophys. Res., 96(D3), 5099–5112. DOI:10.1029/90JD02120 |
| Rutledge, S. A., E. R. Williams, and T. D. Keenan, 1992: The down upper Doppler and electricity experiment (DUNDEE): Overview and preliminary results. Bull. Amer. Meteor. Soc., 73, 3–16. DOI:10.1175/1520-0477(1992)073<0003:TDUDAE>2.0.CO;2 |
| Shackford, C. R., 1960: Radar indications of a precipitation-lightning relationship in New England thunderstorms. J. Meteor., 17, 15–19. DOI:10.1175/1520-0469(1960)017<0015:RIOAPL>2.0.CO;2 |
| Shi, Z., Y. B. Tan, H. Q. Tang, et al., 2015: Aerosol effect on the land–ocean contrast in thunderstorm electrification and lightning frequency. Atmos. Res., 164-165, 131–141. DOI:10.1016/j.atmosres.2015.05.006 |
| Shi, Z., H. Q. Tang, and Y. B. Tan, 2016: Effects of the inductive charging on the electrification and lightning discharges in thunderstorms. Terr. Atmos. Ocean. Sci., 27, 241–251. DOI:10.3319/TAO.2015.12.10.01(A) |
| Takahashi, T., 1978: Riming electrification as a charge generation mechanism in thunderstorms. J. Atmos. Sci., 35, 1536–1548. DOI:10.1175/1520-0469(1978)035<1536:REAACG>2.0.CO;2 |
| Tan, Y. B., S. C. Tao, and B. Y. Zhu, 2006a: Fine-resolution simulation of the channel structures and propagation features of intracloud lightning. Geophys. Res. Lett., 33, L09809. DOI:10.1029/2005GL025523 |
| Tan, Y. B., S. C. Tao, B. Y. Zhu, et al., 2006b: Numerical simulations of the bi-level and branched structure of intracloud lightning flashes. Sci. China Ser. D, 49, 661–672. DOI:10.1007/s11430-006-0661-5 |
| Tan, Y. B., S. C. Tao, B. Y. Zhu, et al., 2007: A simulation of the effects of intra-cloud lightning discharges on the charges and electrostatic potential distributions in a thundercloud. Chinese J. Geophys., 50, 1053–5065. |
| Tan, Y. B., S. C. Tao, Z. W. Liang, et al., 2014: Numerical study on relationship between lightning types and distribution of space charge and electric potential. J. Geophys. Res., 119, 1003–1014. DOI:10.1002/2013JD019983 |
| Tan, Y. B., Z. Shi, Z. L. Chen, et al., 2017: A numerical study of aerosol effects on electrification of thunderstorms. J. Atmos. Solar–Terr. Phys., 154, 236–247. DOI:10.1016/j.jastp.2015.11.006 |
| Tessendorf, S. A., L. J. Miller, K. C. Wiens, et al., 2005: The 29 June 2000 supercell observed during STEPS. Part I: Kinematics and microphysics. J. Atmos. Sci., 62, 4127–4150. DOI:10.1175/JAS3585.1 |
| Vincent, B. R., L. D. Carey, D. Schneider, et al., 2003: Using WSR-88D reflectivity for the prediction of cloud-to-ground lightning: A central North Carolina study. NOAA/National Weather Service Forecast Office, Newport/Morehead City, NC, 35–44. |
| Wang, C. X., 2014: The relationship between vertical airflow characteristics and lightning activity of thunderstorm. Master dissertation, Chinese Academy of Meteorological Sciences, Beijing, China, 66 pp. (in Chinese) |
| Wang, F., Y. J. Zhang, J. Z. Zhao, et al., 2008: The preliminary application of radar data to the lightning warning of isolated storm cells. J. Appl. Meteor. Sci., 19, 153–160. |
| Wang, F., W. S. Dong, Y. J. Zhang, et al., 2009: Case study of big particles effect on lightning initiation in clouds using model. J. Appl. Meteor. Sci., 20, 564–570. |
| Wang, F., Y. J. Zhang, D. Zheng, et al., 2015a: Impact of the vertical velocity field on charging processes and charge separation in a simulated thunderstorm. J. Meteor. Res., 29, 328–343. DOI:10.1007/s13351-015-4023-0 |
| Wang, F., Y. J. Zhang, and D. Zheng, 2015b: Impact of updraft on neutralized charge rate by lightning in thunderstorms: A simulation case study. J. Meteor. Res., 29, 997–1010. DOI:10.1007/s13351-015-5023-9 |
| Wang, J., S. D. Zhou, B. Yang, et al., 2016: Nowcasting cloud-to-ground lightning over Nanjing area using S-band dual-polarization Doppler radar. Atmos. Res., 178-179, 55–64. DOI:10.1016/j.atmosres.2016.03.007 |
| Wiens, K. C., S. A. Rutledge, and S. A. Tessendorf, 2005: The 29 June 2000 supercell observed during STEPS. Part II: Lightning and charge structure. J. Atmos. Sci., 62, 4151–4177. DOI:10.1175/JAS3615.1 |
| Williams, E. R., 1985: Large-scale charge separation in thunderclouds. J. Geophys. Res., 90(D4), 6013–6025. DOI:10.1029/JD090iD04p06013 |
| Williams, E. R., and R. M. Lhermitte, 1983: Radar tests of the precipitation hypothesis for thunderstorm electrification. J. Geophys. Res., 88(C15), 10984–10992. DOI:10.1029/JC088iC15p10984 |
| Workman, E. J., and S. E. Reynolds, 1949: Electrical activity as related to thunderstorm cell growth. Bull. Amer. Meteor. Soc., 30, 142–144. |
| Zheng, D., and D. R. MacGorman, 2016: Characteristics of flash initiations in a supercell cluster with tornadoes. Atmos. Res., 167, 249–264. DOI:10.1016/j.atmosres.2015.08.015 |
| Zhou, Z. M., and X. L. Guo, 2009: 3D modeling on relationships among intracloud lightning, updraft and liquid water content in a severe thunderstorm case. Climatic Environ. Res., 14, 31–44. |
| Ziegler, C. L., D. R. MacGorman, J. E. Dye, et al., 1991: A model evaluation of noninductive graupel–ice charging in the early electrification of a mountain thunderstorm. J. Geophys. Res., 96(D7), 12833–12855. DOI:10.1029/91JD01246 |
 2017, Vol. 31
2017, Vol. 31


